Effect of Incident Rainfall Redistribution by Maize Canopy on Soil Moisture at the Crop Row Scale
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of Experimental Site and Agronomic Management
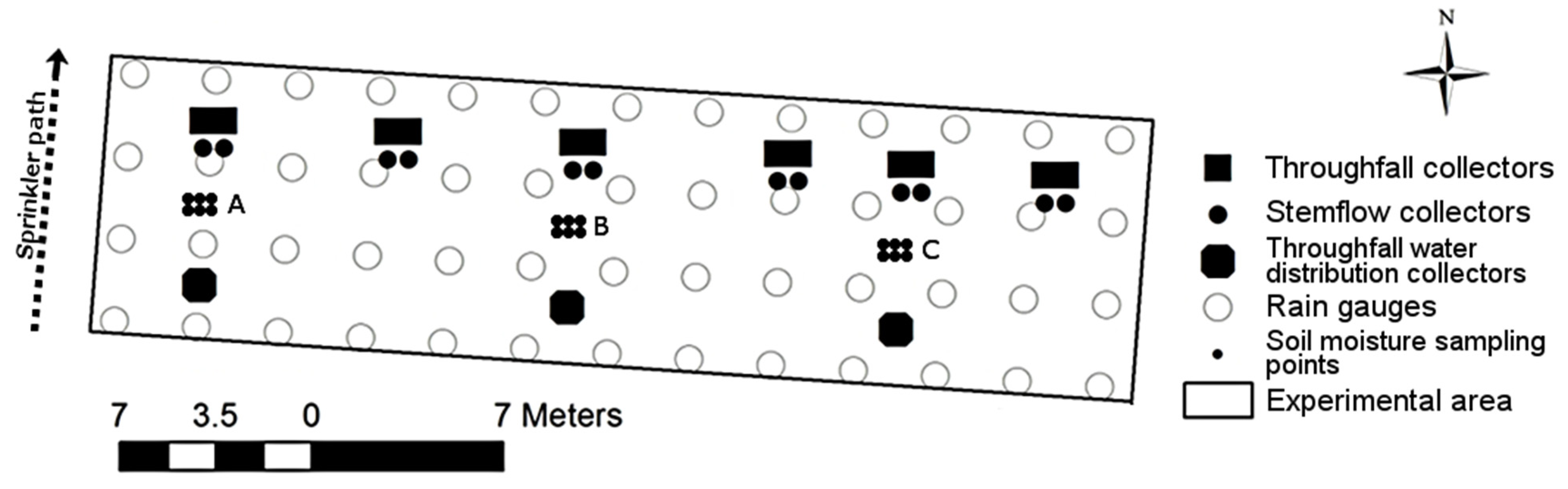
2.2. Stemflow and Throughfall Water Collection

2.3. Soil Moisture Monitoring
2.4. Modelling Canopy Interception Effects with HYDRUS 2D/3D Model
2.4.1. Calibration/Validation of HYDRUS 2D/3D
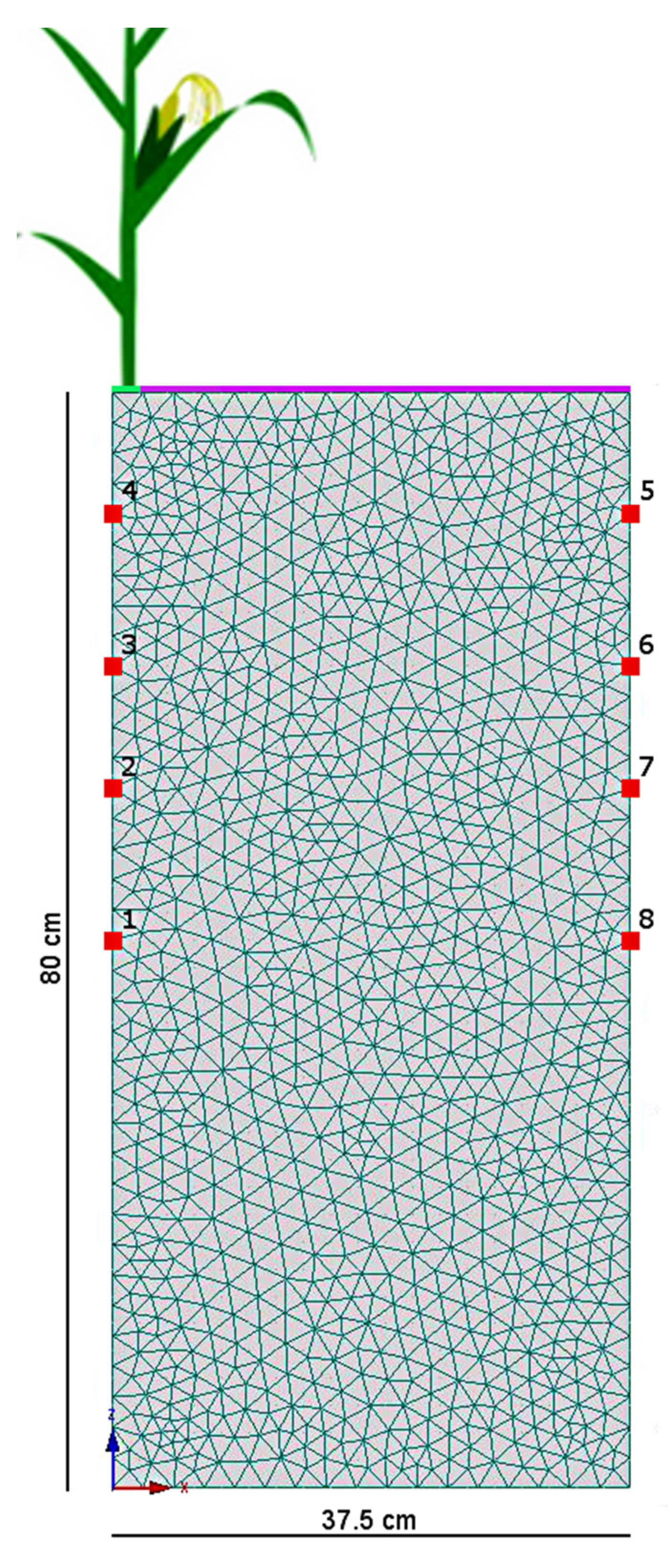
2.4.2. Numerical Simulation of Irrigation Systems with HYDRUS 2D/3D
3. Results
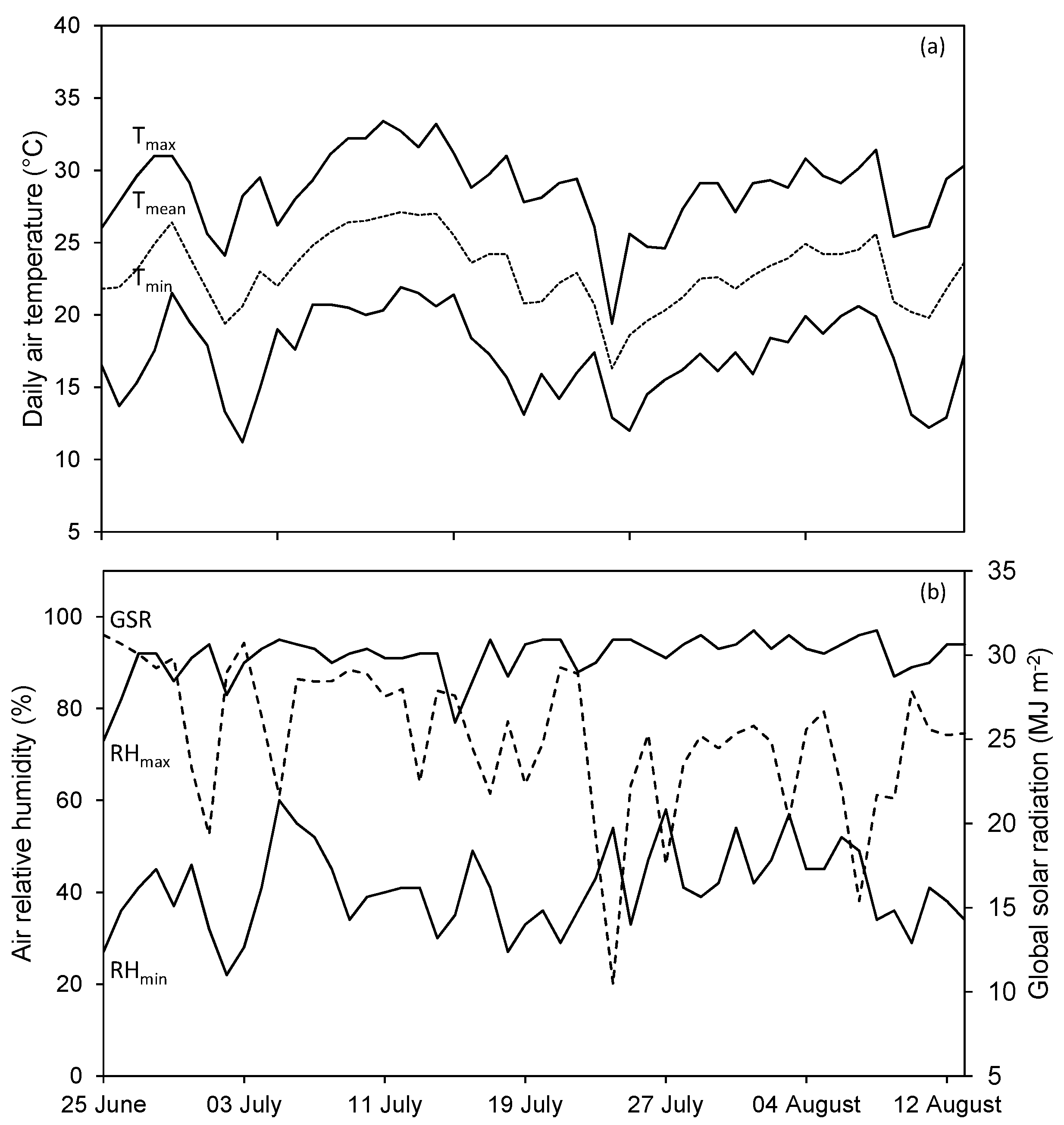
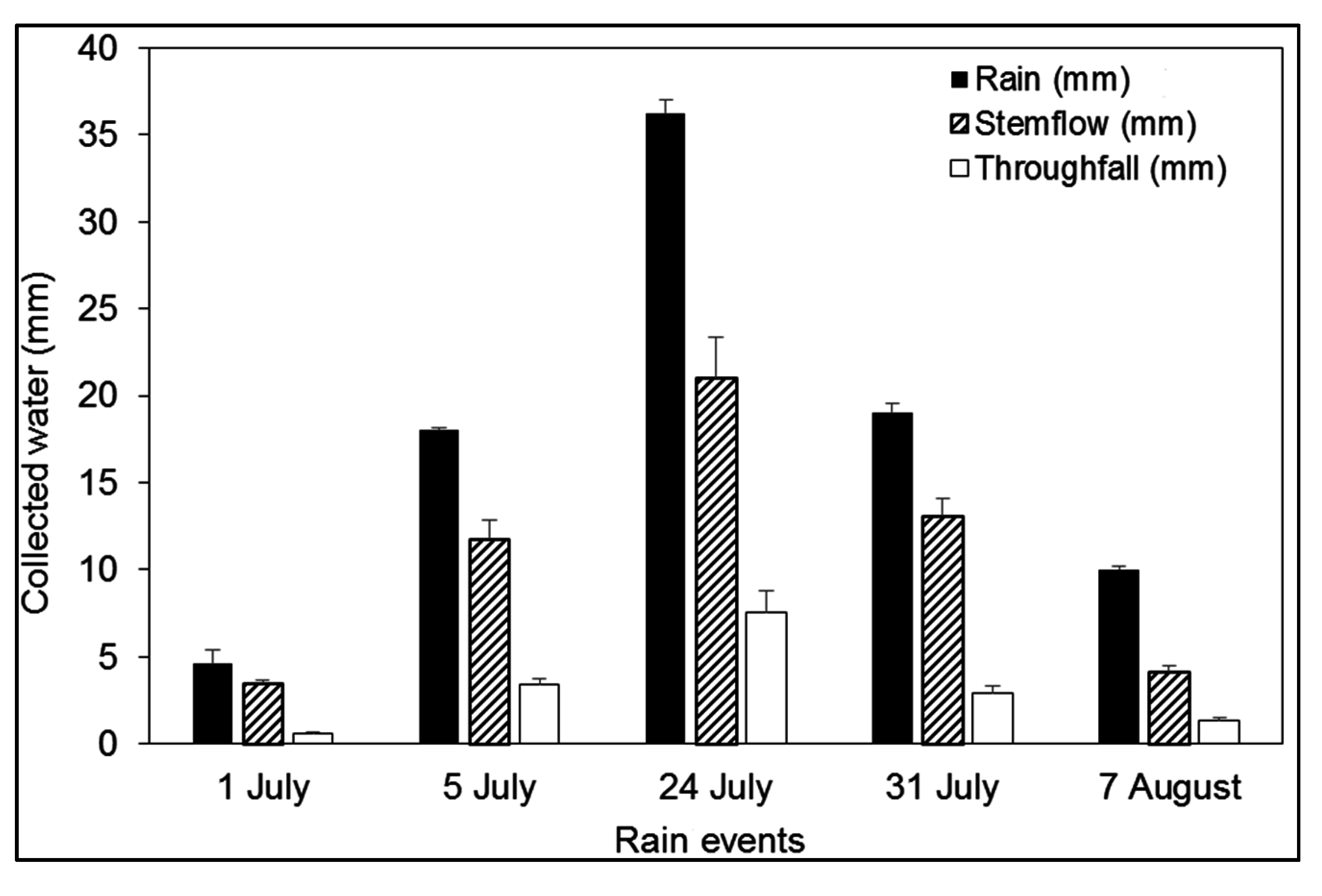
3.1. Rainfall Redistribution by Canopy Interception and Soil Water Dynamics
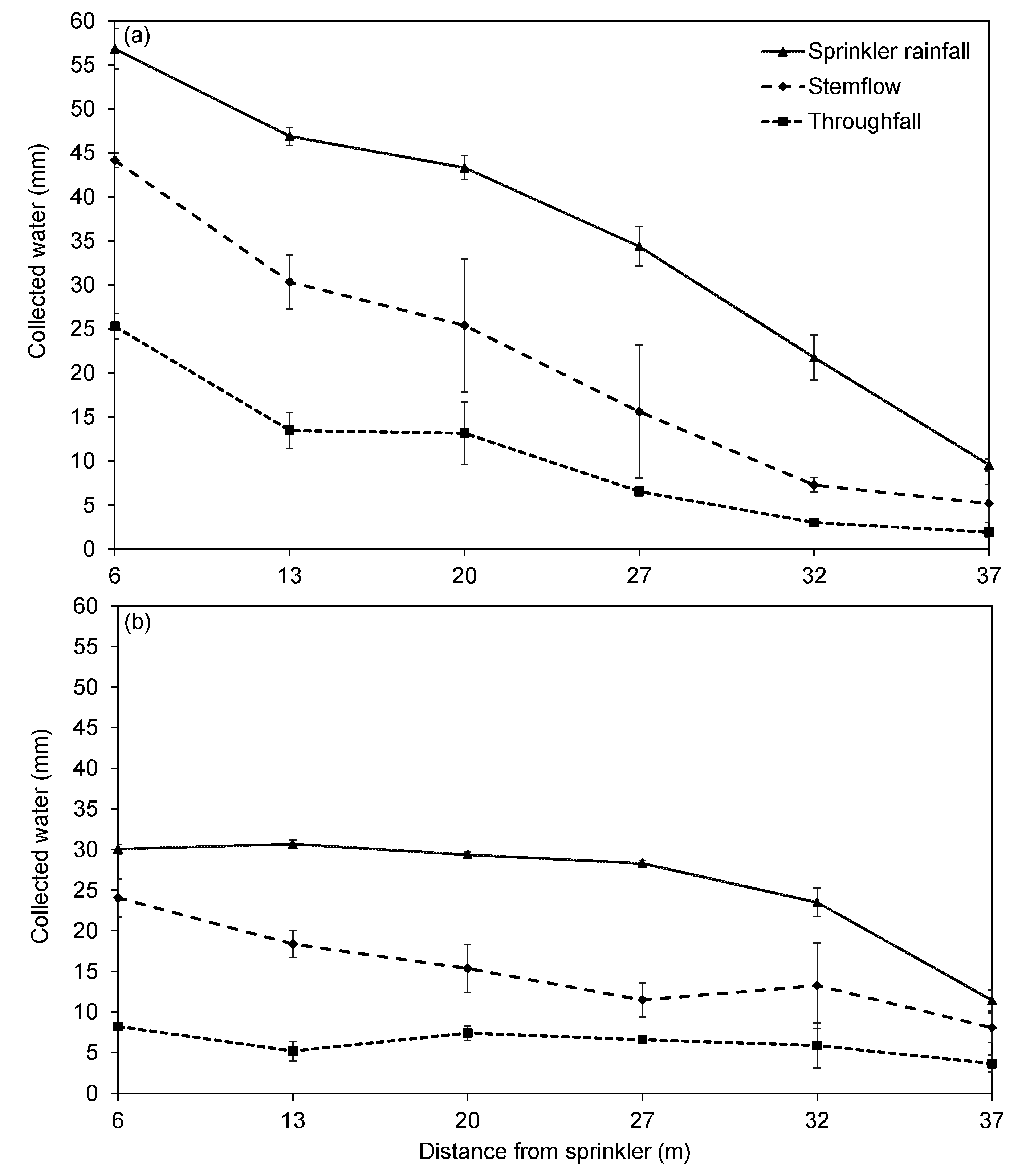
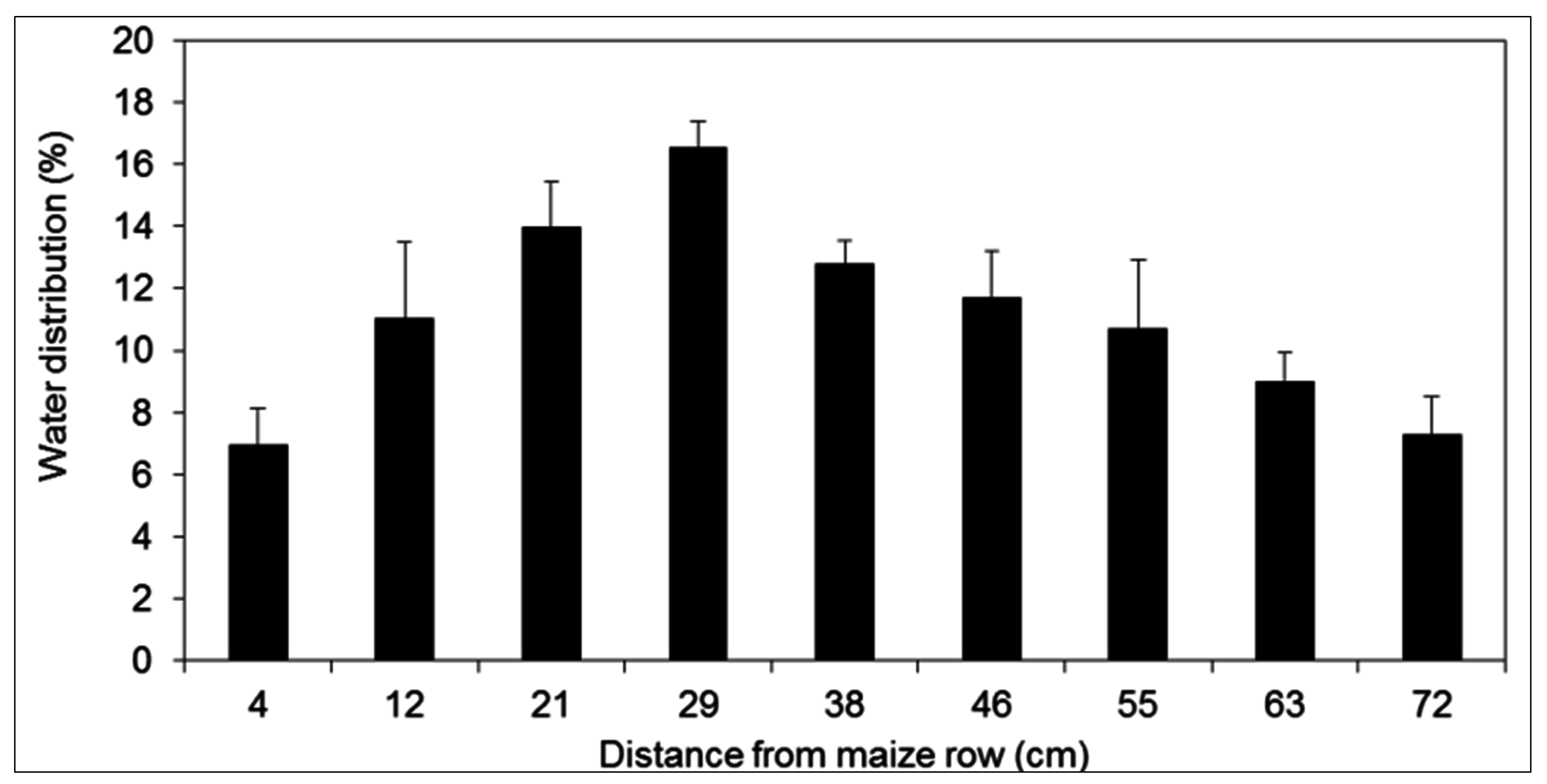
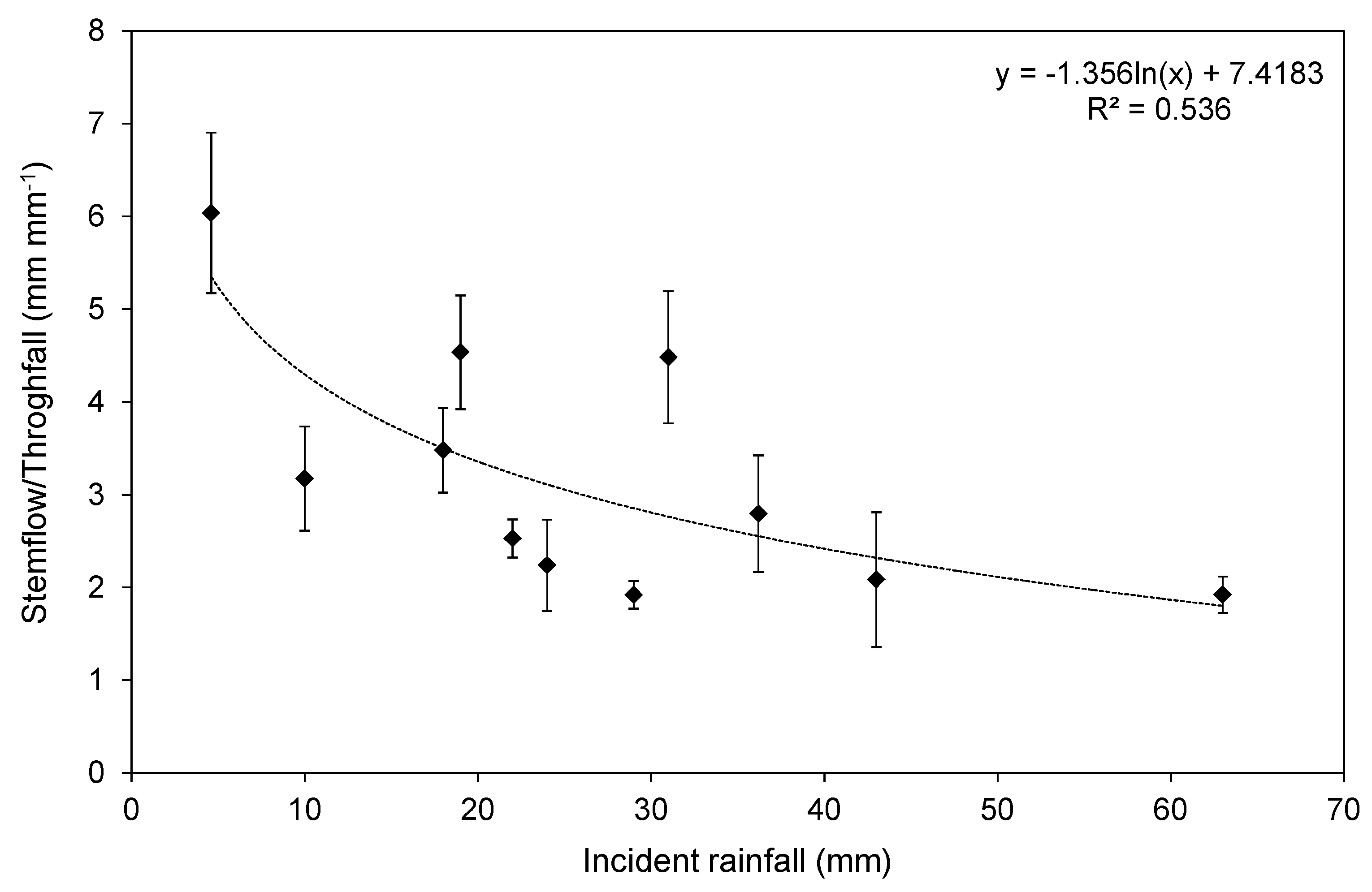
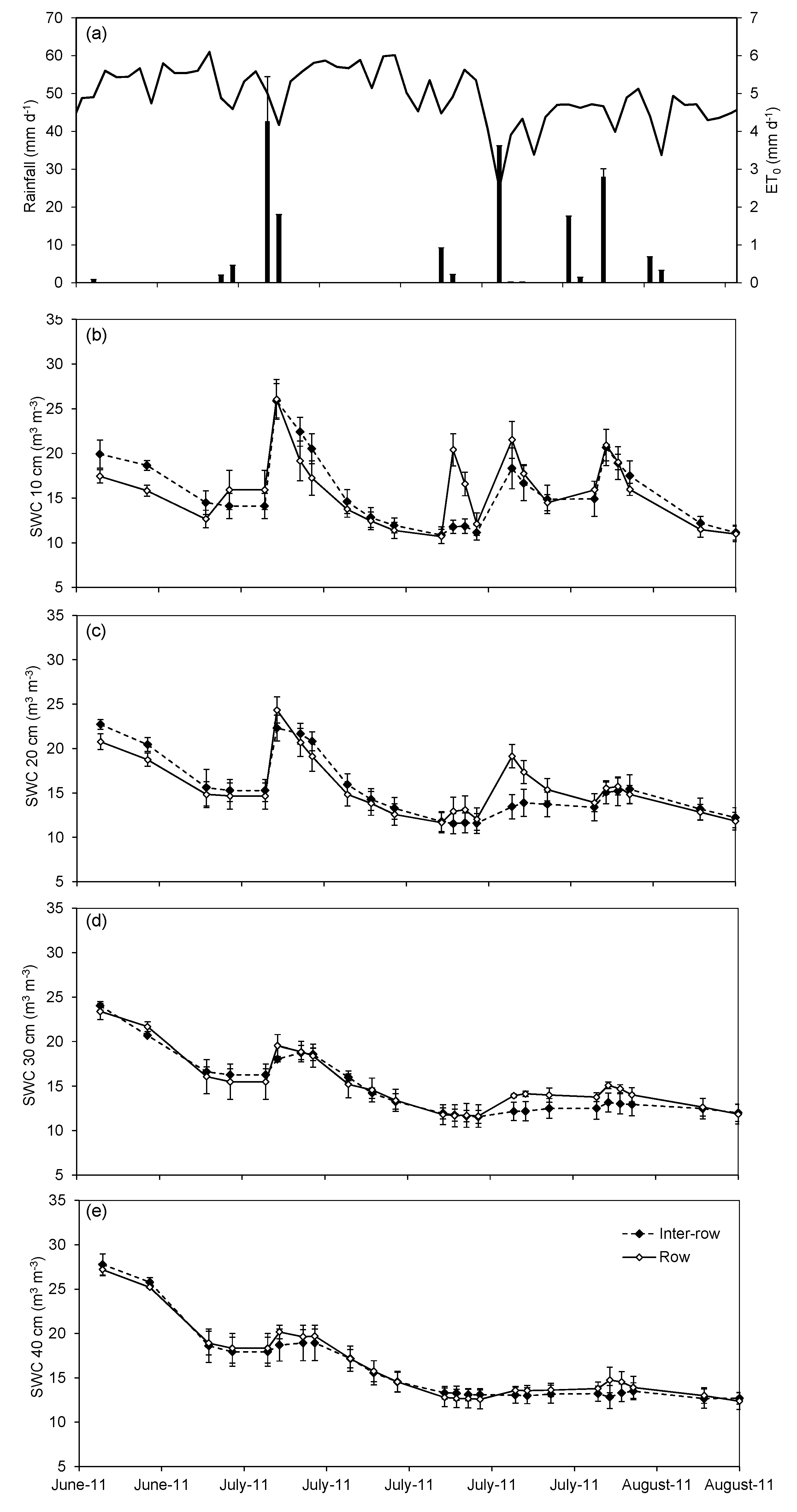
3.2. Inter-Row and Intra-Row Soil Water Dynamics
3.3. Calibration/Validation of HYDRUS 2D/3D
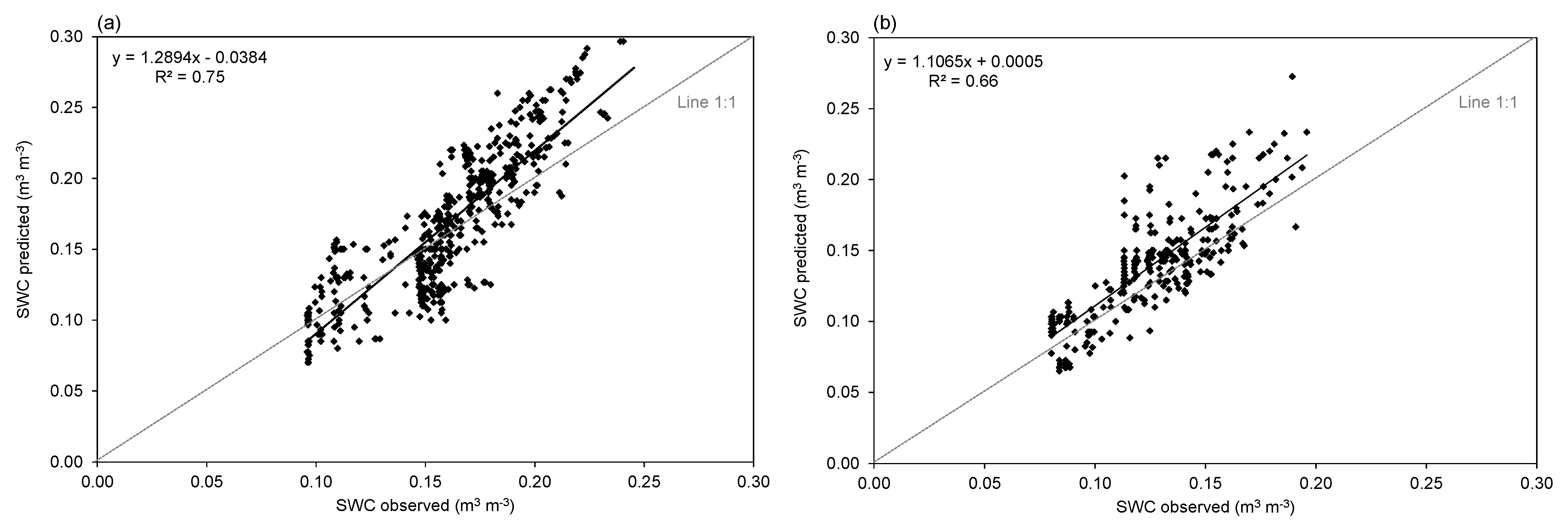
| Site | SWCr a (m3·m−3) | SWCs (m3·m−3) | α b (cm−1) | n c | Ks d (cm·h−1) | SWC (m3·m−3) −330 cm | SWC (m3·m−3) −15,000 cm |
|---|---|---|---|---|---|---|---|
| A | 0.031 | 0.461 | 0.005 | 1.51 | 0.71 | 0.319 | 0.078 |
| B | 0.000 | 0.460 | 0.002 | 1.39 | 0.26 | 0.395 | 0.115 |
| C | 0.071 | 0.460 | 0.006 | 1.52 | 0.48 | 0.324 | 0.109 |
3.4. Numerical Simulations
| Site | Irrigation | Simulations a | RF (mm) | ET (mm) | ETc (mm) | ET/ETc | Drainage (mm) | WCin b (mm) | WCfin c (mm) |
|---|---|---|---|---|---|---|---|---|---|
| A | Full | RU | 210 | 261 | 270 | 0.97 | 0.90 | 172 | 122 |
| ST | 210 | 261 | 270 | 0.97 | 0.91 | 172 | 122 | ||
| LEPA | 210 | 261 | 270 | 0.97 | 1.00 | 172 | 120 | ||
| Deficit 60% | RU | 126 | 217 | 270 | 0.80 | 0.90 | 172 | 82 | |
| ST | 126 | 220 | 270 | 0.81 | 0.90 | 172 | 81 | ||
| LEPA | 126 | 213 | 270 | 0.79 | 0.90 | 172 | 86 | ||
| B | Full | RU | 210 | 241 | 270 | 0.89 | 0.19 | 172 | 142 |
| ST | 210 | 241 | 270 | 0.89 | 0.19 | 172 | 142 | ||
| LEPA | 210 | 243 | 270 | 0.90 | 0.19 | 172 | 138 | ||
| Deficit 60% | RU | 126 | 190 | 270 | 0.70 | 0.19 | 172 | 108 | |
| ST | 126 | 193 | 270 | 0.71 | 0.19 | 172 | 107 | ||
| LEPA | 126 | 186 | 270 | 0.69 | 0.19 | 172 | 113 | ||
| C | Full | RU | 210 | 240 | 270 | 0.89 | 0.34 | 172 | 144 |
| ST | 210 | 241 | 270 | 0.89 | 0.34 | 172 | 144 | ||
| LEPA | 210 | 241 | 270 | 0.89 | 0.35 | 172 | 143 | ||
| Deficit 60% | RU | 126 | 193 | 270 | 0.71 | 0.34 | 172 | 108 | |
| ST | 126 | 196 | 270 | 0.72 | 0.34 | 172 | 106 | ||
| LEPA | 126 | 189 | 270 | 0.70 | 0.34 | 172 | 112 |

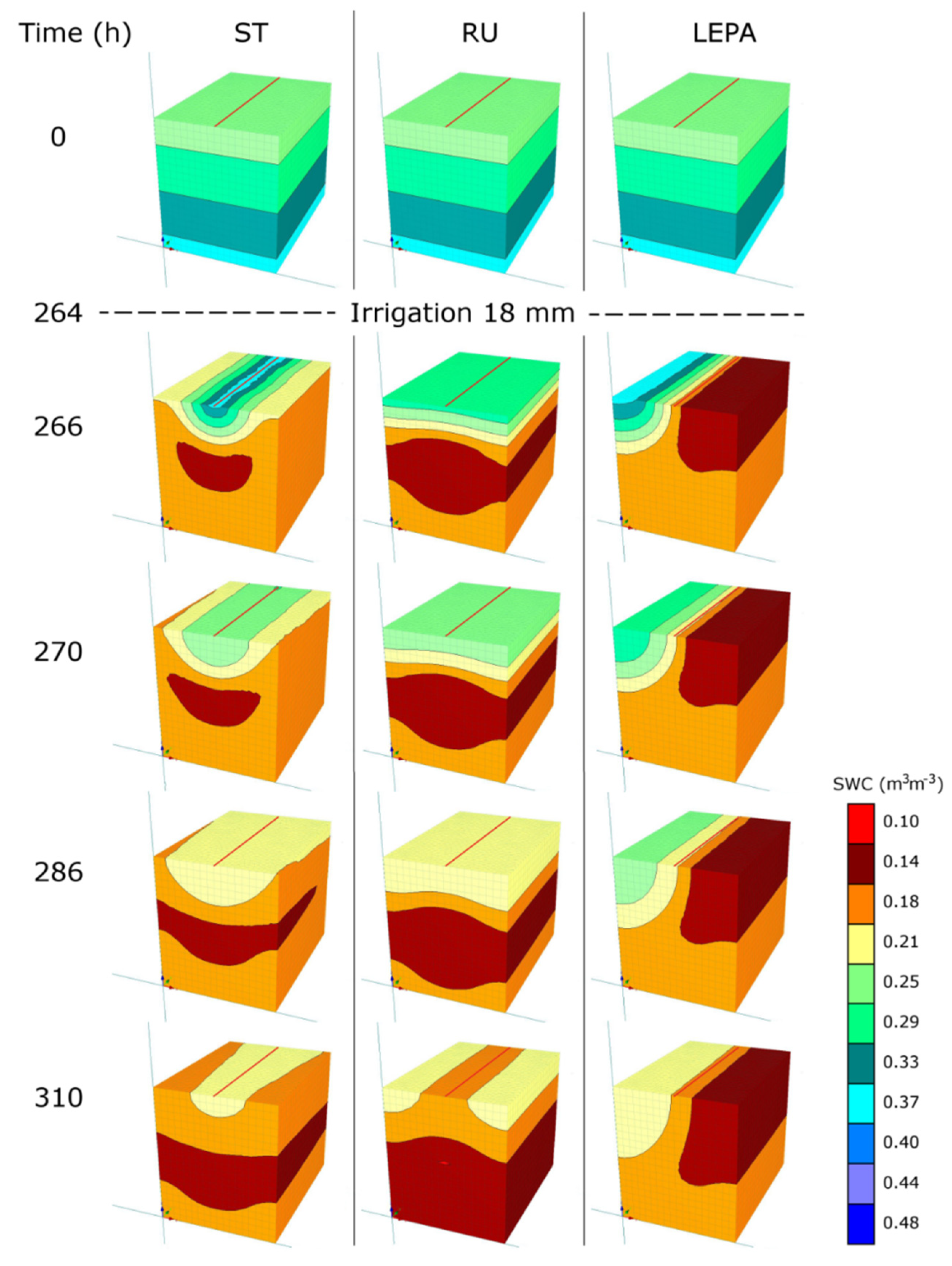
4. Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Pereira, L.S.; Cai, L.G.; Hann, M.J. Farm water and soil management for improved water use in the North China Plain. Irrig. Drain. 2003, 52, 299–317. [Google Scholar]
- Siebert, S.; Döll, P. Quantifying blue and green virtual water contents in global crop production as well as potential production losses without irrigation. J. Hydrol. 2010, 384, 198–217. [Google Scholar] [CrossRef]
- Lamm, F.R.; Manges, H.L. Partitioning of sprinkler irrigation water by a corn canopy. Trans. ASAE 2000, 43, 909–918. [Google Scholar] [CrossRef]
- Frasson, R.P.M.; Krajewski, W.F. Rainfall interception by maize canopy: Development and application of a processed-based model. J. Hydrol. 2013, 489, 246–255. [Google Scholar] [CrossRef]
- Logsdon, S.D.; Sauer, T.J.; Hernandez-Ramirez, G.; Hatfield, J.L.; Kaleita-Forbes, A.L. Effect of corn or soybean row position on soil water. Soil Sci. 2010, 175, 530–534. [Google Scholar] [CrossRef]
- Hupet, F.; Vanclooster, M. Micro-variability of hydrological processes at the maize row scale: Implications for soil water content measurements and evapotranspiration estimates. J. Hydrol. 2005, 303, 247–270. [Google Scholar] [CrossRef]
- Van Weesenbeck, I.; Kachanoski, R. Spatial and temporal distribution of soil water in the tilled layer under a corn crop. Soil Sci. Soc. Am. J. 1988, 52, 363–368. [Google Scholar]
- Paltineanu, I.; Starr, J. Preferential water flow through corn canopy and soil water dynamics across rows. Soil Sci. Soc. Am. J. 2000, 64, 44–54. [Google Scholar] [CrossRef]
- Lyle, W.M.; Bordowsky, J.P. Low energy precision application (LEPA) irrigation system. Trans. ASAE 1981, 24, 1241–1245. [Google Scholar] [CrossRef]
- Schneider, A.D.; Buchleiter, G.W.; Kincaid, D.C. LEPA irrigation developments. In Proceedings of the 4th Decennial Symposium, National Irrigation Symposium, Phoenix, AZ, USA, 14–16 November 2000; pp. 89–96.
- Food and Agriculture Organization (FAO); United Nations Educational, Scientific and Cultural Organization. Soil Map of the World, Revised Legend; FAO: Rome, Italy, 1990. [Google Scholar]
- Borin, M.; Morari, F.; Bonaiti, G.; Paasch, M.; Skaggs, W. Analysis of DRAINMOD performances with different detaiul of soil input data inb the Veneto region of Italy. Agric. Water Manag. 2000, 42, 259–272. [Google Scholar] [CrossRef]
- Norme Internationale (ISO). Matériel D’irrigation Asperseurs Rotatifs Partie 2: Uniformité de la Distribution et Méthodes D’essai. ISO 7749-2; ISO: Lethbridge, AL, Canada, 1990. (In French) [Google Scholar]
- Simunek, J.; Sejna, M.; van Genuchten, M.T. The HYDRUS-2D Software Package for Simulating Two-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media. Version 2.0, IGWMC-TPS-53; International Ground Water Modeling Center, Colorado School of Mines: Golden, CO, USA, 1999. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; Food Agriculture Organization Of the UN: Rome, Italy, 1998. [Google Scholar]
- Dal Ferro, N.; Sartori, L.; Simonetti, G.; Berti, A.; Morari, F. Soil macro and microstructure as affected by different tillage systems and their effects on maize root growth. Soil Till. Res. 2014, 140, 55–65. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water Use and Crop Yield; John Wiley and Sons: New York, NY, USA, 1978. [Google Scholar]
- Chang, C.; Laird, D.A.; Mausbachc, M.J.; Hurburghd, C.R. Near-infrared reflectance spectroscopy–principal components regression analyses of soil properties. Soil Sci. Soc. Am. J. 2001, 65, 480–490. [Google Scholar] [CrossRef]
- Giardini, L. Productivity and Sustainability of Different Cropping Systems; Patron Editore: Bologna, Italy, 2004. [Google Scholar]
- Viscarra Rossel, R.A.; Walvoort, D.J.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Keller, J.; Bliesner, R.D. Sprinkle and Trickle Irrigation; Blackburn Press: Caldwell, NJ, USA, 2000. [Google Scholar]
- Michot, D.; Benderitter, Y.; Dorigny, A.; Nicollaud, B.; King, D.; Tabbagh, A. Spatial and temporal monitoring of soil water content with irrigated corn crop cover using surface electrical resistivity tomography. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Schneider, A.D.; Howell, T.A. LEPA and spray irrigation for grain crops. J. Irrig. Drain. Eng. 1999, 125, 167–172. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martello, M.; Ferro, N.D.; Bortolini, L.; Morari, F. Effect of Incident Rainfall Redistribution by Maize Canopy on Soil Moisture at the Crop Row Scale. Water 2015, 7, 2254-2271. https://doi.org/10.3390/w7052254
Martello M, Ferro ND, Bortolini L, Morari F. Effect of Incident Rainfall Redistribution by Maize Canopy on Soil Moisture at the Crop Row Scale. Water. 2015; 7(5):2254-2271. https://doi.org/10.3390/w7052254
Chicago/Turabian StyleMartello, Marco, Nicola Dal Ferro, Lucia Bortolini, and Francesco Morari. 2015. "Effect of Incident Rainfall Redistribution by Maize Canopy on Soil Moisture at the Crop Row Scale" Water 7, no. 5: 2254-2271. https://doi.org/10.3390/w7052254
APA StyleMartello, M., Ferro, N. D., Bortolini, L., & Morari, F. (2015). Effect of Incident Rainfall Redistribution by Maize Canopy on Soil Moisture at the Crop Row Scale. Water, 7(5), 2254-2271. https://doi.org/10.3390/w7052254







