Hierarchical Classification of Groundwater Pollution Risk of Contaminated Sites Using Fuzzy Logic: A Case Study in the Basilicata Region (Italy)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Intrinsic and Integrated Groundwater Vulnerability
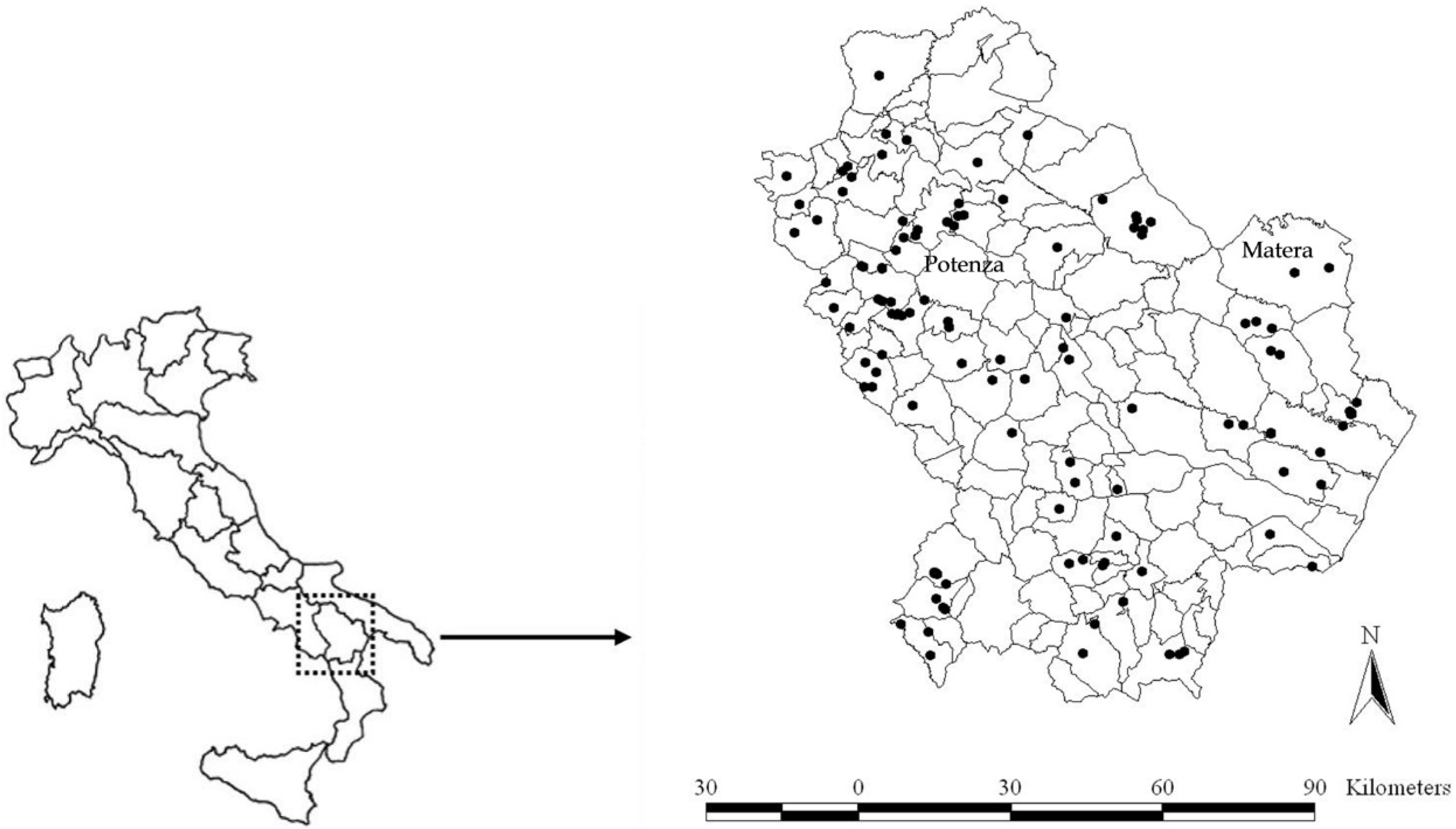
Aquifer Intrinsic Vulnerability: The GNDCI-CNR Method


- identification and definition of hydrological and hydrodynamic characteristics of the area of interest;
- creation of the hydrogeological map and identification of scenario or hydrological and impact scenarios in the area of interest;
- identification, on the basis of the GNDCI-CNR protocol, of the reference scenario or scenarios adaptable to the hydrogeological situation of interest by the consequent assignment of the relative degrees of vulnerability.
- drafting of the aquifer intrinsic vulnerability map accompanied by an appropriate legend.
2.2. Case Study
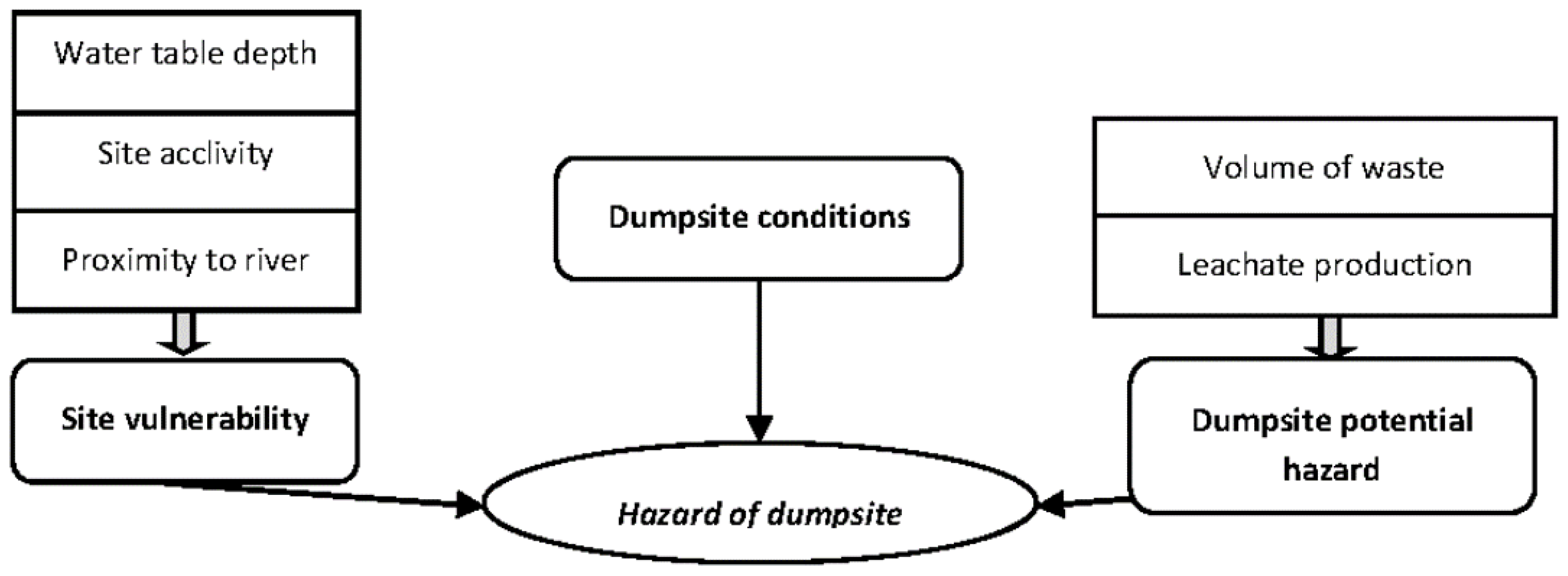
2.2.1. Risk Factors
2.2.2. Water Table Depth
2.2.3. Slope Gradient

2.2.4. River Proximity
2.2.5. Leachate Production
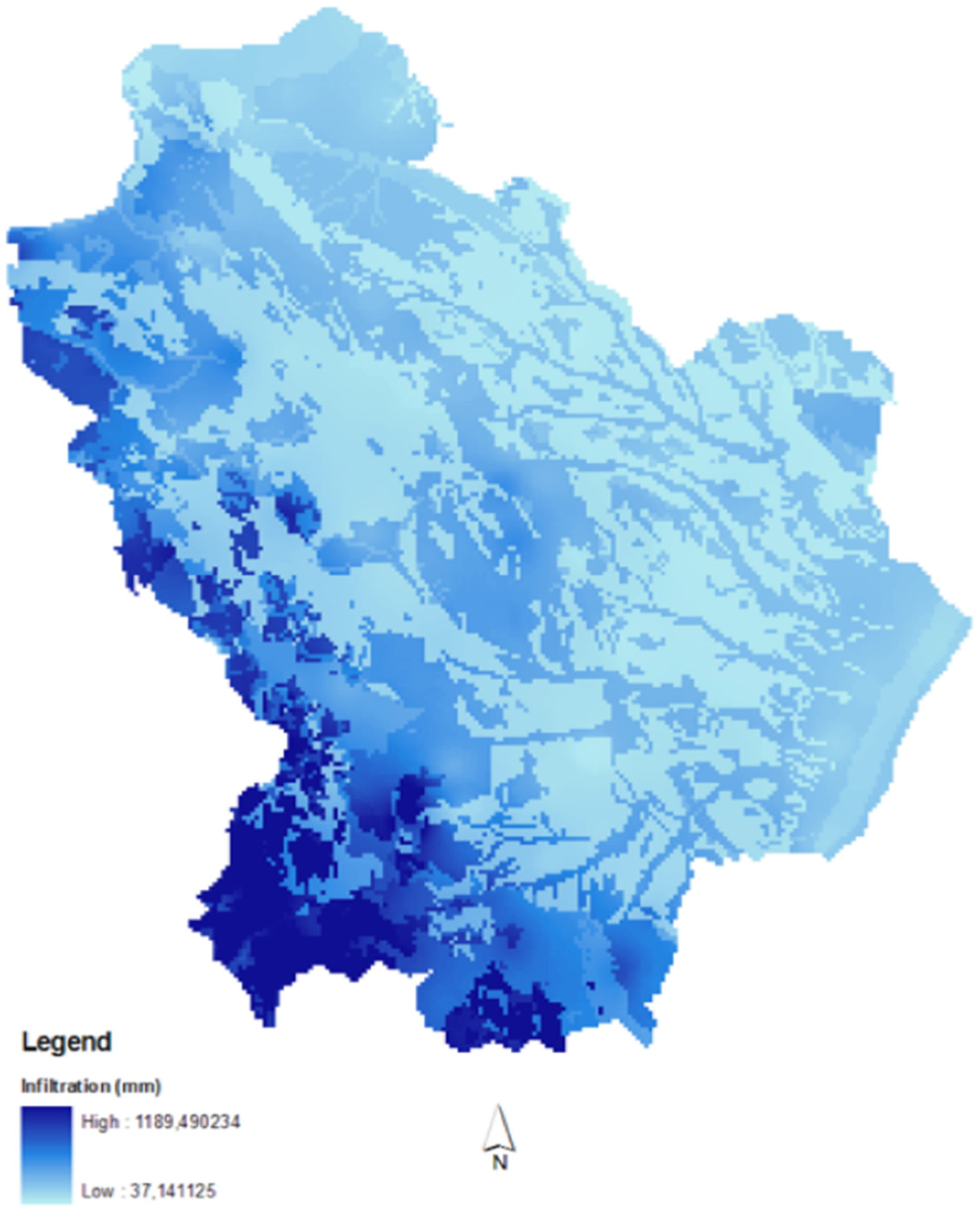
2.3. Assessment of the Pollution Risk of the Illegal Dumpsites of the Basilicata Region: The “Scores and Weights” Method
| Hazardous Factors of Landfills | Weights and Coefficient of Reduction of Risk Factors (R) | |
|---|---|---|
| Waste input rate (waste volume, m3) | <1,000 | 0.1 |
| 1,000–5,000 | 0.3 | |
| 5,000–10,000 | 0.5 | |
| 10,000–20,000 | 0.7 | |
| >20,000 | 1 | |
| Estimate of leachate production (infiltration value, mm) | 0–100 | 0.1 |
| 100–200 | 0.3 | |
| 200–300 | 0.5 | |
| 300–500 | 0.7 | |
| >500 | 1 | |
| Waste types | MSW, MSW + IW | 0.1 |
| non-MSW, non-MSW + MSW | 0.5 | |
| HW, MSW + HW, non-MSW + HW | 1 | |
| Proximity to superficial water (Proximity river index value, adim) | 0–5 | 0.1 |
| 5–10 | 0.5 | |
| >10 | 1 | |
| Water table depth (m) | >5 | 0.1 |
| 2–5 | 0.5 | |
| 0–2 | 1 | |
| Site acclivity (degrees) | >20 | 0.1 |
| 10–20 | 0.3 | |
| 5–10 | 0.7 | |
| 0–5 | 1 | |
| Monitoring system | Present | 0.1 |
| Not present | 1 | |
| Physical state of dumpsite | Without soil cover | 0.3 |
| With soil cover | 1 | |
2.4. Development of the Fuzzy Logic Model for Assessing Aquifer Integrated Vulnerability


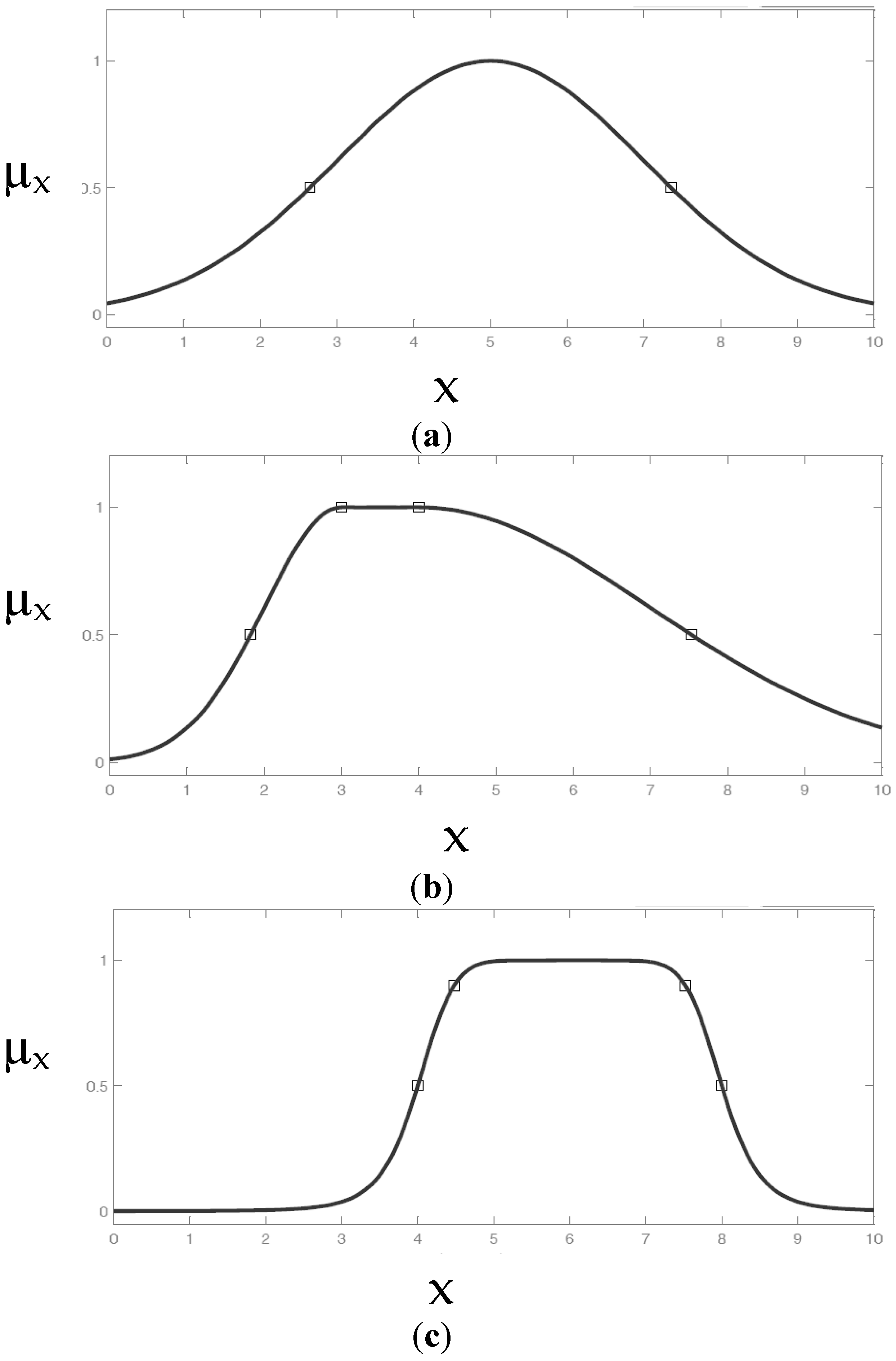
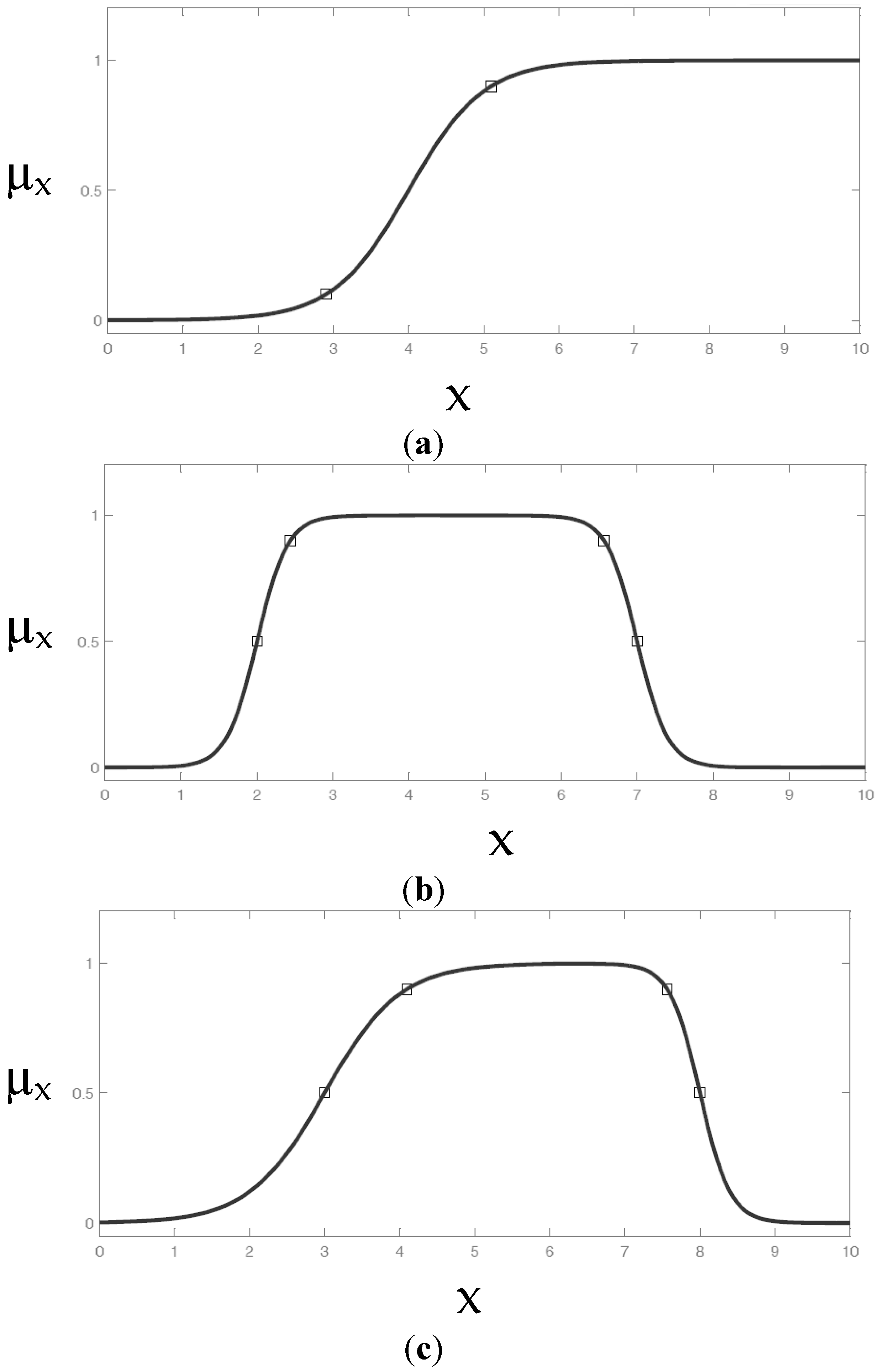
- Centroid method: the chosen numerical value for the output is calculated as the centre of the mass of the fuzzy set;
- Bisector method: the output is the abscissa of the bisector of the area subtended to the fuzzy data set;
- Middle of maximum method: the output value is determined as the average of maximum values (Mom, middle of maximum) (Figure 4);
- Largest of maximum method: the output numerical value is calculated as the maximum of the maximum (Lom: Largest of maximum);
- Smallest of maximum method: the output value is represented by the output minimum value (Som: Smallest of maximum).
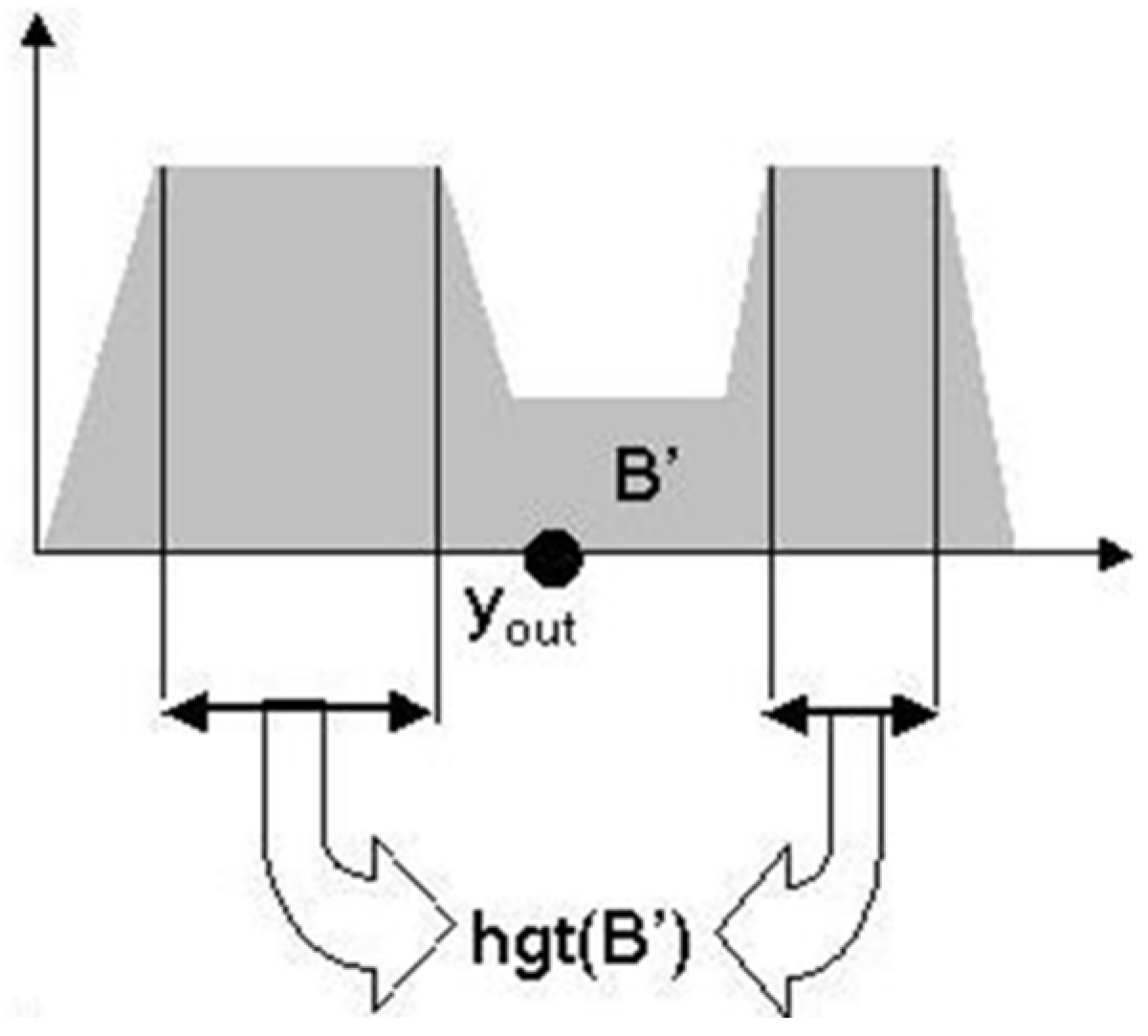

| Defuzzification Method | Gauss2 | Triangular | Trapezoidal | Gbell | Gauss | Disig | Psig | Pi |
|---|---|---|---|---|---|---|---|---|
| Centroid | 0.692 | 0.594 | 0.969 | 0.966 | 0.280 | 0.001 | 0.001 | 0.479 |
| Bisector | 0.687 | 0.945 | 0.945 | 0.030 | 0.940 | 0.118 | 0.114 | 0.815 |
| Mom | 0.009 | 0.009 | 0.009 | 0.009 | 0.012 | 0.008 | 0.011 | 0.013 |
| Lom | 0.009 | 0.009 | 0.009 | 0.018 | 0.012 | 0.010 | 0.014 | 0.023 |
| Som | 0.026 | 0.025 | 0.025 | 0.012 | 0.021 | 0.087 | 0.094 | 0.093 |
| Landfills Hazard | Aquifer Intrinsic Vulnerability | ||||
|---|---|---|---|---|---|
| Very Low | Low | Medium | High | Very High | |
| Very Low | Very Low | Low | Low | Medium | Medium |
| Low | Low | Low | Medium | Medium | High |
| Medium | Low | Medium | Medium | High | High |
| High | Medium | Medium | High | High | Very high |
| Very high | Medium | High | High | Very high | Very high |
3. Results and Discussion
3.1. Aquifer Intrinsic Vulnerability
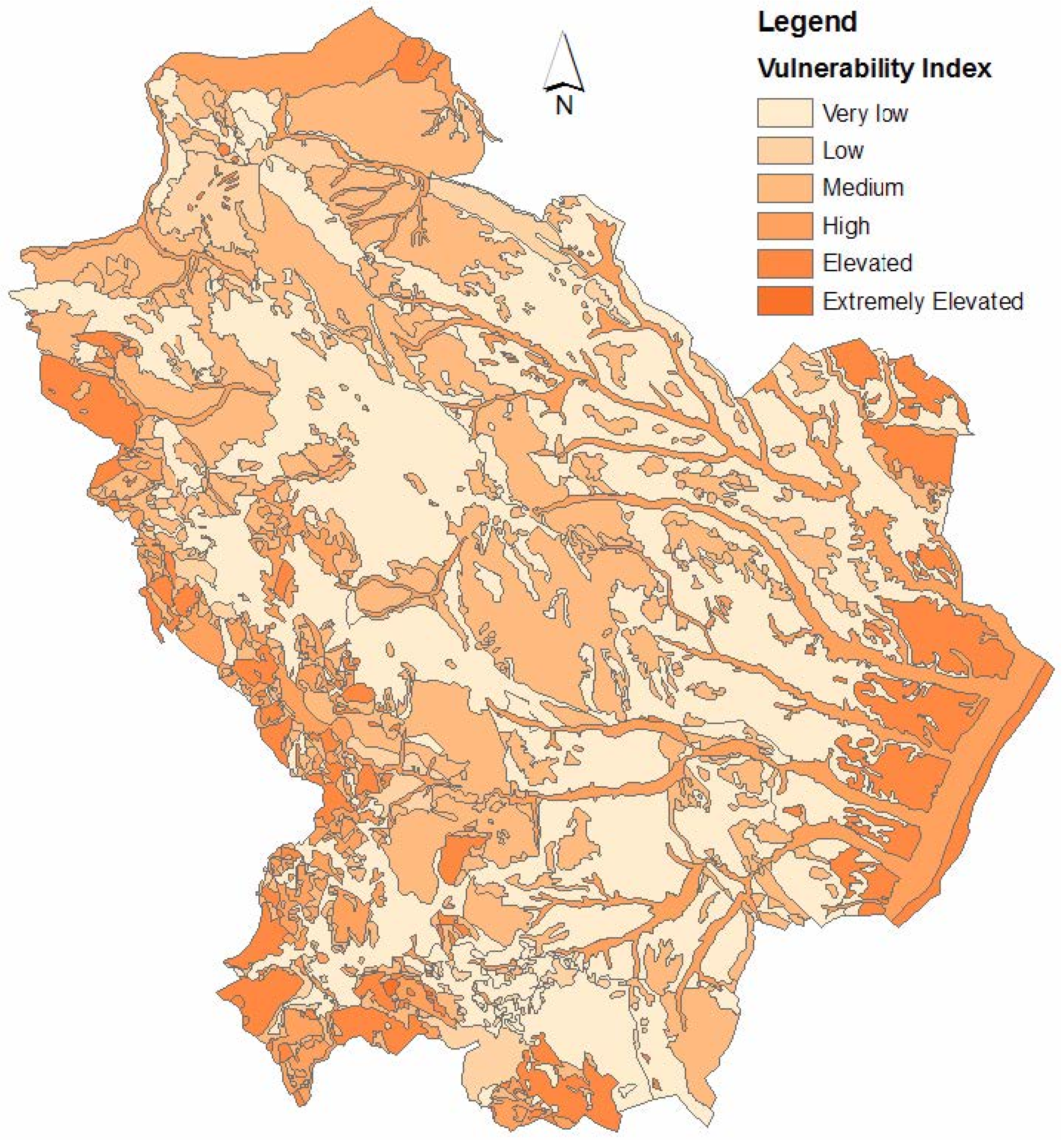
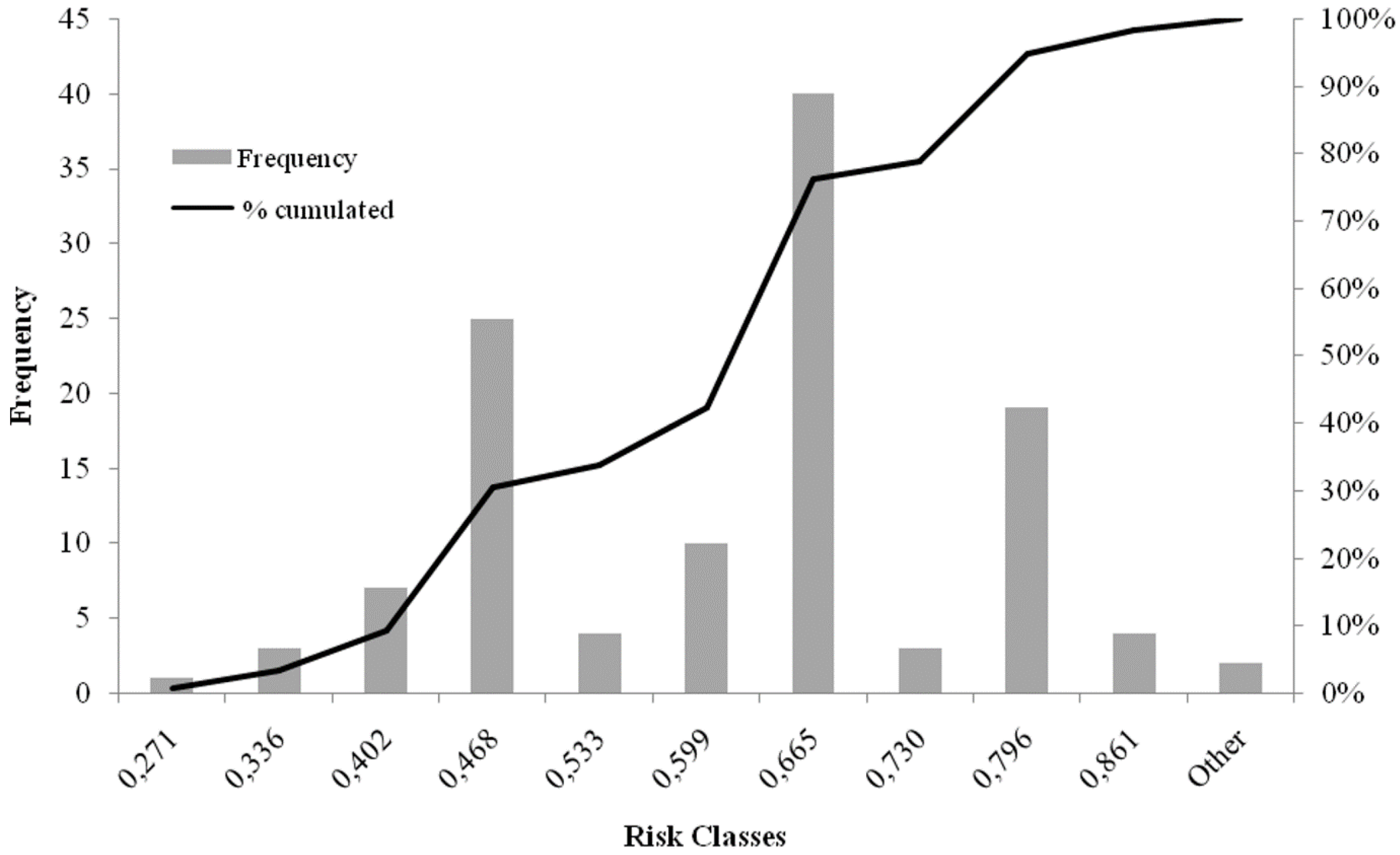
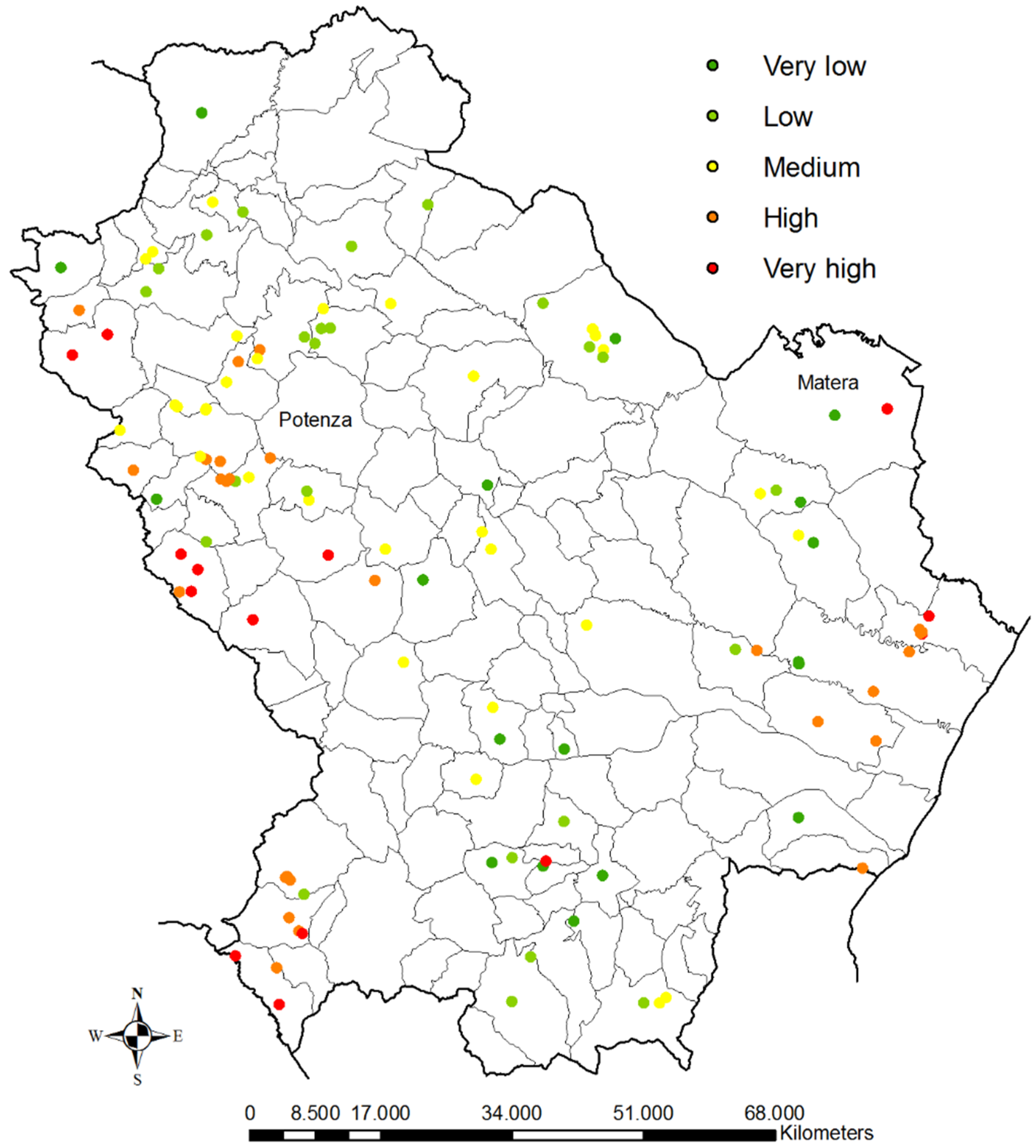
3.2. Results of the Pollution Risk of Dumpsites Obtained with the “Scores and Weights” and the Fuzzy Logic Method
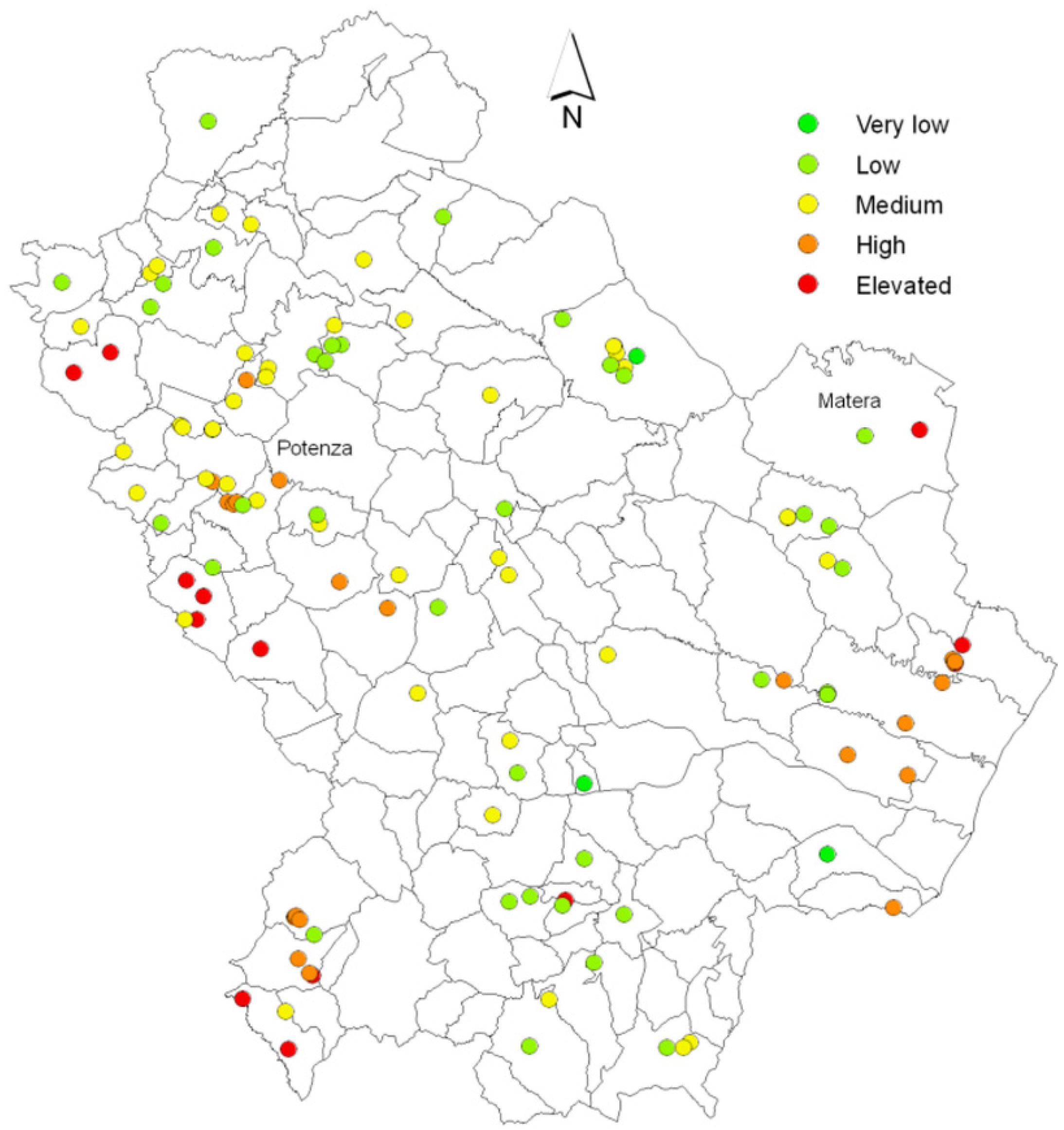
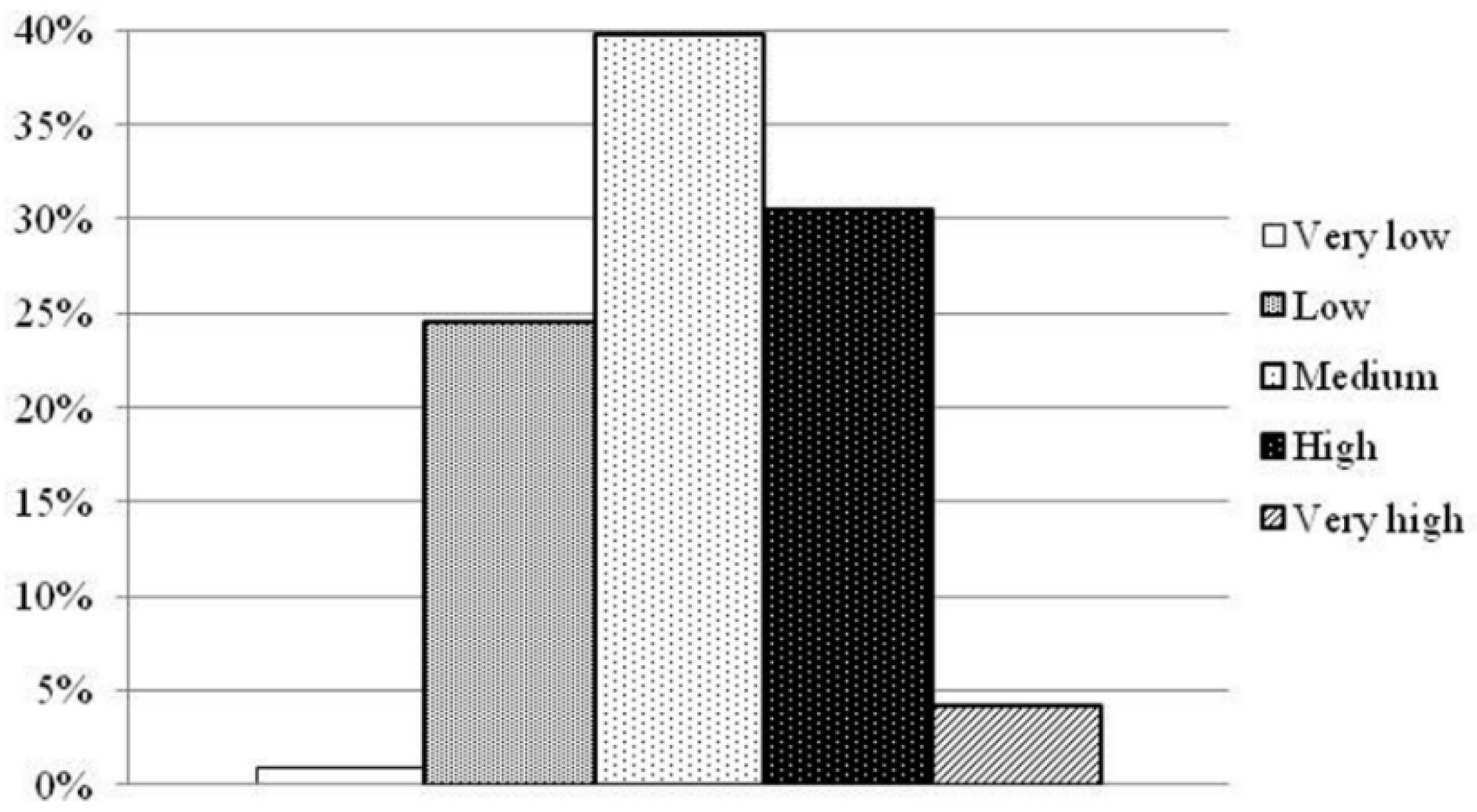
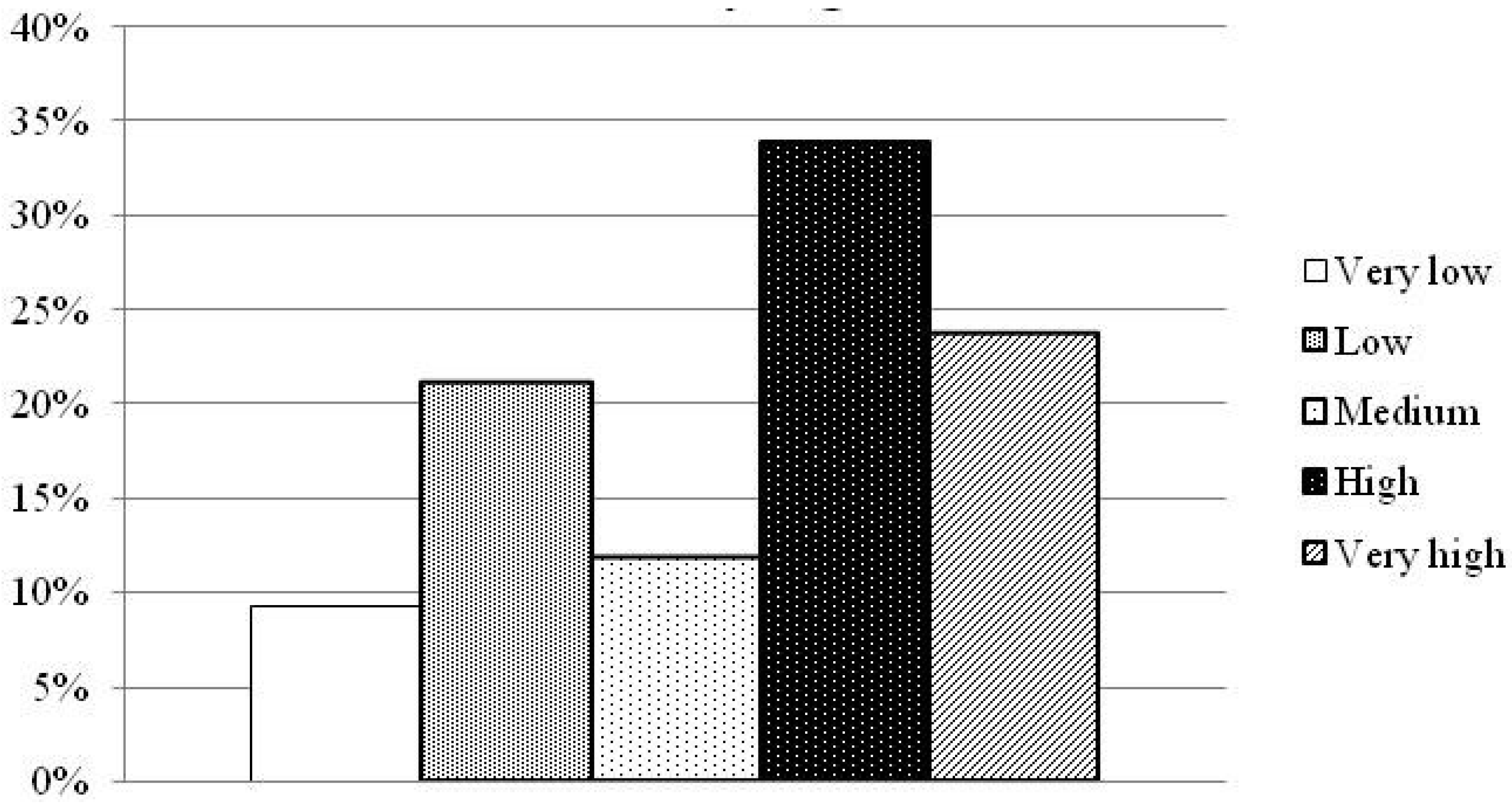
| Dumpsite Pollution Vulnerability Classes | Classes Range |
|---|---|
| Very low | 0.402 |
| Low | 0.468 |
| Medium | 0.599 |
| High | 0.665 |
| Very high | 0.796 |
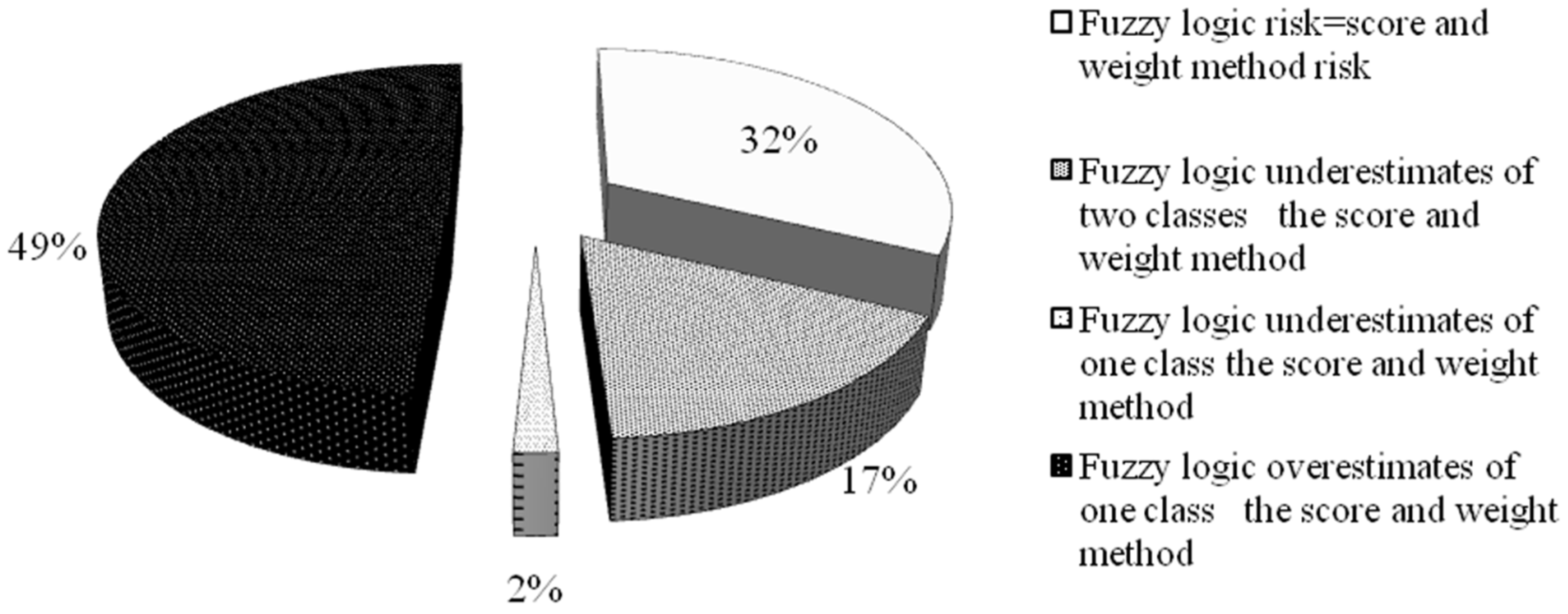
| Statistical Dispersion Indices | Scores and Weight Method | Fuzzy Logic |
|---|---|---|
| Standard deviation | 0.237 | 0.211 |
| Variance | 0.056 | 0.044 |
| Mean | 0.466 | 0.470 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rezaei, F.; Safavi, H.R.; Ahmadi, A. Groundwater vulnerability assessment using fuzzy logic: A case study in the zayandehrood aquifers, Iran. Environ. Manag. 2013, 51, 267–277. [Google Scholar] [CrossRef]
- Shahmaleki, N.; Behbahani, S.M.R.; Massah Bavani, A.R.; Khodaei, K. Comparison between logistic regression, modified DRASTIC and AHP-DRASTIC methods in groundwater vulnerability assessment. J. Environ. Stud. 2013, 38, 79–92. [Google Scholar]
- Jarvis, N. The MACRO Model Technical Description; Swedish University of Agricultural Sciences (SLU); Department of Soil Sciences: Uppsala, Switzerland, 2002. [Google Scholar]
- Merdun, H.; Quisenberry, V.L. Simulation of water and solute transport with MACRO model in Cecil loamysand soil. Aust. J. Soil Res. 2004, 42, 939–951. [Google Scholar] [CrossRef]
- Ma, L.; Ahuja, L.R.; Ascough, J.C.; Shaffer, M.J.; Rojas, K.W.; Malone, R.W.; Cameira, M.R. Integrating System Modeling with Field Research in Agriculture: Application of the Root Zone Water Quality Model; United States Department of Agriculture, Agricultural Research Service (USDA-ARS): Washington, DC, USA, 2000.
- Castiglione, P.; Mohanty, B.P.; Shouse, P.J.; Simunek, J.; van Genuchten, M.T.; Santini, A. Lateral water diffusion in an artificial macroporous system. Vadose Zone J. 2003, 2, 212–221. [Google Scholar] [CrossRef]
- Simunek, J.; Sejna, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media, Version 3.0.; Department of Environmental Sciences, University of California Riverside: Riverside, CA, USA, 2005. [Google Scholar]
- Hutson, J.L. Leachm Model Description and User’s Guide; School of Chemistry, Physics and Earth Sciences, Flinders University of South Australia: Adelaide, Australia, 2003. [Google Scholar]
- Rahman, A. A GIS based DRASTIC model for assessing groundwater vulnerability in shallow aquifer in Aligarh, India. Appl. Geogr. 2008, 28, 32–53. [Google Scholar] [CrossRef]
- Shouyu, C.; Guangtao, F. A DRASTIC-based fuzzy pattern recognition methodology for groundwater vulnerability evaluation. Hydrol. Sci. J. 2003, 48, 211–220. [Google Scholar] [CrossRef]
- Civita, M. Legenda Unificata per le Carte Della Vulnerabilità dei Corpi Idrici Sotterranei/Unified Legend for the Aquifer Pollution Vulnerability Maps; Studi sulla Vulnerabilità degli Acquiferi 1 Pitagora: Bologna, Italy, 1990. [Google Scholar]
- Civita, M. Una metodologia per la definizione e il dimensionamento delle are di salvaguardia delle opere delle opere di presa delle sorgenti normali. Boll. Ass. Min. SUBALPINA 1988, 25, 423–440. [Google Scholar]
- Afshar, A.; Mariño, M.A.; Ebtehaj, M.; Moosavi, J. Rule-based fuzzy system for assessing groundwater vulnerability. J. Environ. Eng. 2007, 133, 532–540. [Google Scholar] [CrossRef]
- Caniani, D.; Lioi, D.S.; Mancini, M.I.; Masi, S. Application of fuzzy logic and sensitivity analysis for soil contamination hazard classification. Waste Manag. 2011, 31, 583–594. [Google Scholar] [CrossRef] [PubMed]
- Dixon, B. Groundwater vulnerability mapping: A GIS and fuzzy rule based integrated tool. Appl. Geogr. 2005, 25, 327–347. [Google Scholar] [CrossRef]
- Gemitzi, A.; Petalas, C.; Tsihrintzis, V.A.; Pisinaras, V.; et al. Assessment of groundwater vulnerability to pollution: A combination of GIS, fuzzy logic and decision making techniques. Environ. Geol. 2006, 49, 653–673. [Google Scholar] [CrossRef]
- Mohammadi, K.; Niknam, R.; Majd, V.J. Aquifer vulnerability assessment using GIS and fuzzy system: A case study in Tehran-Karaj aquifer, Iran. Environ. Geol. 2009, 58, 437–446. [Google Scholar] [CrossRef]
- Uricchio, V.F.; Giordano, R.; Lopez, N. A fuzzy knowledge-based decision support system for groundwater pollution risk evaluation. J. Environ. Manag. 2004, 73, 189–197. [Google Scholar] [CrossRef]
- Sdao, F.; Lioi, D.S.; Pascale, S.; Caniani, D.; Mancini, I.M. Landslide susceptibility assessment by using a neuro-fuzzy model: A case study in the Rupestrian heritage rich area of Matera. Nat. Hazards Earth Syst. Sci. 2013, 13, 395–407. [Google Scholar] [CrossRef]
- Civita, M.; de Maio, M. SINTACS. Un Sistema Parametrico per la Valutazione e la Cartografia Della Vulnerabilità Degli Acquiferi All’inquinamento: Metodologia e Automazione; Pitagora Editrice: Bologna, Italy, 1997. (In Italian) [Google Scholar]
- Rapti-Caputo, D.; Sdao, F.; Masi, S. Pollution risk assessment based on hydrogeological data and management of solid waste landfills. Eng. Geol. 2006, 85, 122–131. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caniani, D.; Lioi, D.S.; Mancini, I.M.; Masi, S. Hierarchical Classification of Groundwater Pollution Risk of Contaminated Sites Using Fuzzy Logic: A Case Study in the Basilicata Region (Italy). Water 2015, 7, 2013-2036. https://doi.org/10.3390/w7052013
Caniani D, Lioi DS, Mancini IM, Masi S. Hierarchical Classification of Groundwater Pollution Risk of Contaminated Sites Using Fuzzy Logic: A Case Study in the Basilicata Region (Italy). Water. 2015; 7(5):2013-2036. https://doi.org/10.3390/w7052013
Chicago/Turabian StyleCaniani, Donatella, Donata Serafina Lioi, Ignazio M. Mancini, and Salvatore Masi. 2015. "Hierarchical Classification of Groundwater Pollution Risk of Contaminated Sites Using Fuzzy Logic: A Case Study in the Basilicata Region (Italy)" Water 7, no. 5: 2013-2036. https://doi.org/10.3390/w7052013
APA StyleCaniani, D., Lioi, D. S., Mancini, I. M., & Masi, S. (2015). Hierarchical Classification of Groundwater Pollution Risk of Contaminated Sites Using Fuzzy Logic: A Case Study in the Basilicata Region (Italy). Water, 7(5), 2013-2036. https://doi.org/10.3390/w7052013





