1. Introduction
Water conflicts are key issues for sustainable water resources management. Under the dual effects of climate change and human activities, many water bodies are polluted to varying degrees, further exacerbating water conflicts [
1,
2]. Ecosystem studies such as water enhancement, water quality risk assessment, and early warnings have drawn much attention across the world [
3]. As important engineering measures are developed to guarantee water supply, irrigation, electricity, and other functions, reservoirs can help solve these issues through the redistribution of runoff in both time and space; therefore, they are widely used throughout the world. Although water demands of each production department (e.g., industrial department, agricultural department, and so on) correspond to different water quality requirements, water quality always needs to be up to its appropriate standard in different water usage [
4]. Accordingly, it is important to forecast water quality accurately, which could provide a scientific decision basis for reservoir management.
Chlorophyll
a is an important component of algae organisms, and its concentration in water bodies is closely related to the type and the quantity of algae [
5]. Therefore, as an important symbol of phytoplankton stock, concentration of chlorophyll
a can reflect water nutritional status, making chlorophyll
a one of the indicators in controlling the eutrophication of lakes and reservoirs. The minimum threshold concentration of chlorophyll
a for eutrophic lakes identified by the Organization for Economic Cooperation and Development (OECD) is 0.008 mg/L. Consequently, there is a need to control the concentration of chlorophyll
a in water to prevent potential eutrophication. For this reason, accurate prediction of chlorophyll
a is a worldwide concern.
The generation mechanism of chlorophyll
a in water is accordingly complex, which is closely related to ecological, environmental, and societal activities. Therefore, the elements involved in the prediction for chlorophyll
a in water are complex accordingly. In the existing literature, prediction models for chlorophyll
a mainly included two categories: statistical regression models [
6] and mechanism models [
7]. Statistical regression models were established with the applications of statistical correlation analysis theory and methods. This means that the sample size had a major influence on prediction accuracy. Moreover, these models usually applied a linear relationship to simplify complex problems, leading to unsatisfactory prediction results under the situation when the limiting factors of chlorophyll
a changed. Mechanism models mainly included the nutrient model, phytoplankton model, and ecological dynamic models such as CE-QUAL-ICM, WASP, CAEDYM, AQUATOX, and ECOPATH [
8,
9,
10]. Based on the principle of hydrodynamics and ecosystem dynamics, these models comprehensively considered the interaction mechanisms among indicators of water resources system and ecosystem, and then predicted the future development of the system accurately. However, these models also had a high demand for data quantity, which was inconvenient for model calibration and verification, leading to a decline in reliability and applicability. Furthermore, due to uncertainty factors such as the concentration of phosphorus input from non-point source pollution, the prediction of chlorophyll
a based on deterministic differential equations was not reasonable [
11]. For this reason, the uncertainty of input parameters and the nonlinearity of the system required further consideration when constructing models.
To improve the accuracy and efficiency of nonlinear system simulations, intelligent algorithms have been applied in recent years [
12]. Widely used intelligent algorithms include the artificial neural network (ANN), the genetic algorithm (GA), the particle swarm algorithm, the wavelet theory, and the projection pursuit algorithm,
etc.; these intelligent algorithms overcome the uncertainty to a certain extent with high simulation precision. In recent years, the support vector machine (SVM) algorithm, which is a new type of machine learning tool based on statistical learning theory, has drawn more attention [
13]. This intelligent algorithm can solve nonlinear system problems and has reasonable generalization ability when using small samples, ameliorating the weaknesses of the above intelligent algorithms, e.g., large sample size requirements and being susceptible to underfitting and overfitting the data for the ANN. The SVM has demonstrated promise for applied studies of water environments, especially for the prediction of hydrologic factors, such as wave height [
14], inflow [
15], and water levels [
16]. Previous studies of chlorophyll
a based on the SVM algorithm often focused on the retrieval of chlorophyll
a in water [
17], although very few results of chlorophyll
a prediction have been reported [
18]. Furthermore, chlorophyll
a is affected by many factors, and irrelevant and redundant information is often hidden in the time series of high dimensional feature vectors, leading to structurally complex models and a decrease of analysis precision and application efficiency of the SVM model when using conventional modeling processes [
19]. To simplify the model structure and avoid the interference of redundant information in chlorophyll
a forecasts, it is desirable to obtain more accurate and reliable prediction results by using SVM models with the most relevant influence factors as input vectors and simple structures. Feature selection is an important approach for getting structurally simplified model by removing those redundant parameters. Cho
et al. [
20] used principal component analysis (PCA) to extract variables for the prediction model of chlorophyll
a. Compared to conventional parameter extraction approaches such as PCA, the GA has a distinct advantage in fast random search. Thus, the SVM model can be expected to get satisfactory prediction results through combing the GA to extract feature variables and simplify the model structure in such complex water bodies as reservoirs, whose water quality variations likely result from a combination of multiple factors. However, the GA-SVM hybrid model needs to be further developed for nonlinear water resources system.
This study developed a hybrid model of GA and SVM algorithms to predict chlorophyll a in the Miyun Reservoir of northern China. Based on the feature selection with the GA, we extracted appropriate input vectors, so that the redundant information was effectively eliminated with the simplified model structure. This model could analyze water quality and its change trend with reliable results, and was of great practical significance in preventing water pollution accidents.
2. Study Area and Data Description
The Miyun Reservoir is located in the Miyun County of Beijing City. Built in 1960, it is the largest reservoir and is a unique surface source of drinking water in Beijing City (
Figure 1). In addition to functioning as a water supply, the Miyun Reservoir also provides irrigation, flood control, power generation, aquaculture, tourism, and other comprehensive benefits. The Miyun Reservoir’s surface area is 183.6 km
2, its maximum depth is 153.93 m, and the maximum volume of reservoir storage is 3.349 × 10
10 m
3. Monitoring data shows that in recent years, the total phosphorus concentration in the reservoir fluctuated between 0.010 and 0.025 mg/L, which means the nutrition status of the water is at a mesotrophication to oligotrophication level. The total nitrogen concentration ranges between 0.62 and 1.43 mg/L, indicating that the nutrition status is at a mild or moderate eutrophication level. Planktonic algae have rich diversities, and the dominant population in various periods is different in the Miyun Reservoir. As for cyanobacterium, from 2001 to 2003 it was the dominant algae from September to October [
21]; from 2008 to 2010, it was the dominant algae from June to September [
22,
23]. Considering the current water quality situation, we should take effective measures to alleviate adverse influences resulting from climate change and human activities on the reservoir.
Figure 1.
The Miyun Reservoir in northern China.
Figure 1.
The Miyun Reservoir in northern China.
In this paper, the Baihe Key Dam in the Miyun Reservoir is taken as the research area. Data for the model establishment and calibration are from the monitored data, including water quality indicators (
i.e., chlorophyll
a in water, total nitrogen, total phosphorus, permanganate index, and dissolved oxygen), hydrological indicators (
i.e., water temperature, pH, transparency, flow, reservoir storage, inflow, outflow, and water level), and meteorological indicators (
i.e., precipitation and temperature). The monthly data from 2000 to 2010 were obtained from the Miyun Reservoir Management Office. Because the Miyun Reservoir is frozen for the period from December to March, the prediction of chlorophyll
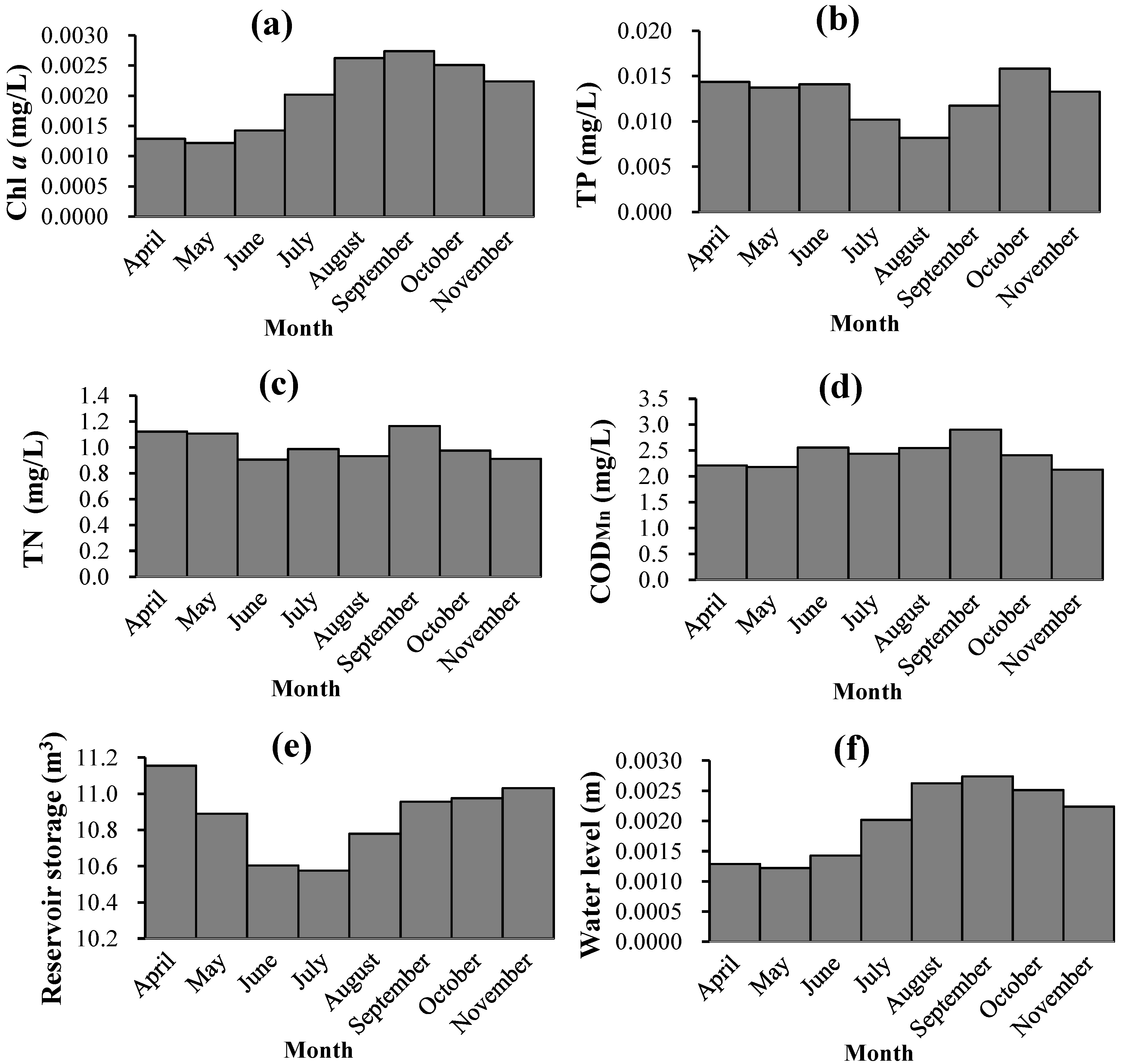
a focused on the period from April to November in each year, and other indicators in the SVM model corresponded to these months. The average monthly variations of parts of these indicators are shown in
Figure 2.
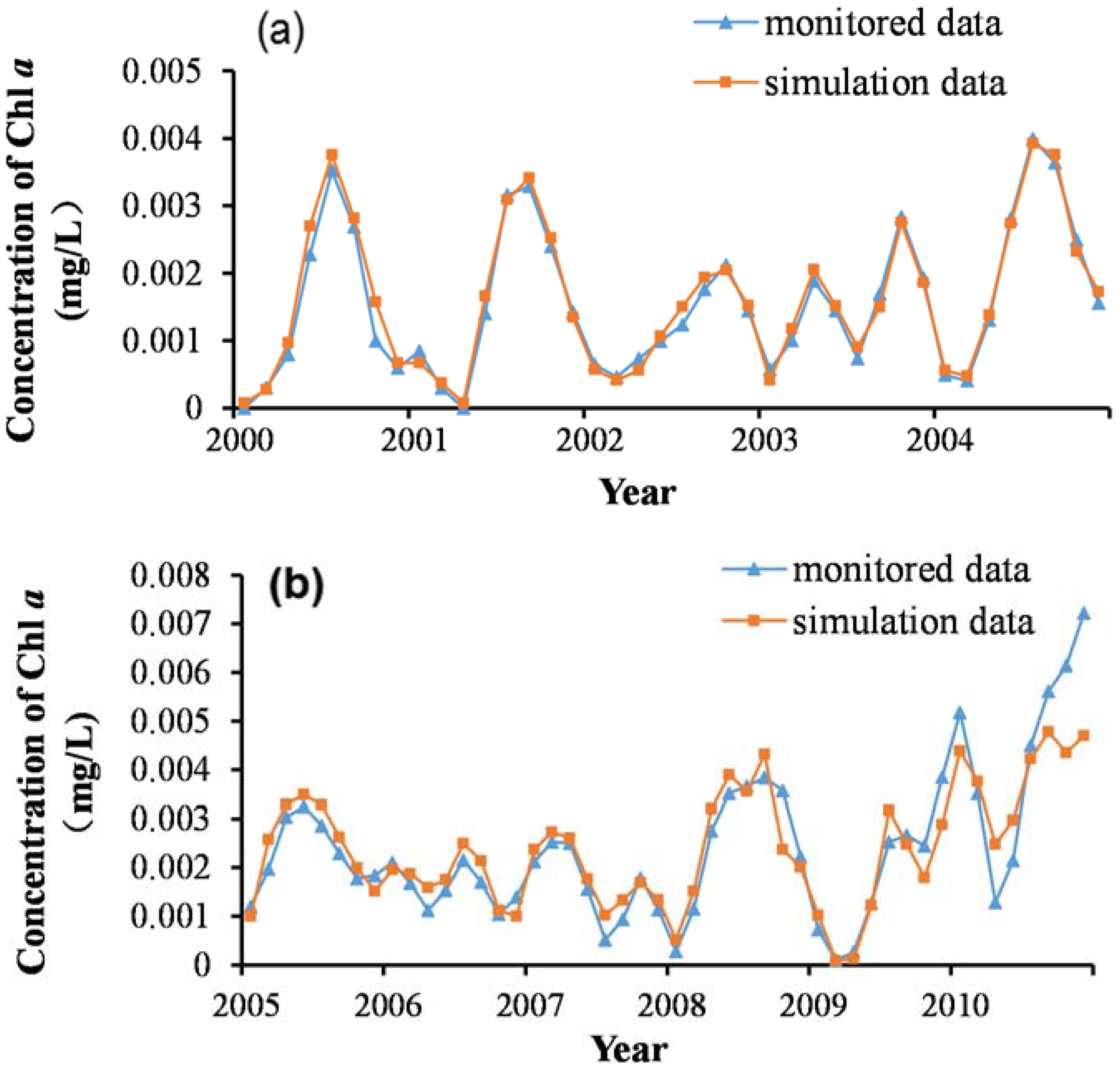
Figure 2.
Water environmental situation in Miyun Reservoir: (a) Concentration of chlorophyll a; (b) TP concentration; (c) TN concentration; (d) CODMn concentration; (e) reservoir storage; and (f) water level.
Figure 2.
Water environmental situation in Miyun Reservoir: (a) Concentration of chlorophyll a; (b) TP concentration; (c) TN concentration; (d) CODMn concentration; (e) reservoir storage; and (f) water level.
3. Methods
Originally proposed in 1985 by Cortes and Vapnik, the SVM algorithm was widely used to solve highly nonlinear classification and regression problems with good generalizability [
24]. The SVM algorithm can be easily applied to other machine learning problems such as function fitting. It is based on the VC dimension theory and the structure risk minimum principle of the statistical learning theory. By seeking the best compromise among the complexities in the model with a limited sample (
i.e., learning accuracy of particular training samples) and learning ability (
i.e., learning ability to identify random sample), the SVM algorithm can achieve the best generalization ability. There are many meteorological and hydrological parameters that influence chlorophyll
a. To avoid blindness in selecting the input vector during the process of chlorophyll
a prediction, this study firstly took feature selection to determine the best input vectors of prediction model with the GA, and then constructed the SVM model with a simplified model structure to achieve the purpose of improving prediction accuracy.
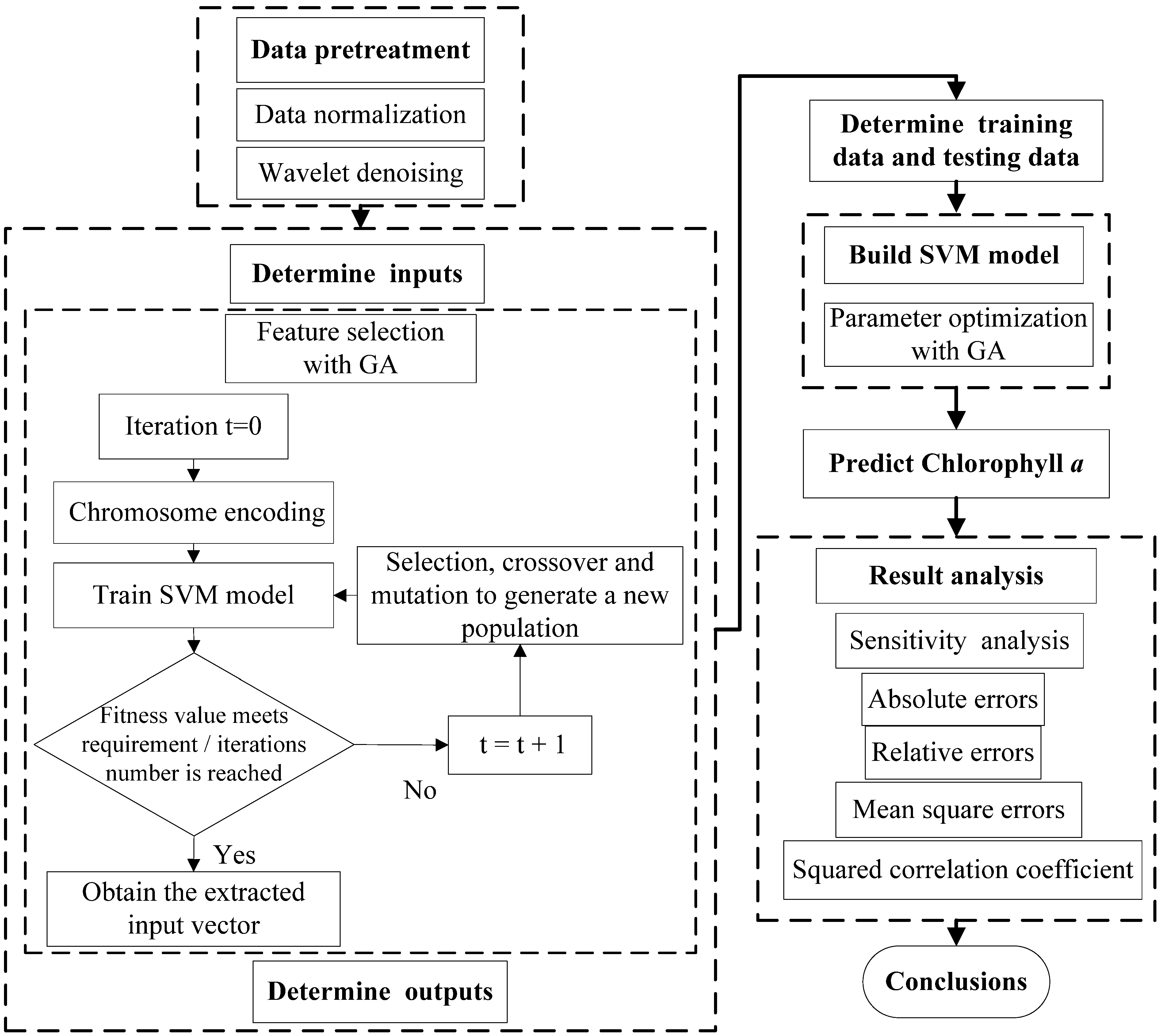
3.1. The Flow Chart for Developing a Simplified Structural GA-SVM Hybrid Model
The penalty factor and kernel function parameters of the SVM model may directly influence simulation results. This study developed a SVM model by using the GA to optimize the input parameters in the SVM model and extract feature parameters with the aim of simplifying the model structure. The flow chart of the simplified structural SVM model based on the GA is shown in
Figure 3. After data pre-treatment, the input and output vectors were determined, and the sample set was divided into a training data set and a testing data set. The GA was applied to optimizing the parameters of the SVM model and extracting input vectors. The SVM model was trained and calibrated with optimal parameters, then used to predict chlorophyll
a in the water. This study applies the LIBSVM software package developed by Lin Chih-Jen
et al., of Taiwan University to run the program on the MATLAB platform [
25].
Figure 3.
The flow chart for developing simplified structural GA-SVM hybrid model for chlorophyll a prediction.
Figure 3.
The flow chart for developing simplified structural GA-SVM hybrid model for chlorophyll a prediction.
3.2. Construction of Chlorophyll a Prediction Model Based on the SVM Algorithm
This paper applied the principle of the SVM algorithm to establish a prediction model for chlorophyll
a in the Miyun Reservoir. The basic principle of the SVM algorithm was to first select a nonlinear mapping algorithm as a kernel function, through which the input vectors were mapped into a high dimensional feature space, and in this space simpler linear regressions can replace complex nonlinear regressions of the original input space [
26]. Then an optimal decision function was produced in the feature space to realize the nonlinear decision function of the original input space, and finally the linear learning method can be applied to solve the classification and regression problems in the input space. This process can be expressed as:
where
y is the output,
yR;
x is the input vector,
xR
n;
w is the matrix of the regression weight vector;
is a non-linear function by which
x is mapped into a high dimensional feature space;
b is a bias; and
b and
w can be obtained with Equation (3). In the mapping process, a kernel function
can be constructed by
. Therefore, we only need to replace the
x or
xi of the original space with
or
, while it is not necessary to know the explicit expression of nonlinear mapping
. In this study, we selected radial basis function (RBF) as the kernel function:
where
xi is the input vector,
xR
n; and γ is the parameter of the RBF kernel function.
In Equation (1), the concentration of chlorophyll a in reservoir water was selected as y in the SVM model, whereas other water quality factors, hydrological factors, and meteorological factors were selected as x in the SVM model. In this way, the concentration of chlorophyll a was predicted based on the other factors. To solve Equation (1), the following regularized risk function (i.e., Equation (3)) was used. These constraints ensured the regression errors of the samples being within the area that was delineated by the error tolerance and the slack variables. Equation (3) can be solved with the Lagrange technique.
Minimize
subject to
where
C is a penalty parameter that determines the penalty degree for the sample classification errors in the optimization problem;
N is the number of the samples of
;
and
are slack variables that penalize training errors by the loss function over the error tolerance (ε);
represents the upper training errors subject to
;
represents the lower training errors subject to ε;
and
can be calculated with Equation (3); and was normally set to 0.001.
Overall, the chlorophyll a simulation with the SVM model depended on the ability to learn the nonlinear causality between the historical data of the concentration of chlorophyll a and its influencing factors (i.e., other water quality factors, hydrological factors, and meteorological factors). The modeling process for the SVM model was introduced below.
Step 1. Determine chlorophyll
a as the output value of the prediction model, with the other indicators as input values:
where
S is reservoir storage,
WI is inflow,
W0 is outflow,
L is water level,
TP is the concentration of total phosphorus in water,
TN is total nitrogen in water,
CODMn is permanganate index in water,
DO is the dissolved oxygen concentration in water,
TW is water temperature,
pH is hydrogenion concentration of water,
SD is water transparency,
TA is temperature, and
P is precipitation.
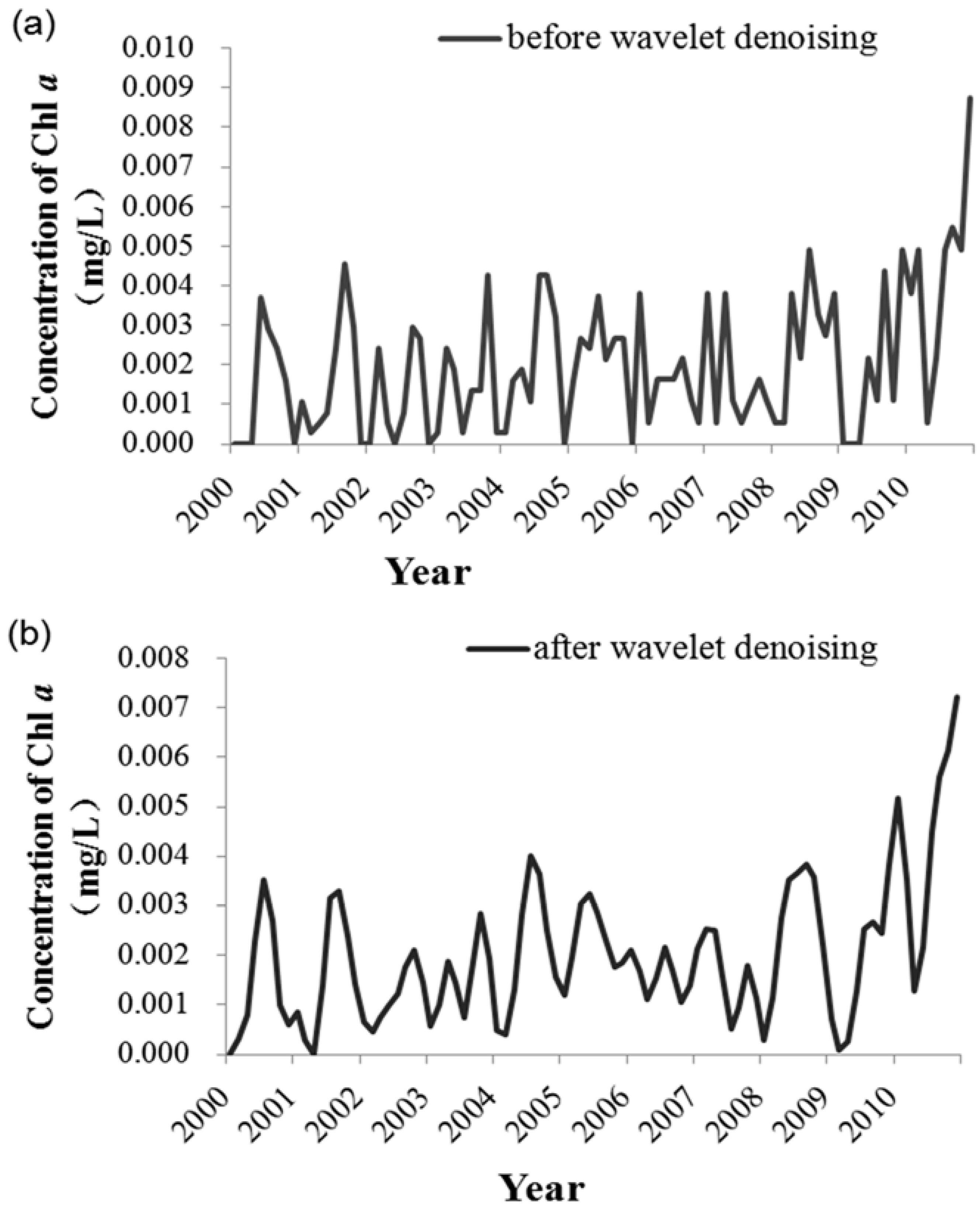
Step 2. Before establishing the SVM model, to extract useful information in the original data and determine the most reasonable and relevant input vectors of the prediction model, this study applied data normalization, wavelet denoising, and feature selection for the data pre-treatment in the MATLAB software. To test the prediction ability of the SVM model, the sample set was divided into separate training and testing sets. Data between 2000 and 2004 were used as the training set, and those between 2005 and 2010 as the testing set. Thus, the testing set data were independent and not used to train the model. In the parameter optimization, the initial conditions of the GA were set: the biggest evolution generation was 100, the largest population was 20, the gap of genetic algorithm was 0.9, and the k-fold cross-validation number was 5.
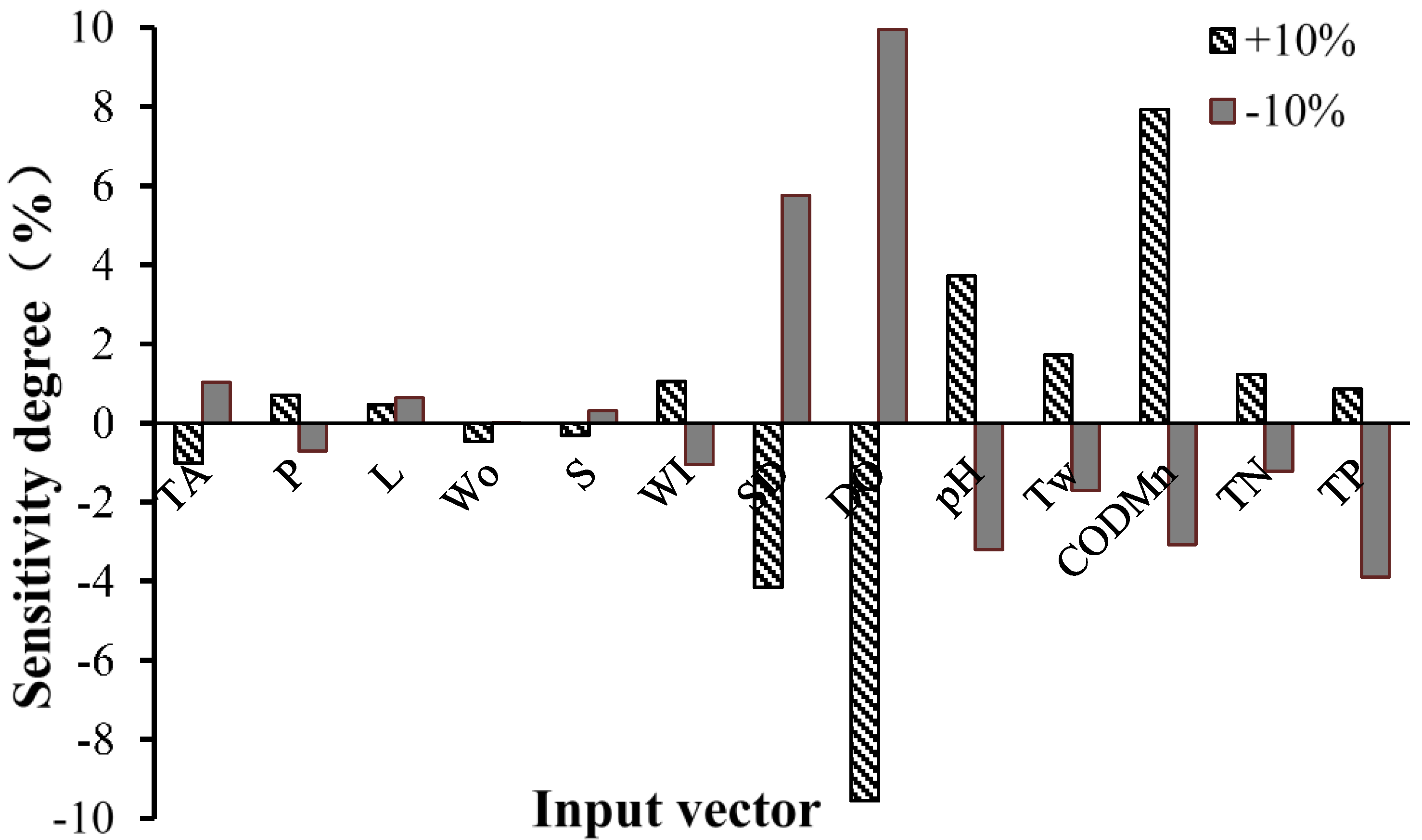
Step 3. To determine the effect of each input indicator to the prediction model, we carried out sensitivity analysis of the chlorophyll a prediction model. The analysis method was to change a particular input variable (increase or decrease by 10%) while the other input variables remained fixed and then applied the established SVM model to re-predict; the variable of the sensitivity model was obtained by calculating the relative changes in chlorophyll a with the output value.
Step 4. To eliminate the irrelevant and redundant information hidden in the time series of high dimensional feature vectors, and reveal the more representative features that influenced the concentration of chlorophyll a in the Miyun Reservoir, we applied feature selection to the input vectors of the SVM model for chlorophyll a simulation by using the GA. Subsequently, we established the hybrid SVM model using the extracted feature vectors and improved prediction accuracy, generalization ability, and efficiency.
3.3. Feature Selection and Parameter Optimization Based on Genetic Algorithm Optimization
The feature means each attribute of the data set. Too many features will increase the complexity of the work, while the accuracy of data mining may not be improved. To pick out the most representative and effective feature vectors of the chlorophyll
a prediction model, we used the GA for feature selection. In addition, considering that the SVM model did not provide a method for selecting the parameter in the RBF kernel function and the penalty parameter (C), we used the GA for optimizing these two parameters in the SVM model. The principle of the GA is based on a specific operation for the structure of objectives, according to a predefined criteria function, to improve the new population by comparing it with the original one. In the process of generation, proper coding was used and the operator was applied to imitate the path of natural selection. Reproduction, crossover, and mutation were taken to operators in the current population [
27]. Procedures of feature selection and parameter optimization with applications of the GA were as follows.
Step 1. Chromosome encoding. In the selection and optimization process, the iterations were set to zero. Chromosomes were encoded with binary coding. Each operator was composed of N codes, where N is the number of characteristic vectors or SVM parameters that need to be optimized. When a number in the operator was 1, it represented the characteristic vector and the parameter was selected; otherwise it was not selected, and the initial population was generated randomly.
Step 2. Evaluation of the fitness function value. Determine the square of the root mean square error in the training phase as the objective function for the fitness value. Then, calculate the fitness function value of the current generation. Choose a certain adaptation level, retaining the individuals whose fitness function value is greater than the adaptation level; these individuals compose the next generation.
Step 3. Selection, crossover and mutation of operators. Apply genetic operation of selection, crossover, and mutation to individuals in the group; the next generation was produced after the genetic optimization.
Step 4. Termination judgment. If the iteration number was greater than the set value, or the accuracy of the fitness function value reached the expected value, then terminate the iteration [
28]. The extracted features and the optimal model parameters were then determined.
3.4. Model Calibration
In order to analyze the performance of the model, four indicators—The absolute error (AE), relative error (RE), root mean square error (RMSE), and square of correlation coefficient (
R2)—Were selected to evaluate the fit and prediction effect of the model. AE represented the deviation between monitoring and prediction values, and RE was the ratio of AE and monitoring values, reflecting the objective accuracy of measurement results. RMSE reflected the performance of the prediction model,
i.e., generally, the smaller the RMSE the better the performance.
R2 represented the degree of linear relevance among the variables,
i.e., the closer
R2 was to 1 the higher the relevance. The expressions of these four indicators were as follows:
where
yi is the real value of the data set,
is prediction value,
is the average of the original data, and
n is the amount of data for the testing set.
5. Conclusions
A GA-based SVM model for predicting the monthly concentration of chlorophyll a of the Miyun Reservoir was constructed. We firstly carried out a sensitivity analysis of the prediction model, and identified that the concentration of chlorophyll a had great sensitivity to seven input indicators. With the GA being used for the removal of redundant features and the feature selection of input vectors, the four most relevant influence factors of chlorophyll a (i.e., total phosphorus, total nitrogen, permanganate index, and reservoir storage) were screened as new input vectors, which were consistent with the results of the sensitivity analysis. With these new input vectors, the prediction model had simpler structure and better prediction accuracy than the model without the feature selection. Due to the stronger correlation of the input vector structure, the simplified GA-SVM model showed improved calibration and prediction ability. This proved that the SVM prediction model was sensitive to the structure of the input variables. In brief, this study proposed an intelligent algorithm for predicting the concentration of chlorophyll a of the reservoir water, which provided an effective tool for the management of reservoirs, especially for an early warning of eutrophication. Besides, this model could solve practical problems with different nutritional load conditions, and its applications can be extended to other reservoirs. In future research, the interaction mechanism of influence factors should be further considered to optimize the parameters used in the developed hybrid model of GA-SVM algorithm to get more reliable results for the prediction of chlorophyll a, and empirical models will be explored to get better application performance in chlorophyll a prediction.