Performance Evaluation for a Contamination Detection Method Using Multiple Water Quality Sensors in an Early Warning System
Abstract
:1. Introduction
2. Materials and Methods
2.1. Pilot-Scale Contaminant Injection and Monitoring System
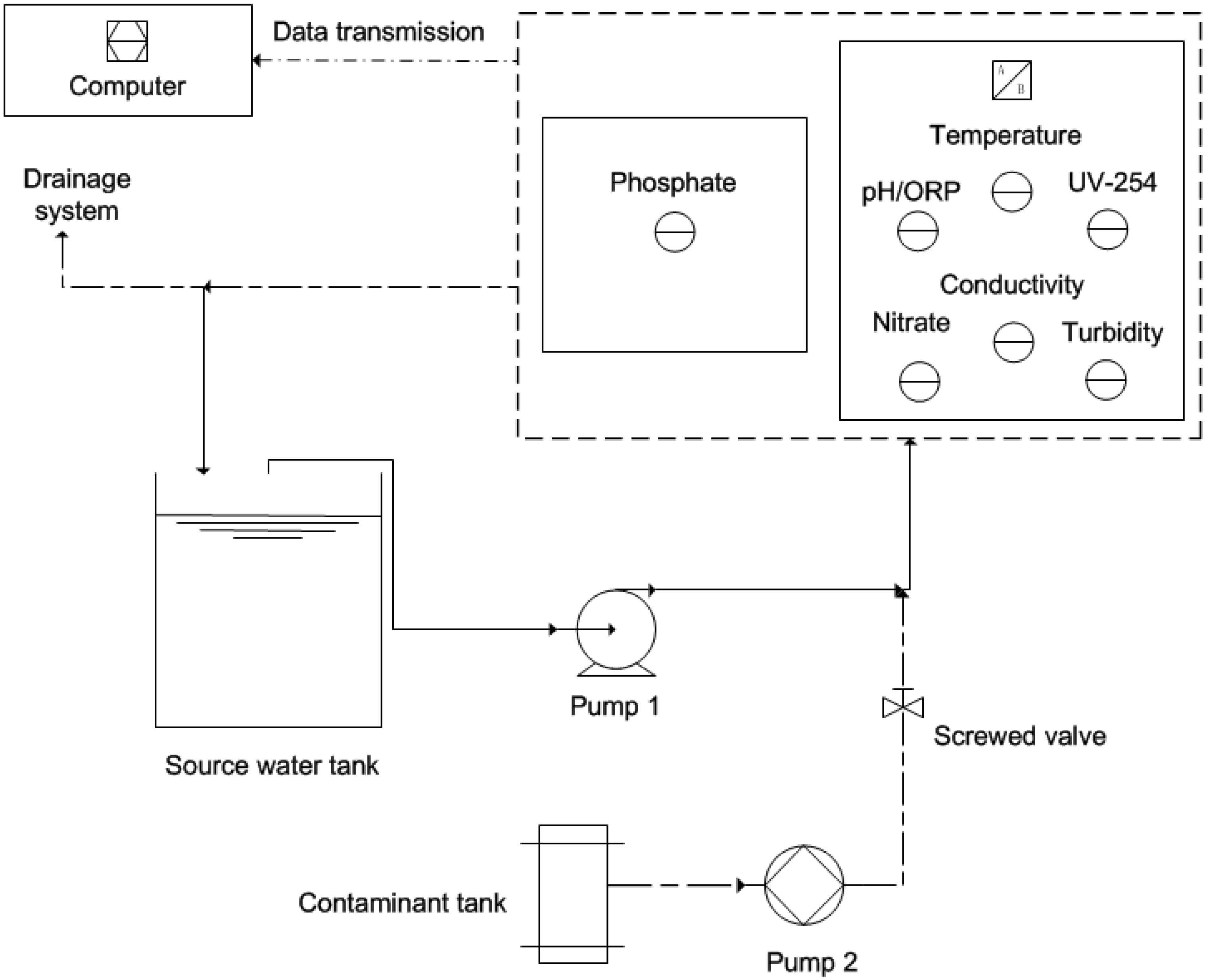
2.2. Sensors Investigated
| Parameter | Sensor Name | Measuring Range | Sensitivity | Measuring Interval |
|---|---|---|---|---|
| Temperature | DPD1R1-WDMP | −10–50 °C | ±0.01 °C | 1 min |
| pH | DPD1R1-WDMP | −2.00–14.00 | ±0.01 | 1 min |
| Turbidity | LXV423.99.10100 | 0.001–4,000 NTU | ±0.001 NTU | 1 min |
| Conductivity | D3725E2T-WDMP | 0–2,000,000 us/cm | ±1 us/cm | 1 min |
| ORP | DRD1R5-WDMP | −1,500–1,500 mV | ±0.5 mV | 1 min |
| UV-254 | LXG418.99.20000 | 0.01–60 1/m | ±0.01 1/m | 1 min |
| Nitrate | LXG.717.99.50000 | 0.1–100.0 mg/L | ±0.1 mg/L | 1 min |
| Phosphate | LXV422.99.20102 | 0.05–15 mg/L | ±0.05 mg/L | 5 min |
2.3. Contaminants Investigated
2.4. Experimental Procedure
2.5. Detection Method
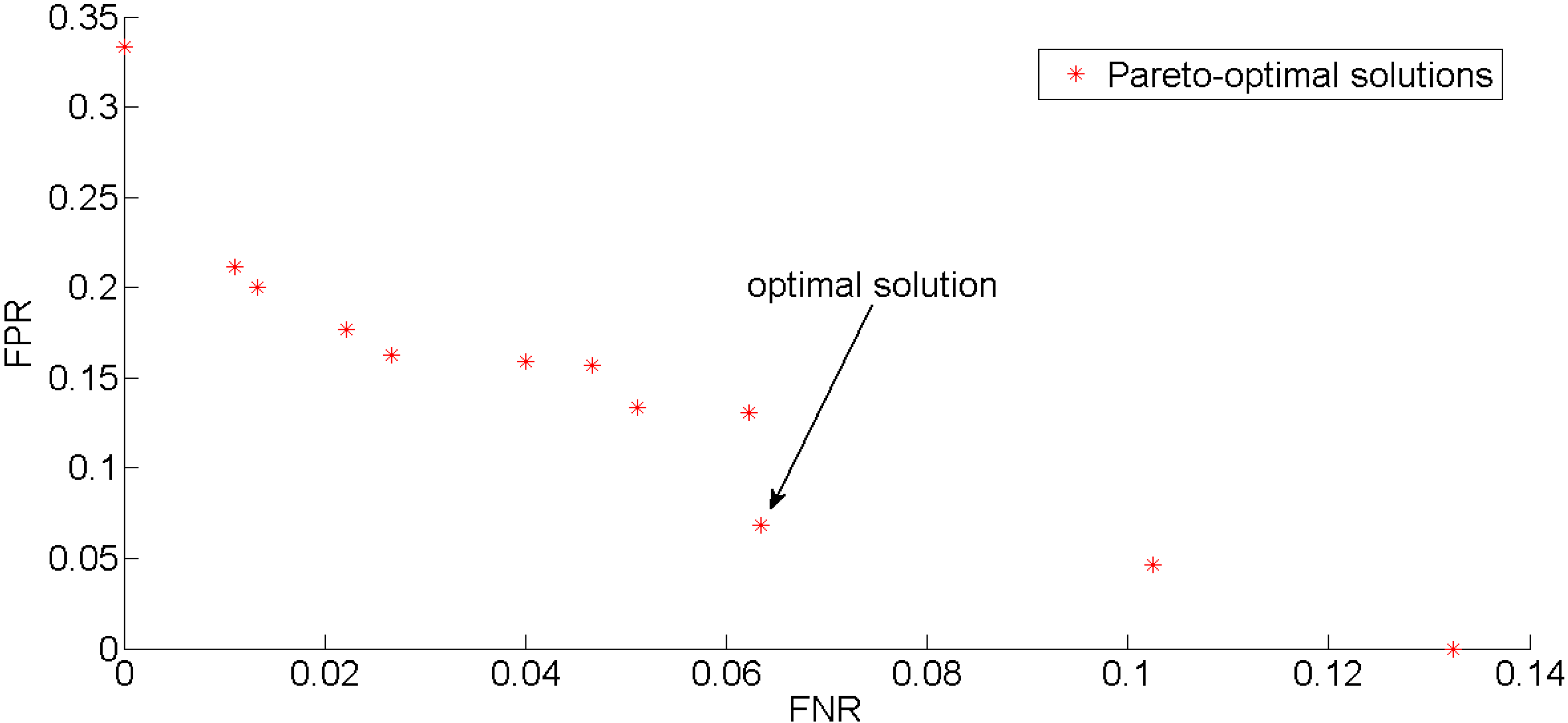
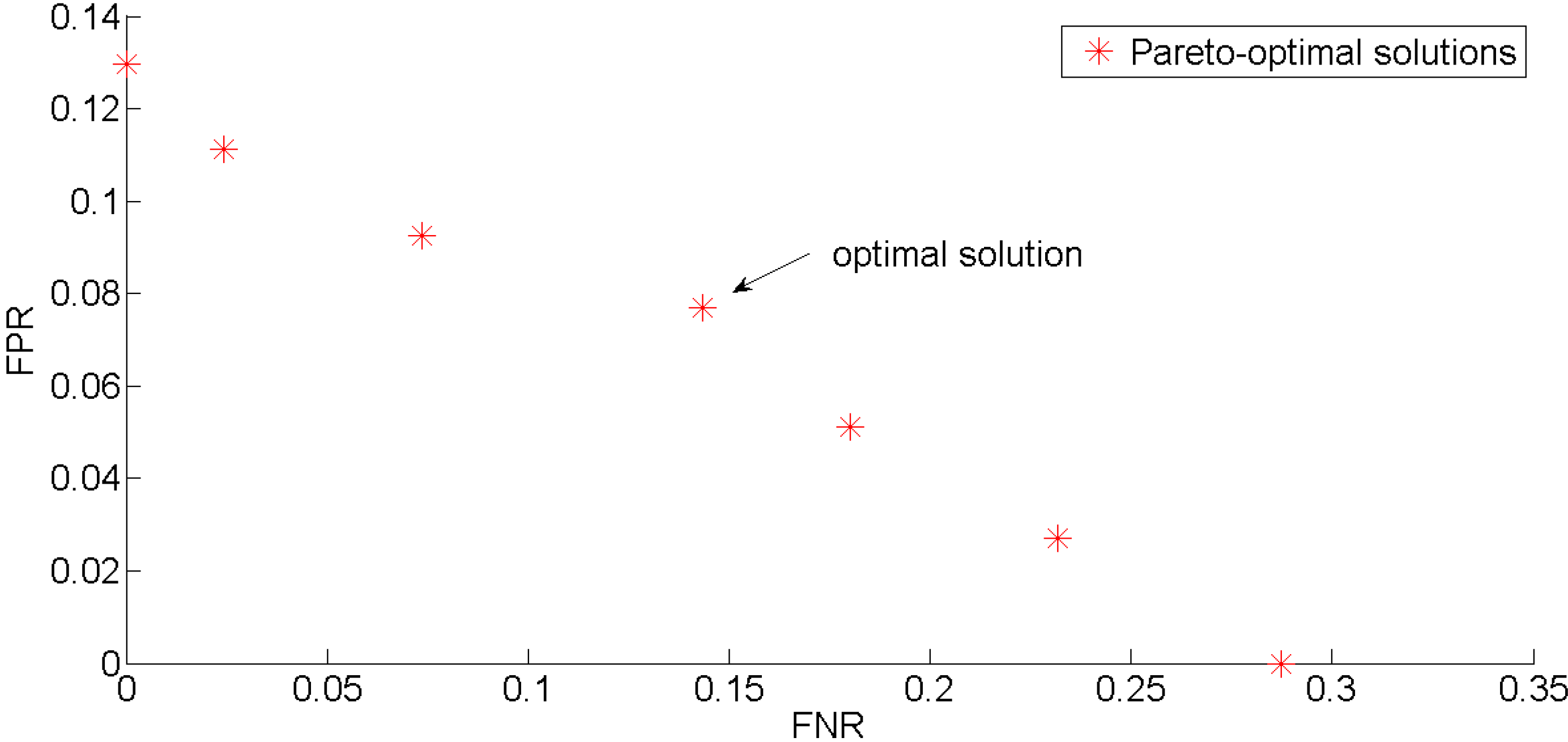
2.6. Parameter Optimization and Validation
| Parameter Name | Value |
|---|---|
| Population | 250 |
| Generation number | 200 |
| Crossover rate | 0.85 |
| Mutation rate | 0.05 |
3. Results and Discussion
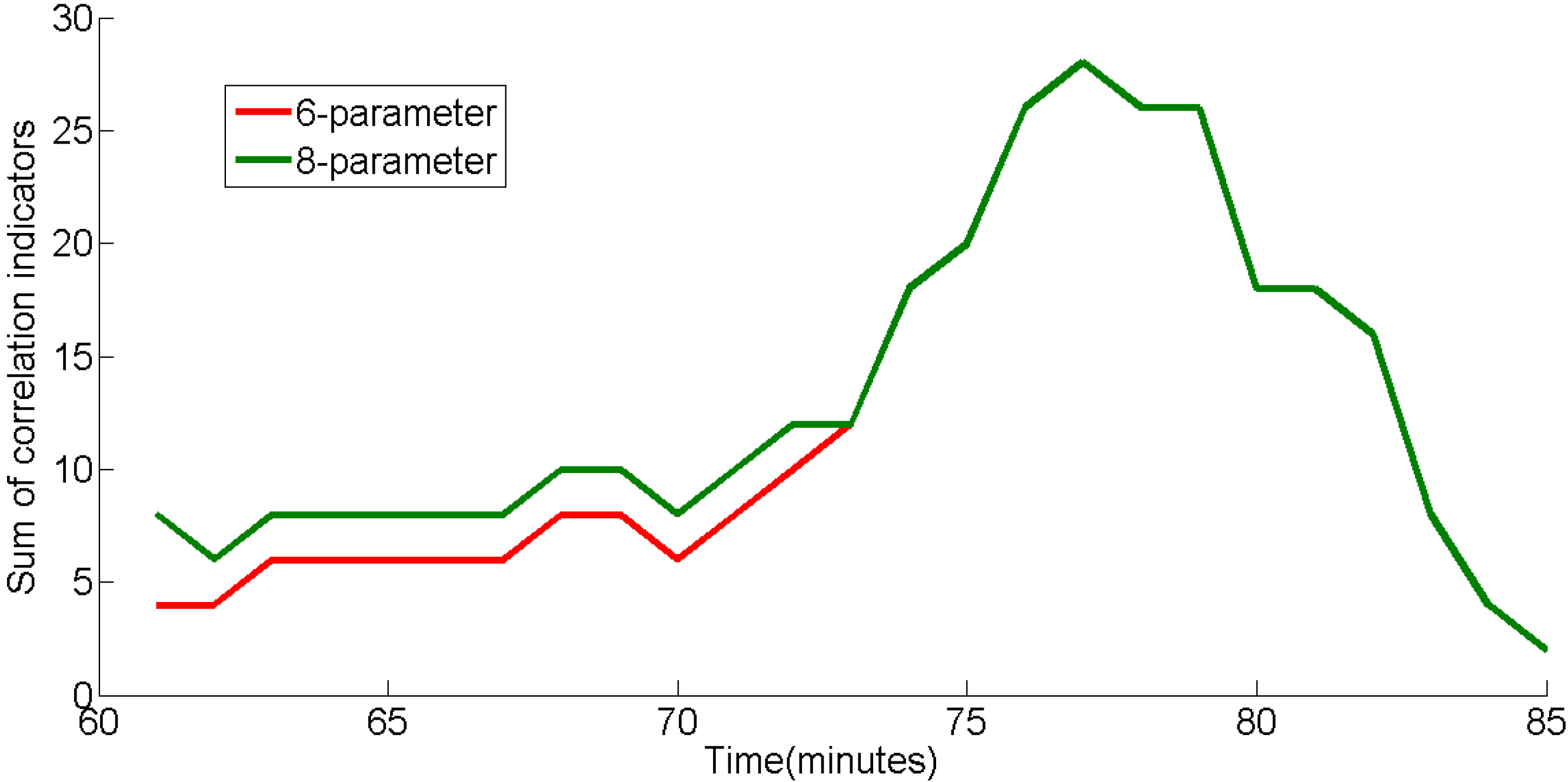
3.1. Correlative Responses
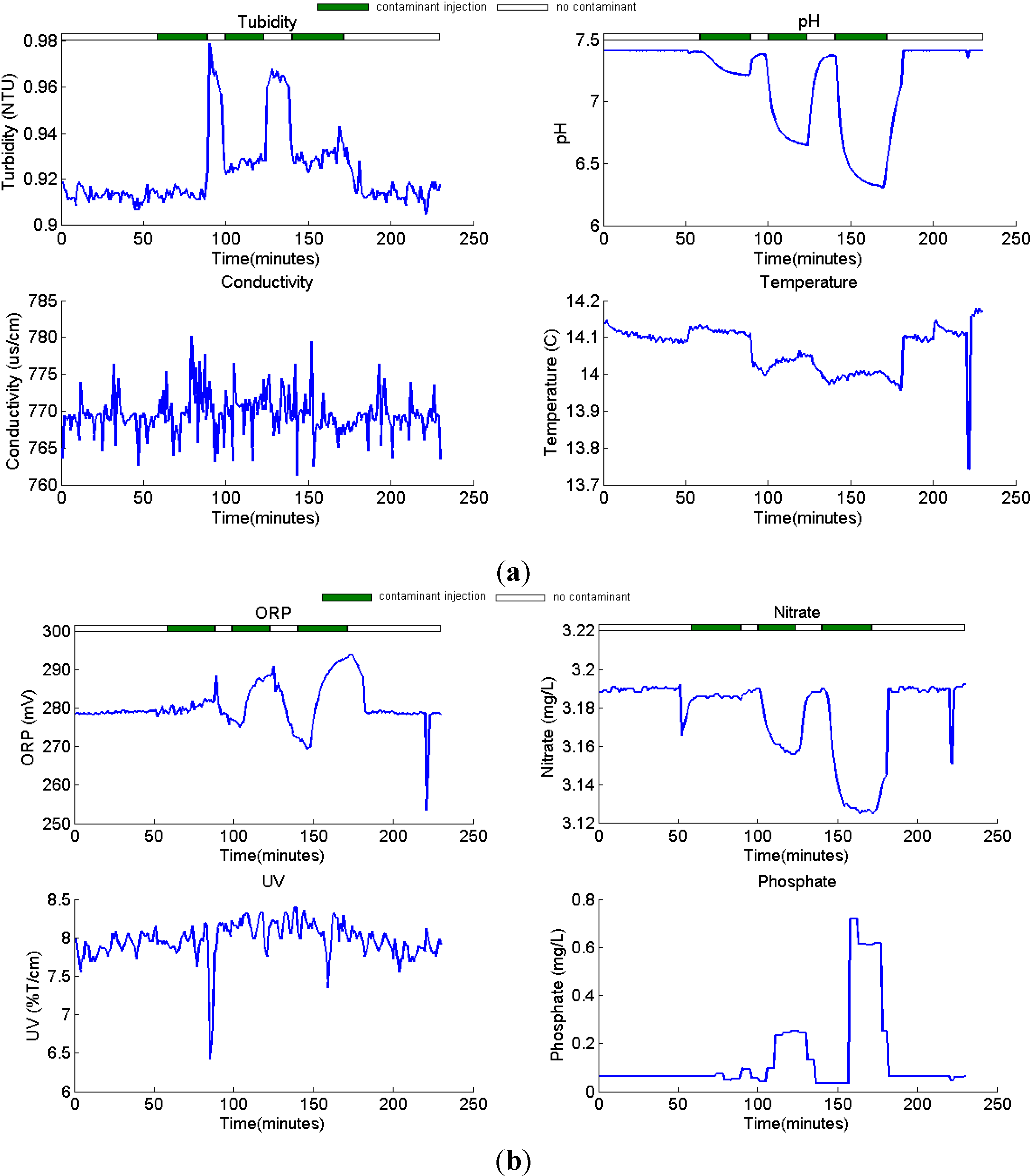
3.2. Parameter Optimization and Validation
| 8-Sensor | Glyphosate-A | Glyphosate-B | ||||
|---|---|---|---|---|---|---|
| Concentration | 0.8 mg/L | 2.0 mg/L | 4.0 mg/L | 0.8 mg/L | 2.0 mg/L | 4.0 mg/L |
| TPR | 88.0% | 96.3% | 96.7% | 95.5% | 100.0% | 100.0% |
| FPR | 6.8% | 6.8% | 6.8% | 0.0% | 0.0% | 0.0% |
3.3. Sensors Selection
| Sensor Name | Turbidity | pH | Conductivity | Temperature | ORP | Nitrate | UV | Phosphate |
|---|---|---|---|---|---|---|---|---|
| Turbidity | 1.000 | −0.447 | −0.024 | 0.383 | 0.618 | −0.424 | −0.068 | 0.313 |
| pH | −0.447 | 1.000 | −0.093 | −0.704 | −0.947 | 0.832 | −0.302 | −0.625 |
| Conductivity | −0.024 | −0.093 | 1.000 | 0.167 | −0.015 | 0.094 | −0.091 | 0.021 |
| Temperature | 0.383 | −0.704 | 0.167 | 1.000 | 0.688 | −0.718 | 0.164 | 0.443 |
| ORP | 0.618 | −0.947 | −0.015 | 0.688 | 1.000 | −0.781 | 0.216 | 0.544 |
| Nitrate | −0.424 | 0.832 | 0.094 | −0.718 | −0.781 | 1.000 | −0.399 | −0.732 |
| UV | −0.068 | −0.302 | −0.091 | 0.164 | 0.216 | −0.399 | 1.000 | 0.274 |
| Phosphate | 0.313 | −0.625 | 0.021 | 0.443 | 0.544 | −0.732 | 0.274 | 1.000 |
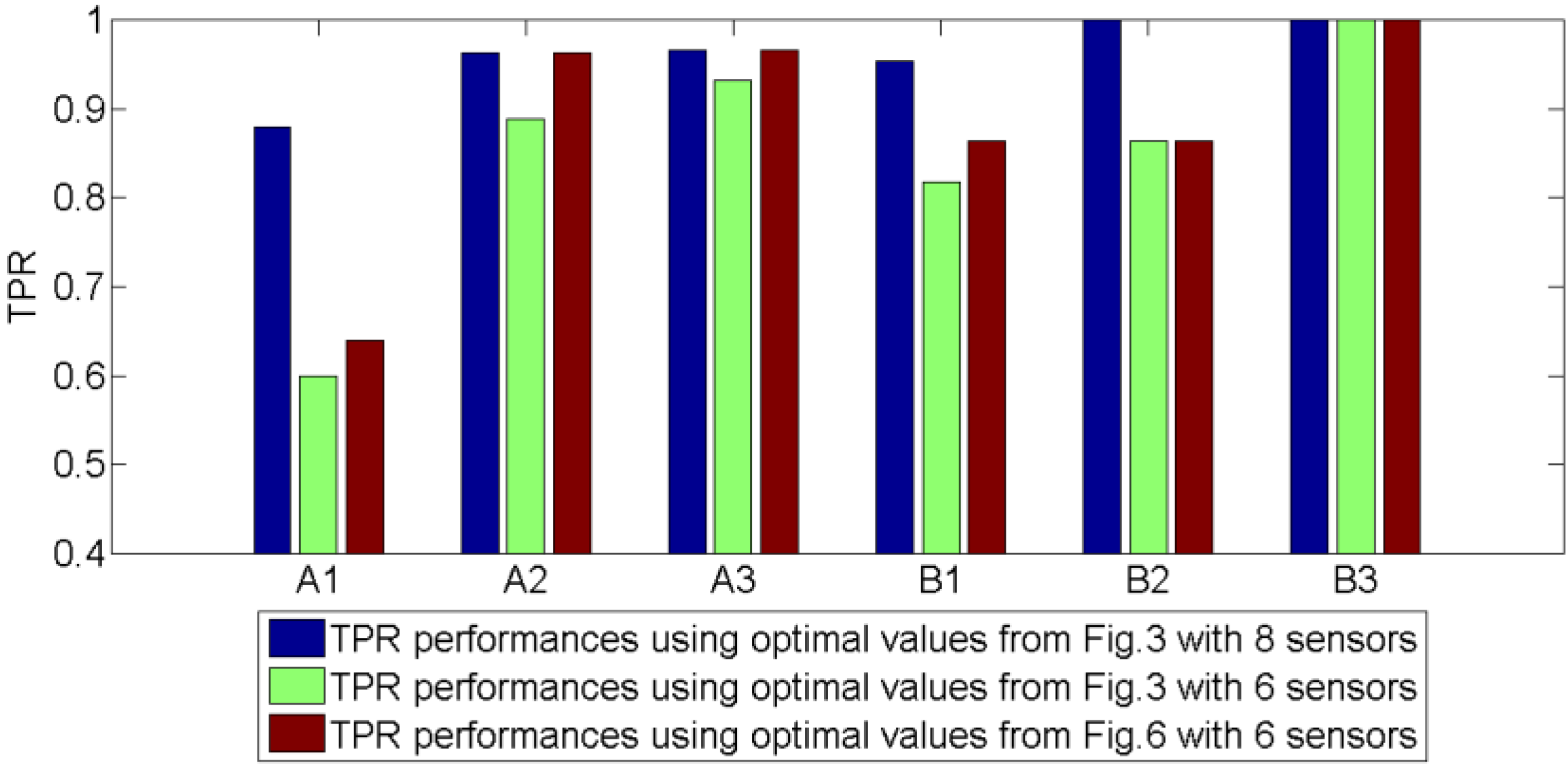
| 6-Sensor | Glyphosate-A | Glyphosate-B | ||||
|---|---|---|---|---|---|---|
| Concentration | 0.8 mg/L | 2.0 mg/L | 4.0 mg/L | 0.8 mg/L | 2.0 mg/L | 4.0 mg/L |
| TPR | 64.0% | 96.3% | 96.7% | 86.4% | 86.4% | 100.0% |
| FPR | 7.6% | 7.6% | 7.6% | 0.0% | 0.0% | 0.0% |
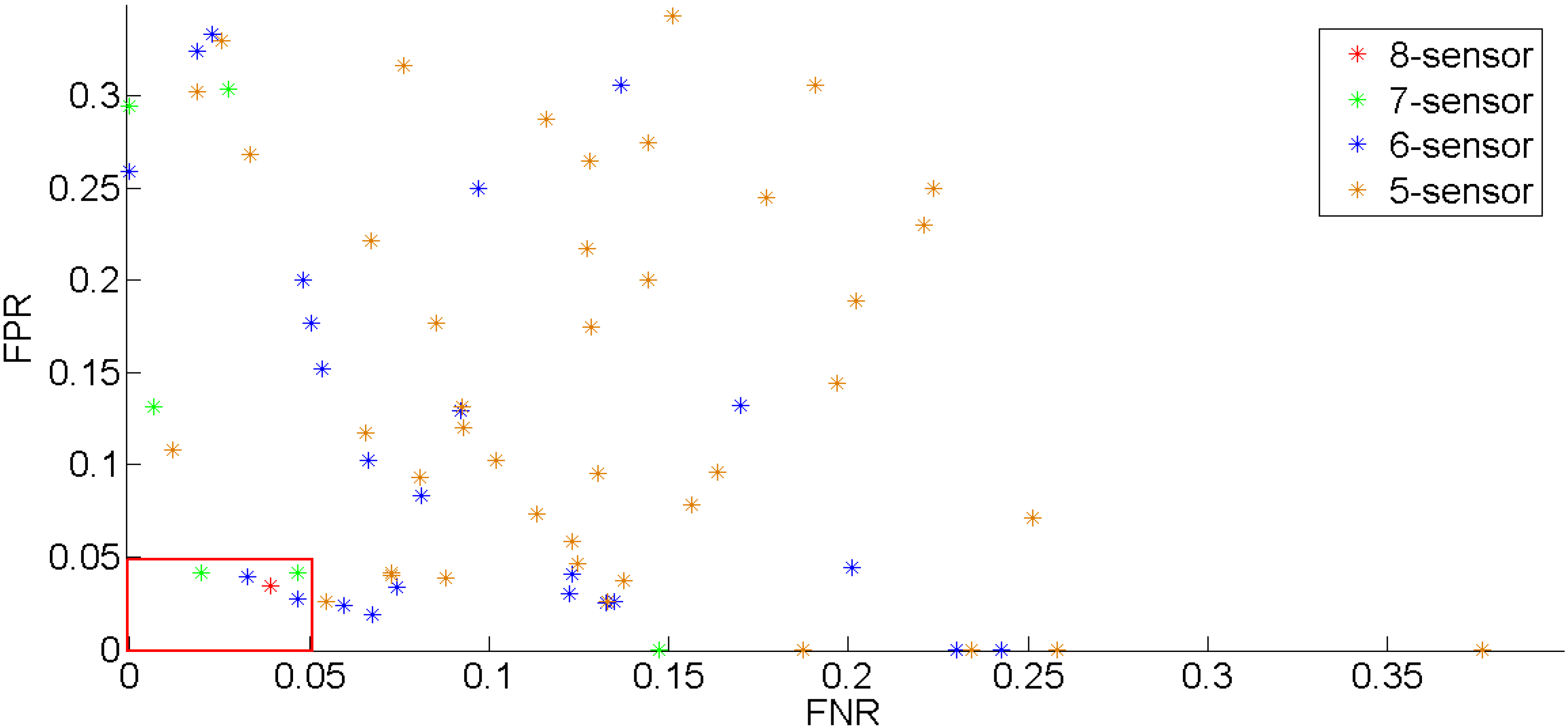
| Number of Sensors | Sensor Names |
|---|---|
| 7 | Turbidity, pH, conductivity, temperature, ORP, nitrate, UV-254 |
| 7 | Turbidity, pH, Conductivity, ORP, Nitrate, UV-254, Phosphate |
| 6 | Turbidity, pH, Conductivity, ORP, Nitrate, Phosphate |
| 6 | Turbidity, pH, Temperature, ORP, Nitrate, Phosphate |
| 5 | Turbidity, pH, ORP, Nitrate, Phosphate |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gullick, R.W.; Grayman, W.M.; Deininger, R.; Males, R.M. Design of early warning monitoring systems for source waters. J. Am. Water Work. Assoc. 2003, 95, 58–72. [Google Scholar]
- Storey, M.V.; van der Gaag, B.; Burns, B.P. Advances in on-line drinking water quality monitoring and early warning systems. Water Res. 2011, 45, 741–747. [Google Scholar] [CrossRef] [PubMed]
- Hasan, J.; States, S.; Deininger, R. Safeguarding the security of public water supplies using early warning systems: A brief review. J. Contemp. Water Res. Educ. 2004, 129, 27–33. [Google Scholar] [CrossRef]
- Hawkins, P.R.; Novic, S.; Cox, P.; Neilan, B.A.; Burns, B.P.; Shaw, G.; Wickramasinghe, W.; Peerapornpisal, Y.; Ruangyuttikarn, W.; Itayama, T.; et al. A review of analytical methods for assessing the public health risk from microcystin in the aquatic environment. J. Water Supply Res. Technol. 2005, 54, 509–518. [Google Scholar]
- Henderson, R.K.; Baker, A.; Murphy, K.R.; Hamblya, A.; Stuetz, R.M.; Khan, S.J. Fluorescence as a potential monitoring tool for recycled water systems: A review. Water Res. 2009, 43, 863–881. [Google Scholar] [CrossRef] [PubMed]
- Marshall, C.P.; Leuko, S.; Coyle, C.M.; Walter, M.R.; Burns, B.P.; Neilan, B.A. Carotenoid analysis of halophilic archaea by resonance raman spectroscopy. Astrobiology 2007, 7, 631–643. [Google Scholar] [CrossRef] [PubMed]
- Pomati, F.; Burns, B.P.; Neilan, B.A. Identification of an Na+-dependent transporter associated with saxitoxin-producing strains of the cyanobacterium anabaena circinalis. Appl. Environ. Microbiol. 2004, 70, 4711–4719. [Google Scholar] [CrossRef] [PubMed]
- De Hoogh, C.J.; Wagenvoort, A.J.; Jonker, F.; van Leerdam, J.A.; Hogenboom, A.C. Hplc-Dad and Q-TOF MS techniques identify cause of Daphnia biomonitor alarms in the River Meuse. Environ. Sci. Technol. 2006, 40, 2678–2685. [Google Scholar] [CrossRef] [PubMed]
- Jeon, J.; Kim, J.H.; Lee, B.C.; Kim, S.D. Development of a new biomonitoring method to detect the abnormal activity of Daphnia magna using automated Grid Counter device. Sci. Total Environ. 2008, 389, 545–556. [Google Scholar] [CrossRef] [PubMed]
- McKenna, S.A.; Wilson, M.; Klise, K.A. Detecting changes in water quality data. J. Am. Water Work. Assoc. 2008, 100, 74–85. [Google Scholar]
- Hall, J.; Zaffiro, A.D.; Marx, R.B.; Kefauver, P.C.; Krishnan, E.R.; Herrmann, J.G. On-Line water quality parameters as indicators of distribution system contamination. J. Am. Water Work. Assoc. 2007, 99, 66–77. [Google Scholar]
- Yang, Y.J.; Haught, R.C.; Goodrich, J.A. Real-Time contaminant detection and classification in a drinking water pipe using conventional water quality sensors: Techniques and experimental results. J. Environ. Manag. 2009, 90, 2494–2506. [Google Scholar] [CrossRef]
- Kroll, D.; King, K. The utilization on-line of common parameter monitoring as a surveillance tool for enhancing water security. Spec. Publ. R. Soc. Chem. 2006, 302, 89–98. [Google Scholar]
- Liu, S.; Che, H.; Smith, K.; Chang, T. A real time method of contaminant classification using conventional water quality sensors. J. Environ. Manag. 2015, 154, 13–21. [Google Scholar] [CrossRef]
- Hart, D.; McKenna, S.A.; Klise, K.; Cruz, V.; Wilson, M. CANARY: A water quality event detection algorithm development tool. In Proceedings of the World Environmental and Water Resources Congress, Tampa, FL, USA, 15–19 May 2007; pp. 1–9.
- Klise, K.A.; McKenna, S.A. Water quality change detection: Multivariate algorithms. In Proceedings of the Defense and Security Symposium, International Society for Optics and Photonics, Kissimmee, FL, USA, 17 April 2006.
- Allgeier, S.; Murray, R.; Mckenna, S.; Shalvi, D. Overview of Event Detection Systems for WaterSentinel; United States Environmental Protection Agency: Washington, DC, USA, 12 December 2005. [Google Scholar]
- Raciti, M.; Cucurull, J.; Nadjm-Tehrani, S. Anomaly detection in water management systems. In Critical Infrastructure Protection; Springer: Berlin/Heidelberg, Germany, 2012; pp. 98–119. [Google Scholar]
- Perelman, L.; Arad, J.; Housh, M.; Ostfeld, A. Event detection in water distribution systems from multivariate water quality time series. Environ. Sci. Technol. 2012, 46, 8212–8219. [Google Scholar] [CrossRef] [PubMed]
- Arad, J.; Housh, M.; Perelman, L.; Ostfeld, A. A dynamic thresholds scheme for contaminant event detection in water distribution systems. Water Res. 2013, 47, 1899–1908. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Che, H.; Smith, K.; Chen, L. Contamination event detection using multiple types of conventional water quality sensors in source water. Environ. Sci. Process. Impacts 2014, 16, 2028–2038. [Google Scholar] [CrossRef] [PubMed]
- Che, H.; Liu, S. Contaminant detection using multiple conventional water quality sensors in an early warning system. Procedia Eng. 2014, 89, 479–487. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Sweetapple, C.; Fu, G.T.; Butler, D. Multi-Objective optimisation of wastewater treatment plant control to reduce greenhouse gas emissions. Water Res. 2014, 55, 52–62. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhu, X.P.; Fu, G.T.; Zhou, H.C.; Wang, H. The impacts of climate change on water diversion strategies for a water deficit reservoir. J. Hydroinform. 2014, 16, 872–889. [Google Scholar] [CrossRef]
- Berardi, L.; Giustolisi, O.; Savic, D.A.; Kapelan, Z. An effective multi-objective approach to prioritisation of sewer pipe inspection. Water Sci. Technol. 2009, 60, 841–850. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.M.; Butler, D.; Brazier, R.; Heathwaite, L.; Khu, S.T. Using genetic algorithms to calibrate a water quality model. Sci. Total. Environ. 2007, 374, 260–272. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Che, H.; Liu, S.; Smith, K. Performance Evaluation for a Contamination Detection Method Using Multiple Water Quality Sensors in an Early Warning System. Water 2015, 7, 1422-1436. https://doi.org/10.3390/w7041422
Che H, Liu S, Smith K. Performance Evaluation for a Contamination Detection Method Using Multiple Water Quality Sensors in an Early Warning System. Water. 2015; 7(4):1422-1436. https://doi.org/10.3390/w7041422
Chicago/Turabian StyleChe, Han, Shuming Liu, and Kate Smith. 2015. "Performance Evaluation for a Contamination Detection Method Using Multiple Water Quality Sensors in an Early Warning System" Water 7, no. 4: 1422-1436. https://doi.org/10.3390/w7041422
APA StyleChe, H., Liu, S., & Smith, K. (2015). Performance Evaluation for a Contamination Detection Method Using Multiple Water Quality Sensors in an Early Warning System. Water, 7(4), 1422-1436. https://doi.org/10.3390/w7041422





