On Approaches to Analyze the Sensitivity of Simulated Hydrologic Fluxes to Model Parameters in the Community Land Model
Abstract
:1. Introduction
2. Methods
2.1. Site Description
2.2. Model Parameterization
2.3. Response Variables and Metrics
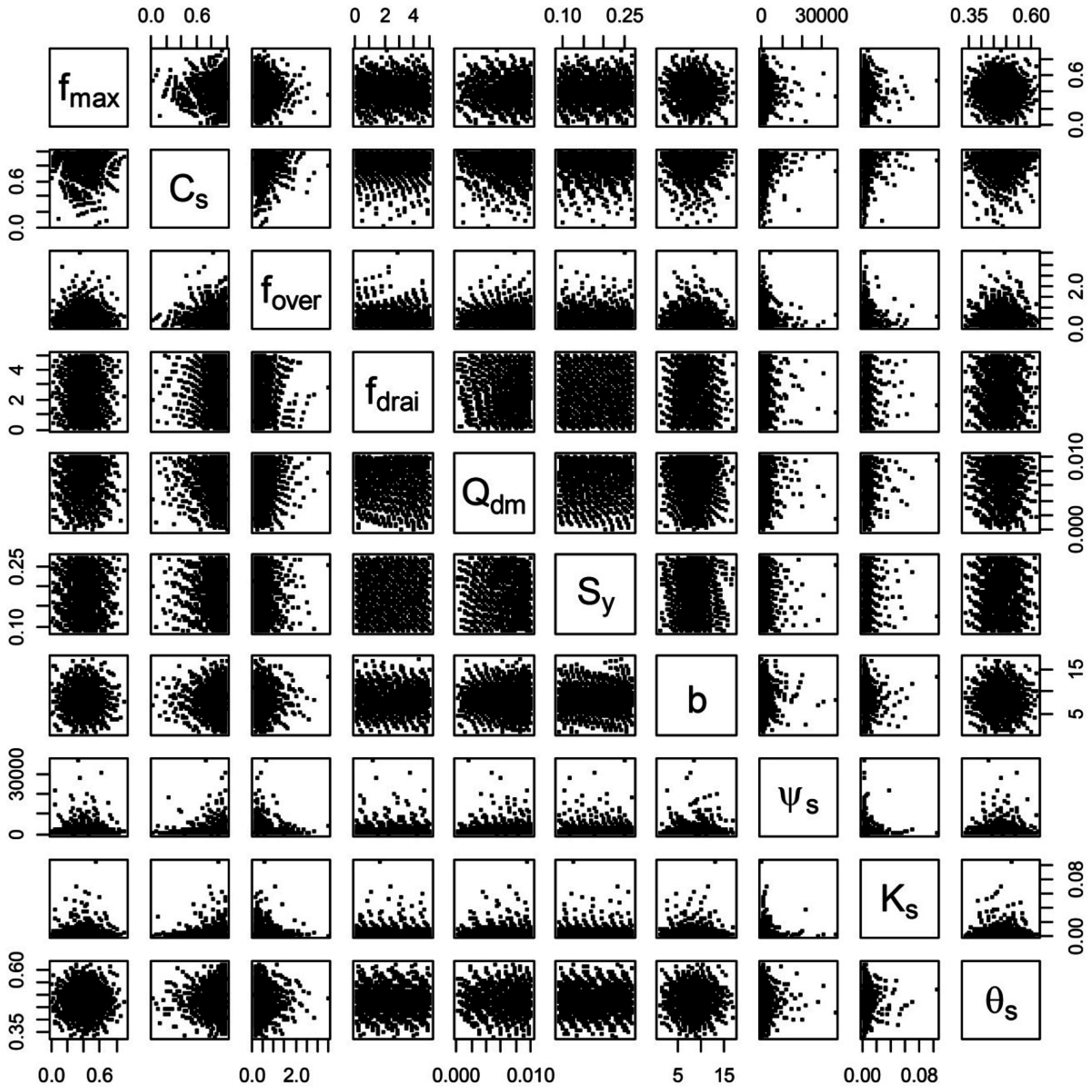
2.4. Effective Sampling and Sensitivity Analysis Methods
2.4.1. Sampling Methods
2.4.2. Sensitivity Analysis Approaches
ANOVA Based on GLM
GCV Based on the MARS Model
SRC Based on the LM
ANOVA Based on SVM
3. Results and Discussion
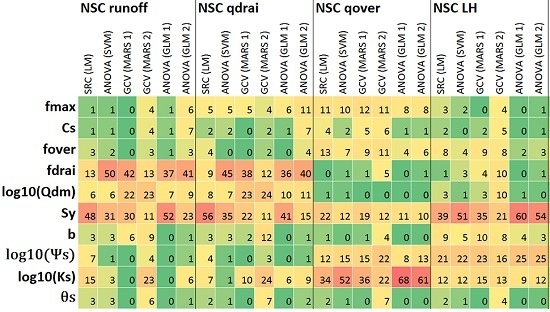
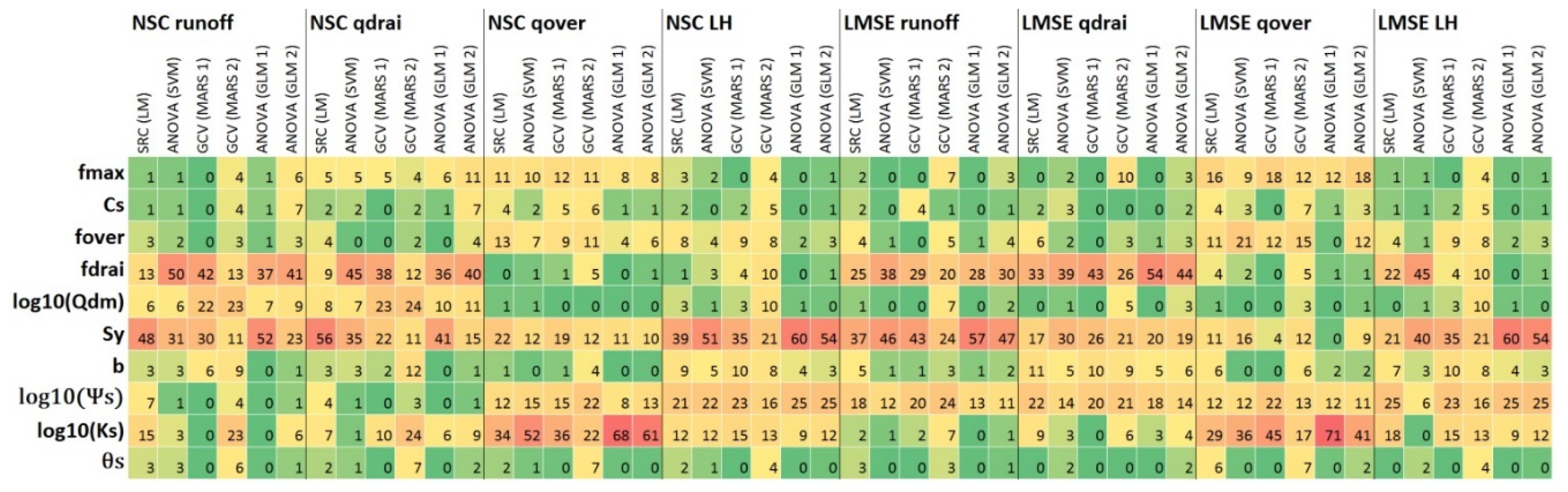
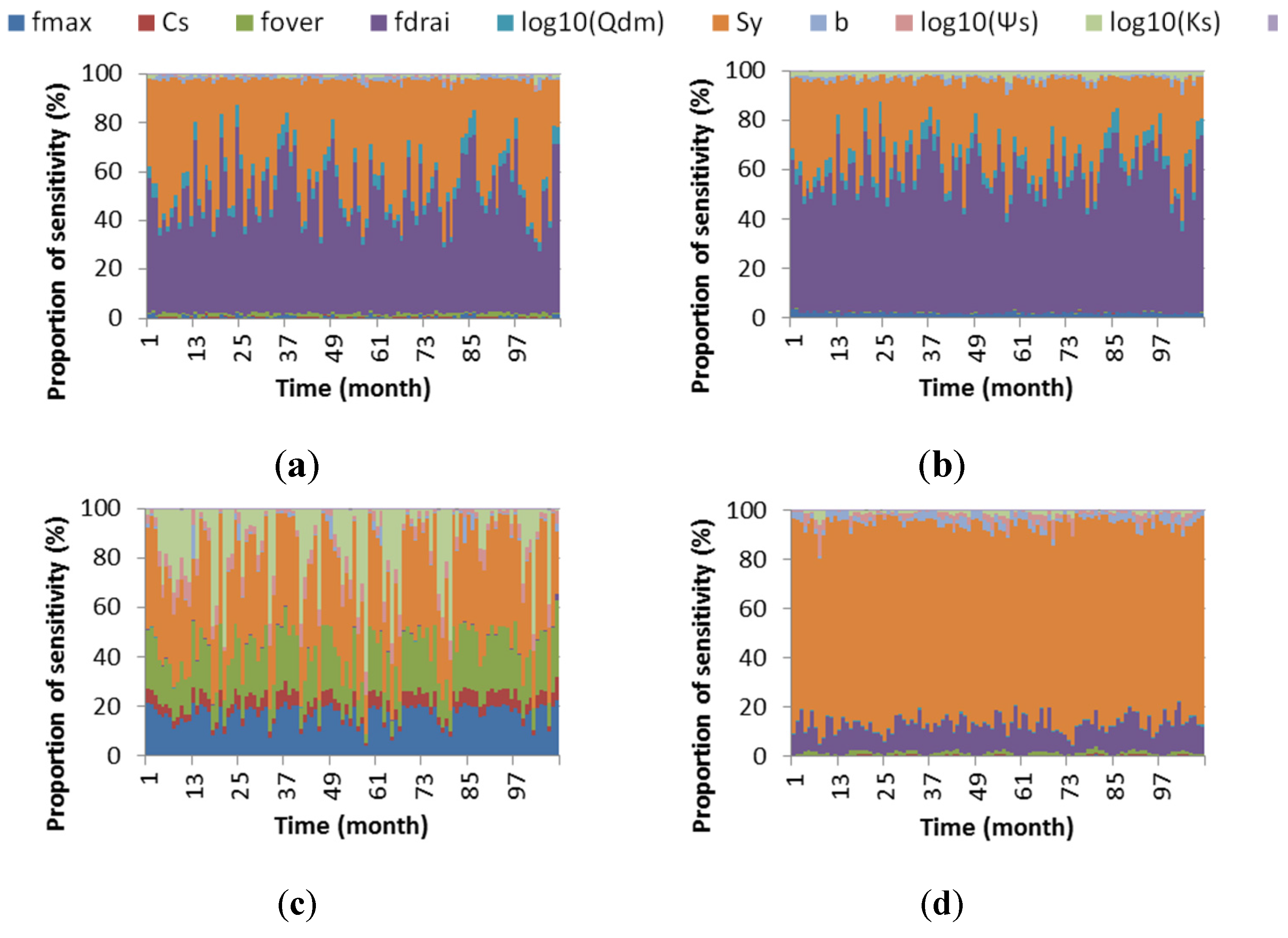
3.1. Effects of Choices of Response Variables/Metrics
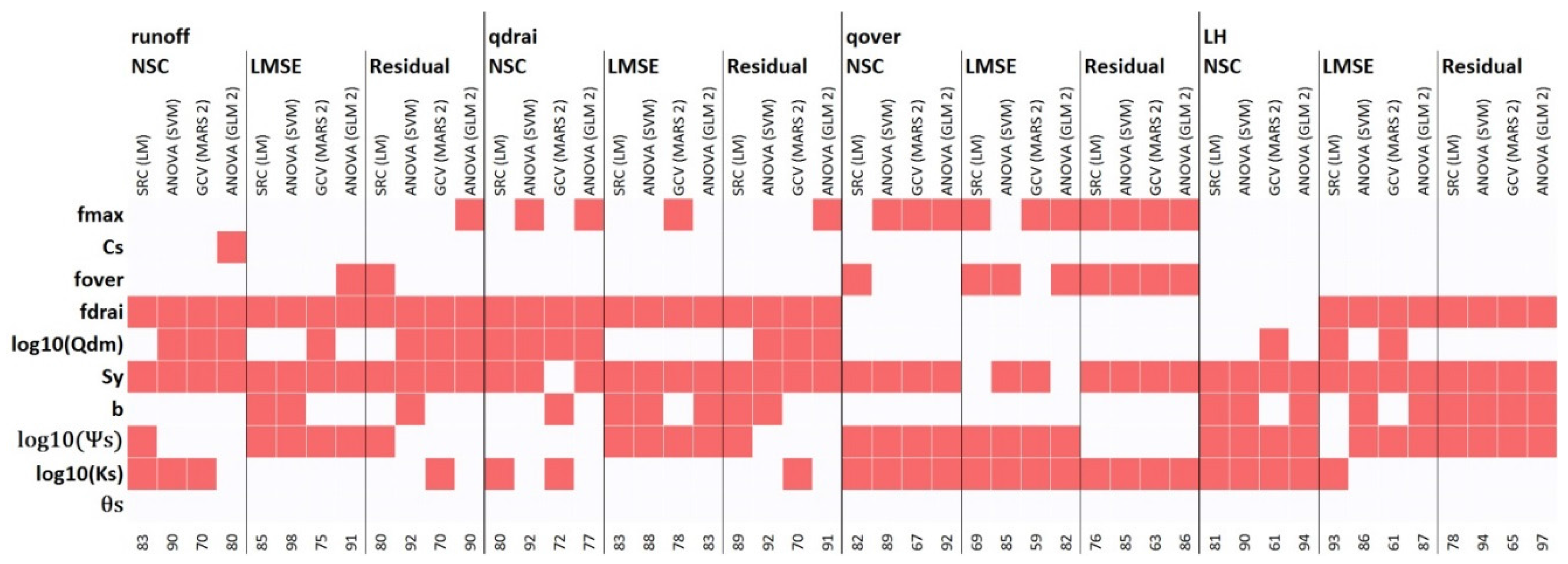
3.2. Effects of Choices of SA Approach
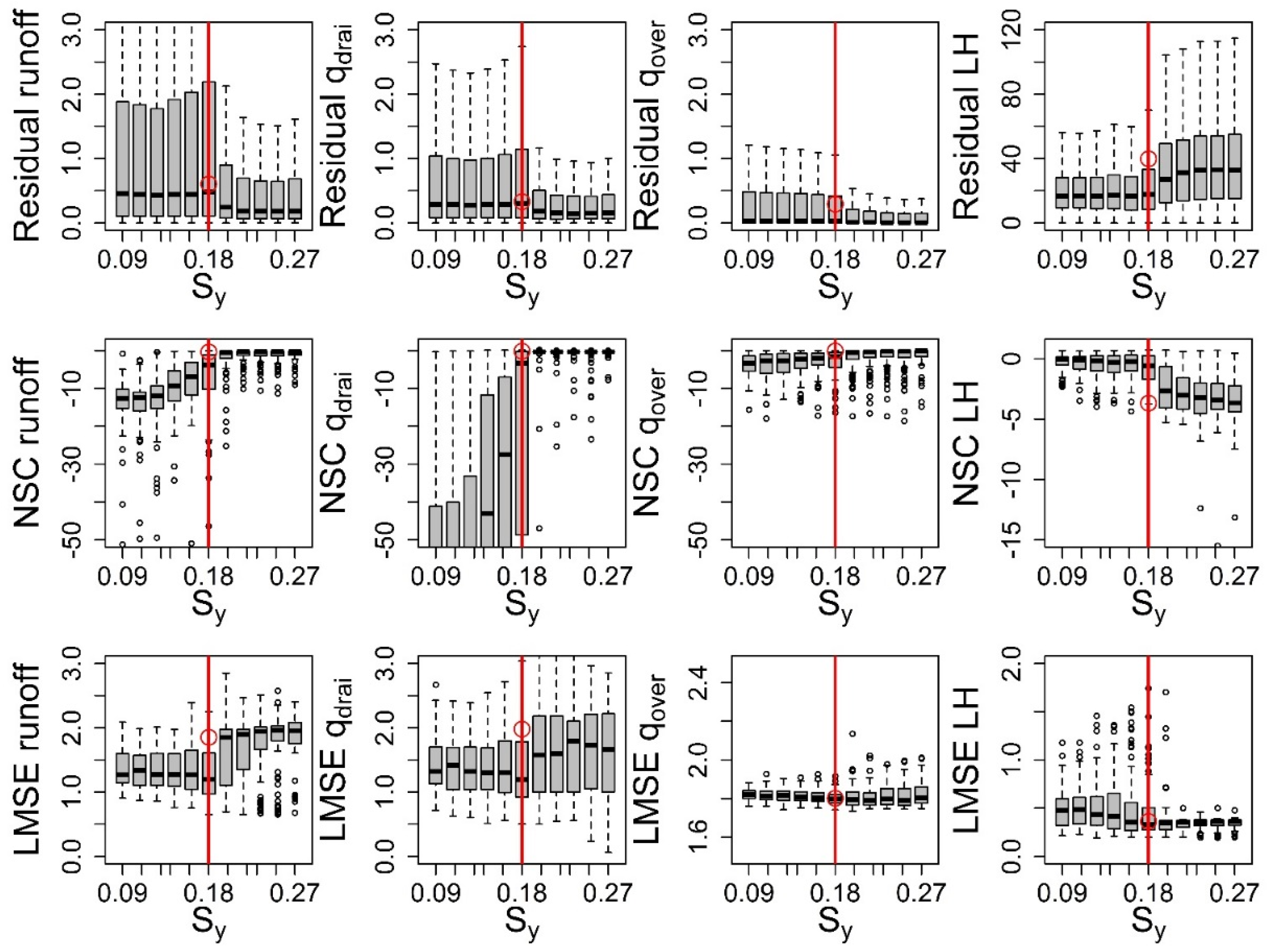
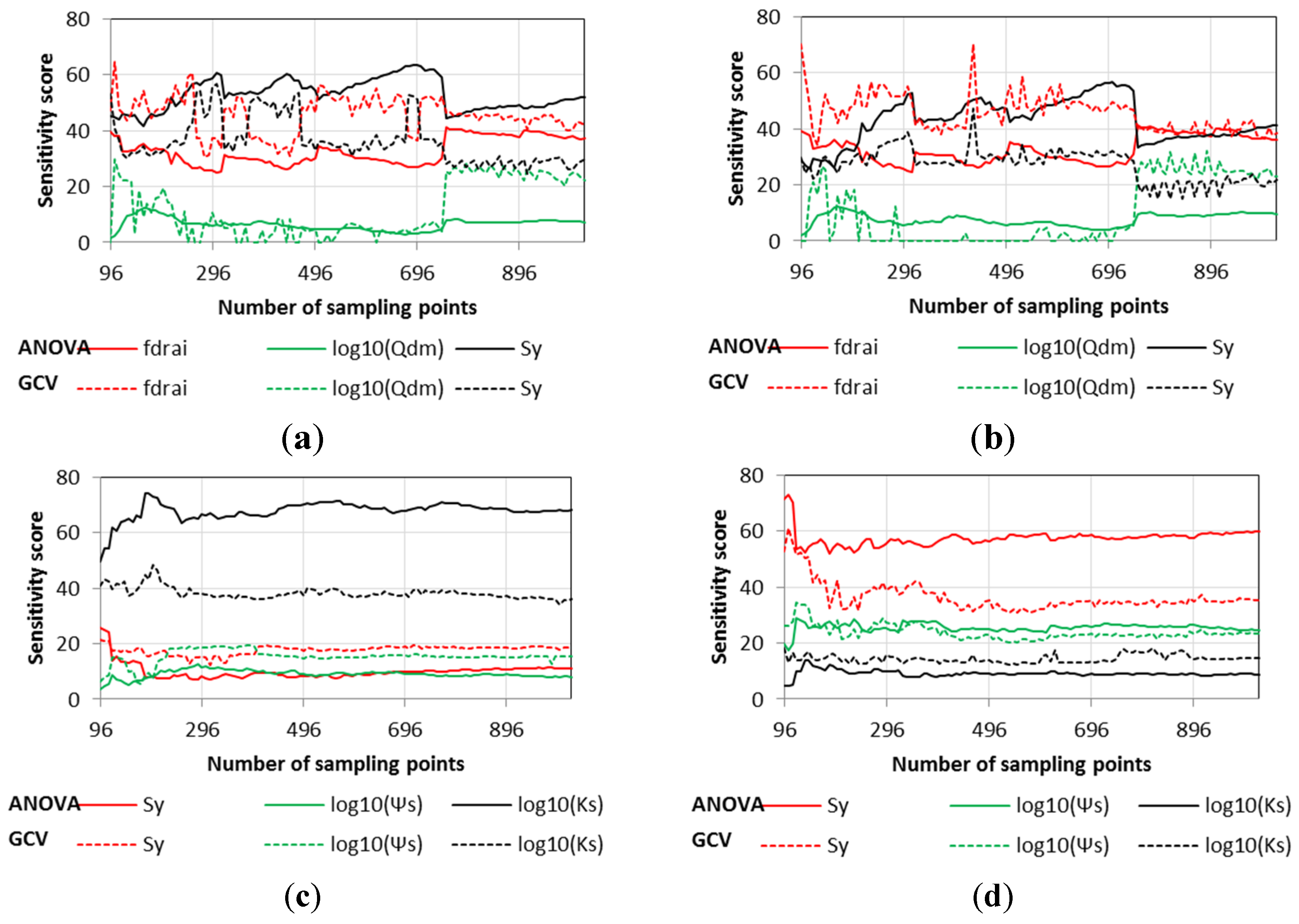
3.3. Convergence, Under-Sampling Issues, and Model Verification
4. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Henderson-Sellers, A.; Pitman, A.J.; Love, P.K.; Irannejad, P.; Chen, T.H. The Project for Intercomparison of Land-Surface Parameterization Schemes (Pilps)—Phase-2 and Phase-3. Bull. Am. Meteorol. Soc. 1995, 76, 489–503. [Google Scholar] [CrossRef]
- Henderson-Sellers, A.; Chen, T.H.; Nakken, M. Predicting global change at the land-surface: The project for intercomparison of land-surface parameterization schemes (PILPS) (phase 4). In Proceedings of the Seventh American Meteorological Society (AMS) symposium on global change studies, Atlanta, GA, USA, 28 January–2 February 1996; pp. 59–66.
- Bastidas, L.A.; Hogue, T.S.; Sorooshian, S.; Gupta, H.V.; Shuttleworth, W.J. Parameter sensitivity analysis for different complexity land surface models using multicriteria methods. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Hou, Z.; Huang, M.; Leung, L.R.; Lin, G.; Ricciuto, D.M. Sensitivity of surface flux simulations to hydrologic parameters based on an uncertainty quantification framework applied to the Community Land Model. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Göhler, M.; Mai, J.; Cuntz, M. Use of eigendecomposition in a parameter sensitivity analysis of the Community Land Model. J. Geophys. Res. Biogeosci. 2013, 118, 904–921. [Google Scholar] [CrossRef]
- Nasybulin, E.; Xu, W.; Engelhard, M.H.; Nie, Z.; Burton, S.D.; Cosimbescu, L.; Gross, M.E.; Zhang, J.-G. Effects of Electrolyte Salts on the Performance of Li-O-2 Batteries. J. Phys. Chem. C 2013, 117, 2635–2645. [Google Scholar] [CrossRef]
- Oleson, K.W.; Dai, Y.J.; Bonan, G.B.; Bosilovich, M.; Dickinson, R.; Dirmeyer, P.; Hoffman, F.M.; Houser, P.R.; Levis, S.; Niu, Y.; et al. Technical Description f Version 4.0 of the Community Land Model (CLM); National Center for Atomospheric Research: Boulder, CO, USA, 2010. [Google Scholar]
- Lawrence, D.M.; Oleson, K.W.; Flanner, M.G.; Thornton, P.E.; Swenson, S.C.; Lawrence, P.J.; Zeng, Z.; Yang, Z.L.; Levis, S.; Sakaguchi, K.; et al. Parameterization Improvements and Functional and Structural Advances in Version 4 of the Community Land Model. J. Adv. Model. Earth Syst. 2011, 3, 27. [Google Scholar]
- Leng, G.; Huang, M.; Tang, Q.; Gao, H.; Leung, L.R. Modeling the effects of groundwater-fed irrigation on terrestrial hydrology over the conterminous United States. J. Hydrometeorol. 2014, 15, 957–972. [Google Scholar] [CrossRef]
- Lei, H.; Huang, M.; Leung, R.; Yang, D.; Shi, X.; Mao, J.; Hayes, D.J.; Schwalm, C.R.; Wei, Y.; Liu, S. Sensitivity of global terrestrial gross primary production to hydrologic states simulated by the Community Land Model using two runoff parameterizations. J. Adv. Model. Earth Syst. 2014, 6. [Google Scholar] [CrossRef]
- Stöckli, R.; Lawrence, D.M.; Niu, G.-Y.; Oleson, K.W.; Thornton, P.E.; Yang, Z.-L.; Bonan, G.B.; Denning, A.S.; Running, S.W. Use of FLUXNET in the Community Land Model development. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Niu, G.-Y.; Yang, Z.-L.; Dickinson, R.; Dickinson, R.; Gulden, L.E.; Gulden, L.E. A simple TOPMODEL-based runoff parameterization (SIMTOP) for use in global climate models. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Huang, M.; Hou, Z.; Leung, L.R.; Ke, Y.; Liu, Y.; Fang, Z.; Sun, Y. Uncertainty Analysis of Runoff Simulations and Parameter Detectability in the Community Land Model—Evidence from MOPEX Basins and Flux Tower Sites. J. Hydrometeorol. 2013, 14, 1754–1772. [Google Scholar] [CrossRef]
- Liu, Y.; Gupta, H.V.; Sorooshian, S.; Bastidas, L.A.; Shuttleworth, W.J. Exploring parameter sensitivities of the land surface using a locally coupled land-atmosphere model. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Van Griensven, A.; Meixnera, T.; Grunwaldb, S.; Bishopb, T.; Diluzioc, M.; Srinivasand, R. A global sensitivity analysis tool for the parameters of multi-variable catchment models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Campolongo, F.; Cariboni, J.; Saltelli, A. An effective screening design for sensitivity analysis of large models. Environ. Model. Softw. 2007, 22, 1509–1518. [Google Scholar] [CrossRef]
- Borgonovo, E.; Castaings, W.; Tarantola, S. Model emulation and moment-independent sensitivity analysis: An application to environmental modelling. Environ. Model. Softw. 2012, 34, 105–115. [Google Scholar] [CrossRef]
- Pan, W.; Bao, J.; Lo, C.; Lai, K.; Agarwal, K.; Koeppel, B.J.; Khaleel, M. A general approach to develop reduced order models for simulation of solid oxide fuel cell stacks. J. Power Sources 2013, 232, 139–151. [Google Scholar] [CrossRef]
- Bao, J.; Xu, Z.; Lin, G.; Fang, Y. Uncertainty quantification for evaluating impacts of caprock and reservoir properties on pressure buildup and ground surface displacement during geological CO2 sequestration. Greenh. Gases Sci. Technol. 2013, 3, 338–358. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Aiken, L.S.; West, S.G. Multiple Regression: Testing and Interpreting Interactions; Sage Publications Inc.: Thousand Oaks, CA, USA, 1991. [Google Scholar]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Sobol, I.M. On the distribution of points in a cube and the approximate evaluation of integrals. USSR Comput. Math. Math. Phys. Engl. Transl. 1967, 7, 86–112. [Google Scholar] [CrossRef]
- Friedman, J.H. Fitting funcctions to noisy data in high dimensions. In Proceedings of the 20th Symposium on the Interface, Reston, VA, USA, 20–23 April 1988.
- Anscombe, F.J. The Validity of Comparative Experiments. J. R. Stat. Soc. Ser. A 1948, 111, 181–211. [Google Scholar] [CrossRef]
- Box, G.E.P. Some Theorems on Quadratic Forms Applied in the Study of Analysis of Variance Problems, I. Effect of Inequality of Variance in the One-Way Classification. Ann. Math. Stat. 1954, 25, 290–302. [Google Scholar] [CrossRef]
- McCullagh, P.; Nelder, J. Generalized Linear Models, 2nd ed.; CRC press: Boca Raton, FL, USA, 1989. [Google Scholar]
- Chambers, J.M.; Hastie, T.J. Statistical Models in S; Chapman and Hall/CRC: Boca Raton, FL, USA, 1992. [Google Scholar]
- Friedman, J.H.; Silverman, B.W. Flexible Parsimonious Smoothing and Additive Modeling; Stanford Linear Accelerator: Stanford, CA, USA, 1987. [Google Scholar]
- Friedman, J.H. Fast MARS; Tech. Report LCS110; Stanford University: Stanford, CA, USA, 1993. [Google Scholar]
- Drucker, H.; Burges, C.J.C.; Kaufman, L.; Smola, A.J.; Vapnik, V. Advances in Neural Information Processing Systems 9 (NIPS). In Proceedings of Neural Information Processing Systems 1996, Denver, CO, USA, 2–5 December 1996; pp. 155–161.
- Smola, A.J.; Scholkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Tong, C. PSUADE User’s Manual; Lawrence Livermore National Laboratory: Livermore, CA, USA, 2009.
- Williams, C.K.I. Prediction with Gaussian Processes: From Linear Regression to Linear Prediction and Beyond. In Learning and Inference in Graphical Models; Kluwer: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Mehrotra, K.; Mohan, C.K.; Ranka, S. Elements of Artificial Neural Networks; Massachusetts Institute of Technology Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Sun, Y.; Hou, Z.; Huang, M.; Tian, F.; Leung, L.R. Inverse modeling of hydrologic parameters using surface flux and runoff observations in the Community Land Model. Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 5077–5119. [Google Scholar] [CrossRef]
- Ray, J.; Hou, Z.; Huang, M.; Sargsyan, K.; Swiler, L. Bayesian Calibration of the Community Land Model using Surrogates. SIAM J. Uncertain. Quantif. 2015, 31, 199–233. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- MODIS Global Evapotranspiration Project (MOD16). Available online: http://www.ntsg.umt.edu/project/mod16 (accessed on 1 December 2015).
- Lyne, V.D.; Hollick, M. Stochastic time-variable rainfall-runoff modelling. In Hydrology and Water Resources Symposium; Institution of Engineers Australia: Perth, Australia, 1979; pp. 89–92. [Google Scholar]
- Niu, G.Y.; Yang, Z.-L.; Dickinson, R.E.; Gulden, L.E.; Su, H. Development of a simple groundwater model for use in climate models and evaluation with Gravity Recovery and Climate Experiment data. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Woodbury, A.D. A FORTRAM program to produce minimum relative entropy distributions. Comput. Geosci. 2004, 30, 131–138. [Google Scholar] [CrossRef]
- Hou, Z.; Rubin, Y. On minimum relative entropy concepts and prior compatibility issues in vadose zone inverse and forward modeling. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory and Model Parameter Estimation; Society of Industrial and Applied Mahematics (SIAM): Philadelphia, PA, USA, 2005. [Google Scholar]
- Bratley, P.; Fox, B.L. Algorithm 659: Implementing Sobol’s Quasirandom Sequence Generator. ACM Trans. Math. Softw. 1988, 14, 88–100. [Google Scholar] [CrossRef]
- Tong, C. Toward a More Robust Variance-Based Global Sensitivity Analysis of Model Outputs; Lawrence Livermore National Laboratory: Livermore, CA, USA, 2007.
- Nossent, J.; Elsen, R.; Bauwens, W. Sobol’ sensitivity analysis of a complex environmental model. Environ. Model. Softw. 2011, 26, 1515–1525. [Google Scholar] [CrossRef]
- Pleming, J.B.; Manteufel, R.D. Replicated Latin Hypercube Sampling. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Austin, TX, USA, 18–21 April 2005.
- Lee, L.A.; Carslaw, K.S.; Pringle, K.J.; Mann, G.W.; Sprackle, D.V. Emulation of a complex global aerosol model to quantify sensitivity to uncertain parameters. Atmos. Chem. Phys. Discuss. 2011, 11, 12253–12273. [Google Scholar] [CrossRef]
- Lee, L.A.; Carslaw, K.S.; Pringle, K.J.; Mann, G.W. Mapping the uncertainty in global CCN using emulation. Atmos. Chem. Phys. Discuss. 2012, 12, 14089–14114. [Google Scholar] [CrossRef]
- Björck, Å. Numerical Methods for Least Squares Problems; Society of Industrial and Applied Mahematics (SIAM): Philadelphia, PA, USA, 1996. [Google Scholar]
- Rao, C.R.; Toutenburg, H.; Shalabh; Heumann, C. Linear Models: Least Squares and Alternatives. In Springer Series in Statistics; Springer: New York, NJ, USA, 1999. [Google Scholar]
- Allison, P.D. Tesing for interaction in multiple regression. Am. J. Sociol. 1977, 83, 144–153. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley: Boston, MA, USA, 1977. [Google Scholar]
- Benjamini, Y. Opening the box of a boxplot. Am. Stat. 1988, 42, 257–262. [Google Scholar]
- Rousseeuw, P.J.; Ruts, I.; Tukey, J.W. The Bagplot: A Bivariate Boxplot. Am. Stat. 1999, 53, 382–387. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, J.; Hou, Z.; Huang, M.; Liu, Y. On Approaches to Analyze the Sensitivity of Simulated Hydrologic Fluxes to Model Parameters in the Community Land Model. Water 2015, 7, 6810-6826. https://doi.org/10.3390/w7126662
Bao J, Hou Z, Huang M, Liu Y. On Approaches to Analyze the Sensitivity of Simulated Hydrologic Fluxes to Model Parameters in the Community Land Model. Water. 2015; 7(12):6810-6826. https://doi.org/10.3390/w7126662
Chicago/Turabian StyleBao, Jie, Zhangshuan Hou, Maoyi Huang, and Ying Liu. 2015. "On Approaches to Analyze the Sensitivity of Simulated Hydrologic Fluxes to Model Parameters in the Community Land Model" Water 7, no. 12: 6810-6826. https://doi.org/10.3390/w7126662
APA StyleBao, J., Hou, Z., Huang, M., & Liu, Y. (2015). On Approaches to Analyze the Sensitivity of Simulated Hydrologic Fluxes to Model Parameters in the Community Land Model. Water, 7(12), 6810-6826. https://doi.org/10.3390/w7126662