An Indirect Simulation-Optimization Model for Determining Optimal TMDL Allocation under Uncertainty
Abstract
:1. Introduction
2. Materials and Methods
2.1. BRRT-EILP Model
2.2. Application to the Swift Creek Reservoir Watershed
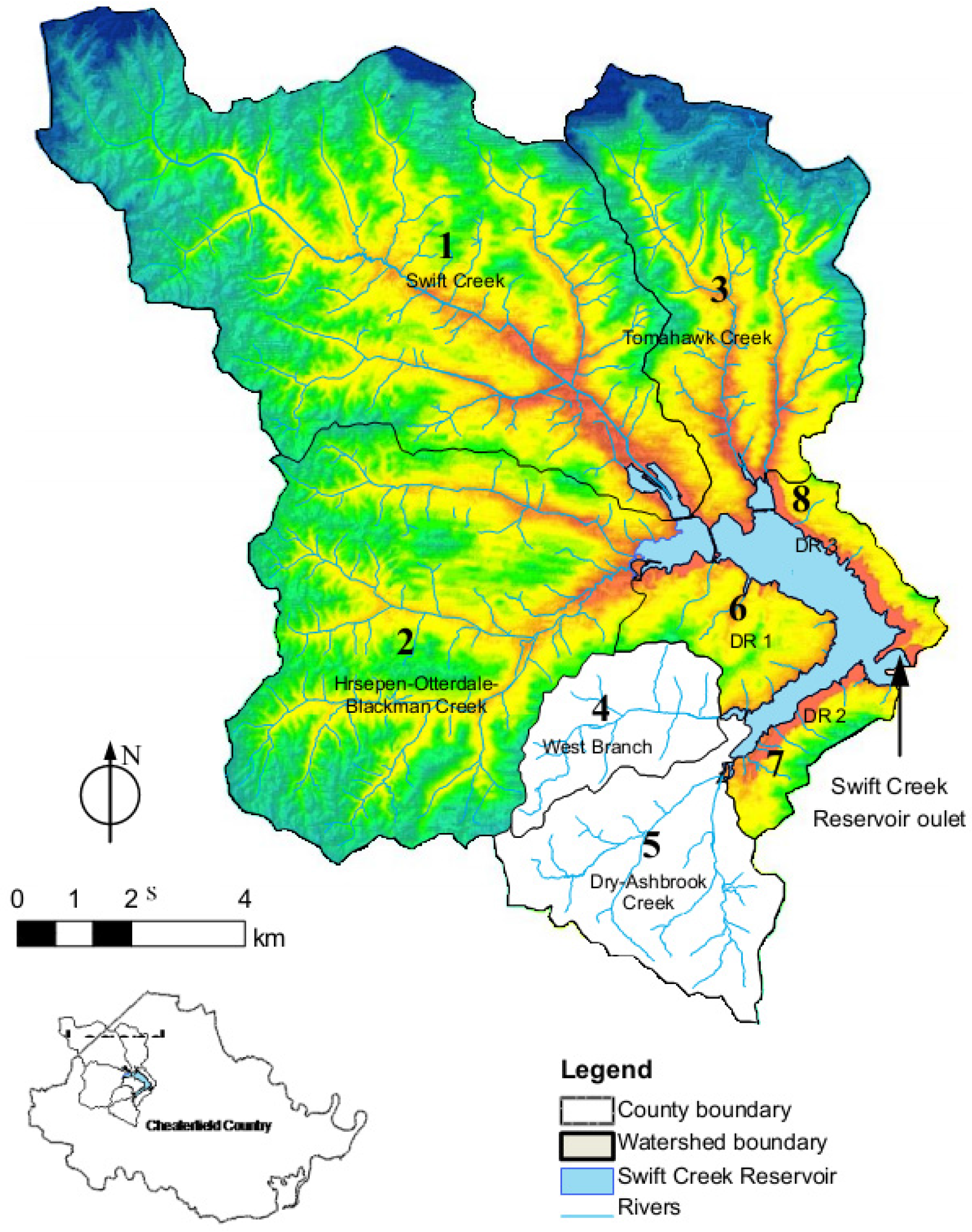
| Sub-Watershed j | Area, km2 | ci1, kg | ci2, kg |
|---|---|---|---|
| 1. Swift Creek | 59.47 | 4451.7 | 157.4 |
| 2. Horsepen-Otterdale-Blackman Creek | 40.47 | 5169.3 | 388.4 |
| 3. Tomahawk Creek | 25.30 | 2677.2 | 126.8 |
| 4. West Branch | 7.50 | 286.7 | 87.9 |
| 5. Dry-Ashbrook Creek | 14.52 | 516.5 | 161.1 |
| 6. Direct runoff (1) | 3.73 | 1916.3 | 114.2 |
| 7. Direct runoff (2) | 6.13 | 1000.7 | 90.2 |
| 8. Direct runoff (3) | 3.31 | 471.7 | 146.1 |
| Total | 160.4 | 16,490 | 1272 |
2.3. Algorithmic Processes
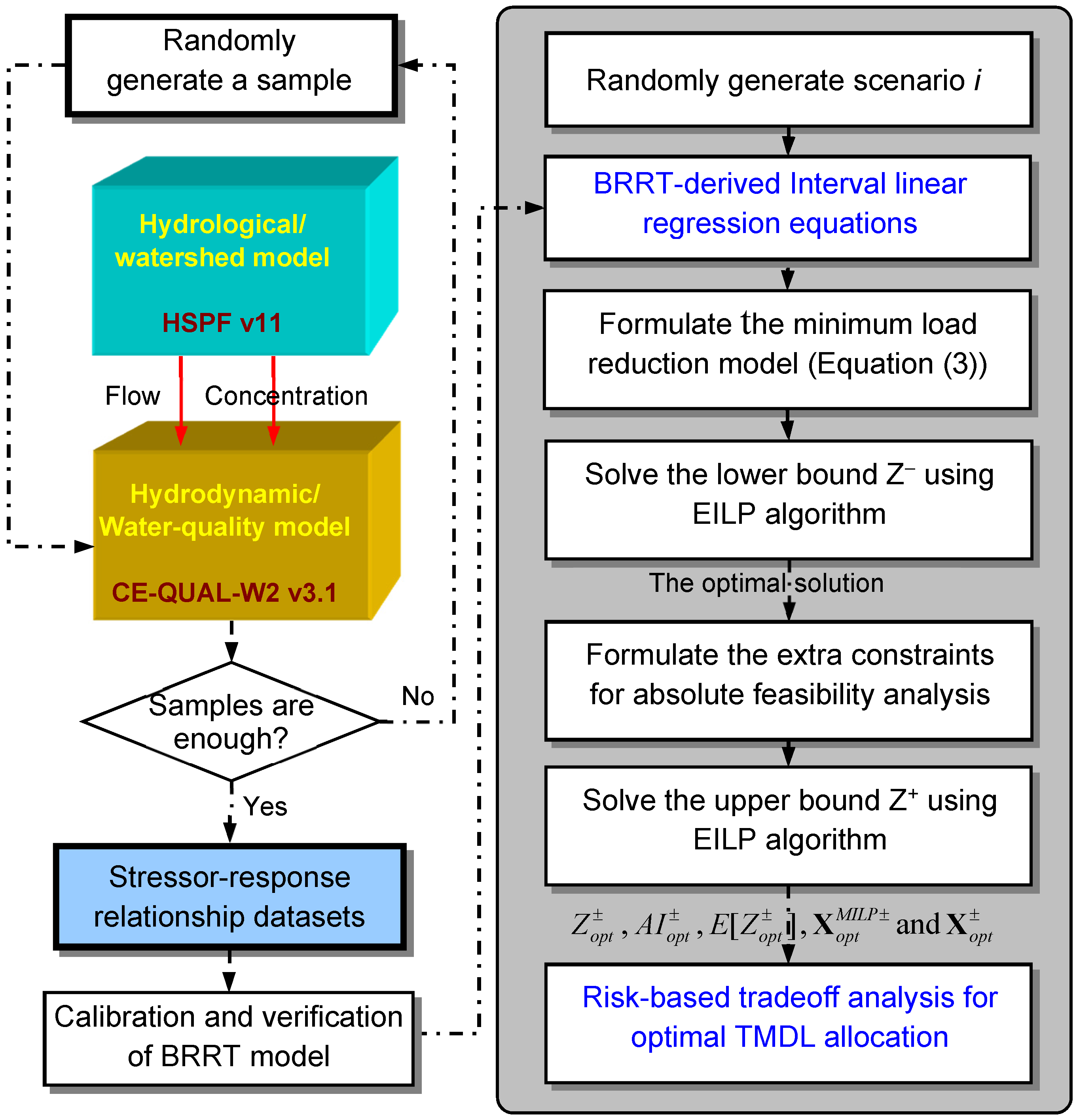
3. Results
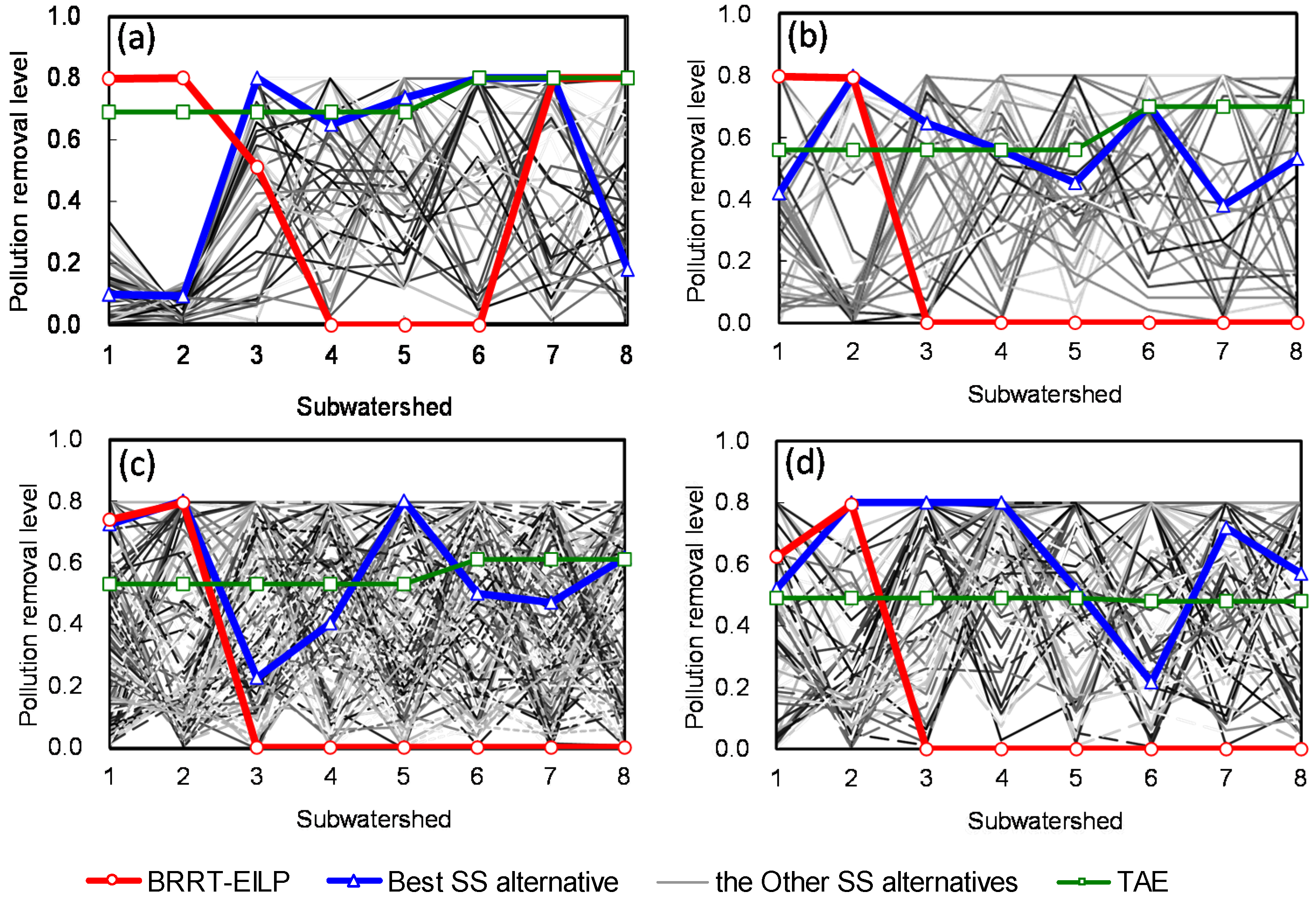
| Sub-watershed j | Minimum Total Load Reduction of Inorganic Nitrogen | Minimum Total Load Reduction of Inorganic Phosphorus | ||||||||||
| Scenario 1 (Chl-a: [14, 15] μg/L) | Scenario 2 (Chl-a: [13, 15] μg/L) | Scenario 3 (Chl-a: [12, 15] μg/L) | Scenario 1 | Scenario 2 | Scenario 3 | |||||||
| * | *, kg | , kg | , kg | , kg | , kg | , kg | ||||||
| 1 | [0.42, 0.42] | [1870, 1870] | [0.42, 0.42] | [1870, 1870] | [0.42, 0.42] | [1870, 1870] | [0.62, 0.74] | [98.2, 116.2] | [0.62, 0.8] | [98.2, 125.6] | [0.62, 0.8] | [98.2, 125.6] |
| 2 | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0.79, 0.79] | [308, 308] | [0.79, 0.79] | [308, 308] | [0.79, 0.8] | [308, 310.7] |
| 3 | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0.51] | [0, 64.8] |
| 4 | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] |
| 5 | [0, 0.23] | [0, 120] | [0, 0.71] | [0, 360] | [0, 0.8] | [0, 413] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] |
| 6 | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0.12] | [0, 238] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] |
| 7 | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0.8] | [0, 72.2] |
| 8 | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0.8] | [0, 116.9] |
| Total load reduction | [1870, 1989] | [1870, 2235] | [1870, 2521] | [406.2, 424.2] | [406.2, 433.6] | [406.2, 690.2] | ||||||
| 1929.5 | 2052.5 | 2195.5 | 415.2 | 419.9 | 548.2 | |||||||
Minimum Total Load Reductions of Inorganic Nitrogen
4. Discussion
| Method | Calibration | New Application |
|---|---|---|
| BRRT-EILP model | 33 h | 1 min |
| Direct SOM framework | ~10 days | ~10 days |


5. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- USEPA. Allocating Loads and Wasteloads, Technical Support Documents, Total Maximum Daily Load (TMDL); US EPA Press: Washington, DC, USA, 2003.
- Jia, Y.B.; Culver, T.B. Robust optimization for total maximum daily load allocations. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Cerco, C.F.; Noel, M.R.; Kim, S.C. Three-dimensional management model for lake washington, part ii: Eutrophication modeling and skill assessment. Lake Reserv. Manag. 2006, 22, 115–131. [Google Scholar] [CrossRef]
- Cole, T.; Wells, S.A. CE-QUAL-W2: A Two-Dimensional, Laterally Averaged, Hydrodynamic and Water Quality Model, Version 3.1; US Army Engineering and Research Development Center: Vicksburg, MS, USA, 2003. [Google Scholar]
- Boesch, D.F. The gulf of Mexico’s dead zone. Science 2004, 306, 977–978. [Google Scholar] [CrossRef]
- Dhar, A.; Datta, B. Optimal operation of reservoirs for downstream water quality control using linked simulation optimization. Hydrol. Process. 2008, 22, 842–853. [Google Scholar] [CrossRef]
- He, L.; Huang, G.H.; Lu, H.W. Health-risk-based groundwater remediation system optimization through clusterwise linear regression. Environ. Sci. Technol. 2008, 42, 9237–9243. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Huang, G.H.; Zeng, G.M.; Lu, H.W. An integrated simulation, inference, and optimization method for identifying groundwater remediation strategies at petroleum-contaminated aquifers in western canada. Water Res. 2008, 42, 2629–2639. [Google Scholar] [CrossRef]
- Huang, G.H.; Huang, Y.F.; Wang, G.Q.; Xiao, H.N. Development of a forecasting system for supporting remediation design and process control based on NAPL-biodegradation simulation and stepwise-cluster analysis. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Rejani, R.; Jha, M.K.; Panda, S.N. Simulation-optimization modelling for sustainable groundwater management in a coastal basin of orissa, india. Water Resour. Manag. 2009, 23, 235–263. [Google Scholar] [CrossRef]
- Saadatpour, M.; Afshar, A. Waste load allocation modeling with fuzzy goals; simulation-optimization approach. Water Resour. Manag. 2007, 21, 1207–1224. [Google Scholar] [CrossRef]
- Zhou, F.; Chen, G.X.; Huang, Y.F.; Yang, J.Z.; Feng, H. An adaptive moving finite volume scheme for modeling flood inundation over dry and complex topography. Water Resour. Res. 2013, 49, 1914–1928. [Google Scholar] [CrossRef]
- Zhou, F.; Chen, G.X.; Noelle, S.; Guo, H.C. A well-balanced stable generalized riemann problem scheme for shallow water equations using adaptive moving unstructured triangular meshes. Int. J. Numer. Methods Fluids 2013, 73, 266–283. [Google Scholar] [CrossRef]
- Qin, X.S.; Huang, G.H.; Chakma, A. A stepwise-inference-based optimization system for supporting remediation of petroleum-contaminated sites. Water Air Soil Pollut. 2007, 185, 349–368. [Google Scholar] [CrossRef]
- Guo, H.C.; Gao, W.; Zhou, F. Three-level trade-off analysis for decision making in environmental engineering under interval uncertainty. Eng. Optim. 2014, 46, 377–392. [Google Scholar] [CrossRef]
- Huang, G.H. A stepwise cluster-analysis method for predicting air-quality in an urban-environment. Atmos. Environ. B Urban Atmos. 1992, 26, 349–357. [Google Scholar] [CrossRef]
- Sahinidis, N.V. Optimization under uncertainty: State-of-the-art and opportunities. Comput. Chem. Eng. 2004, 28, 971–983. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, W.; Cai, Y.L.; Guo, H.C.; Zhou, F. Joint optimization of population pattern and end-of-pipe control under uncertainty for lake dianchi water-quality management. Fresenius Environ. Bull. 2012, 21, 3693–3704. [Google Scholar]
- Zhou, F.; Huang, G.H.; Chen, G.X.; Guo, H.C. Enhanced-interval linear programming. Eur. J. Oper. Res. 2009, 199, 323–333. [Google Scholar] [CrossRef]
- Birge, J.R.; Louveaux, F.V. Introduction to Stochastic Programming; Springer: New York, NY, USA, 1997. [Google Scholar]
- Zou, R.; Liu, Y.; Riverson, J.; Parker, A.; Carter, S. A nonlinearity interval mapping scheme for efficient waste load allocation simulation-optimization analysis. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Zou, R.; Lung, W.S.; Wu, J. An adaptive neural network embedded genetic algorithm approach for inverse water quality modeling. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Zhou, F.; Guo, H.C.; Chen, G.X.; Huang, G.H. The interval linear programming: A revisit. J. Environ. Inform. 2008, 11, 1–10. [Google Scholar] [CrossRef]
- Iorgulescu, I.; Beven, K.J. Nonparametric direct mapping of rainfall-runoff relationships: An alternative approach to data analysis and modeling? Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.G. Classification and Regression Trees; Wadsworth International Group: Belmont, CA, USA, 1984. [Google Scholar]
- Zhou, F.; Shang, Z.Y.; Zeng, Z.Z.; Piao, S.L.; Ciais, P.; Raymond, P.; Wang, X.H.; Wang, R.; Chen, M.P.; Yang, C.L.; et al. New model for capturing the variations of fertilizer-induced emission factors of n2o. Glob. Biogeochem. Cycles 2015, 29. [Google Scholar] [CrossRef]
- Harmel, R.D.; Cooper, R.J.; Slade, R.M.; Haney, R.L.; Arnold, J.G. Cumulative uncertainty in measured streamflow and water quality data for small watersheds. Trans. ASABE 2006, 49, 689–701. [Google Scholar] [CrossRef]
- Wu, J.; Zou, R.; Yu, S.L. Uncertainty analysis for coupled watershed and water quality modeling systems. J. Water Resour. Plann. Manag. 2006, 132, 351–361. [Google Scholar] [CrossRef]
- Wetzel, R.G. Limnology—Lake and River Ecosystems, 3rd ed.; Academic Press: New York, NY, USA, 2001. [Google Scholar]
- U.S. Environmental Protection Agency (USEPA). Protocol for Developing Nutrient TMDLs; EPA 841-B-99-007; Office of Water (4503F), United States Environmental Protection Agency: Washington, DC, USA, 1999.
- Conley, D.J.; Paerl, H.W.; Howarth, R.W.; Boesch, D.F.; Seitzinger, S.P.; Havens, K.E.; Lancelot, C.; Likens, G.E. Ecology controlling eutrophication: Nitrogen and phosphorus. Science 2009, 323, 1014–1015. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, F.; Dong, Y.; Wu, J.; Zheng, J.; Zhao, Y. An Indirect Simulation-Optimization Model for Determining Optimal TMDL Allocation under Uncertainty. Water 2015, 7, 6634-6650. https://doi.org/10.3390/w7116634
Zhou F, Dong Y, Wu J, Zheng J, Zhao Y. An Indirect Simulation-Optimization Model for Determining Optimal TMDL Allocation under Uncertainty. Water. 2015; 7(11):6634-6650. https://doi.org/10.3390/w7116634
Chicago/Turabian StyleZhou, Feng, Yanjun Dong, Jing Wu, Jiangli Zheng, and Yue Zhao. 2015. "An Indirect Simulation-Optimization Model for Determining Optimal TMDL Allocation under Uncertainty" Water 7, no. 11: 6634-6650. https://doi.org/10.3390/w7116634
APA StyleZhou, F., Dong, Y., Wu, J., Zheng, J., & Zhao, Y. (2015). An Indirect Simulation-Optimization Model for Determining Optimal TMDL Allocation under Uncertainty. Water, 7(11), 6634-6650. https://doi.org/10.3390/w7116634





