Estimating Groundwater Recharge in the Semiarid Al-Khazir Gomal Basin, North Iraq

Abstract

The mean annual recharge of Al-Khazir Gomal Basin was estimated as a basis for decision makers regarding the renewability and sustainability of groundwater. For this purpose, two approaches were used: hydrograph analysis and water table fluctuation (WTF). The long-term mean daily stream-flow records of Al-Khazir River (1969–1981) were used to estimate groundwater discharge by base-flow hydrograph separation and displacement recession curve methods. Four base-flow separation methods were used; one is the graphical separation method, and three are automated separation methods included in the web-based Hydrograph Analysis Tool. The annual recharge estimated by WTF was 111.6 mm/y, and the average annual recharge estimated by the four base-flow separation methods was 125.8 mm/y. Estimating recharge by the water table fluctuation method does not incorporate spatial variability contained in the whole watershed, because the specific yield did not represent the entire basin. However, the hydrograph analysis method can give a comprehensive estimation of the net integrated recharge for the entire watershed, which includes different recharge mechanisms. The displacement recession curve method deviates a lot (>30 mm/y) from the other methods, which indicates that this method may not be suitable to apply in such large watersheds.

1. Introduction

Compared to other Middle Eastern countries, Iraq is considered a wealthy country with respect to water resources. These resources, however, are becoming more and more constrained due to population growth, climate change and decreasing surface water inflow from neighboring countries (Turkey, Syria and Iran). In the last decade, the demand for groundwater in Al-Khazir Gomal Basin to meet domestic, agricultural and industrial needs has increased; therefore, groundwater resource management is an important issue in this area, especially with regard to potential agricultural and industrial projects. A major parameter needed for groundwater resource management is groundwater recharge.

It is difficult to find a single reliable method for measuring groundwater recharge due to the complexity of this phenomenon and the large variety of situations encountered [1]. For the estimation of groundwater recharge, it is thus important to select methods that are suitable for the study area with regard to the available data, objectives, scale, accuracy, cost and expected recharge mechanism. Practicing hydrologists typically make the best estimates of recharge possible by the use of methods that are relatively direct in their application and require only commonly available hydrologic data [2]. Using the water budget for a basin in estimating recharge as a residual component has an inherent drawback, because the accuracy of the recharge estimation depends on the accuracy of the other components of the water budget. This limitation is critical when the magnitude of the recharge rate is small compared to that of the other variables, in particular ET [3]. Hydrograph analysis, especially the base-flow separation and discharge recession, is one of the methods used to estimate the net regional recharge and requires neither complex conceptual modeling nor detailed knowledge of soil types and land use and land cover practices.

Eckhardt [4] identified the base-flow as a stream-flow component that reacts slowly to rainfall and is usually associated with water discharged from groundwater storage. Normally, groundwater discharge is approximately equal to recharge [5,6]. This assumption is justified if interflow, evapotranspiration from riparian areas, interaction with the underlying aquifer and neighboring basins and anthropogenic factors are thought to have a minimal effect. In this case, one can use this recharge in the evaluation of water resources over a large area. Accordingly, base-flow separation is considered a straightforward and easy method to estimate regional recharge and a good strategy for understanding the dynamics of groundwater discharge to streams.

Many researchers used several methods to estimate the contribution of groundwater to stream-flow through hydrograph analysis (e.g., [6,7,8]), and a useful review of the development of base-flow separation techniques was reported by Smakhtin [9]. Most of these studies describe the base-flow characteristics of streams, identify the regional differences in these flow characteristics and evaluate the interaction between surface and ground-water. These methods experienced a revival and became easier and more convenient through the application of the automated methods developed by Rutledge [10,11], Arnold et al. [12], Sloto and Crouse [13] and Eckhardt [14]. However, only a few researchers have focused on estimating recharge through stream-flow data analyzing (e.g., [14,15,16,17,18]). These studies revealed the feasibility of using hydrograph analysis for estimating the regional integrated recharge compared with costly monitoring water balance, percolation models and tracer methods. Szilang et al. [17] and Lee et al. [18] estimated the long-term mean annual groundwater recharge on a regional scale by using the water budget coupled with base-flow records. This technique was easy to implement, and its results compared well with the long-term mean groundwater recharge estimated previously.

The displacement recession curve method can be used to estimate groundwater recharge directly from stream-flow records. The method is based on the hypothesis that the stream-flow-recession curve is displaced upward during periods of groundwater recharge. Accordingly, groundwater recharge during an event can be estimated on the basis of work by Rorabaugh [15]. Rutledge [10] coded RECESS to determine the master recession curve (MRC) and the recession index (K), which are used in RORA [19] for estimating the recharge in each rainstorm event by the displacement recession curve method. The aim of this paper was using an automated analysis procedure by the programs described above and the automated base-flow separation methods included in the web-based Hydrograph Analysis Tool (WHAT) system. This will help to reduce the subjectivity of the manual method and increase the speed of analysis.

To avoid overestimation of the annual base-flow caused by rainstorm events, several investigators, such as Rutledge [11,12,20,21], Lee et al. [18] and Chen and Lee [22], recommended the usage of stable base-flow in the dry season as the average value over the year. For this purpose, the stable base-flow analysis is applied in this study to obtain more reliable results.

Validation of recharge estimation is difficult to carry out, because recharge cannot be measured directly [23]. Therefore, much of the literature recommends the use of multiple methods in estimating recharge. This study aims to estimate the recharge by the hydrograph analysis approach and water table fluctuation method to provide relevant recharge values for the semiarid Alkhazir Gomal Basin to ensure sustainable use of groundwater.

2. Study Area

Al-Khazir Gomal River Basin spans an area of 3185 km² and is located in the northern part of Iraq at the border of the high and low folded zones (Figure 1). Shaded relief has been used to highlight the topographic features of the basin. The surface elevation ranges from 216 m at the lowest point, close to the watershed outlet, to 2165 m at the highest point, in the mountainous area in the far northern parts. The basin is crossed by the Al-Khazir River and its tributary, the Gomel River, which meet near Bardarash Mountain. The annual stream-flow of the perennial Al-Khazir River measured at Manguba station near the outlet of the basin is 7.4 × 10⁸ m³/y [24].

According to the aridity index [21], the study area is classified as a semiarid to dry subhumid region, which has a distinct continental interior of a Mediterranean climate type, characterized by hot and dry summers and cold rainy winters. The average annual rainfall in the basin of around 650 mm occurs from October to April, and it is almost dry in the rest of the year. The mean annual temperature is 20 °C, and the potential evapotranspiration is 1500 mm/y.

Approximately 46% of the watershed in the northern part of the area is considered as a mountainous region and is occupied mostly by the Aqra-Bekhme and Qamchuqa formations (Cretaceous), as well as the Pilaspi Formation (Middle Eocene). Theses formations consist mainly of limestone and constitute the fractured aquifer system. The remainder of the area is covered by agricultural plain, which mainly consists of the Bia Hassan Formation (Pliocene) and Quaternary sediments. The last two formations represent the most important intergranular aquifer system in the basin.

According to the geological and structural settings, the basin is divided by Al-Sam and Hanna [25] into three regions. The first region (mountainous area) is located to the north of Aqra Mountain and has little significance in terms of hydrogeology, because it has small granular and fractured aquifers restricted on the longitudinal and narrow synclines. The second region in the middle part of the basin represents a broad syncline between Aqra and Bardarash mountains, covering an area of 1224 km². The aquifer in this region consists of thick beds of conglomerate and sandstone alternated with thin layers of claystone and siltstone. This aquifer is considered the main and most important aquifer with regard to the quality and quantity of groundwater. The third region is specified by a triangular outlet area that has the same hydrogeological conditions as the second region, but is separated from it by the Bardarash Mountains. Most human activities are concentrated in the second region, which occupies 38% of the basin and includes many towns and villages. Rain-fed agriculture is one of the most important activities of the peoples in this region. Domestic use is the main use of groundwater in the basin, in addition to the irrigation of small home farms. Industrial activities are limited to one drinking-water bottling plant and quarries of sand and gravel along Al-Khazir River.

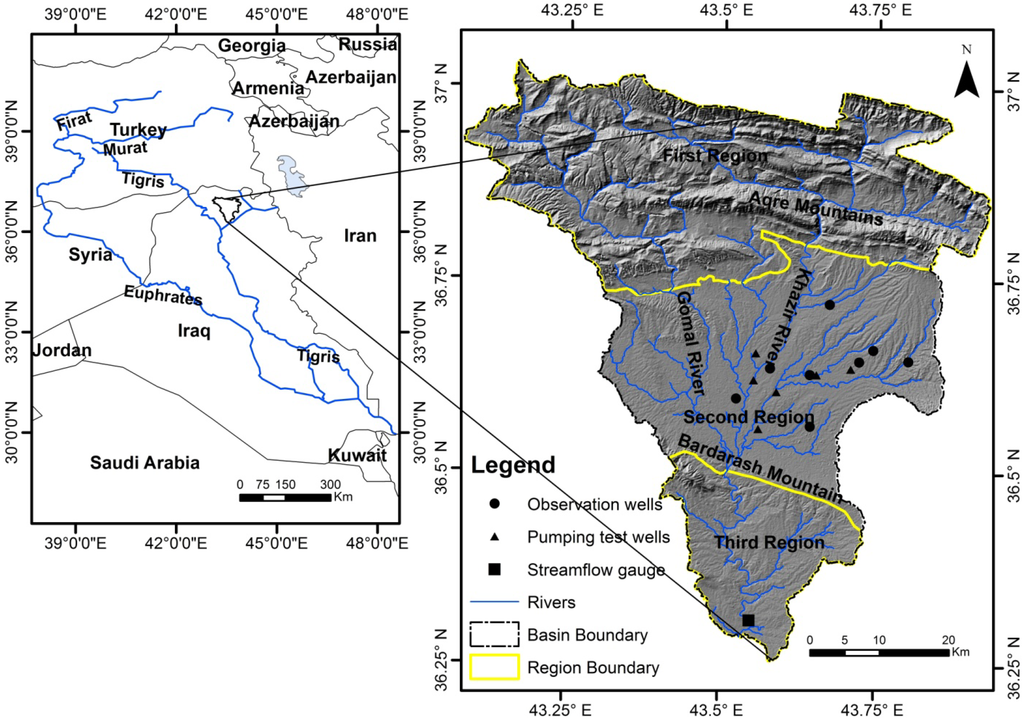
Figure 1. Map of Al-Khazir Gomel basin illustrating the basin boundary, the three regions’ boundaries, the stream-flow gauge and pumping and observation wells.

Figure 1. Map of Al-Khazir Gomel basin illustrating the basin boundary, the three regions’ boundaries, the stream-flow gauge and pumping and observation wells.

3. Methodology

Groundwater recharge is estimated by two methods: hydrograph analysis and water table fluctuation. In hydrograph analysis, two approaches are used, namely base-flow separation and a displacement recession curve. Figure 2 is a flowchart showing the methodology that has been used in estimating recharge. Below, a brief description of these methods is given.

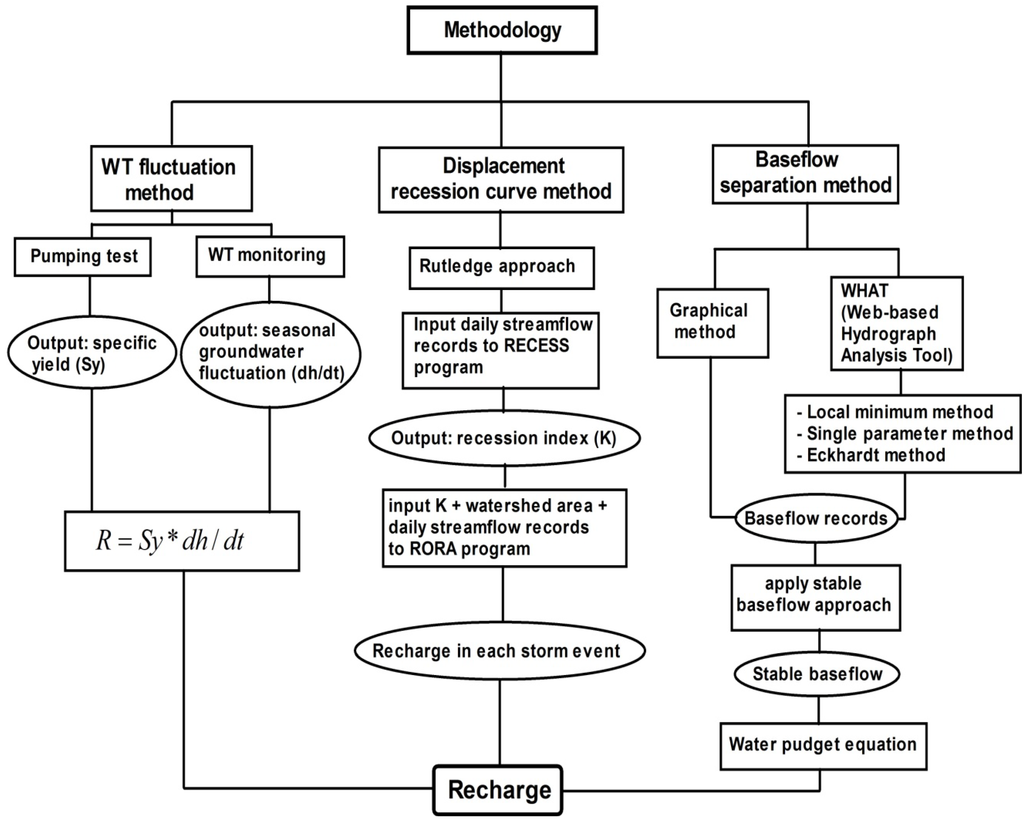
Figure 2. Flowchart showing the methodology of the recharge estimation by base-flow separation methods, the displacement recession curve method and the water table (WT) fluctuation method.

Figure 2. Flowchart showing the methodology of the recharge estimation by base-flow separation methods, the displacement recession curve method and the water table (WT) fluctuation method.

3.1. Base-Flow SEPARATION

The stream-flow can acquire a modified base-flow situation, due to the extensive abstraction from the groundwater storage, the use of water resources directly from the stream and interruption by diversion of runoff or harvesting mechanisms. Therefore, the pristine continuous daily stream-flow discharge records for the period of 1969–1981 are selected in this study to ensure that the anthropogenic effects on the river discharge are at minimum. Below, a brief explanation of the four base-flow separation methods is given.

3.1.1. Graphical Method (Constant Slope Method)

The essence of this method is an interpolation connecting the beginning of the rising limb to the estimated end of the direct runoff period through the following steps:

• Identify the start of direct runoff;
• Estimate the duration of the direct runoff period N after the peak of the storm by the empirical relationship (N = A^0.2) proposed by Linsley et al. [26], where N is the number of the days after the peak and A is the area of the watershed in square miles (Mi²) above the gauge station;
• Draw a line connecting the start of direct runoff to the end (inflection point after N days). This is the base-flow hydrograph (Figure 3).

For convenience, the graphical separation was executed using the Excel add-in, Chart Image to Data [27] instead of the traditional graphical separation method. In this approach, the daily stream-flow hydrograph chart with a linear axis is converted to an image, and the add-in can help to indicate the values of the base-flow by digitizing the hygrograph’s curve in the chart image to get (X, Y) values representing the base-flow values with time. After creating the curve of the base-flow from the (X, Y) values, the area under the curve can be integrated to calculate the annual base-flow.

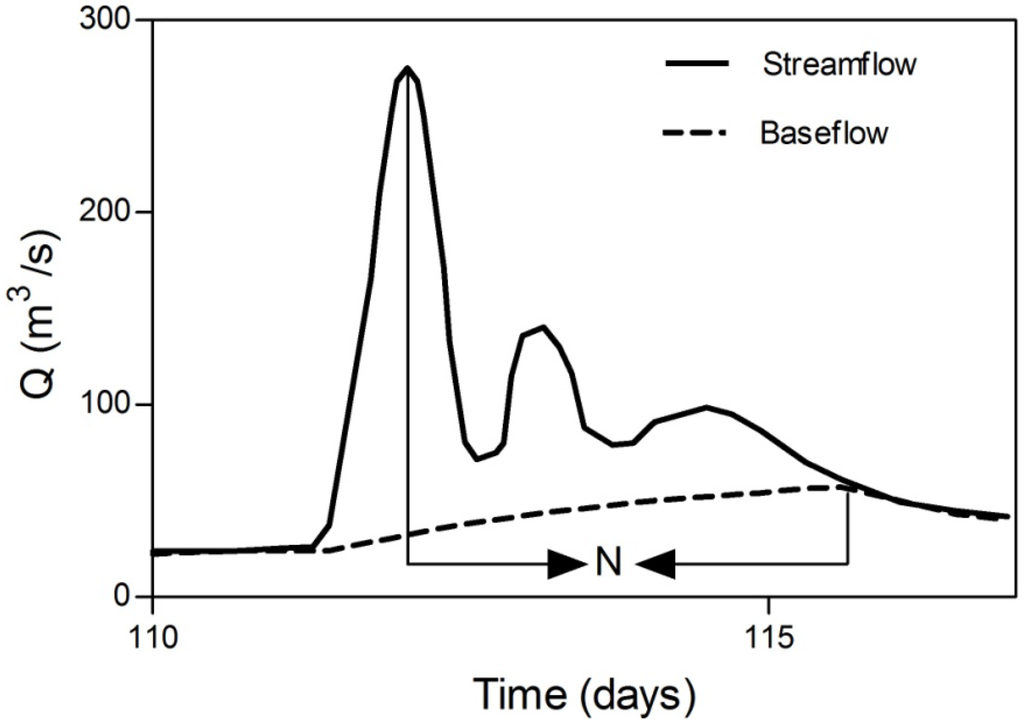
Figure 3. Graphical separation method (constant slope method).

Figure 3. Graphical separation method (constant slope method).

3.1.2. Automated Web GIS-Based Hydrograph Analysis Tool (WHAT)

The WHAT system coded by Engel [28] offers three base-flow separation modules: BFLOW digital filter (single parameter method), Eckhardt digital filters and the local minimum method. Digital filter methods divide the stream-flow hydrograph into high frequency (direct runoff) and low frequency (base-flow) components [29]. Although the technique has no true physical basis, it is objective and reproducible [12]. Below, brief explanations for these three automated methods are given:

• Single parameter method: The digital filter technique BFLOW software filter was developed based on Equation (1), which is known as a single parameter equation filter ([14,29,30]).

  $$R_t=\text{α}{R}_{t-1}+\frac{\left(1+\text{α}\right)}{2}\left(Q_t-Q_{t-1}\right)$$

  (1)

where R_t is the filtered surface runoff (quick response) at the t time step (one day); Q is the original stream-flow and α the base-flow filter parameter (0.925). The value of 0.925 was determined by Arnold et al. [12] to give realistic results compared to manual separation techniques.

Base-flow, B, is calculated with the equation:

B = Q_t − R_t

(2)

• Eckhardt method: Eckhardt [14] proposed in Equation (3) two parameters in the digital filter base-flow, the base-flow filter parameter α (0.98) and BFI_max (base-flow index (BFI); the maximum value of long-term ratio of base-flow to total stream-flow). To reduce the subjective influence of using BFI_max, Eckhardt [14] proposed that BFI_max in perennial and ephemeral streams with porous aquifers be 0.8 and 0.5, respectively, and 0.25 with a hard rock aquifer. In this study, a BFI_max value of 0.8 was used.

  $$B_t=\frac{\left(1-BF{I}_{\text{max}}\right)\times \text{ α }\times B_{t-1}+\left(1-\text{α}\right)\times BF{I}_{\text{max}}\times Q_t}{1-\text{α }\times BF{I}_{\text{max}}}$$

  (3)

where B_t is the filtered base-flow at the t time step, B_t−1 is the filtered base-flow at the t − 1 time step, BFI_max is the maximum value of long-term ratio of base flow to total stream-flow, α is the filter parameter and Q_t is the total stream-flow at the t time step.

• Local minimum method: The local minimum method begins by constructing a sequence of “local minima”. The procedure depends on determining the lowest discharge value in one half of the interval minus one day (0.5(2N − 1) days) before and after the day being considered and then connects the adjacent local minimum by an interpolated line [13].

To avoid overestimation caused by rainstorm events, Chen and Lee [22] proposed a stable base-flow analysis to obtain more reliable results. In this study, the diagrams of the stable base-flow analysis (Figure 4) are used to determine the annual stable base-flow values in the four aforementioned methods. The procedure of the stable-base-flow analysis is described by Lee et al. [18] as follows:

(1)

Obtain monthly base-flow from the base-flow-record estimation;

(2)

Obtain long-term mean monthly base-flow. In our case, this was done for the period 1969 to 1981;

(3)

Perform data processing by sorting and accumulating the long-term mean monthly base-flow. In this way, a new series of long-term mean monthly accumulated base-flow values is obtained;

(4)

Choose the most stable (near-linear) segment and obtain the slope of the stable base-flow;

(5)

Use linear interpolation in the remaining months; finally, the mean annual base-flow is obtained.

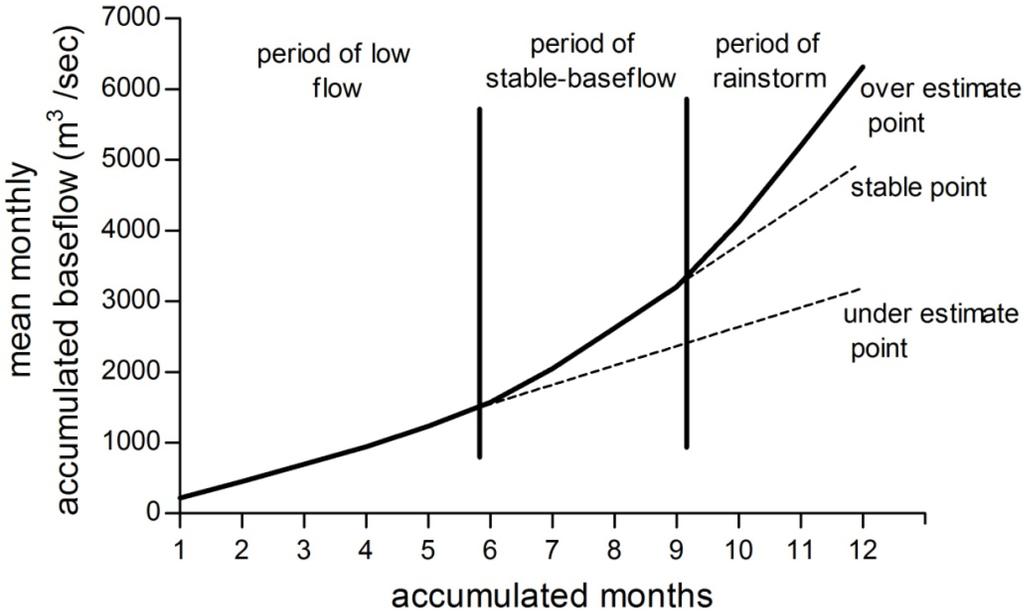
Figure 4. The diagram of the stable base-flow analysis.

Figure 4. The diagram of the stable base-flow analysis.

The dimensionless base-flow index (BFI), which is the ratio of base-flow (Q_b) to the total stream runoff (Q), is calculated for base-flow records and stable base-flow.

$$BFI=\frac{Q_{\text{b}}}{Q}$$

(4)

According to Schicht and Walton [31] the recharge can be estimated from the water budget approach using Equation (5). This equation simply states that all water reaching the water table flows out of the basin as groundwater flow, discharges to the surface, evaporates, or is held as storage:

$$R=(Q_{\text{off}}^{\text{gw}}-Q_{\text{on}}^{\text{gw}})+Q^{\text{bf}}+E{T}^{\text{gw}}+\Delta S^{\text{gw}}$$

(5)

Where, R is recharge; $Q_{\text{off}}^{\text{gw}}$ is groundwater flows out the basin; $Q_{\text{on}}^{\text{gw}}$ is groundwater flows in the basin; Q^bf is base-flow; ET^gw is ET from the groundwater table; ΔS^gw is change in groundwater storage.

Al-Khazir Gomal Basin is surrounded by mountains on all sides; therefore, the basin can be considered as a closed system and the river as the main outlet. In addition, the evapotranspiration from the water table can be neglected due to the deep groundwater table, which is 19 m on average (it reaches 40 m upstream and not more than 3 m downstream). As a result, most of the items on the right side of Equation (5), except for Q^bf, can be neglected, and the net recharge can be estimated as:

R ≅ Q^bf

(6)

3.2. Displacement Recession Curve Method

The RECESS program [32] is used to determine the master recession curve (MRC) of stream-flow records for the period 1969–1981 when all flow can be considered to be groundwater discharge. The program uses a cyclic interactive procedure for selecting several periods of continuous recession (recession segments) (Figure 6) and determines a best fit equation for the rate of recession as a function of the logarithm of flow. Then, the coefficients of this equation are used to derive the MRC and, finally, to determine the recession index (K), which represents the recession rate in days per log cycle. The critical time Tc, representing the time at which the recession become linear, can be determined from Equation (7). The detailed procedure of this process is given in Rutledge [19].

T_c = 0.2144K

(7)

The RORA program [19] is not a hydrograph separation method; rather, recharge is determined from displacement of the stream-flow recession curve according to the theory of groundwater drainage. The program uses the displacement recession curve technique of Rorabaugh [15] to estimate groundwater recharge from each storm event. To estimate the average recharge for the period 1969–1981, the value of K and the watershed area are entered, together with the daily stream-flow records, into the RORA program. The displacement recession curve procedure (Figure 5) states that after an instantaneous recharge event, if the resulting groundwater discharge (Q) at critical time (Tc) is known, the recharge can be approximated for the entire drainage basin upstream of the gage using Rutledge’s equation (Equation (8), [19]), which is modified from Rorabaugh’s equation.

$$R\cong \frac{2\left(Q_1-Q_2\right)K}{2.3026}$$

(8)

where R is the volume of recharge, Q₁ is the groundwater discharge at a critical time after the peak of the previous recession curve, Q₂ is the groundwater discharge at the critical time after the peak on the current recession curve and K is the recession index.

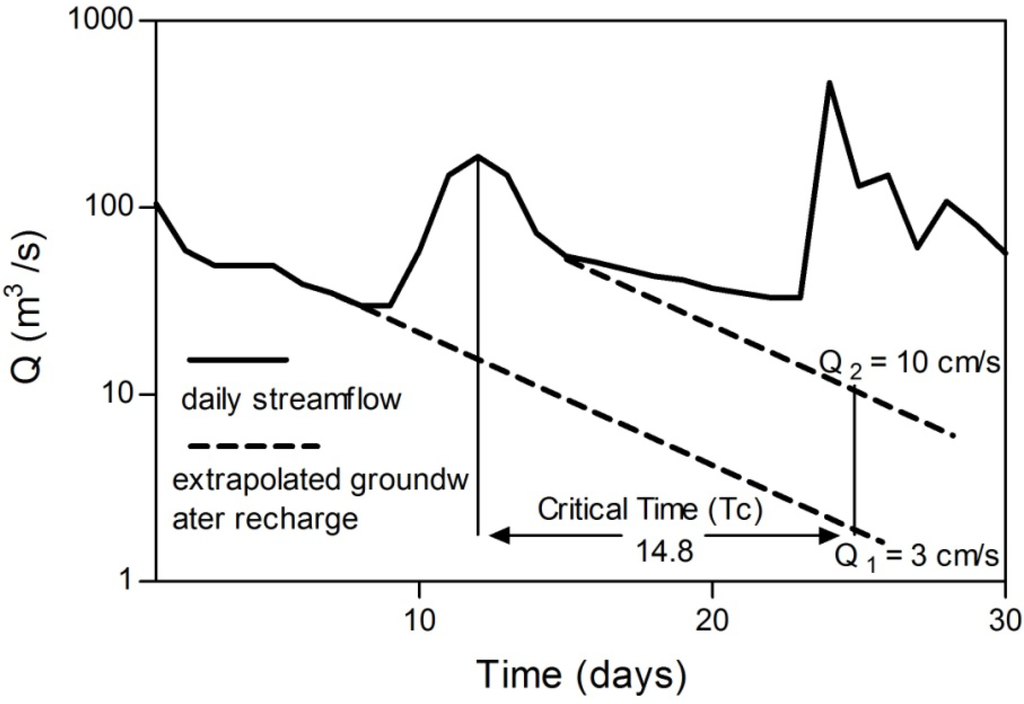
Figure 5. Procedure of the displacement recession curve method.

Figure 5. Procedure of the displacement recession curve method.

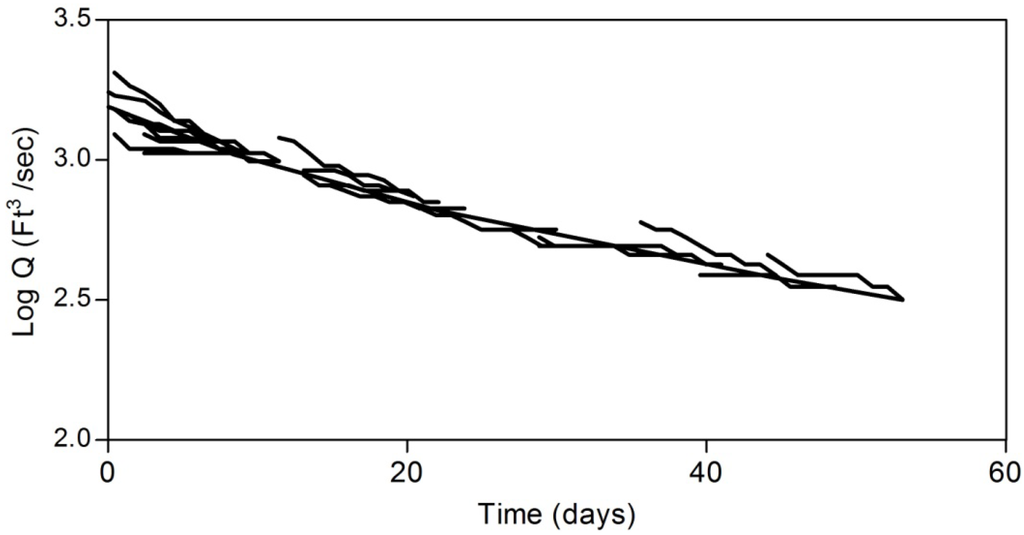
Figure 6. Recession segments and master recession curve (MRC) for the period 1969–1981 determined by the RECESS program.

Figure 6. Recession segments and master recession curve (MRC) for the period 1969–1981 determined by the RECESS program.

3.3. Water Table Fluctuation Method

The water table fluctuation method is based on the assumption that a rise in groundwater level in an unconfined aquifer is due to recharged water reaching the groundwater table; it requires data about specific yield and changes in water levels over time. The advantages of this approach include its simplicity and insensitivity to the mechanism by which water moves through the unsaturated zone [33]. However, it is difficult to determine a representative value for specific yield and to ensure that the fluctuation in water levels is a result of recharge and does not result from changes in atmospheric pressure, the presence of entrapped air or anthropogenic effects. Recharge is calculated as:

$$R=\frac{S_{\text{y }}.\Delta h}{\Delta t}$$

(9)

where R = recharge; S_y = specific yield; Δh = change in water table elevation and Δt = the time period.

4. Results and Discussion

The results of the annual base-flow separation records, annual stable base-flow and base-flow indices are shown in Table 1. The study found out that all methods were significantly correlated with each other, and the bivariate correlation coefficients for the annual base-flow calculated between the graphical method and single parameter method, Eckhardt method and local minimum method were 0.95, 0.93 and 0.89, respectively, at p < 0.01. The relatively weak relation between the graphical and local minimum methods is due to the fact that the local minimum method does not consider flow duration [34], so it overestimates base-flow in long periods of runoff (Figure 7). The outputs of the Eckhardt separation method were more reliable and closer to the graphical method. This may be due to the use of two parameters (α and BFI_max) in the digital filter base-flow, where the BFI_max parameter takes the physical properties of the basin into account.

Table 1. Annual base-flow records, stable base-flow and their base-flow indices.

Method	Base-Flow Records (m3/y)	Base-Flow Indices (BFI)	Stable Base-flow records (m3/y)	Stable Base-Flow Indices (BFI)
Graphical method	4.9 × 108	0.68	3.8 × 108	0.52
Single parameter method	5.51 × 108	0.75	4.2 × 108	0.56
Eckhardt method	5.1 × 108	0.69	3.9 × 108	0.52
Local minimum method	5.48 × 108	0.75	4.2 × 108	0.56

Table 1. Annual base-flow records, stable base-flow and their base-flow indices.

Method	Base-Flow Records (m3/y)	Base-Flow Indices (BFI)	Stable Base-flow records (m3/y)	Stable Base-Flow Indices (BFI)
Graphical method	4.9 × 108	0.68	3.8 × 108	0.52
Single parameter method	5.51 × 108	0.75	4.2 × 108	0.56
Eckhardt method	5.1 × 108	0.69	3.9 × 108	0.52
Local minimum method	5.48 × 108	0.75	4.2 × 108	0.56

If one takes climate conditions in the study area into account, for example in the case of average rainfall of 650 mm/y, potential evapotranspiration of 1400–1500 mm/y and the physical catchment properties, the base-flow index should be in the range of 0.5–0.6, depending on previous studies in regions with the same conditions [31,32,33]. Therefore, the stable base-flow was applied to the four base-flow separation methods to avoid overestimation in base-flow records. Accordingly, the stable base-flow values were used to estimate the integrated net annual recharge after applying Equations (5) and (6), and the results were 131, 131, 122 and 119 mm/y for the local minimum method, single parameter digital filter, Eckhardt method and graphical method, respectively.

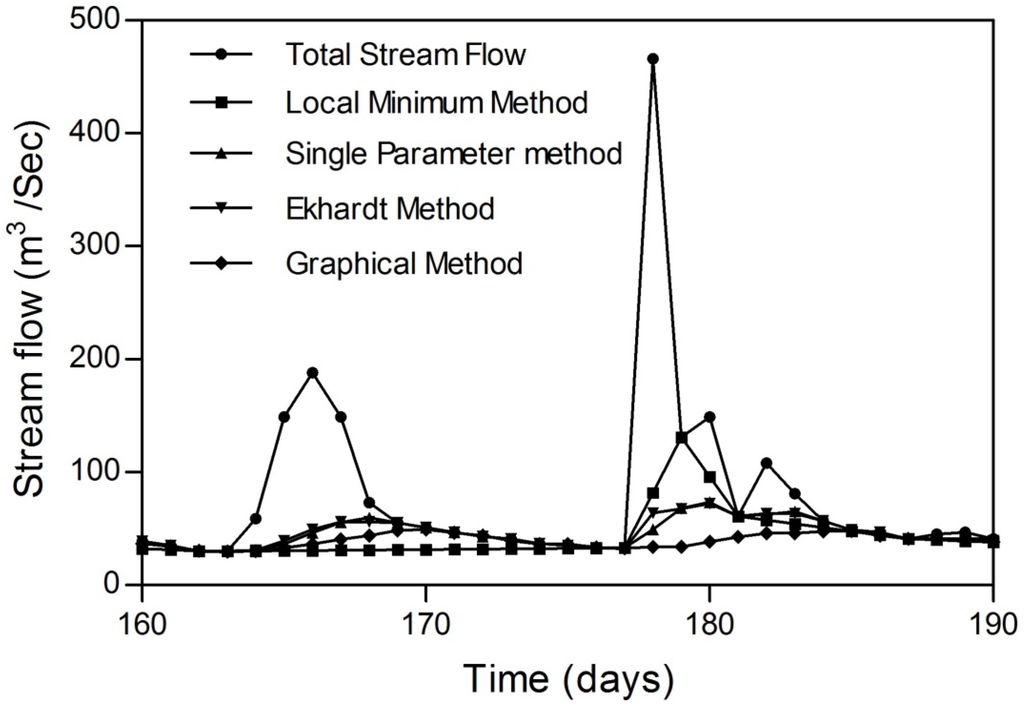
Figure 7. The base-flow separation methods.

Figure 7. The base-flow separation methods.

The high value of recharge obtained by the displacement recession curve method (157 mm/y) results from the assumption inherent in this method. This assumption states that the recharge occurs instantaneously and uniformly directly after a rainstorm [15], which is not the case, especially for large watershed areas. Therefore, this will affect the defined days that fit the requirement of antecedent recession. In spite of setting the antecedent recession as eight days (nearly double the N value), the recharge is still much higher than any of the other methods, which reflects the effect of the large watershed area in increasing the interflow and the surface runoff duration. Therefore, this method is unsuitable for estimating recharge in large areas.

Groundwater recharge estimated by the water table fluctuation method depends on the maximum (April) and minimum (October) groundwater levels for the period (2006–2011). These data are obtained from eight observation wells monitored by the Department of Well Drilling in Aqra district. The average fluctuation in these wells is 0.794 m. Seasonal change in the water table seems to increase toward the eastern side with an increase in groundwater depth and a decrease in the hydraulic conductivity. Wells near the center of the watershed show less seasonal water table fluctuation, because of the high hydraulic conductivity and mutual feeding between aquifer and river.

The specific yield was determined to be 0.14 by conducting pumping tests in six locations. Pumping tests were performed by the Directorate of Regional and Applied Geology [25]. The depth to the water table in the observation wells pre- and post-wet season is shown in Figure 8, and the locations of observation and pumping wells are shown in Figure 1. The declination of the water table with time is clear from year to year, especially in the deep groundwater wells. By applying Equation (9), the recharge is estimated to be 111.6 mm/y. The final results of the estimated recharge and the recharge percentage of annual rainfall and annual river discharge are illustrated in Figure 9.

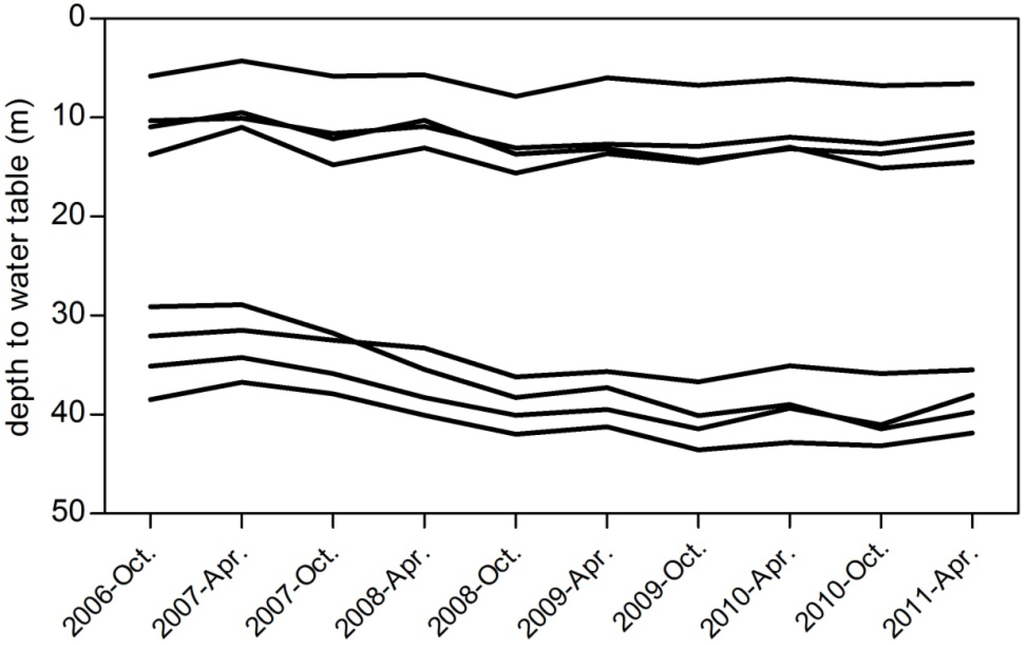
Figure 8. Depth to the water table in observation wells pre- (October) and post-wet season (April).

Figure 8. Depth to the water table in observation wells pre- (October) and post-wet season (April).

Estimation of groundwater recharge by groundwater table fluctuation (111.6 mm/y) seems more reasonable compared with the average stable base-flow (125.75 mm/y) measured by the four separation methods if one takes into consideration the climate conditions of the semiarid to dry sub-humid region. The variation in estimating groundwater recharge between the hydrograph analysis approach and the water table fluctuation approach is due to the following reasons:

• Recharge estimated by the hydrograph analysis method represents an integrated long-term recharge over a large area in different mechanisms (diffuse recharge and focused recharge through river bed leakage). However, the main source of recharge calculated by water table (WT) fluctuation is diffuse recharge, and it is less affected by indirect recharge, especially in areas far away from the main river course;
• Base-flow may be overestimated by bank storage, which is considered as a short-term storage discharge, in addition to snow melt in the spring season;
• The probability of leakage from the confined system becomes higher downstream, because the difference in hydrostatic pressure increases with the decreasing of the unconfined aquifer thickness;
• Recharge obtained by the WT fluctuation method does not represent the entire watershed, because neither monitoring wells nor pumping test wells cover the entire watershed area.

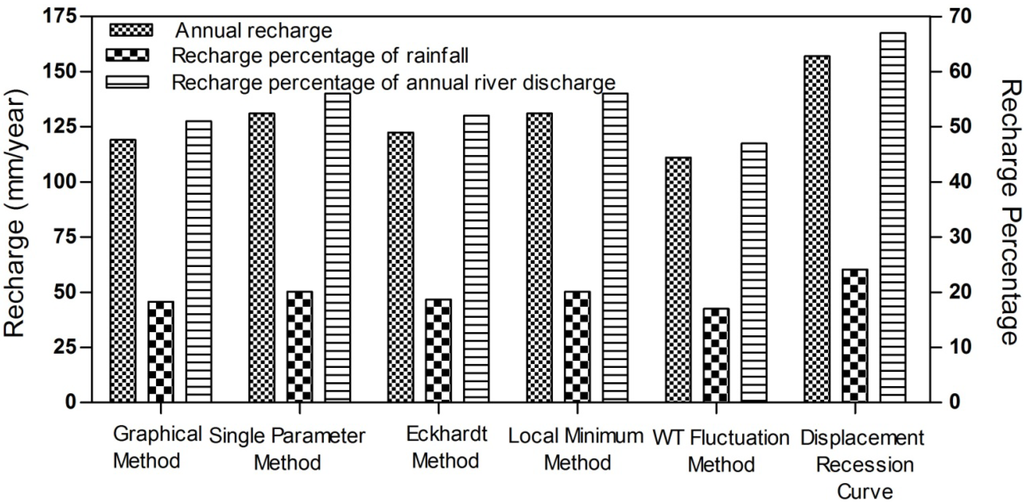
Figure 9. Estimated recharge using the base-flow separation methods (graphical method, single parameter method, Eckhardt method, local minimum method), WT fluctuation method and displacement recession curve method.

Figure 9. Estimated recharge using the base-flow separation methods (graphical method, single parameter method, Eckhardt method, local minimum method), WT fluctuation method and displacement recession curve method.

In general, the difference between recharge estimated by WT fluctuation (17% of rainfall) and the recharge estimated by the four base-flow separation methods (19.25% of rainfall) was 11.6%. This difference is due to the fact that each method uses different algorithms and depends on uncertain assumptions. The displacement recession curve method seems not to be suitable; due to the large deviation from any of the other methods (24% of rainfall). However, the results seem to be acceptable if one takes into account the high infiltration capacity of the basin, which consists mainly of gravel and sand, the presence of the direct (diffuse) recharge and the indirect (focused) recharge mechanism beneath Al-Khazir River and the ephemeral streams.

The chemical analyses of the groundwater in this basin (not presented here) support the reliability of the results (the groundwater type was Ca-HCO₃, and the average total dissolved solid (TDS) and Cl were 406 and 3.5 mg/L, respectively). This indicates renewable groundwater, the short residence time of the water near the surface and a high infiltration capacity. In addition, the analysis of stable isotopes (deuterium and O¹⁸) of groundwater showed a match and a very slight shift from the local meteoric water line, which means that the recharged water is not affected by high evaporation. Moreover, rainfall happens in the cold months when evapotranspiration is minimal, and thus, more water will be available to contribute to groundwater recharge.

5. Conclusions

In this study, the long-term integrated groundwater recharge was estimated in semiarid to dry to subhumid Al-Khazir Gomal Basin using the available daily river discharge and groundwater table fluctuation data. In spite of the limitations and simple assumptions inherent in these approaches, they are considered valuable approaches, because they do not require detailed knowledge of land use, land cover, soil characteristics or any complex numerical model; they only require long-term daily stream-flow records, monitored groundwater levels and the specific yield of the aquifer materials. The recharge estimated by the methods applied is useful for regional studies and for validating the mass balance techniques in the case of unconfined aquifers [30], where recharge in mass the balance technique is calculated as a residual component with high uncertainty.

The Khazir River system is considered pristine so far, and the groundwater is under sustainable use. The main use of groundwater in the basin is for domestic use. However, when planning future industrial and agricultural projects, the local authorities in the basin should take into consideration that the annual groundwater exploitation should not exceed half of the minimum recharge estimated by these methods (1.7 × 10⁸ m³/y) to ensure a sustainable use of groundwater and to save the river environment.