Identifying Major Factors Affecting Groundwater Change in the North China Plain with Grey Relational Analysis
Abstract
:1. Introduction
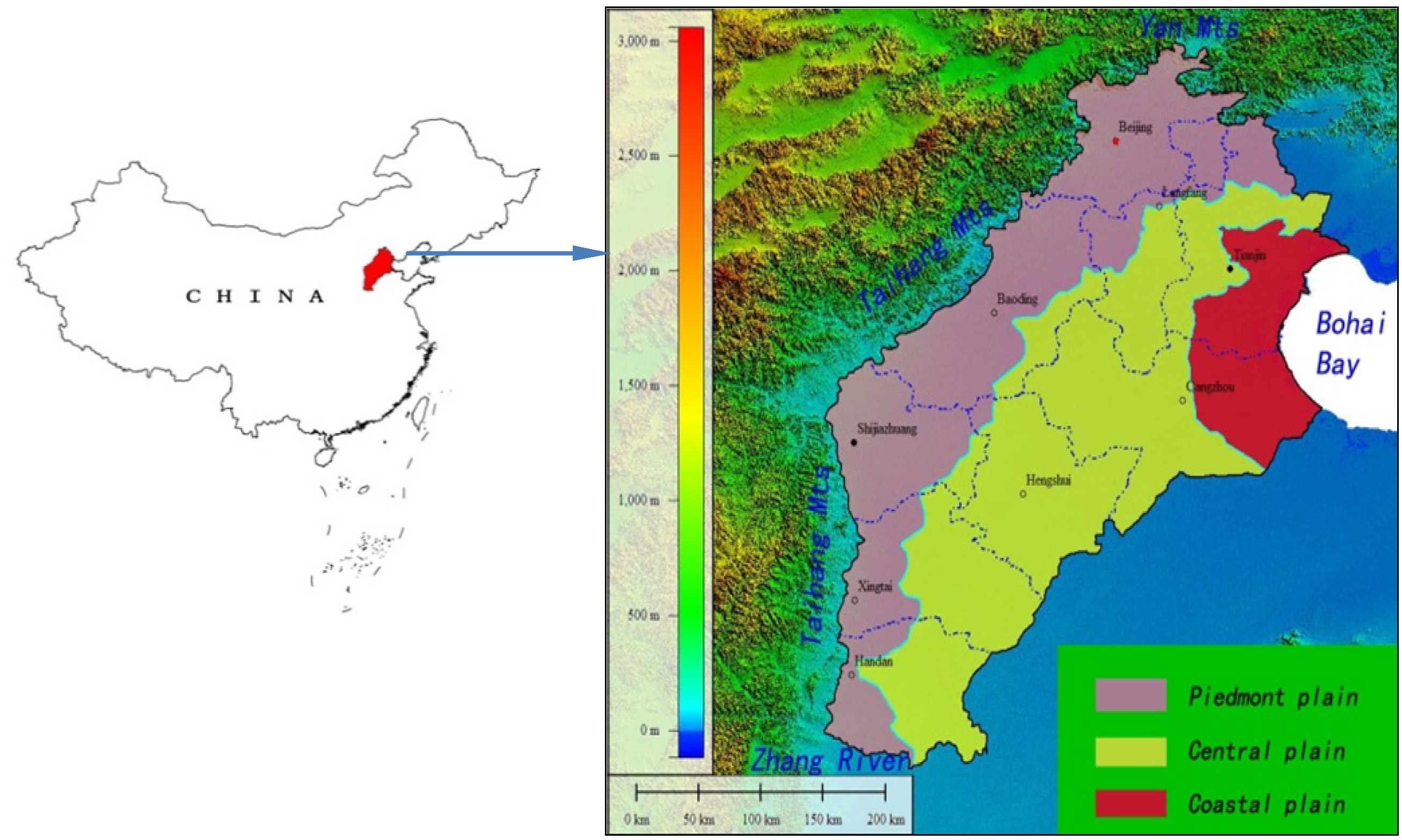
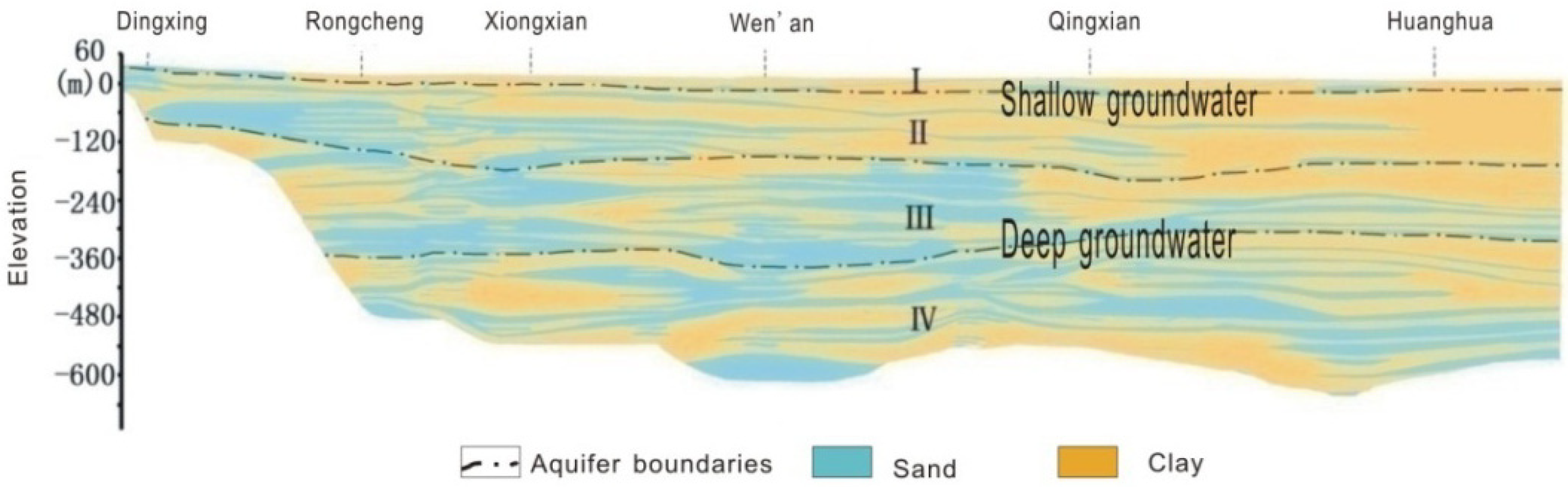
2. Study Area and Hydrogeologic Setting
3. Methods
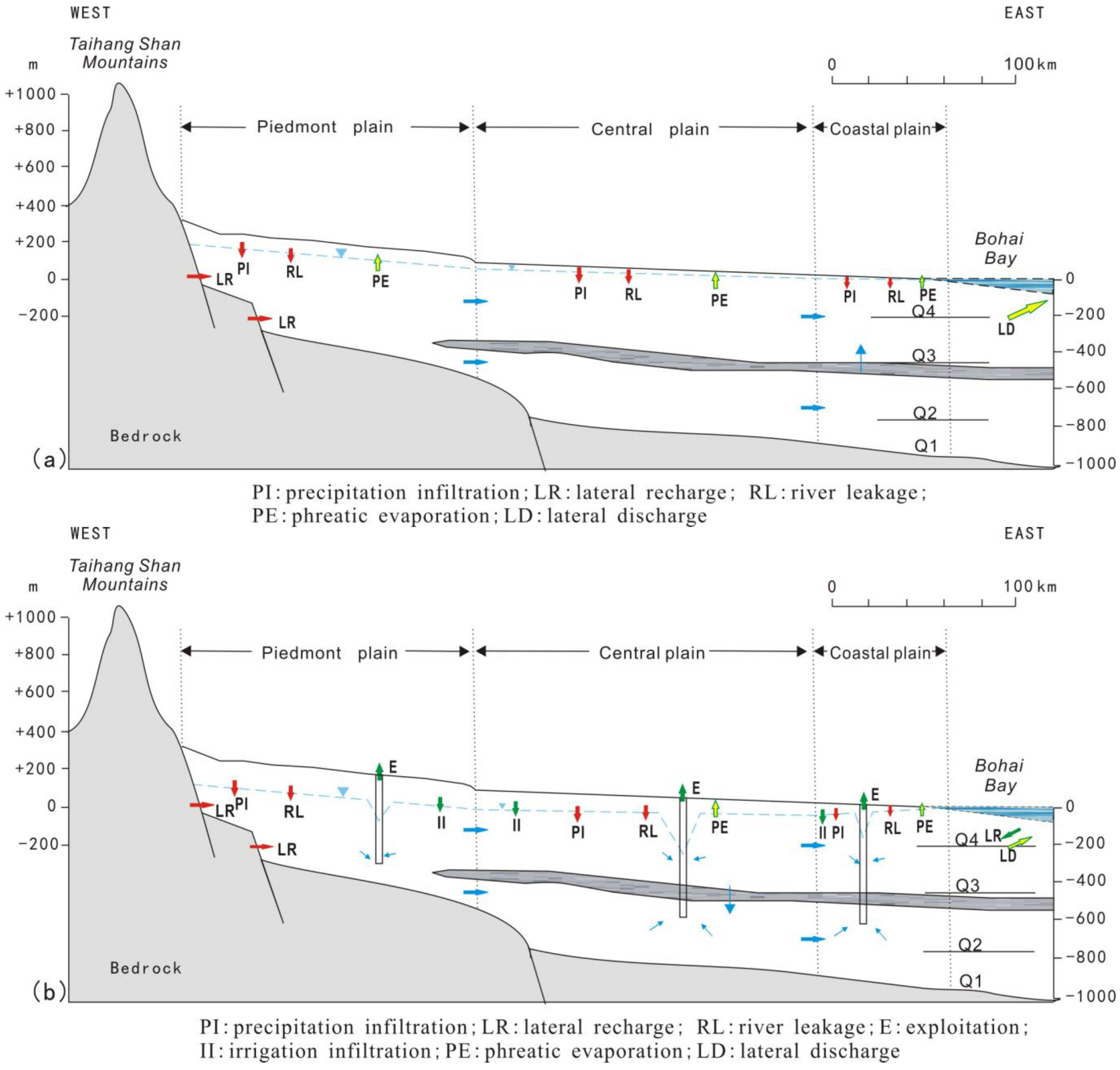
3.1. Groundwater Flow Model
3.2. Grey Relational Analysis
3.2.1. Basic Idea
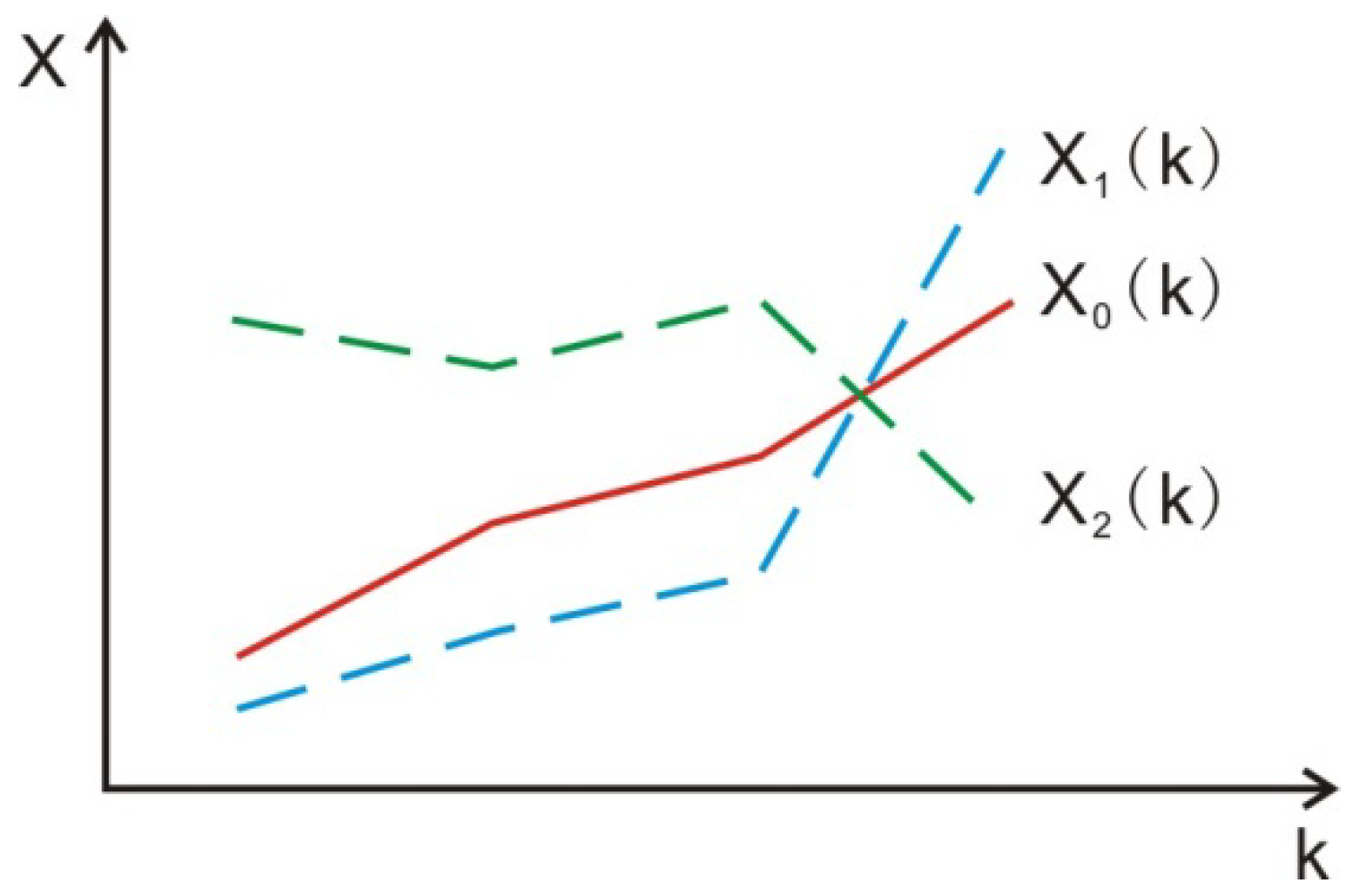
3.2.2. Basic Approach







4. Results and Discussion
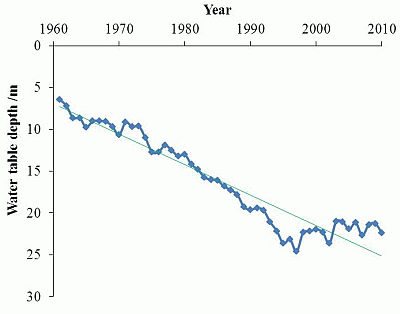
4.1. Groundwater Flow Dynamics
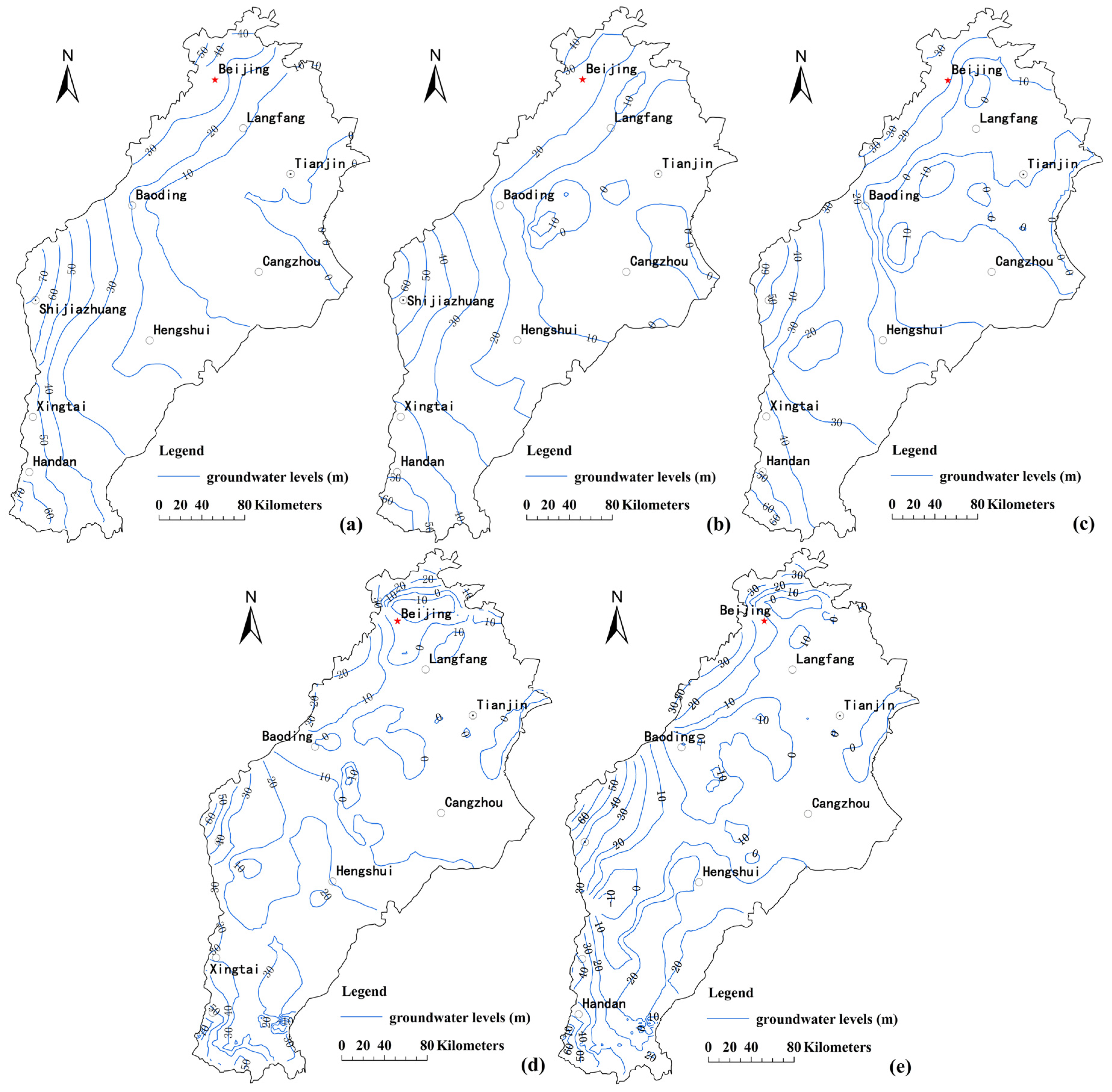
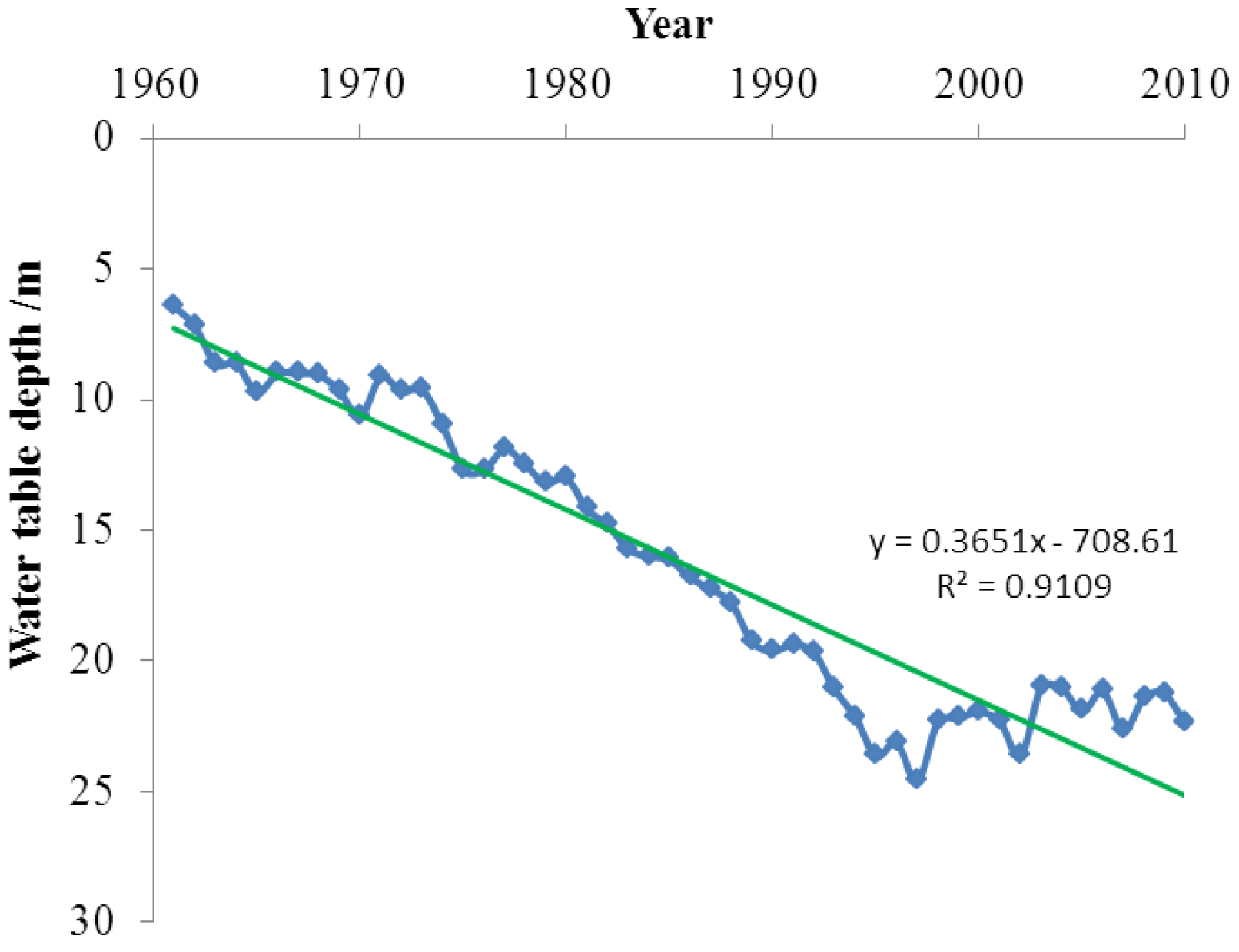
4.2. Factors Influencing Groundwater Levels
4.2.1. Climate Change
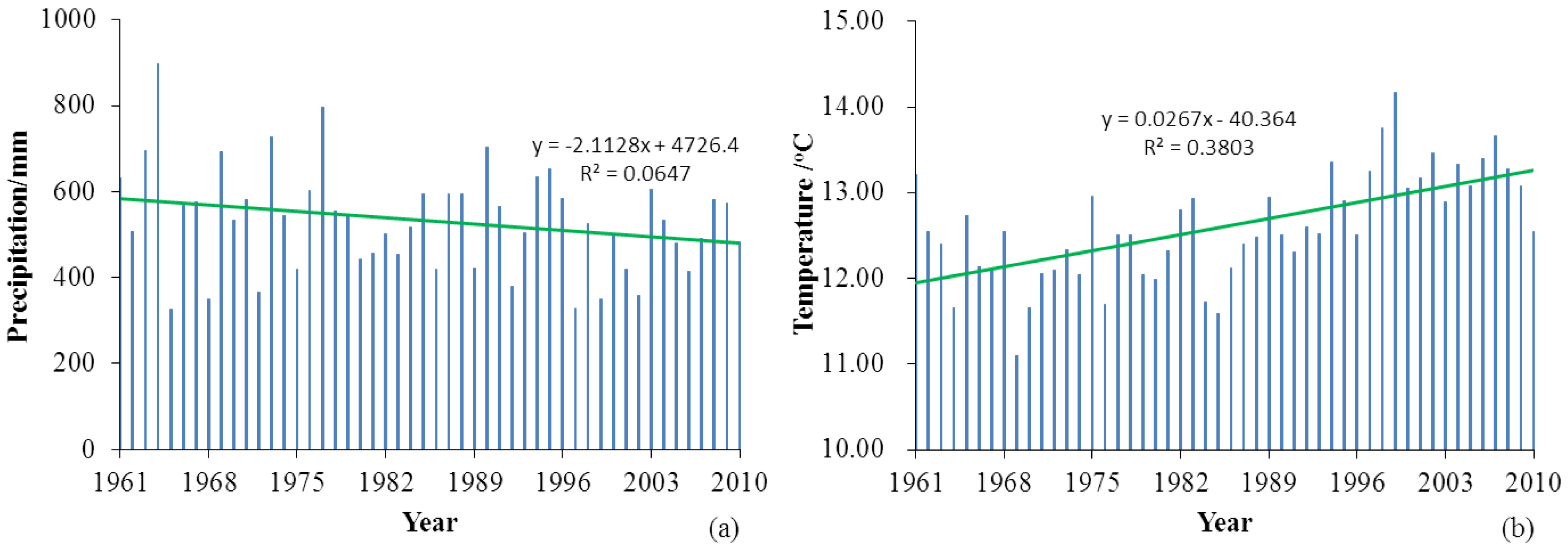
| Item | Mann–Kendall test | ||
|---|---|---|---|
| Z0 | β | H0 | |
| Precipitation | −1.58 | −1.78 | S |
| Temperature | 4.48 | 0.028 | C |
4.2.2. Human Activities
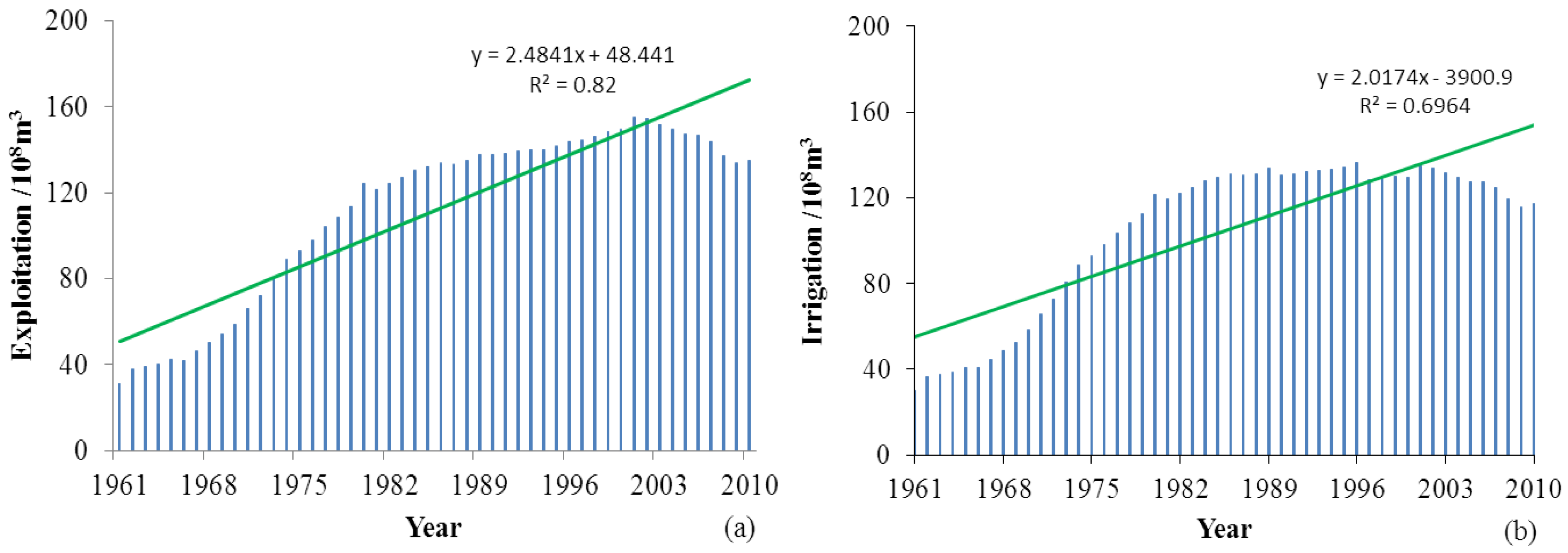
4.3. GRA between Water Table Depth and Influencing Factors
| n | X0 | X1 | X2 | X3 | X4 | X5 |
|---|---|---|---|---|---|---|
| 1 | 0.397 | 0.863 | 1.515 | 0.277 | 1.886 | 0.551 |
| 2 | 0.444 | 0.690 | 1.511 | 0.337 | 1.886 | 0.670 |
| 3 | 0.533 | 0.947 | 1.386 | 0.347 | 1.886 | 0.689 |
| 4 | 0.532 | 1.224 | 1.039 | 0.357 | 1.886 | 0.709 |
| 5 | 0.601 | 0.447 | 1.483 | 0.378 | 1.886 | 0.753 |
| 6 | 0.556 | 0.776 | 1.261 | 0.377 | 1.886 | 0.750 |
| 7 | 0.555 | 0.787 | 1.248 | 0.413 | 1.886 | 0.822 |
| 8 | 0.559 | 0.478 | 1.513 | 0.450 | 1.886 | 0.895 |
| 9 | 0.597 | 0.944 | 1.203 | 0.487 | 1.886 | 0.969 |
| 10 | 0.658 | 0.727 | 1.227 | 0.524 | 1.886 | 1.076 |
| 11 | 0.564 | 0.963 | 1.623 | 0.588 | 1.252 | 0.643 |
| 12 | 0.599 | 0.609 | 1.873 | 0.647 | 1.252 | 0.711 |
| 13 | 0.593 | 1.207 | 1.519 | 0.720 | 1.252 | 0.791 |
| 14 | 0.679 | 0.903 | 1.601 | 0.796 | 1.252 | 0.871 |
| 15 | 0.783 | 0.695 | 1.572 | 0.832 | 1.252 | 0.909 |
| 16 | 0.784 | 0.998 | 1.449 | 0.874 | 1.252 | 0.961 |
| 17 | 0.734 | 1.322 | 1.475 | 0.929 | 1.252 | 1.015 |
| 18 | 0.772 | 0.919 | 1.525 | 0.970 | 1.252 | 1.061 |
| 19 | 0.815 | 0.905 | 1.385 | 1.018 | 1.252 | 1.101 |
| 20 | 0.802 | 0.735 | 1.408 | 1.109 | 1.252 | 1.191 |
| 21 | 0.876 | 0.851 | 0.843 | 1.088 | 0.514 | 0.913 |
| 22 | 0.913 | 0.938 | 0.840 | 1.112 | 0.514 | 0.933 |
| 23 | 0.971 | 0.849 | 0.790 | 1.138 | 0.514 | 0.955 |
| 24 | 0.988 | 0.966 | 0.761 | 1.168 | 0.514 | 0.980 |
| 25 | 0.995 | 1.109 | 0.649 | 1.184 | 0.514 | 0.993 |
| 26 | 1.038 | 0.782 | 0.805 | 1.196 | 0.514 | 1.005 |
| 27 | 1.065 | 1.108 | 0.707 | 1.193 | 0.514 | 0.999 |
| 28 | 1.099 | 1.108 | 0.752 | 1.208 | 0.514 | 1.005 |
| 29 | 1.189 | 0.787 | 0.811 | 1.234 | 0.514 | 1.026 |
| 30 | 1.210 | 1.313 | 0.654 | 1.232 | 0.514 | 1.001 |
| 31 | 1.197 | 1.293 | 0.629 | 1.235 | 0.737 | 1.143 |
| 32 | 1.215 | 0.868 | 0.707 | 1.249 | 0.737 | 1.155 |
| 33 | 1.302 | 1.154 | 0.705 | 1.251 | 0.737 | 1.158 |
| 34 | 1.367 | 1.448 | 0.705 | 1.253 | 0.737 | 1.161 |
| 35 | 1.459 | 1.493 | 0.690 | 1.265 | 0.737 | 1.171 |
| 36 | 1.427 | 1.335 | 0.671 | 1.287 | 0.737 | 1.191 |
| 37 | 1.519 | 0.752 | 0.740 | 1.294 | 0.737 | 1.119 |
| 38 | 1.379 | 1.201 | 0.635 | 1.308 | 0.737 | 1.127 |
| 39 | 1.370 | 0.801 | 0.705 | 1.329 | 0.737 | 1.136 |
| 40 | 1.355 | 1.146 | 0.701 | 1.336 | 0.737 | 1.130 |
| 41 | 1.377 | 0.980 | 0.833 | 1.388 | 0.737 | 1.234 |
| 42 | 1.459 | 0.840 | 0.834 | 1.382 | 0.596 | 1.228 |
| 43 | 1.298 | 1.418 | 0.688 | 1.356 | 0.596 | 1.205 |
| 44 | 1.299 | 1.247 | 0.726 | 1.335 | 0.596 | 1.187 |
| 45 | 1.353 | 1.125 | 0.729 | 1.315 | 0.596 | 1.169 |
| 46 | 1.307 | 0.967 | 0.641 | 1.314 | 0.596 | 1.168 |
| 47 | 1.399 | 1.149 | 0.656 | 1.287 | 0.596 | 1.144 |
| 48 | 1.320 | 1.361 | 0.525 | 1.228 | 0.596 | 1.092 |
| 49 | 1.313 | 1.343 | 0.523 | 1.195 | 0.596 | 1.063 |
| 50 | 1.383 | 1.132 | 0.525 | 1.209 | 0.596 | 1.074 |
| n | Δ01 | Δ02 | Δ03 | Δ04 | Δ05 |
|---|---|---|---|---|---|
| 1 | 0.466 | 1.118 | 0.120 | 1.489 | 0.154 |
| 2 | 0.246 | 1.068 | 0.107 | 1.442 | 0.226 |
| 3 | 0.415 | 0.854 | 0.186 | 1.354 | 0.157 |
| 4 | 0.692 | 0.507 | 0.175 | 1.354 | 0.177 |
| 5 | 0.154 | 0.883 | 0.222 | 1.286 | 0.152 |
| 6 | 0.220 | 0.705 | 0.179 | 1.330 | 0.194 |
| 7 | 0.231 | 0.692 | 0.142 | 1.331 | 0.267 |
| 8 | 0.081 | 0.954 | 0.109 | 1.327 | 0.336 |
| 9 | 0.347 | 0.607 | 0.110 | 1.289 | 0.372 |
| 10 | 0.069 | 0.569 | 0.134 | 1.228 | 0.418 |
| 11 | 0.399 | 1.059 | 0.024 | 0.688 | 0.079 |
| 12 | 0.009 | 1.274 | 0.048 | 0.652 | 0.112 |
| 13 | 0.614 | 0.926 | 0.127 | 0.659 | 0.198 |
| 14 | 0.224 | 0.922 | 0.117 | 0.573 | 0.192 |
| 15 | 0.088 | 0.789 | 0.048 | 0.469 | 0.126 |
| 16 | 0.214 | 0.665 | 0.090 | 0.468 | 0.177 |
| 17 | 0.588 | 0.741 | 0.194 | 0.517 | 0.281 |
| 18 | 0.148 | 0.753 | 0.199 | 0.480 | 0.290 |
| 19 | 0.091 | 0.571 | 0.203 | 0.437 | 0.287 |
| 20 | 0.068 | 0.606 | 0.307 | 0.449 | 0.389 |
| 21 | 0.026 | 0.033 | 0.212 | 0.362 | 0.037 |
| 22 | 0.025 | 0.074 | 0.199 | 0.399 | 0.020 |
| 23 | 0.122 | 0.181 | 0.167 | 0.456 | 0.016 |
| 24 | 0.022 | 0.227 | 0.180 | 0.473 | 0.008 |
| 25 | 0.114 | 0.346 | 0.188 | 0.481 | 0.002 |
| 26 | 0.257 | 0.233 | 0.158 | 0.524 | 0.034 |
| 27 | 0.044 | 0.358 | 0.128 | 0.550 | 0.066 |
| 28 | 0.008 | 0.347 | 0.109 | 0.585 | 0.094 |
| 29 | 0.403 | 0.379 | 0.044 | 0.675 | 0.164 |
| 30 | 0.103 | 0.556 | 0.022 | 0.696 | 0.209 |
| 31 | 0.096 | 0.567 | 0.039 | 0.459 | 0.054 |
| 32 | 0.347 | 0.508 | 0.034 | 0.477 | 0.060 |
| 33 | 0.148 | 0.597 | 0.050 | 0.564 | 0.144 |
| 34 | 0.080 | 0.662 | 0.114 | 0.630 | 0.206 |
| 35 | 0.034 | 0.769 | 0.194 | 0.722 | 0.288 |
| 36 | 0.092 | 0.756 | 0.140 | 0.690 | 0.236 |
| 37 | 0.767 | 0.779 | 0.225 | 0.782 | 0.400 |
| 38 | 0.178 | 0.744 | 0.071 | 0.642 | 0.252 |
| 39 | 0.570 | 0.665 | 0.041 | 0.633 | 0.234 |
| 40 | 0.209 | 0.654 | 0.019 | 0.617 | 0.224 |
| 41 | 0.397 | 0.544 | 0.011 | 0.640 | 0.143 |
| 42 | 0.619 | 0.625 | 0.077 | 0.863 | 0.231 |
| 43 | 0.120 | 0.610 | 0.058 | 0.702 | 0.093 |
| 44 | 0.052 | 0.573 | 0.036 | 0.703 | 0.112 |
| 45 | 0.228 | 0.624 | 0.038 | 0.757 | 0.184 |
| 46 | 0.340 | 0.666 | 0.008 | 0.710 | 0.139 |
| 47 | 0.250 | 0.743 | 0.112 | 0.803 | 0.256 |
| 48 | 0.041 | 0.795 | 0.092 | 0.724 | 0.228 |
| 49 | 0.030 | 0.790 | 0.118 | 0.717 | 0.251 |
| 50 | 0.251 | 0.858 | 0.175 | 0.787 | 0.309 |
| n | ξ1 | ξ2 | ξ3 | ξ4 | ξ5 |
|---|---|---|---|---|---|
| 1 | 0.609 | 0.393 | 0.860 | 0.327 | 0.827 |
| 2 | 0.748 | 0.405 | 0.874 | 0.334 | 0.764 |
| 3 | 0.637 | 0.460 | 0.798 | 0.349 | 0.824 |
| 4 | 0.512 | 0.589 | 0.807 | 0.349 | 0.806 |
| 5 | 0.827 | 0.451 | 0.767 | 0.361 | 0.829 |
| 6 | 0.769 | 0.508 | 0.803 | 0.353 | 0.791 |
| 7 | 0.760 | 0.512 | 0.838 | 0.353 | 0.732 |
| 8 | 0.902 | 0.432 | 0.872 | 0.353 | 0.685 |
| 9 | 0.677 | 0.545 | 0.871 | 0.360 | 0.662 |
| 10 | 0.915 | 0.561 | 0.846 | 0.371 | 0.635 |
| 11 | 0.646 | 0.406 | 0.972 | 0.514 | 0.905 |
| 12 | 0.990 | 0.363 | 0.941 | 0.527 | 0.868 |
| 13 | 0.542 | 0.439 | 0.853 | 0.524 | 0.788 |
| 14 | 0.765 | 0.440 | 0.863 | 0.559 | 0.792 |
| 15 | 0.894 | 0.479 | 0.940 | 0.608 | 0.854 |
| 16 | 0.774 | 0.522 | 0.892 | 0.609 | 0.805 |
| 17 | 0.553 | 0.495 | 0.791 | 0.584 | 0.722 |
| 18 | 0.833 | 0.491 | 0.787 | 0.602 | 0.716 |
| 19 | 0.891 | 0.560 | 0.783 | 0.625 | 0.718 |
| 20 | 0.917 | 0.545 | 0.704 | 0.618 | 0.652 |
| 21 | 0.969 | 0.959 | 0.776 | 0.668 | 0.955 |
| 22 | 0.970 | 0.910 | 0.786 | 0.646 | 0.977 |
| 23 | 0.858 | 0.802 | 0.814 | 0.614 | 0.982 |
| 24 | 0.974 | 0.764 | 0.803 | 0.606 | 0.993 |
| 25 | 0.867 | 0.678 | 0.796 | 0.602 | 1.000 |
| 26 | 0.740 | 0.758 | 0.823 | 0.581 | 0.959 |
| 27 | 0.946 | 0.671 | 0.852 | 0.569 | 0.919 |
| 28 | 0.992 | 0.677 | 0.872 | 0.554 | 0.888 |
| 29 | 0.644 | 0.658 | 0.945 | 0.518 | 0.818 |
| 30 | 0.878 | 0.567 | 0.974 | 0.511 | 0.778 |
| 31 | 0.885 | 0.562 | 0.952 | 0.613 | 0.934 |
| 32 | 0.677 | 0.589 | 0.958 | 0.604 | 0.926 |
| 33 | 0.833 | 0.549 | 0.938 | 0.563 | 0.836 |
| 34 | 0.903 | 0.523 | 0.867 | 0.536 | 0.781 |
| 35 | 0.958 | 0.486 | 0.791 | 0.501 | 0.717 |
| 36 | 0.890 | 0.490 | 0.840 | 0.513 | 0.756 |
| 37 | 0.486 | 0.482 | 0.765 | 0.482 | 0.645 |
| 38 | 0.805 | 0.494 | 0.914 | 0.531 | 0.743 |
| 39 | 0.561 | 0.522 | 0.949 | 0.534 | 0.757 |
| 40 | 0.778 | 0.526 | 0.978 | 0.541 | 0.765 |
| 41 | 0.647 | 0.572 | 0.988 | 0.532 | 0.837 |
| 42 | 0.540 | 0.538 | 0.906 | 0.457 | 0.760 |
| 43 | 0.861 | 0.544 | 0.929 | 0.509 | 0.888 |
| 44 | 0.935 | 0.559 | 0.955 | 0.508 | 0.868 |
| 45 | 0.762 | 0.538 | 0.953 | 0.490 | 0.800 |
| 46 | 0.682 | 0.522 | 0.993 | 0.505 | 0.841 |
| 47 | 0.745 | 0.494 | 0.868 | 0.475 | 0.741 |
| 48 | 0.949 | 0.477 | 0.890 | 0.501 | 0.762 |
| 49 | 0.964 | 0.479 | 0.862 | 0.503 | 0.744 |
| 50 | 0.744 | 0.458 | 0.808 | 0.480 | 0.702 |
| γi | 0.792 | 0.549 | 0.868 | 0.511 | 0.809 |
| Grey relational order | 3 | 4 | 1 | 5 | 2 |
5. Conclusions
Acknowledgements
Authors Contributions
Conflicts of Interest
References
- Kemper, K. Groundwater—From development to management. Hydrogeol. J. 2004, 12, 3–5. [Google Scholar] [CrossRef]
- De Vries, J.; Simmers, I. Groundwater recharge: An overview of processes and challenges. Hydrogeol. J. 2002, 10, 5–17. [Google Scholar] [CrossRef]
- Chen, H.; Wang, S.; Gao, Z.; Hu, Y. Artificial Neural Network Approach for Quantifying Climate Change and Human Activities Impacts on Shallow Groundwater Level—A Case Study of Wuqiao in North China Plain; IEEE: New York, NY, USA, 2010. [Google Scholar]
- Hsu, K.-C.; Yeh, H.-F.; Chen, Y.-C.; Lee, C.-H.; Wang, C.-H.; Chiu, F.-S. Basin-scale groundwater response to precipitation variation and anthropogenic pumping in Chih-ben watershed, Taiwan. Hydrogeol. J. 2012, 20, 499–517. [Google Scholar] [CrossRef]
- Hao, X.; Chen, Y.; Xu, C.; Li, W. Impacts of climate change and human activities on the surface runoff in the Tarim river basin over the last fifty years. Water Resour. Manag. 2008, 22, 1159–1171. [Google Scholar] [CrossRef]
- Bloomfield, J.P.; Gaus, I.; Wade, S.D. A method for investigating the potential impacts of climate-change scenarios on annual minimum groundwater levels. Water Environ. J. 2003, 17, 86–91. [Google Scholar] [CrossRef]
- Scibek, J.; Allen, D.M. Modeled impacts of predicted climate change on recharge and groundwater levels. Water Resour. Res. 2006, 42, W11405. [Google Scholar]
- Waibel, M.S.; Gannett, M.W.; Chang, H.; Hulbe, C.L. Spatial variability of the response to climate change in regional groundwater systems—Examples from simulations in the deschutes basin, oregon. J. Hydrol. 2013, 486, 187–201. [Google Scholar] [CrossRef]
- Konikow, L.; Kendy, E. Groundwater depletion: A global problem. Hydrogeol. J. 2005, 13, 317–320. [Google Scholar] [CrossRef]
- Shah, T.; Molden, D.; Sakthivadivel, R.; Seckler, D. Global groundwater situation: Opportunities and challenges. Eco. Polit. Wkly. 2001, 36, 4142–4150. [Google Scholar]
- Wada, Y.; van Beek, L.P.H.; van Kempen, C.M.; Reckman, J.W.T.M.; Vasak, S.; Bierkens, M.F.P. Global depletion of groundwater resources. Geophys. Res. Lett. 2010, 37, L20402. [Google Scholar]
- Manca, F.; Capelli, G.; La Vigna, F.; Mazza, R.; Pascarella, A. Wind-induced salt-wedge intrusion in the Tiber river mouth (Rome–Central Italy). Environ. Earth Sci. 2014. [Google Scholar] [CrossRef]
- Custodio, E. Aquifer overexploitation: What does it mean? Hydrogeol. J. 2002, 10, 254–277. [Google Scholar] [CrossRef]
- Zheng, C.; Liu, J.; Cao, G.; Kendy, E.; Wang, H.; Jia, Y. Can China cope with its water crisis?—Perspectives from the North China Plain. Ground Water 2010, 48, 350–354. [Google Scholar] [CrossRef]
- Liu, C.; Yu, J.; Kendy, E. Groundwater exploitation and its impact on the environment in the North China Plain. Water Int. 2001, 26, 265–272. [Google Scholar] [CrossRef]
- Fei, Y.; Zhang, Z.; Zhang, F.E.; Wang, Z.; Chen, Z.; Chen, J.; Qian, Y.; Li, Y. An analysis of the influence of human activity and climate change on water resources of the North China Plain. Acta Geosci. Sin. 2007, 28, 567–571. (In Chinese) [Google Scholar]
- Fei, Y.; Miao, J.; Zhang, Z.; Chen, Z.; Song, H.; Yang, M. Analysis on evolution of groundwater depression cones and its leading factors in North China Plain. Resour. Sci. 2009, 31, 394–399. (In Chinese) [Google Scholar]
- Zhu, L.; Gong, H.; Li, X.; Li, Y.; Su, X.; Guo, G. Comprehensive analysis and artificial intelligent simulation of land subsidence of Beijing, China. Chin. Geogr. Sci. 2013, 23, 237–248. [Google Scholar] [CrossRef]
- Zhang, Z.; Fei, Y.; Chen, Z.; Zhao, Z.; Xie, Z.; Wang, Y.; Miao, J.; Yang, L.; Shao, J.; Jin, M.; et al. Investigation and Assessment of Sustainable Utilization of Groundwater Resources in the North China Plain; Geological Publishing House: Beijing, China, 2009. [Google Scholar]
- Yo-Ping, H.; Chi-Chang, H. The integration and application of fuzzy and grey modeling methods. Fuzzy Sets Syst. 1996, 78, 107–119. [Google Scholar] [CrossRef]
- Ju-Long, D. Control problems of grey systems. Syst. Control Letters 1982, 1, 288–294. [Google Scholar] [CrossRef]
- Deng, J. The theory and method of socioeconomic grey systems. Soc. Sci. China 1984, 6, 47–60. (In Chinese) [Google Scholar]
- Wong, H.; Hu, B.; Ip, W.; Xia, J. Change-point analysis of hydrological time series using grey relational method. J. hydrol. 2006, 324, 323–338. [Google Scholar] [CrossRef]
- Lin, J.; Lin, C. The use of the orthogonal array with grey relational analysis to optimize the electrical discharge machining process with multiple performance characteristics. Int. J. Mach. Tools Manuf. 2002, 42, 237–244. [Google Scholar] [CrossRef]
- Kung, C.-Y.; Wen, K.-L. Applying grey relational analysis and grey decision-making to evaluate the relationship between company attributes and its financial performance—A case study of venture capital enterprises in taiwan. Decis. Support. Syst. 2007, 43, 842–852. [Google Scholar] [CrossRef]
- Gau, H.S.; Hsieh, C.Y.; Liu, C.W. Application of grey correlation method to evaluate potential groundwater recharge sites. Stoch. Environ. Res. Risk Assess. 2006, 20, 407–421. [Google Scholar] [CrossRef]
- Du, W.; Wei, X.; Li, P.; Li, P.; Han, Y. Dynamic evolutionary tendency of groundwater in irrigationdistrict in changing environment and its driving factors. J. Drain. Irrig. Mach. Eng. 2013, 31, 993–999. (In Chinese) [Google Scholar]
- Yeh, Y.; Su, M.; Tsou, I. Forecasting of groundwater level using grey modeling. J. Taiwan Water Conserv. 1995, 43, 66–73. [Google Scholar]
- Chen, W. Groundwater in Hebei Province; Earthquake Publishing House: Beijing, China, 1999. [Google Scholar]
- McDonald, M.G.; Harbaugh, A.W. A Modular Three-Dimensional Finite-Difference Ground-Water Flow Model; Scientific Publications Company: Reston, VA, USA, 1984. [Google Scholar]
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; McDonald, M.G. Modflow-2000, the US Geological Survey Modular Ground-Water Model: User Guide to Modularization Concepts and the Ground-Water Flow Process; US Geological Survey: Reston, VA, USA, 2000.
- Harbaugh, A.W. Modflow-2005, the US Geological Survey Modular Ground-Water Model: The Ground-Water Flow Process; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2005.
- La Vigna, F.; Demiray, Z.; Mazza, R. Exploring the use of alternative groundwater models to understand the hydrogeological flow processes in an alluvial context (Tiber river, Rome, Italy). Environ. Earth Sci. 2014, 71, 1115–1121. [Google Scholar] [CrossRef]
- La Vigna, F.; Mazza, R.; Capelli, G. Detecting the flow relationships between deep and shallow aquifers in an exploited groundwater system, using long-term monitoring data and quantitative hydrogeology: The Acque Albule basin case (Rome, Italy). Hydrol. Process. 2013, 27, 3159–3173. [Google Scholar]
- Zhang, Z.; Shen, Z.; Xue, Y. Groundwater Environment Evolution in the North China Plain; Geological Publishing House: Beijing, China, 2000. [Google Scholar]
- Zhang, Y.; Li, G. Long-term evolution of cones of depression in shallow aquifers in the North China Plain. Water 2013, 5, 677–697. [Google Scholar] [CrossRef]
- Deng, J. The Primary Methods of Grey System Theory; Hua Zhong University of Science and Technology Press: Wuhan, China, 2005. [Google Scholar]
- Cao, G.; Zheng, C.; Scanlon, B.R.; Liu, J.; Li, W. Use of flow modeling to assess sustainability of groundwater resources in the North China Plain. Water Resour. Res. 2013, 49, 159–175. [Google Scholar] [CrossRef]
- Xia, J.; Liu, C.; Ding, Y.; Jia, S.; Lin, C. Water Issues Vision in China; Science Publishing House: Beijing, China, 2011. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Oxford: Griffin, UK, 1955. [Google Scholar]
- Partal, T.; Kahya, E. Trend analysis in turkish precipitation data. Hydrol. Process. 2006, 20, 2011–2026. [Google Scholar] [CrossRef]
- Ip, W.C.; Zhang, L.; Wong, H.; Xia, J. Multi-scale variability and trends of precipitation in North China. Water Resour. 2011, 38, 18–28. [Google Scholar] [CrossRef]
- Kuang, Z.; Ji, Z.; Lin, Y. Wavelet analysis of rainfall data in North China. Clim. Environ. Res. 2000, 5, 312–317. (In Chinese) [Google Scholar]
- Tan, F.; Wang, J.; Song, Y. Characteristic of cliamte change in the North China Plain for recent 45 years. Meteorol. Mon. 2010, 36, 40–45. (In Chinese) [Google Scholar]
- Fei, Y. Evolution and Conservation of Groundwater in Hebei Plain to the South of Beijing and Tianjin; Hohai University: Nanjing, China, 2006. [Google Scholar]
- Xu, X. A Study of Numerical Simulation for Groundwater Flow in the Beijing Plain; China University of Geosciences (Beijing): Beijing, China, 2006. [Google Scholar]
- Yang, Y.; Li, X.; Wang, L.; Li, C.; Liu, Z. Characteristics of the groundwater level regime and effect factors in the plain region of Tianjin city. Geol. Surv. Res. 2011, 34, 313–320. (In Chinese) [Google Scholar]
- Zhang, G.; Fei, Y.; Wang, J.; Yan, M.; Yu, C.; Wang, G.; Wang, H.; Feng, H.; Liu, Z.; Liu, K.; et al. Adaptation between Irrigation Agriculture and Groundwater in North China Plain; Science Press: Beijing, China, 2012. [Google Scholar]
- Zhang, G.; Fei, Y.; Liu, C.; Yan, M.; Wang, J. Adaptation between irrigation intensity and groundwater carrying capacity in North China Plain. Trans. Chin. Soc. Agric. Eng. 2013, 29, 1–10. (In Chinese) [Google Scholar]
- Xu, Y. Evaluation of groundwater level drawdown driving forces in the Hebei plain to the south of Beijing and Tianjin. Prog. Geogr. 2003, 22, 490–498. (In Chinese) [Google Scholar]
- Sophocleous, M. From safe yield to sustainable development of water resources—The Kansas experience. J. Hydrol. 2000, 235, 27–43. [Google Scholar] [CrossRef]
- Alley, W.M.; Reilly, T.E.; Franke, O.L. Sustainability of Ground-Water Resources; US Department of the Interior, US Geological Survey: Reston, VA, USA, 1999.
- Galloway, D.L. Evolving Issues and Practices in Managing Ground-Water Resources. US Department of the Interior, US Geological Survey: Reston, VA, USA, 2003. [Google Scholar]
- Liu, J.; Zheng, C.M.; Zheng, L.; Lei, Y.P. Ground water sustainability: Methodology and application to the North China Plain. Ground Water 2008, 46, 897–909. [Google Scholar]
- Wang, L.; Ma, C. A study on the environmental geology of the Middle Route Project of the South–North water transfer. Eng. Geol. 1999, 51, 153–165. [Google Scholar] [CrossRef]
- Changjiang Water Resources Commission of the Ministry of Water Resources. The south-to-north water transfer project planning (2001 revision). Chin. Water Resour. 2003, 1, 48–55. (In Chinese) [Google Scholar]
- Zhang, Y.; Li, G.-M. Influence of South-to-North Water Diversion on major cones of depression in North China Plain. Environ. Earth Sci. 2014, 71, 3845–3853. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, X.; Li, G.; Zhang, Y. Identifying Major Factors Affecting Groundwater Change in the North China Plain with Grey Relational Analysis. Water 2014, 6, 1581-1600. https://doi.org/10.3390/w6061581
Li X, Li G, Zhang Y. Identifying Major Factors Affecting Groundwater Change in the North China Plain with Grey Relational Analysis. Water. 2014; 6(6):1581-1600. https://doi.org/10.3390/w6061581
Chicago/Turabian StyleLi, Xue, Guomin Li, and Yuan Zhang. 2014. "Identifying Major Factors Affecting Groundwater Change in the North China Plain with Grey Relational Analysis" Water 6, no. 6: 1581-1600. https://doi.org/10.3390/w6061581
APA StyleLi, X., Li, G., & Zhang, Y. (2014). Identifying Major Factors Affecting Groundwater Change in the North China Plain with Grey Relational Analysis. Water, 6(6), 1581-1600. https://doi.org/10.3390/w6061581