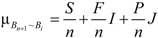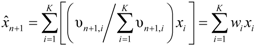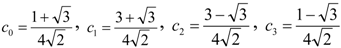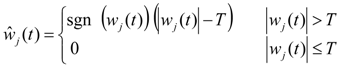Application of Set Pair Analysis-Based Similarity Forecast Model and Wavelet Denoising for Runoff Forecasting
Abstract
:1. Introduction
2. SPA-SF Model
2.1. SPA Principles
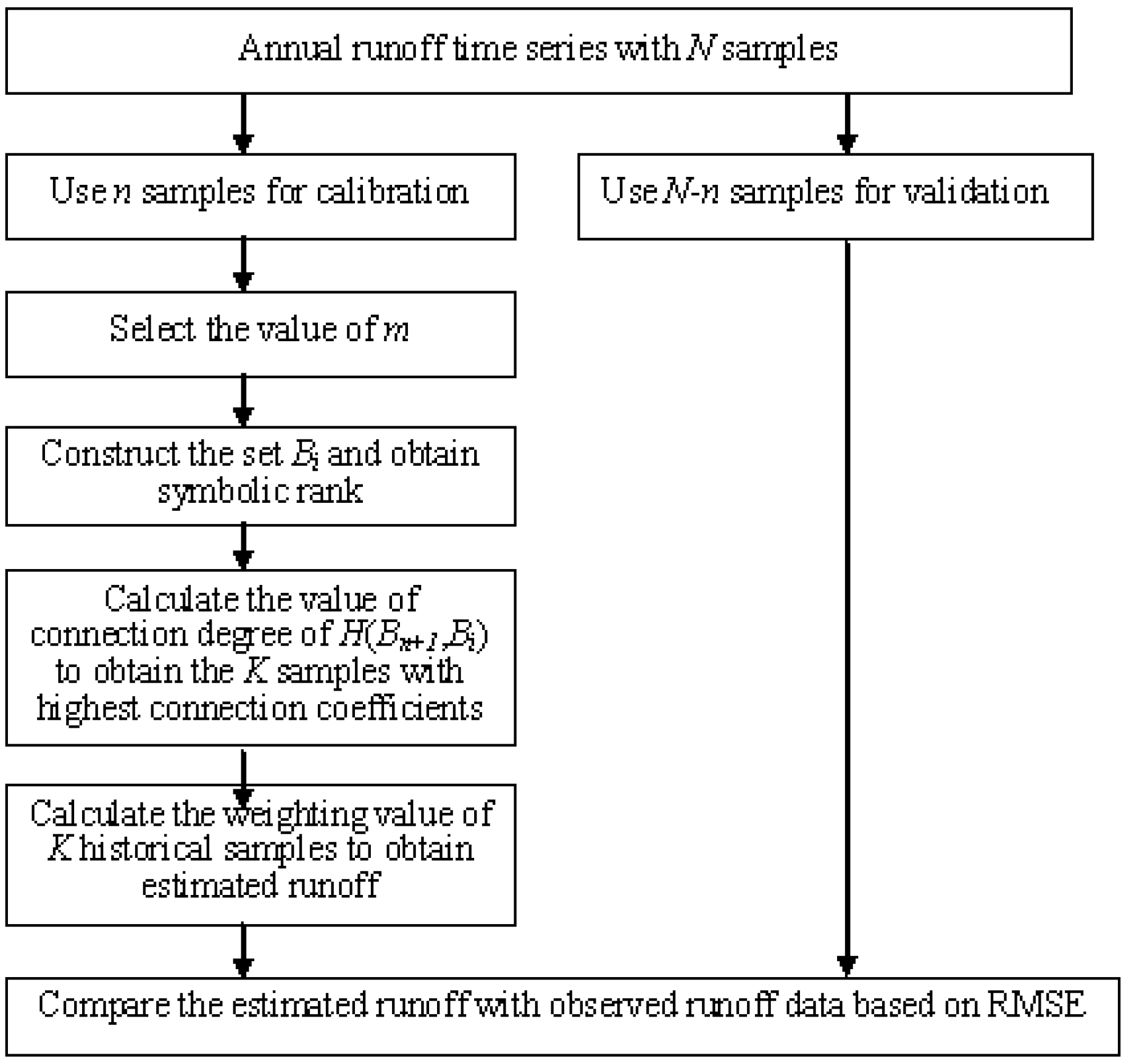
2.2. SPA-SF Model and Its Application to Forecast Runoff
| Sets | Elements in sets | Subsequent values | ||||
|---|---|---|---|---|---|---|
| B1 | x1 | x2 | x3 | ... | xm | xm+1 |
| B2 | x2 | x3 | x4 | ... | xm+1 | xm+2 |
| B3 | x3 | x4 | x5 | ... | xm+2 | xm+3 |
| ... | ... | ... | ... | ... | ... | ... |
| Bn−m | xn−m | xn−m+1 | xn−m+2 | ... | xn−1 | xn |
| Bn+1 | xn−m+1 | xn−m+2 | xn−m+3 | ... | xn | xn+1 |
- (1)
- The appropriate value of m is selected through the analysis.
- (2)
- Process the various elements in set Bi to obtain their symbolic rank according to certain classification criteria. Use the mean deviation to classify the elements. Calculate the average μj and the average absolute deviation dj (j = 1,2…,m) of the impact factor (i.e., the same element in the set). The elements in set Bi can be classified into Classes I, II and III according to (0, μj − 0.5dj), (μj − 0.5dj, μj + 0.5dj)and (μj + 0.5dj, ∞), respectively.
- (3)
- Construct the current set Bn + 1, according to the classification standard of the quantified symbols. Construct the set pair, H(Bn + 1, Bi), and count the number of identical statistical symbols (i.e., identity). Count the number of statistical symbols with one difference (i.e., differences), such as Class II vs. I, or Class II vs. III. Count the number of statistical symbols with two differences (i.e., compositionality), such as Class III vs. I. Calculate the connection degree for each set pair. The connection degree μBn+1~Bi, which describes the relationship between Bn+1 and Bi, is defined as [20]:where S is the number of identities, F is the number of differences, P is the number of oppositionality and S + F + P = n. I is the uncertainty factor of the difference. The value of I is selected in the interval (−1, 1), depending on various circumstances. Occasionally, I only plays the role of a differentially labeled element. J is the antithesis coefficient; J = −1, and occasionally, J plays the role of the opposition mark.
- (4)
- When the values of I and J are reasonably chosen, Equation (1) becomes a value called the connection coefficient, denoted by μ′Bn+1~Bi. In this study, the values of I and J were chosen as 0.5 and −1 [20], respectively. Thus, the connection coefficient of set pair H(Bn+1, Bi) and μ′Bn+1~Bi can be obtained.
- (5)
- The K historical samples, which are the most similar to Bn+1 based on the maximum of connection coefficients μ′Bn+1~Bi are determined. The value of K can be empirically determined or obtained from the connection coefficients that exceed a certain threshold K ≤ n0.5. Typically, the choice of K depends on the specific circumstances of the study. In this study, the suitable value of K was chosen based on the largest values of the connection coefficients, μ′Bn+1~Bi. The relative weights corresponding to the K historical samples can be determined from the relative membership degree, υn+1,i, corresponding to the connection coefficients, μ′Bn+1~Bi. The prediction of xn+1 can be obtained from the weighted average of the K historical samples, as follows [20]:
3. Wavelet Denoising
3.1. Wavelet Transforms and Daubechies Wavelet Coefficients
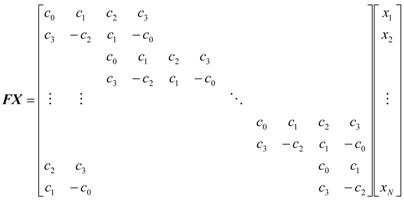

3.2. Wavelet Denoising Procedure
- (1)
- Choose an appropriate wavelet function and number of resolution level M. The original one-dimensional time series is decomposed into an approximation at resolution level M and detailed signals at various resolution levels by using wavelet transform.
- (2)
- Below fixed thresholds, the absolute values of detailed signals, wj (t) (j = 1, 2,…, M), are set to zero at each resolution level. The subscript, j, represents the j-th resolution levels. The absolute values of detailed signals that exceed fixed thresholds are treated as the difference between the values of detailed signals and thresholds as follows [24].Equation (6) gives the threshold quantifications used to obtain the processed detailed signals at each resolution level during wavelet denoising. The approximation usually does not perform threshold quantifications.
- (3)
- Wavelet reconstruction can derive the denoised time series data from the approximation at resolution level M and processed detailed signals (ŵj (t)) at all resolution levels.
4. Application and Analysis
4.1. The Proposed Method Combining SPA-SF and Wavelet Denoising
4.2. Determining Thresholds
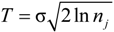
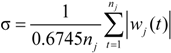
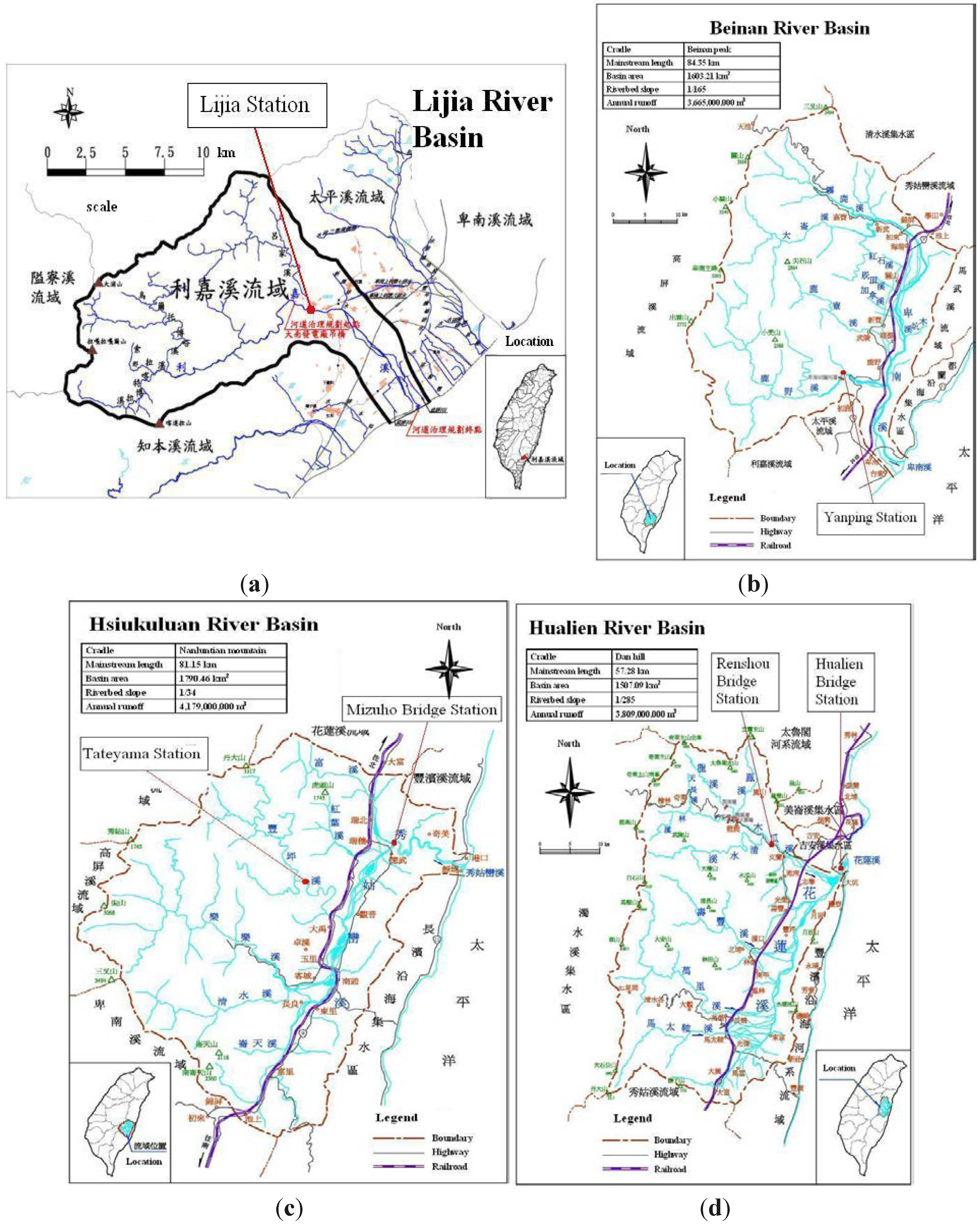
4.3. Collection and Collation of Research Data
| Name of stations | Name of rivers | Name of river basins | Drainage basin area (km2) |
|---|---|---|---|
| Lijia | Lijia River | Lijia River | 148.62 |
| Yanping | Kano River | Beinan River | 476.16 |
| Tateyama | Fung Ping River | Hsiukuluan River | 249.40 |
| Mizuho Bridge | Hsiukuluan River | Hsiukuluan River | 1538.81 |
| Renshou Bridge | Mugua River | Hualien River | 425.92 |
| Hualien Bridge | Hualien River | Hualien River | 1506.00 |
4.4. Comparison of Models
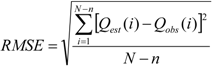
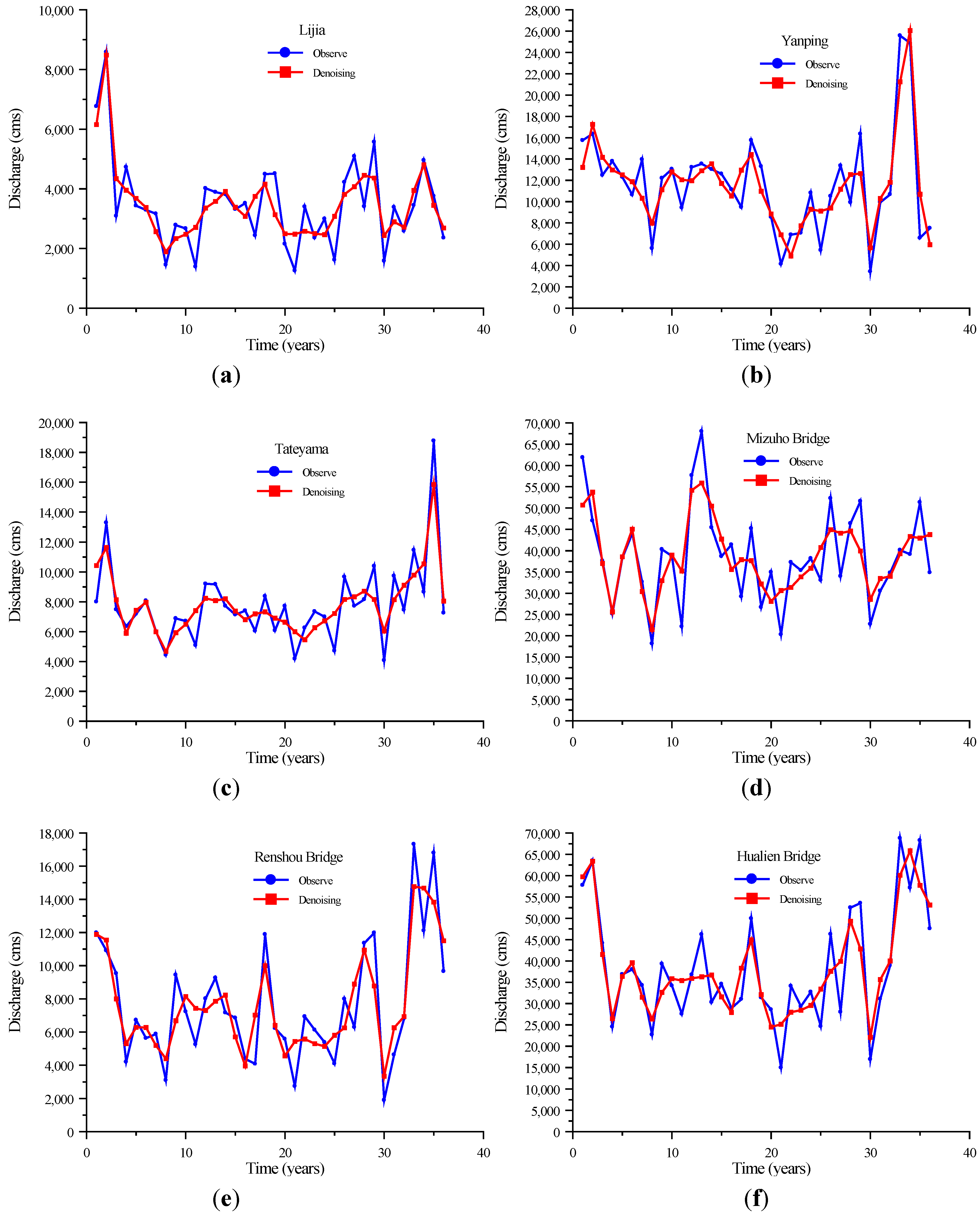
5. Results and Discussion
| Sets | xi | xi+1 | xi+2 | xi+3 | xi+4 | Subsequent values xi+5 | Identity | Differences | Compositionality | Connection coefficients |
|---|---|---|---|---|---|---|---|---|---|---|
| B1 | III | III | III | I | II | 37,977 | 0.4 | 0.2 | 0.4 | 0.1 |
| B2 | III | III | I | II | II | 34,293 | 0.2 | 0.4 | 0.4 | 0.0 |
| B3 | III | I | II | III | II | 22,702 | 0.6 | 0.4 | 0.0 | 0.8 |
| B4 | I | II | III | II | I | 39,307 | 0.4 | 0.4 | 0.2 | 0.4 |
| B5 | II | II | II | I | II | 34,200 | 0.0 | 0.8 | 0.2 | 0.2 |
| B6 | II | II | I | I | II | 27,551 | 0.2 | 0.6 | 0.2 | 0.3 |
| B7 | II | I | III | II | I | 36,767 | 0.6 | 0.4 | 0.0 | 0.8 |
| B8 | I | II | II | I | II | 46,204 | 0.0 | 0.6 | 0.4 | -0.1 |
| B9 | II | II | I | II | III | 30,304 | 0.0 | 0.6 | 0.4 | -0.1 |
| B10 | II | I | II | III | II | 34,553 | 0.4 | 0.6 | 0.0 | 0.7 |
| B11 | I | II | III | II | II | 28,901 | 0.2 | 0.6 | 0.2 | 0.3 |
| B12 | II | III | II | II | I | 31,007 | 0.2 | 0.6 | 0.2 | 0.3 |
| B13 | III | II | II | I | II | 49,942 | 0.2 | 0.6 | 0.2 | 0.3 |
| B14 | II | II | I | II | III | 31,395 | 0.0 | 0.6 | 0.4 | −0.1 |
| B15 | II | I | II | III | II | 28,567 | 0.4 | 0.6 | 0.0 | 0.7 |
| B16 | I | II | III | II | I | 14,963 | 0.4 | 0.4 | 0.2 | 0.4 |
| B17 | II | III | II | I | I | 34,098 | 0.2 | 0.4 | 0.4 | 0.0 |
| B18 | III | II | I | I | II | 29,349 | 0.2 | 0.4 | 0.4 | 0.0 |
| B19 | II | I | I | II | I | 32,706 | 0.4 | 0.4 | 0.2 | 0.4 |
| B20 | I | I | II | II | II | 24,671 | 0.2 | 0.6 | 0.2 | 0.3 |
| B21 | I | II | II | II | I | 46,275 | 0.2 | 0.6 | 0.2 | 0.3 |
| B22 | II | I | II | I | III | 28,012 | 0.2 | 0.4 | 0.4 | 0.0 |
| B23 | I | II | I | III | I | 52,494 | 0.4 | 0.2 | 0.4 | 0.1 |
| B24 | II | I | III | I | III | 53,543 | 0.4 | 0.2 | 0.4 | 0.1 |
| B25 | I | III | I | III | III | 16,919 | 0.2 | 0.0 | 0.8 | −0.6 |
| B26 | III | I | III | III | I | – | – | – | – | – |
| Lijia | Yanping | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Year | Observe (m3/s) | SPA-SF (m3/s) | SPA-SFW (m3/s) | Year | Observe (m3/s) | SPA-SF (m3/s) | SPA-SFW (m3/s) | ||
| 2003 | 3,385 | 3,051 | 2,192 | 2003 | 9,928 | 8,174 | 9,844 | ||
| 2004 | 2,587 | 2,774 | 2,920 | 2004 | 10,674 | 14,195 | 9,477 | ||
| 2005 | 3,448 | 2,890 | 2,789 | 2005 | 25,568 | 7,635 | 11,234 | ||
| 2006 | 4,954 | 3,880 | 4,492 | 2006 | 24,889 | 13,261 | 13,037 | ||
| 2007 | 3,757 | 2,943 | 4,029 | 2007 | 6,589 | 8,547 | 8,487 | ||
| 2008 | 2,357 | 3,124 | 2,151 | 2008 | 7,510 | 4,147 | 9,844 | ||
| RMSE | 691 | 619 | RMSE | 9,013 | 7,707 | ||||
| Tateyama | Mizuho Bridge | ||||||||
| Year | Observe (m3/s) | SPA-SF (m3/s) | SPA-SFW (m3/s) | Year | Observe (m3/s) | SPA-SF (m3/s) | SPA-SFW (m3/s) | ||
| 2003 | 9,730 | 6,403 | 6,725 | 2003 | 30,552 | 34,723 | 34,158 | ||
| 2004 | 7,455 | 6,901 | 7,117 | 2004 | 34,808 | 38,753 | 32,795 | ||
| 2005 | 11,458 | 8,154 | 7,047 | 2005 | 40,134 | 38,702 | 37,280 | ||
| 2006 | 8,664 | 8,207 | 8,765 | 2006 | 39,159 | 32,655 | 45,371 | ||
| 2007 | 18,772 | 5,639 | 7,411 | 2007 | 51,320 | 44,931 | 52,029 | ||
| 2008 | 7,257 | 8,207 | 6,939 | 2008 | 34,877 | 51,015 | 42,048 | ||
| RMSE | 5,713 | 5,128 | RMSE | 7,943 | 4,391 | ||||
| Renshou Bridge | Hualien Bridge | ||||||||
| Year | Observe (m3/s) | SPA-SF (m3/s) | SPA-SFW (m3/s) | Year | Observe (m3/s) | SPA-SF (m3/s) | SPA-SFW (m3/s) | ||
| 2003 | 4,624 | 7,428 | 4,225 | 2003 | 31,077 | 29,734 | 31,007 | ||
| 2004 | 6,783 | 4,851 | 5,628 | 2004 | 38,921 | 37,552 | 36,088 | ||
| 2005 | 17,327 | 6,896 | 7,834 | 2005 | 68,780 | 34,293 | 34,293 | ||
| 2006 | 12,114 | 5,135 | 5737 | 2006 | 57,138 | 28,371 | 29,611 | ||
| 2007 | 16,804 | 11,979 | 11,979 | 2007 | 68,247 | 28,901 | 34,707 | ||
| 2008 | 9,657 | 6,939 | 7,166 | 2008 | 47,589 | 30,673 | 41,024 | ||
| RMSE | 5,770 | 5,192 | RMSE | 25,347 | 22,815 | ||||
| Name of stations | SPA-SF | SPA-SFW | AR |
|---|---|---|---|
| Lijia | 691 | 619 | 1,061 |
| Yanping | 9,013 | 7,707 | 9,141 |
| Tateyama | 5,713 | 5,128 | 4,674 |
| Mizuho Bridge | 7,943 | 4,391 | 9,030 |
| Renshou Bridge | 5,770 | 5,192 | 6,036 |
| Hualien Bridge | 25,347 | 22,815 | 21,146 |
| Average | 9,080 | 7,642 | 8,515 |
| Name of stations | m = 1 | m = 2 | m = 3 | m = 4 | m = 5 |
|---|---|---|---|---|---|
| Lijia | 0.31699 | 0.25847 | 0.25648 | −0.03414 | 0.13865 |
| Yanping | 0.22231 | 0.26237 | 0.15771 | −0.14061 | 0.43697 |
| Tateyama | 0.08698 | 0.30733 | 0.47995 | 0.11940 | −0.00456 |
| Mizuho Bridge | 0.31934 | 0.13720 | 0.39881 | 0.18277 | −0.05631 |
| Renshou Bridge | 0.21177 | 0.09370 | 0.22852 | 0.28814 | 0.14405 |
| Hualien Bridge | 0.06826 | 0.21847 | 0.36847 | 0.20636 | 0.12162 |
6. Conclusions
Conflicts of Interest
References
- Wu, C.L.; Chau, K.W. Data-driven models for monthly streamflow time series prediction. Eng. Appl. Artif. Intell. 2010, 23, 1350–1367. [Google Scholar] [CrossRef]
- Montanari, A. Large sample behaviors of the generalized likelihood uncertainty estimation (GLUE) in assessing the uncertainty of rainfall-runoff simulations. Water Resourc. Res. 2005, 41. [Google Scholar] [CrossRef]
- Wang, W.S.; Li, Y.Q. Set pair analysis of water resources and hydrology. South-to-north water divers. Water Sci. Technol. 2011, 9, 27–32. (in Chinese). [Google Scholar]
- Jin, J.L.; Wei, Y.M.; Wang, W.S. Set pair analysis based on similarity forecast model of water resources. J. Hydroelectr. Eng. 2009, 28, 72–77. (in Chinese). [Google Scholar]
- Zhao, K. Set Pair Analysis and Its Preliminary Applications; Zhejiang Science and Technology Press: Hangzhou, China, 2000. (in Chinese) [Google Scholar]
- Jiang, Y.L.; Xu, C.F.; Yao, Y.; Zhao, K.Q. Systems information in set pair analysis and its applications. In proceedings of 2004 International Conference on Machine Learning and Cybernetics, Shanghai, China, 26–29 August 2004.
- Li, H.M.; Fu, Q. Highest floodlevel prediction based on set pair analysis similarity forecast model. J. Heilongjiang Hydraul. Eng. 2010, 3, 30–32. (in Chinese). [Google Scholar]
- Gao, J.; Sheng, Z. Method and application of set pair analysis classified prediction. J. Syst. Eng. 2002, 7, 458–462. (in Chinese). [Google Scholar]
- Nourani, V.; Rahimi, A.Y.; Nejad, F.H. Conjunction of ANN and threshold based wavelet de-noising approach for forecasting suspended sediment load. Int. J. Manag. Inf. Technol. 2013, 3, 9–26. [Google Scholar]
- Nejad, F.H.; Nourani, V. Elevation of wavelet denoising performance via an ANN-based streamflow forecasting model. Int. J. Comput. Sci. Manag. Res. 2012, 1, 764–770. [Google Scholar]
- Chang, S.G.; Yu, B.; Vetterli, M. Adaptive wavelet thresholding for image denoising and compression. IEEE Trans. Image Process 2000, 9, 1532–1546. [Google Scholar] [CrossRef]
- Lim, Y.H.; Lye, L.M. Denoising of streamflow series affected by tides using wavelet methods. In Proceeding of Annual Conference of the Canadian Society for Civil Engineering, Montréal, Québec, Canada, 5–8 June 2002.
- Liu, G.H.; Qian, J.L.; Wang, J.J. Study of flood forecast based on wavelet soft-threshold technology and ANN. J. Hydroelectr. Eng. 2004, 23, 5–10. (in Chinese). [Google Scholar]
- Wang, X.J.; Fei, S.M. Application of wavelet analysis to hydrological runoff simulation. Water Resour. Power 2007, 25, 1–3. (in Chinese). [Google Scholar]
- Wang, H.R.; Ye, L.T.; Liu, C.M.; Yang, C.; Liu, P. Problems in wavelet analysis of hydrologic series and some suggestions on improvement. Progr. Nat. Sci. 2007, 17, 80–86. [Google Scholar] [CrossRef]
- Cui, L.; Chi, D.; Wu, S. Forecasting precipitation using gray topological with wavelet denoising. J. Liaoning Tech. Univ. 2009, 28, 853–856. (in Chinese). [Google Scholar]
- Wang, W.H.; Hu, S.X.; Li, Y.Q. Wavelet transform method for synthetic generation of daily streamflow. Water Resour. Manag. 2011, 25, 41–57. [Google Scholar] [CrossRef]
- Chou, C.M. A threshold based wavelet denoising method for hydrological data modelling. Water Resour. Manag. 2011, 25, 1809–1830. [Google Scholar] [CrossRef]
- Li, A.Y.; Lu, J.H. Annual runoff forecasting based on wavelet de-noising SPA model. Adv. Mater. Res. 2012, 356, 2301–2306. [Google Scholar]
- Wang, W.S.; Zhang, X.; Jin, J.L.; Ding, J.; Wang, H. Methods of Uncertainty Analysis for Hydrology; Science Press: Beijing, China, 2011. (in Chinese) [Google Scholar]
- Wang, W.S.; Ding, J.; Lee, Y.Q. Hydrological Wavelet Analysis; Chemical industry Press: Beijing, China, 2005. (in Chinese) [Google Scholar]
- Mallat, S.G. A theory for multiresolution signal decomposition: the wavelet representation. IEEE Trans. Pattern Anal. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Lin, Z.S.; Zheng, Z.W. Diagnosis Technology of Climate Using Wavelet; Meteorology Press: Beijing, China, 1999. (in Chinese) [Google Scholar]
- Donoho, D.L.; Johnstone, J.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Taiwan River Restoration Network. Available online: http://trrn.wra.gov.tw/trrn/controlRiver/index.do (accessed on 17 November 2013).
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chou, C.-M. Application of Set Pair Analysis-Based Similarity Forecast Model and Wavelet Denoising for Runoff Forecasting. Water 2014, 6, 912-928. https://doi.org/10.3390/w6040912
Chou C-M. Application of Set Pair Analysis-Based Similarity Forecast Model and Wavelet Denoising for Runoff Forecasting. Water. 2014; 6(4):912-928. https://doi.org/10.3390/w6040912
Chicago/Turabian StyleChou, Chien-Ming. 2014. "Application of Set Pair Analysis-Based Similarity Forecast Model and Wavelet Denoising for Runoff Forecasting" Water 6, no. 4: 912-928. https://doi.org/10.3390/w6040912
APA StyleChou, C.-M. (2014). Application of Set Pair Analysis-Based Similarity Forecast Model and Wavelet Denoising for Runoff Forecasting. Water, 6(4), 912-928. https://doi.org/10.3390/w6040912