Abstract
In this study, a two-stage inexact credibility-constrained programming (TICP) method is developed for identifying the efficiency of water trading under multiple uncertainties. TICP can tackle uncertainties expressed as probabilistic distributions, discrete intervals and fuzzy sets. It can also provide an effective linkage between the benefits to the system and the associated economic penalties attributed to the violation of the predefined policies for water resource allocation. The developed TICP method is applied to a real case of water resource allocation management and planning in the Kaidu-kongque River Basin, which is a typical arid region in Northwest China. Different water resource allocation policies based on changes to the water permit and trading ratio levels are examined. The results indicate that the efficiencies of water trading are sensitive to the degrees of satisfaction (i.e., interval credibility levels), which correspond to different water resource management policies. Furthermore, the comparison of benefits and shortages between trading and non-trading schemes implies that trading is more optimal and effective than non-trading. The results are helpful for making decisions about water allocation in an efficient way and for gaining insight into the tradeoffs between water trading and economic objectives.
1. Introduction
In the past few decades, the pressures of human population and patterns of economic development have led to the shrinking of available water resources worldwide, while water shortage has become a critical factor in the global water crisis. It is a challenge for water resource managers and planners to maintain sustainable development under situations of increasing population, developing economies and changing climate. Particularly in many semiarid and arid regions, water shortage and an unreliable water supply have been regarded as one major obstacle to regional sustainable development for watershed systems [1,2,3,4]. Water trading is useful for allocating water resources optimally, which increases the economic productivity of water by encouraging its movement from low to high valued use. Under the situation of limited water resources, markets can also provide incentives to adopt water saving policies [5]. Water trading can balance limited water resources between the allocation for human use and the streamflow, especially in semi-arid and arid regions, such that several water trading programs have been established and are under development throughout the world [6,7,8]. However, the uncertainties existing in practical water trading programs are often related to errors in the acquired data, variations in spatial and temporal units and the incompleteness or impreciseness of the observed information, which leads to difficulties in planning water trading scientifically [9]. Consequently, the effective planning of water resource management under such uncertainties and complexities is important for facilitating sustainable socio-economic development for watershed systems [10].
Two-stage stochastic programming (TSP) is effective in dealing with problems for which an analysis of policy scenarios is desired and the uncertainties can be expressed as probabilistic distributions [11,12]. In TSP, an initial decision must be made before the realization of random variables (first-stage decision), and then, a corrective action can be taken after random events have taken place (second-stage decision) [13]. This implies that a second-stage decision can be used to minimize “penalties” that may appear, due to some infeasibility [14]. TSP has been widely used for water resource management and planning over the past few decades. For example, Maqsood et al. [15] developed an interval-fuzzy two-stage stochastic programming method for planning water resource management systems associated with multiple uncertainties, in which interval fuzzy programming methods were introduced into a TSP framework. Kenneth et al. [16] developed a TSP method for tackling uncertainties expressed as probability density functions for water availability. Li et al. [17] proposed an interval-parameter two-stage stochastic nonlinear programming method for supporting decisions about water-resource allocation within a multi-reservoir system, where uncertainties expressed as both probability distributions and discrete intervals were reflected. Vidoli [18] evaluated water resource services by integrating conditional, robust, nonparametric frontier and multivariate adaptive regression splines into a TSP framework. In general, TSP can provide an effective linkage between policies and the economic penalties, which has the advantages of reflecting the complexities of system uncertainties, as well as analyzing policy scenarios when the pre-regulated targets are violated. However, the major problem of TSP is that the increased data requirement for specifying the probability distributions of coefficients may affect their practical applicability [19]. One potential approach to better account for more complex uncertainties is to introduce an interval-parameter programming (IPP) technique into the TSP framework. IPP is an alternative for handling uncertainties in the model’s left- and/or right-hand sides, as well as those that cannot be quantified as membership or distribution functions, since interval numbers are acceptable as its uncertain inputs. Moreover, in practical water resource management problems, uncertainties may be related to errors in the acquired data, variations in spatial and temporal units and the incompleteness or impreciseness of the observed information in water resource management [10,20]. Fuzzy programming (FP) is effective in handling ambiguous coefficients of objective functions and constraints caused by imprecision and vagueness, when the quality and quantity of uncertain information is often not satisfactory enough to be presented as a probabilistic distribution. Previously, a number of FP techniques, such as the fuzzy-stochastic [21,22], interactive fuzzy [23] and robust methods [24,25], were developed to deal with uncertainties in decision making problems. Fuzzy credibility-constrained programming (FCP) is effective in reflecting the fuzziness inherited with parameters associated with subjective considerations, which would be useful in the presence of weaker sources of information. FCP can measure the confidence levels in a fuzzy water system to tackle uncertainties expressed as fuzzy sets, when detailed information is not able to be presented by interval or stochastic numbers [26,27,28,29]. However, few studies have been reported on the application of FCP techniques to water resource management and planning [30,31,32]. Therefore, one potential approach to better account for multiple uncertainties and economic penalties is to introduce the IPP and FCP concepts into the TSP framework; this will lead to a two-stage inexact credibility-constrained programming (TICP) method.
The aim of this study is to develop such a TICP method for identifying a cost-effective water trading policy under multiple uncertainties. The TICP is an integrated optimization technique for tackling uncertainties expressed as discrete intervals, probability distributions and fuzzy sets. The TICP method will be applied to a real case study of water resource management in the Kaidu-kongque River Basin, which is one of the aridest regions in Northwest China. The degrees of satisfaction for the given constraints will be represented using interval credibility levels, which can provide scientific support for large-scale regional water-resource management under uncertainty conditions at the watershed level. A number of policy scenarios that are associated with different decreasing levels of the water permit and trading ratio will be analyzed, which can help in gaining insight into the tradeoff between water trading and economic objectives.
2. Methodology
When uncertainties of the right-hand side of the model are expressed as probability density functions (pdfs) and decisions need to be made periodically over time, the problem can be formulated as a two-stage stochastic programming (TSP) model [33]. A general TSP linear model can be formulated as follows:
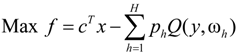 subject to:
where x is the vector of the first-stage decision variables, cTx is the first-stage benefits, ω is the random events after the first-stage decisions are made, ph is the probability of an event, ωh, Q(y, ωh) is the recourse at the second-stage under the occurrence of the event, ωh, and
subject to:
where x is the vector of the first-stage decision variables, cTx is the first-stage benefits, ω is the random events after the first-stage decisions are made, ph is the probability of an event, ωh, Q(y, ωh) is the recourse at the second-stage under the occurrence of the event, ωh, and 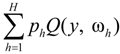 is the expected value of the second-stage penalties [12]. However, the parameter of a model may fluctuate within a certain interval, and it is difficult to state a meaningful probability distribution for this variation. Interval-parameter programming (IPP) can deal with uncertainties in objective function and system constraints, which can be expressed as intervals without distribution information. An interval number, x±, can be defined as an interval with a known lower-bound and upper-bound, but unknown distribution information [34,35]. It can be expressed as [x−, x+], representing a number (or an interval), which can have a minimum value of x− and a maximum one of x+.
is the expected value of the second-stage penalties [12]. However, the parameter of a model may fluctuate within a certain interval, and it is difficult to state a meaningful probability distribution for this variation. Interval-parameter programming (IPP) can deal with uncertainties in objective function and system constraints, which can be expressed as intervals without distribution information. An interval number, x±, can be defined as an interval with a known lower-bound and upper-bound, but unknown distribution information [34,35]. It can be expressed as [x−, x+], representing a number (or an interval), which can have a minimum value of x− and a maximum one of x+.
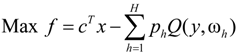
Ax ≤ b
T(ωh)x + W(ωh) = g(ωh), ∀h = 1, 2, …, H
x ≥ 0
y(ωh) ≥ 0
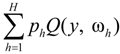 is the expected value of the second-stage penalties [12]. However, the parameter of a model may fluctuate within a certain interval, and it is difficult to state a meaningful probability distribution for this variation. Interval-parameter programming (IPP) can deal with uncertainties in objective function and system constraints, which can be expressed as intervals without distribution information. An interval number, x±, can be defined as an interval with a known lower-bound and upper-bound, but unknown distribution information [34,35]. It can be expressed as [x−, x+], representing a number (or an interval), which can have a minimum value of x− and a maximum one of x+.
is the expected value of the second-stage penalties [12]. However, the parameter of a model may fluctuate within a certain interval, and it is difficult to state a meaningful probability distribution for this variation. Interval-parameter programming (IPP) can deal with uncertainties in objective function and system constraints, which can be expressed as intervals without distribution information. An interval number, x±, can be defined as an interval with a known lower-bound and upper-bound, but unknown distribution information [34,35]. It can be expressed as [x−, x+], representing a number (or an interval), which can have a minimum value of x− and a maximum one of x+.
x+ = [x−, x+] = {a ∊ x ǀ x− ≤ a ≤ x+ }
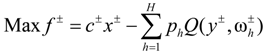
A±x± ≤ b±
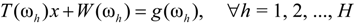
x± ≥ 0

Let 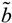 be a fuzzy set of imprecise right-hand sides with possibility distributions. The triangular fuzzy membership function is the most popular possibility distribution, and it is adopted in this study, due to its computational efficiency. Accordingly, the credibility of the constraint Ax ≤
be a fuzzy set of imprecise right-hand sides with possibility distributions. The triangular fuzzy membership function is the most popular possibility distribution, and it is adopted in this study, due to its computational efficiency. Accordingly, the credibility of the constraint Ax ≤ 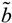 could be defined as follows [32]:
could be defined as follows [32]:
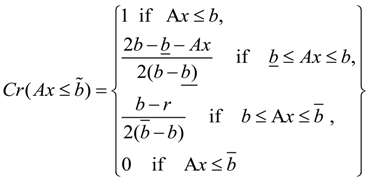
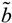 be a fuzzy set of imprecise right-hand sides with possibility distributions. The triangular fuzzy membership function is the most popular possibility distribution, and it is adopted in this study, due to its computational efficiency. Accordingly, the credibility of the constraint Ax ≤
be a fuzzy set of imprecise right-hand sides with possibility distributions. The triangular fuzzy membership function is the most popular possibility distribution, and it is adopted in this study, due to its computational efficiency. Accordingly, the credibility of the constraint Ax ≤ 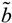 could be defined as follows [32]:
could be defined as follows [32]:
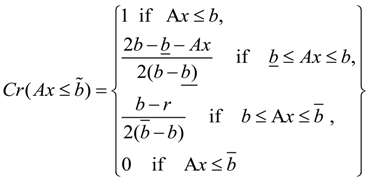
Thereby, a general credibility constrained problem can be formulated as follows:
subject to:
 where λ is the credibility level. In the optimization process for management and planning, it is usually assumed that the credibility level should be no less than 0.5 [32]. Thus, Equation (5b) can be rewritten as:
where λ is the credibility level. In the optimization process for management and planning, it is usually assumed that the credibility level should be no less than 0.5 [32]. Thus, Equation (5b) can be rewritten as:
 where it can be transformed into a deterministic constraint as follows:
where it can be transformed into a deterministic constraint as follows:
Max ƒ = cT X

x ≥ 0

Ax ≤ b + (1 − 2λ)(b − b)
Therefore, by incorporating the creditability constraints equation into the ITSP framework, a two-stage inexact credibility-constrained programming (TICP) model can be formulated as follows:
 subject to:
subject to:
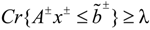

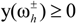

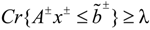

x± ≥ 0
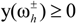
Then, an interactive two-step solution algorithm is proposed for solving the TICP model, which is different from normal interval analysis and best/worst-case analysis [12,34,35]. The TICP model can be transformed into two sets of deterministic submodels, which correspond to the lower and upper bounds of the desired objective function value. The resulting solutions can provide intervals for the objective function and decision variables with different levels of risk in violating the constraints. When the objective is ƒ+, which corresponds to the upper bound of the objective function value, it can be formulated as follows:
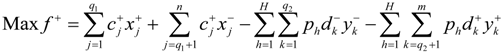 subject to:
subject to:





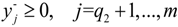
 where c+j (j = 1,2,…,q1) > 0; c+j (j = q1 + 1, q1 + 2,…,n) < 0; d+k (j = 1,2,…,q2) > 0; d+k (j = q2 + 1, q2 + 2,…,m) < 0;
where c+j (j = 1,2,…,q1) > 0; c+j (j = q1 + 1, q1 + 2,…,n) < 0; d+k (j = 1,2,…,q2) > 0; d+k (j = q2 + 1, q2 + 2,…,m) < 0;  when
when  ,
,  when
when 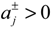 and λ- = the lower bound of the credibility level value.
and λ- = the lower bound of the credibility level value.
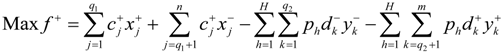





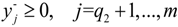

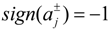 when
when 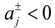 ,
,  when
when 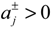 and λ- = the lower bound of the credibility level value.
and λ- = the lower bound of the credibility level value. The optimal solution of Model (9), including  for j = 1 to q1,
for j = 1 to q1,  for j = q1 + 1 to n,
for j = q1 + 1 to n, 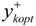 for k = 1 to q2 and
for k = 1 to q2 and  for k = q2 + 1 to m, can be obtained. Accordingly, the second submodel corresponding to the lower bound of the objective function value can be formulated as:
for k = q2 + 1 to m, can be obtained. Accordingly, the second submodel corresponding to the lower bound of the objective function value can be formulated as:
 subject to:
subject to:
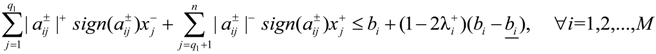

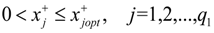
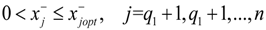
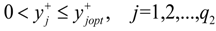

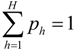
 for j = 1 to q1,
for j = 1 to q1,  for j = q1 + 1 to n,
for j = q1 + 1 to n, 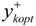 for k = 1 to q2 and
for k = 1 to q2 and  for k = q2 + 1 to m, can be obtained. Accordingly, the second submodel corresponding to the lower bound of the objective function value can be formulated as:
for k = q2 + 1 to m, can be obtained. Accordingly, the second submodel corresponding to the lower bound of the objective function value can be formulated as:

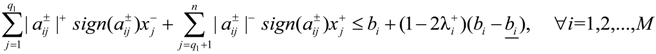

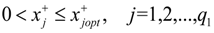
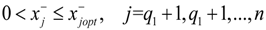
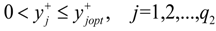

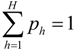
Thereby, optimal solutions of Model (10) can be gained, including  for j = 1 to q1,
for j = 1 to q1,  for j = q1 + 1 to n,
for j = q1 + 1 to n,  for k = 1 to q2 and
for k = 1 to q2 and 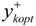 for k = q2 + 1 to m. Therefore, by integrating the solutions of the two submodels, the solution of the TICP model can be generated.
for k = q2 + 1 to m. Therefore, by integrating the solutions of the two submodels, the solution of the TICP model can be generated.
 for j = 1 to q1,
for j = 1 to q1,  for j = q1 + 1 to n,
for j = q1 + 1 to n,  for k = 1 to q2 and
for k = 1 to q2 and 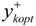 for k = q2 + 1 to m. Therefore, by integrating the solutions of the two submodels, the solution of the TICP model can be generated.
for k = q2 + 1 to m. Therefore, by integrating the solutions of the two submodels, the solution of the TICP model can be generated.The solution process of TICP can be summarized as follows:
- Step 1: Formulate the TICP model.
- Step 2: Transform the TICP model into two submodels, where the submodel corresponding to ƒ+ is desired first, since the objective is to maximize ƒ±.
- Step 3: Obtain the optimal solutions by solving the ƒ+ submodel under each λ.
- Step 4: Formulate and solve the ƒ- submodel by importing optimal solutions from the ƒ+ submodel into the ƒ-submodel under each λ.
- Step 5: Obtain the optimal solution interval value under each λ.
3. Case Study
The Kaidu River and the Kongque River are the branches of the Tarim River formed from the middle of mountain Tian to Lake Bositeng and are about 610 km- and 785 km-long, respectively. The Kaidu-kongque River Basin is located in the middle reach of the Tarim River Basin, which is approximately 62 × 103 km2 [36] (as shown in Figure 1). It is a typical arid region, due to an extremely dry climate and a low and uneven distribution of rainfall. For example, the climate in the basin is extremely dry, with the average rainfall being about 273 mm/year, which is more than 80% of the total annual precipitation fall from May to September and less than 20% of the total fall from November to the following April [37]. The basin includes six counties (i.e., Kuerle, Yanqi, Hejing, Heshuo, Bohu and Yuli) and has a population of more than one million [36]. It is suitable for the growth of crops, such as wheat, corn, sugar beet, tomato and fruit, which have provided high-speed growth in agricultural product processing and manufacturing. Moreover, the rich mineral and oil resources of the basin form an industrial structure dominated by mining, the chemical industry and the fossil oil industry, while textiles, electric power, papermaking and transportation are keeping pace with the development of the mainstay industries. The water demands of four users (e.g., municipal, agricultural, industrial and ecological) in six districts rely on the river’s streamflow, which is mainly derived from upstream flow, snow melt and rainfall. Due to the dry climate, low-rainfall and high evaporation, the water supply capacity of the river is quite low, which presents difficulties in satisfying the water demands from the six counties. Particularly in recent years, the demand for water has reached the limits of what the natural system can provide, so that water shortage could become a major obstacle to social and economic development for this region. Unfortunately, in the study of the basin, there is a lack of effective tools for facilitating efficient, equitable and sustainable water resource management. Therefore, population growth, the food security challenge, industrial sector development and the potential threat of climate change elevate the attention given to efficient and sustainable water management [38].
Water trading can solve conflicts caused by water shortage [39,40], not only improving the net benefit for the system, but also saving water, while respecting hydrological, environmental, food security, economic development, population growth and institutional constraints. Under an allocated water permit, trading can release surplus water to remedy the losses from water deficiency, achieving a higher profitability. However, a number of variations caused by factitious factors and natural factors exist in the trading system, which bring more complexities and uncertainties to the water trading system. For example, less observation and insufficient data create uncertainties in data inputting, and natural uncertainties generate many stochastic factors in the trading system, such as streamflow water, demand and water-allocation targets; fluctuations can be associated with the net benefit for the system. These complexities could become further compounded by not only interactions among the uncertain parameters, but also their economic implications [2]. Therefore, the proposed TICP model can be used in water trading for optimally allocating limited water resources to facilitate regional sustainability with a maximized benefit for the system.
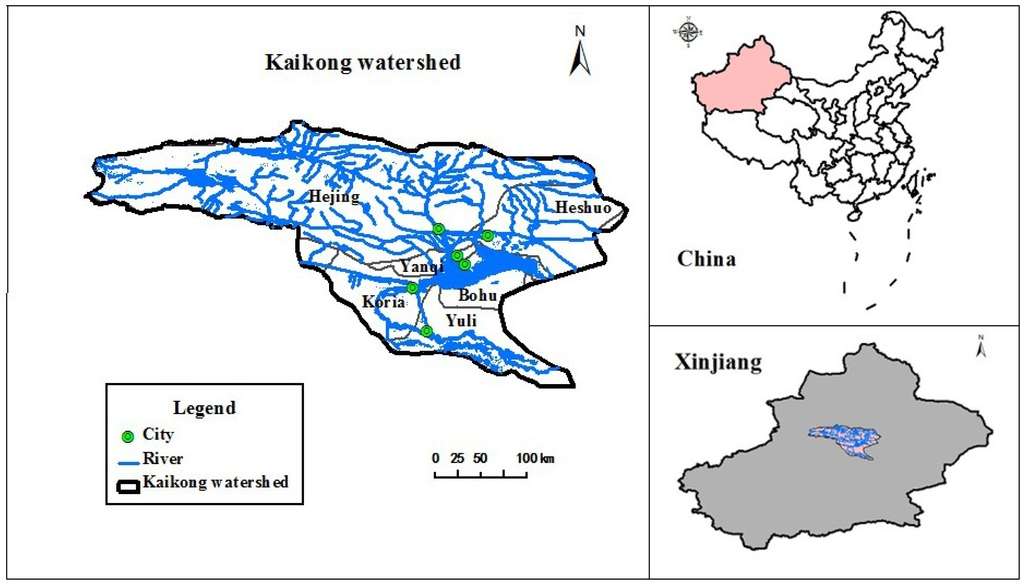
Figure 1.
The study area.
A manager (e.g., a valley authority or water resources bureau) is responsible for allocating water resources to multiple users (e.g., residential, industrial, agricultural and ecological) in the Kaidu-kongque River Basin and aims to create a plan to effectively allocate the uncertain supply of water to every user in order to satisfy the users’ demand and to maximize the overall benefit for the system. In order to recover the ecological system of the lower reach of the watershed, the manager has obligated water to maintain the water level of the river first. Water permits have been allocated to each user by a manager in the beginning of this year, which are based on the water utilization of last year. Nevertheless, allocations are made once per year, which will be adjusted by the water manager next year. When variations emerge in this year, system disruption risk attributable to the uncertainties may influence the benefits for the system and water supplies tremendously. This leads to a problem of recourse for planning water resource allocation with a maximized economic benefit and a minimized system failure risk.
On the basis of the local management policy, water availability is allocated to users for consumption by the percentage of the water permits, which leads to water surpluses and water shortages, but not to trading, when water is not tradable. The benefits for the system denote the profit of the economic production in proportion to the pre-regulated economic targets, while the system’s recourse penalties denote the loss for a shortage. With the purpose of obtaining a more effective water allocation, a water trading program can be established, in which water permits being traded at a higher value substitute for the allocation to each user proportionally. When water is tradable, water permits being allocated to users by cubic meters, water shortages and surpluses emerge, due to the difference between water targets, permits and availability. Therefore, retributions for water permits would be acquired, with which water shortages and surpluses could join in the water market for trading based on the law of value. Since the water market can provide an equal and effective manner of allocating water, water shortages and surpluses reallocated by water trading led to water permits being reattributed. Under such a situation, the manager can reduce the water permits to release appropriate water permits for trade in the water market according to the actual water requirements, which achieves a maximized benefit for the system, while considering the trading costs (the trading cost is smaller than the loss of the shortage). Moreover, multiple uncertainties may exist in water allocation and trading processes (e.g., uncertain data and the probability distribution of water availability), which affect water resource management planning. Thus, the manager will formulate a TICP model for water trading to maximize the entire benefit for the system, which can satisfy the goal of water use reduction and allow for reflection on complex uncertainties. When water is tradable, the TICP model can be formulated as follows:
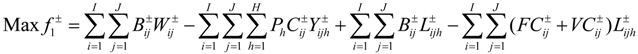 Subject to the:
Subject to the:
 presents the net benefit of the entire system with trading (US$),
presents the net benefit of the entire system with trading (US$), 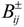 is net benefit to user i in district j per volume of water being delivered (US$/103 m3),
is net benefit to user i in district j per volume of water being delivered (US$/103 m3),  is the water demand target for user i in district j (106 m3),
is the water demand target for user i in district j (106 m3),  is the total water availability of the entire system under probability Ph (106 m3), Ph denotes the probability of random water availability
is the total water availability of the entire system under probability Ph (106 m3), Ph denotes the probability of random water availability 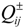 under level h (%),
under level h (%), 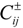 is the economic loss to user i in district j per volume of water not being delivered (US$/103 m3),
is the economic loss to user i in district j per volume of water not being delivered (US$/103 m3), 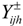 is the water deficiency for user i in district j when demand
is the water deficiency for user i in district j when demand  is not met (106 m3),
is not met (106 m3), 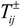 is the allocated allowable water permit to user i in district j (106 m3), λ is the credibility level, which measures the degrees of satisfaction of the constraints, d is the percentage of the reduced total allowable water allocation,
is the allocated allowable water permit to user i in district j (106 m3), λ is the credibility level, which measures the degrees of satisfaction of the constraints, d is the percentage of the reduced total allowable water allocation,  is the water released to user i in district j when the total water availability exceeds the allowable water reallocation with trading scheme (106 m3),
is the water released to user i in district j when the total water availability exceeds the allowable water reallocation with trading scheme (106 m3),  is the trading fixed cost to user i in district j with trading scheme (US$/103 m3),
is the trading fixed cost to user i in district j with trading scheme (US$/103 m3), 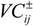 is the variable trading cost to user i in district j with trading scheme (US$/103 m3),
is the variable trading cost to user i in district j with trading scheme (US$/103 m3), 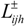 is the amount of water trading from other water sources to user i in district j with trading scheme (106 m3) and tʹijh / tijh is the ratio of water trading from other water sources to user i in district j with the trading scheme.
is the amount of water trading from other water sources to user i in district j with trading scheme (106 m3) and tʹijh / tijh is the ratio of water trading from other water sources to user i in district j with the trading scheme.
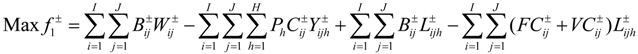
- (1)
- Constraints of water permit:

- (2)
- Constraints of water shortage:
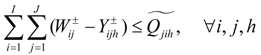
- (3)
- Constraints of water surplus:

- (4)
- Constraints of water trading:

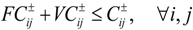
- (5)
- Constraints of technical:
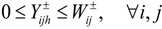
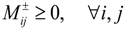
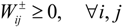
 presents the net benefit of the entire system with trading (US$),
presents the net benefit of the entire system with trading (US$), 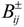 is net benefit to user i in district j per volume of water being delivered (US$/103 m3),
is net benefit to user i in district j per volume of water being delivered (US$/103 m3),  is the water demand target for user i in district j (106 m3),
is the water demand target for user i in district j (106 m3),  is the total water availability of the entire system under probability Ph (106 m3), Ph denotes the probability of random water availability
is the total water availability of the entire system under probability Ph (106 m3), Ph denotes the probability of random water availability 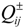 under level h (%),
under level h (%), 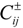 is the economic loss to user i in district j per volume of water not being delivered (US$/103 m3),
is the economic loss to user i in district j per volume of water not being delivered (US$/103 m3), 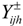 is the water deficiency for user i in district j when demand
is the water deficiency for user i in district j when demand  is not met (106 m3),
is not met (106 m3), 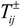 is the allocated allowable water permit to user i in district j (106 m3), λ is the credibility level, which measures the degrees of satisfaction of the constraints, d is the percentage of the reduced total allowable water allocation,
is the allocated allowable water permit to user i in district j (106 m3), λ is the credibility level, which measures the degrees of satisfaction of the constraints, d is the percentage of the reduced total allowable water allocation,  is the water released to user i in district j when the total water availability exceeds the allowable water reallocation with trading scheme (106 m3),
is the water released to user i in district j when the total water availability exceeds the allowable water reallocation with trading scheme (106 m3),  is the trading fixed cost to user i in district j with trading scheme (US$/103 m3),
is the trading fixed cost to user i in district j with trading scheme (US$/103 m3), 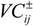 is the variable trading cost to user i in district j with trading scheme (US$/103 m3),
is the variable trading cost to user i in district j with trading scheme (US$/103 m3), 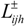 is the amount of water trading from other water sources to user i in district j with trading scheme (106 m3) and tʹijh / tijh is the ratio of water trading from other water sources to user i in district j with the trading scheme.
is the amount of water trading from other water sources to user i in district j with trading scheme (106 m3) and tʹijh / tijh is the ratio of water trading from other water sources to user i in district j with the trading scheme.Table 1 shows basic economic data and trading costs, which are estimated indirectly based on the statistical yearbook of the Xinjiang Uygur Autonomous Region in the Uygur Autonomous Region, 2005–2010, and the water price for the Xinjiang Autonomous Region. Values of 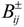 and
and 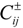 are estimated according to different users’ gross national product in different counties indirectly, the upper bound values of which are estimated as the highest from the yearbook (2005–2010) and the lower bound values of which are the opposite. For example, the net benefit (
are estimated according to different users’ gross national product in different counties indirectly, the upper bound values of which are estimated as the highest from the yearbook (2005–2010) and the lower bound values of which are the opposite. For example, the net benefit ( 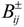 ) for the agricultural user in Hejing County is estimated by the gross amount of crops (i.e., wheat, corn, tomato, cotton and fruit) and the total water demand (net benefit = gross amount of crops/total water demand). From 2005 to 2010, the highest net benefit was 1860 US$/103 m3 in 2008, which was estimated by the gross amount of crops (i.e., wheat = 45.1 × 106 US$; oil plant = 11.3 × 106 US$; tomato = 15.93 × 106 US$; cotton t = 44.02 × 106 US$ and other crops = 47.33 × 106 US$) and the water demand (i.e., wheat = 24.1 × 106 m3; oil plant = 2.91 × 106 m3; tomato = 3.41 × 106 m3; cotton = 29.4 × 106 m3 and other crops = 28.18 × 106 m3). Meanwhile, the lowest net benefit was 1530 US$/103 m3 in 2005. Therefore, the interval value of the net benefit is acquired as [1530, 1860] US$/103 m3, which is on the basis of the highest and lowest value of the net benefit. The method calculated for the net benefit of the agricultural user in Hejing County can be applied to other users, districts and even other economic data.
) for the agricultural user in Hejing County is estimated by the gross amount of crops (i.e., wheat, corn, tomato, cotton and fruit) and the total water demand (net benefit = gross amount of crops/total water demand). From 2005 to 2010, the highest net benefit was 1860 US$/103 m3 in 2008, which was estimated by the gross amount of crops (i.e., wheat = 45.1 × 106 US$; oil plant = 11.3 × 106 US$; tomato = 15.93 × 106 US$; cotton t = 44.02 × 106 US$ and other crops = 47.33 × 106 US$) and the water demand (i.e., wheat = 24.1 × 106 m3; oil plant = 2.91 × 106 m3; tomato = 3.41 × 106 m3; cotton = 29.4 × 106 m3 and other crops = 28.18 × 106 m3). Meanwhile, the lowest net benefit was 1530 US$/103 m3 in 2005. Therefore, the interval value of the net benefit is acquired as [1530, 1860] US$/103 m3, which is on the basis of the highest and lowest value of the net benefit. The method calculated for the net benefit of the agricultural user in Hejing County can be applied to other users, districts and even other economic data.  is a basic form of trading cost, which is estimated by the actual price of water exceed water permit in Kaidu-kongque Basin.
is a basic form of trading cost, which is estimated by the actual price of water exceed water permit in Kaidu-kongque Basin. 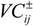 is estimated according to the opportunity cost of water, which is affected by a number of factors, such as the scarcity of water resources, the relationship between supply and demand and the status of socio-economic development. Table 2 shows policy data
is estimated according to the opportunity cost of water, which is affected by a number of factors, such as the scarcity of water resources, the relationship between supply and demand and the status of socio-economic development. Table 2 shows policy data 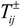 , which are acquired from the water permits of the water authority of Uygur Autonomous Region from 2005 to 2010 directly. Additionally, water target
, which are acquired from the water permits of the water authority of Uygur Autonomous Region from 2005 to 2010 directly. Additionally, water target  is estimated by the users’ actual water usage in recent years, which takes the situation of economic development into consideration. The value of
is estimated by the users’ actual water usage in recent years, which takes the situation of economic development into consideration. The value of  should be derived by conducting statistical analyses with the results of the annual streamflow of the Kaidu-kongque River (2005–2010). Due to the rainy seasons in the Kaidu-kongque River Basin, more than 80% of the total annual precipitation falls from May to September, and less than 20% of the total falls from November to the following April [37]. Therefore, the total water availability can be converted to several levels. Table 3 shows the total water availability of the Kaidu-kongque River Basin under several level probabilities.
should be derived by conducting statistical analyses with the results of the annual streamflow of the Kaidu-kongque River (2005–2010). Due to the rainy seasons in the Kaidu-kongque River Basin, more than 80% of the total annual precipitation falls from May to September, and less than 20% of the total falls from November to the following April [37]. Therefore, the total water availability can be converted to several levels. Table 3 shows the total water availability of the Kaidu-kongque River Basin under several level probabilities.
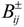 and
and 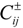 are estimated according to different users’ gross national product in different counties indirectly, the upper bound values of which are estimated as the highest from the yearbook (2005–2010) and the lower bound values of which are the opposite. For example, the net benefit (
are estimated according to different users’ gross national product in different counties indirectly, the upper bound values of which are estimated as the highest from the yearbook (2005–2010) and the lower bound values of which are the opposite. For example, the net benefit ( 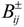 ) for the agricultural user in Hejing County is estimated by the gross amount of crops (i.e., wheat, corn, tomato, cotton and fruit) and the total water demand (net benefit = gross amount of crops/total water demand). From 2005 to 2010, the highest net benefit was 1860 US$/103 m3 in 2008, which was estimated by the gross amount of crops (i.e., wheat = 45.1 × 106 US$; oil plant = 11.3 × 106 US$; tomato = 15.93 × 106 US$; cotton t = 44.02 × 106 US$ and other crops = 47.33 × 106 US$) and the water demand (i.e., wheat = 24.1 × 106 m3; oil plant = 2.91 × 106 m3; tomato = 3.41 × 106 m3; cotton = 29.4 × 106 m3 and other crops = 28.18 × 106 m3). Meanwhile, the lowest net benefit was 1530 US$/103 m3 in 2005. Therefore, the interval value of the net benefit is acquired as [1530, 1860] US$/103 m3, which is on the basis of the highest and lowest value of the net benefit. The method calculated for the net benefit of the agricultural user in Hejing County can be applied to other users, districts and even other economic data.
) for the agricultural user in Hejing County is estimated by the gross amount of crops (i.e., wheat, corn, tomato, cotton and fruit) and the total water demand (net benefit = gross amount of crops/total water demand). From 2005 to 2010, the highest net benefit was 1860 US$/103 m3 in 2008, which was estimated by the gross amount of crops (i.e., wheat = 45.1 × 106 US$; oil plant = 11.3 × 106 US$; tomato = 15.93 × 106 US$; cotton t = 44.02 × 106 US$ and other crops = 47.33 × 106 US$) and the water demand (i.e., wheat = 24.1 × 106 m3; oil plant = 2.91 × 106 m3; tomato = 3.41 × 106 m3; cotton = 29.4 × 106 m3 and other crops = 28.18 × 106 m3). Meanwhile, the lowest net benefit was 1530 US$/103 m3 in 2005. Therefore, the interval value of the net benefit is acquired as [1530, 1860] US$/103 m3, which is on the basis of the highest and lowest value of the net benefit. The method calculated for the net benefit of the agricultural user in Hejing County can be applied to other users, districts and even other economic data.  is a basic form of trading cost, which is estimated by the actual price of water exceed water permit in Kaidu-kongque Basin.
is a basic form of trading cost, which is estimated by the actual price of water exceed water permit in Kaidu-kongque Basin. 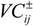 is estimated according to the opportunity cost of water, which is affected by a number of factors, such as the scarcity of water resources, the relationship between supply and demand and the status of socio-economic development. Table 2 shows policy data
is estimated according to the opportunity cost of water, which is affected by a number of factors, such as the scarcity of water resources, the relationship between supply and demand and the status of socio-economic development. Table 2 shows policy data 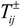 , which are acquired from the water permits of the water authority of Uygur Autonomous Region from 2005 to 2010 directly. Additionally, water target
, which are acquired from the water permits of the water authority of Uygur Autonomous Region from 2005 to 2010 directly. Additionally, water target  is estimated by the users’ actual water usage in recent years, which takes the situation of economic development into consideration. The value of
is estimated by the users’ actual water usage in recent years, which takes the situation of economic development into consideration. The value of  should be derived by conducting statistical analyses with the results of the annual streamflow of the Kaidu-kongque River (2005–2010). Due to the rainy seasons in the Kaidu-kongque River Basin, more than 80% of the total annual precipitation falls from May to September, and less than 20% of the total falls from November to the following April [37]. Therefore, the total water availability can be converted to several levels. Table 3 shows the total water availability of the Kaidu-kongque River Basin under several level probabilities.
should be derived by conducting statistical analyses with the results of the annual streamflow of the Kaidu-kongque River (2005–2010). Due to the rainy seasons in the Kaidu-kongque River Basin, more than 80% of the total annual precipitation falls from May to September, and less than 20% of the total falls from November to the following April [37]. Therefore, the total water availability can be converted to several levels. Table 3 shows the total water availability of the Kaidu-kongque River Basin under several level probabilities.Table 1 shows basic economic data and trading costs, which are estimated indirectly based on the statistical yearbook of the Xinjiang Uygur Autonomous Region in the Uygur Autonomous Region, 2005–2010, and the water price for the Xinjiang Autonomous Region. Values of 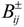 and
and 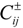 are estimated according to different users’ gross national product in different counties indirectly, the upper bound values of which are estimated as the highest from the yearbook (2005–2010) and the lower bound values of which are the opposite. For example, the net benefit (
are estimated according to different users’ gross national product in different counties indirectly, the upper bound values of which are estimated as the highest from the yearbook (2005–2010) and the lower bound values of which are the opposite. For example, the net benefit ( 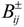 ) for the agricultural user in Hejing County is estimated by the gross amount of crops (i.e., wheat, corn, tomato, cotton and fruit) and the total water demand (net benefit = gross amount of crops/total water demand). From 2005 to 2010, the highest net benefit was 1860 US$/103 m3 in 2008, which was estimated by the gross amount of crops (i.e., wheat = 45.1 × 106 US$; oil plant = 11.3 × 106 US$; tomato = 15.93 × 106 US$; cotton t = 44.02 × 106 US$ and other crops = 47.33 × 106 US$) and the water demand (i.e., wheat = 24.1 × 106 m3; oil plant = 2.91 × 106 m3; tomato = 3.41 × 106 m3; cotton = 29.4 × 106 m3 and other crops = 28.18 × 106 m3). Meanwhile, the lowest net benefit was 1530 US$/103 m3 in 2005. Therefore, the interval value of the net benefit is acquired as [1530, 1860] US$/103 m3, which is on the basis of the highest and lowest value of the net benefit. The method calculated for the net benefit of the agricultural user in Hejing County can be applied to other users, districts and even other economic data.
) for the agricultural user in Hejing County is estimated by the gross amount of crops (i.e., wheat, corn, tomato, cotton and fruit) and the total water demand (net benefit = gross amount of crops/total water demand). From 2005 to 2010, the highest net benefit was 1860 US$/103 m3 in 2008, which was estimated by the gross amount of crops (i.e., wheat = 45.1 × 106 US$; oil plant = 11.3 × 106 US$; tomato = 15.93 × 106 US$; cotton t = 44.02 × 106 US$ and other crops = 47.33 × 106 US$) and the water demand (i.e., wheat = 24.1 × 106 m3; oil plant = 2.91 × 106 m3; tomato = 3.41 × 106 m3; cotton = 29.4 × 106 m3 and other crops = 28.18 × 106 m3). Meanwhile, the lowest net benefit was 1530 US$/103 m3 in 2005. Therefore, the interval value of the net benefit is acquired as [1530, 1860] US$/103 m3, which is on the basis of the highest and lowest value of the net benefit. The method calculated for the net benefit of the agricultural user in Hejing County can be applied to other users, districts and even other economic data.  is a basic form of trading cost, which is estimated by the actual price of water exceed water permit in Kaidu-kongque Basin.
is a basic form of trading cost, which is estimated by the actual price of water exceed water permit in Kaidu-kongque Basin. 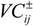 is estimated according to the opportunity cost of water, which is affected by a number of factors, such as the scarcity of water resources, the relationship between supply and demand and the status of socio-economic development. Table 2 shows policy data
is estimated according to the opportunity cost of water, which is affected by a number of factors, such as the scarcity of water resources, the relationship between supply and demand and the status of socio-economic development. Table 2 shows policy data 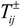 , which are acquired from the water permits of the water authority of Uygur Autonomous Region from 2005 to 2010 directly. Additionally, water target
, which are acquired from the water permits of the water authority of Uygur Autonomous Region from 2005 to 2010 directly. Additionally, water target  is estimated by the users’ actual water usage in recent years, which takes the situation of economic development into consideration. The value of
is estimated by the users’ actual water usage in recent years, which takes the situation of economic development into consideration. The value of  should be derived by conducting statistical analyses with the results of the annual streamflow of the Kaidu-kongque River (2005–2010). Due to the rainy seasons in the Kaidu-kongque River Basin, more than 80% of the total annual precipitation falls from May to September, and less than 20% of the total falls from November to the following April [37]. Therefore, the total water availability can be converted to several levels. Table 3 shows the total water availability of the Kaidu-kongque River Basin under several level probabilities.
should be derived by conducting statistical analyses with the results of the annual streamflow of the Kaidu-kongque River (2005–2010). Due to the rainy seasons in the Kaidu-kongque River Basin, more than 80% of the total annual precipitation falls from May to September, and less than 20% of the total falls from November to the following April [37]. Therefore, the total water availability can be converted to several levels. Table 3 shows the total water availability of the Kaidu-kongque River Basin under several level probabilities.
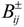 and
and 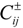 are estimated according to different users’ gross national product in different counties indirectly, the upper bound values of which are estimated as the highest from the yearbook (2005–2010) and the lower bound values of which are the opposite. For example, the net benefit (
are estimated according to different users’ gross national product in different counties indirectly, the upper bound values of which are estimated as the highest from the yearbook (2005–2010) and the lower bound values of which are the opposite. For example, the net benefit ( 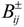 ) for the agricultural user in Hejing County is estimated by the gross amount of crops (i.e., wheat, corn, tomato, cotton and fruit) and the total water demand (net benefit = gross amount of crops/total water demand). From 2005 to 2010, the highest net benefit was 1860 US$/103 m3 in 2008, which was estimated by the gross amount of crops (i.e., wheat = 45.1 × 106 US$; oil plant = 11.3 × 106 US$; tomato = 15.93 × 106 US$; cotton t = 44.02 × 106 US$ and other crops = 47.33 × 106 US$) and the water demand (i.e., wheat = 24.1 × 106 m3; oil plant = 2.91 × 106 m3; tomato = 3.41 × 106 m3; cotton = 29.4 × 106 m3 and other crops = 28.18 × 106 m3). Meanwhile, the lowest net benefit was 1530 US$/103 m3 in 2005. Therefore, the interval value of the net benefit is acquired as [1530, 1860] US$/103 m3, which is on the basis of the highest and lowest value of the net benefit. The method calculated for the net benefit of the agricultural user in Hejing County can be applied to other users, districts and even other economic data.
) for the agricultural user in Hejing County is estimated by the gross amount of crops (i.e., wheat, corn, tomato, cotton and fruit) and the total water demand (net benefit = gross amount of crops/total water demand). From 2005 to 2010, the highest net benefit was 1860 US$/103 m3 in 2008, which was estimated by the gross amount of crops (i.e., wheat = 45.1 × 106 US$; oil plant = 11.3 × 106 US$; tomato = 15.93 × 106 US$; cotton t = 44.02 × 106 US$ and other crops = 47.33 × 106 US$) and the water demand (i.e., wheat = 24.1 × 106 m3; oil plant = 2.91 × 106 m3; tomato = 3.41 × 106 m3; cotton = 29.4 × 106 m3 and other crops = 28.18 × 106 m3). Meanwhile, the lowest net benefit was 1530 US$/103 m3 in 2005. Therefore, the interval value of the net benefit is acquired as [1530, 1860] US$/103 m3, which is on the basis of the highest and lowest value of the net benefit. The method calculated for the net benefit of the agricultural user in Hejing County can be applied to other users, districts and even other economic data.  is a basic form of trading cost, which is estimated by the actual price of water exceed water permit in Kaidu-kongque Basin.
is a basic form of trading cost, which is estimated by the actual price of water exceed water permit in Kaidu-kongque Basin. 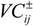 is estimated according to the opportunity cost of water, which is affected by a number of factors, such as the scarcity of water resources, the relationship between supply and demand and the status of socio-economic development. Table 2 shows policy data
is estimated according to the opportunity cost of water, which is affected by a number of factors, such as the scarcity of water resources, the relationship between supply and demand and the status of socio-economic development. Table 2 shows policy data 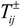 , which are acquired from the water permits of the water authority of Uygur Autonomous Region from 2005 to 2010 directly. Additionally, water target
, which are acquired from the water permits of the water authority of Uygur Autonomous Region from 2005 to 2010 directly. Additionally, water target  is estimated by the users’ actual water usage in recent years, which takes the situation of economic development into consideration. The value of
is estimated by the users’ actual water usage in recent years, which takes the situation of economic development into consideration. The value of  should be derived by conducting statistical analyses with the results of the annual streamflow of the Kaidu-kongque River (2005–2010). Due to the rainy seasons in the Kaidu-kongque River Basin, more than 80% of the total annual precipitation falls from May to September, and less than 20% of the total falls from November to the following April [37]. Therefore, the total water availability can be converted to several levels. Table 3 shows the total water availability of the Kaidu-kongque River Basin under several level probabilities.
should be derived by conducting statistical analyses with the results of the annual streamflow of the Kaidu-kongque River (2005–2010). Due to the rainy seasons in the Kaidu-kongque River Basin, more than 80% of the total annual precipitation falls from May to September, and less than 20% of the total falls from November to the following April [37]. Therefore, the total water availability can be converted to several levels. Table 3 shows the total water availability of the Kaidu-kongque River Basin under several level probabilities.
Table 1.
Economic data and trading costs.
| District | User | |||
|---|---|---|---|---|
| i = 1 | i = 2 | i = 3 | i = 4 | |
| Municipality | Agriculture | Industry | Ecology | |
| Net benefits (unit: US$/103 m3) | ||||
| j = 1 Kuerle county | [6030, 6670] | [2320, 2520] | [4530, 4670] | [1960, 2120] |
| j = 2 Yanqi county | [5500, 6040] | [1420, 1560] | [2600, 2930] | [1680, 1930] |
| j = 3 Hejing county | [4670, 4800] | [1530, 1860] | [3730, 3810] | [1540, 1780] |
| j = 4 Heshuo county | [5300, 5530] | [2010, 2340] | [3440, 3620] | [1660, 1940] |
| j = 5 Bohu county | [4910, 5100] | [1780, 2010] | [3620, 3740] | [1530, 1840] |
| j = 6 Yuli county | [4600, 5260] | [2230, 2460] | [3220, 3440] | [1690, 1990] |
| Penalties (unit: US$/103 m3) | ||||
| j = 1 Kuerle county | [9045, 10005] | [3480, 3765] | [6795, 7005] | [2940, 3180] |
| j = 2 Yanqi county | [8250, 9060] | [2130, 2340] | [3900, 4395] | [2520, 2895] |
| j = 3 Hejing county | [7005, 7200] | [2295, 2790] | [5595, 5725] | [2310, 2670] |
| j = 4 Heshuo county | [7950, 8295] | [3015, 3510] | [5160, 5430] | [2190, 2490] |
| j = 5 Bohu county | [7365, 7650] | [2670, 3015] | [5430, 5610] | [2295, 2760] |
| j = 6 Yuli county | [6900, 7890] | [3345, 3690] | [4830, 5160] | [2535, 2985] |
| Trading fix cost (unit: US$/103 m3) | ||||
| j = 1 to 6 | [3050, 3150] | [550, 650] | [2400, 2600] | [280, 350] |
| Trading variable cost (unit: US$/103 m3) | ||||
| j = 1 to 6 | [1200, 1350] | [700, 800] | [150, 200] | [100, 150] |
Since linguistic terms are encountered in the practical process of data acquisition associated with human subjective judgment, scales of linguistic terms have been established [41]. Semantic scales are used to present the credibility levels of decision makers (i.e., quite, very, almost and practical degree of satisfaction corresponding to λ = 0.6 to 0.9) and violated constraints (i.e., quite, very, almost and practical violation risk level corresponding to λ = 0.4 to 0.1). There is a strong negative correlation between credibility levels and violated levels (i.e., credibility levels + violated levels = 1), in which is manifest the relationship between the degree of satisfaction and the violation risk level. For example, the quite satisfied constraint (λ = 0.6) corresponds to the quite violated constraint (r = 0.4), which indicates a high satisfaction degree corresponding to a low violation risk. By setting the acceptable semantic terms of decision makers, acceptable interval credibility levels can then be generated. In order to ensure that the constraints would be practically satisfied and not violated in the study system, the credibility level, λ, in this model is set as [0.6, 0.9] [32]. In this study, two cases were examined based on different water resource management policies. Case 1 was based on a policy for a 5% decrease in the water permit and a 100% trading ratio. Case 2 was based on a policy for a 10% decrease in the water permit and a 90% trading ratio. Since the credibility level, λ, in this model is set as [0.6, 0.9], different violation risk levels of water availability and water resource constraints are considered in two cases, which can help in analyzing different water resource management policies under the credibility levels.

Table 2.
Water targets and water permits.
| District | User | |||
|---|---|---|---|---|
| i = 1 | i = 2 | i = 3 | i = 4 | |
| Municipality | Agriculture | Industry | Ecology | |
| Water target (unit: 106 m3) | ||||
| j = 1 Kuerle County | [8.80, 14.00] | [258.00, 275.00] | [53.30, 620.00] | [56.00, 76.00] |
| j = 2 Yanqi County | [6.00, 8.20] | [158.00, 165.00] | [28.00, 39.00] | [31.00, 47.00] |
| j = 3 Hejing County | [2.40, 4.30] | [81.00, 88.00] | [16.00, 20.10] | [14.70, 23.00] |
| j = 4 Heshuo County | [0.24, 0.50] | [9.70, 10.10] | [1.78, 2.25] | [1.28, 2.60] |
| j = 5 Bohu County | [2.20, 4.30] | [75.00, 85.00] | [15.60, 19.00] | [13.70, 23.00] |
| j = 6 Yuli County | [4.60, 6.00] | [110.00, 120.00] | [21.60, 27.00] | [24.00, 33.00] |
| Allocated allowable water permit (unit: 106 m3) | ||||
| j = 1 Kuerle County | [9.72, 13.75] | [261.60, 275.08] | [55.44, 61.89] | [59.56, 75.65] |
| j = 2 Yanqi County | [[6.64, 8.14] | [158.33, 162.87] | [30.31, 36.65] | [32.26, 44.79] |
| j = 3 Hejing County | [2.89, 4.23] | [82.22, 84.50] | [15.70, 19.01] | [17.08, 23.24] |
| j = 4 Heshuo County | [0.36, 0.53] | [9.11, 9.38] | [1.89, 2.11] | [1.69, 2.70] |
| j = 5 Bohu County | [2.56, 4.09] | [78.89, 81.84] | [15.78, 18.41] | [15.58, 22.58] |
| j = 6 Yuli County | [4.94, 5.87] | [110.56, 117.41] | [22.33, 26.42] | [25.56, 32.29] |

Table 3.
Probability levels and total water availabilities.
| District | Level | Probability | User | |||
|---|---|---|---|---|---|---|
| i = 1 | i = 2 | i = 3 | i = 4 | |||
| Municipality | Agriculture | Industry | Ecology | |||
| Total water availability (unit: 106 m3) | ||||||
| j = 1 Kuerle County | h = 1 (low) | 0.6 | [6.57, 10.67] | [202.32, 216.00] | [43.47, 49.96] | [42.30, 58.50] |
| h = 2 (medium) | 0.3 | [7.30, 11.85] | [224.80, 240.00] | [48.30, 55.51] | [47.00, 65.00] | |
| h = 3 (high) | 0.1 | [8.03, 13.04] | [247.28, 264.00] | [53.13, 61.06] | [51.70, 71.50] | |
| j = 2 Yanqi County | h = 1 (low) | 0.6 | [4.77, 6.38] | [124.02, 128.70] | [22.86, 29.41] | [22.95, 35.55] |
| h = 2 (medium) | 0.3 | [5.30, 7.09] | [137.80, 143.00] | [25.40, 32.68] | [25.50, 39.50] | |
| h = 3 (high) | 0.1 | [5.83, 7.80] | [151.58, 157.30] | [27.94, 35.95] | [28.05, 43.45] | |
| j = 3 Hejing County | h = 1 (low) | 0.6 | [1.89, 3.24] | [66.11, 68.40] | [12.96, 16.29] | [11.43, 17.82] |
| h = 2 (medium) | 0.3 | [2.10, 3.60] | [73.45, 76.00] | [14.40, 18.10] | [12.70, 19.80] | |
| h = 3 (high) | 0.1 | [2.31, 3.96] | [80.80, 83.60] | [15.84, 19.91] | [13.97, 21.78] | |
| j = 4 Heshuo County | h = 1 (low) | 0.6 | [0.19, 0.38] | [7.90, 8.19] | [1.40, 1.62] | [0.88, 1.90] |
| h = 2 (medium) | 0.3 | [0.21, 0.42] | [8.78, 9.10] | [1.55, 1.80] | [0.98, 2.11] | |
| h = 3 (high) | 0.1 | [0.23, 0.46] | [9.66, 10.01] | [1.71, 1.98] | [1.08, 2.32] | |
| j = 5 Bohu County | h = 1 (low) | 0.6 | [1.79, 3.33] | [58.50, 65.70] | [12.69, 15.38] | [11.16, 18.20] |
| h = 2 (medium) | 0.3 | [1.99, 3.70] | [65.00, 73.00] | [14.10, 17.09] | [12.40, 20.23] | |
| h = 3 (high) | 0.1 | [2.19, 4.07] | [71.50, 80.30] | [15.51, 18.80] | [13.64, 22.25] | |
| j = 6 Yuli County | h = 1 (low) | 0.6 | [3.69, 4.75] | [86.85, 93.82] | [17.64, 21.79] | [19.35, 26.10] |
| h = 2 (medium) | 0.3 | [4.10, 5.28] | [96.50, 104.25] | [19.60, 24.21] | [21.50, 29.00] | |
| h = 3 (high) | 0.1 | [4.51, 5.81] | [106.15, 114.67] | [21.56, 26.63] | [23.65, 31.90] | |
4. Result Analysis
4.1. Results under Different Credibility Levels
Figure 2 shows the results of optimal water allocations for municipal, agricultural, industrial and ecological users in the six counties of the study basin under Case 1 when λ = 0.6 and 0.9. Results indicate that a shortage in the water supply would be generated if the pre-regulated target could not be satisfied (i.e., shortage = targeted value − available inflow). Under such a situation, the actual water allocation would be the difference between the pre-regulated target and the probabilistic shortage (i.e., allocation = target − shortage). Each allocated water flow is the difference between the promised target and the probabilistic shortage under a given stream condition with an associated probability level, which indicates that different violation levels would result in varied water-allocation patterns. For example, under Case 1 (λ = 0.6), the optimized targets of municipal, agricultural, industrial and ecological users (in Bohu County, j = 5) would be 4.95 × 106 m3, 97.75 × 106 m3, 21.85 × 106 m3 and 28.75 ×106 m3, respectively. When inflow is high, shortages would be [0.19, 1.28] × 106 m3, [3.82, 12.11] × 106 m3, [2.55, 2.55] × 106 m3 and [6.59, 7.06] × 106 m3; correspondingly, the actual allocations would be [3.66, 4.75] × 106 m3, [85.65, 93.93] × 106 m3, [19.30, 19.30] × 106 m3 and [18.81, 19.29] × 106 m3. The total amount of allocated water to Bohu County would be from 127.42 × 106 m3 to 137.27 × 106 m3; however, its total water demand would be 153.3 × 106 m3, indicating that there would be a shortage, even though the inflow is high. Due to more than 80% of the total annual precipitation falls from May to September in the study region, falls in other months were much less. Therefore, when inflows are medium or low, the shortage would be strengthened, whereas each user would have to obtain water from other sources to satisfy its essential demands.
Meanwhile, several λ levels were examined by different combinations of the fuzzy sets, which achieved different water availabilities, water targets and varied water-allocations under Case 1. When λ = 0.6, higher water availability corresponding to the lower credibility satisfaction levels would lead to lower water deficiency, which produced a higher water allocation. While λ = 0.9, lower water availability corresponding to the higher credibility satisfaction levels would produce the opposite result. Therefore, as shown in Figure 2, the amount of water allocation when λ = 0.6 is greater than that when λ = 0.9, implying that a low credibility level could result in a high water allocation level in the trading program. For example, when λ = 0.6, optimized target of municipal users in Bohu County (j = 5) was 4.95 ×106 m3. When inflow is high, shortages would be [0.19, 1.28] × 106 m3; correspondingly, the actual allocations would be [3.66, 4.75] × 106 m3. Meanwhile, when λ = 0.9, a lower water resource permit and water availability would correspond to the higher credibility satisfaction levels. The optimized municipal target for Bohu County (j = 5) was 4.95 × 106 m3. When inflow is high, shortages would be [0.21, 1.32] × 106 m3; correspondingly, the actual allocations would be [1.32, 4.75] × 106 m3. This implies that different λ levels lead to different credibility satisfaction levels and violation risks in the water planning system, corresponding to different water availabilities, which lead to different shortages and allocations.
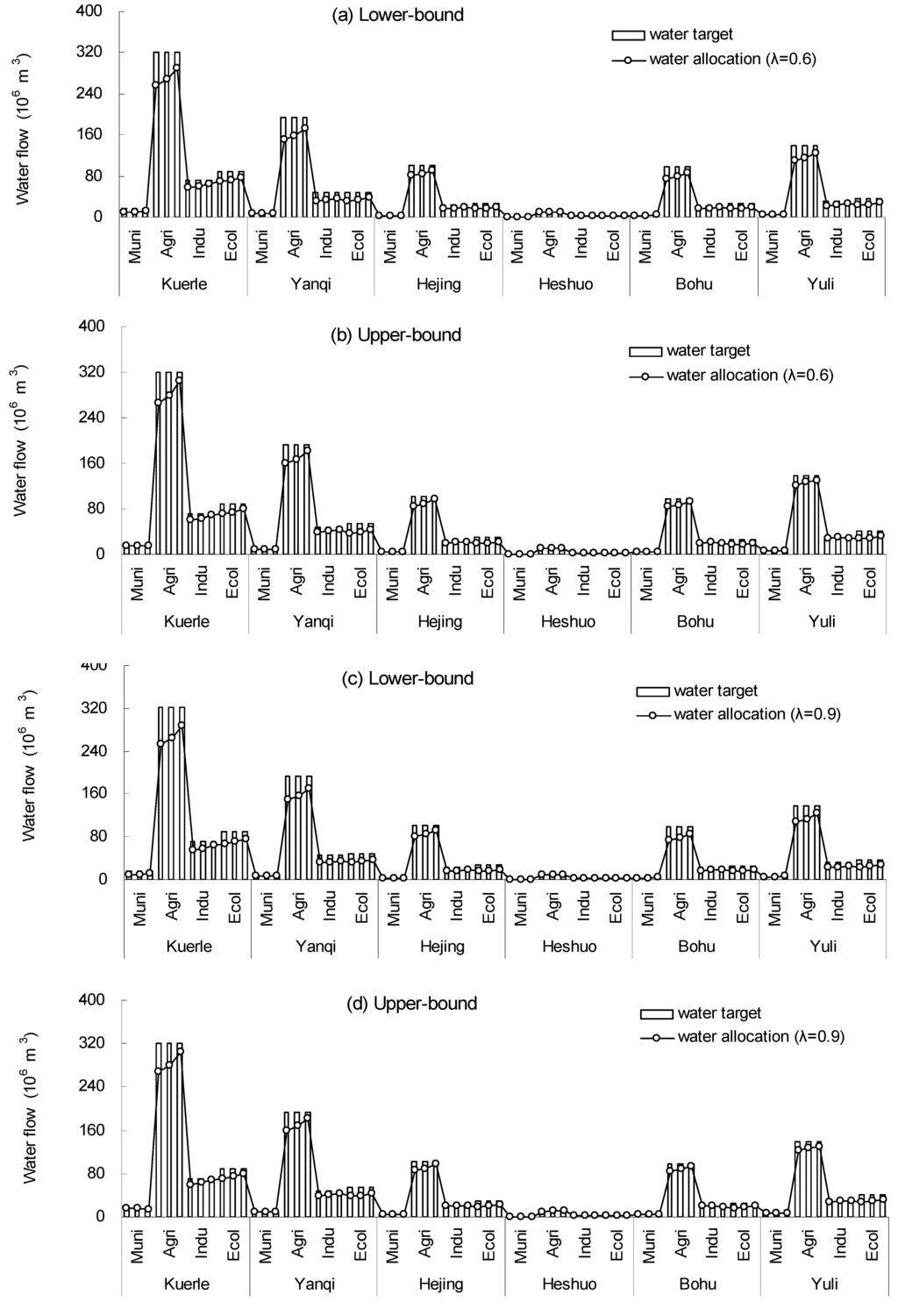
Figure 2.
Solutions for water allocation under Case 1 (λ = 0.6 and 0.9).
Meanwhile, several λ levels were examined by different combinations of the fuzzy sets, which achieved different water availabilities, water targets, and varied water allocations under Case 1. When λ = 0.6, higher water availability corresponding to the lower credibility satisfaction levels would lead to lower water deficiency, which produced a higher water allocation. While λ = 0.9, lower water availability corresponding to the higher credibility satisfaction levels would produce the opposite result. Therefore, as shown in Figure 2, the amount of water allocation when λ = 0.6 is greater than that when λ = 0.9, implying that a low credibility level could result in a high water allocation level in the trading program. For example, when λ = 0.6, the optimized target for municipal users in Bohu County (j = 5) was 4.95 ×106 m3. When inflow is high, shortages would be [0.19, 1.28] × 106 m3; correspondingly, the actual allocations would be [3.66, 4.75] × 106 m3. Meanwhile λ = 0.9, lower water resource permit and water availability would correspond to the higher credibility satisfaction levels. Optimized targets of municipal in Bohu County (j = 5) was 4.95 × 106 m3. When inflow is high, shortages would be [0.21, 1.32] × 106 m3; correspondingly, the actual allocations would be [1.32, 4.75] × 106 m3. It replied that different λ levels led to different credibility satisfactions and violation risks in water planning system, corresponding to different water availabilities, which lead to different shortages, and allocations.
Different policies in water resources planning would result in varied shortages, targets, allocations and trading amounts. Figure 3 presents water shortages under the two cases (λ = 0.9), which indicated that water shortages changed by decreasing the water permits. Water shortages would occur if the available water resource could not meet the regulated targets, which indicated that the shortages were associated with water targets and water availability. In the study basin, water targets are often determined before total water inflows are known, which generates a problem of recourse for water allocation caused by variations between targets and water availabilities. Due to water deficiency in the study region, water permits have been allocated in advance, so as to save more water or to obtain higher benefits. By decreasing water permits, less water would be allowanced, but more water would be released to trade, which leads to much more shortage under Case 2 than under Case 1. For example, water shortages of municipal users in Kuerle County (j = 1) would be [1.31, 6.29] × 106 m3 at the low level, [0.62, 5.86] × 106 m3 at the medium level and [0.66, 4.99] × 106 m3 at the high level under Case 1 (λ = 0.6), while it would be [1.31, 6.39] × 106 m3 at the low level, [0.62, 5.96] × 106 m3 at the medium level and [1.54, 5.11] × 106 m3 at the high level under Case 2 (λ = 0.6). Moreover, shortages are affected by the randomness of water availabilities. Due to a special climate situation, when the flow is high in the wet season, the shortages may be relatively low under advantageous conditions and would be increased when the flow is low in the dry season.
Figure 4 presents the results for water allocations under the two cases (λ = 0.6), which indicated that the allocated water changed by decreasing the water permits. Results demonstrated that higher water permits lead to a lower shortage, resulting in a lower allocation. Meanwhile, lower water permits generate the opposite result. For example, the water allocation of municipal users in Yuli County (j = 6) would be [5.12, 6.34] × 106 m3 at the low level, [5.35, 6.64] × 106 m3 at the medium level and [5.82, 6.22] × 106 m3 at the high level under case 1 (λ = 0.6), while it would be [5.12, 6.20] × 106 m3 at the low level, [5.35, 6.50] × 106 m3 at the medium level and [5.82, 5.91] × 106 m3 at the high level under Case 2 (λ = 0.6). The results of water allocations under the two cases indicated that different water allocations would be achieved, due to different shortages, based on different policies. It is implied that water allocations were sensitive to water permitting, since different water permits led to different shortages, resulting in different water allocations. Figure 5 presents the amount of water trading under different water permit and trading ratios. In the study region, due to the extremely dry climate, low rainfall and high evaporation rate, the losses from a water shortage are serious. Thus, trading was introduced to reduce the losses from, shortages and to obtain greater benefits. When the losses from water shortages are generated, each user would need to obtain water from released water and other sources to satisfy its essential demands. For example, the amount of water trading for agricultural users in Heshuo County (j = 4) would be [1.48, 1.62] × 106 m3 at the low level, [0.70, 1.16] × 106 m3 at the medium level and [0, 1.36] × 106 m3 at the high level under Case 1 (λ = 0.9), while it would be [1.05, 1.46] × 106 m3 at the low level, [0.25, 0.65] × 106 m3 at the medium level and [0, 0] × 106 m3 at the high level under Case 2 (λ = 0.9). The solutions indicated that the amount of trading based on shortages was relatively low under advantageous conditions and rose in the dry season. Meanwhile, by decreasing the water permit and trading ratios, the more the water surplus remedies the water shortage, the less is the amount of water trading from other sources. Moreover, the amount of water trading is sensitive to trading cost, particular in assuming different water polices. Under the situation of water permit and trading ratio change, the amount of water trading changes dissimilarly, due to the law of value. More released water permits lead to a greater difference in the amount of water trading, while a smaller trading ratio obtains a tremendous change in water trading. For example, in Figure 5, the amount of water trading for agricultural users in Yanqi County (j = 2) would be [7.54, 7.54] × 106 m3 at the low level under Case 1 (λ = 0.9), while it would be [0, 6.65] × 106 m3 at the low level under Case 2 (λ = 0.9). The difference of water trading between Case 1 and Case 2 was caused by the lowest trading cost and limited trading resources.
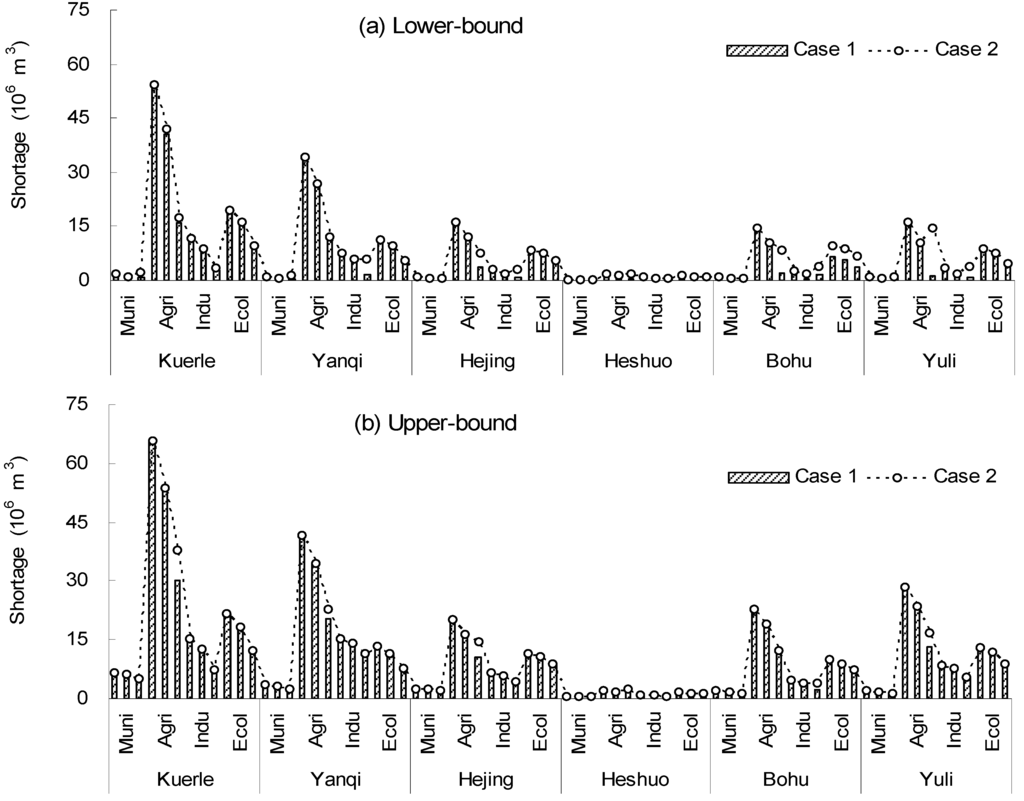
Figure 3.
Solutions for water shortage under case 1 and case 2 (λ = 0.6).
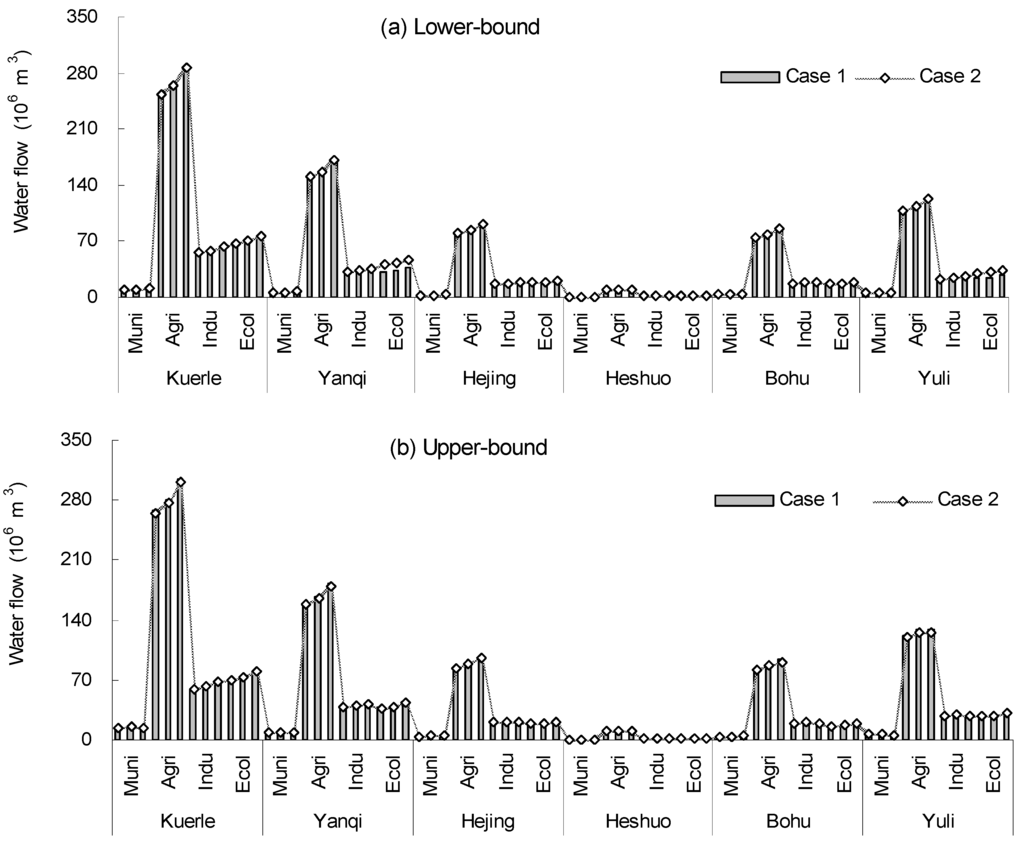
Figure 4.
Solutions for water allocation under Case 1 and Case 2 (λ = 0.9).
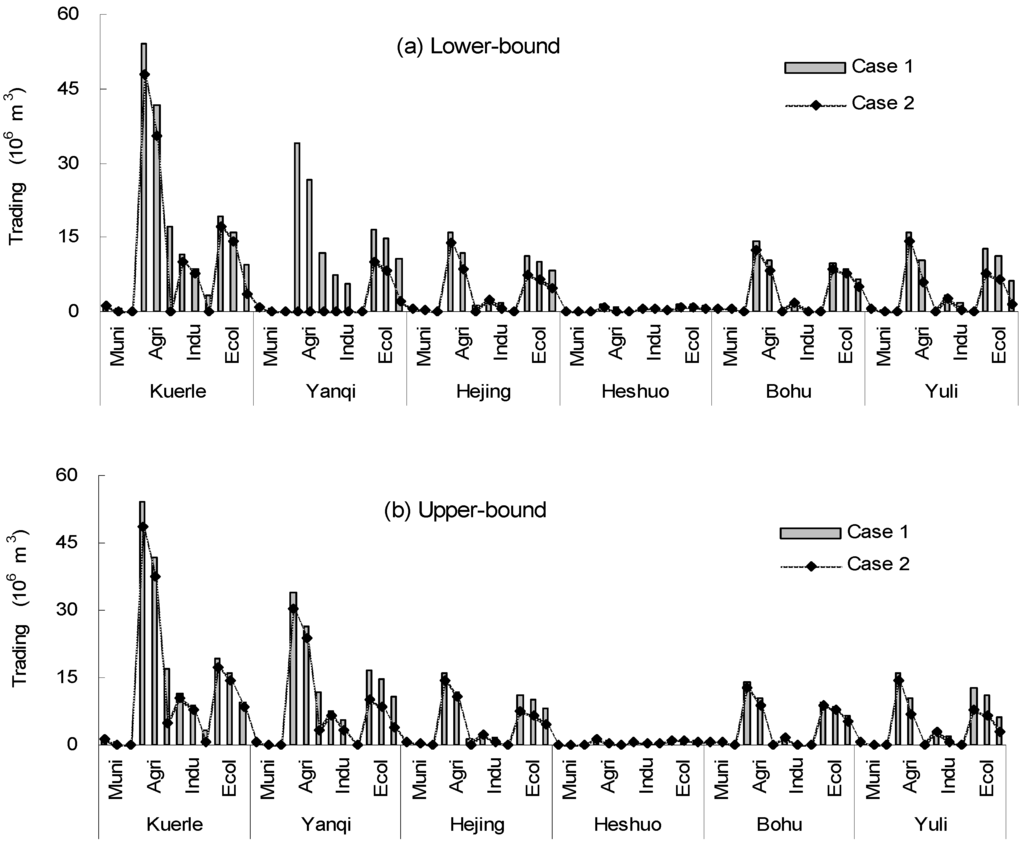
Figure 5.
Solutions for water trading under Case 1 and Case 2 (λ = 0.6).
4.2. Comparison of Trading and Non-Trading Schemes
Figure 6 shows the solutions for the optimized net benefit for the system obtained from the TICP model with trading and non-trading schemes, which are the sum of the first-stage benefit from the water allocation and the second-stage random losses of water deficiency. The lower-bound benefits for the system could result in a lower risk of violating the allowable water permit. Conversely, a higher benefit would lead to a higher probability of violating the allowance. Consequently, there is a tradeoff between the net benefit for the system and the water permit violation risk. In Figure 6, the net benefit for the system would be achieved as [0.77, 2.28] × 109 US$ (λ = 0.6) and [0.68, 2.20] × 109 US$ (λ = 0.9) under Case 1. By decreasing the water permit, the benefits for the system would be [0.51, 1.89] × 109 US$ (λ = 0.6) and [0.47, 1.82] × 109 US$ (λ = 0.9) under Case 2, which indicates that the net benefit for the system would decrease by decreasing the water permit and trading ratio. However, the net benefit for the system under the two cases with the trading scheme was much higher than that with the non-trading scheme (i.e., [0.47, 1.81] × 109 US$ when λ = 0.6 and [0.31, 1.77] × 109 US$ when λ = 0.9). Comparing the net benefit for the system under trading and that under non-trading, the efficiency of trading and non-trading would be acquired. This implies that trading through water markets is likely to increase and improve economic efficiency overall.
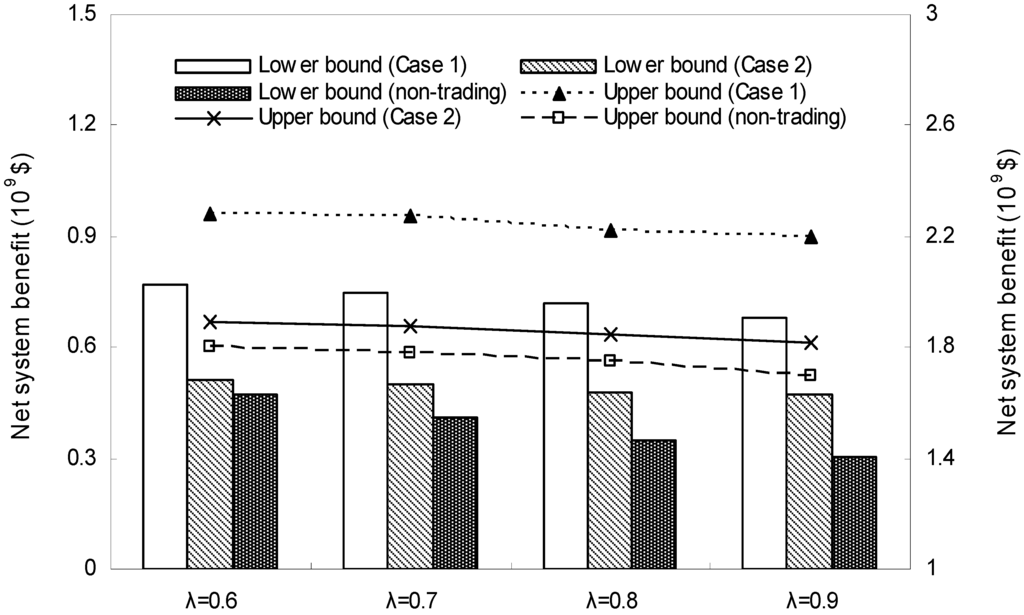
Figure 6.
Benefits for the system under Case 1 and Case 2 (λ = 0.6 to 0.9) with the trading scheme and non-trading scheme.
Meanwhile, water shortages would reduce through water trading, by releasing more water surplus and obtaining other sources of water to remedy water deficiencies. Figure 7 shows the solutions for water shortage under Case 1 (λ = 0.6) with the trading scheme and non-trading scheme, which indicated that water shortages with the trading scheme were much smaller than with the non-trading scheme. For example, water shortages for industrial users in Hejing County (j = 3) with the trading scheme would be [0, 4.24] × 106 m3 at the low level, [1.78, 5.74] × 106 m3 at the medium level and [2.73, 6.50] × 106 m3 at the high level under Case 1 (λ = 0.6), while with the non-trading scheme, they would be [1.96, 6.55] × 106 m3 at the low level, [1.78, 8.05] × 106 m3 at the medium level and [2.73, 8.81] × 106 m3 at the high level. This implies that markets can provide incentives for adopting water saving practices, since market prices make the opportunity cost of water explicit to users. Therefore, water trading was considered as an effective way for not only reducing the shortages of water systems, but also for gaining a higher net benefit for the system in an arid region.
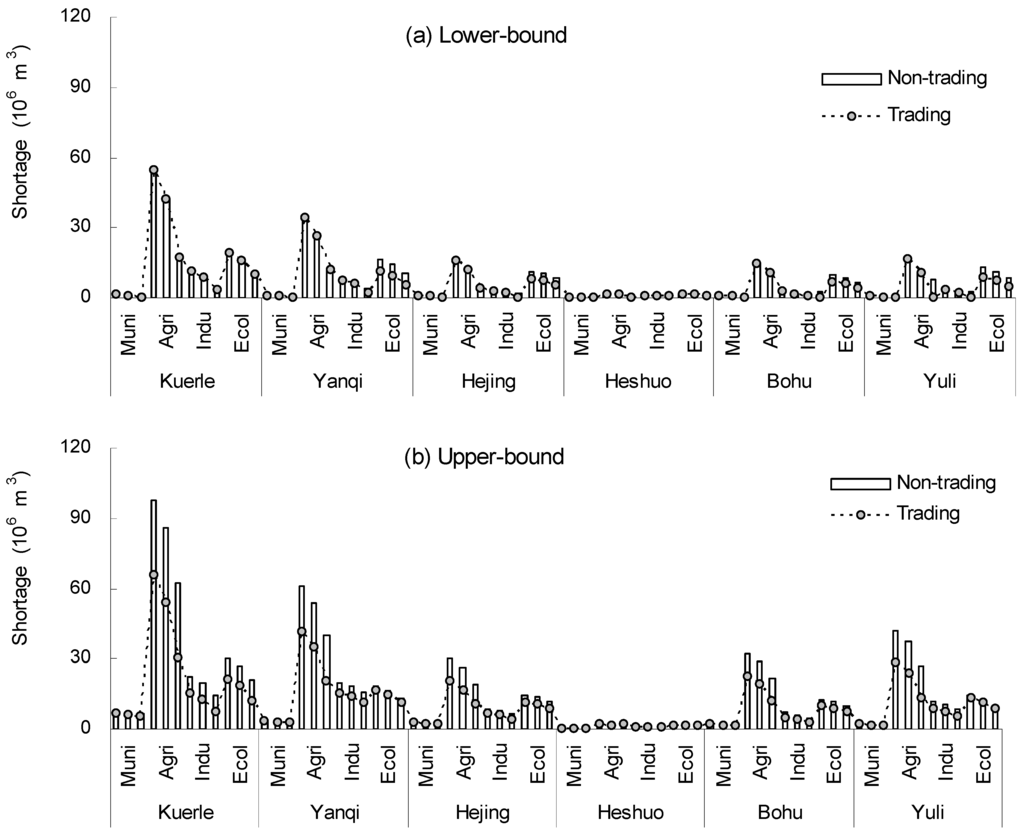
Figure 7.
Solutions shortages under Case 1 (λ = 0.6) with the trading scheme and non-trading scheme.
5. Conclusions
In this study, a two-stage inexact credibility-constrained programming (TICP) method has been developed for identifying the efficiency of water trading policy under multiple uncertainties. The TICP can incorporate uncertainties presented as intervals, probability distributions and fuzzy sets within its modeling framework. It can quantify the effectiveness of water trading, which can deal with system uncertainties between the allocation policy and violation risk. In the proposed model, the credibility constrained programming method, which is derived from fuzzy possibility theory, was incorporated to account for the imprecision associated with the goals of water trading and to make full use of the available information. Fuzzy membership functions were used to encode the possibilistic distribution of the parameters, and credibility was proposed to measure the satisfaction level of the fuzzy constraints. It can deal with water resource allocation problems resulting from randomness in the total water supply and uncertainties represented as interval credibility constrained programming in the water trading system. The significant advantage of the TICP model is that it can reflect the tradeoffs between the predefined economic targets and the associated water shortage penalties, as well as the fuzziness of the water availability.
The developed method has been applied to the Kaidu-kongque River Basin for water trading under uncertainties of water supply and demand. The study region is a typical arid region, in which water shortage and unreliable water supply impede the sustainable development of the regional economy and society in watershed systems. The TICP can facilitate reducing the risks of establishing a water trading program, and the developed method will support decision makers in allocating water resources effectively. Based on the regional situation of water resources, a number of different policy cases based on arid characteristics were listed for comparison. The resulting analysis shows that trading is much more effective than non-trading under some designated situations, which not only increases the economic benefits according to the law of value, but also provides incentives for adopting water saving policies. Water shortage can be remedied by water trading, resulting in loss reduction and improving the benefits for the system. Therefore, trading is an efficient way for allocating water resources optimally, which should be considered in water resource management to remedy the limitation of polices. The results of the case study indicate that the effectiveness of a trading program is sensitive to the water permit and trading ratio; thus the water permit and trading ratio should be considered as a primary factor for policy formulations in water resource management. Therefore, a manager of water resources in the Kaidu-kongque River Basin should adjust the water policies based on regional development, to release appropriate water permits for water trading, which cannot only remedy the losses of water deficiency, but also improve the efficiency of the water resource system. Meanwhile, the policies of the trading ratio should be formulated by the relationships between water availability and regional sustainable development (e.g., economic development, social progress and ecological protection), since fallacious policies of the trading ratio would lead to water trading failure in response to the trading cost and other opportunity costs.
Acknowledgments
This research was supported by the National Natural Science Foundation for Distinguished Young Scholars (grant no. 51225904), the Natural Sciences Foundation of China (grant nos. 51379075 and 51190095), the 111 Project (B14008), and the Program for Innovative Research Team in University (IRT1127).The authors are grateful to the editors and the anonymous reviewers for their insightful comments and helpful suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bates, B.C.; Kundzewicz, Z.W.; Wu, S.; Palutikof, J.P. Climate Change and Water. In Technical Paper of the Intergovernmental Panel on Climate Change; IPCC Secretariat: Geneva, Switzerland, 2008. [Google Scholar]
- Huang, Y.; Li, Y.P.; Chen, X.; Ma, Y.G. Optimization of irrigation water resources for agricultural sustainability in Tarim River Basin, China. Agric. Water Manag. 2012, 107, 74–85. [Google Scholar] [CrossRef]
- Hassan, Q.K.; Sekhon, N.S.; Magai, R.; McEachern, P. Reconstruction of snow water equivalent and snow depth using remote sensing data. J. Environ. Inform. 2012, 20, 67–74. [Google Scholar]
- Su, L.Y.; Christensen, P.; Liu, J.L. Comparative study of water resource management and policies for ecosystems in China and Denmark. J. Environ. Inform. 2013, 21, 72–83. [Google Scholar] [CrossRef]
- Calatrava, J.; Garrido, A. Spot water markets and risk in water supply. Agric. Econ. 2005, 33, 131–143. [Google Scholar] [CrossRef]
- Zaman, A.M.; Malano, H.M.; Davidson, B. An integrated water trading–allocation model, applied to a water market in Australia. Agric. Water Manag. 2009, 96, 149–159. [Google Scholar] [CrossRef]
- Youkhana, E.; Laube, W. Virtual water trade: A realistic policy option for the countries of the Volta Basin in West Africa? Water Policy 2009, 11, 569–581. [Google Scholar] [CrossRef]
- Luo, B.; Maqsood, I.; Gong, Y.Z. Modeling climate change impacts on water trading. Sci. Total Environ. 2010, 408, 2034–2041. [Google Scholar] [CrossRef]
- Dominguez, D.; Truffer, B.; Gujer, W. Tackling uncertainties in infrastructure sectors through strategic planning: The contribution of discursive approaches in the urban water sector. Water Policy 2010, 13, 299–316. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H.; Chen, X. Multistage scenario-based interval-stochastic programming for planning water resources allocation. Stoch. Environ. Res. Risk Assess. 2009, 23, 781–792. [Google Scholar] [CrossRef]
- Ahmed, S.; Tawarmalani, M.; Sahinidis, N.V. A finite branch-and-bound algorithm for two-stage stochastic integer programs. Math. Program. 2004, 100, 355–377. [Google Scholar] [CrossRef]
- Li, Z.; Huang, G.; Zhang, Y.; Li, Y. Inexact two-stage stochastic credibility constrained programming for water quality management. Resourc. Conserv. Recycl. 2013, 73, 122–132. [Google Scholar] [CrossRef]
- Lu, H.W.; Huang, G.H.; Zeng, G.M.; Maqsood, I.; He, L. An inexact two-stage fuzzy-stochastic programming model for water resource management. Water Resour. Manag. 2008, 22, 991–1016. [Google Scholar] [CrossRef]
- Birge, J.R.; Louveaux, F.V. Introduction to Stochastic Programming; Springer-Verlag: New York, NY, USA, 1997. [Google Scholar]
- Maqsood, I.; Huang, G.H.; Huang, Y. ITOM: An interval-parameter two-stage optimization model for stochastic planning of water resources systems. Stoch. Environ. Res. Risk Assess. 2005, 19, 125–133. [Google Scholar] [CrossRef]
- Kenneth, W.H. Two-stage decision-making under uncertainty and stochasticity: Bayesian Programming. Adv. Water Resour. 2007, 30, 641–664. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H. Interval-parameter two-stage stochastic nonlinear programming for water resource management under uncertainty. Water Resour. Manag. 2008, 22, 681–698. [Google Scholar] [CrossRef]
- Vidoli, F. Evaluating the water sector in Italy through a two stage method using the conditional robust nonparametric frontier and multivariate adaptive regression splines. Eur. J. Oper. Res. 2011, 3, 584–595. [Google Scholar]
- Li, Y.P.; Huang, G.H. Two-stage planning for sustainable water-quality management under uncertainty. J. Environ. Manag. 2009, 90, 2402–2413. [Google Scholar] [CrossRef]
- Freeze, R.A.; Massmann, J.; Smith, L.; Sperling, T.; James, B. Hydrogeological decision analysis: 1. A framework. Ground Water 1990, 28, 738–766. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H. Fuzzy-stochastic-based violation analysis method for planning water resource management systems with uncertain information. Inf. Sci. 2009, 179, 4261–4276. [Google Scholar] [CrossRef]
- Nazemi, A.R.; Akbarzadeh, M.R.; Hosseini, S.M. Fuzzy-stochastic linear programming in water resources engineering. Stoch. Environ. Res. Risk Assess. 2002, 2, 167–174. [Google Scholar]
- Lee, C.S.; Chang, S.P. Interactive fuzzy optimization for an economic and environmental balance in a river system. Water Res. 2005, 39, 221–231. [Google Scholar] [CrossRef]
- Bertsimas, D.; Sim, M. The price of robustness. Oper. Res. 2004, 52, 35–53. [Google Scholar] [CrossRef]
- Doolse, G.; Kingwell, R. Robust mathematical programming for natural resource modeling under parametric uncertainty. Nat. Resourc. Modell. 2010, 23, 283–302. [Google Scholar]
- Liu, S.S.; Papageorgiou, L.G.; Gikas, P. Integrated management of nonconventional water resources in anhydrous islands. Water Resourc. Manag. 2012, 26, 359–375. [Google Scholar] [CrossRef]
- Vylder, F.D.; Sundt, B. Constrained credibility estimators in the regression model. Scand. Actuar. J. 1982, 1, 27–31. [Google Scholar]
- Liu, B.; Liu, Y.K. Expected value of fuzzy variable and fuzzy expected value models. IEEE Trans. Fuzzy Syst. 2002, 10, 45–50. [Google Scholar]
- Punyangarm, V.; Yanpirat, P.; Charnsethikul, P.; Lertworasirikul, S. A Credibility Approach for Fuzzy Stochastic Data Envelopment Analysis (FSDEA). In Proceedings of the 7th Asia Pacific Industrial Engineering and Management Systems Conference, Bangkok, Thailand, 17–20 December, 2006.
- Luo, S.X.; Li, F.C.; Qiu, J.Q.; Li, L.X. Credibility-Based General Hartley Measure and Its Application on Fuzzy Programming. In Proceedings of the IEEE 2004 International Conference on Machine Learning and Cybernetics, Shanghai, China, 26–29 August, 2004.
- Rong, A.; Lahdelma, R. Fuzzy chance constrained linear programming model for optimizing the scrap charge in steel production. Eur. J. Oper. Res. 2008, 186, 53–64. [Google Scholar]
- Zhang, Y.M.; Huang, G.H. Inexact credibility constrained programming for environmental system management. Resour. Conserv. Recycl. 2011, 55, 1–7. [Google Scholar]
- Li, Y.P.; Huang, G.H.; Nie, S.L. An interval-parameter multistage stochastic programming model for water resource management under uncertainty. Adv. Water Resour. 2006, 29, 776–1377. [Google Scholar] [CrossRef]
- Huang, G.H. A hybrid inexact-stochastic water management model. Eur. J. Oper. Res. 1998, 107, 137–158. [Google Scholar] [CrossRef]
- Fan, R.; Huang, G.H. A robust two-step method for solving interval linear programming problems within an environmental management context. J. Environ. Inform. 2012, 19, 1–12. [Google Scholar] [CrossRef]
- Xinjiang Uygur Autonomous Bureau of statistics. The statistical yearbook of Xinjiang Uygur Autonomous Region in Uygur Autonomous Region 2005–2011; Xinjiang Uygur Autonomous Bureau of statistics: Uruemqi, China, 2012; in Chinese.
- Huang, Y.; Li, Y.P.; Chen, X.; Bao, A.M.; Zhou, M. Simulation-based optimization method for water resource management in Tarim River Basin, China. Sci. Direct 2010, 2, 1451–1460. [Google Scholar]
- Abdelaziz, A.G.; Frank, A.W. Gains from expanded irrigation water trading in Egypt: An integrate basin approach. Ecol. Econ. 2010, 69, 2535–2548. [Google Scholar] [CrossRef]
- Richard, A.; Wildman, J.; Noelani, A.F. Management of water shortage in the colorado river basin: Evaluating current policy and the viability of interstate water trading. J. Am. Water Resourc. Assoc. 2012, 48, 411–422. [Google Scholar] [CrossRef]
- Luo, B.; Huang, G.H.; Zou, Y.; Yin, Y.Y. Toward quantifying the effectiveness of water trading under uncertainty. Environ. Manag. 2007, 83, 181–190. [Google Scholar] [CrossRef]
- Jiménez, M.; Arenas, M.; Bilbao, A. Linear programming with fuzzy parameters: An interactive method resolution. Eur. J. Oper. Res. 2007, 177, 1599–1609. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).