Self-Powered Desalination of Geothermal Saline Groundwater: Technical Feasibility
Abstract
:1. Introduction
2. Theory
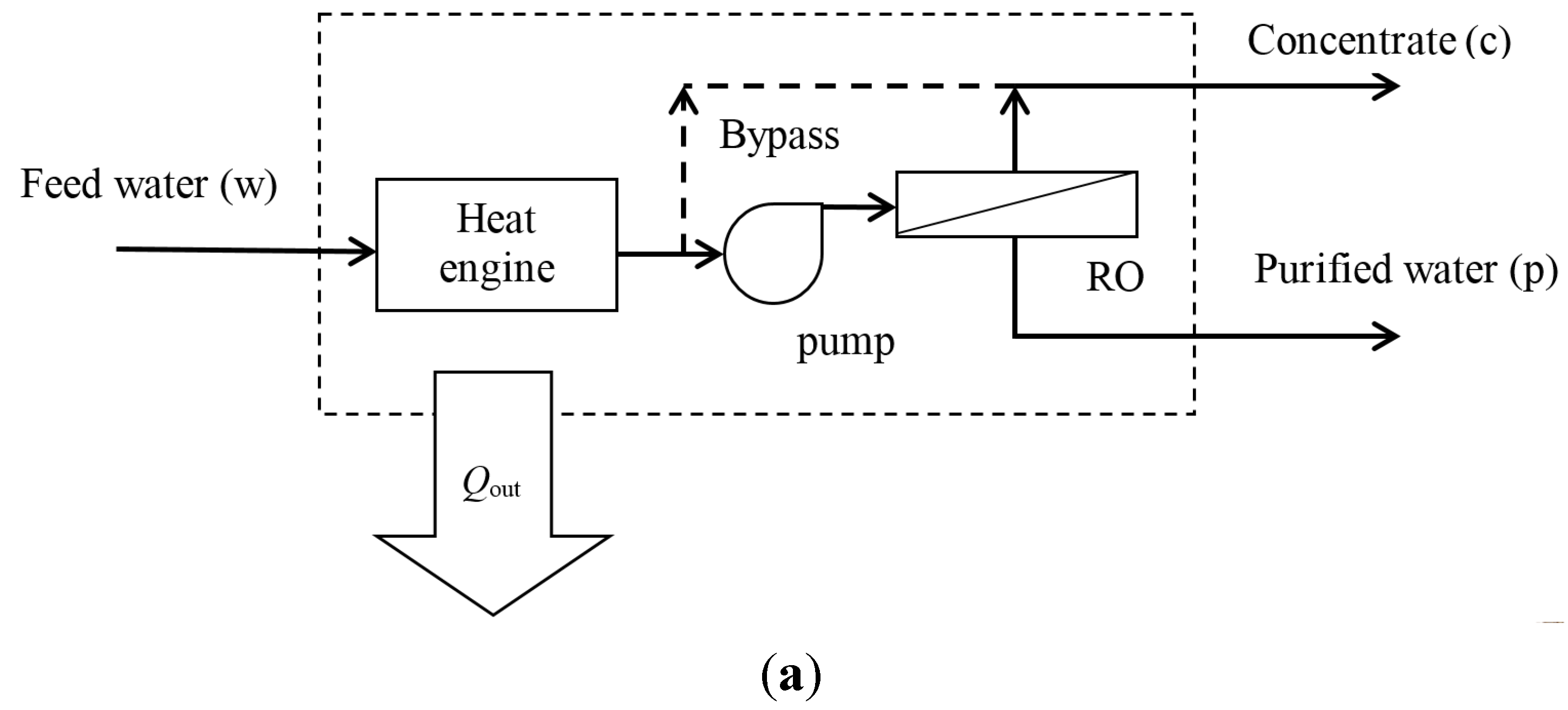
2.1. Exergy Analysis
- The purified water is free of salt i.e., the rejection fraction is 100%. Indeed, most modern desalination technologies typically achieve rejection fractions well above 95%. This assumption is conservative, in that lower rejection fractions will generally require less energy, so the separation will be accomplished more readily.
- The energy consumptions of auxiliary processes (e.g., pre-treatment and post-treatment) are not considered. Due to the varied nature of these processes, however, they are not amenable to a generalised thermodynamic analysis. (In practice, auxiliary processes are important and these will later be discussed in outline in relation to specific case studies).
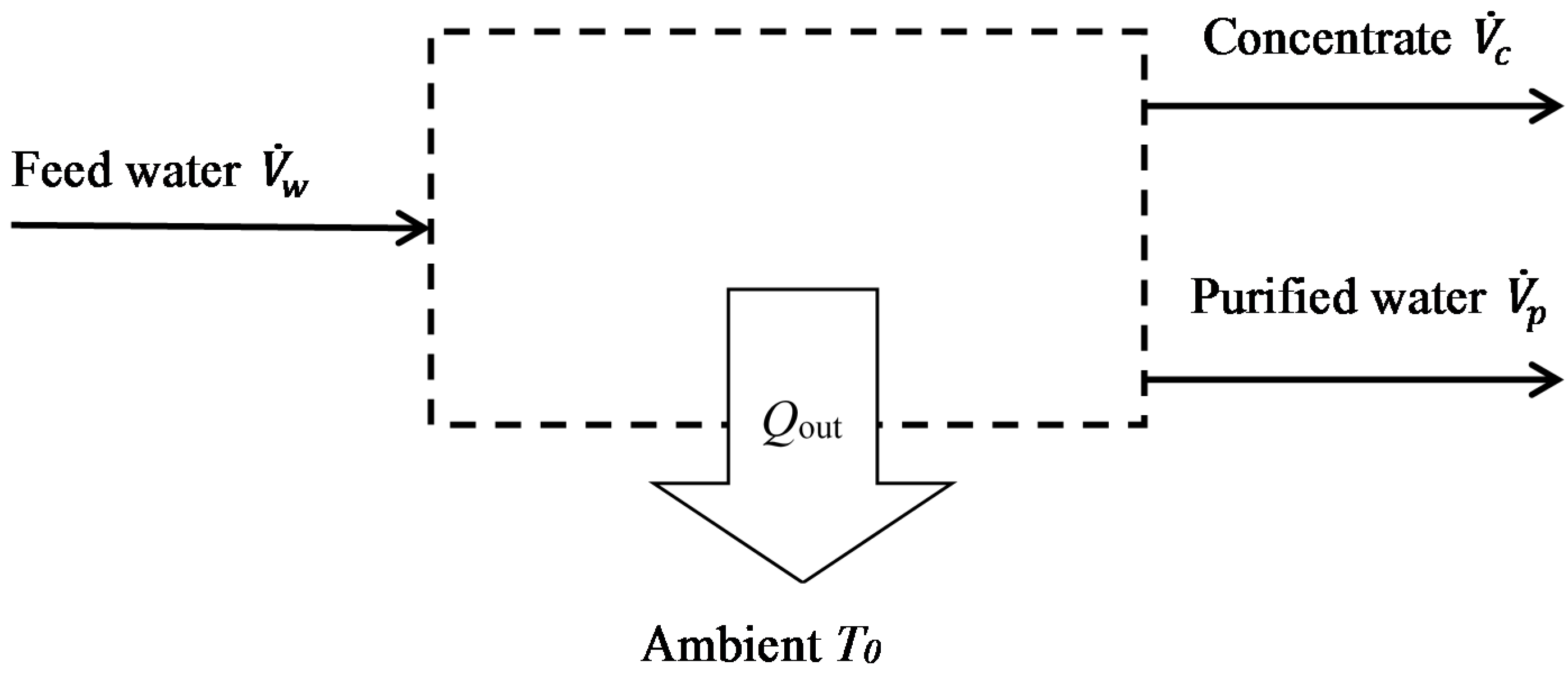
- Similarly, energy needed to lift the water from the source, and potential or kinetic energy associated with the pressure of the source water, are neglected.
- Assumptions valid for dilute solutions are used: the density and specific heat capacity are considered independent of concentration, and osmotic pressure is considered proportional to the molar concentration of salt. This is justified by the fact that groundwater sources studied here have salt concentrations <10,000 mg/kg.
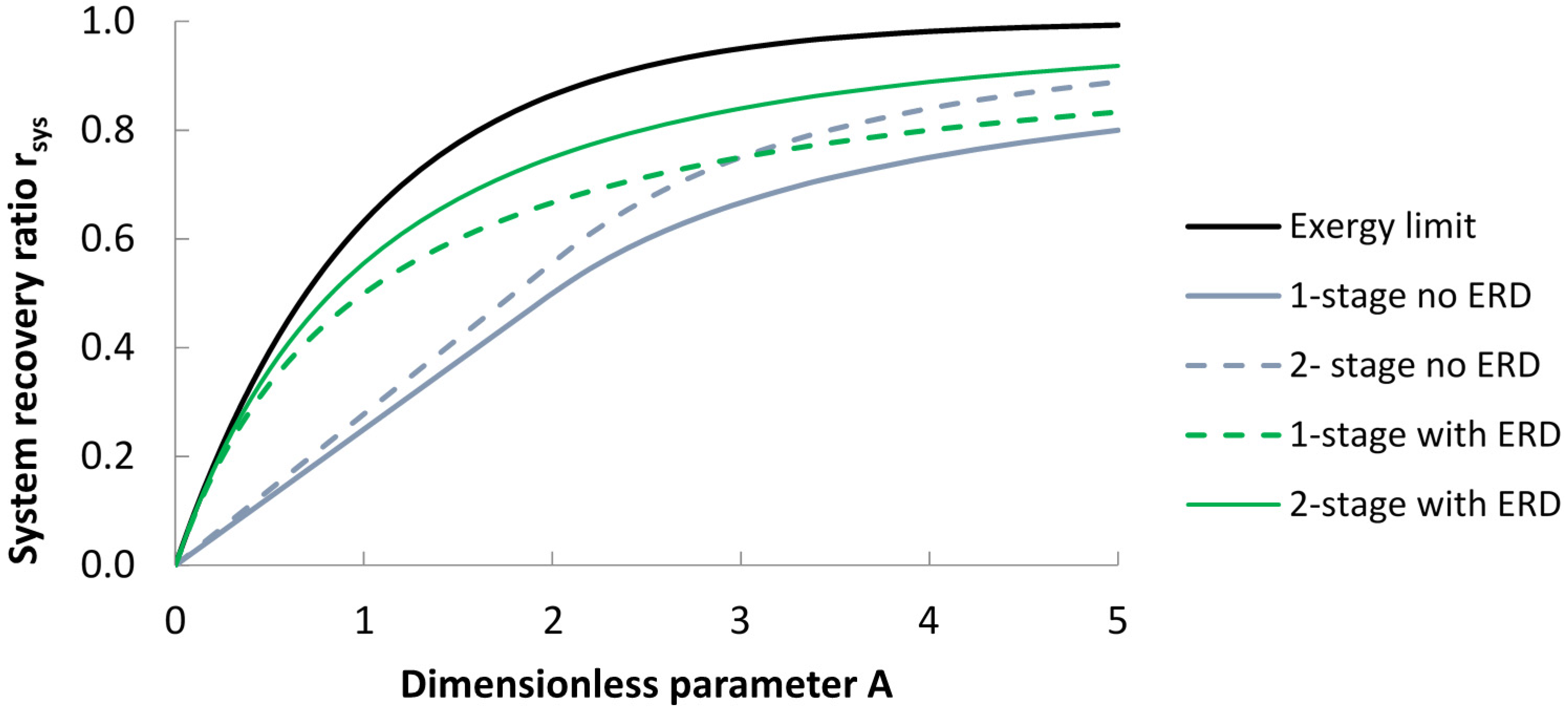
2.2. Reverse Osmosis System
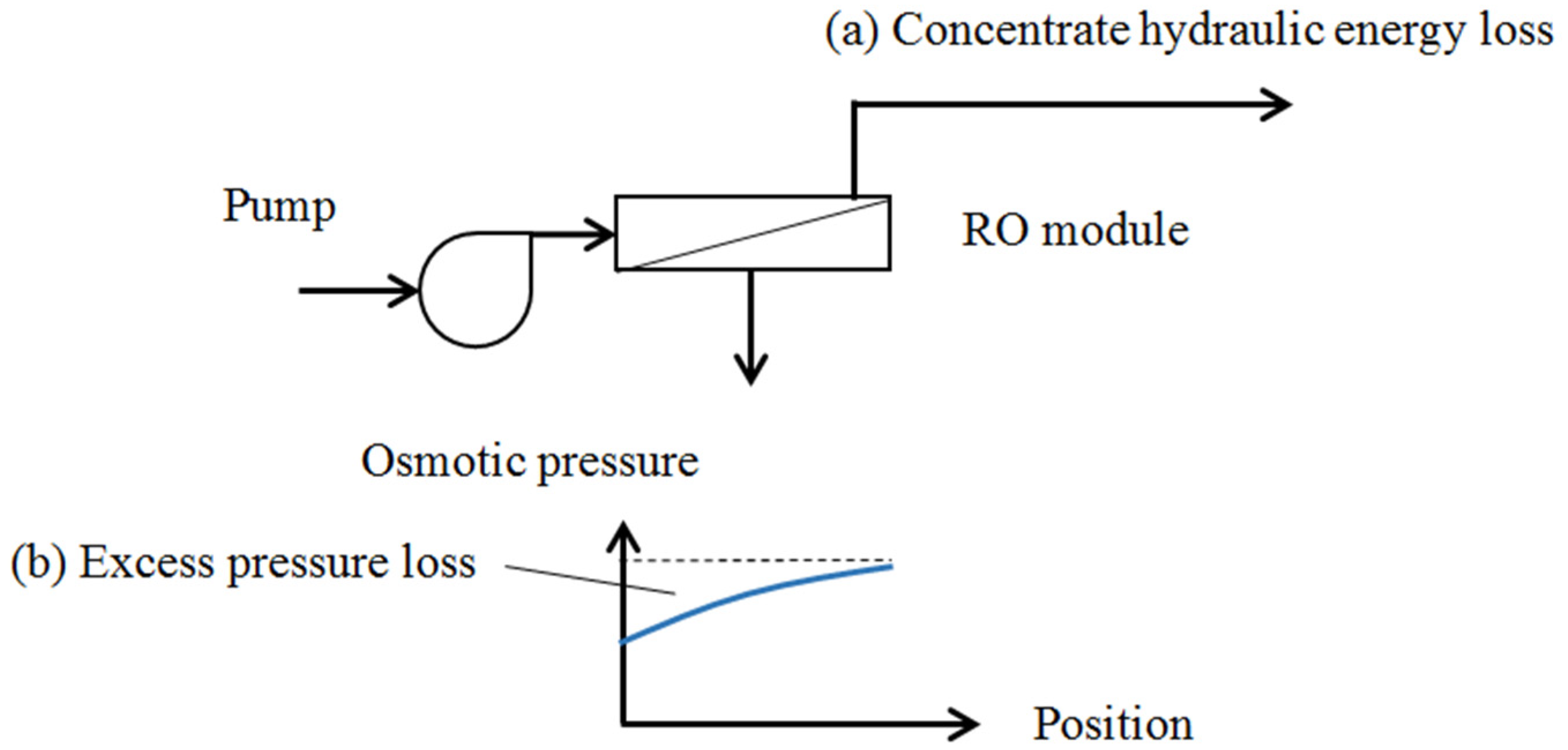
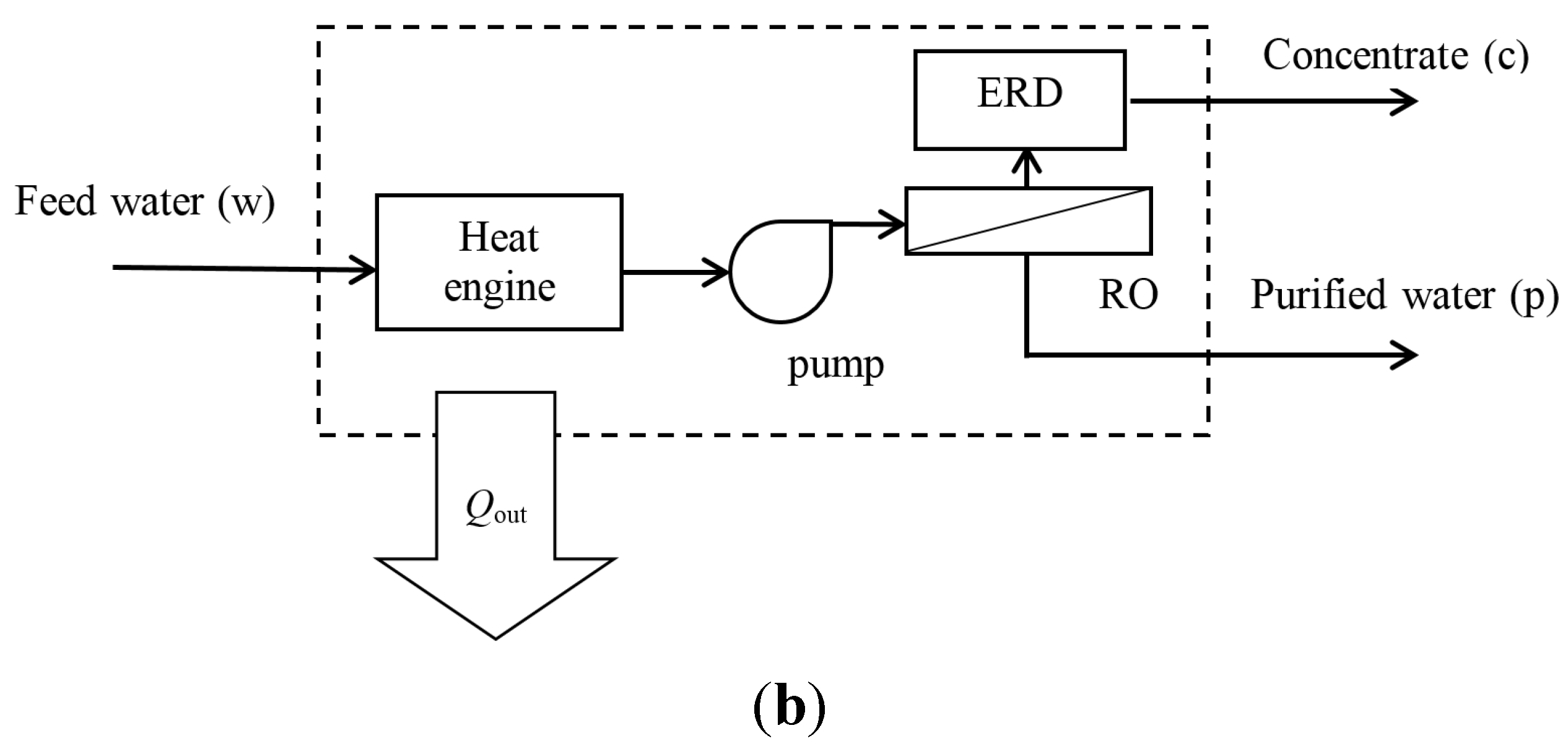
| Configuration | Without Energy Recovery Device | With Energy Recovery Device |
|---|---|---|
| 1-stage | When A < 2 (bypass): | |
| When A ≥ 2 (no bypass): | ||
| 2-stage | When A < 2 (bypass): | |
| rsys = 0.278 A | ||
| When A ≥ 2 (no bypass): | ||
| Ideal (batch system, or infinite number of stages with ERD). | rsys = 1 − e−A | |
| Location | Configuration * | Feedwater Concentration | Osmotic Pressure Posm | Recovery r | Reported SECreal | Semi-Ideal SECsideal | Loss Ratio εRO | Capacity | Year Reported | Reference |
|---|---|---|---|---|---|---|---|---|---|---|
| mg kg−1 | kPa | kWh m−3 | kWh m−3 | m3/day | ||||||
| Kerkennah, Tunisia | 1-stage no ERD | 3,700 | 293 ** | 0.75 | 1.1 | 0.150 | 0.14 | 4,700 | 2003 | [28] |
| Chino, California (train A) | 1-stage no ERD | 950 | 62 | 0.809 | 0.490 | 0.0353 | 0.07 | 8,300 | 2011 | [29] |
| Chino, California (train A—optimised) | 1-stage no ERD | 950 | 62 | 0.9 | 0.441 | 0.044 | 0.10 | 8,300 | 2012 | [25] |
| Large Element Study § | 1-stage no ERD | 2,200 | 175 | 0.75 | 0.88 | 0.090 | 0.10 | 189,000 | 2004 | [26,30] |
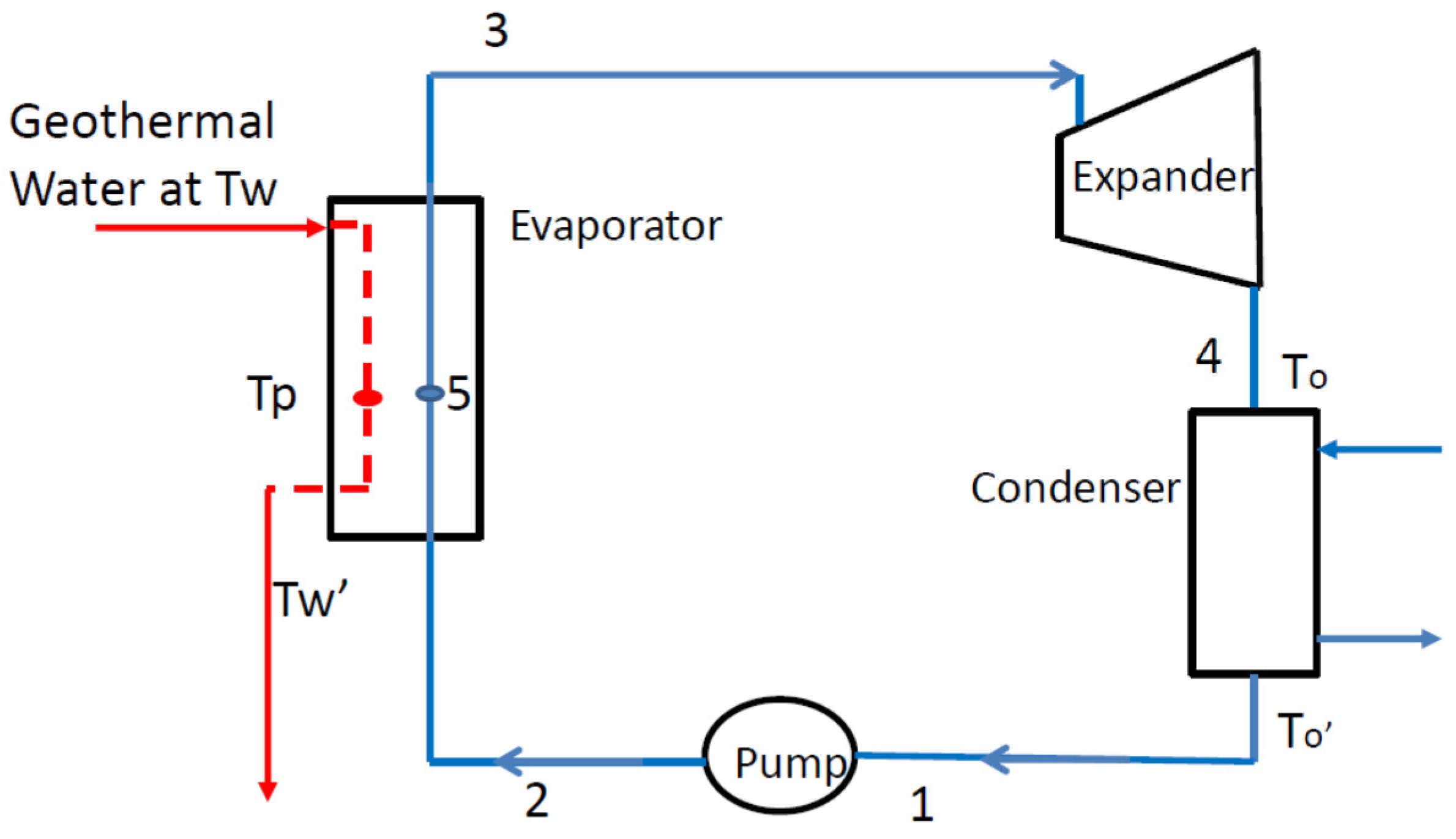
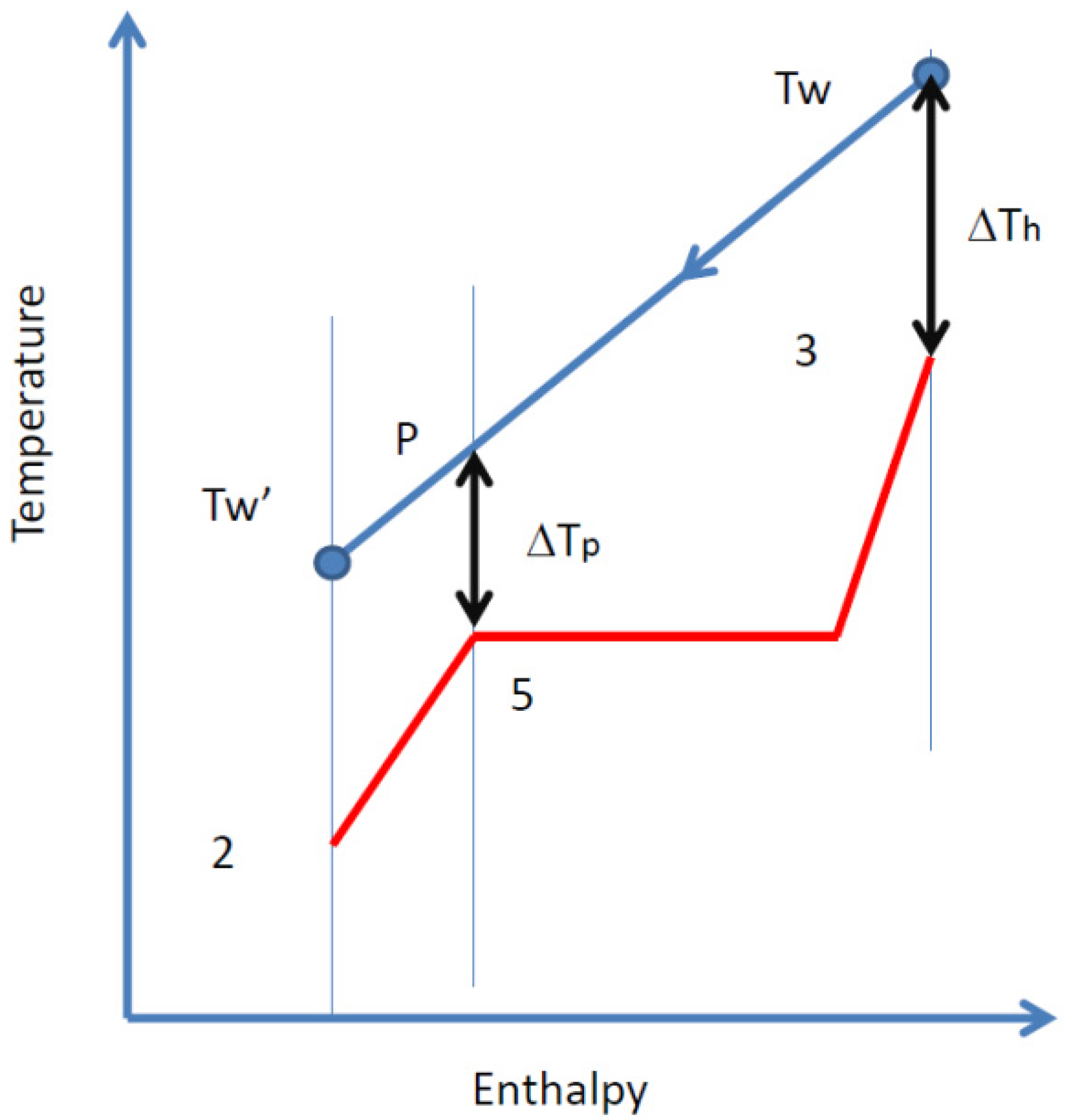
2.3. Organic Rankine Cycle
- -
- Dry expansion to avoid wet vapour and erosion in the turbine;
- -
- Non-corrosive, non-flammable and non-toxic fluid;
- -
- High molecular weight to reduce the turbine nozzle velocity;
- -
- Low ozone depletion potential (ODP) and global warming potential (GWP).
| Fluid | ASHRAE Designation | Mol. Weight (kg/kmol) | Critical Temperature Tc (°C) | Critical Pressure Pc (MPa) | Latent Heat (at 25 °C) (kJ/kg) | ODP | GWP |
|---|---|---|---|---|---|---|---|
| [33] | [34] | [34] | [34] | [34] | [35] | [35] | |
| 1,1,1-trifluoroethane | R143a | 84.04 | 72.7 | 3.76 | 159.3 | 0 | 4470 |
| difluoromethane | R32 | 52.02 | 78.1 | 5.78 | 270.9 | 0 | 500 |
| propane | R290 | 44.10 | 96.7 | 4.25 | 335.3 | 0 | 3.3 |
| 1,1,1,2-tetrafluoroethane | R134a | 102.03 | 101.0 | 4.06 | 177.8 | 0 | 1430 |
| Ammonia | R717 | 17.03 | 132.3 | 11.33 | 1166 | 0 | 0 |
3. Case Studies
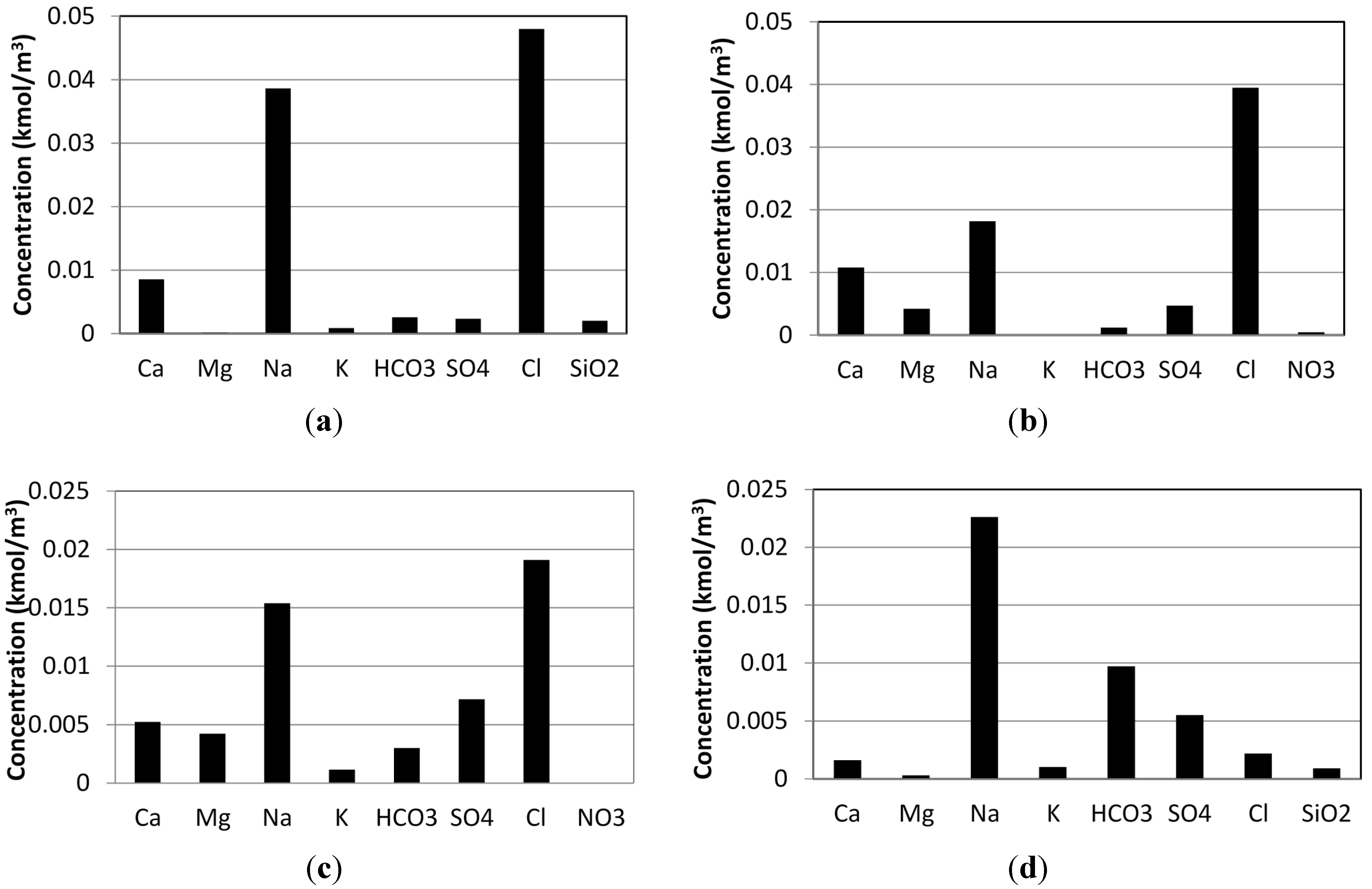
3.1. Case Study 1: Tuwa, Gujarat
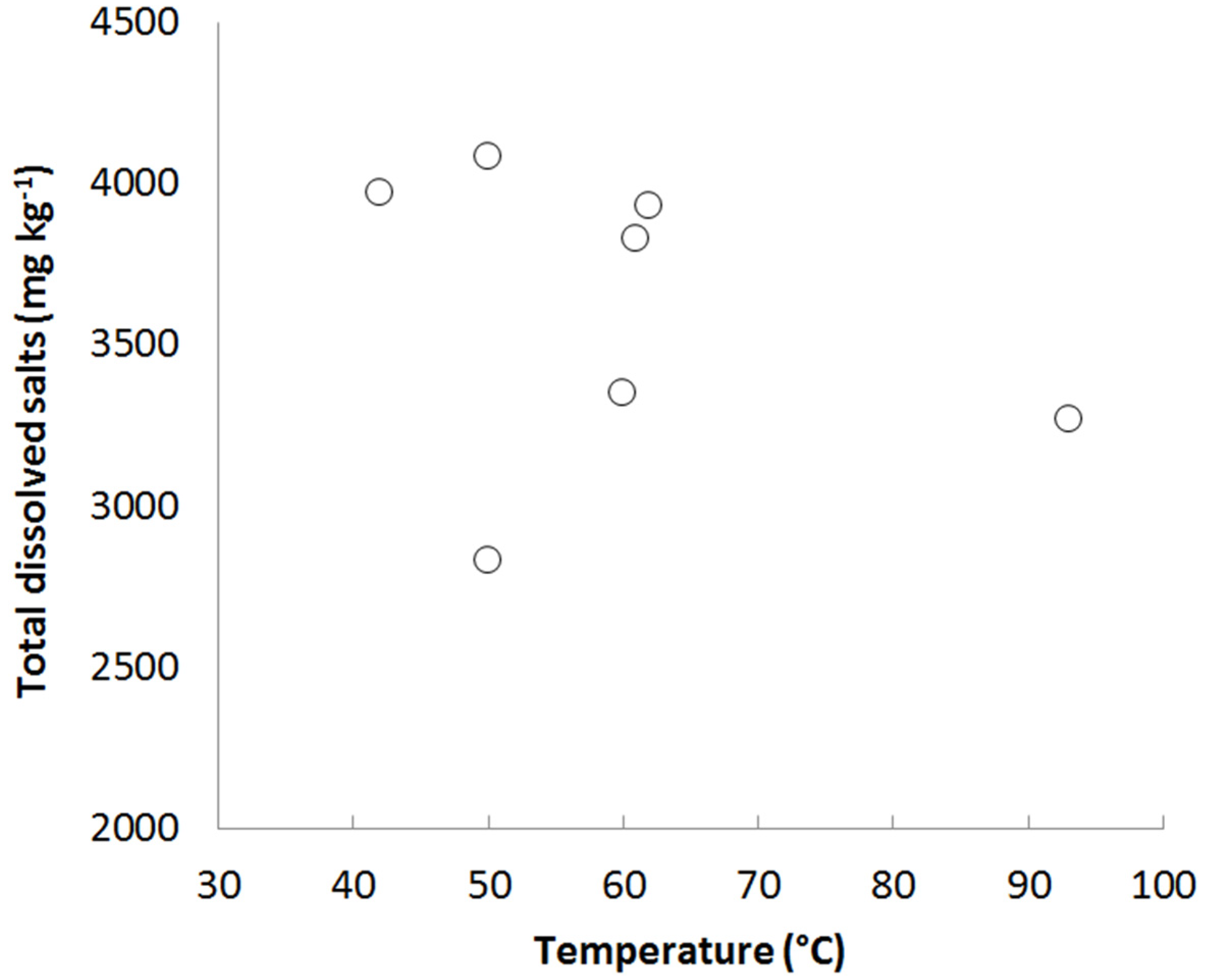
3.2. Case Study 2: Salbukh, Najd Plateau, Saudi Arabia
3.3. Case Study 3: Kebili Geothermal Field, Tunisia
3.4. Case Study 4: Eynal Spring, Simav Geothermal Field, Turkey
4. Results
| Case Study | ||||
|---|---|---|---|---|
| 1. Tuwa—Gujarat (India) | 2. Salbukh—(Saudi Arabia) | 3. Kebili—(Tunisia) | 4. Eynal—(Turkey) | |
| Total salt concentration (mg/kg) | 3350 | 1800 | 2440 | 1830 |
| Osmotic Pressure (kPa) | 245 | 117 | 119 | 97.5 |
| Source temperature T1 | 60 | 70 | 70 | 96 |
| Ambient temperature T0 | 41 | 44 | 38 | 31 |
| Parameter A | 9.4 | 36.1 | 54.1 | 261.2 |
| ψORC (R290) | 0.3085 | 0.3271 | 0.373 | 0.4503 |
| εRO | 0.10 | 0.10 | 0.10 | 0.10 |
| Areal | 0.29 | 1.18 | 2.02 | 11.76 |
| Maximum rsys | ||||
| Ideal exergetic limit * | >0.99 | >0.99 | >0.99 | >0.99 |
| Semi-ideal **: | ||||
| 1-stage RO (no ERD) | 0.894 | 0.972 | 0.982 | >0.99 |
| 2-stage RO (no ERD) | 0.963 | >0.99 | >0.99 | >0.99 |
| 1-stage RO (with ERD) | 0.904 | 0.973 | 0.982 | >0.99 |
| 2-stage RO (with ERD) | 0.969 | >0.99 | >0.99 | >0.99 |
| Real §: | ||||
| 1-stage RO (no ERD) | 0.073 | 0.295 | 0.505 | 0.915 |
| 2-stage RO (no ERD) | 0.081 | 0.328 | 0.561 | 0.975 |
| 1-stage RO (with ERD) | 0.225 | 0.542 | 0.669 | 0.922 |
| 2-stage RO (with ERD) | 0.238 | 0.605 | 0.752 | 0.979 |
| Case Study | |||||
|---|---|---|---|---|---|
| 1. Tuwa—Gujarat (India) | 2. Salbukh—(Saudi Arabia) | 3. Kebili—(Tunisia) | 4. Eynal—(Turkey) | ||
| Source temperature Tw | 60 | 70 | 70 | 96 | |
| Ambient temperature T0 | 41 | 44 | 38 | 31 | |
| R143a | ψORC | 0.286 | 0.359 | 0.366 | 0.563 |
| (Pevap, Pcond) | (2390,2000) | (2756,2115) | (2756,1850) | (3700,1550) | |
| R290 (propane) | ψORC | 0.3085 | 0.3271 | 0.373 | 0.4503 |
| (Pevap, Pcond) | (1754,1468) | (1899,1570) | (1899,1370) | (2408,1165) | |
5. Discussion
5.1. Pre- and Post-Treatment
| Case Study | Scaling Issue | Pre-Treatment |
|---|---|---|
| 1: Tuwa, Gujarat | Calcium sulphate precipitation would limit recovery to about 0.3High silica level | Use anti-scalants e.g., phosphonates (or work at lower recovery) |
| 2: Salbukh, Saudi Arabia | Calcium sulphate already near saturation | Anti-scalant or water softening by cation-exchange resin |
| 3: Kebili, Tunisia | ||
| 4: Eynal Spring, Turkey | Calcium sulphate precipitation would limit recovery to about 0.5Significant silica level | Use anti-scalants e.g., phosphonates (or work at lower recovery) |
5.2. Equipment Design for Performance and Low Cost
6. Conclusions
Nomenclature
| A | dimensionless parameter defined by Equation (9) |
| ṁ | mass flow (kg s−1) |
| n | moles of solute (kmol) |
| P | pressure (kPa) |
| r | recovery ratio |
| R | gas constant ( = 8.314 kJ·kmol−1·K−1) |
| T | temperature (K or °C) |
| V | volume (m3) |
volumetric flow (m3·s−1) | |
| W | mechanical work (kJ) |
| Ẇ | rate of mechanical work (kW) |
| SEC | specific energy consumption (kJ m−3 or kWh m−3) |
Greek letters
| ε | loss ratio |
| η | energy efficiency |
| ψ | exergy efficiency |
Subscripts
| c | concentrate |
| cond | condenser |
| evap | evaporator |
| ideal | ideal |
| p | purified water (permeate), or pinch point |
| ORC | organic Rankine cycle |
| osm | osmotic |
| real | real |
| RO | reverse osmosis |
| s | relating to work of desalination |
| sideal | semi-ideal |
| sys | system |
| t | relating to conversion of thermal energy to work |
| w | feedwater at system inlet |
| w’ | feedwater at outlet to heat exchanger |
| 0 | ambient |
| 0’ | at condenser outlet |
| 1 | at pump inlet |
| 2 | at pump outlet |
| 3 | at evaporator outlet |
| 4 | at expander outlet |
| 5 | pinch point |
Abbreviations
| ERD | Energy Recovery Device |
| GWP | Global Warming Potential |
| MSF | Multi-stage Flash Unit |
| ODP | Ozone Depleting Potential |
| ORC | Organic Rankine Cycle |
| RO | Reverse Osmosis |
Acknowledgments
Author Contributions
Appendix: Calculation of Osmotic Pressures
Conflicts of Interest
References
- Lund, J.W.; Freeston, D.H.; Boyd, T.L. Direct utilization of geothermal energy in 2010 worldwide. Geothermics 2011, 40, 159–180. [Google Scholar] [CrossRef]
- Dincer, I.; Hepbasli, A.; Ozgener, L. Geothermal energy resources. In Encyclopedia of Energy Engineering and Technology; CRC Press (Taylor and Francis Group): Boca Raton, FL, USA, 2007; pp. 744–752. [Google Scholar]
- Awerbuch, L.; Lindemuth, T.E.; May, S.C.; Rogers, A.N. Geothermal energy recovery process. Desalination 1976, 9, 325–336. [Google Scholar] [CrossRef]
- Bourouni, K.; Chaibi, M.; Martin, R.; Tadrist, L. Heat Transfer and evaporation in geothermal desalination units. Appl. Energy 1999, 64, 129–147. [Google Scholar] [CrossRef]
- Mohamed, A.M.I.; El Minshawy, N.A.S. Humidification-dehumidification desalination system driven by geothermal energy. Desalination 2009, 249, 602–608. [Google Scholar] [CrossRef]
- Mahmoudi, H.; Spahis, N.; Goosen, M.F.; Ghaffour, N.; Drouiche, N.; Ouagued, A. Application of geothermal energy for heating and fresh water production in a brackish water greenhouse desalination unit: A case study from Algeria. Renew. Sust. Energy Rev. 2010, 14, 512–517. [Google Scholar] [CrossRef]
- Bouguecha, S.; Dhahb, M. Fluidised bed crystalliser and air gap membrane distillation as a solution to geothermal water desalination. Desalination 2003, 152, 237–244. [Google Scholar] [CrossRef]
- Mathioulakis, E.; Belessiotis, V.; Delyannis, E. Desalination by using alternative energy: Review and state-of-the-art. Desalination 2007, 152, 346–365. [Google Scholar] [CrossRef]
- Koroneos, C.; Roumbas, G. Geothermal waters heat integration for the desalination of sea water. Desalin. Water Treat. 2012, 37, 69–76. [Google Scholar] [CrossRef]
- Li, C.; Besarati, S.; Goswami, Y.; Stefanokos, E.; Chen, H. Reverse osmosis desalination driven by low temperature supercritical organic Rankine cycle. Appl. Energy 2013, 102, 1071–1080. [Google Scholar] [CrossRef]
- Manolakos, D.; Papadakis, G.; Kyritsis, S.; Bouzianas, K. Experimental evaluation of an autonomous low-temperature solar Rankine cycle system for reverse osmosis desalination. Desalination 2007, 203, 366–374. [Google Scholar] [CrossRef]
- Igobo, O.N.; Davies, P.A. Low-temperature organic Rankine cycle engine with isothermal expansion for use in desalination. Desalin. Water Treat. 2014. [Google Scholar] [CrossRef]
- El-Emam, R.S.; Dincer, I. Exergy and exergoecomomic analyses and optimization of geothermal Rankine cycle. Appl. Therm. Eng. 2013, 59, 435–444. [Google Scholar] [CrossRef]
- Madhawa Hettiarachchi, H.D.; Golubovic, M.; Worek, W.M.; Ikegami, Y. Optimum design criteria for an Organic Rankine cycle using low-temperature geothermal heat sources. Energy 2007, 32, 1698–1706. [Google Scholar] [CrossRef]
- Cerci, Y. Exergy analysis of a reverse osmosis desalination plant in California. Desalination 2002, 142, 257–266. [Google Scholar] [CrossRef]
- El-Emam, R.S.; Dincer, I. Thermodynamic and thermoeconomic analyses of seawater reverse osmosis desalination plant with energy recovery. Energy 2014, 64, 154–163. [Google Scholar] [CrossRef]
- Nafey, A.S.; Sharaf, M.A. Combined solar organic Rankine cycle with reverse osmosis desalination process: Energy, exergy and cost evaluations. Renew. Energy 2010, 35, 2571–2580. [Google Scholar] [CrossRef]
- Tchanche, B.F.; Lambrinos, G.; Frangoudakis, A.; Papadakis, G. Exergy analysis of micro-organic Rankine power cycles for a small scale solar driven reverse osmosis desalination system. Appl. Energy 2010, 87, 1295–1306. [Google Scholar] [CrossRef]
- Bejan, A. Advanced Engineering Thermodynamics; Wiley: New York, NY, USA, 1988. [Google Scholar]
- Feistel, R. A Gibbs function for seawater thermodynamics for −6 to 80 °C and salinity up to 120 g kg−1. Deep Sea Res. I 2008, 55, 1639–1671. [Google Scholar]
- Mistry, K.H.; Hunter, H.A.; Lienhard, J.H. Effect of composition and nonideal solution behavior on desalination calculations for mixed electrolyte solutions with comparison to seawater. Desalination 2013, 318, 34–47. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Lienhard, J.H.; Zubair, S.M. Thermophysical properties of seawater: A review of existing correlations and data. Desalin. Water Treat. 2010, 16, 354–380. [Google Scholar] [CrossRef]
- Qiu, T.; Davies, P.A. Comparison of configurations for high-recovery inland desalination systems. Water 2012, 4, 690–706. [Google Scholar] [CrossRef]
- Elimelech, M.; Phillip, W.A. The future of seawater desalination: Energy, technology and the environment. Science 2011, 333, 712–717. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Noh, B. Validation of model-based validation of brackish water reverse osmosis (BWRO) desalination. Desalination 2012, 304, 20–24. [Google Scholar] [CrossRef]
- Bartels, C.; Bergman, R.; Hallan, M.; Henthorne, L.; Knappe, P.; Lozier, J.; Metcalfe, P.; Peery, M.; Shelby, I. Industry Consortium Analysis of Large Reverse Osmosis and Nanofiltration Element Diameters; Desalination and Water Purification Research and Development Report No. 114; US Bureau of Reclamation: Denver, CO, USA, 2004. [Google Scholar]
- He, C.; Liu, C.; Gao, H.; Li, Y.; Wu, S.; Xu, J. The optimal evaporation temperature and working fluids for subcritical organic Rankine cycle. Energy 2012, 38, 136–143. [Google Scholar] [CrossRef]
- Fethi, K. Optimization of energy consumption in the 3300 m3/d RO Kerkennah plant. Desalination 2003, 157, 145–149. [Google Scholar] [CrossRef]
- Li, M. Optimal plant operation of brackish water reverse osmosis (BWRO) desalination. Desalination 2012, 239, 61–68. [Google Scholar] [CrossRef]
- Pearce, G.K. UF/MF pre-treatment to RO in seawater and wastewater reuse applications: A comparison of energy costs. Desalination 2008, 222, 66–73. [Google Scholar] [CrossRef]
- Chen, H.; Goswami, D.Y.; Stefanokos, E.K. A review of thermoadynamic cycles and working fluids for the conversion of low grade heat. Renew. Sust. Energy Rev. 2010, 14, 3059–3067. [Google Scholar] [CrossRef]
- Nguyen, T.Q.; Slawnwhite, J.D.; Goni Boulama, K. Power generation from residual industrial heat. Energy Conv. Manag. 2010, 51, 2220–2229. [Google Scholar] [CrossRef]
- Doerr, R.G. Refrigerants; ASHRAE Handbook: Atlanta, GA, USA, 2001; Chapter 19. [Google Scholar]
- Klein, S.A. Engineering Equation Solver (EES); F-Chart Software: Madison, WI, USA, 2013. [Google Scholar]
- Environment Canada, Govt. of Canada. Available online: http://www.ec.gc.ca/Air/ (accessed on 15 October 2014).
- Khennich, M.; Galanis, N. Thermodynamic analysis and optimization of power cycles sing a finite low temperature heat source. Int. J. Energy Res. 2012, 36, 871–885. [Google Scholar] [CrossRef]
- World Meteorological Organisation (WMO). Available online: http://www.wmo.int (accessed on 16 Janurary 2014).
- Singh, G. Salinity-related desertification and management strategies: Indian experience. Land Degrad. Dev. 2009, 20, 367–385. [Google Scholar] [CrossRef]
- Minissale, A.; Chandrasekharam, D.; Vaselli, O.; Magro, G.; Tassi, F.; Pansini, G.L.; Bhramhabut, A. Geochemistry, geothermics and relationship to active tectonics of Gujarat and Rajasthan thermal discharges, India. J. Volcanol. Geotherm. Res. 2003, 127, 19–32. [Google Scholar] [CrossRef]
- Electricity and Cogeneration Regulatory Authority (ECRA). Annual Statistical Booklet and Seawater Desalination Industries; ECRA: Riyadh, Saudi Arabia, 2012. [Google Scholar]
- Sobhani, R.; Abahusayn, M.; Gabelich, C.J.; Rosso, D. Energy footprint analysis of brackish groundwater desalination with zero liquid discharge in inland areas of the Arabian Peninsula. Desalination 2012, 291, 106–116. [Google Scholar] [CrossRef]
- Agoun, A. Exploitation of the Continental Intercalaire Aquifer at the Kebili Geothermal Field, Tunisia; Report No 2; UN University Geothermal Training Programme: Reykjavík, Iceland, 2000. [Google Scholar]
- Bourouni, K.; Chaibi, M.T. Application of geothermal energy for brackish water desalination in South of Tunisia. In Proceedings of World Geothermal Congress, Antalya, Turkey, 24–29 April 2005.
- Bourouni, K.; Chaibi, M.T. Geothermal water cooling systems in Tunisia—Design and practice. In Proceedings of World Geothermal Congress, Antalya, Turkey, 24–29 April 2005.
- Bayram, A.F.; Simsek, S. Hydrogeochemical isotopic survey of Kütahya-Simav geothermal field. In Proceedings of World Geothermal Congress, Antalya, Turkey, 24–29 April 2005.
- Fritzmann, C.; Löwenberg, J.; Wintgens, T.; Melin, T. State-of-the-art reverse osmosis desalination. Desalination 2007, 216, 1–76. [Google Scholar] [CrossRef]
- Schäfer, A.; Broeckmann, A.; Richards, B.S. Renewable energy powered membrane technology: 1. Development and characterization of a photovoltaic hybrid membrane system. Environ. Sci. Technol. 2007, 41, 998–1003. [Google Scholar] [CrossRef] [PubMed]
- Qiu, T.Y.; Igobo, O.N.; Davies, P.A. DesaLink: Solar-powered desalination of brackish groundwater giving high output and high recovery. Desalin. Water Treat. 2013, 51, 1279–1289. [Google Scholar] [CrossRef]
- Robinson, R.A.; Stokes, R.H. Electrolyte Solutions; Butterworths: London, UK, 1959. [Google Scholar]
- Robinson, R.A. The vapour pressure and osmotic equivalence of sea water. J. Mar. Biol. Assoc. UK 1954, 33, 449–455. [Google Scholar] [CrossRef]
- Sarbar, M.; Convington, A.K.; Nuttall, R.L.; Goldberg, R.N. The activity and osmotic coefficients of aqueous sodium bicarbonate solutions. J. Chem. Thermodyn. 1982, 14, 967–976. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Davies, P.A.; Orfi, J. Self-Powered Desalination of Geothermal Saline Groundwater: Technical Feasibility. Water 2014, 6, 3409-3432. https://doi.org/10.3390/w6113409
Davies PA, Orfi J. Self-Powered Desalination of Geothermal Saline Groundwater: Technical Feasibility. Water. 2014; 6(11):3409-3432. https://doi.org/10.3390/w6113409
Chicago/Turabian StyleDavies, Philip A., and Jamel Orfi. 2014. "Self-Powered Desalination of Geothermal Saline Groundwater: Technical Feasibility" Water 6, no. 11: 3409-3432. https://doi.org/10.3390/w6113409
APA StyleDavies, P. A., & Orfi, J. (2014). Self-Powered Desalination of Geothermal Saline Groundwater: Technical Feasibility. Water, 6(11), 3409-3432. https://doi.org/10.3390/w6113409