An Approach Using a 1D Hydraulic Model, Landsat Imaging and Generalized Likelihood Uncertainty Estimation for an Approximation of Flood Discharge
Abstract
:1. Introduction
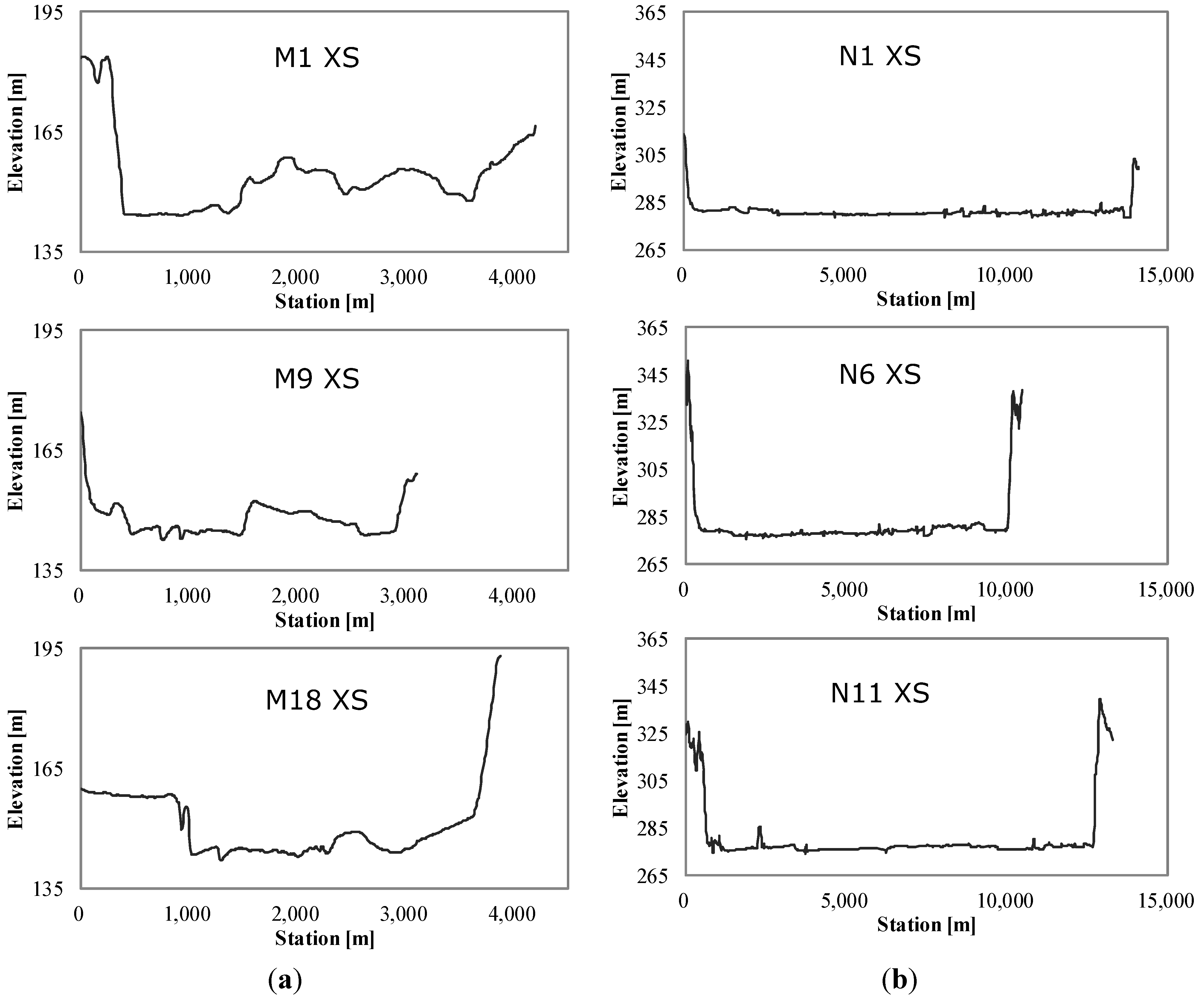
2. Study Area and Data Set
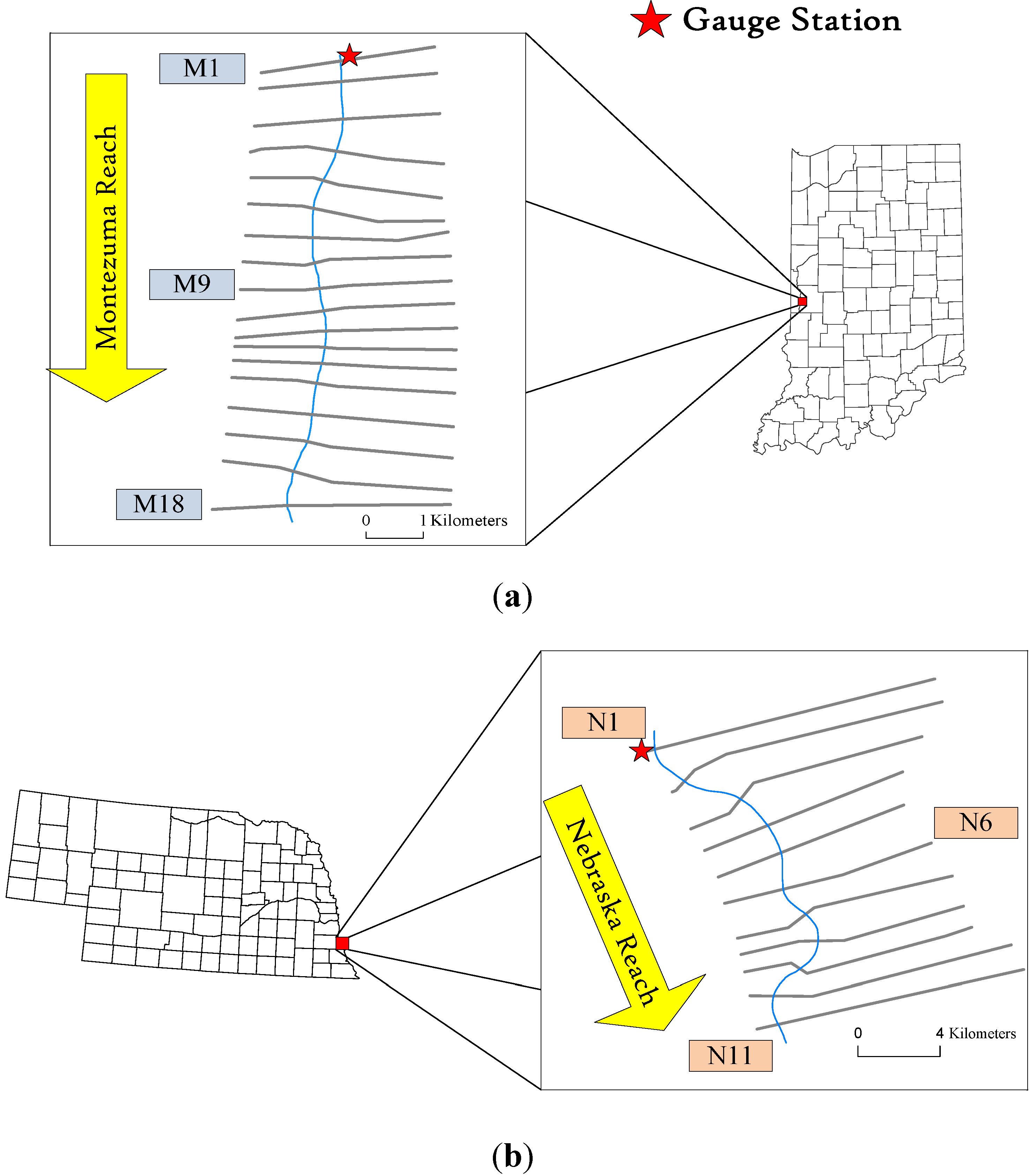
| Study Reach | River length (km) | Mean bed slope (m/km) | Number of cross-section | Mean width of cross-section (km) | Mean spacing cross-section (km) |
|---|---|---|---|---|---|
| Montezuma | 9 | 0.25 | 18 | 3.61 | 0.53 |
| Nebraska | 19 | 0.21 | 11 | 12.84 | 1.90 |
| 2001 NLCD Classification | Manning’s n | Source | ||
|---|---|---|---|---|
| Minimum | Normal | Maximum | ||
| Open Water | 0.025 | 0.030 | 0.033 | [35] |
| Developed, Open Space | 0.010 | 0.013 | 0.160 | [36] |
| Developed, Low Intensity | 0.038 | 0.050 | 0.063 | [36] |
| Developed, Medium Intensity | 0.056 | 0.075 | 0.094 | [36] |
| Developed, High Intensity | 0.075 | 0.100 | 0.125 | [36] |
| Barren Land | 0.025 | 0.030 | 0.035 | [35] |
| Deciduous Forest | 0.100 | 0.120 | 0.160 | [35] |
| Evergreen Forest | 0.100 | 0.120 | 0.160 | [35] |
| Mixed Forest | 0.100 | 0.120 | 0.160 | [35] |
| Scrub/Shrub | 0.035 | 0.050 | 0.070 | [35] |
| Grassland/Herbaceous | 0.025 | 0.030 | 0.035 | [35] |
| Pasture/Hay | 0.030 | 0.040 | 0.050 | [35] |
| Cultivated Crops | 0.025 | 0.035 | 0.045 | [35] |
| Woody Wetlands | 0.080 | 0.100 | 0.120 | [35] |
| Emergent Herbaceous Wetland | 0.075 | 0.100 | 0.150 | [35] |
| Study Reach | USGS gauge station | For flood discharge on Landsat imagery | For a peak flow of the flood event | ||
|---|---|---|---|---|---|
| Date of Landsat image | Discharge at gauge station (m3/s) | Date of peak flow | Discharge at gauge station (m3/s) | ||
| Montezuma | 03340500 | 11 June 2008 | 1450 | 8 June 2008 | 2197 |
| Nebraska | 06807000 | 9 July 2011 | 6031 | 7 July 2011 | 6258 |
3. Methodology
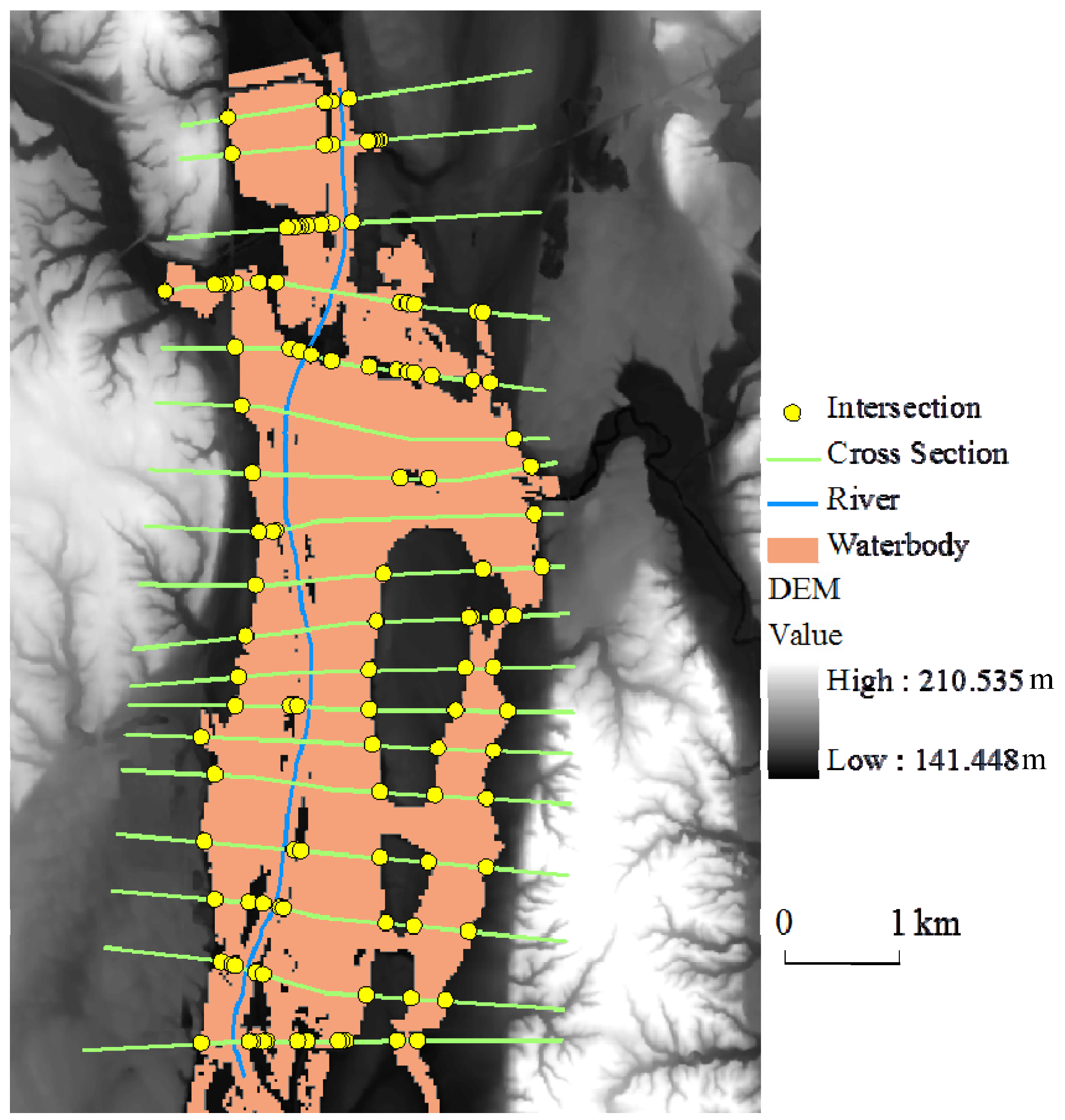
3.1. Extraction of the Observed Data from Landsat 5 TM Satellite Imagery
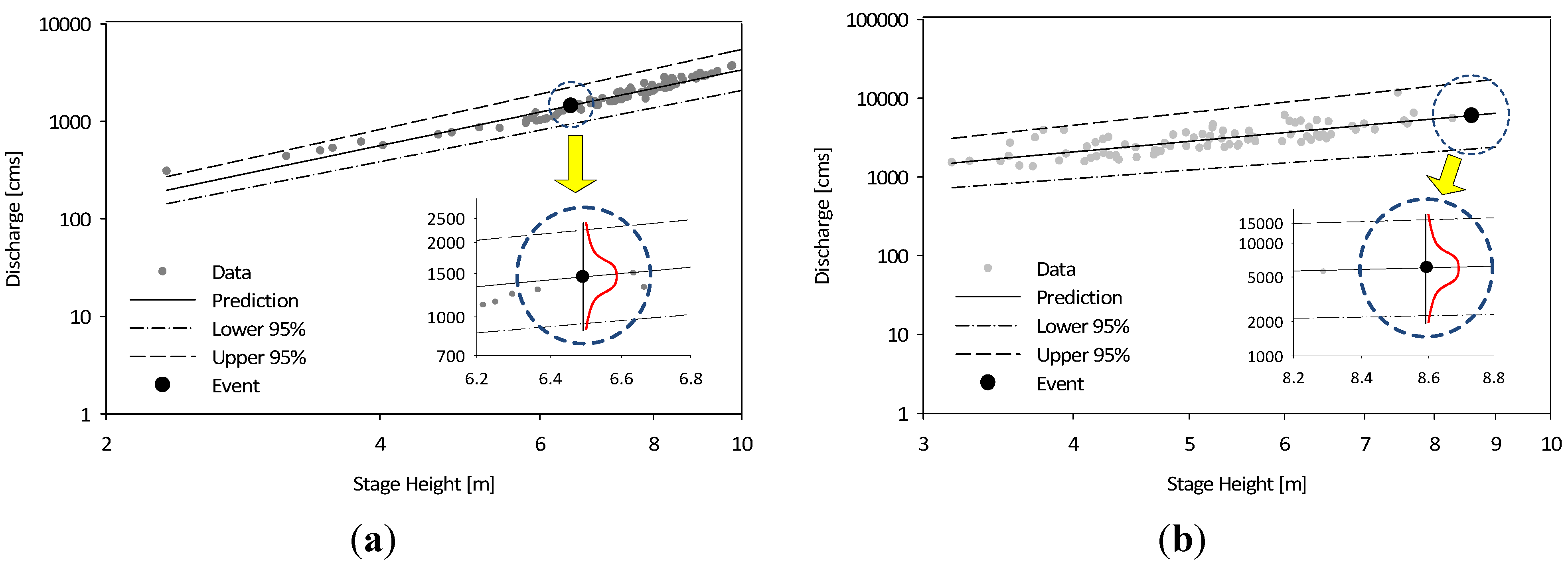
3.2. Approximation of Flood Discharge Using HEC-RAS and the GLUE Methodology
3.2.1. Monte Carlo Simulation Using HEC-RAS

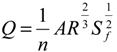
3.2.2. Approximation of Flood Discharge Using the GLUE Methodology

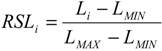
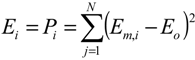
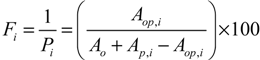

4. Results and Discussion
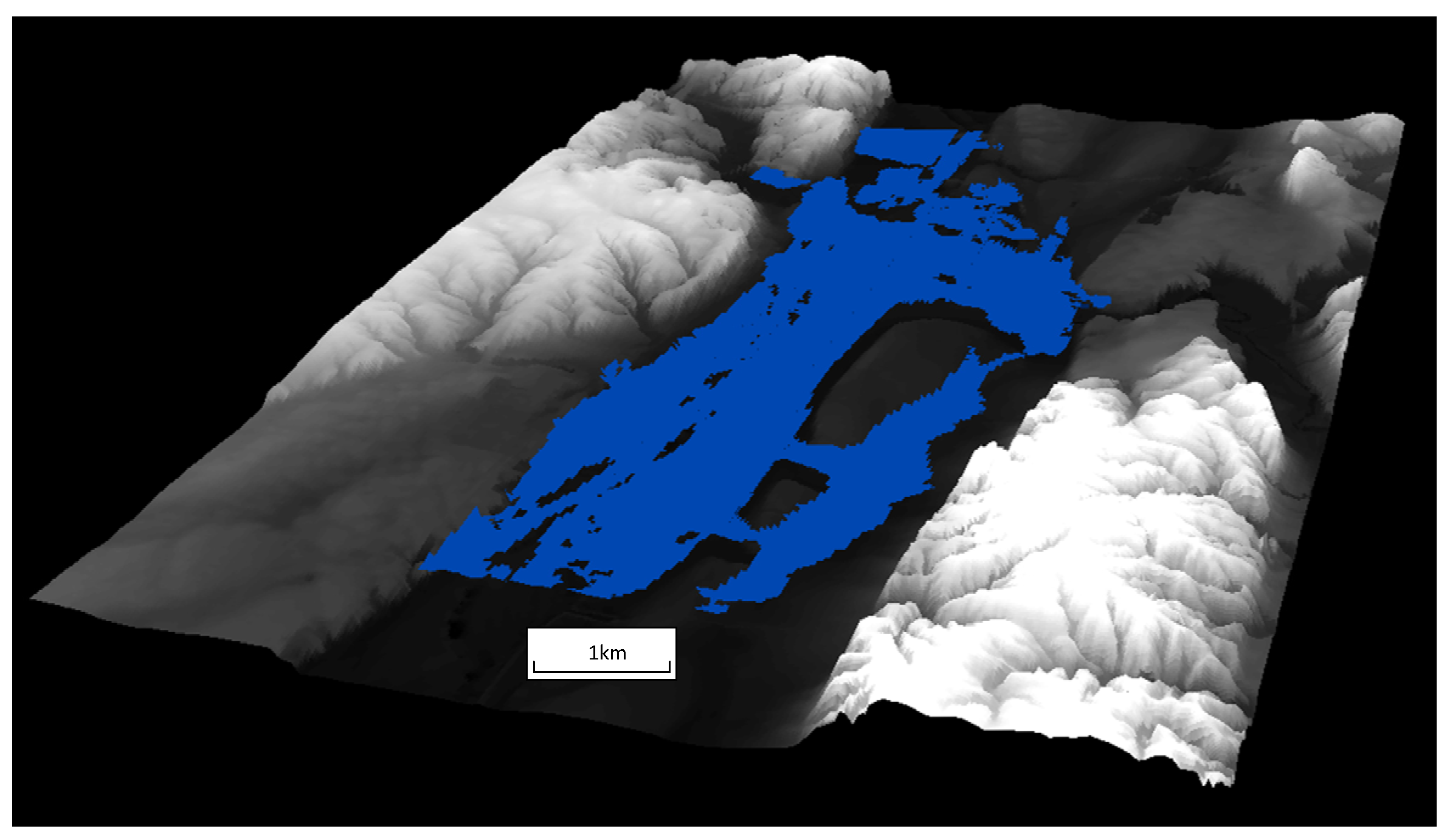
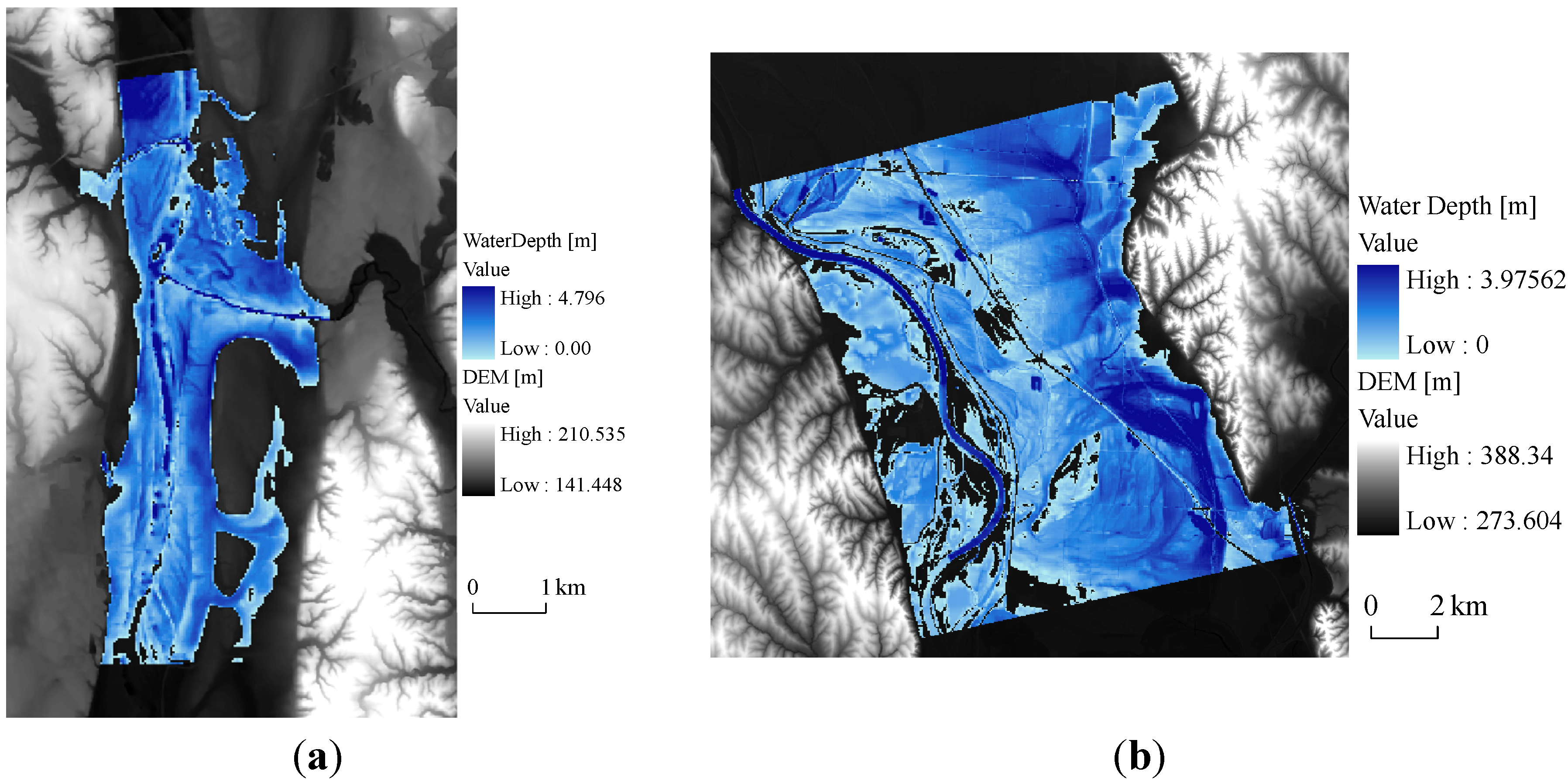
4.1. Extraction of the Observed Data from Landsat 5 TM Satellite Imagery

4.2. Approximation of Flood Discharge Using HEC-RAS and the GLUE Methodology
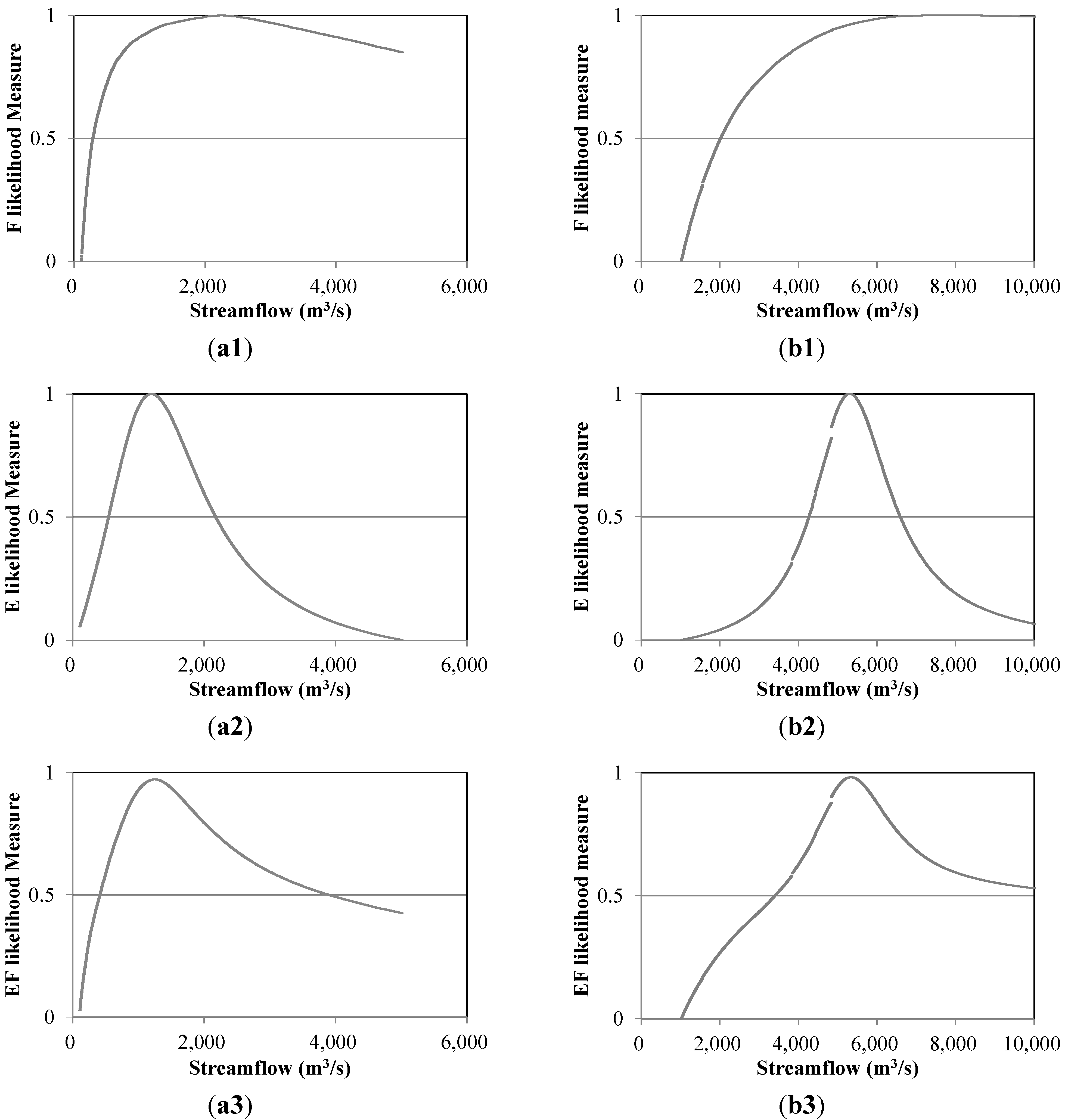
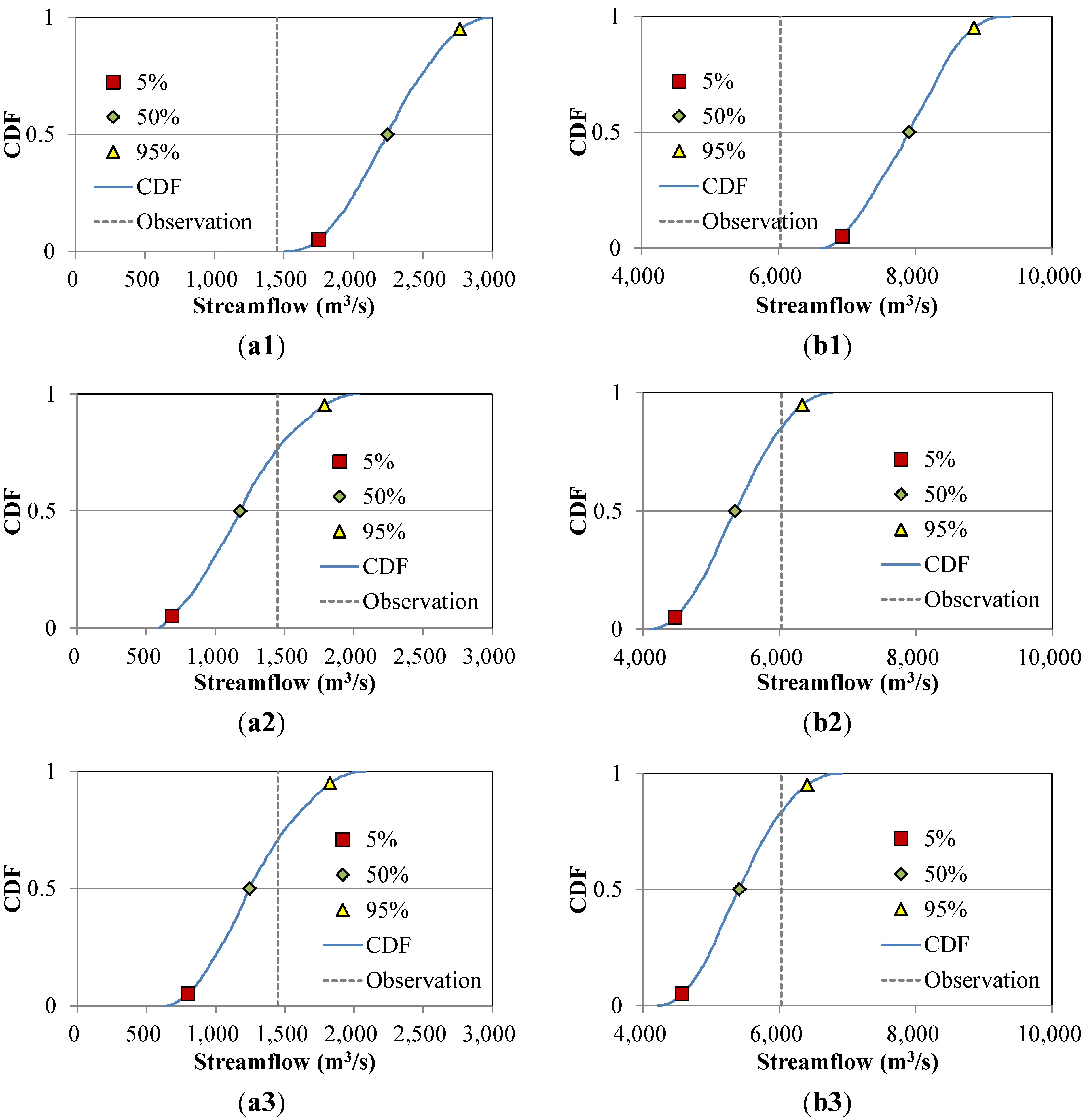
| Likelihood Measure | CDF | Discharge (m3/s) | |
|---|---|---|---|
| Montezuma | Nebraska | ||
| F | 0.05 | 1752 | 6938 |
| 0.50 | 2247 | 7911 | |
| 0.95 | 2769 | 8862 | |
| E | 0.05 | 687 | 4471 |
| 0.50 | 1179 | 5346 | |
| 0.95 | 1788 | 6344 | |
| EF | 0.05 | 801 | 4576 |
| 0.50 | 1245 | 5413 | |
| 0.95 | 1827 | 6412 | |
| Observation | 1450 | 6030 | |
5. Summary and Conclusions
- This study demonstrates that Landsat imagery can be used as secondary source for discharge estimation in a data-poor environment. The water-body extracted from the Landsat imagery can be used in conjunction with a hydraulic model to estimate flood discharge. However, the use of Landsat imagery in a small-scale study can produce relatively more uncertainty in reading water surface elevation from a DEM (10 m × 10 m) than in a large-scale study, due to the coarse resolution (30 m × 30 m) of a Landsat image. Therefore, flood information obtained from Landsat imagery in planning flood risk management in a data-poor environment is more appropriate for larger rivers. The approximated flood discharge estimated for the Nebraska reach is 5413 m3/s, and 1245 m3/s for the Montezuma reach. The relative errors between the gauged data and the approximations are 10% for the Nebraska reach and 14% for the Montezuma reach, respectively.
- In the GLUE methodology, the different results between E Likelihood measure and F likelihood measure showed subjectivity on the selection of criteria meeting informal likelihood measure. However, when considering the physical conditions of the study reach, such as the shape of the valley, size of the reach, and the flood intensity, the informal likelihood measure in the GLUE methodology can enhance the ability of finding improved flood information in data-poor environment. In addition, each likelihood measure is differently responded corresponding to the random discharge, but produces common results in flood discharge estimation for both study reaches. For example, the approximated discharge for both reaches is overestimated for F likelihood measure on the spatial flood extent and underestimated for E likelihood measure on the observed water surface elevation. In addition, the combination (EF likelihood) of two likelihood measures estimates discharge closest to the observed discharge at gauge station.
Acknowledgments
Conflicts of Interest
References
- Stedinger, J.R.; Vogel, R.M. Foufoula-Georgiou E. Frequency Analysis of Extreme Events. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Ramachandra, R.A.; Hamed, K.H. Flood Frequency Analysis; CRC Press: Boca Raton, FL, USA, 2000; p. 350. [Google Scholar]
- Vogel, R.M.; McMahon, T.A.; Chiew, F. Floodflow frequency model selection in Australia. J. Hydrol. 1993, 146, 421–449. [Google Scholar] [CrossRef]
- Klemeš, V. Tall tales about tails of hydrological distributions. J. Hydrol. Engrg. ASCE 2003, 5, 232–239. [Google Scholar] [CrossRef]
- Mitosek, H.T.; Strupczewski, W.G.; Singh, V.P. Three procedures for selection of annual flood peak distribution. J. Hydrol. 2006, 323, 57–73. [Google Scholar] [CrossRef]
- Laio, F.; di Baldassarre, G.; Montanari, A. Model selection techniques for the frequency analysis of hydrological extremes. Water Resour. Res. 2009, 45, W07416. [Google Scholar] [CrossRef]
- Dalrymple, T. Flood Frequency Analyses; USGS Water Supply Paper 1543-A; USGS: Reston, VA, USA, 1960. [Google Scholar]
- Viviroli, D.; Zappa, M.; Schwanbeck, J.; Gurtz, J.; Weingartner, R. Continuous simulation for flood estimation in ungauged mesoscale catchments of Switzerland—Part I: Modelling framework and calibration results. J. Hydrol. 2009, 377, 191–207. [Google Scholar] [CrossRef]
- Viviroli, D.; Mittelbach, H.; Gurtz, J.; Weingartner, R. Continuous simulation for flood estimation in ungauged mesoscale catchments of Switzerland—Part II: Parameter regionalisation and flood estimation results. J. Hydrol. 2009, 377, 208–225. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Serinaldi, F. Design hydrograph estimation in small and ungauged watersheds: Continuous simulation method versus event-based approach. Hydrol. Process. 2012, 26, 3124–3134. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Oberstadler, R.; Honsch, H.; Huth, D. Assessment of the mapping capabilities of ERS-1 SAR data for flood mapping: A case study of Germany. Hydrol. Process. 1997, 10, 1415–1425. [Google Scholar] [CrossRef]
- Sivapalan, M.; Takeuchi, K.; Franks, S.W.; Gupta, V.K.; Karambiri, H.; Lakshim, V.; Liang, X.; McDonnell, J.J.; Mendiondo, E.M.; Connell, O.; et al. IAHS decade on predictions in ungauged basins (PUB), 2003–2012: Shaping an exciting future for the hydrological sciences. Hydrol. Sci. J. 2003, 48, 857–880. [Google Scholar] [CrossRef]
- Montanari, M.; Hostache, R.; Matgen, P.; Schumann, G.; Pfister, L.; Hoffmann, L. Calibration and sequential updating of a coupled hydrologic–hydraulic model using remote sensing-derived water stages. Hydrol. Earth Syst. Sci. 2009, 13, 367–380. [Google Scholar] [CrossRef]
- Smith, L.C. Satellite remote sensing of river inundation area, stage and discharge: A review. Hydrol. Process. 1997, 11, 1427–1439. [Google Scholar] [CrossRef]
- Pan, F.; Nichols, J. Remote sensing of river stage using the cross sectional inundation area—River stage relationship (IARSR) constructed from digital elevation model data. Hydrol. Process. 2012. [Google Scholar] [CrossRef]
- Bates, P.D.; Horritt, M.S.; Smith, C.N.; Mason, D. Integrating remote sensing observations of flood hydrology and hydraulic modelling. Hydrol. Process. 1997, 11, 1777–1796. [Google Scholar] [CrossRef]
- Sun, W.C.; Ishidaira, W.H.; Bastola, S. Prospects for calibrating rainfall-runoff models using satellite observations of river hydraulic variables as surrogates for in situ river discharge measurements. Hydrol. Process. 2012, 26, 872–882. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Moller, D.; Smith, L.C.; Dingman, S.L. Estimating discharge in rivers using remotely sensed hydraulic information. J. Hydrol. 2005, 309, 191–209. [Google Scholar] [CrossRef]
- Getirana, A.C.V.; Peters-Lidard, C. Estimating water discharge from large radar altimetry datasets. Hydrol. Earth Sys. Sci. 2013, 17, 923–933. [Google Scholar] [CrossRef]
- Durand, M.; Andreadis, K.M.; Alsdorf, D.E.; Lettenmaier, D.P.; Moller, D.; Wilson, M. Estimation of bathymetric depth and slope from data assimilation of swath altimetry into a hydrodynamic model. Geophys. Res. Letters 2008, 35, L20401. [Google Scholar] [CrossRef]
- Neal, J.; Schumann, G.; Bates, P.; Buytaert, W.; Matgen, P.; Pappenberger, F. A data assimilation approach to discharge estimation from space. Hydrol. Process. 2009, 23, 3641–3649. [Google Scholar] [CrossRef]
- Hostache, R.; Lai, X.; Monnier, J.; Puech, C. Assimilation of spatially distributed water levels into a shallow-water flood model. Part II: Use of a remote sensing image of Mosel river. J. Hydrol. 2010, 390, 257–268. [Google Scholar] [CrossRef]
- Matgen, P.; Montanari, M.; Hostache, R.; Pfister, L.; Hoffmann, L.; Plaza, D.; Pauwels, V.R.N.; de Lannoy, G.J.M.; de Keyser, R.; Savenije, H.H.G. Towards the sequential assimilation of SAR-derived water stages into hydraulic models using the particle filter: Proof of concept. Hydrol. Earth Syst. Sci. 2010, 14, 1773–1785. [Google Scholar] [CrossRef]
- Beven, K.J.; Binley, A.M. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Romanowicz, R.; Beven, K.J. Dynamic real-time prediction of flood inundation probabilities. Hydrol. Sci. J. 1998, 43, 181–196. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.J.; Hunter, N.M.; Bates, P.D.; Gouweleeuw, B.T.; Thielen, J.; de Roo, A.P.J. Cascading model uncertainty from medium range weather forecasts (10 days) through a rainfall-runoff model to flood inundation predictions within the European Flood Forecasting System (EFFS). Hydrol. Earth Syst. Sci. 2005, 9, 381–393. [Google Scholar] [CrossRef]
- Pappenberger, F.; Matgen, P.; Beven, K.; Henry, J.; Pfister, L.; de Fraipont, P. Influence of uncertain boundary conditions and model structure on flood inundation predictions. Adv. Water Resour. 2006, 29, 1430–1449. [Google Scholar] [CrossRef]
- Mantovan, P.; Todini, E. Hydrological forecasting uncertainty assessment: Incoherence of the GLUE methodology. J. Hydrol. 2006, 330, 368–381. [Google Scholar] [CrossRef]
- Beven, K.J.; Smith, P.J.; Freer, J.E. Comment on “Hydrological forecasting uncertainty assessment: Incoherence of the GLUE methodology” by Pietro Mantovan and Ezio Todini. J. Hydrol. 2007, 338, 315–318. [Google Scholar] [CrossRef]
- Beven, K.J.; Smith, P.J.; Freer, J.E. So just why would a modeller choose to be incoherent? J. Hydrol. 2008, 354, 15–32. [Google Scholar] [CrossRef]
- USGS Landsat Missions Home Page. Available online: http://landsat.usgs.gov/ (accessed on 26 September 2013).
- The National Map Viewer and Download Platform. Available online: http://seamless.usgs.gov/ (accessed on 26 September 2013).
- Moore, M.R. Development of a High-Resolution 1D/2D Coupled Flood Simulation of Charles City, Iowa. Master’s thesis, University of Iowa, Iowa city, IA, USA, May 2011. [Google Scholar]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Calenda, G.C.; Mancini, C.P.; Volpi, E. Distribution of extreme peak floods of the Tiber River from the XV century. Adv. Water Resour. 2005, 28, 615–625. [Google Scholar] [CrossRef]
- National Water Information System: Web Interface. USGS Water Resources. USGS 03340500. Available online: http://waterdata.usgs.gov/usa/nwis/uv?03340500 (accessed on 26 September 2013).
- National Water Information System: Web Interface. USGS Water Resources. USGS 06807000. Available online: http://waterdata.usgs.gov/usa/nwis/uv?site_no=06807000 (accessed on 26 September 2013).
- Tou, J.T.; Gonzales, R.C. Pattern Recognition Principles. Isodata Algorithm, Pattern Classification by Distance Functions; Addison-Wesley: Reading, MA, USA, 1974; pp. 97–104. [Google Scholar]
- Richards, J.A. Remote Sensing Digital Image Analysis: An Introduction, 2nd ed.; Springer-Verlag: Berlin, Germany, 1993. [Google Scholar]
- Castañeda, C.; Herrero, J.; Casterad, M.A. Facies identification within the playalakes of the Monegros Desert, Spain, with field and satellite data. Catena 2005, 63, 39–63. [Google Scholar] [CrossRef]
- Lang, M.W.; McCarty, G.W. LiDAR intensity for improved detection of inundation below the forest canopy. Wetlands 2009, 29, 1166–1178. [Google Scholar] [CrossRef]
- Thomas, N.E.; Huang, C.; Goward, S.N.; Powell, S.; Rishmawi, K.; Schleeweis, K.; Hinds, A. Validation of north American forest disturbance dynamics derived from Landsat time series stacks. Remote Sens. Environ. 2011, 115, 19–32. [Google Scholar] [CrossRef]
- Khan, S.I.; Hong, Y.; Wang, J.; Yilmaz, K.K.; Gourley, J.J.; Adler, R.F.; Brakenridge, G.R.; Policelli, F.; Habib, S.; Irwin, D. Satellite remote sensing and hydrologic modeling for flood inundation mapping in Lake Victoria basin: Implications for hydrologic prediction in ungauged basins. IEEE Trans. Geosci. Remote Sens. 2011, 49, 85–95. [Google Scholar] [CrossRef]
- Song, C.; Woodcock, C.E.; Seto, K.C.; Pax-Lenney, M.; Macomber, S.A. Classification and change detection using Landsat TM data: When and how to correct atmospheric effects. Remote Sens. Environ. 2001, 75, 230–244. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers (USACE). HEC–RAS Hydraulic Reference Manual; Hydrologic Engineering Center: Davis, CA, USA, 2006. [Google Scholar]
- Pappenberger, F.; Beven, K.; Horritt, M.; Blazkova, S. Uncertainty in the calibration of effective roughness parameters in HEC-RAS using inundation and downstream level observations. J. Hydrol. 2005, 302, 46–69. [Google Scholar] [CrossRef]
- Horritt, M.S. A methodology for the validation of uncertain flood inundation models. J. Hydrol. 2006, 326, 153–165. [Google Scholar] [CrossRef]
- Fewtrell, T.J.; Bates, P.D.; Horritt, M.; Hunter, N.M. Evaluating the effect of scale in flood inundation modelling in urban environments. Hydrol. Process. 2008, 22, 5107–5118. [Google Scholar] [CrossRef]
- Hicks, F.E.; Peacock, T. Suitability of HEC-RAS for flood forecasting. Can. Water Resour. J. 2005, 30, 159–174. [Google Scholar] [CrossRef]
- Meselhe, E.A.; Pereira, J.F.; Georgiou, I.Y.; Allison, M.A.; McCorquodale, J.A.; Davis, M.A. Numerical Modeling of Mobile-Bed Hydrodynamics in the Lower Mississippi River. American Society of Civil Engineers. In Proceedings of the World Environmental and Water Resources Congress (EWRI), Providence, RI, USA, 16–20 May 2010; pp. 1433–1442.
- Hornberger, G.M.; Spear, R.C. An approach to the preliminary analysis of environmental systems. J. Environ. Manag. 1981, 12, 7–18. [Google Scholar]
- Young, P.C. The Validity and Credibility of Models for Badlydefined Systems. Uncertainty and Forecasting of Water Quality; van Straten, B., Ed.; Springer: Berlin, Germany, 1983; pp. 69–98. [Google Scholar]
- Beven, K.J. Environmental Modelling: An Uncertain Future? Routledge: London, UK, 2009. [Google Scholar]
- Wang, X.; Frankenberger, J.R.; Kladivko, E.J. Uncertainties in DRAINMOD predictions of subsurface drain flow for an Indiana silt loam using the GLUE methodology. Hydrol. Process. 2006, 20, 3069–3084. [Google Scholar] [CrossRef]
- Blasone, R.S.; Madsen, H.; Rosbjerg, D. Uncertainty assessment of integrated distributed hydrological models using GLUE with Markov chain Monte Carlo sampling. J. Hydrol. 2008, 353, 18–32. [Google Scholar] [CrossRef]
- Blasone, R.S.; Vrugt, J.A.; Madsen, H.; Rosbjerg, D.; Robinson, B.A.; Zyvoloski, G.A. Generalized likelihood uncertainty estimation (GLUE) using adaptive Markov chain Monte Carlo sampling. Adv. Water Resour. 2008, 31, 630–648. [Google Scholar] [CrossRef]
- Hornberger, G.M.; Cosby, B.J. Selection of parameter values in environmental models using sparse data: A case study. Appl. Math. Comp. 1985, 17, 335–355. [Google Scholar]
- Kiczko, A.; Pappenberger, F.; Romanowicz, R.J. Flood Risk Analysis of the Warsaw Reach of the Vistula River. In ERB 2006: Uncertainties in the ‘Monitoring-Conceptualisation-Modelling’ Sequence of Catchment Research; European Network of Experimental and Representative Basins (ERB): Luxembourg, 2007. [Google Scholar]
- Aronica, G.; Hankin, B.G.; Beven, K.J. Uncertainty and equifinality in calibrating distributed roughness coefficients in a flood propagation model with limited data. Adv. Water Resour. 1998, 22, 349–365. [Google Scholar] [CrossRef]
- Hunter, N.M.; Bates, P.D.; Horritt, M.S.; de Roo, A.P.T.; Werner, M.G.F. Utility of different data types for calibrating flood inundation models within a GLUE framework. Hydrol. Earth Syst. Sci. 2005, 9, 412–430. [Google Scholar] [CrossRef]
- Schumann, G.; Cutler, M.; Black, A.; Matgen, P.; Pfister, L.; Hoffmann, L.; Pappenberger, F. Evaluating uncertain flood inundation predictions with uncertain remotely sensed water stages. Int. J. River Basin Manag. 2008, 6, 187–199. [Google Scholar] [CrossRef]
- Horritt, M.S.; Bates, P.D. Evaluation of 1D and 2D numerical models for predicting river flood inundation. J. Hydrol. 2002, 268, 87–89. [Google Scholar] [CrossRef]
- Schumann, G.; Bates, P.D.; Horritt, M.S.; Matgen, P.; Pappenberger, F. Progress in integration of remote sensing derived flood extent and stage data and hydraulic models. Rev. Geophys. 2009, 47. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Schumann, G.; Bates, P.D. A technique for the calibration of hydraulic models using uncertain satellite observations of flood extent. J. Hydrol. 2009, 367, 276–282. [Google Scholar] [CrossRef]
- Horritt, M.S.; Bates, P.D. Predicting floodplain inundation: Raster-based modelling versus the finite element approach. Hydrol. Process. 2001, 15, 825–842. [Google Scholar] [CrossRef]
- Aronica, G.; Bates, P.D.; Horritt, M.S. Assessing the uncertainty in distributed model predictions using observed binary pattern information within GLUE. Hydrol. Process. 2002, 16, 2001–2016. [Google Scholar] [CrossRef]
- Bates, P.D.; Horritt, M.S.; Aronica, G.; Beven, K.J. Bayesian updating of flood inundation likelihoods conditioned on flood extent data. Hydrol. Process. 2004, 18, 3347–3370. [Google Scholar] [CrossRef]
- Pappenberger, F.; Frodsham, K.; Beven, K.J.; Romanowicz, R.; Matgen, P. Fuzzy set approach to calibrating distributed flood inundation models using remote sensing observation. Hydrol. Earth Syst. Sci. 2007, 11, 739–752. [Google Scholar] [CrossRef]
- Cook, A.; Merwade, V. Effect of topographic data, geometric configuration and modeling approach on flood inundation mapping. J. Hydrol. 2009, 377, 131–142. [Google Scholar] [CrossRef]
- Sanders, B.F. Evaluation of on-line DEMs for flood inundation modeling. Adv. Water Resour. 2007, 30, 1831–1843. [Google Scholar] [CrossRef]
- Zheng, T.; Wang, Y. Mapping flood extent using a simple DEM-inundation model. North Carol. Geographer. 2007, 15, 1–19. [Google Scholar]
- Bates, P.D.; Horritt, M.S.; Hunter, N.M.; Mason, D.C.; Cobby, D.M. Numerical Modelling of Floodplain Flow. In Computational Fluid Dynamics:Applications in Environmental Hydraulics; Bates, P., Ferguson, L., Eds.; John Wiley and Sons Ltd.: Chichester, UK, 2005. [Google Scholar]
- Fewtrell, T.J.; Neal, J.C.; Bates, P.D.; Harison, P.J. Geometric and structural river channel complexity and the prediction of urban inundation. Hydrol. Process. 2011, 25, 3173–3186. [Google Scholar] [CrossRef]
- Jung, Y.; Merwade, V. Uncertainty quantification in flood inundation mapping using generalized likelihood uncertainty estimate and sensitivity analysis. J. Hydrol. Eng. 2012, 17, 507–520. [Google Scholar] [CrossRef]
- Bales, J.D.; Wagner, C.R. Sources of uncertainty in flood inundation maps. J Flood Risk Manag. 2009, 2, 139–147. [Google Scholar] [CrossRef]
- Merwade, V.M.; Olivera, F.; Arabi, M.; Edleman, S. Uncertainty in flood inundation mapping—Current issues and future directions. ASCE J. Hydrol. Eng. 2008, 13, 608–620. [Google Scholar] [CrossRef]
- Pan, F.; Liao, J.; Li, X.; Guo, H. Application of the inundation area-lake level rating curves constructed from the SRTM DEM to retrieving lake levels from satellite measured inundation areas. Comput. Geosci. 2013, 52, 168–176. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Jung, Y.; Merwade, V.; Yeo, K.; Shin, Y.; Lee, S.O. An Approach Using a 1D Hydraulic Model, Landsat Imaging and Generalized Likelihood Uncertainty Estimation for an Approximation of Flood Discharge. Water 2013, 5, 1598-1621. https://doi.org/10.3390/w5041598
Jung Y, Merwade V, Yeo K, Shin Y, Lee SO. An Approach Using a 1D Hydraulic Model, Landsat Imaging and Generalized Likelihood Uncertainty Estimation for an Approximation of Flood Discharge. Water. 2013; 5(4):1598-1621. https://doi.org/10.3390/w5041598
Chicago/Turabian StyleJung, Younghun, Venkatesh Merwade, Kyudong Yeo, Yongchul Shin, and Seung Oh Lee. 2013. "An Approach Using a 1D Hydraulic Model, Landsat Imaging and Generalized Likelihood Uncertainty Estimation for an Approximation of Flood Discharge" Water 5, no. 4: 1598-1621. https://doi.org/10.3390/w5041598
APA StyleJung, Y., Merwade, V., Yeo, K., Shin, Y., & Lee, S. O. (2013). An Approach Using a 1D Hydraulic Model, Landsat Imaging and Generalized Likelihood Uncertainty Estimation for an Approximation of Flood Discharge. Water, 5(4), 1598-1621. https://doi.org/10.3390/w5041598




