Abstract
Bioretention cells are an urban stormwater management technology used to address both water quality and quantity concerns. A lack of region-specific design guidelines has limited the widespread implementation of bioretention cells, particularly in cold climates. In this paper, experimental data are used to construct a multiple linear regression model to predict hydrological performance of bioretention cells. Nine different observed parameters are considered as candidates for regressors, of which inlet runoff volume and duration, and initial soil moisture were chosen. These three variables are used to construct six different regression models, which are tested against the observations. Statistical analysis showed that the amount of runoff captured by a bioretention cell can be successfully predicted by the inlet runoff volume and event duration. Historical data is then used to calculate runoff volume for a given duration, in different catchment types. This data is used in the regression model to predict bioretention cell performance. The results are then used to create a design tool which can assist in estimating bioretention cell size to meet different performance goals in southern Alberta. Examples on the functionality of the design tool are provided.
1. Introduction
Urban stormwater runoff is defined as the overland flow that occurs after a precipitation event in urbanized areas. These areas are characterized by a higher fraction of impervious surfaces as compared to natural, undeveloped areas. An increase in impervious surfaces, such as roofs, roads and parking lots can lead to higher runoff volumes with higher flow rates, lower evapotranspiration and lower infiltration [1]. This can increase the risk of flooding in downstream waterways and contribute to the degradation of water quality; in fact urban stormwater runoff is considered to be a leading cause of degradation of surface waters [2,3,4]. In response to the detrimental effects of runoff, a site design strategy known as Low Impact Development (or LID), has been widely adopted and aims to control, capture and treat runoff at the source and promotes sustainable water management [5]. For LID, structural and non-structural practices are implemented on site such that the post-development hydrology and water quality mimics or improves from the pre- or undeveloped conditions [3,6,7].
Bioretention cells, also known as rain gardens, are small, terrestrial, soil and plant based infiltration and treatment basins. They consist of a highly porous engineered soil media topped with dense vegetation and organic ground cover (such as mulch) (see Figure 1 for a schematic of the bioretention cell used in this study). Urban runoff is routed to the cell, where it infiltrates into the media. The runoff can exit the cell via an under-drain beneath the cell, percolate into the surrounding sub-soils, or a combination of both depending on the design [7]. The surface layer acts to attenuate the peak discharge and time of concentration of the incoming flow [8,9] as well as to provide storage if the runoff intensity is higher than the infiltration capacity. Losses to the surrounding sub-soils, plant uptake and storage in soil media contribute to runoff volume reduction.
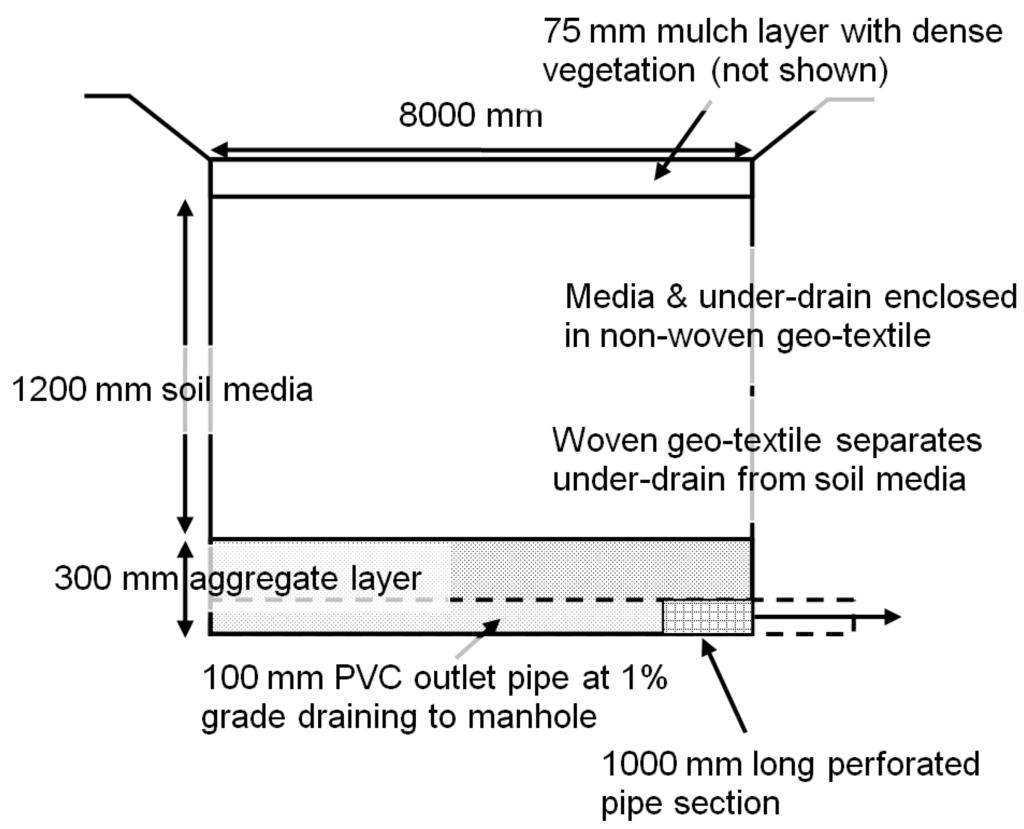
Figure 1.
An example of a bioretention cell in Calgary, Canada.
Bioretention cells are used to address both runoff quantity and quality concerns. This paper will focus only on the quantity (i.e., hydrological) component, specifically the ability of a bioretention cell to decrease or capture the amount of runoff it receives. Other hydrological performance indicators include the change in peak flow rate and the lag time of the outlet hydrograph. The ability of a bioretention cell to decrease or capture runoff volume has been reported in a number of studies. Experiments on both the field and laboratory scale have shown that the cells can capture 100% of influent volumes from small to medium size events, and between 33%–80% for larger events [5,10,11,12]. The large variability in performance in these studies can be attributed to the fact that current design guidelines are highly empirical and are not optimized for region specific differences in geological characteristics and climatic conditions [1]. Thus bioretention cells may not perform with the same efficacy as intended if implemented without considerations for regional differences.
A number of bioretention cell design guidelines have been developed in the United States; a summary of some of these has been provided in [13]. In most cases, the functionality of these guidelines is limited by location and climate, as described above. This is especially poignant in cold climate regions, particularly in prairie regions, where bioretention cell hydrology is unique [14,15]. Cold climate conditions are characterized by frozen soil, higher snowmelt volumes and lower runoff intensity from snowmelt, and repeating freeze-thaw cycles [15]. Thus, guidelines developed in warm or temperate regions may not be applicable in cold regions.
To overcome these limitations, a number of physically-based numerical models have been created to predict bioretention cell performance [13]. The overall objective of these models is to ascertain whether a particular design guideline is appropriate for the desired application or performance targets. Additionally, these models can predict the effects of design changes on performance. Examples include the RECARGA [16] and RECHARGE [17] models, based on the Richards and Green-Ampt equations, respectively. The models were developed in Wisconsin, USA and they have been adopted by the state government [13]. Heasom et al. [18] developed a model using the HEC-HMS system that treats the bioretention cell as a reservoir and uses a weir system to control the outflow. Similar rainfall-runoff approach models were created using SWMM by [19,20].
However, a major drawback of using physically-based models is the data needed for simulations, which may not be easily available, as well difficulties in model calibration. This is especially true when a number of “sub-models” representing different processes (e.g., rainfall-runoff, infiltration, evapotranspiration) are lumped together [21]. In addition to this, it may be difficult to mimic local characteristics using these models, for example, the frequent freeze-thaw cycles experienced in regions like Calgary, Canada. In contrast to physically-based models, data-driven models are based on the analysis of the data characterizing a system, i.e., the bioretention cell, with limited or no assumptions regarding the nature of the physical system being modeled. Typically, the model is defined on the basis of the connections between concurrent input and output variables [21]. An advantage of this approach is that, there is potential for establishing strong relationships between bioretention cell performance (i.e., the output variable) and widely available input variables (e.g., precipitation depth or air temperature). If so, the ability to predict bioretention cell performance may be much simpler than relying on physically-based models that require more intensive and specialized data requirements. By using region-specific data, a data-driven model offers the potential of predicting bioretention cell performance in that region.
In this paper, a data-driven model is proposed to predict region-specific bioretention cell performance in Calgary, Canada. The use of a bioretention cell to address stormwater runoff concerns has been explored in Calgary [15,22]. However, to date, no comprehensive regional design guidelines or numerical models (data-driven or other) have been developed for bioretention cell use in Calgary. The city is characterized by prairie hydrology that experiences frequent freeze-thaw cycles through the winter months. These unique characteristics require specific considerations in design guidelines before widespread bioretention implementation can occur. The objectives of this research are to simulate bioretention cell performance using a data-driven model and then to use the results from the simulations to create a design tool to assist in sizing bioretention cells to meet performance targets. The research presented here uses data from Calgary; however this methodology can be applied to develop region-specific tools for any location.
The model described in this paper uses experimental data from a bioretention cell to construct and validate a multiple linear regression (MLR) model. The regressors were selected based on statistical analysis of the available parameters collected via field-scale experiments. The best performing model was used to predict bioretention cell performance under different conditions, using historical observations. These processes are described in detail below.
2. Methods and Materials
2.1. Site Description and Experiment Procedure
The bioretention cell used for the experiments is located in southwest Calgary. The cell was constructed in 2005 for experimental purposes. As such, the cell is not operational and no runoff drains to it. The bioretention cell measures 8 m wide by 4 m long, with a depth of 1.5 m. The cell consists of dense, native vegetation on the surface along with a 75 mm mulch layer. The soil media used in the cell is classified as loam to sandy-loam. The media is enclosed with a permeable geotextile, allowing moisture in the cell to drain into the surrounding sub-soils. Details on the design of the bioretention cell are included in [15,22].
Since the bioretention cell is experimental and offline, a runoff distribution system was designed to mimic precipitation events. Synthetic stormwater runoff was created using stormwater from a stormwater pond and sediment used for road de-icing. The runoff was applied to the cell using a variable speed pump and series of hoses. The volume, flow rate and duration of each experiment aimed to mimic storm events of different frequencies that occur in Calgary. The synthetic runoff drained through the bioretention cell to the under-drain layer, where a perforated pipe channeled the runoff to a manhole that was equipped with monitoring equipment. Details on the synthetic runoff system and experimental procedure are listed in [15,22].
2.2. Data Collection and Analysis
For each experiment on the bioretention cell, a number of different hydrological parameters were collected. Details on sampling methods have been previously described in [15]. The pertinent parameters used for this research include the volume of synthetic runoff applied (Vi) and released (Vo) from the bioretention cell, the corresponding flow rates Qi and Qo, and the duration of the two hydrographs, ti and to. The initial (θi), peak (θp) and final (θf) moisture level of the soil media was measured at four depths: 150, 300, 500 and 1000 mm below the surface of the cell. A number of climatic parameters, including air temperature (T), radiation, wind speed and direction, and precipitation were also collected. In addition to these, a number of variables were calculated from the observed data, including peak and center of mass flow rates and the time to peak for both inlet and outlet hydrographs and the delay or lag-time between the peaks and center of mass.
Candidates for regressors were chosen from this collection of data based on correlation analysis. However, since the objective of this research is to use a data-driven model to predict performance, a function of Vo, all parameters that were directly influenced by Vo were not considered as regressors. This limited the candidates to the following nine parameters: T, Vi, ti, influent peak flow rate and center-of mass flow rate (labeled Qpi and Qci, respectively) and θi at four depths. Pearson’s correlation coefficient and significance tests (estimated with Student’s t-test) were carried out on these parameters to determine which had the highest influence on the dependent variable Vo.
Bioretention cell performance was defined as, and limited to, the change in runoff volume between the inlet and outlet. It is defined as:
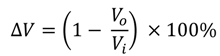 where ΔV = change in runoff volume between inlet and outlet of the bioretention cell (%); Vo = volume of effluent (m3); and Vi = volume of influent (m3). A value of ΔV less than 100% indicates a decrease in runoff volume between the inlet and outlet, or a lower volume of effluent than influent.
where ΔV = change in runoff volume between inlet and outlet of the bioretention cell (%); Vo = volume of effluent (m3); and Vi = volume of influent (m3). A value of ΔV less than 100% indicates a decrease in runoff volume between the inlet and outlet, or a lower volume of effluent than influent.
2.3. Model Construction
In this study an MLR model was used as the data-driven technique to predict bioretention cell performance. The independent variables were selected from the larger group of observed variables, based on correlation analysis. The general form of the regression equation was:
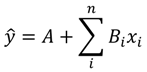 where xi are the independent variables, A and Bi are the regression coefficients and n is the total number of regressors used. Different permutations of regressors were used to create six different models, which are summarized in Section 4 below. For each regression analysis, the logarithms of the data were used as inputs into the model to overcome the nonlinearity between the independent and dependent variables. These models were evaluated using the coefficient of determination (R2), root mean square error (RMSE), mean absolute error (MAE) and the corrected Akaike information criterion (AICc). These error statistics were calculated using the following equations:
where xi are the independent variables, A and Bi are the regression coefficients and n is the total number of regressors used. Different permutations of regressors were used to create six different models, which are summarized in Section 4 below. For each regression analysis, the logarithms of the data were used as inputs into the model to overcome the nonlinearity between the independent and dependent variables. These models were evaluated using the coefficient of determination (R2), root mean square error (RMSE), mean absolute error (MAE) and the corrected Akaike information criterion (AICc). These error statistics were calculated using the following equations:
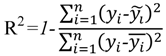
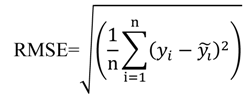
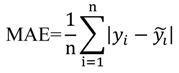
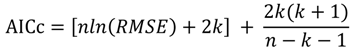 where n is the number of sample points used and k is the number of parameters in each regression model. For each model, approximately two thirds of the available data was used for constructing model and the remaining data were used for validation.
where n is the number of sample points used and k is the number of parameters in each regression model. For each model, approximately two thirds of the available data was used for constructing model and the remaining data were used for validation.
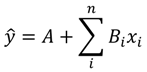
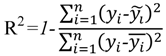
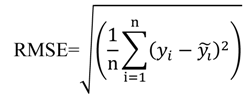
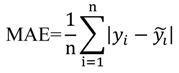
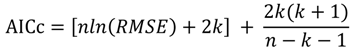
3. Experimental and Data Analysis Results
A total of 24 experiments were conducted on the bioretention cell; data corresponding to the experiments are listed in Table 1 below. The volume of synthetic runoff applied to the cell ranged from approximately 3720 L to 17,990 L with experiment durations ranging from 14 min to 116 min. Eight experiments were conducted in cold climate conditions; cold climate was defined as when air temperature was less than 5 °C. The average change in volume between the inlet and outlet was 91.5%, calculated using Equation (1). The performance was significantly lower (i.e., higher Vo) for the cold climate experiments. The reasons for the differences in the two climatic conditions are discussed in detail in [15].

Table 1.
Summary of data collected from the 24 field experiments.
| ID | T | Vi | ti | Qpi | Qci | θi-1 | θi-2 | θi-3 | θi-4 | Vo |
|---|---|---|---|---|---|---|---|---|---|---|
| (°C) | (L) | (min) | (L/s) | (L/s) | (m3/m3) | (m3/m3) | (m3/m3) | (m3/m3) | (L) | |
| S1 | 14 | 8,004 | 116 | 2.62 | 1.11 | 0.230 | 0.249 | 0.282 | 0.402 | 739 |
| S2 | 22 | 7,520 | 21 | 13.04 | 4.08 | 0.307 | 0.250 | 0.284 | 0.403 | 162 |
| S3 | 20 | 7,736 | 36 | 11.52 | 3.31 | 0.299 | 0.302 | 0.328 | 0.433 | 237 |
| S4 | 13 | 7,943 | 31 | 8.83 | 4.73 | 0.313 | 0.308 | 0.324 | 0.421 | 586 |
| F1 | 11 | 8,230 | 34 | 11.79 | 4.02 | 0.597 | 0.312 | 0.179 | 0.410 | 394 |
| F2 | 9 | 8,120 | 32 | 10.59 | 4.34 | 0.307 | 0.351 | 0.482 | 0.465 | 728 |
| F3* | −1 | 4,739 | 28 | 6.22 | 2.33 | 0.459 | 0.358 | 0.399 | 0.513 | 3 |
| W1* | 3 | 3,919 | 19 | 6.43 | 3.35 | 0.236 | 0.353 | 0.346 | 0.370 | 0 |
| Sp1* | 4 | 3,866 | 21 | 7.03 | 2.23 | 0.236 | 0.353 | 0.346 | 0.370 | 0 |
| Sp2 | 9 | 8,601 | 27 | 11.37 | 4.49 | 0.335 | 0.391 | 0.357 | 0.392 | 909 |
| Sp3 | 16 | 3,877 | 14 | 9.67 | 3.28 | 0.335 | 0.391 | 0.357 | 0.392 | 5 |
| S5 | 12 | 8,395 | 34 | 6.30 | 3.39 | 0.335 | 0.391 | 0.357 | 0.392 | 409 |
| S6 | 22 | 7,842 | 36 | 7.45 | 4.28 | 0.181 | 0.286 | 0.278 | 0.314 | 479 |
| S7 | 15 | 4,848 | 17 | 6.53 | 4.81 | 0.335 | 0.391 | 0.357 | 0.392 | 0 |
| S8 | 17 | 4,857 | 16 | 6.06 | 3.89 | 0.326 | 0.385 | 0.340 | 0.388 | 0 |
| S9 | 17 | 3,717 | 21 | 7.28 | 4.81 | 0.389 | 0.434 | 0.395 | 0.429 | 0 |
| S10+ | 21 | 17,995 | 88 | 8.30 | 1.91 | 0.364 | 0.414 | 0.368 | 0.405 | 3,253 |
| F4* | −10 | 8,840 | 61 | 3.35 | 2.33 | 0.417 | 0.460 | 0.376 | 0.368 | 2,282 |
| W2* | 5 | 8,398 | 62 | 8.03 | 1.88 | 0.179 | 0.347 | 0.306 | 0.356 | 1,005 |
| W3* | 2 | 9,014 | 68 | 5.46 | 1.51 | 0.292 | 0.454 | 0.372 | 0.404 | 1,883 |
| W4* | −4 | 8,951 | 69 | 9.70 | 2.89 | 0.130 | 0.189 | 0.267 | 0.362 | 1,293 |
| W5* | 5 | 8,581 | 64 | 5.18 | 1.62 | 0.158 | 0.242 | 0.320 | 0.372 | 2,311 |
| S11 | 19 | 6,922 | 67 | 4.79 | 1.03 | 0.307 | 0.337 | 0.321 | 0.357 | 424 |
| S12 | 10 | 8,868 | 67 | 5.08 | 1.71 | 0.423 | 0.457 | 0.404 | 0.407 | 2,044 |
Notes: * Cold climate experiments, when T ≤ 5 °C; + Analysis concluded that experiment S10 was an outlier, with respect to the magnitude of Vi and was removed from further calculations; θi-1, θi-2, θi-3 and θi-4 refer to soil moisture measured 150, 300, 500 and 1,000 mm below the surface of the bioretention cell.
A correlation analysis was conducted to determine the associations between Vo and the other nine parameters. Figure 2 shows pair-by-pair scatter plots of Vo and these parameters. The figure illustrates that a single parameter cannot be used to describe all the variance in Vo. Correlation coefficients were calculated for each pair; Vo was significantly (with a p-value < 0.05) correlated with Vi (Pearson’s correlation coefficient r, was calculated to be 0.73) and ti (r = 0.64). Non-significant (with a p-value > 0.05) correlation was found between Vo and θi-2 (the soil moisture measured 300 mm below the surface, with r = 0.14). Based on this, the candidates for regressors for the MLR were reduced from the original nine to Vi, ti and θi-2. Figure 3 shows pair-by-pair scatter plots of these three parameters versus Vo; in this figure the values plotted are the logarithm of the original observations. The linear correlation between these variables is clearer after the transformation. It should be noted that for events F3 to Sp1, Sp3 and S7 to S9, Vo was less than 10 L (in fact, Vo was equal to zero for five of the seven cases, i.e., no effluent drained from the bioretention cell); these values were replaced with values of 1 L to facilitate the log-transformation. As such, experiments producing minimal effluent volume were considered to be of the same population (with the higher effluent volumes arising from a different population due to different generating mechanisms) with a very small variance. Thus, all effluent volumes less than 0.1% of the inlet volume, or 10 L, were assigned a value of 1 L.
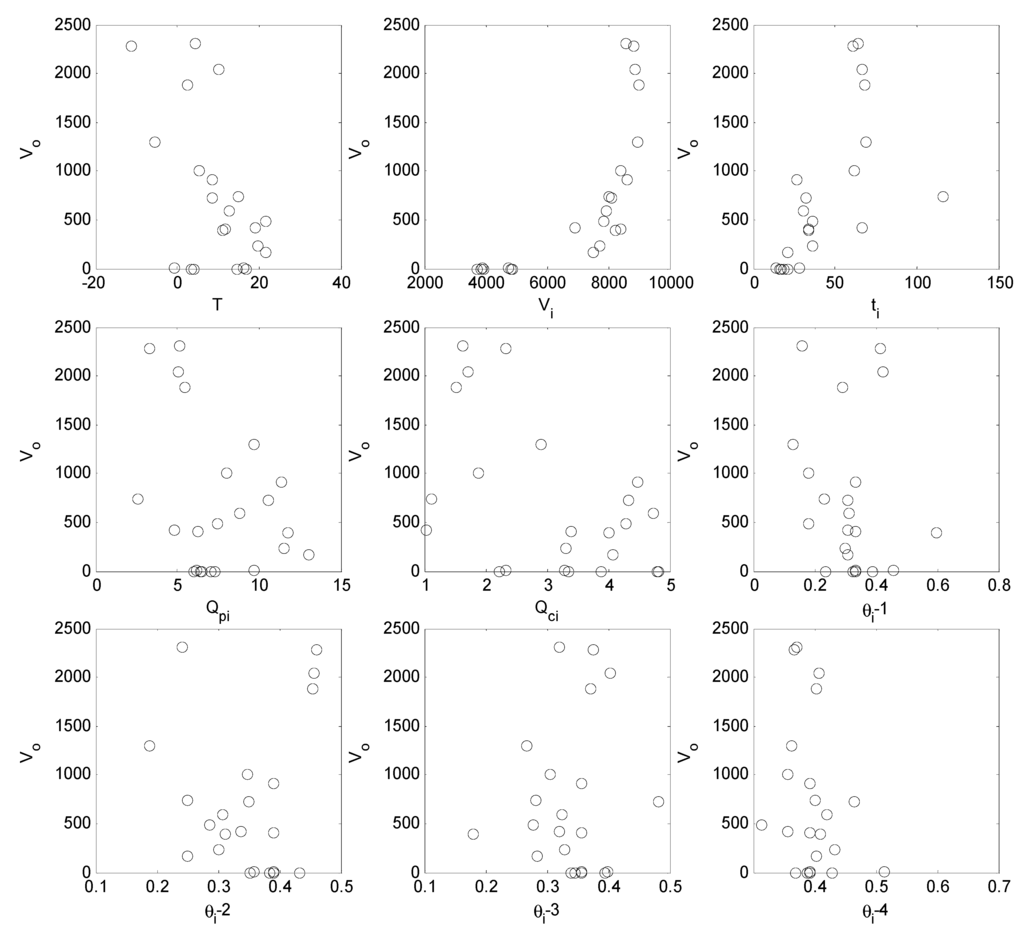
Figure 2.
Pair by pair scatter plots of Vo and the nine independent variables.
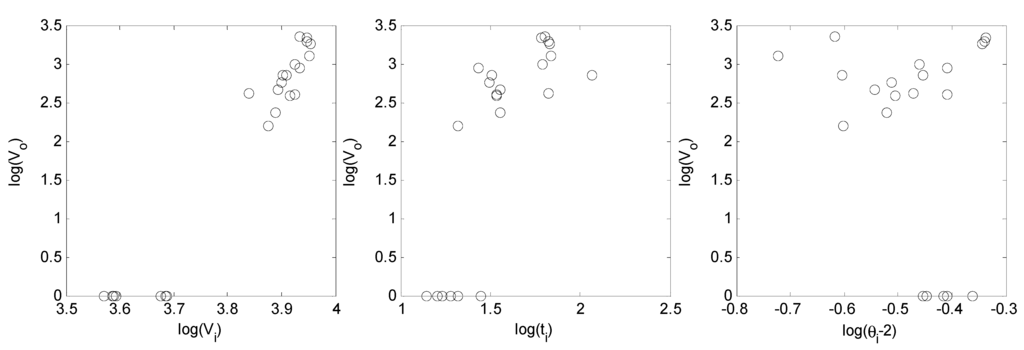
Figure 3.
Pair by pair scatter plots of log-transformed Vo, the two significantly correlated variables, Vi, and ti, and weakly correlated θi-2.
4. Model Construction and Validation
After the candidate regressors to predict Vo were identified, the data was divided for model construction and validation; 15 data points were used for model construction and 8 were used for validation. The data were split to ensure an equal representation of cold climate events in both sets as well as no significant deviation from the population mean. Table 2 summarizes statistics of the original and the divided data, and identifies the experiment ID that corresponds to each data set.

Table 2.
Summary of statistics of all experiments, construction and validation data sets for the three regressor candidates and Vo.
| Statistic | Vi (L) | ti (min) | θi-2 (m3/m3) | Vo (L) |
|---|---|---|---|---|
| All experiments | ||||
| Mean | 7034 | 42 | 0.347 | 691 |
| Standard Deviation | 1955 | 25 | 0.073 | 770 |
| Experiments used for construction: | ||||
| S1, S2, S3, F3, W1, SP2, SP3, S5, S7, S9, F4, W2, W3, S11, S12 | ||||
| Mean | 6893 | 44 | 0.371 | 673 |
| Standard Deviation | 2050 | 29 | 0.068 | 799 |
| Experiments used for validation: | ||||
| S4, F1, F2, SP1, S6, S8, W4, W5 | ||||
| Mean | 7299 | 38 | 0.303 | 724 |
| Standard Deviation | 1866 | 19 | 0.064 | 763 |
The construction data set was then used to construct six MLR models using Equation (2) with different combinations of the regressors. The models are summarized in Table 3, which lists the regressors used and the values of regression coefficients for each. Based on the error statistics for both the construction and validation sets (summarized in Table 3), Model 2 which used Vi and ti as the regressors, emerged as the best performing model. Model 2 outperformed the other models based on a collective evaluation of error statistics, rather than leading in a single category. An advantage of using Model 2 to predict bioretention performance is that these two variables are typically readily available from historical records, and thus can be easily used to predict bioretention cell performance, without the need for other detailed site characteristics (e.g., soil type or the degree of imperviousness in upstream catchment area).

Table 3.
Summary of six multiple linear regression (MLR) model results, including regressors, xi used, the constant term A, coefficients Bi, and error statistics for both model construction (top row) and model validation (bottom row).
| Model # | Input | A | B1 | B2 | B3 | R2 | RMSE | MAE | AICc | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | x1 | log(Vi) | −33.94 | 9.39 | - | - | 0.98 | 0.195 | 0.136 | −22.2 |
| 0.98 | 0.161 | 0.109 | −11.9 | |||||||
| 2 | x1 | log(Vi) | −30.60 | 8.14 | 0.91 | - | 0.99 | 0.128 | 0.086 | −28.5 |
| x2 | log(ti) | 0.98 | 0.178 | 0.145 | −11.1 | |||||
| 3 | x1 | log(Vi) | −33.74 | 9.42 | 0.71 | - | 0.98 | 0.191 | 0.123 | −22.5 |
| x2 | log(θi-2) | 0.98 | 0.203 | 0.144 | −10.1 | |||||
| 4 | x1 | log(Vi) | −30.34 | 8.16 | 0.93 | 0.77 | 0.99 | 0.120 | 0.079 | −29.5 |
| x2 | log(ti) | |||||||||
| x3 | log(θi-2) | 0.97 | 0.221 | 0.164 | −9.41 | |||||
| 5 | x1 | log(ti) | −4.46 | 4.08 | - | - | 0.58 | 0.901 | 0.616 | 0.744 |
| 0.68 | 0.721 | 0.553 | −0.050 | |||||||
| 6 | x1 | log(ti) | −4.25 | 4.09 | 0.53 | - | 0.59 | 0.888 | 0.600 | 0.526 |
| x2 | log(θi-2) | 0.65 | 0.754 | 0.600 | −0.408 | |||||
Figure 4 below shows a comparison of the observed and predicted data using Model 2. The figure shows that the model can accurately predict both the lower (~0 L) and higher end of the observed Vo. It is important to note this model was designed so that predicted Vo values between 0 L and 10 L were set equal to 1 L to be consistent with the rule used described in Section 3. This assumes that predicted low effluent volumes (between 0 L and 10 L) are essentially the same population as the case when no runoff drains from the bioretention cell. Figure 4 also shows that the observed and predicted values closely follow the 1:1 line, in both the construction and validation data sets.
The upper and lower limits of the input data for Model 2 are influenced by the data used to construct the model. Vi ranged from 3720 L to 9100 L, while ti ranged from 14 min to 116 min. The application of the model is approximately limited to these values. Furthermore, the limit of the predicted values of this model are bounded by Vo = 0 L (100% of inlet runoff captured) and by Vo ≤ Vi (maximum outlet runoff cannot be greater than inlet runoff). Therefore, it is important to ensure that the input variables used for prediction do not exceed the upper limits of Vi and ti.
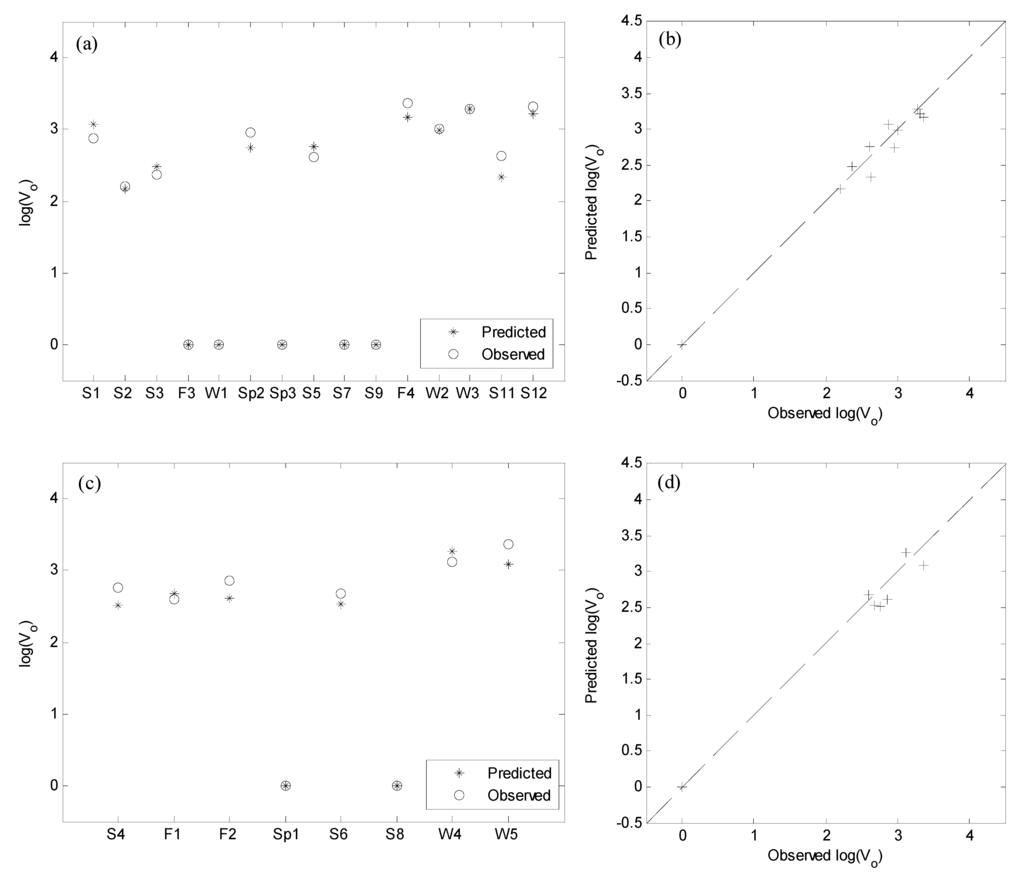
Figure 4.
Model 2 results: time series comparison of observed and predicted log(Vo) for (a) construction, and (c) validation data sets; and comparison of predicted and observed data sets for (b) construction and (d) validation data sets.
5. Model Application
One of the objectives of this research was to use an MLR model to create a design tool to assist in designing bioretention cells, for region-specific applications. To do this, historical precipitation depth and duration data for Calgary were used to predict Vo using the developed model. An important intermediate step in this process is the conversion of the precipitation depth to Vi. A method that accounts for the size of a bioretention cell and the size and degree of imperviousness of its upstream catchment is used and described below.
Historical precipitation and duration data was collected from Environment Canada [23]. The data, part of the Short Duration Rainfall Intensity-Duration-Frequency Data set, includes the maximum precipitation depth observed in Calgary (Calgary Int’l A, ID: 3031093) at nine event durations. The data from 1947 to 2007 (with six years data missing) includes event durations from 5 min to 24 h. Figure 5 summarizes the maximum precipitation depths at each interval for the 60 year period. Note that events with a duration of less than 10 min and more than 6 h were excluded in the figure and in the proceeding analysis, as this data does not meet the criteria for the MLR model outlined in Section 4.
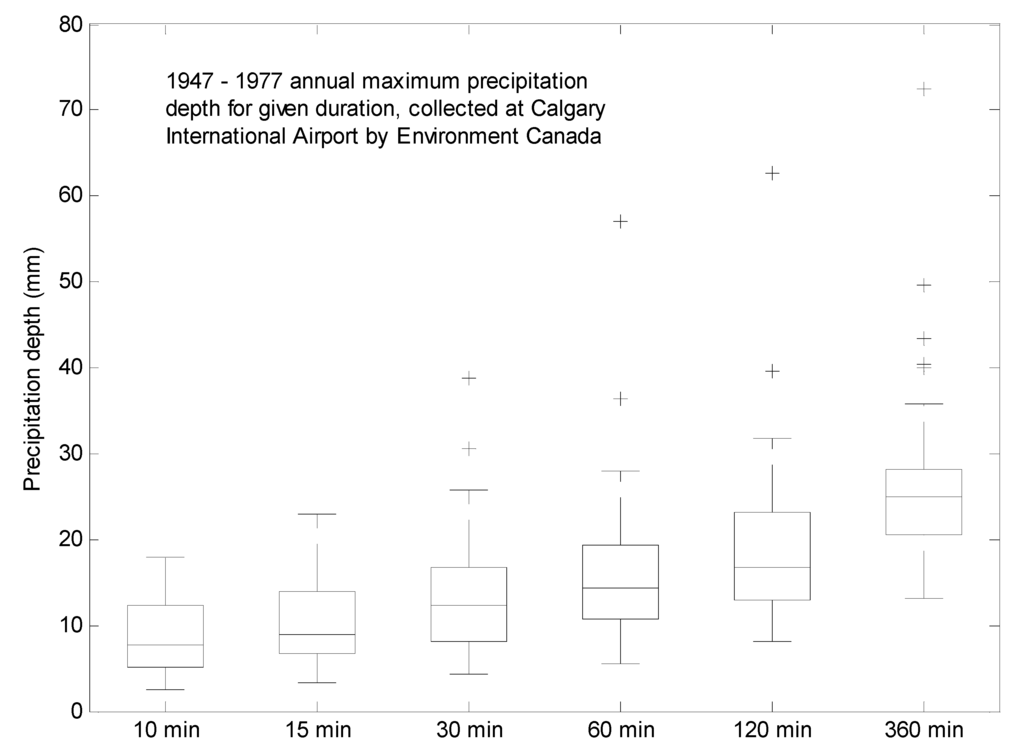
Figure 5.
Summary of historical maximum precipitation depth and corresponding duration for Calgary, collected from Environment Canada for the years 1947–2007.
The volume of runoff generated in a catchment from a given precipitation depth is a function of both the area and the degree of imperviousness of the catchment. Both these factors need to be included to calculate Vi from the historical precipitation depths. First, the area of the catchment has to be defined; typical guidelines recommend that a bioretention cell should be sized from 5% to 20% of the catchment area [24,25]. For this research, four different catchment sizes were used, where bioretention cell area (which was equal to 32 m2 for the experiments) was 5%, 10%, 15% and 20% of the total catchment area. The corresponding catchment areas are 160, 213.3, 320 and 640 m2.
Second, the amount of impervious area of the catchment area has to be defined. A typical residential area in Calgary will have an impervious area of 40% whereas in commercial areas or parking lots it can be as high as 100% (i.e., 100% of the catchment has impervious surfaces). For the application of the MLR model, four different levels of impervious areas were used: 100%, 80%, 60% and 40%, representing typical catchment characteristics found in urban areas. For example, for a 320 m2 catchment, if the amount of impervious area in a catchment is 40%, the area of the impervious surfaces is 128 m2.
A ratio known as the Impervious to Pervious Ratio (I/P) was introduced [15,26]. I/P is the ratio of the upstream impervious area (I) to the area of the pervious bioretention cell (P) that receives the runoff. Thus, continuing from the example above, the impervious fraction (I) is 128 m2, while the bioretention area (i.e., P) is 32 m2, meaning the I/P = 128 m2/32 m2 = 4. The I/P approach is useful since it can combine both factors: the total area, and the imperviousness of the catchment, into a single relationship which can be formulated as:
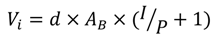 where Vi = volume of influent (m3); d = precipitation depth (m); AB = bioretention cell area (m2); and I/P = Impervious to Pervious Ratio. Equation (7) takes into account the runoff generated from the impervious area in the catchment and also the precipitation that occurs on the bioretention cell itself. A summary of the I/P calculated for the 16 combinations of catchment size and impervious areas are shown below in Table 4. Though Equation (7) shows that Vi is a function of the area of bioretention cell, AB, this is not explicitly necessary, and Equation (7) can be rewritten in a more general form as:
where Vi = volume of influent (m3); d = precipitation depth (m); AB = bioretention cell area (m2); and I/P = Impervious to Pervious Ratio. Equation (7) takes into account the runoff generated from the impervious area in the catchment and also the precipitation that occurs on the bioretention cell itself. A summary of the I/P calculated for the 16 combinations of catchment size and impervious areas are shown below in Table 4. Though Equation (7) shows that Vi is a function of the area of bioretention cell, AB, this is not explicitly necessary, and Equation (7) can be rewritten in a more general form as:
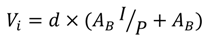
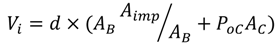
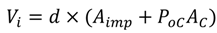 where Aimp is the impervious area of the catchment (m2); PoC is the size of the bioretention cell as a percentage of the total area of the catchment, e.g., between 5% and 20% (%); and AC is the area of the catchment that drains for the bioretention cell (m2).
where Aimp is the impervious area of the catchment (m2); PoC is the size of the bioretention cell as a percentage of the total area of the catchment, e.g., between 5% and 20% (%); and AC is the area of the catchment that drains for the bioretention cell (m2).
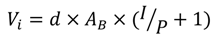
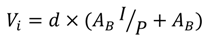
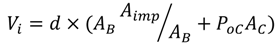
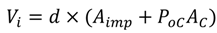

Table 4.
Summary of I/P values calculated for 16 different combinations of catchment size and percent impervious area in the catchment.
| Percent Impervious Area | Percentage of catchment size | |||
|---|---|---|---|---|
| 5% | 10% | 15% | 20% | |
| 100% | 20 | 10 | 6.7 | 5 |
| 80% | 16 | 8 | 5.3 | 4 |
| 60% | 12 | 6 | 4 | 3 |
| 40% | 8 | 4 | 2.7 | 2 |
After the I/P values were determined, Vi values were computed for the entire historical data set. Values of Vi that exceeded 9,100 L were excluded from further analysis. These values were then used as input in Model 2. The resultant Vo, determined from the model output, were used to calculate ΔV using Equation (1). The results are plotted in Figure 6 below. The figure shows predicted ΔV values versus the precipitation depth at six different duration intervals. Further, at each duration, the ΔV values are further categorized by I/P values. The solid black lines represent predicted values calculated by the model, whereas the dashed lines are extrapolation of the predicted trends.
To illustrate the functionality of the figure, take the following examples: given an event with a duration of 60 min and depth of 30 mm, the expected ΔV, for a bioretention cell sized to an I/P of 8, is approximately 90%. Conversely, if ΔV is known a priori, for example development regulations stipulate that 80% of runoff must be captured, the figure can be used to determine the necessary I/P ratio. This ratio can be used to calculate the size of the bioretention cell needed, assuming that the total catchment size is known, to meet the performance goals, for a given “design event”. For example, to capture 80% of runoff generated from a 25 mm, 120 min event, the figure shows that the necessary I/P of the cell has to be 8 or lower. However, if the “design event” is, for example, 25 mm over 60 min, the I/P value can be up to 10 to meet the runoff reduction goals. This increase can be achieved by either decreasing the size of the bioretention cell, relative to the size of the catchment, or more impervious surfaces can be added to the catchment, or a combination of both.
These examples show how Figure 6, which was developed using local experimental and historical data, can be used as a design tool to size bioretention cells for use in Calgary. Once the performance targets are known, different sizes can be explored using this figure, based on catchment characteristics and available area. Limitations of the tool include the maximum permissible Vi, and also the characteristics of the experimental bioretention cell used to generate the data.
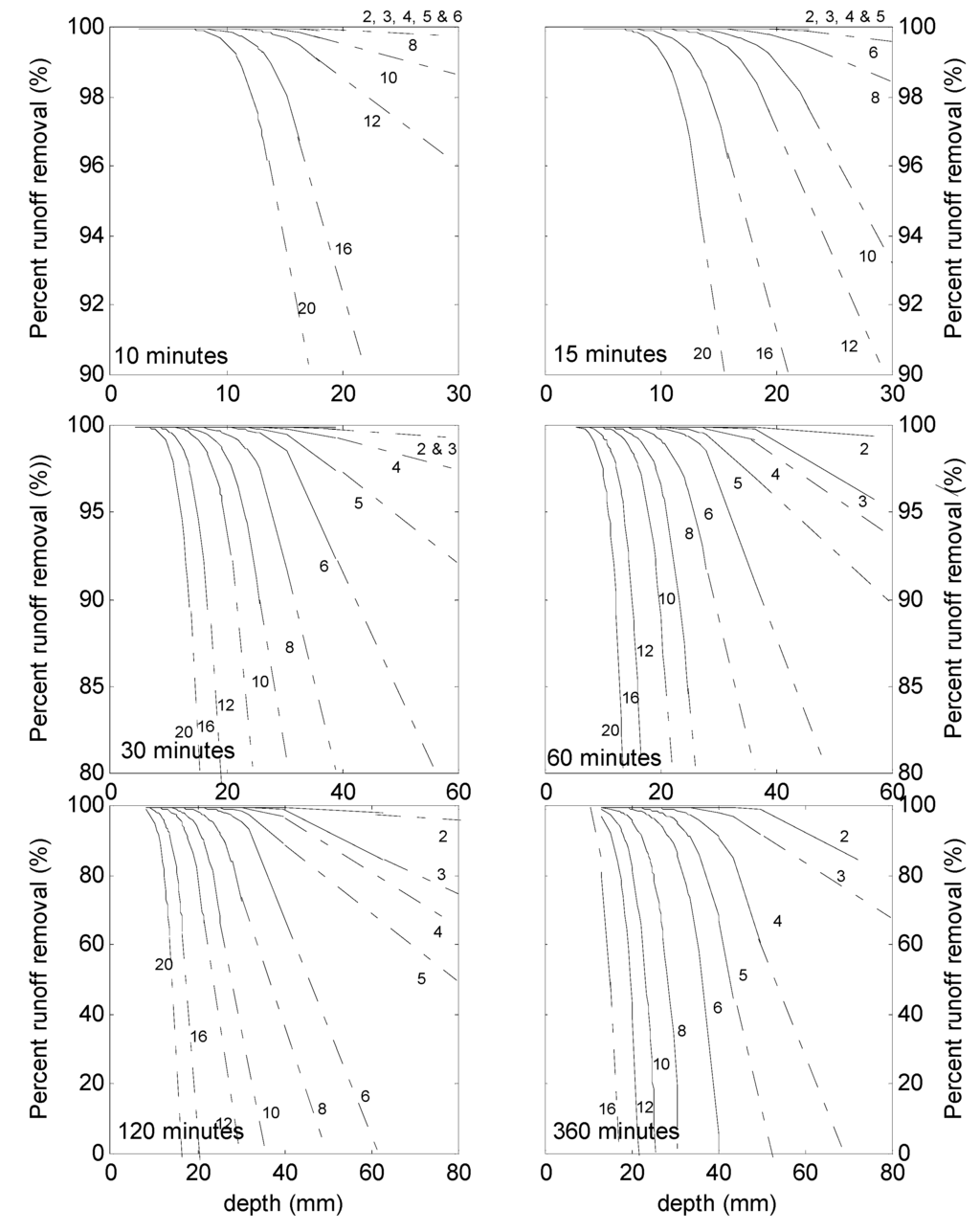
Figure 6.
Bioretention cell design guide for Calgary: runoff volume reduction as a function of precipitation depth, duration and I/P ratio.
6. Conclusions
LID is a sustainable water management strategy that aims to integrate water management into the urban fabric. As a site design strategy, LID can be considered more than just a stormwater control technology; it is a tool that promotes a full spectrum of ecosystem benefits. LID, including bioretention cells, are an emerging technique of addressing urban stormwater management: techniques that move away from traditional practices of expanding urban infrastructure, to providing engineering answers at the lot-level.
Bioretention cells are a proven technology to address urban runoff concerns in cold climate conditions, like that of Calgary, Canada [15,22]. This paper developed a novel method to create a design tool to assist in bioretention design, for Calgary, that takes region-specific design considerations into account. Currently, no guidelines or models exist to design bioretention cells for use in Calgary. In this paper, experimental data was used to create a data-driven model to predict bioretention cell performance, specifically the amount of runoff captured. This research shows that the volume of runoff draining to a bioretention cell and the duration of a precipitation event can be successfully used to predict bioretention cell performance. The model performed well with respect to R2 (0.991), RMSE (0.128), MAE (0.086) and AIC (−28.8). Historical precipitation depth and duration was then used to predict bioretention cell performance under 16 different catchment characteristics, including varied levels of imperviousness and catchment size. These results were collated and extrapolated to create a novel design tool, shown in Figure 6. This figure was then used to demonstrate how future bioretention cell design size can be estimated if performance targets are known. An example also showed how bioretention cell performance can be estimated if the size and characteristics of the catchment are known. Though the methodology was applied to only one case study, Calgary, it can be applied in any region where the relevant data is available.
Future research should focus on advancing this technique by expanding the scope of performance parameters. Other hydrological performance parameters, such as peak flow reduction, are closely correlated with the decrease in runoff volume, and a data-driven technique may be applied to predict these parameters as well. Similarly, future work should focus on predicting water quality performance by using the hydrological performance as an indicator.
Acknowledgments
The authors would like to thank the National Science and Engineering Resource Council of Canada for funding this research and A. Montgomery of Mechanical Engineering, University of Victoria for her assistance and suggestions. We would also like to thank three anonymous reviewers for their helpful suggestions to improve this article.
References
- Davis, A.P.; Traver, R.G.; Hunt, W.F.; Lee, R.; Brown, R.A.; Olszewski, J.M. Hydrologic performance of bioretention storm-water. J. Hydrol. Eng. 2012, 17, 604–614. [Google Scholar] [CrossRef]
- Marsalek, J.; Rochfort, Q.; Savic, D. Urban water as a part of integrated catchment management. In Frontiers in Urban Water Management, 1st; Maksimovic, C., Tejada-Guibert, J.A., Eds.; IWA Publishing: Cornwall, UK, 2001; pp. 37–84. [Google Scholar]
- Nordberg, M.; Thorolfsson, S.T. Low impact development and bioretention areas in cold climates. In Critical Transitions in Water and Environmental Resources Management, Proceedings of the World Water and Environmental Resources Congress, Salt Lake City, UT, USA, 27 June–1 July 2004; pp. 3409–3418.
- Hunt, W.F.; Smith, J.T.; Jadlocki, S.J.; Hathaway, J.M.; Eubanks, P.R. Pollutant removal and peak flow mitigation by a bioretention cell in urban Charlotte, N.C. J. Environ. Eng. 2008, 134, 403–408. [Google Scholar] [CrossRef]
- Environmental Protection AgencyOffice of WaterLow Impact Development (LID): A Literature Review; EPA Document # EPA-841-B-00-005, 1st ed; U.S. Environmental Protection Agency: Washington, DC, USA, 2000.
- Davis, A.P. Field performance of bioretention: Hydrology impacts. J. Hydrol. Eng. 2008, 13, 90–95. [Google Scholar] [CrossRef]
- Bioretention Manual; Environmental Services Division, Department of Environmental Resources, Prince George’s County, Maryland: Largo, MD, USA, 2007.
- Davis, A.P.; Shokouhian, M.; Himanshu, S.; Minami, C. Water quality improvement through bioretention media: Nitrogen and phosphorus removal. Water Environ. Res. 2006, 78, 284–293. [Google Scholar] [CrossRef]
- Hunt, W.F.; Jarrett, A.R.; Smith, J.T.; Sharkey, L.J. Evaluating bioretention hydrology and nutrient removal at three field sites in North Carolina. J. Irrig. Drain. Eng. 2006, 132, 600–608. [Google Scholar]
- Ermilio, J.R.; Traver, R.G. Hydrologic and pollutant removal performance of a bio-infiltration BMP. In Examining the Confluence of Environmental and Water Concerns, Proceedings of the 2006 World Environmental and Water Resources Congress, Omaha, NE, USA, 21–25 May 2006.
- Hatt, B.E.; Fletcher, T.D.; Deletic, A. Hydrologic and pollutant removal performance of biofiltration systems at the field scale. J. Hydrol. 2009, 365, 310–321. [Google Scholar] [CrossRef]
- Traver, R.G.; Prokop, M. Effectiveness of a bioinfiltration BMP. In Proceedings of the World Water and Environmental Resources Congress, Philadelphia, PA, USA, 23–26 June 2003.
- Roy-Poirier, A.; Champagne, P.; Filion, Y. Review of bioretention system research and design: Past, present and future. J. Environ. Eng. 2010, 136, 878–889. [Google Scholar] [CrossRef]
- University of North HampshireStormwater CentreBioretention System. In 2005 Data Report, 1st ed; University of New Hampshire: Durham, NH, USA, 2005.
- Khan, U.T.; Valeo, C.; Chu, A.; van Duin, B. Bioretention cell efficacy in cold climates: Part 1 Hydrologic performance. Can. J. Civil Eng. 2012, 39, 1210–1221. [Google Scholar] [CrossRef]
- Dussaillant, A.R.; Cozzetto, K.; Brander, K.; Potter, K.W. Green-ampt model of a rain garden and comparison to Richard’s equation model. In Sustainable Planning and Development; Beriatos, E., Brebbia, C.A., Coccossis, H., Kungolos, A., Eds.; WIT Press: Southampton, UK, 2003; pp. 891–900. [Google Scholar]
- Dussaillant, A.R.; Wu, C.H.; Potter, K.W. Richard’s equation model of a rain garden. J. Hydrol. Eng. 2004, 9, 219–225. [Google Scholar] [CrossRef]
- Heasom, W.; Traver, R.G.; Welker, A. Hydrologic modelling of a bioinfiltration best management practice. J. Am. Water Resour. Assoc. 2006, 42, 1329–1347. [Google Scholar] [CrossRef]
- Lucas, W.C. Design of integrated bioinfiltration-detention urban retrofits with continuous simulation methods. In Great Rivers, Proceedings of the 2009 World Environmental and Water Resources Congress, Kansas City, MO, USA; 2009. [Google Scholar]
- Poresky, A.L.; Palhegyi, G.E. Design and modeling of bioretention for hydro modification control: An assessment of alternative model representations. In LID for Urban Ecosystem and Habitat Protection, Proceedings of the 2008 International Low Impact Development Conference, Seattle, WA, USA; 2009. [Google Scholar]
- Solomatine, D.P.; Ostfeld, A. Data-driven modelling: Some past experiences and new approaches. J. Hydroinform. 2008, 10, 3–22. [Google Scholar] [CrossRef]
- Khan, U.T.; Valeo, C.; Chu, A.; van Duin, B. Bioretention cell efficacy in cold climates: Part 2 Water quality performance. Can. J. Civil Eng. 2012, 39, 1222–1233. [Google Scholar] [CrossRef]
- Intensity-Duration-Frequency (IDF) Files. Canada’s National Climate Data and Information Archive Web Page. Available online: http://www.climate.weatheroffice.gc.ca/prods_servs/index_e.html (accessed on 29 September 2012).
- Hunt, W.F.; Jarrett, A.R. Evaluating bioretention areas from two field sites in North Carolina. In Critical Transitions in Water and Environmental Resources Management, Proceedings of the World Water and Environmental Resources Congress, Salt Lake City, UT, USA, 2004; pp. 797–806.
- Lanarc Consultants Ltd.Kerr Wood Leidal AssociatesNgan, G. Infiltration rain garden. In Stormwater Source Control Guidelines 2005; Greater Vancouver Regional District: Vancouver, Canada, 2005; pp. 43–52. [Google Scholar]
- Brown, C. Characteristics of Solids Removal and Clogging Processes in Two Types of Permeable Pavement.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).