Profitability of Nitrification Inhibitors for Abatement of Nitrate Leaching on a Representative Dairy Farm in the Waikato Region of New Zealand
Abstract
:1. Introduction
2. Background
3. Model
3.1. Farm Model
3.2. Parameter Values
- The structure of the model is based on that of an optimisation model that was subject to peer review in [32].
- The ability of the model to report results that are consistent with real-world observations is presented in Section 4.1.
4. Results and Discussion
4.1. Base Output
| Variable | Without inhibitors | With inhibitors | Difference (%) |
|---|---|---|---|
| N inhibitor application (ha) | - | 97 | - |
| Farm profit ($ ha−1) | 1705 | 1744 | +2.3 |
| Stocking rate (cows ha−1) | 3.03 | 3.19 | +5.3 |
| Milk production (kg MS cow−1) | 311 | 311 | 0 |
| Milk production (kg MS ha−1) | 942 | 992 | +5.3 |
| N fertiliser application (kg ha−1) | 166 | 165 | −0.6 |
| N leaching (kg N ha−1) | 37 | 34 | −8.8 |
| Total feed (t DM ha−1) | 17.76 | 18.66 | +5.1 |
| Total grazed pasture (t DM ha−1) | 16.18 | 16.89 | +4.4 |
| Total grass silage (t DM ha−1) | 1.44 | 1.63 | +13.2 |
| Total maize silage (t DM ha−1) | 0.139 | 0.156 | +12.2 |
| Total energy per cow (MJ cow−1) | 54,749 | 54,518 | −0.4 |
| Lactation length (days) | 270 | 270 | 0 |
4.2. Value of Nitrification Inhibitors under Standard Assumptions
4.3. Impact of Milk Price on Nitrification Inhibitor Use
| Variable | Low milk price | High milk price | |
|---|---|---|---|
| Without and with inhibitors | Without inhibitors | With inhibitors | |
| N inhibitor application (ha) | - | - | 100 |
| Farm profit ($ ha−1) | 656 | 2,763 | 2,850 |
| Stocking rate (cows ha−1) | 2.99 | 3.08 | 3.24 |
| Milk production (kg MS cow−1) | 306 | 314 | 314 |
| N fertiliser application (kg ha−1) | 133 | 190 | 188 |
| N leaching (kg N ha−1) | 35 | 39 | 35 |
| Total feed (t DM ha−1) | 17.53 | 18.04 | 18.97 |
| Total grazed pasture (t DM ha−1) | 15.86 | 16.4 | 17.15 |
| Total grass silage (t DM ha−1) | 1.44 | 1.5 | 1.66 |
| Total maize silage (t DM ha−1) | 0.221 | 0.136 | 0.152 |
| Total energy per cow (MJ cow−1) | 54,642 | 54,573 | 54,573 |
| Lactation length (days) | 270 | 270 | 270 |
4.4. Impacts of Nitrification Inhibitors on Leaching Loads
| Decrease in nitrate leaching (%) | Abatement cost ($) a | Stocking rate (cows ha−1) | Milk production (kg MS cow−1) | Maize silage (kg ha−1) | N fertiliser (kg ha−1) |
|---|---|---|---|---|---|
| 0 | 0 | 3.03 | 311 | 139 | 166 |
| 10 | 64 | 3.01 | 309 | 175 | 152 |
| 20 | 146 | 2.99 | 306 | 215 | 135 |
| 30 | 335 | 2.86 | 305 | 223 | 108 |
| 40 | 479 | 2.7 | 309 | 154 | 103 |
| 50 | 624 | 2.53 | 314 | 75 | 100 |
| 60 | 950 | 2.22 | 316 | 0 | 85 |
| 70 | 1,444 | 1.78 | 316 | 0 | 68 |
| Decrease in nitrate leaching (%) | Abatement cost ($) a | Stocking rate (cows ha−1) | Milk production (kg MS cow−1) | Maize silage (kg ha−1) | N fertiliser (kg ha−1) | Nitri. inhibitor (ha) |
|---|---|---|---|---|---|---|
| 0 | 0 | 3.19 | 311 | 156 | 165 | 97 |
| 10 | 9 | 3.19 | 310 | 161 | 163 | 97 |
| 20 | 56 | 3.19 | 309 | 182 | 153 | 109 |
| 30 | 137 | 3.17 | 307 | 222 | 137 | 109 |
| 40 | 325 | 2.99 | 308 | 184 | 119 | 109 |
| 50 | 486 | 2.83 | 312 | 114 | 111 | 109 |
| 60 | 682 | 2.64 | 315 | 46 | 102 | 109 |
| 70 | 1,162 | 2.2 | 316 | 0 | 85 | 109 |
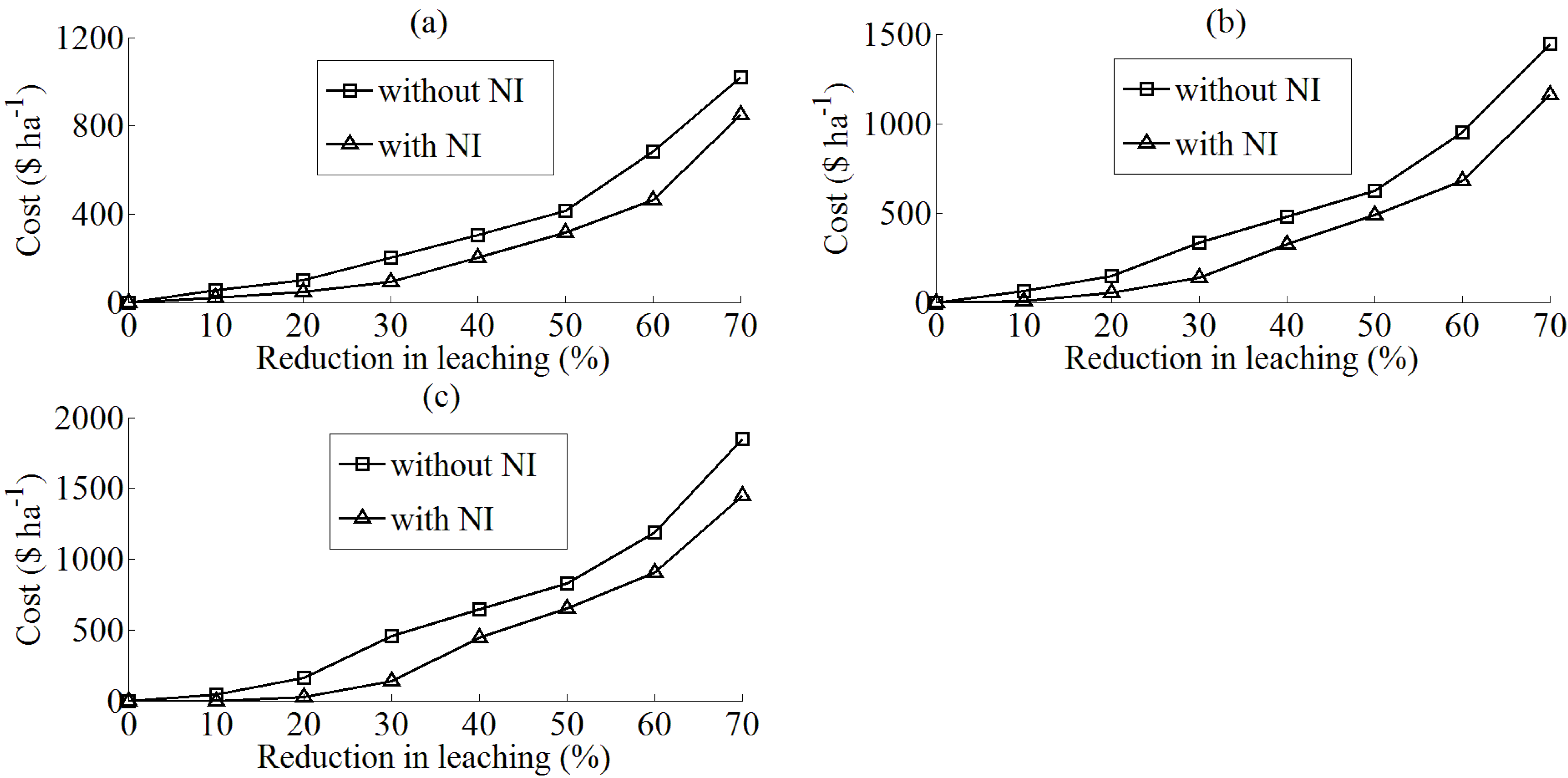
4.5. Use of Nitrification Inhibitors under Different Model Assumptions
| Parameter values | Key model output | |||||
|---|---|---|---|---|---|---|
| Milk price ($ t MS−1) | Cost of inhibitor ($ ha−1) | Increase in pasture (%) | Farm profit ($ ha−1) | Stocking rate (cows ha−1) | Inhibitor use (ha) | N leaching (kg N ha−1) |
| 4140 | 100 | 0 | 656 | 2.99 | 0 | 35 |
| 4140 | 100 | 5 | 656 | 2.99 | 0 | 35 |
| 4140 | 100 | 10 | 702 | 3.17 | 109 | 32 |
| 4140 | 100 | 15 | 777 | 3.26 | 109 | 32 |
| 4140 | 160 | 0 | 656 | 2.99 | 0 | 35 |
| 4140 | 160 | 5 | 656 | 2.99 | 0 | 35 |
| 4140 | 160 | 10 | 656 | 2.99 | 0 | 35 |
| 4140 | 160 | 15 | 717 | 3.26 | 109 | 32 |
| 4140 | 220 | 0 | 656 | 2.99 | 0 | 35 |
| 4140 | 220 | 5 | 656 | 2.99 | 0 | 35 |
| 4140 | 220 | 10 | 656 | 2.99 | 0 | 35 |
| 4140 | 220 | 15 | 664 | 3.21 | 81 | 33 |
| 5140 | 100 | 0 | 1705 | 3.03 | 0 | 37 |
| 5140 | 100 | 5 | 1711 | 3.11 | 97 | 33 |
| 5140 | 100 | 10 | 1801 | 3.20 | 109 | 33 |
| 5140 | 100 | 15 | 1904 | 3.29 | 109 | 34 |
| 5140 | 160 | 0 | 1705 | 3.03 | 0 | 37 |
| 5140 | 160 | 5 | 1705 | 3.03 | 0 | 37 |
| 5140 | 160 | 10 | 1744 | 3.19 | 97 | 34 |
| 5140 | 160 | 15 | 1844 | 3.29 | 109 | 34 |
| 5140 | 220 | 0 | 1705 | 3.03 | 0 | 37 |
| 5140 | 220 | 5 | 1705 | 3.03 | 0 | 37 |
| 5140 | 220 | 10 | 1705 | 3.05 | 109 | 37 |
| 5140 | 220 | 15 | 1784 | 3.29 | 109 | 34 |
| 6140 | 100 | 0 | 2764 | 3.08 | 0 | 39 |
| 6140 | 100 | 5 | 2790 | 3.17 | 100 | 34 |
| 6140 | 100 | 10 | 2890 | 3.23 | 109 | 34 |
| 6140 | 100 | 15 | 3027 | 3.32 | 109 | 35 |
| 6140 | 160 | 0 | 2764 | 3.08 | 0 | 39 |
| 6140 | 160 | 5 | 2764 | 3.08 | 0 | 39 |
| 6140 | 160 | 10 | 2850 | 3.24 | 100 | 35 |
| 6140 | 160 | 15 | 2967 | 3.32 | 109 | 35 |
| 6140 | 220 | 0 | 2764 | 3.08 | 0 | 39 |
| 6140 | 220 | 5 | 2764 | 3.08 | 0 | 39 |
| 6140 | 220 | 10 | 2799 | 3.24 | 96 | 35 |
| 6140 | 220 | 15 | 2907 | 3.32 | 109 | 35 |
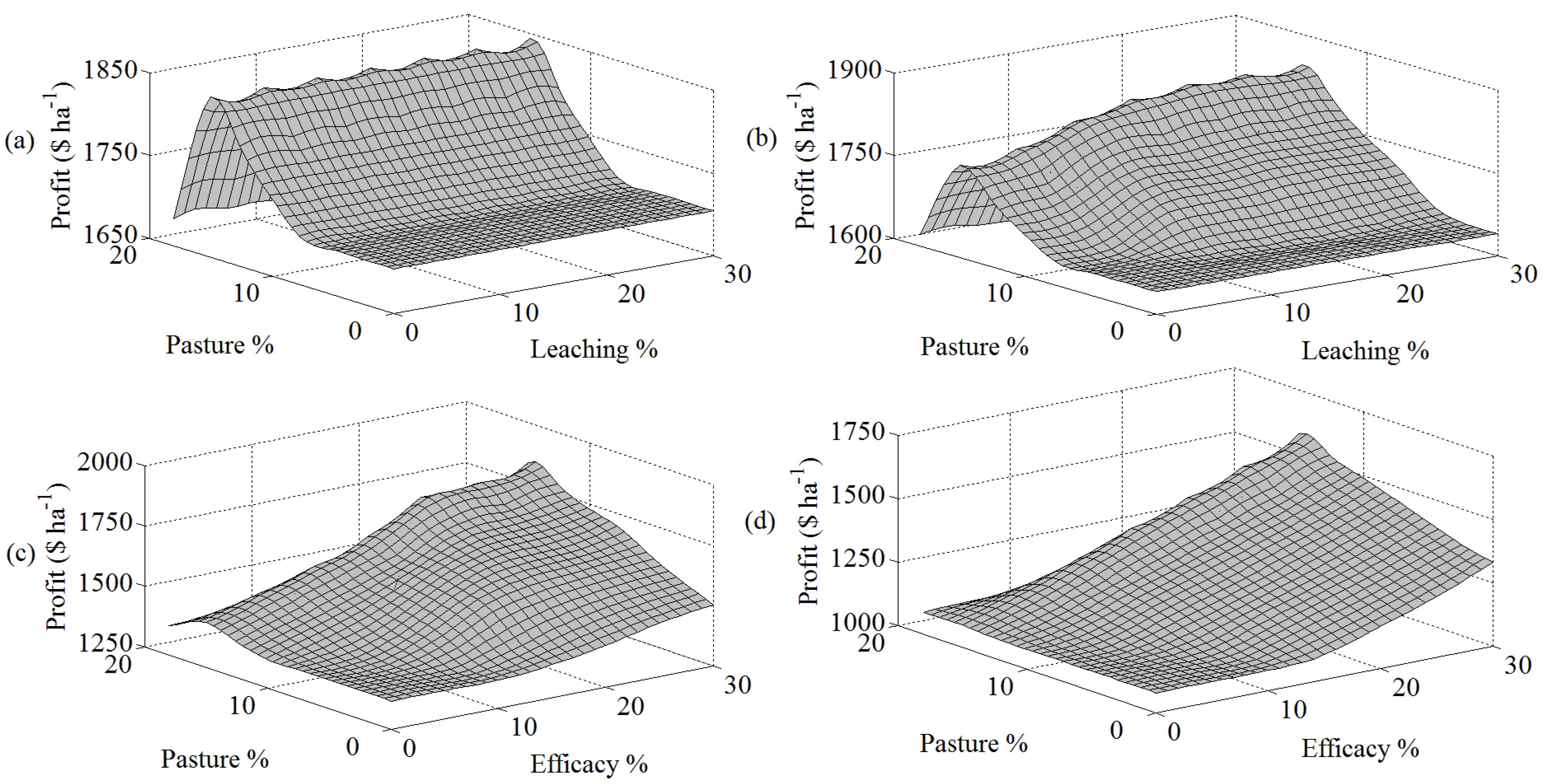
5. Conclusions
References
- Monaghan, R.M.; Hedley, M.J.; Di, H.J.; McDowell, R.W.; Cameron, K.C.; Ledgard, S.F. Nutrient management in New Zealand pastures—Recent developments and future issues. New Zeal. J. Agr. Res. 2007, 50, 181–201. [Google Scholar] [CrossRef]
- European Commission. Report on the Implementation of Council Directive 91/676/EEC; European Commission: Brussels, Belgium, 2010. [Google Scholar]
- Centre for European Agricultural Studies (CEAS). Environmental Impact of Dairy Production in the European Union; CEAS: Wye, England, 2000. [Google Scholar]
- Almasri, M.N.; Kaluarachchi, J.J. Implications of on-ground nitrogen loading and soil transformations on groundwater quality management. J. Am. Water Resour. Assoc. 2004, 40, 165–186. [Google Scholar] [CrossRef]
- Monaghan, R.M.; de Klein, C.A.M.; Muirhead, R.W. Prioritisation of farm scale remediation efforts for reducing losses of nutrients and faecal inhibitor organisms to waterways: A case study of New Zealand dairy farming. J. Environ. Manag. 2007, 87, 609–622. [Google Scholar] [CrossRef]
- Vant, W.; Petch, T. Nitrogen and Phosphorous in Our Freshwaters: Effects and Targets; Environment Waikato: Hamilton, New Zealand, 2006.
- Morgan, C.; Wolverton, A. Water quality trading in the United States: Trading programs and one-time offset agreements. Water Policy 2008, 10, 73–93. [Google Scholar] [CrossRef]
- Pannell, D.J. Public benefits, private benefits, and policy intervention for land-use change for environmental benefits. Land Econ. 2008, 84, 225–240. [Google Scholar]
- Ridley, A.; Pannell, D.J. The role of plants and plant-based R&D in managing dryland salinity in Australia. Aust. J. Exp. Agr. 2005, 45, 1341–1355. [Google Scholar] [CrossRef]
- Pannell, D.J.; Marshall, G.R.; Barr, N.; Curtis, A.; Vanclay, F.; Wilkinson, R. Understanding and promoting adoption of conservation practices by rural landholders. Aust. J. Exp. Agr. 2006, 46, 1407–1424. [Google Scholar] [CrossRef]
- Rabotyagov, S.S.; Jha, M.K.; Campbell, T. Impact of crop rotation on optimal selection of conservation practices for water quality protection. J. Soil Water Conserv. 2009, 65, 369–380. [Google Scholar] [CrossRef]
- Vigiak, O.; Newham, L.T.H.; Whitford, J.; Roberts, A.M.; Rattray, D.; Melland, A.R. Integrated farming systems and landscape processes to assess management impacts on suspended sediment loads. Environ. Model. Softw. 2011, 26, 144–162. [Google Scholar] [CrossRef]
- Kennedy, A.M.; Wilson, P.N. Reduced tillage systems as economical dust mitigation strategies. J. Soil Water Conserv. 2009, 64, 61–69. [Google Scholar] [CrossRef]
- Weersink, A.; Jeffrey, S.; Pannell, D.J. Farm-level modelling for bigger issues. Rev. Agr. Econ. 2002, 24, 123–140. [Google Scholar] [CrossRef]
- Bathgate, A.; Pannell, D.J. Economics of deep-rooted perennials in Southern Australia. Agr. Water Manag. 2002, 53, 117–132. [Google Scholar] [CrossRef]
- John, M.; Pannell, D.J.; Kingwell, R.S. Climate change and the economics of farm management in the face of land degradation: Dryland salinity in Western Australia. Can. J. Agr. Econ. 2005, 53, 443–459. [Google Scholar] [CrossRef]
- McConnell, K.E. An economic model of soil conservation. Am. J. Agr. Econ. 1983, 65, 83–89. [Google Scholar] [CrossRef]
- Di, H.J.; Cameron, K.C. The use of a nitrification inhibitor, dicyanamide (DCD), to reduce nitrate leaching from cow urine patches in a grazed dairy pasture under irrigation. Soil Use Manag. 2002, 18, 395–403. [Google Scholar] [CrossRef]
- Di, H.J.; Cameron, K.C. Reducing environmental impact of agriculture by using a fine particle suspension nitrification inhibitor to decrease nitrate leaching from grazed pastures. Agr. Ecosyst. Environ. 2005, 109, 202–212. [Google Scholar] [CrossRef]
- Monaghan, R.M. The BMP toolbox—Selecting the right best management practice for mitigating farming impacts on water quality. In Nutrient Management in a Rapidly Changing World; Currie, L.D., Yates, L.J., Eds.; Massey University: Palmerston North, New Zealand, 2009; pp. 328–334. [Google Scholar]
- Moir, J.; Cameron, K.C.; Di, H.J. Effects of the nitrification inhibitor dicyanamide on soil mineral N, pasture yield, nutrient uptake and pasture quality in a grazed pasture system. Soil Use Manag. 2007, 23, 111–120. [Google Scholar] [CrossRef]
- Doole, G.J. Indirect instruments for nonpoint pollution control with multiple, dissimilar agents. J. Agr. Econ. 2010, 61, 680–696. [Google Scholar] [CrossRef]
- Livestock Improvement Corporation (LIC). 2008/09 Dairy Statistics; Livestock Improvement Corporation: Hamilton, New Zealand, 2009. [Google Scholar]
- Environment Waikato (EW). The Condition of Rural Water and Soil in the Waikato Region: Risks and Opportunities; EW: Hamilton, New Zealand, 2008.
- Di, H.J.; Cameron, K.C. Treating grazed pasture soil with a nitrification inhibitor, eco-NTM, to decrease nitrate leaching in a deep sandy soil under spray irrigation—A lysimeter study. New Zeal. J. Agr. Res. 2004, 47, 351–361. [Google Scholar] [CrossRef]
- Meneer, J.C.; Sprosen, M.S.; Ledgard, S.F. Effect of timing and formulation of dicyandiamide (DCD) application on nitrate leaching and pasture production in a bay of plenty pastoral soil. New Zeal. J. Agr. Res. 2008, 51, 377–385. [Google Scholar] [CrossRef]
- Sprosen, M.S.; Ledgard, S.F.; Lindsey, S.B. Effect of rate and form of dicyandiamide application on nitrate leaching and pasture production from a volcanic ash soil in the Waikato. New Zeal. J. Agr. Res. 2009, 52, 47–55. [Google Scholar] [CrossRef]
- Di, H.J.; Cameron, K.C.; Shen, J.P.; He, J.Z.; Winefield, C.S. A lysimeter study of nitrate leaching from grazed grassland as affected by a nitrification inhibitor, dicyanamide, and relationships with ammonia oxidising bacteria and archaea. Soil Use Manag. 2010, 25, 454–461. [Google Scholar] [CrossRef]
- MacDonald, K.A.; Williams, Y.; Dobson-Hill, B. Effectiveness of a nitrification inhibitor (DCn) on a coastal Taranaki dairy farm. Proc. New Zeal. Grassland Assoc. 2010, 72, 147–152. [Google Scholar]
- Molloy, L. Soils in the New Zealand Landscape: The Living Mantle; New Zealand Society of Soil Science: Palmerston North, New Zealand, 1988. [Google Scholar]
- Ministry of Agriculture and Forestry (MAF). Pastoral Sector Overview; Ministry of Agriculture and Forestry: Wellington, New Zealand, 2009.
- McCall, D.G.; Clark, D.A.; Stachurski, L.J.; Penno, J.W.; Bryant, A.M.; Ridler, B.J. Optimised dairy grazing systems in the Northeast United States and New Zealand. I. Model description and evaluation. J. Dairy Sci. 1999, 82, 1795–1807. [Google Scholar] [CrossRef] [PubMed]
- Dexcel. Feed Information Sheet; Dexcel: Hamilton, New Zealand, 2008. [Google Scholar]
- Dexcel. Average Pasture Growth Data for New Zealand Dairy Farms; Dexcel: Hamilton, New Zealand, 2008. [Google Scholar]
- Moir, J.; Lincoln University: Lincoln, New Zealand. 2010. Personal communication.
- Wheeler, D.M.; Ledgard, S.F.; Monaghan, R.M.; McDowell, R.W.; de Klein, C.A.M. OVERSEER Nutrient Budget Model—What it is, what it does. In Implementing Sustainable Nutrient Management Strategies in Agriculture; Currie, L.D., Hanly, J.A., Eds.; Massey University: Palmerston North, New Zealand, 2006; pp. 231–236. [Google Scholar]
- Whistler, D.; White, K.J.; Wong, S.D.; Bates, D. SHAZAM Version 10 User’s Manual; Northwest Econometrics: Gibsons, FL, USA, 2004. [Google Scholar]
- Newham, L.T.H.; Letcher, R.A.; Jakeman, A.J.; Kobayashi, T. A framework for integrated hydrologic, sediment, and nutrient export modelling for catchment-scale management. Environ. Model. Softw. 2004, 19, 1029–1038. [Google Scholar] [CrossRef]
- Thomas, S.M.; Ledgard, S.F.; Francis, G.S. Improving estimates of nitrate leaching for quantifying New Zealand’s indirect nitrous oxide emissions. Nutr. Cycl. Agroecosys. 2005, 73, 213–226. [Google Scholar] [CrossRef]
- Wheeler, D.M.; van der Weerden, T.; Shepherd, M.A. Description of a cut and carry model within OVERSEER® nutrient budgets. In Farming’s Future—Minimising Footprints and Maximising Margins; Currie, L.D., Lindsay, C.L., Eds.; Massey University: Palmerston North, New Zealand, 2010; pp. 203–211. [Google Scholar]
- AgFirst Waikato. Upper Waikato Nutrient Efficiency Study; AgFirst Waikato: Hamilton, New Zealand, 2009. [Google Scholar]
- Financial Budget Manual 2008; Chaston, T. (Ed.) Lincoln University: Christchurch, New Zealand, 2008.
- DairyNZ. DairyNZ Economic Survey 2007–08; DairyNZ: Hamilton, New Zealand, 2009. [Google Scholar]
- Longhurst, R.D.; Smeaton, D.C. Improved Nutrient Efficiency through Integrated Catchment Management in Little Waipa and Waipapa; AgResearch: Hamilton, New Zealand, 2008. [Google Scholar]
- Brooke, A.; Kendrick, D.; Meeraus, A.; Raman, R. GAMS—A User’s Guide; GAMS Development Corporation: Washington, DC, USA, 2008. [Google Scholar]
- McCarl, B.A.; Apland, J.D. Validation of linear programming models. South. J. Agr. Econ. 1986, 68, 155–164. [Google Scholar]
- Doole, G.J.; Ramilan, T.; Pannell, D.J. Framework for evaluating management interventions for water quality improvement across multiple agents. Environ. Model. Softw. 2011, 26, 860–872. [Google Scholar] [CrossRef]
- Makowski, D.; Hendrix, E.M.T.; van Ittersum, M.K.; Rossing, W.A.H. A framework to study nearly optimal solutions of linear programming models developed for agricultural land use exploration. Ecol. Model. 2000, 131, 65–77. [Google Scholar] [CrossRef]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Doole, G.J.; Paragahawewa, U.H. Profitability of Nitrification Inhibitors for Abatement of Nitrate Leaching on a Representative Dairy Farm in the Waikato Region of New Zealand. Water 2011, 3, 1031-1049. https://doi.org/10.3390/w3041031
Doole GJ, Paragahawewa UH. Profitability of Nitrification Inhibitors for Abatement of Nitrate Leaching on a Representative Dairy Farm in the Waikato Region of New Zealand. Water. 2011; 3(4):1031-1049. https://doi.org/10.3390/w3041031
Chicago/Turabian StyleDoole, Graeme J., and Upa H. Paragahawewa. 2011. "Profitability of Nitrification Inhibitors for Abatement of Nitrate Leaching on a Representative Dairy Farm in the Waikato Region of New Zealand" Water 3, no. 4: 1031-1049. https://doi.org/10.3390/w3041031
APA StyleDoole, G. J., & Paragahawewa, U. H. (2011). Profitability of Nitrification Inhibitors for Abatement of Nitrate Leaching on a Representative Dairy Farm in the Waikato Region of New Zealand. Water, 3(4), 1031-1049. https://doi.org/10.3390/w3041031




