Wind–Wave and Swell Separation and Typhoon Wave Responses on the Dafeng Shelf (Northern Jiangsu)

Abstract

This study analyzes wave data from Typhoons Hinnamnor and Muifa in 2022, improves the traditional one-dimensional wind–wave and swell separation method (PM method), and proposes a wind–wave and swell separation strategy suitable for the Dafeng sea area during typhoon events. Combining this with the WH enables high-precision separation of wind–wave and swell. A numerical model of MIKE21 SW waves was established based on the superposition of the Holland typhoon wind field and the ERA5 background wind field. Furthermore, the study conducts controlled variable experiments through numerical simulations to systematically quantify the differential effects of the maximum wind speed radius (RMW), translation speed, and track geometry. The mathematical model in this study couples MIKE 21 SW and MIKE 21 FM, importing hydrodynamic conditions through FM as key variables into the SW model. This enables real-time data exchange during the computational process, thereby yielding results that better align with physical reality. The results from factorial sensitivity experiments demonstrate that the significant wave height and average period of offshore waves, far from the typhoons, significantly increase with the expansion of the maximum wind speed radius, with wave heights at offshore points reaching a maximum of 7.5 m. Specifically, when the RMW increased by 50%, the wave height increased by 2.5 m. The wave characteristics of landing typhoons are more influenced by terrain effects and the location of typhoon landfall. Additionally, changes in typhoon translation speed lead to a first increase and then a decrease in significant wave height. The typhoon’s path significantly affects the propagation direction and energy distribution of waves. In the Dafeng area, distant typhoons often generate long-period swells, which continuously exert high loads on actual engineering foundations. These findings inform early warning systems and the design of shelf-aware port and coastal infrastructure in northern Jiangsu and similar regions.

1. Introduction

With continuous societal development, increasing attention has been focused on the exploitation and utilization of ocean resources. However, the development of these resources faces complex environmental risks, particularly the impacts of extreme weather events. During a typhoon’s impact, the wave field is mainly composed of wind-generated waves directly caused by the typhoon’s wind force, and low-frequency swells that generated during wave propagation. Among these, wind waves are fluctuations induced by the direct wind forcing on the water’s surface, characterized by high frequency, short wavelength, and steepness. In contrast, swells are waves formed after the wind forcing ceases or when there are abrupt changes in wind direction and speed, resulting from the energy transfer and attenuation of wind waves. Swells are typically characterized by low-frequency and long-wavelength and have a gentle slope. Therefore, studying the characteristics of wind waves and swells in typhoon conditions is crucial for the disaster prevention and mitigation in typhoon-prone areas.

A numerical wave model of the Dafeng coastal zone was constructed using the MIKE 21 SW module. Based on the predefined model parameters, the variations in significant wave height, wave period, and mean wave direction under different typhoon forcing conditions were examined systematically. This allowed for a systematic analysis of the wave characteristics in the study area during typhoon events.

Currently, wave–swell separation methods can be broadly classified into two categories. The first category is based on wave characteristic parameters such as wave height, period, and wave age [1,2]. The second category is based on wave spectra. Depending on the dimensionality of the wave spectrum, spectral-based separation methods can be further divided into two-dimensional (2D) and one-dimensional (1D) spectral approaches.

The 2D spectral method, first proposed by Gerling et al. [3], distinguishes wind sea and swell components by simultaneously analyzing the wave directional spectrum and wind vector information, based on the fundamental physics of wind-to-wave energy transfer [4]. The 1D spectral method, on the other hand, relies on the one-dimensional frequency spectrum to perform the separation. Numerous studies on wind sea spectra have demonstrated that the peak frequency of the wind sea spectrum is proportional to the separation frequency between wind sea and swell. In 1984, Earle [5], based on the fully developed wind sea spectrum model (Pierson–Moskowitz, PM spectrum), proposed an empirical formula for the separation frequency as a function of wind speed and gravitational acceleration, expressed as follows:

$$f_s=0.8f_{PM}$$

(1)

where f_PM is the peak frequency of the Pierson–Moskowitz (PM) spectrum, defined as:

$$f_{PM}=0.13{\displaystyle \frac{g}{U_{10}}}$$

(2)

In the above equations, U₁₀ represents the wind speed at a height of 10 m above the sea surface, and g denotes the acceleration due to gravity.

The portion of the spectrum with frequencies higher than the separation frequency corresponds to the wind sea component, while the portion with frequencies lower than the separation frequency corresponds to the swell component. As a simple and effective one-dimensional wind–wave and swell separation method, the PM approach [6] requires almost no use of wave spectral parameters. Portilla and Goda [7,8] proposed a method based on the overshoot phenomenon, referred to as the Overshoot Parameter (OP) method, whose criterion is based on dividing the spectral peak of the observed wave system (i.e., the peak value of the measured wave spectrum) by the spectral peak of a fully developed PM spectrum corresponding to the same peak frequency. This ratio is defined as a parameter and can be expressed as:

$$\lambda ={\displaystyle \frac{S\left(f_m\right)}{S_{PM}\left(f_m\right)}}$$

(3)

where f_m is the peak frequency in the wave spectrum; S(f_m) denotes the spectral peak value of the wave system at the frequency f_m; and S_PM(f_m) represents the spectral peak value of the Pierson–Moskowitz (PM) spectrum at the same frequency f_m. If λ > 1, the wave system is classified as wind sea; otherwise, it is classified as swell.This method does not rely on the availability of wind speed or wind direction information, making it easy to implement for operational applications.

Liu et al. [9] investigated the WH method and its modified version. Extensive practical applications have shown that the modified WH method performs well in wind–wave and swell separation under conditions of low or rapidly decreasing wind speeds. However, when the significant wave height is less than 0.5 m, the modified WH method becomes more sensitive to variations in wind speed. Kim and Chen et al. [10,11] proposed a two-dimensional spectral decoupling scheme based on S-band Doppler radar ocean wave directional spectrum inversion technology. Under conditions lacking real-time wind field data, the method achieved separation accuracy comparable to that of wind-driven models by introducing wave age parameterization constraints.

Wave numerical simulation is a method that uses wave models to simulate and forecast wave fields. At present, commonly used wave models include the third-generation model WAVEWATCH III (WW3), as well as nearshore wave models such as SWAN and MIKE 21 SW. With the development of wave numerical models and the advancement of computational techniques, the study of typhoon swell propagation characteristics has gradually shifted toward numerical simulation. Nie et al. [12] applied the Holland model in combination with ERA background wind field data to construct simulated wind fields for the dual typhoon events “Bolaven” and “Tembin.” Based on these wind fields, numerical experiments of typhoon-induced waves were carried out using the MIKE 21 SW module. Liu et al. [13] simulated and analyzed global wave conditions over a ten-year period and pointed out that oceanic swells are primarily generated by the Southern Ocean storm belt and subsequently propagate into other ocean basins.

Currently, research on the sedimentary dynamics of the Dafeng tidal flats has revealed their complexity, yet the data and models supporting in-depth studies of storm-surge remain inadequate. The Dafeng coast experiences strong tidal dynamics and intense suspended sediment transport. Current research often focuses on the individual effects of tides, tidal currents, or wind waves. There is a lack of detailed observation and mechanistic studies on how the complex non-linear interactions between wind waves and tidal currents affect the local hydrodynamic environment, sediment transport, and geomorphological evolution. The novelty of this study lies in the construction of a high-fidelity numerical model that simulates wave evolution characteristics under multiple typhoon track scenarios, thereby systematically quantifying the mechanisms through which various typhoon factors influence energy transfer and distribution within the wave field of the Dafeng coastal area.

In summary, existing studies have predominantly focused on typhoon intensity, while the investigation of wave characteristics in this region—particularly those related to long-period waves—remains insufficient. In this study, a combined wind–wave and swell separation strategy is proposed, which integrates the improved PM method with the WH method. The resulting separation compensates for the accuracy limitations that arise when applying one-dimensional (1D) methods in the absence of the necessary conditions for two-dimensional (2D) spectral separation of wind sea and swell components. In terms of numerical simulation, this study focuses on the differentiated impacts of key typhoon parameters, including the radius of maximum wind speed, translation speed, and track. The objective is to systematically quantify the influence mechanisms of these typhoon factors on wave energy transfer and distribution in the Dafeng sea area. By simulating the evolution of wave spectra under multiple typhoon path scenarios, the study reveals the spatiotemporal response characteristics of typhoon-induced waves in the specific region. The results not only enhance the understanding of the physical mechanisms of typhoon-generated waves but also provide a scientific basis for developing targeted disaster prevention and mitigation strategies to effectively reduce typhoon-induced losses in the Dafeng sea area.

The remainder of this paper is organized as follows. Section 2 introduces the improved wind–wave and swell separation method and the verification of the numerical model. Section 3 presents the configuration of differentiated typhoon parameters and analyzes the corresponding variations in swell characteristics and wave spectral features. Finally, Section 4 provides the conclusions and offers recommendations for future research.

2. Materials and Methods

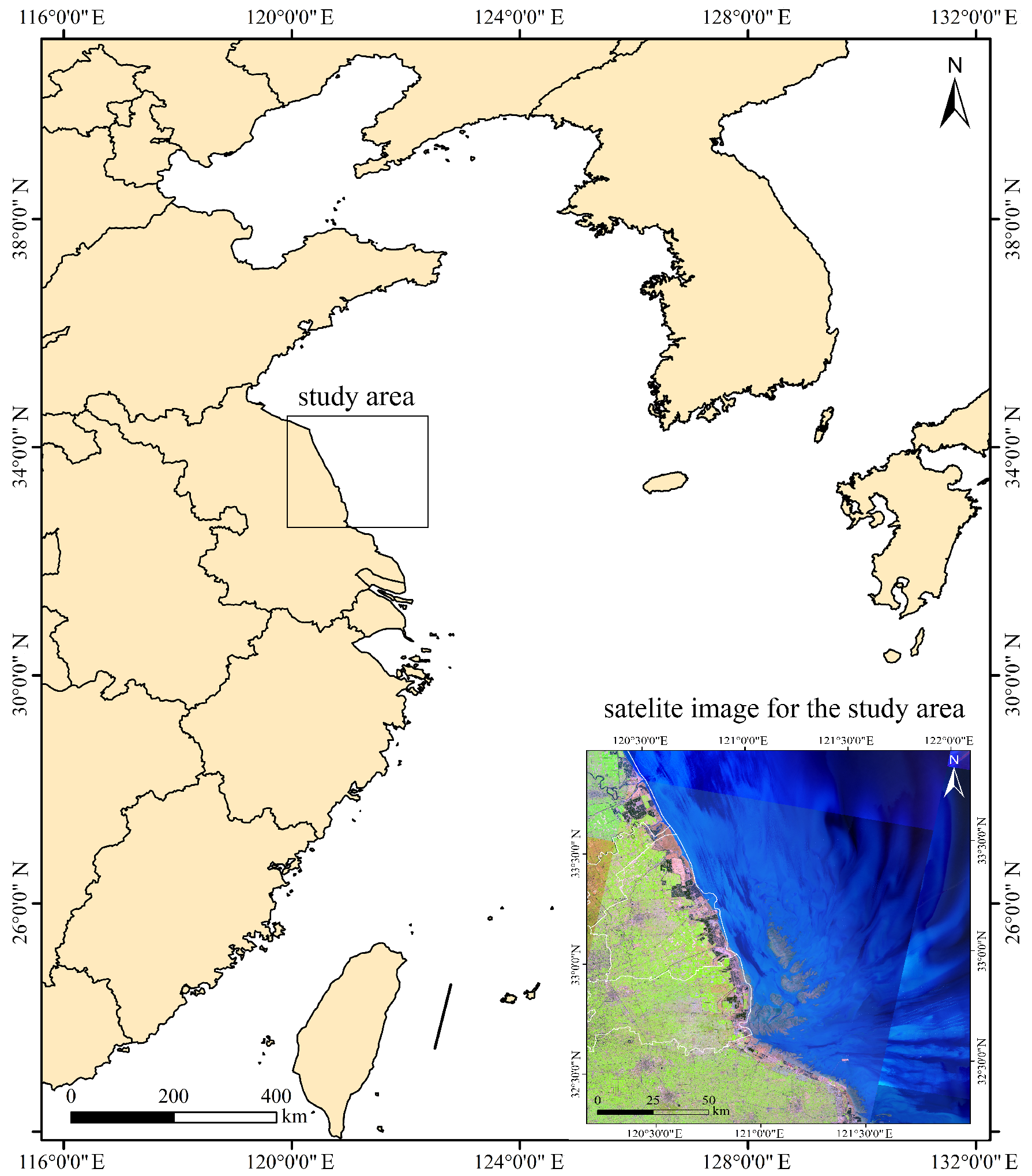
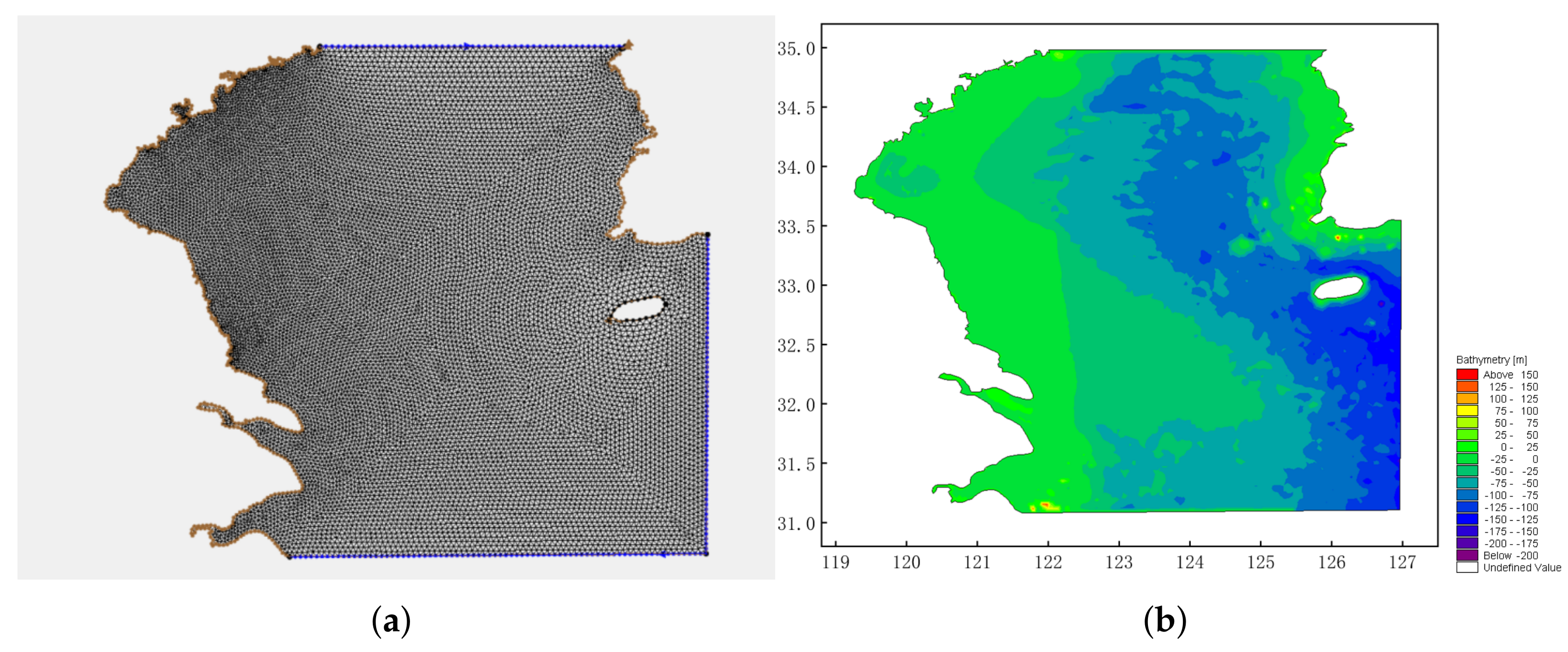
2.1. Study Area and Observations

The continental shelf in the Yancheng Dafeng area, part of the broad South Yellow Sea shelf, is characterized by an extremely gentle gradient and shallow waters (typically ranging from 10 to 20 m deep), featuring a unique radial sand ridge system. Concurrently, this marine area is dominated by a robust regular semidiurnal tide, exhibiting a medium to large tidal range (averaging 2.5–4.0 m) and associated strong reversing tidal currents. The combination of this gentle, shallow topography and the powerful tidal regime creates a highly dynamic and complex sediment dynamic environment, marked by intense wave-tide-sediment interactions. Observations include data from an offshore buoy (OSB-W7) and a nearshore AWAC. Figure 1 shows the study area and the locations of the buoy (OSB-W7) and AWAC sites. Shoreline data were obtained from the GSHHS (Global Self-consistent, Hierarchical, High-resolution Shoreline) fractal-optimized coastline database. The wave reanalysis data were derived from the WW3 (WaveWatch III) model, with a computational domain covering the area from 5° S to 50° N and 99° E to 155° E, at a spatial resolution of 0.1° × 0.1°.

Wave measurement Site 1 used an OSB-W7 wave buoy system developed by Zhongshan Tanhai Co., Ltd. (Zhongshan, China), deployed at coordinates 121.12° E and 33.51° N. The depth of the water at this site exceeds 20 m, with continuous 24-h observations conducted daily from September 2022 to October 2023. Measurements were taken hourly, with each record containing no fewer than 100 individual wave events, including parameters such as wave height and period.

Wave measurement Site 2 used an AWAC-600 kHz system manufactured by Nortek (Vestby, Norway), deployed at coordinates 121.26° E and 33.75° N.

Table 1. Locations of wave measurement sites.

Parameter	OSB-W7	AWAC
Longitude	121.12 E	121.26 E
Latitude	33.51 N	33.75 N

lists the specific locations of both measurement sites.

Typhoon parameter data for Typhoons Muifa, Hinnamnor, and Bavi were obtained from the China Meteorological Administration “http://typhoon.nmc.cn/ (accessed on 15 September 2024)”.

2.2. Validation and Experiments

The MIKE 21 SW model results were validated against in situ measurements. The validation method involved a correlation analysis between the simulated and observed significant wave heights and significant wave periods. The measurement sites were located at 33°44.8′ N, 121°15.6′ E and 33°30.6′ N, 121°6.93′ E, with a uniform water depth of 7 m. During the wind–wave and swell separation process using the MIKE 21 SW model, a dynamic critical frequency approach was adopted, with 0.59 Hz was defined as the maximum critical frequency for separation.

The root-mean-square (RMSE) was calculated using the standard formula, and the correlation coefficient was determined based on the Pearson correlation method. The data were obtained from wave buoy and AWAC field measurements, as well as MIKE 21 SW simulation outputs, covering the period from 1 September 2022 to 30 September 2022 in the Dafeng sea area.

2.3. Wind–Wave and Swell Separation

We applied a practical 1D separation strategy based on a classical PM split frequency and an improved WH split, with parameters calibrated against 2D partitions. A commonly used one-dimensional (1D) method is the PM method. The PM method (wind speed method) requires only the wind speed U measured at a height of 10 m above the sea surface to determine the separation frequency f_s. The empirical formula is given in Equation (1). f_PM is the peak frequency of the PM spectrum, and its expression is given in Equation (2).

According to previous studies and engineering practice, this method tends to overestimate the wind wave component. The target of this study is the swell propagating from offshore to nearshore during typhoon events, under which the sea surface wind speed is generally higher than under normal conditions. Therefore, a proportional amplification of the separation frequency in the PM method is considered. By multiplying the separation frequency f_s by different amplification factors, it was found that when using 1.1 f_s as the modified separation frequency, the root mean square (RMSE) between the separation result and the two-dimensional (2D) method was minimized. Hence, this study adopts 1.1 f_s as the improved PM method for subsequent analysis. Using the given wave spectrum and the corresponding separation frequency, the representative wave height and period of wind waves and swell can be calculated separately. The significant wave height H_S and mean wave period T_S of swell can be expressed as:

$$H_S=4\sqrt{m_{0s}},T_Z=\sqrt{{\displaystyle \frac{m_{0s}}{m_{2s}}}}$$

(4)

where m_0s and m_2s are obtained from:

$$m_{ns}={\int }_{f_s}^{f_{\max }}{f}^{n}S\left(f\right)df,n=0,2$$

(5)

In this study, four commonly used one-dimensional (1D) wind-wave and swell separation methods were employed: the PM method, the improved PM method, the WH method, and the spectral integration method. Each set of results was compared with the separation results obtained by the two-dimensional (2D) method, and both the correlation coefficient (CORR) and root mean square (RMSE) were analyzed to evaluate the performance of each 1D separation method.

The correlation coefficient (CORR) is a statistical indicator used to measure the strength and the direction of the linear relationship between two variables. The Pearson correlation coefficient, one of the most widely used measures of correlation, quantifies the degree of linear association between two continuous variables. Its calculation formula is given by:

$$r={\displaystyle \frac{\sum XY-\frac{\sum X\sum Y}{N}}{\sqrt{\left(\sum X^2-\frac{{(\sum X)}^2}{N}\right)\left(\sum Y^2-\frac{{(\sum Y)}^2}{N}\right)}}}$$

(6)

where r denotes the Pearson correlation coefficient; X represents the significant wave height of swell separated by the 1D method; Y represents the significant wave height of swell separated by the 2D method; and N is the number of data samples. The larger the absolute value of the correlation coefficient, indicating higher accuracy in distinguishing between wind waves and swell. The dataset utilized in this study comprises over 200,000 measured data points of original wave height and wave period, supplemented by simulated wave data with a temporal resolution of 30-s intervals. The sample size of simulated data exceeds 10,000 instances, varying in accordance with the total simulation duration. The root mean square (RMSE) is calculated as follows:

$$RMSE=\sqrt{{\displaystyle \frac{1}{m}}\sum _{i=1}^m{(X_i-Y_i)}^2}$$

(7)

where X_i and Y_i denote the paired values obtained from the 1D and 2D separation methods, respectively, and m represents the total number of data samples.

2.4. Wave Model

In this study, a two-dimensional (2D) refined computational mesh of the Yellow Sea was constructed using the Surface-water Modeling System (SMS), as shown in Figure 2. The open boundary extends from a coastal point at 121.65° E, 30.01° N to a point on the Korean Peninsula at 127.97° E, 34.72° N. Regarding grid resolution, the boundary resolution in the Dafeng sea area is 0.002 km. The entire computational domain consists of 13,480 nodes and 26,262 triangular elements.

In this study, the global topographic reference system ETOPO, jointly developed by the National Geophysical Data Center (NGDC) and the National Oceanic and Atmospheric Administration (NOAA), was adopted. A dynamic data fusion strategy was employed to spatially interpolate and couple the high-precision topographic framework of ETOPO 2022 with locally measured bathymetric data. The resulting bathymetric distribution is shown in Figure 2.

In the model setup, the driving wind field was generated using the Holland (1980) [14] parametric typhoon wind field model with an axisymmetric wind structure. The parameterizations of whitecapping, quadruplet interactions, bottom friction, and depth-induced breaking were all kept as the model default settings.

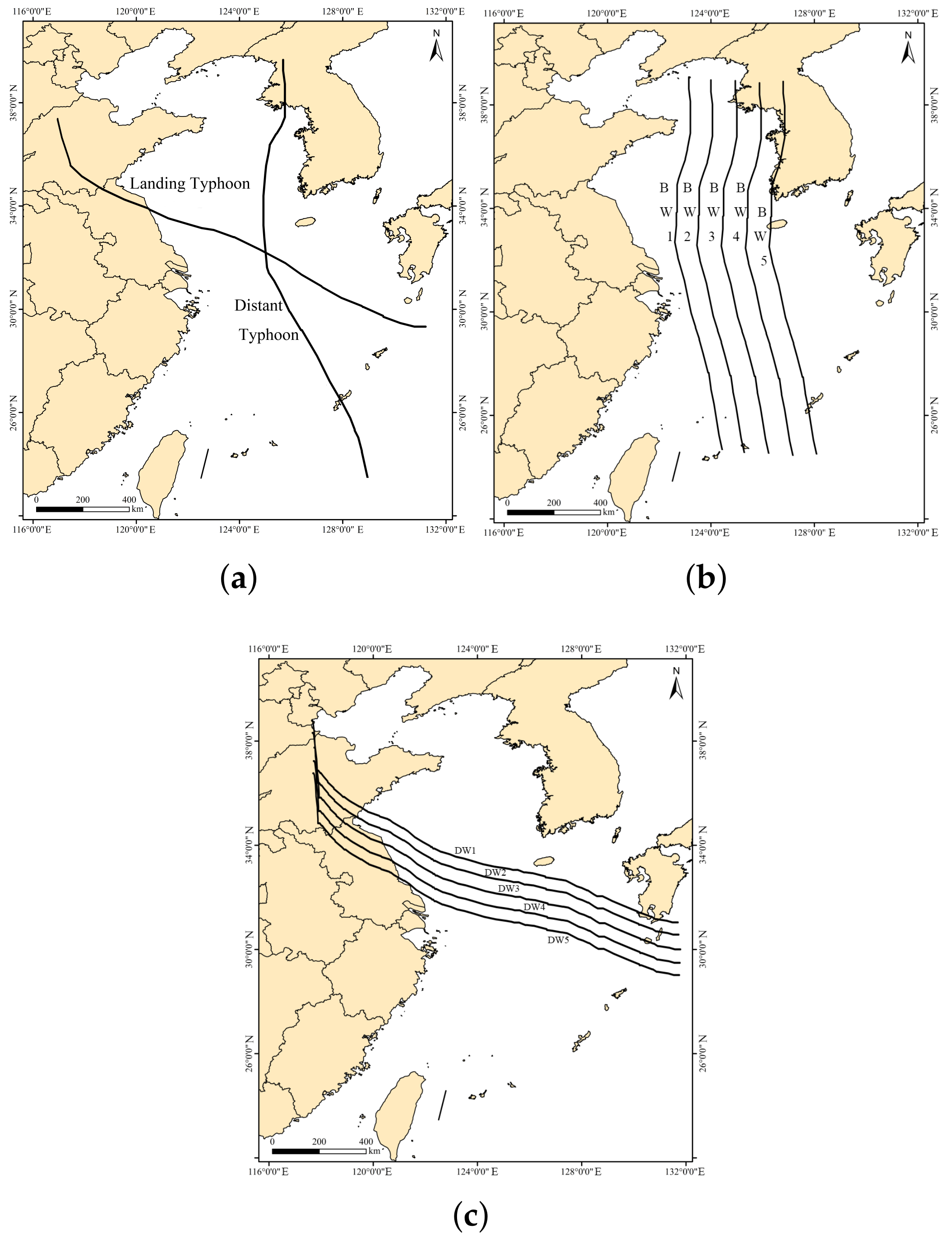
2.5. Typhoon Parameter Sensitivity Analysis

In this study, the radius of maximum wind (RMW), translation speed, and typhoon track were selected as the core control variables [15]. The primary rationale is that the RMW directly determines the extent of the typhoon’s strong wind region (i.e., the effective fetch length), which governs the spatial scale of wave growth. The translation speed influences the wave development stage through the “wind duration–fetch equilibrium” relationship, while different typhoon tracks determine the interaction patterns between wave propagation direction and coastal topography [16].

The typhoon tracks were selected from two representative events: the offshore-type Typhoon Bavi (BW, 2020, No. 8) and the landfall-type Typhoon Damrey (DW, 2012, No. 10). The fundamental parameters of these two typhoons are listed in

Table 2. Characteristic typhoon parameters.

Parameter	Typhoon Bavi	Typhoon Damrey
Minimum Central Pressure P (hpa)	950	960
Maximum Wind Speed V (m/s)	45	40
Radius of Maximum Wind (km)	42–58	47–63

, and their corresponding tracks are illustrated in Figure 3. Three groups of sensitivity experiments were designed for this study (

Table 3. Design table for numerical simulation experiment on the influence of distant typhoon parameters on wave characteristics.

Group	RMW (km)	Translation Speed (m/s)	Typhoon Track
1	RMW1 RMW0 = 0.7RMW1 RMW2 = 1.3RMW1 RMW3 = 1.5RMW1	V1	BW1
2	RMW1	V1 V2 = 0.5V1 V3 = 0.75V1 V4 = 1.5V1 V5 = 2.0V1	BW1
3	RMW1	V1	BW1 BW2 BW3 BW4 BW5

and

Table 4. Design table for numerical simulation experiment on the influence of landing typhoon parameters on wave characteristics.

Group	RMW (km)	Translation Speed (m/s)	Typhoon Track
1	RMW1 RMW0 = 0.7RMW1 RMW2 = 1.3RMW1 RMW3 = 1.5RMW1	V1	DW1
2	RMW1	V1 V2 = 0.5V1 V3 = 0.75V1 V4 = 1.5V1 V5 = 2.0V1	DW1
3	RMW1	V1	DW1 DW2 DW3 DW4 DW5

).

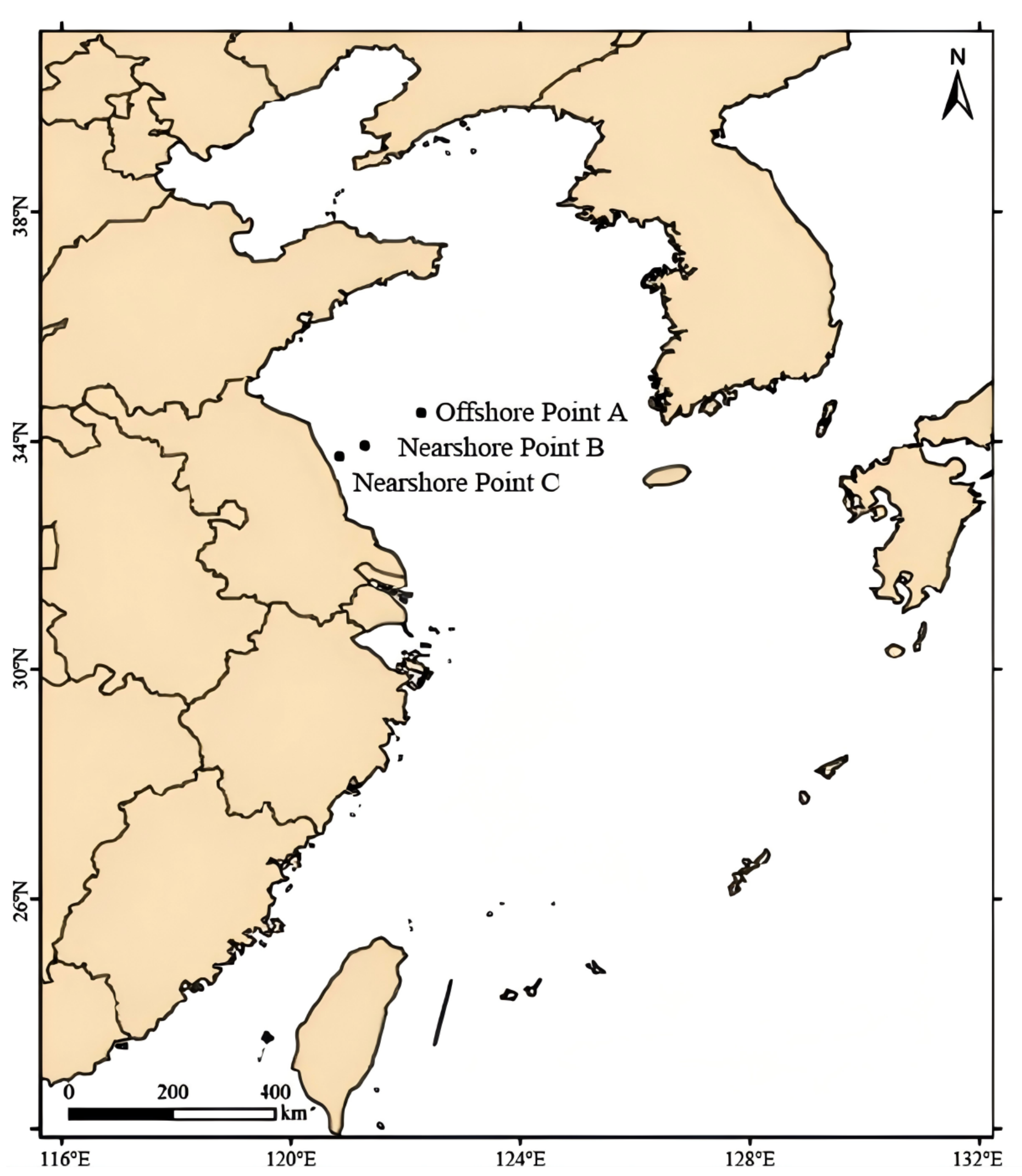
2.6. Observation Points and Locations

To systematically investigate the propagation mechanism of typhoon waves from offshore to nearshore and the influence of coastal topography, three characteristic monitoring points were established in this study. The first is the deep-water swell energy input zone (offshore Point A, water depth 22 m); the second is the nearshore Point B (water depth 12 m) located in the natural shoreline wave attenuation transition zone; and the third is the nearshore Point C (water depth 8 m) within the port engineering impact area. Figure 4 shows the locations of the three points, representing the distinct effects of swell generation, natural dissipation, and human activities, respectively.

3. Results and Disscussion

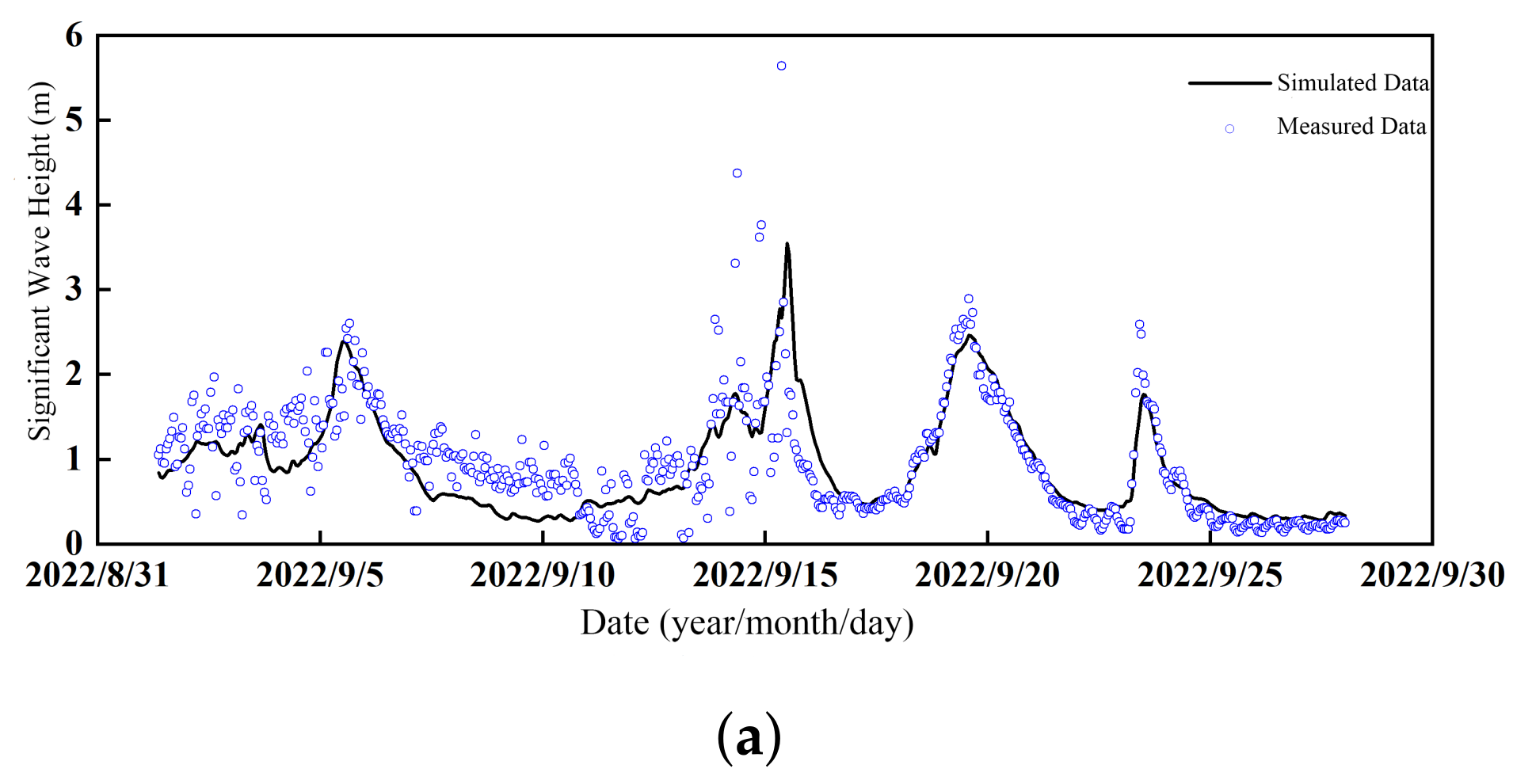
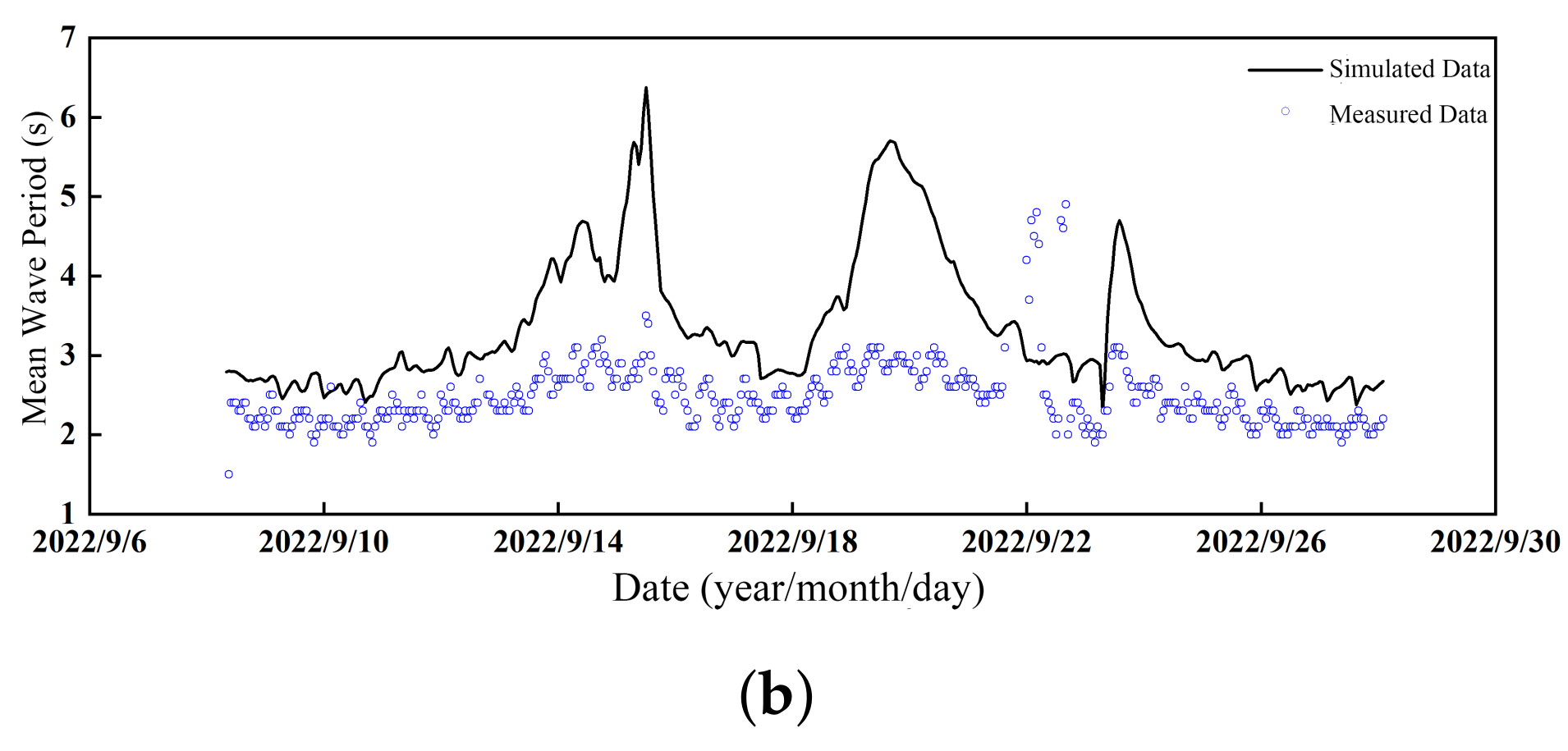
3.1. Numerical Model Validation

Figure 5 presents the comparison between the simulated results obtained from the MIKE 21 SW model and the measured data at the same observation points. As shown in the figures, the simulated significant wave height closely matches the observed values, and the simulated mean wave period exhibits a consistent trend with the buoy measurements during the typhoon events.

Table 5. Characteristic typhoon parameters table.

	Mixed Wave		Swell
Variable	Hs	Tm	Hs	Tm
RMSE	0.386	1.168	0.317	1.679
r	0.800	0.579	0.601	0.304

summarizes the correlation coefficients and root mean square (RMSE) between the simulated and observed significant wave heights and wave periods. As indicated in Table 5, the correlation coefficient for the simulated significant wave height under mixed sea conditions reaches 0.8, demonstrating a strong agreement. Therefore, the model is capable of accurately reproducing the wave dynamics in the Dafeng sea area during typhoon conditions.

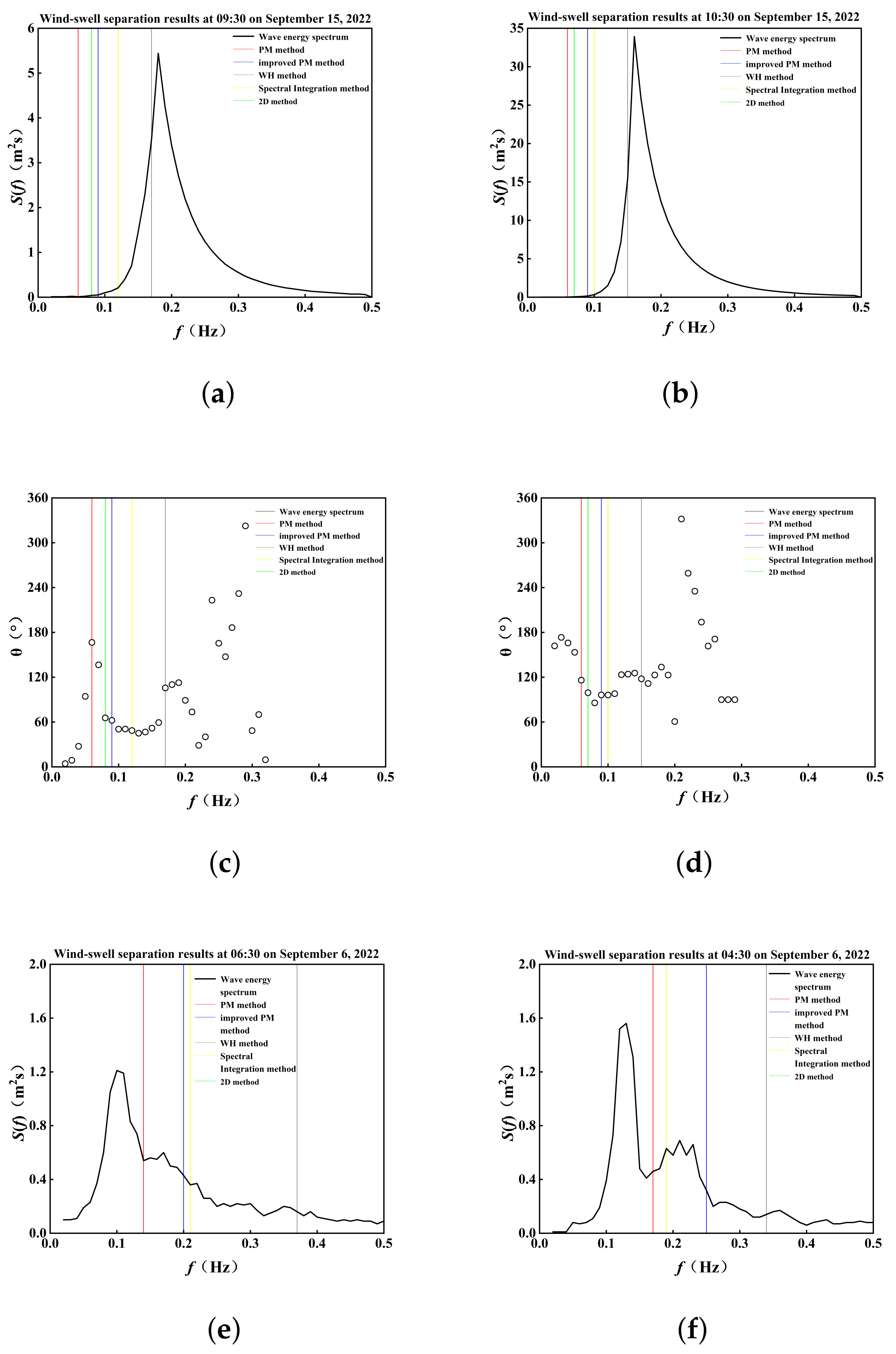
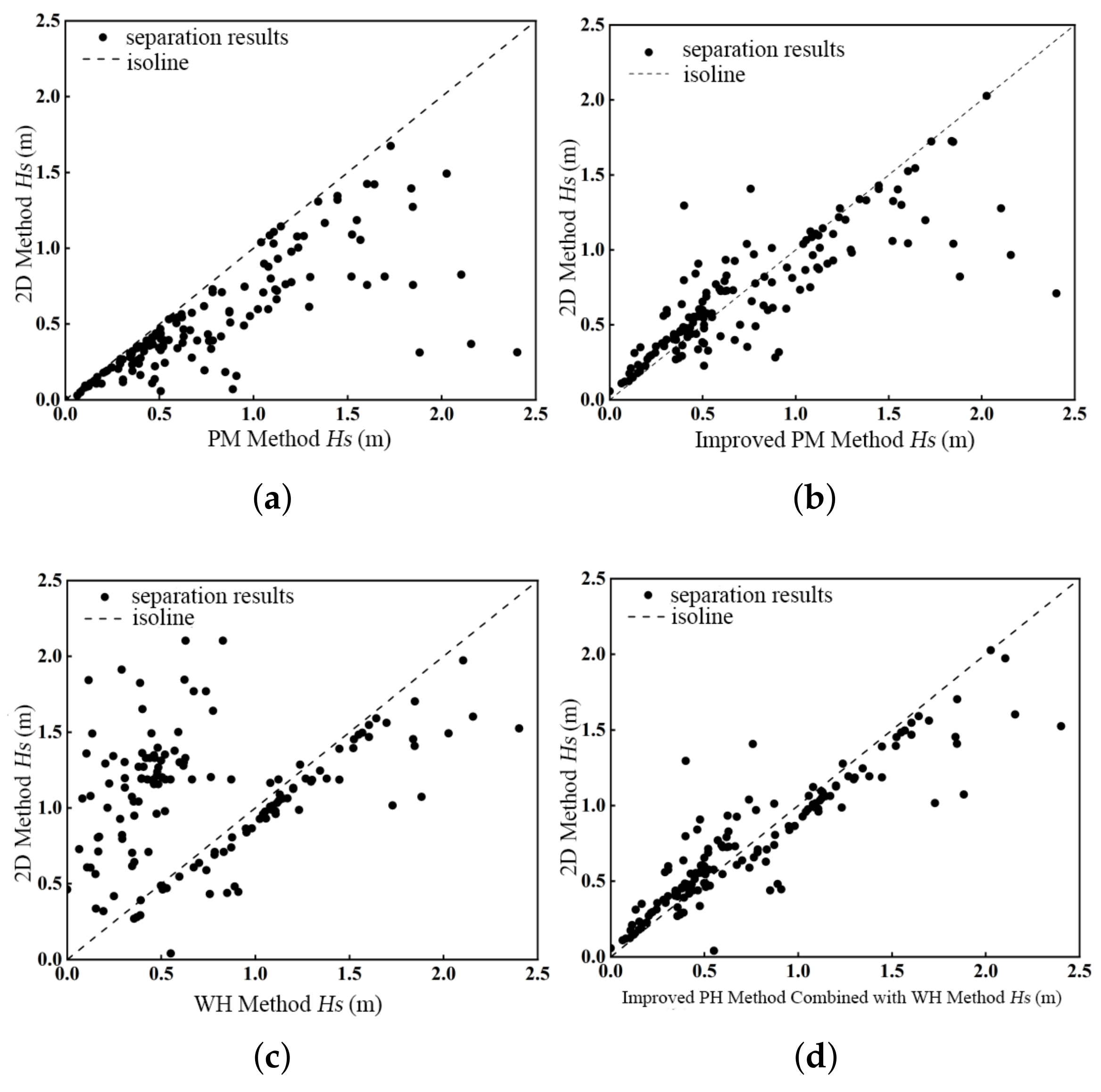
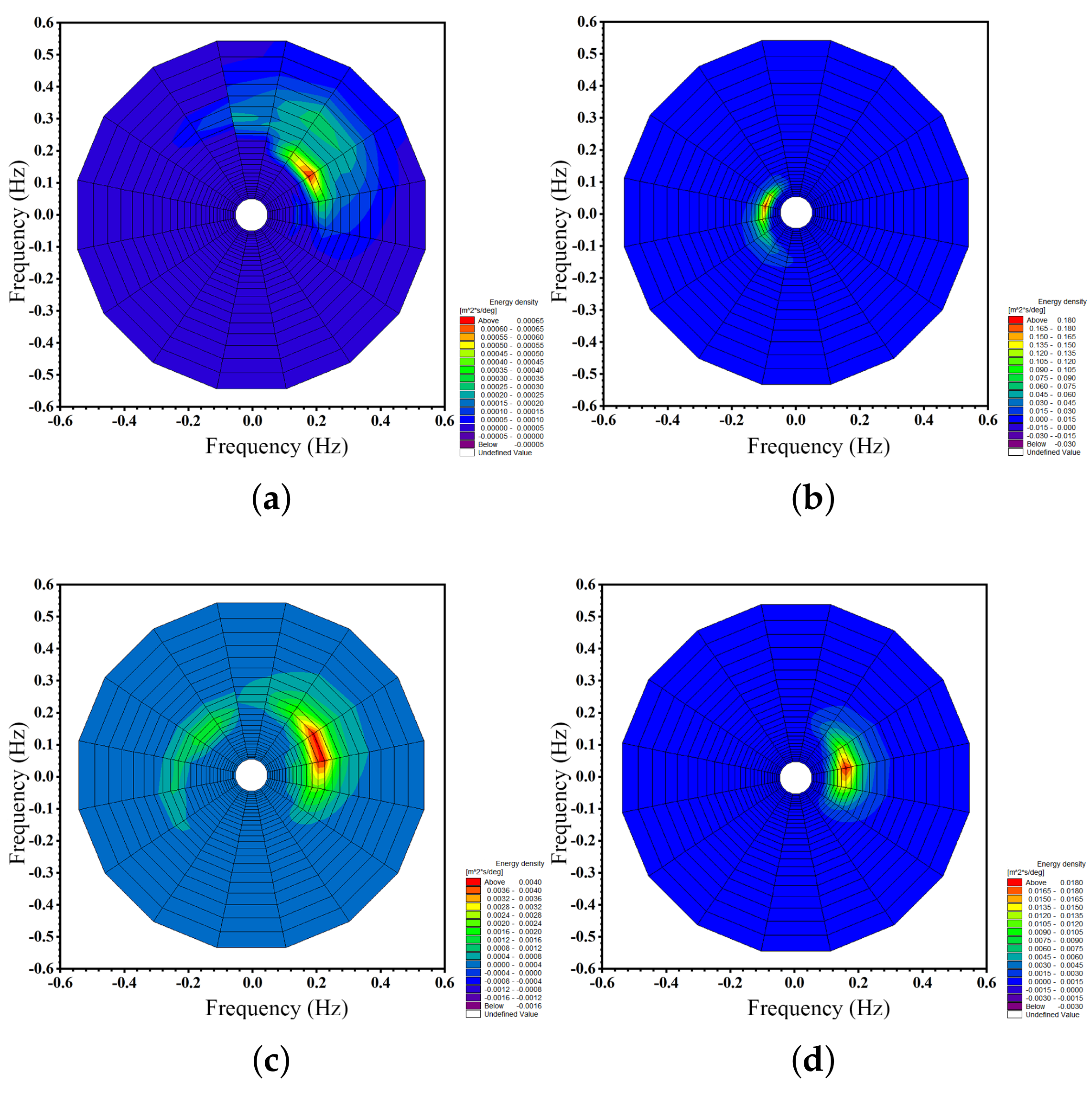
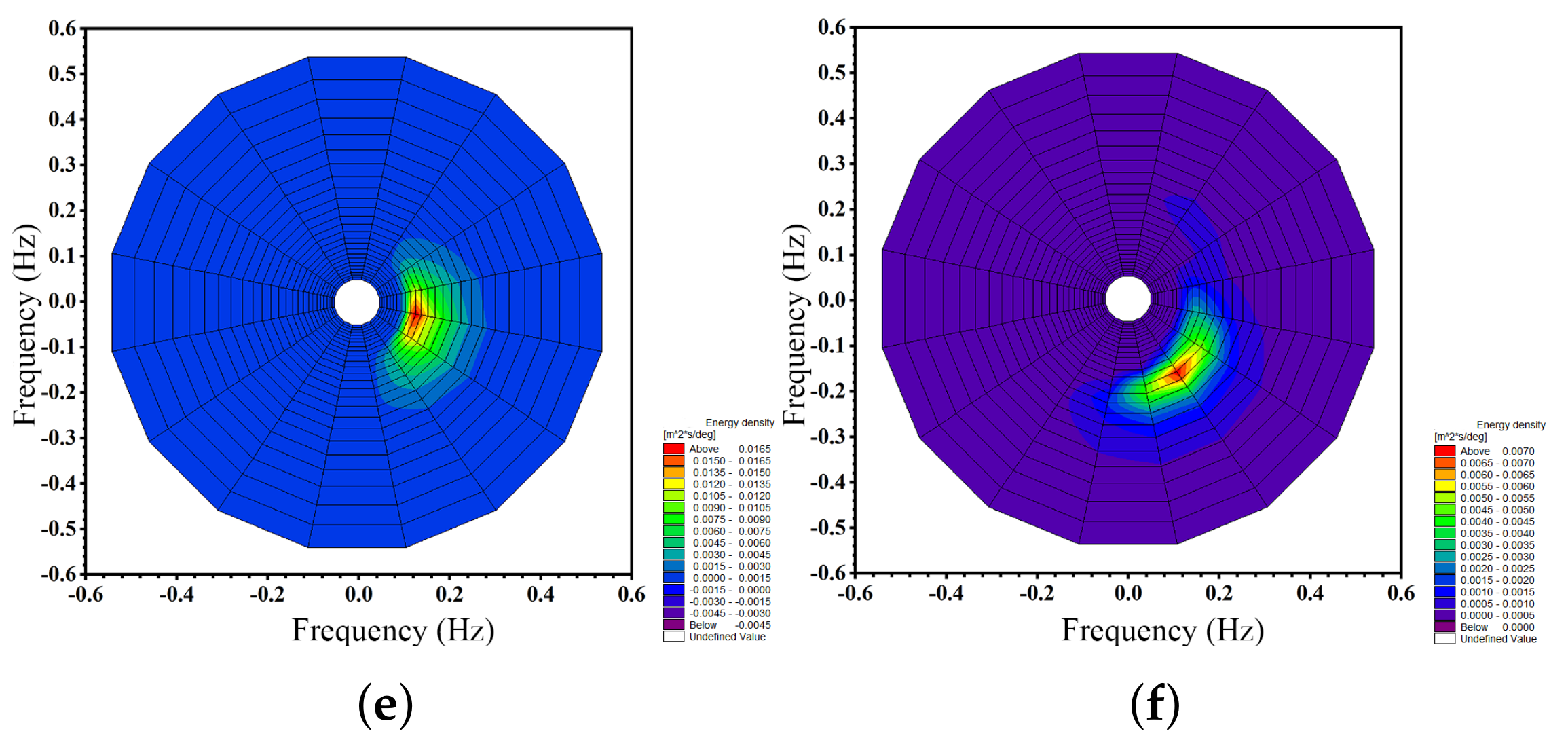
3.2. Wind–Wave and Swell Separation Results

Focusing on the measured wave data from the Dafeng sea area, two representative scenarios were selected—one dominated by wind waves and the other dominated by swell. Using both one-dimensional (1D) and two-dimensional (2D) separation methods, the wind sea and swell components in this region were effectively distinguished. The results of various separation methods are clearly illustrated in Figure 6.

Figure 6 presents the separation results at 09:30 and 10:30 on 15 September 2022. The single-peaked shape of the energy spectrum indicates the presence of only one wave system, suggesting that the sea state at this time was purely wind-dominated. At 09:30 on the 15th, the wind speed U was 17.4 m/s. Based on this wind speed, different wind–wave and swell separation methods yielded corresponding cutoff frequencies f_s: the red vertical line represents the f_s calculated by the PM method (0.05725 Hz); the blue vertical line represents the f_s obtained by the improved PM method (0.087 Hz); the gray vertical line indicates the f_s derived from the WH method (0.17 Hz); the yellow vertical line corresponds to the f_s computed by the spectral integration method (0.12 Hz), determined from the relationship between the peak frequency and the cutoff frequency; and the green vertical line represents the f_s calculated by the 2D method.

At 04:30 on 6 September, the wind speed was 7.4 m/s. During this period, wind waves were relatively weak, and the sea state was dominated by swell. Under such conditions, wind–wave and swell separation was performed, and the peak frequency f_p of the energy spectrum at 04:30 on the 6th was 0.1 Hz. In the figure, the red vertical line represents the separation frequency f_s calculated by the PM method (0.14 Hz); the blue vertical line represents the f_s obtained by the improved PM method (0.20 Hz); the gray vertical line corresponds to the f_s derived from the WH method (0.37 Hz); and the yellow vertical line indicates the f_s calculated by the spectral integration method (0.20 Hz).

At 06:30 on the 6th, the peak frequency f_p of the power spectrum was also 0.1 Hz. The gray vertical line represents the f_s calculated by the WH method (0.34 Hz), while the yellow vertical line represents the f_s obtained from the spectral integration method (0.19 Hz). The PM method yielded a separation frequency f_s of 0.17 Hz; the fixed-frequency method gave f_s = 0.10 Hz; and the improved PM method produced f_s = 0.25 Hz.

In the previous section, it was introduced that, given the separation frequency of a known wave spectrum, the significant wave height and wave period of wind waves and swells can be calculated using Equation (4). Next, the Pearson correlation coefficient (r) and the root mean square (RMSE) are used to analyze the correlation between the separation results of each 1D method and those of the 2D method. The statistical comparisons are presented in

Table 6. The similarity between the significant wave height of the swell separated by four 1D methods and the standard value.

	PM Method	Improved PM Method	WH Method	Spectral Integration Method
RMSE	0.634	0.758	0.274	0.349
r	0.509	0.378	0.691	0.574

.

As shown in Figure 7, the standard PM method tends to overestimate the swell wave height. A comparison with the improved PM method reveals that the clustering of the separation results is significantly enhanced. However, the improved PM method still shows reduced accuracy when the actual swell height is large, tending to underestimate the swell wave height. The WH method, on the other hand, tends to overestimate the swell wave height when the swell is relatively small. Considering the advantages and limitations of these two approaches, this study proposes a combined strategy: when the sea state is dominated by swells, the WH method is used for wind–wave and swell separation; when it is dominated by wind waves, the improved PM method is applied. The results show that this strategy increases the correlation coefficient r from 0.758 and 0.274 to 0.830, effectively compensating for the weaknesses of each individual method.

3.3. Simulation Results of Wave Parameters Under Different Typhoon Conditions

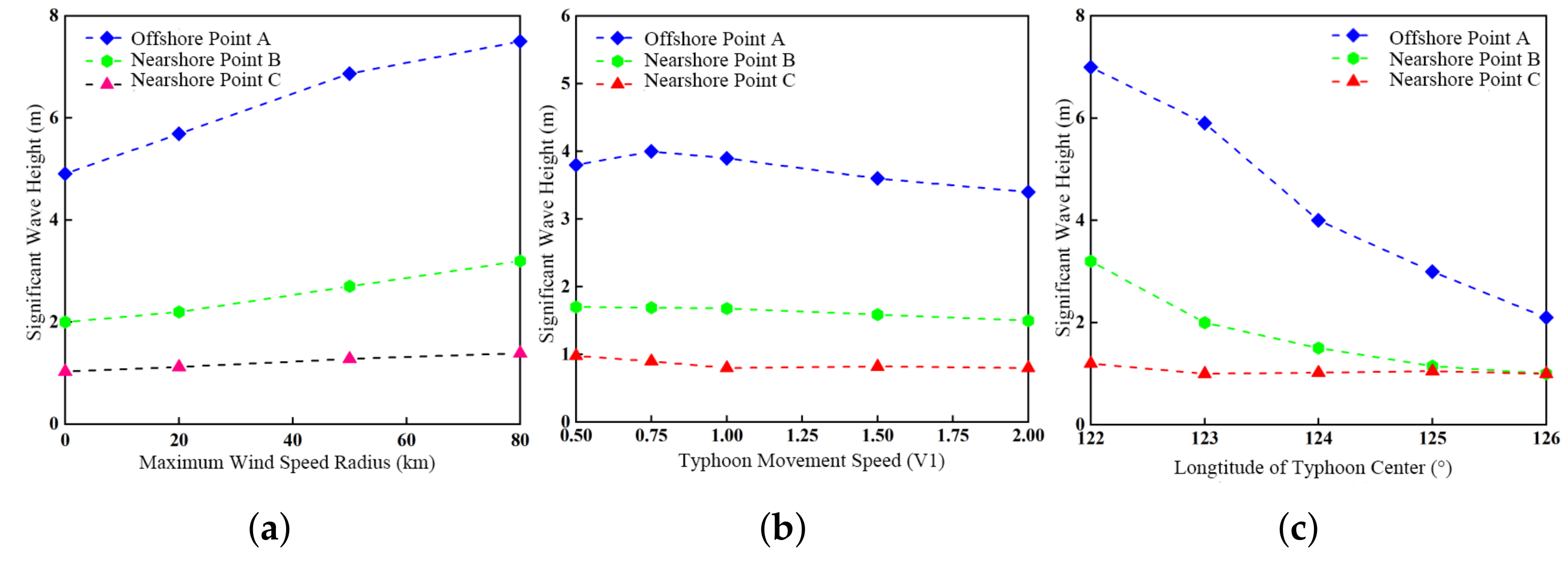
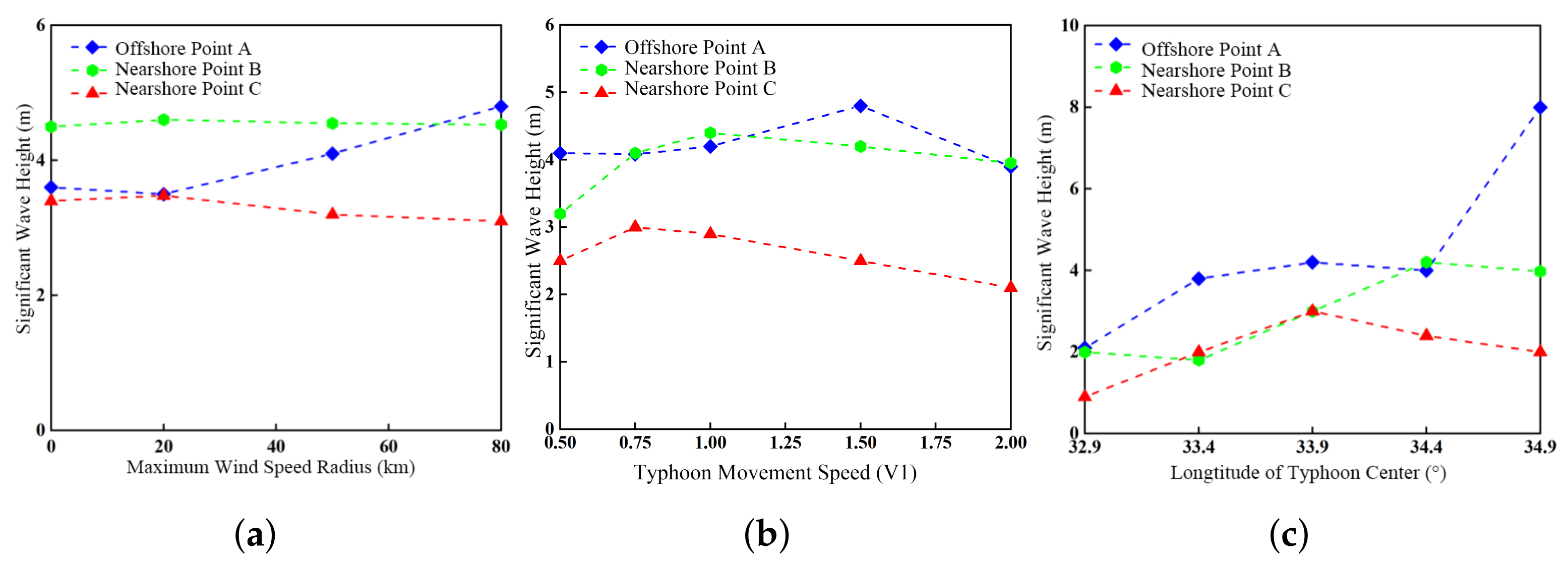
3.3.1. Significant Wave Height of Swell

Figure 8 and Figure 9 illustrate the relationship between the maximum significant wave height, the mean significant wave height, and the radius of maximum wind speed during typhoon events. During distant typhoons, as the radius of maximum wind speed increases, the difference in significant wave height between offshore Point A and nearshore Point B gradually increases. In contrast, during landing typhoons (as shown in Figure 9), the maximum significant wave height at offshore Point A is strongly influenced by the radius of maximum wind speed, increasing by about 1.5 m. By comparison, nearshore Points B and C are less affected, with their maximum significant wave heights remaining relatively stable around 4.8 m and 3.0 m, respectively. This phenomenon is closely related to the geographical locations and surrounding environments of the nearshore points.

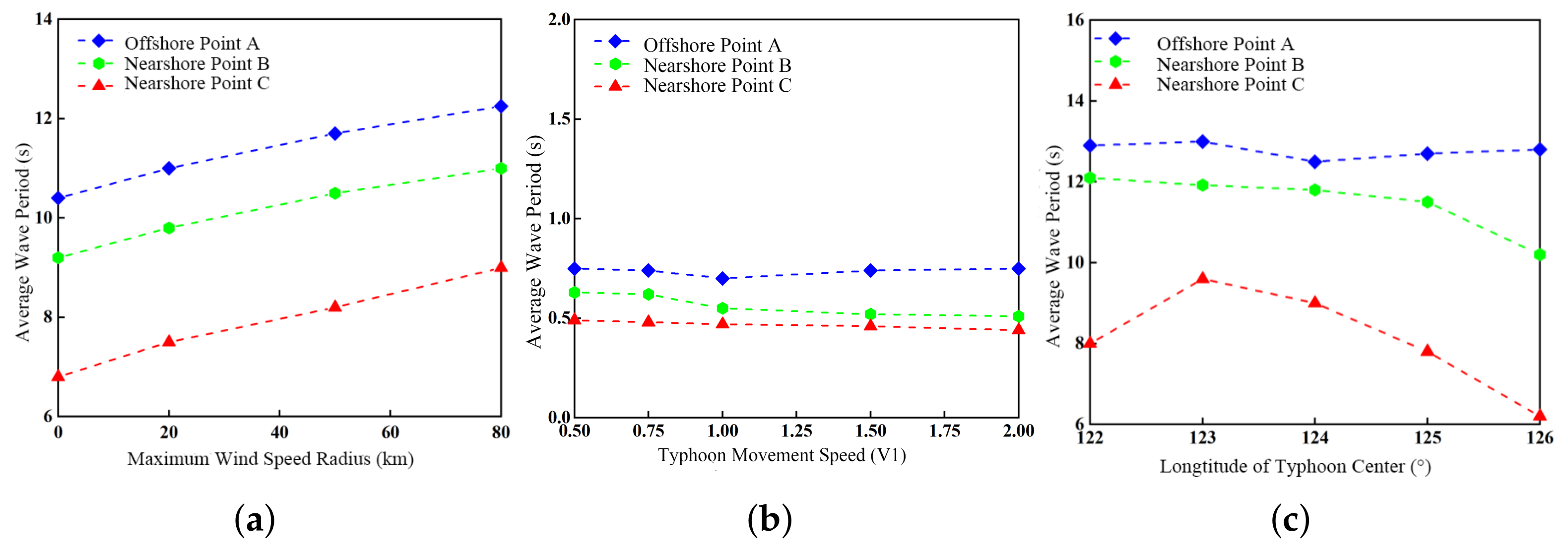
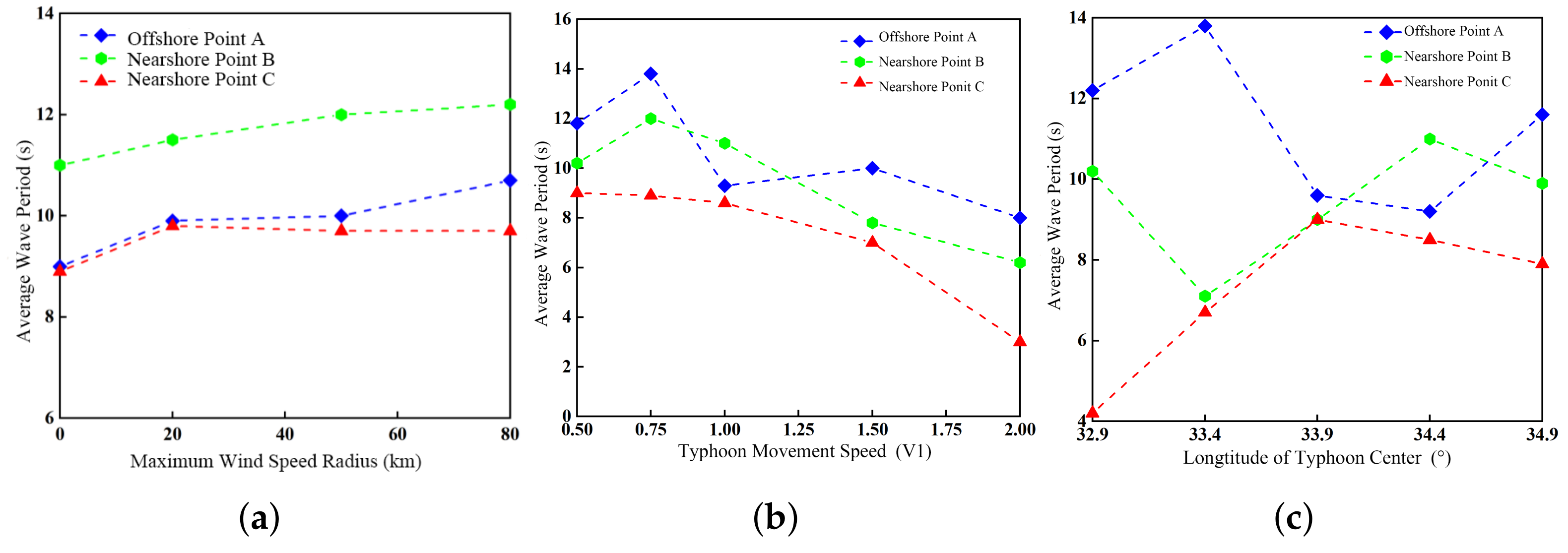
3.3.2. Average Wave Period of Swell

During distant typhoons (as shown in Figure 10), the maximum values of the mean wave period at offshore Point A and nearshore Points B and C increase monotonically with enlargement of the maximum wind speed radius. Meanwhile, the maximum mean period at offshore Point A is consistently greater than that at nearshore Points B and C. This is because, as offshore swells generated by distant typhoons propagate toward the coast, factors such as topography and decreasing water depth causes a reduction in the mean swell period [17].

During landing typhoons (as shown in Figure 11), the maximum mean wave period also increases with the maximum wind speed radius. However, in this case, the maximum mean period at nearshore Point B exceeds that at offshore Point A. This is mainly due to the effects of coastal topography and energy dissipation during swell propagation after the typhoon makes landfall.

Additionally, the maximum mean wave period at nearshore Points B and C first increases and then decreases with the increase in typhoon movement speed. This response pattern reflects the competing effects between wind forcing duration and fetch-length constraints on wave development. When translation speed is low, the prolonged wind forcing duration allows waves to develop toward a more fully developed state with longer periods, following classical wave growth theory. However, when the typhoon moves very slowly, the localized wind forcing may not provide sufficient spatial fetch for additional energy input, and energy dissipation processes (whitecapping, bottom friction) become more significant. Conversely, when translation speed exceeds an optimal value, the abbreviated wind forcing duration prevents full wave development, resulting in shorter mean periods despite higher energy input rates [18,19].

During distant typhoons, as the latitude of the typhoon center increases, the maximum mean wave period at offshore Point A and nearshore Point B gradually decreases. Because the farther the typhoon center is from the coast, the weaker the effects of topography and water depth on the swell become, resulting in smoother propagation and smaller variations in wave period. At nearshore Point C, coastal refraction and bathymetric effects become significant. Wave refraction in shallow water (governed by Snell’s law) rotates wave directions toward shore-normal, concentrating energy in certain coastal segments. Combined with shoaling effects, this creates energy focusing, enhancing wave heights at Point C. Bottom friction preferentially dissipates high-frequency components, while the complex shelf bathymetry causes partial wave reflection and scattering. These processes collectively modify both the wave period and the direction at nearshore locations. During landing typhoons, when the typhoon center is located at 33.4° N, there is a large difference between the maximum mean wave periods at offshore Point A and nearshore Points B and C. This occurs because, at this position, the typhoon path passes near the coast, causing locally generated waves to dominate at nearshore observation points, while the swell component is weakened by geometric shadowing and strong bottom dissipation in shallow water.

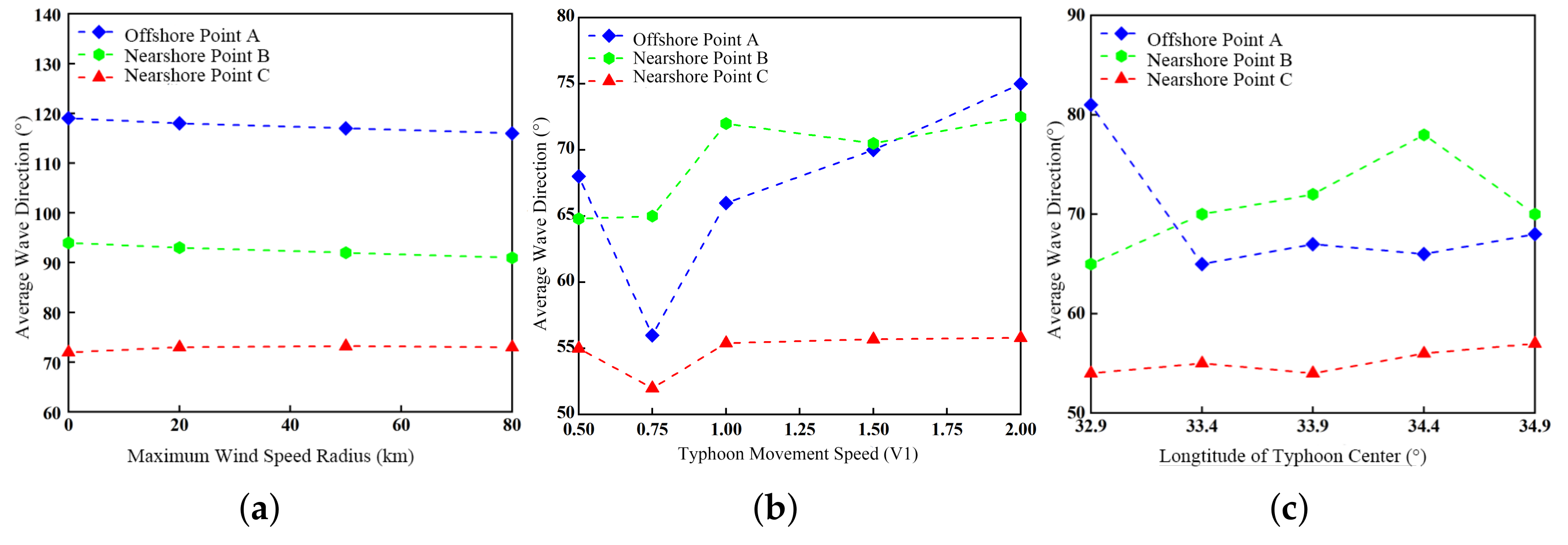
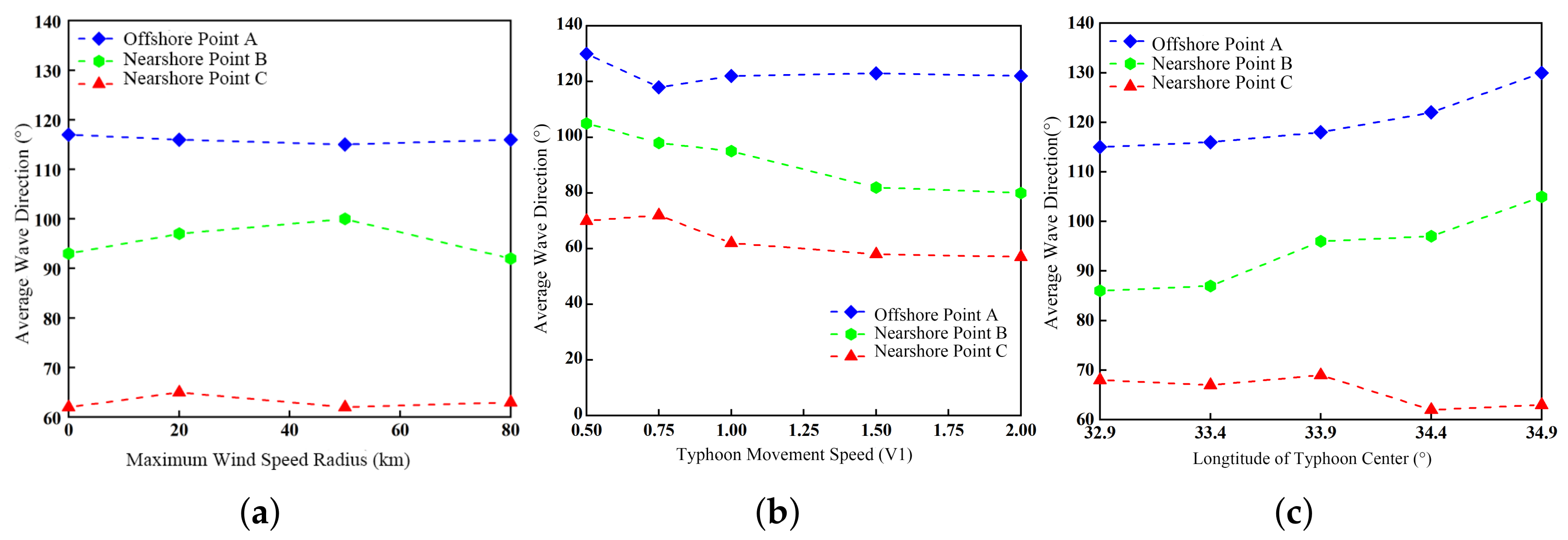
3.3.3. Average Wave Direction of Swell

Figure 12 and Figure 13 illustrate the variation in the mean wave direction under different typhoon parameters. For both distant typhoons and landing typhoons, as the radius of maximum wind speed increases, the mean wave directions at offshore Point A and nearshore Points B and C show a slight decreasing trend but remain generally stable. It is worth noting that the wave direction at offshore Point A slightly shifts from ESE to E, while the dominant wave direction at nearshore Point B remains mainly around E, and at nearshore Point C, it stays around ENE.

Under the influence of distant typhoons, as the typhoon’s moving speed increases, the mean wave direction at offshore Point A gradually shifts from ENE to E. During landing typhoons, the mean wave direction at Point A turns from SE to ESE as the typhoon’s moving speed increases, and the mean wave direction at Point B shifts from ESE to E.

For distant typhoons, when the typhoon track moves eastward and the typhoon center longitude increases, the mean swell direction tends to rotate toward the southeast. In contrast, during landing typhoons, as the typhoon track shifts northward, the mean wave directions at offshore Point A and nearshore Point B both tend to deflect toward the southeast, while the mean wave direction at nearshore Point C shifts northward by about 8°.

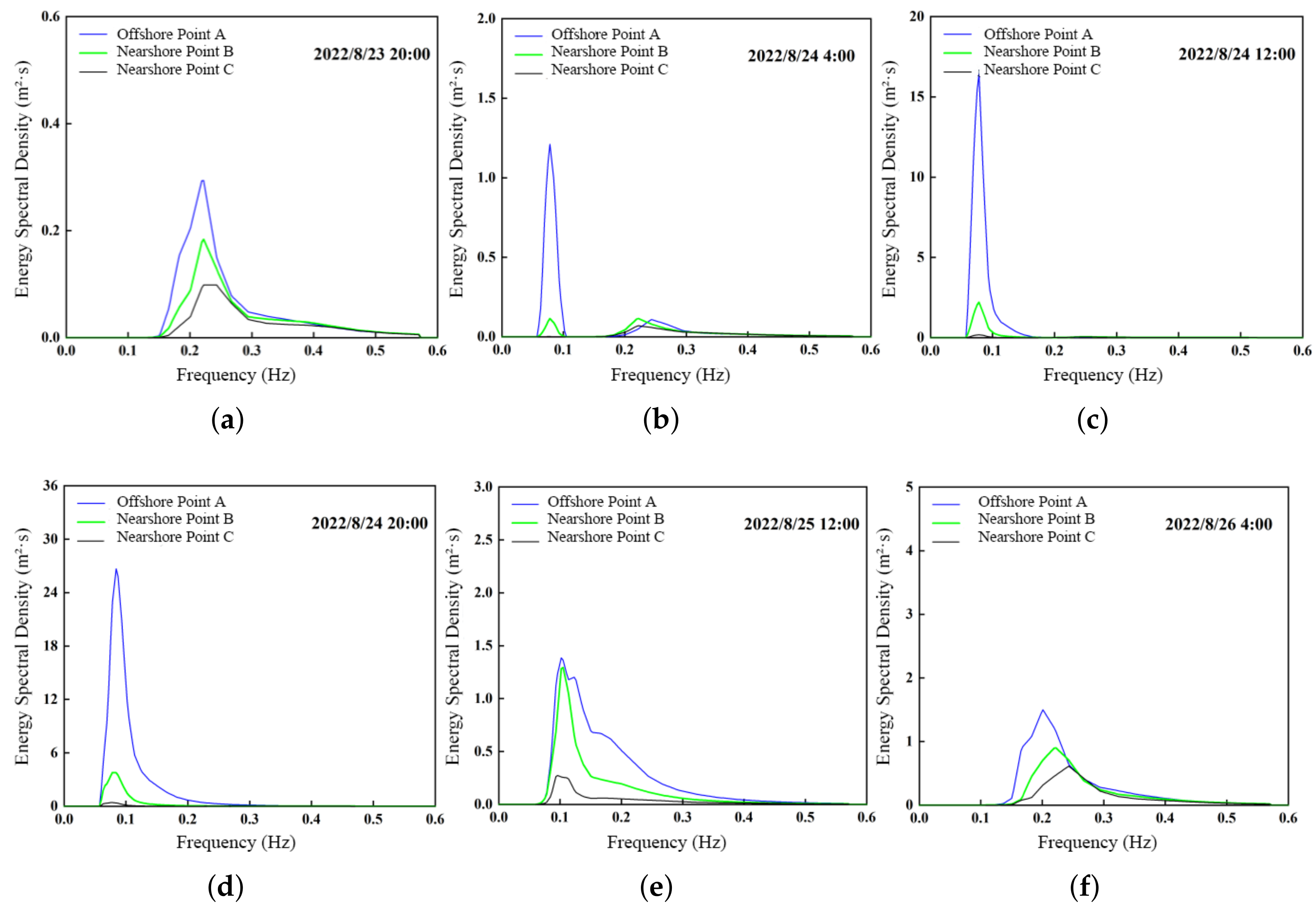
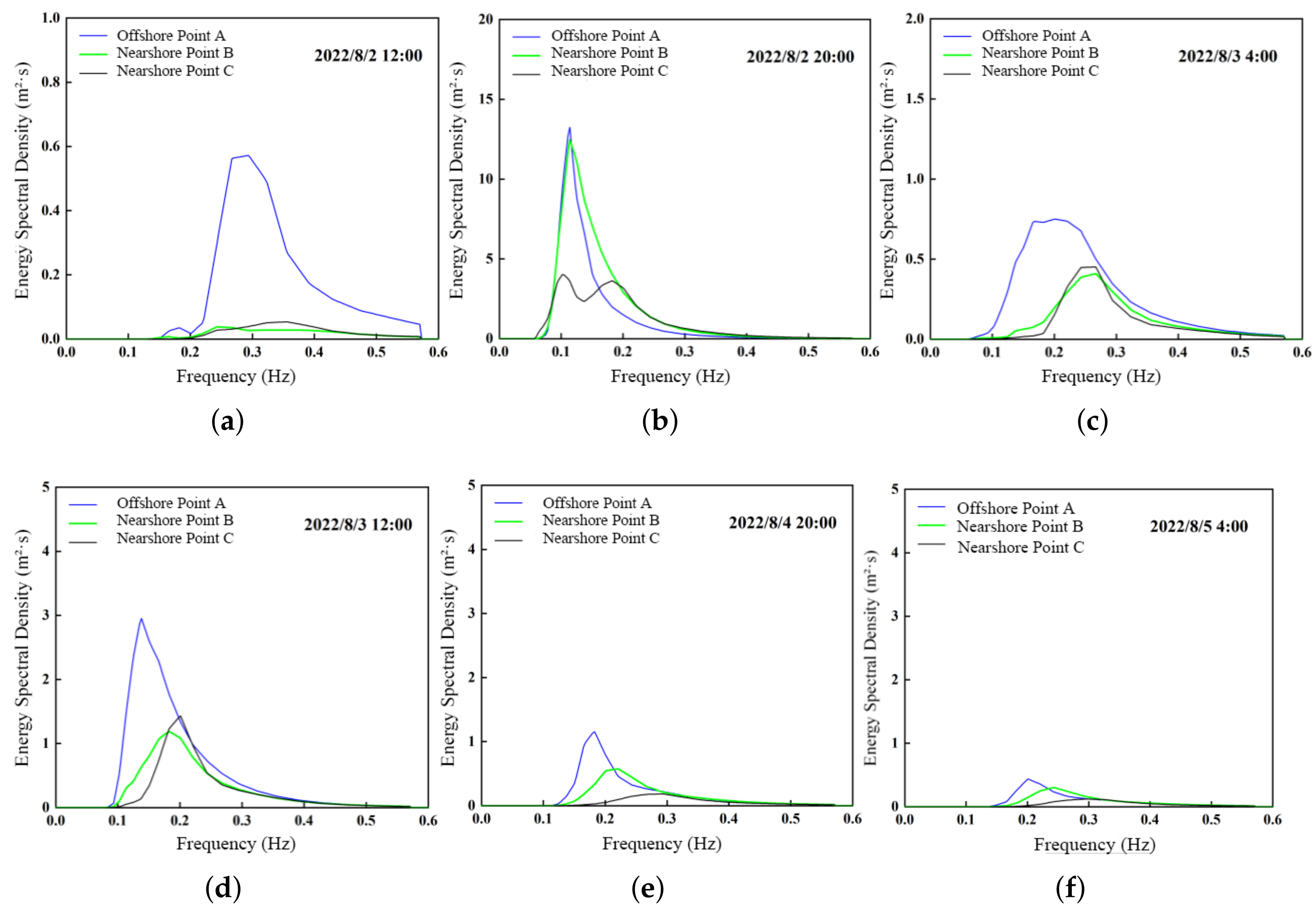
3.3.4. Characteristics of the Wave Spectrum

Figure 14 illustrates the wave energy spectra in the Dafeng sea area from 20:00 on 23 August to 04:00 on 26 August during the distant typhoon event. As shown in the figure, at 20:00 on 23 August, when the typhoon intensity reached the super typhoon level, the observed spectrum exhibited a single-peak type, with the spectral peak frequency concentrated at 0.22 Hz and the corresponding spectral energy density less than 0.4 m²·s, representing the pre-typhoon sea state. By 04:00 on 24 August, as the typhoon moved northward, the low-frequency energy gradually increased, forming two distinct wave systems. The first system had a spectral peak frequency of 0.08 Hz, corresponding to the swell component, while the second system had a spectral peak frequency of 0.24 Hz, close to the multi-year mean frequency of the Dafeng area, corresponding to the wind sea component. From 04:00 to 20:00 on 24 August, with the typhoon moving further north and the distance between the typhoon center and the Dafeng area decreasing to approximately 300 km, the spectral peak energy significantly increased and became more concentrated, shifting from 0.22 Hz to the lower-frequency region around 0.08 Hz. At 20:00, the spectral energy density reached its maximum value of 27 m²·s, and the spectrum appeared narrow and sharp. Between 04:00 and 20:00 on 25 August, the spectral shape broadened, the long-period wave energy gradually decreased, and the peak frequency shifted toward higher frequencies. By 04:00 on 26 August, the peak frequency had increased to 0.2 Hz, indicating that the typhoon had moved away from the area and the swell gradually dissipated, with local wind waves regaining dominance.

From offshore point A to nearshore point C, the spectral peak energy decreased, and the nearshore site—being farther from the typhoon center—showed the largest peak frequency. This indicates that wave energy gradually dissipated as waves propagated from offshore to nearshore. Moreover, as the waves traveled from nearshore point B to nearshore point C, their energy was further attenuated due to the effects of coastal topography and bathymetry.

As shown in Figure 15, the directional spectra reveal distinct wave evolution stages during the distant typhoon event. On 23 August, before the typhoon formed, the spectrum indicates that the sea state was dominated by locally generated wind waves. On 24 August, under the influence of the typhoon, the sea state transitioned into a mixed wave condition, and after the typhoon moved away, wind waves once again became dominant. The energy density of the distant typhoon was mainly concentrated in the NNE–E directions. During the period of maximum significant wave height, the spectral peak frequency was concentrated around 0.1 Hz. As the typhoon moved away on 25 and 26 August, the swell energy decayed and wind waves became dominant.

When the representative observation point was located to the southwest of the typhoon center, the wave spectrum was dominated by low-frequency swell. As the typhoon approached the coast and moved northwestward relative to the observation point, the spectrum showed a combination of wind waves and swell. Subsequently, the swell gradually disappeared, and wind waves became the dominant component. During the passage of the landing typhoon, low-frequency swell gradually propagated into the region and shifted northeastward, with the sea state characterized mainly by mixed waves. The spectral peak frequency was concentrated around 0.15 Hz. Before and after landfall, the wind direction in the Dafeng sea area shifted from southeast to northwest under the influence of the typhoon’s regional circulation, resulting in swells generated at different times propagating in opposite directions.

In summary, the swell induced by distant typhoons is characterized by a relatively concentrated wave direction (NNE–E) and a longer period, which can exert a sustained high load on one side of coastal structures such as offshore wind turbine foundations (e.g., the wave-facing side of monopile foundations). Therefore, particular attention should be paid to the cumulative fatigue damage of these structural components.

During the passage of landing typhoons, the Dafeng sea area experiences swells from both the eastern (southeasterly winds) and western (northwesterly winds) sides of the typhoon, resulting in the coexistence of waves traveling in opposite directions. When the typhoon makes landfall along the Jiangsu coast, the Yellow Sea exhibits coexisting swells from the southeast and northwest directions, with regional wave directions differing by more than 90°. Such multi-directional wave superposition may lead to a sudden increase in wave height. The coexistence of multi-directional swells significantly increases the complexity of the sea state and should be given special attention in disaster prevention and mitigation efforts.

This study acknowledges several limitations. The wind field parameterization relies on the Holland (1980) [14] model with best-track data, which carries ±5–10% uncertainty in pressure difference and maximum wind radius. The model does not account for current-wave coupling, which could underestimate wave changes in regions with strong tidal currents. The spectral resolution of 0.01 Hz may introduce aliasing at very low frequencies (<0.05 Hz), affecting long-period swell estimates. Validation is based on September 2022 only, which may not fully represent the range of typhoon intensities in this region. Despite these limitations, the model’s wave height predictions (R² = 0.80) are sufficient for characterizing typhoon-wave interactions (Figure 16 and Figure 17).

4. Conclusions

This study focuses on the typhoon-prone Dafeng sea area and systematically investigates the quantitative influence mechanisms of typhoon parameters on swell characteristics. Based on the analysis of field wave observations collected during Typhoons Hinnamnor (2022 No. 11) and Muifa (2022 No. 12), the traditional one-dimensional (1D) wind–wave and swell separation method (PM method) was improved, and a dynamic hybrid separation strategy combining the modified PM method and the WH method was proposed. By superimposing the Holland typhoon wind field and the ERA5 background wind field, a high-resolution MIKE21 SW numerical wave model was constructed. The model accurately reproduces the wave evolution process under typhoon influence in the Dafeng sea area, with a significant wave height simulation error of only 0.386 m. The main conclusions are as follows:

• The improved PM method, obtained by introducing a scaling coefficient, was compared with the standard PM method, the fixed-frequency method, and the WH method under both wind-sea-dominated and swell-dominated conditions. By combining the improved PM and WH methods, the overall separation accuracy was enhanced by 21% compared to using a single method, significantly improving applicability under complex typhoon wave conditions.
• The significant swell height is strongly influenced by the radius of maximum wind (RMW). As RMW increases from RMW0 to RMW3, the significant swell height increases from 2 m to 3.5 m, and the mean period lengthens by approximately 2 s, generating stronger and broader swells. When the typhoon translation speed is reduced to half its reference value, the significant wave height increases by about 1.2 m, and the mean period extends by 2 s. In terms of energy input, faster-moving typhoons produce concentrated but short-lived energy transfer, generating shorter-period swells; slower-moving typhoons provide more uniform and persistent forcing, producing higher-energy, longer-period swells. When the translation speed increases to 1.5 times the reference value, wave height reaches a maximum; beyond that, further acceleration results in a decrease in height. When the typhoon track passes closer to a given area, the significant swell height increases by approximately 0.8 m compared with the normal track. During distant typhoons, as the path shifts eastward (BW1 → BW5), the dominant wave direction in the directional spectrum rotates from 30° to 100°. In contrast, during landfalling typhoons (DW1 → DW5), the dominant wave direction at nearshore Point B shifts from 100° to 300°.
• The significant wave height at offshore points responds more sensitively to variations in the RMW than that at nearshore points. Moreover, the faster the typhoon moves, the smaller the difference in significant wave height between offshore and nearshore sites. Distant typhoons generate larger offshore swells (up to 7.5 m), which propagate faster and exhibit longer periods. In contrast, landfalling typhoons produce mixed wind–wave and swell systems nearshore, with maximum wave heights approximately 60% of those offshore. During distant typhoon events, the spectral peak period is generally longer than that of landfalling typhoons. Distant typhoons primarily generate swells, whereas landfalling typhoons tend to produce mixed wind–wave and swell conditions. The propagation speed of swells is faster than that of the typhoon center, reaching up to twice the typhoon’s translation speed.
• Under distant typhoon conditions, waves exhibit swell-dominated, long-period characteristics, with spectral peak periods ranging from 12 s to 14 s and dominant swell directions of N–NE. These conditions can impose sustained high loads on the wave-facing sides of offshore structures (e.g., monopile foundations), necessitating careful attention to cumulative fatigue damage in foundation components. Under landfalling typhoon conditions, waves are characterized by mixed wind–wave and swell systems with shorter periods (9 s–12 s) and highly variable dominant directions. The regional wave direction can shift abruptly by up to 90°, and the coexistence of multi-directional swells may result in sudden increases in wave height. Such multi-directional wave interactions significantly increase the complexity of the sea state and warrant focused attention in coastal disaster prevention and mitigation strategies.
• This study on surge characteristics in the Dafeng sea area during typhoons primarily focuses on landfalling and offshore-moving typhoon types, while excluding atypical tracks and interactions between multiple typhoon systems. Furthermore, research gaps remain regarding the precise mechanisms of surge generation and its interactions with other marine environmental factors during typhoon events. Future research should expand the typhoon dataset and temporal scope, investigate wave interactions during concurrent typhoons, deploy additional wave monitoring stations to analyze regional wave responses under diverse wind conditions, and enhance studies on beach evolution in response to surge dynamics. Specifically for the silt-sediment coast and active sandbar system of Dafeng Port, quantitative assessment of extreme surge impacts on estuarine bar geomorphology during typhoons warrants prioritized investigation.