A Water Resources Scheduling Model for Complex Water Networks Considering Multi-Objective Coordination

Abstract

Complex water networks face prominent contradictions among flood control, water supply, and ecological protection, and traditional scheduling models struggle to address multi-dimensional water security challenges. To solve this problem, this study proposes a multi-objective coordinated water resources scheduling model for complex water networks, taking the Taihu Lake Basin as a typical case. First, a multi-objective optimization indicator system covering flood control, water supply, and aquatic ecological environment was constructed, including 12 key indicators such as drainage efficiency of key outflow hubs and water supply guarantee rate. Second, a dynamic variable weighting strategy was adopted to convert the multi-objective optimization problem into a single-objective one by adjusting indicator weights according to different scheduling periods. Finally, a combined solving mode integrating a basin water quantity-quality model and a joint scheduling decision model was established, optimized using the particle swarm optimization (PSO) algorithm. Under the 1991-Type 100-Year Return Period Rainfall scenario, three scheduling schemes were designed: a basic scheduling scheme and two enhanced discharge schemes modified by lowering the drainage threshold of the Xinmeng River Project. Simulation and decision results show that the enhanced discharge scheme with the lowest drainage threshold achieves the optimal performance with an objective function value of 98.8. Compared with the basic scheme, it extends the flood season drainage days of the Jiepai Hub from 32 to 43 days, increases the average flood season discharge of the Xinmeng River to the Yangtze River by 9.5%, and reduces the maximum water levels of Wangmuguan, Fangqian, Jintan, and Changzhou (III) stations by 5 cm, 5 cm, 4 cm, and 4 cm, respectively. This model effectively overcomes technical bottlenecks such as conflicting multi-objectives and complex water system structures, providing theoretical and technical support for multi-objective coordinated scheduling of water resources in complex water networks.

1. Introduction

Complex water networks serve as the core carrier of water resource circulation and socio-economic development in river basins, serving multiple functions: flood control and drainage, water supply, and ecological protection [1,2,3]. The level of scheduling optimization directly impacts regional water security, sustainable socio-economic development, and ecological health [4,5]. Typical complex water network areas represented by the Taihu Lake Basin in the Yangtze River Delta are characterized by intertwined rivers and lakes, dense water conservancy projects, dense populations, and developed economies. They also face prominent flood risks, urgent water supply demands, and sensitive ecological environments [6,7]. In recent years, affected by the dual impacts of climate change and human activities, extreme rainfall, droughts, and other disasters have occurred frequently [8]. Conflicts between flood control, water supply, and ecological protection goals in the basin are increasingly acute. Traditional decentralized, single-objective scheduling models can no longer address multi-dimensional, composite water security challenges [9]. Therefore, conducting research on joint water resources scheduling in complex water networks to achieve multi-objective coordination holds significant theoretical and practical significance for improving the efficiency of regional water resource allocation, reducing disaster risks, and maintaining ecological balance.

Currently, academics and practical management departments have carried out extensive research and practice on water resources scheduling. In terms of scheduling methods, early studies focused on single-objective optimization, such as reservoir flood control or water supply scheduling models based on linear programming and dynamic programming, which achieve single-objective optimal solutions by simplifying constraints. Specifically, regarding multi-objective coordinated scheduling for complex water networks, existing studies have made remarkable progress but still have obvious gaps. In the construction of multi-objective indicator systems, scholars have gradually expanded from traditional flood control and water supply dual objectives to integrated ecological and water quality indicators [4,10]. For example, Wang et al. established a multi-objective system for regional water resources scheduling, which provided a solid foundation for multi-objective coordination in general regional contexts [4]. However, when applied to complex lake-basin coupled water networks such as the Taihu Lake Basin, the indicator system lacks specific differentiation and does not fully capture the unique hydraulic coupling characteristics between rivers and lakes—an aspect that is particularly critical for scheduling optimization in such complex water systems. In terms of weighting strategy optimization, common methods include subjective weighting (e.g., AHP, Delphi) and objective weighting (e.g., entropy weight, CRITIC) [10]. However, most studies adopted fixed weight coefficients, which cannot dynamically adjust according to seasonal hydrological scenarios (e.g., flood season vs. non-flood season), leading to poor adaptability of scheduling schemes [11]. In the aspect of scheduling model coupling, researchers have integrated hydrodynamic models with intelligent algorithms—such as coupling MIKE 11 with genetic algorithms for river network scheduling [12]—but few studies have fully coupled water quantity and water quality processes. Wu et al. (2025) made valuable contributions by verifying the impact of the Xinmeng River Project on lake water quality, providing important empirical support for understanding the project’s environmental effects [13]. For the scenario of multi-objective coordinated scheduling in complex water networks, however, the integration of water quality simulation into the optimization framework remains to be realized—an integration that is particularly critical for achieving comprehensive coordination of water quantity and quality goals. In terms of engineering application adaptation, existing models are mostly designed for mature water conservancy projects, and there is a lack of targeted scheduling frameworks for newly commissioned projects, resulting in a disconnect between theoretical optimization and practical operation [14]. These gaps indicate that the existing research has not yet fully addressed the technical challenges of multi-objective coordination in complex water networks, highlighting the necessity of this study. In terms of scheduling methods, early studies focused on single-objective optimization, such as reservoir flood control or water supply scheduling models based on linear programming and dynamic programming, which achieve single-objective optimal solutions by simplifying constraints.

With in-depth research and the development of computer technology, intelligent optimization algorithms (e.g., genetic algorithms, particle swarm optimization algorithms, differential evolution algorithms) and multi-objective evolutionary algorithms (e.g., NSGA-II, MOPSO) have been widely applied to multi-objective scheduling problems, providing decision support by generating Pareto non-dominated solution sets [10]. In practice, management departments mostly conduct scheduling based on empirical rules or single-objective priorities, such as the Water Diversion from the Yangtze River to Taihu Lake project and the joint flood control scheduling of cascade reservoirs groups in the Yangtze River Basin, which have achieved certain results in specific scenarios [13,15,16]. However, the core challenge of scheduling in complex water networks lies in the complexity of multi-objective coordination: on one hand, natural contradictions exist between flood control, water supply, and ecological protection goals across temporal and spatial scales, such as the conflict between rapid drainage for flood control during the flood season and water storage for supply after the flood season, and the trade-off between water diversion for water quality improvement and engineering operation cost control; on the other hand, scheduling demands vary across basin, regional, and urban levels, and the interest demands of upstream and downstream, left and right banks are intertwined, further increasing the difficulty of multi-objective coordination [12,17,18]. Although existing multi-objective optimization algorithms can generate non-dominated solution sets, they insufficiently consider the strong coupling characteristics of complex water networks, and the selection of solution sets relies on subjective judgments. It is difficult to form scheduling schemes that balance scientific rigor and practical operability, and the systematicness and effectiveness of multi-objective coordination have not been fully realized [14].

Despite these advances, four critical literature gaps remain unaddressed, which restricts the practical application of multi-objective coordinated scheduling in complex water networks. First, most existing multi-objective studies adopt fixed weighting methods or static Pareto solution sets, lacking dynamic weight adjustment strategies tailored to different hydrological scenarios (e.g., flood control vs. water supply periods). This leads to poor adaptability of scheduling schemes to temporal and spatial variations in water resource demands. Second, existing algorithms fail to fully account for the strong hydraulic coupling and nonlinear relationships among numerous water conservancy projects in complex water networks, resulting in optimization results that deviate from practical engineering operations. Third, the integration of water quantity scheduling, water quality simulation, and ecological protection objectives is inadequate—most studies either separate water quantity and quality management or treat ecological indicators as secondary constraints, failing to achieve truly comprehensive multi-objective coordination. Fourth, few studies have integrated optimization models with the operational rules of newly constructed hydraulic projects, leading to a disconnect between theoretical optimization and on-the-ground implementation. These gaps highlight the urgent need for a more systematic and adaptive multi-objective scheduling framework.

The technical bottlenecks faced by water resources scheduling in complex water networks further restrict the improvement of optimization effects. First, the comprehensiveness and correlation of objectives require consideration of multiple dimensions including flood control safety, water supply guarantee, water quality improvement, and ecological maintenance. Each objective has different physical dimensions and optimization directions, making direct quantitative coordination difficult [11]. Second, complex water networks have intricate structures and numerous water conservancy projects (including reservoirs, pumping stations, sluices, etc.), with close hydraulic connections and significant nonlinear characteristics between projects, increasing the difficulty of scheduling model construction [19]. Third, water quantity and quality simulation is the foundation of scheduling optimization. However, complex water networks span large temporal and spatial scales and are influenced by multiple factors. Simulations involve extensive parameter calibration and numerical calculations, with each simulation requiring substantial computation time. This makes it difficult for traditional optimization algorithms to achieve efficient solving within the feasible region, preventing rapid optimal solution acquisition through iteration like in single reservoir scheduling [20]. These bottlenecks hinder existing scheduling methods from balancing optimization accuracy and computational efficiency in complex water networks, limiting the practical application of multi-objective coordinated scheduling.

To address this issue, this study takes the Taihu Lake Basin as a typical case and conducts systematic research to break through technical bottlenecks, focusing on the core demand of multi-objective coordinated scheduling in complex water networks. First, based on scheduling demands at basin, regional, and urban levels, a multi-objective optimization indicator system covering three major areas (flood control, water supply, and ecological environment) is constructed, comprehensively including key indicators such as drainage efficiency, water supply guarantee rate, and water quality improvement degree. Second, corresponding objective functions for each domain are established, clarifying the optimization direction and constraint conditions of different indicators. Third, an innovative variable weighting strategy is adopted to dynamically adjust the weights of each objective according to different hydrological scenarios (flood control period, water supply period, ecological environment period, etc.), converting the multi-objective optimization problem into a single-objective optimization problem to simplify solving complexity. Finally, a combined solving mode of basin water quantity-quality model and joint scheduling decision model is adopted, combining intelligent algorithms to improve computational efficiency. This study effectively overcomes complex water network technical bottlenecks—multiple conflicting objectives, intricate water system structures, dense hydraulic projects, and heavy computational loads—via an integrated technical process: indicator system construction, objective function establishment, dynamic weighting transformation, and combined model solving. It thereby provides novel theoretical and technical support for the multi-objective coordinated scheduling of water resources in such complex systems.

2. Methodology

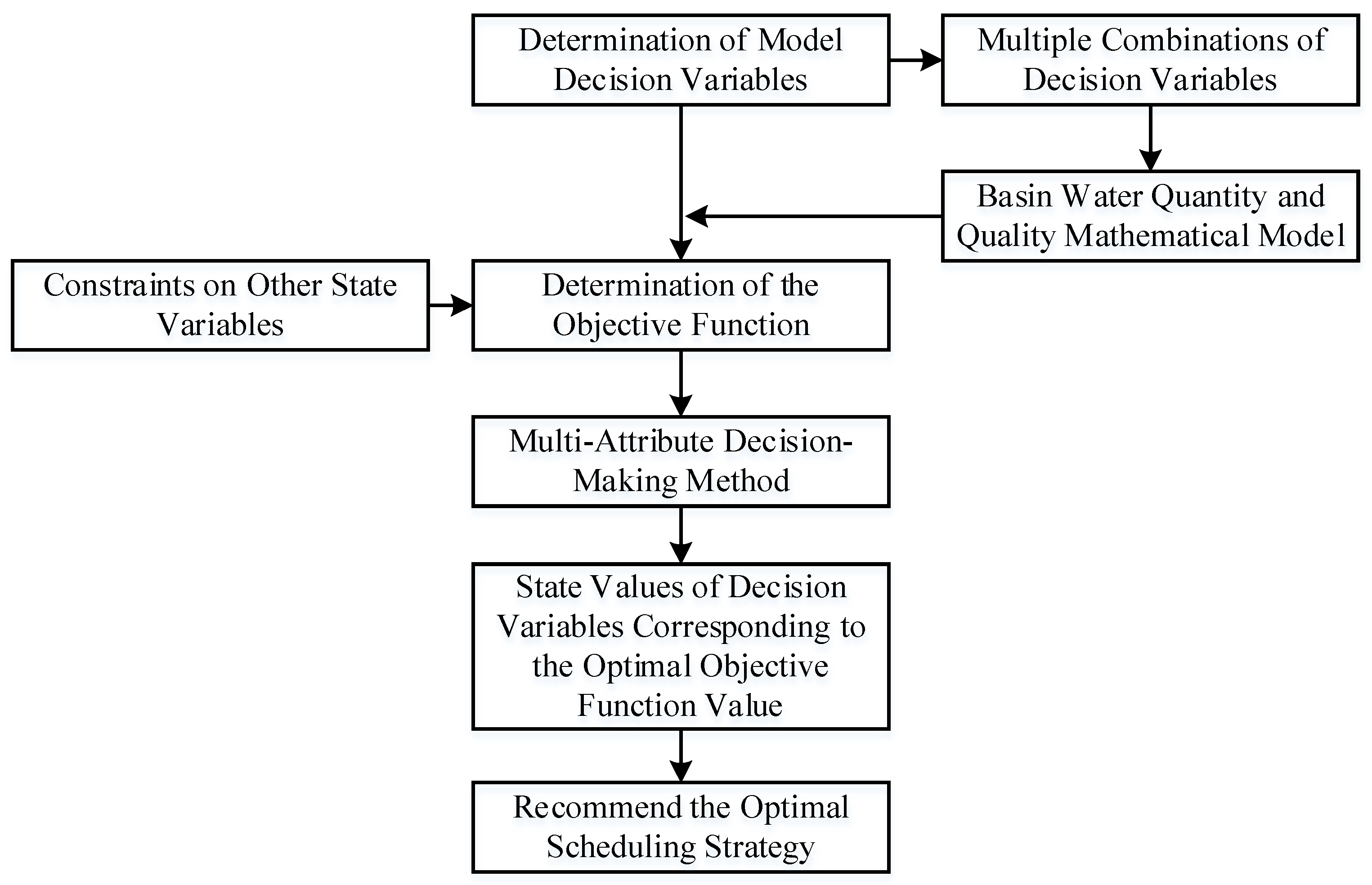
To realize multi-objective coordinated water resources scheduling in complex water networks, this study establishes an integrated technical framework (see Figure 1) that integrates indicator system construction, objective function formulation, constraint definition, and combined model solving. This framework operates through a systematic and sequential process to ensure scientificity and operability.

First, a comprehensive multi-objective optimization indicator system is constructed to cover the core demands of flood control, water supply, and aquatic ecological protection. These indicators, selected based on principles of systematicness, conciseness, importance, and independence, provide quantitative criteria for evaluating scheduling effects. Second, targeted objective functions are established for each domain, clarifying the optimization direction of flood control safety, water supply guarantee, and ecological health. Third, seven key constraint conditions are defined, including water balance, water level, flow rate, flow velocity, water quality, water quality balance, and engineering operation, to limit the feasible solution space and ensure consistency with practical engineering operations. Fourth, a combined solving mode is adopted: the basin water quantity-quality model serves as the foundation to simulate dynamic changes in water level, discharge, and water quality under different scenarios, while the particle swarm optimization (PSO) algorithm is applied to optimize scheduling alternatives, improving the efficiency and accuracy of solution acquisition.

This integrated framework seamlessly connects each technical link, from demand-oriented indicator design to constraint-based model construction, and finally to algorithm-driven optimization. It effectively addresses technical challenges such as conflicting multi-objectives, complex hydraulic connections, and heavy computational loads in complex water networks, providing a systematic and operable technical path for coordinated scheduling. The weight determination method (AHP) adopted in this study is only a supporting link within the framework, used to balance the relative importance of different objectives under specific scenarios, and does not affect the integrity and applicability of the overall technical system.

Regarding the implementation form of dynamic adjustment in this framework: it is designed with dual adaptability to meet different practical needs. In this case study, dynamic adjustment is implemented as an offline setting—specific weight combinations for different scheduling periods are predetermined based on historical hydrological characteristics, regional scheduling priorities, and expert experience. This design ensures that the scheduling scheme is stable and reliable, avoiding excessive fluctuations caused by frequent adjustments and aligning with the actual operation habits of water conservancy projects. Meanwhile, the framework has inherent extensibility for real-time adjustment: if high-frequency real-time monitoring data (e.g., real-time rainfall, water level, water quality, and water demand) are available, the dynamic adjustment mechanism can be integrated with a data-driven module. The system can automatically update objective weights or scheduling parameters based on the deviation between real-time operational status and preset thresholds, realizing adaptive adjustment during operation. This real-time mode requires support from mature monitoring infrastructure and efficient algorithm response capabilities, which is not the focus of the current study but constitutes a key direction for future application expansion and technical upgrading.

2.1. Decision Indicators

Decision indicators refer to the undetermined control variables or operating variables involved in optimal decision problems that are related to constraints and objective functions. The corresponding state of a set of decision variables constitutes a solution to the optimal decision problem.

The decision indicators of the model are determined by the control indicators involved in the operation of water conservancy projects in river network areas. Complex river networks usually have numerous water conservancy projects, and their operation has complex nonlinear relationships with regional water level, quantity, and quality indicators. This study selects the operation control indicators that have relatively strong sensitive relationships with water quantity and water quality objectives as the decision variables of the joint scheduling model. This study selects decision indicators from three aspects: the fields of flood control objectives, water supply objectives, and aquatic ecological environment objectives, ensuring that the joint scheduling schemes can meet the comprehensive water quantity and water quality scheduling needs of the areas involved in the project. When selecting indicators, the principles of systematicness, conciseness, importance, and independence should be followed.

2.1.1. Decision Indicators for Flood Control Objectives

Four indicators in the field of flood control objectives are selected as decision variables, including the drainage efficiency of key outward discharge hubs, the exceedance risk of flood control representative stations above the protection standard, the regional outward discharge coefficient, and the satisfaction degree of pre-discharge objectives.

(1) Drainage efficiency of key outward discharge hubs DS

$$DS=Q/Q_d\cdot {(Z/Z_w)}^{-1}$$

(1)

where Q denotes the actual discharge flow at the control section of key outward discharge hub; Q_d represents the maximum designed flow capacity of key outward discharge hub; Z is the actual water level of basin and regional representative stations during the scheduling period; Z_w stands for the flood control warning water level of basin and regional representative stations. The drainage efficiency of key outward discharge hubs (DS) is a higher-is-better indicator.

(2) Exceedance risk of flood control representative stations above the protection standard CB

$$CB=(H_f(t)-H_w)/H_w\cdot \delta t$$

(2)

where $H_f(t)$ is the water level of the flood control representative station at time t; H_w denotes the flood control guaranteed water level of the flood control representative station; $\delta t$ represents the duration of exceedance above the protection standard.

(3) Regional outward discharge coefficient WP

$$WP=P/(R+W)$$

(3)

where P denotes the outward discharge volume of a specific region within a certain period; R represents the local water yield of the same region during the same period; W is the incoming water volume from other regions entering the same region.

(4) Satisfaction degree of pre-discharge objectives PY

For the objectives of pre-discharge scheduling for lakes, reservoirs, and other water bodies, the PY indicator value for the satisfaction degree of pre-discharge objectives is set according to the degree to which the current water level meets the pre-discharge objectives.

2.1.2. Decision Indicators for Water Supply Objectives

Four indicators in the field of water supply objectives are selected as decision variables, including the water supply efficiency of water diversion and supply projects, the water level satisfaction degree of water supply representative stations, the improvement degree of water quality indicators (NH3-N/DO/TN/TP/COD) in water sources, and the compliance guarantee rate of water quality indicators (NH3-N/DO/TP/COD) in water sources.

(1) Water supply efficiency of water diversion and supply projects η

$$\eta ={\displaystyle \frac{R}{Y}}$$

(4)

where R is the water supply volume of the water diversion and supply project; Y denotes the water diversion volume of the water diversion and supply project. The water supply efficiency of the water diversion and supply project is a higher-is-better indicator.

(2) Water level satisfaction degree of water supply representative stations PG

$$PG={\displaystyle \sum _{t=1}^{T}sgn(H_g(t)-H^s)}$$

(5)

where $H_g(t)$ is the water level of water supply representative station at time t; $H^s$ denotes the minimum allowable average water level of water supply representative station; sgn(*) is the sign function—if the * is greater than 0, the value of sgn(*) is 1; otherwise, it is 0. The water level satisfaction degree (satisfaction duration) of water supply representative stations is a higher-is-better indicator.

(3) Improvement degree of water quality indicators (NH3-N/DO/TN/TP/COD) in water sources ID

$$I{D}^x={\displaystyle \frac{R^x(1)-R^x(T)}{R^x(1)}}$$

(6)

where $R^x(t)$ is the concentration value of the water quality indicator x at time t.

(4) Compliance guarantee rate of water quality indicators (NH3-N/DO/TP/COD) in water sources PQ

$$P{Q}^x={\displaystyle \frac{T{Q}^x}{T}}={\displaystyle \frac{{\displaystyle \sum _{t=1}^T\mathrm{sgn}(R^x(t)-R_u^x)\cdot \Delta t}}{T}}$$

(7)

where $R^x(t)$ is the concentration value of water quality indicator x in water sources at time t; $R_u^x$ denotes the critical compliance value of water quality indicator x; $\Delta t$ represents the scheduling time step; T is the length of the scheduling period. The compliance guarantee rate of water quality indicators (NH3-N/DO/TN/TP/COD) in water sources is a higher-is-better indicator.

2.1.3. Decision Indicators for Aquatic Ecological Environment Objectives

(1) Guarantee rate of ecological water level PW

$$PW={\displaystyle \frac{{\displaystyle \sum _{t=1}^{T}sgn(WL(t)-W{L}_B)}}{T}}$$

(8)

where $W{L}_B$ is the ecological water level of the representative section; $WL(t)$ denotes the water level of the representative section at a certain time t.

(2) Improvement degree of water quality in the scheduling impact area WD

$$W{D}^x={\displaystyle \frac{P{T}^x(1)-P{T}^x(T)}{P{T}^x(1)}}$$

(9)

where $P{T}^x(t)$ is the concentration value of water quality indicator x at the representative section of the scheduling impact area at time t. The improvement degree of water quality indicators (NH3-N/DO/TN/TP/COD) at representative section of the scheduling impact area is a higher-is-better indicator.

(3) Improvement degree of flow velocity at the representative section WL

$$WL={\displaystyle \frac{v(1)-v(T)}{v(1)}}$$

(10)

where $v(t)$ is the flow velocity at the representative section of the river channel at time t. The improvement degree of flow velocity at the representative section is a higher-is-better indicator.

(4) Water diversion cost W

Although the water diversion cost seems to be an economic accounting indicator, it is deeply bound to the “pressure, state, and response” of the aquatic ecological environment. Essentially, it serves as an “economic reflection” and “regulatory lever” of the aquatic ecological environment status, thus being incorporated into the aquatic ecological environment indicator system. This study adopts water diversion volume to measure water diversion cost, comprehensively taking into account water diversion time and water diversion scale:

$$W={\displaystyle \sum _1^T{Q}_p(t)}$$

(11)

where $Q_p(t)$ is the water diversion flow at time t. Water diversion cost is a lower-is-better indicator.

2.1.4. Indicator Normalization

To eliminate the impact of different physical dimensions among indicators on the calculation results, indicator normalization is performed. Suppose there are m alternatives, each including n indicators; then the eigenvalue matrix for the n indicators is as follows:

$$X={(x_{ij})}_{m\times n}=\left[\begin{array}{llll}{x}_{11}& x_{12}& \dots & x_{1n}\\ x_{21}& x_{22}& \dots & x_{2n}\\ ⋮& ⋮& & ⋮\\ x_{m1}& x_{m2}& \dots & x_{mn}\end{array}\right]$$

(12)

where $x_{ij}$ is the j-th indicator of the i-th alternative.

According to the following equation, the eigenvalue matrix X = (x_ij)_m×n is normalized to obtain the normalized matrix R = (r_ij)_m×n.

Higher-is-better indicators:

$$r_{ij}={\displaystyle \frac{x_{ij}-\min x_{ij}}{\max x_{ij}-\min x_{ij}}}$$

(13)

Lower-is-better indicators:

$$r_{ij}={\displaystyle \frac{\max x_{ij}-x_{ij}}{\max x_{ij}-\min x_{ij}}}$$

(14)

where r_ij denotes the normalized indicator value of the j-th indicator for the i-th alternative; $\max x_{ij}$ represents the maximum eigenvalue of indicator j in the overall set; $\min x_{ij}$ denotes the minimum eigenvalue of indicator j in the overall set. Handling of constant columns: If all values of the j-th indicator across all alternatives are identical (i.e., $\max x_{ij}=\min x_{ij}$), the denominator in Equations (13) and (14) becomes zero, leading to undefined results. For such cases, the normalized value of the j-th indicator for all alternatives is uniformly set to $r_{ij}=0$. This handling is based on two rationales: (1) A constant indicator means it has no discriminatory power among alternatives (all schemes perform equally well in this dimension), so assigning a uniform minimum normalized value 0 avoids distorting the comprehensive evaluation; (2) This method maintains consistency with the normalization interval [0, 1] and does not affect the relative weight of other discriminatory indicators in the objective function calculation. These normalization equations (Equations (13) and (14)) are derived based on the classic linear normalization logic, adapted to the study’s multi-objective evaluation needs. They eliminate dimensional differences among indicators while preserving the relative order of performance, which is consistent with the core requirements of complex water network scheduling evaluation.

2.2. Indicator Weights

Weight coefficient determination can be achieved through subjective weighting methods and objective weighting methods. This study adopts the analytic hierarchy process (AHP) among subjective weighting methods to determine the indicator weights of the optimization model, fully considering expert opinions and the role of each indicator in practical scheduling to make the results more in line with practical scenarios.

2.3. Objective Functions

The objectives of joint water resources scheduling in complex water networks typically cover multiple dimensions, such as flood control, water supply, environment, ecology, society, and economy. The incommensurability and conflicting nature among these objectives are the core characteristics of adaptive water resources scheduling problems. To balance and coordinate the relationships between different objectives, two common processing methods are adopted: one is to construct a multi-objective optimal scheduling model based on different objectives, obtain a non-inferior solution set by solving the model, and then select the optimal solution from the set using decision-making methods; the other is to assign differentiated weights to different objectives and convert the multi-objective problem into a comprehensive single-objective optimization problem through methods such as linear weighting. In view of the complexity of each objective, the second processing method is adopted in this study.

The objective function of the water resources scheduling model can be written as:

$$\max W\left(x\right)=\left[{\alpha }_i{f}_1\left(x_i\right),{\beta }_j{f}_2\left(x_j\right),{\gamma }_k{f}_3\left(x_k\right)\right]$$

(15)

where f₁, f₂ and f₃ respectively correspond to the objective areas of flood control, water supply, and aquatic ecological environment; ${\alpha }_i$, ${\beta }_j$ and ${\gamma }_k$ are the weights of decision variables for the objective areas of flood control, water supply, and water environment, respectively.

(1) Objectives of flood control

$$\max f_1=\max f_1\left({\alpha }_{1,i}D{S}_i+{\displaystyle \frac{{\alpha }_{2,i}}{C{B}_i}}+{\alpha }_{3,i}W{P}_i+{\alpha }_{4,i}PY\right)$$

(16)

(2) Objectives of water supply

$$\max f_2=\max f_2\left({\beta }_{1,j}{\eta }_j+{\beta }_{2,j}P{G}_j+{\beta }_{3,j}I{D}_j^x+{\beta }_{4,j}P{Q}_j^x\right)$$

(17)

(3) Objectives of aquatic ecological environment

$$\max f_3=\max f_3\left({\gamma }_{1,k}P{W}_k+{\gamma }_{2,k}W{D}_k^x+{\gamma }_{3,k}W{L}_k+{\displaystyle \frac{{\gamma }_{4,k}}{W_k}}\right)$$

(18)

The overall objective function (Equation (15)) is originally constructed to integrate the three core objective domains (flood control, water supply, aquatic ecological environment). It adopts a linear weighting approach tailored to the dynamic scheduling characteristics of the Taihu Lake Basin, converting multi-objective optimization into a solvable single-objective problem [21]. The sub-objective functions (Equations (16)–(18)) are derived by quantifying the key evaluation indicators (Section 2.1) and aligning with practical scheduling priorities, ensuring the model’s relevance to engineering operations [12,22,23].

2.4. Constraint Conditions

The constraint conditions of the water resources scheduling model cover seven key aspects: water balance constraints, water level constraints, flow rate constraints, flow velocity constraints, water quality constraints, water quality balance constraints, and engineering operation constraints. Detailed descriptions are as follows:

(1) Water balance constraints

For key units of the water resources system (e.g., reservoirs, pumping stations, sluices), the water balance relationship must be satisfied in any time period t. Specifically, the inflow volume of the n-th unit during period t equals the sum of the outflow volume, the change in storage capacity (difference between the end-of-period and start-of-period storage capacities of the n-th unit in period t), and the water loss within the unit during period t.

(2) Water level constraints

The water level of units such as reservoirs and river channels must comply with specific minimum and maximum limits in different periods. These limits are formulated to meet multi-dimensional needs including flood control, water supply, navigation, and ecological protection, ensuring the safe and effective operation of the water system. For the n-th unit in period t, its actual water level must be within the range defined by the allowable minimum and maximum water levels.

(3) Flow rate constraints

In addition to water level constraints, units such as reservoirs, sluices, turbines, and key river sections are subject to flow rate limits in different periods. These constraints are primarily determined by factors such as pre-established scheduling rules and inherent engineering characteristics (e.g., structural design parameters). For the n-th unit in period t, the actual flow rate must be bounded by the allowable minimum and maximum flow rates.

(4) Flow velocity constraints

Flow velocity constraints apply to units including river representative sections and flow channels of water conservancy projects. To ensure ecological health (e.g., maintaining suitable habitat conditions for aquatic organisms) and engineering safety (e.g., preventing channel scouring or silting), the flow velocity of the n-th unit in period t must be maintained within the range of allowable minimum and maximum flow velocities.

(5) Water quality constraints

Key water quality indicators (e.g., NH3-N, DO, TP, COD) of each unit must meet the preset minimum water quality standards. For the n-th unit in period t, the concentration of each water quality indicator must not be lower than the specified minimum target value, ensuring compliance with water use requirements (e.g., drinking water supply, ecological base flow) and environmental regulations.

(6) Water quality balance constraints

This constraint is quantitatively described by a coupled water quantity and quality model. It reflects the dynamic balance between water quality indicators of the unit and key processes such as inflow/outflow transport, pollutant generation, and transformation within the unit over different time periods, ensuring the consistency of water quality simulation results with actual environmental processes.

(7) Engineering operation constraints

This category mainly includes constraints related to the operational performance and scheduling modes of numerous water conservancy projects. Specific constraints include, but are not limited to, the maximum water-carrying capacity of engineering structures (e.g., sluice gate opening limits, pumping station capacity constraints), fixed scheduling operation protocols (e.g., priority of water supply over ecological water release), and safety operation thresholds (e.g., maximum allowable operational duration of pumping units).

2.5. Optimization Method

An alternative optimization model based on the particle swarm optimization (PSO) algorithm is adopted to optimize the set of scheduling alternatives, with the optimization process relying on the simulation results of water quantity and water quality.

3. Case Study

3.1. Study Area

The study was conducted in the Taihu Lake Basin (see Figure 2), a typical complex water network situated in the Yangtze River Delta of eastern China. Covering an area of approximately 36,900 km², the basin spans Jiangsu Province, Zhejiang Province, Anhui Province, and Shanghai Municipality. It is characterized by a complex river-lake interconnection (with Taihu Lake as the central water body), dense distribution of hydraulic structures (e.g., the Xinmeng River Project), high population density, and advanced socio-economic development—collectively posing substantial demands for flood control, water supply security, and ecological protection.

Climatologically, the basin features a subtropical monsoon climate, with an annual average precipitation of 1100–1200 mm, 60–70% of which occurs in the flood season (May–September). Notably, under the influence of global climate change, extreme rainfall events (e.g., the 1991-type extreme rainfall scenario adopted in this study) have become increasingly frequent, leading to acute trade-offs among multi-objective water resources management. These inherent characteristics render the Taihu Lake Basin an ideal prototype for validating the proposed multi-objective coordinated scheduling model.

Taking the Taihu Lake Basin as a typical case (see Figure 1), this study uses the 1991-type 100-year return period rainfall flood control scenario. The whole year is divided into 9 scheduling periods (

Table 1. Identification of Scheduling Periods for Joint Scheduling Decision-Making under the 1991-Type 100-Year Return Period Rainfall Scenario.

No.	Date	Scheduling Period
1	Jan. 3–Mar. 23	Water Supply and Aquatic Ecological Scheduling Period
2	Mar. 26–May 3	Flood Control Scheduling Period
3	May 4–May 8	Aquatic Ecological Scheduling Period
4	May 10–May 23	Aquatic Ecological Scheduling Period
5	May 24–Aug. 2	Flood Control Scheduling Period
6	Aug. 4–Aug. 7	Aquatic Ecological Scheduling Period
7	Aug. 8–Aug. 17	Flood Control Scheduling Period
8	Aug. 18–Aug. 25	Aquatic Ecological Scheduling Period
9	Aug. 27–Dec. 30	Water Supply and Aquatic Ecological Scheduling Period

), including flood control periods, aquatic ecological scheduling periods, and water supply–aquatic ecological scheduling periods. The indicator weight combinations in different periods are listed in

Table 2. Indicator Weight Combinations in Different Periods.

Indicator	Weight
	Flood Control Scheduling Period	Water Supply Scheduling Period	Aquatic Ecological Scheduling Period
DS	0.4620	0.3991	0.3112
CB	0.2239	0.2222	0.2587
WP	0.0862	0.1098	0.1441
PY	0.0534	0.0727	0.0905
η	0.0534	0.0532	0.0471
PG	0.0415	0.0532	0.0360
ID	0.0251	0.0367	0.0360
PQ	0.0231	0.0155	0.0307
PW	0.0100	0.0127	0.0238
WD	0.0100	0.0127	0.0149
WL	0.0076	0.0062	0.0035
W	0.0038	0.0062	0.0035

.

Weight coefficient determination can be achieved through subjective weighting methods and objective weighting methods. Our proposed general methodological framework supports flexible selection of weighting methods: AHP is adopted in this study, and it can be replaced by other methods based on research objectives, data availability, or practical application scenarios.

In this specific case study of the Taihu Lake Basin, we selected the analytic hierarchy process (AHP) to determine the indicator weights, which is a conventional and mature method in water resources scheduling research. The implementation follows standard AHP procedures: 5 experts (with extensive experience in Taihu Lake Basin water management or related research) conducted pairwise comparisons of the relative importance of the three objective domains (flood control, water supply, aquatic ecological environment) and their respective 12 indicators across different scheduling periods. The expert judgments were quantified using the Saaty 1–9 scale, and consistency verification was performed to ensure rationality of the results. All judgment matrices passed the consistency test, with consistency ratio (CR) values ranging from 0.01 to 0.08 (below the critical threshold of 0.1), confirming no logical contradictions in the pairwise comparison results. Given that this is a well-recognized and routine operation in relevant research, detailed steps of the pairwise comparison and judgment matrix construction were not elaborated in the original manuscript to avoid redundant content.

The weight determination process fully considers expert experience and practical scheduling priorities, ensuring that the calculated weights are consistent with the actual operation needs of the Taihu Lake Basin. For readers interested in the detailed judgment matrix and calibration process, complete documentation is available from the corresponding author upon request.

3.2. Design of Scheduling Schemes

For the 1991-Type 100-Year Return Period Rainfall Scenario, three scheduling schemes are designed in this case study, including the basic scheduling scheme (JC scheme) and two enhanced discharge schemes for the Xinmeng River Project (FH1-XM1 and FH1-XM2 schemes), with the latter two modified based on the JC scheme. The scheduling rules of each scheme are formulated according to three types of Taihu Lake water level scenarios, and the specific operations of the Xinmeng River Jiepai Hub and Benniu Hub Sluice under different scenarios are as follows:

3.2.1. JC Scheme

When the water level of Taihu Lake is above or equal to the flood control level, the Jiepai Hub operates based on the Fangqian water level: the sluice is closed when the Fangqian water level is lower than 4.2 m; the sluice is opened for drainage when the Fangqian water level ranges from 4.2 m to 4.6 m; both the sluice and pumps are opened for drainage when the Fangqian water level is 4.6 m or higher. For the Benniu Hub Sluice, it remains fully open when the Fangqian water level is below 4.2 m, and the sluice is opened for drainage (with a discharge not exceeding 128 m³/s) when the Fangqian water level is 4.2 m or higher.

When the water level of Taihu Lake is between the water transfer limit level and the flood control level, the scheduling rules of the Jiepai Hub are adjusted as follows: the sluice is opened for drainage when the Fangqian water level is 4.2 m or higher; the sluice is closed when the Fangqian water level ranges from 3.7 m to 4.2 m; the sluice is appropriately opened for water diversion when the Fangqian water level is below 3.7 m. Corresponding to this scenario, the Benniu Hub Sluice is closed if the water level at the Benniu Hub of the Beijing-Hangzhou Grand Canal is lower than or equal to 5.1 m (and open for drainage if higher) when the Fangqian water level is below 3.7 m; it remains fully open when the Fangqian water level ranges from 3.7 m to 4.2 m; and the sluice is opened for controlled drainage when the Fangqian water level is 4.2 m or higher.

When the water level of Taihu Lake is below the water transfer limit level, the Jiepai Hub conducts drainage when the Fangqian water level is 4.2 m or higher and water diversion when the Fangqian water level is below 4.2 m. The scheduling rules of the Benniu Hub Sluice are consistent with those in the “water transfer limit level ~ flood control level” scenario.

3.2.2. FH1-XM1 Scheme

The scheduling rules of this scheme are identical to those of the JC scheme in the “water transfer limit level~flood control level” and “below water transfer limit level” scenarios. Only in the scenario where the Taihu Lake water level is above or equal to the flood control level, the scheduling thresholds of the two hubs are adjusted during the period from May 1 to September 30: for the Jiepai Hub, the sluice is closed when the Fangqian water level is below 4.0 m, opened for drainage when the Fangqian water level ranges from 4.0 m to 4.6 m, and both the sluice and pumps are opened for drainage when the Fangqian water level is 4.6 m or higher; for the Benniu Hub Sluice, it remains fully open when the Fangqian water level is below 4.0 m, and the sluice is opened for drainage (with a discharge not exceeding 128 m³/s) when the Fangqian water level is 4.0 m or higher. Outside the period from May 1 to September 30, the scheduling rules are the same as those of the JC scheme.

3.2.3. FH1-XM2 Scheme

Similar to the FH1-XM1 scheme, its scheduling rules are consistent with the JC scheme in the “water transfer limit level~flood control level” and “below water transfer limit level” scenarios. The adjustment is only made in the “Taihu Lake water level ≥ flood control level” scenario during the period from May 1 to September 30: the sluice closing threshold of the Jiepai Hub is reduced to 3.8 m (closed when the Fangqian water level is below 3.8 m, opened for drainage when ranging from 3.8 m to 4.6 m, and both sluice and pumps opened when ≥4.6 m); the fully open threshold of the Benniu Hub Sluice is also adjusted to 3.8 m (fully open when the Fangqian water level is below 3.8 m, and opened for drainage with a discharge not exceeding 128 m³/s when ≥3.8 m). Outside the period from May 1 to September 30, the scheduling rules follow the JC scheme.

3.3. Results

3.3.1. Simulation of Scheduling Schemes

A water quantity and quality simulation model is adopted to conduct simulations for each scheme. The coupled model adopted in this study is a mature tool that has been widely verified and applied in the Taihu Lake Basin [13], integrating 1D river network water quantity balance and water quality migration-transformation processes. Its core functions in this research include: simulating dynamic changes in water level and discharge in the basin’s main river network under different scheduling schemes; predicting the concentration variations in key water quality indicators (NH3-N, DO, TP, COD) concerned in this study; and providing quantitative input for the evaluation of water quality-related decision indicators (e.g., improvement degree of water quality, compliance guarantee rate).

The model’s reliability is guaranteed through two aspects: first, key parameters (e.g., longitudinal dispersion coefficient, pollutant decay coefficient) are calibrated and verified using long-term hydrological and water quality monitoring data from the Taihu Lake Basin Administration, with simulation errors meeting the technical requirements of water resources scheduling research; second, the model has been successfully applied in previous studies on water resources optimization scheduling and water quality improvement in the Taihu Lake Basin, demonstrating good adaptability to the region’s complex water network characteristics [13].

Given that the core focus of this paper is the multi-objective coordinated scheduling method rather than the development of the coupled water quantity and quality model itself, detailed mathematical expressions, parameter sensitivity analysis, and comprehensive verification results of the model are not elaborated here.

(1) Regional and Taihu Lake Water Levels

High water levels in the western lake area and Taihu Lake directly reflect the regulatory effect of the Xinmeng River’s enhanced discharge schemes. Under the 1991-Type 100-Year Return Period Rainfall scenario, the maximum water levels at Wangmuguan, Fangqian, Jintan, and Changzhou (III) stations under the JC scheme are 6.35 m, 5.73 m, 6.51 m, and 5.64 m, respectively. Among these stations, Fangqian and Changzhou (III) have relatively long durations of exceeding the guaranteed water level, with 22 days and 19 days, respectively; the maximum water level of Taihu Lake is 4.49 m. The regional water level hydrographs of the FH1-XM1 and FH1-XM2 schemes are basically consistent with that of the JC scheme. However, as the reference water level for drainage scheduling of the Xinmeng River decreases, the maximum water levels in the region and Taihu Lake show a decreasing trend, as illustrated in Figure 3.

(2) Discharge of the Xinmeng River to the Yangtze River

Under the 1991-Type 100-Year Return Period Rainfall scenario, the average discharge of the Xinmeng River Jiepai Hub to the Yangtze River during the flood control period is 75 m³/s for the JC scheme, while those for the FH1-XM1 and FH1-XM2 schemes are 81 m³/s and 82 m³/s, respectively, as shown in Figure 4.

3.3.2. Joint Scheduling Decision Calculation

In this scenario, the calculation of the joint scheduling model focuses on decision indicators related to the flood control objective domain. For the calculation of each indicator, the drainage efficiency of key outflow hubs targets the Xinmeng River Project; the exceedance risk of guaranteed water level at flood control representative stations mainly considers stations in the upper reaches of the basin (e.g., Wangmuguan, Fangqian, Jintan, Changzhou (III)) and Taihu Lake. The normalized results of each indicator are shown in

Table 3. Normalized Results of Decision Indicators for the Enhanced Discharge Schemes of the Xinmeng River Project.

Schemes	Scheduling Period	DS	CB	WP	PY	η	PG	ID				PQ			PW	WD				WL	W
								COD	NH3-N	TP	TN	COD	NH3-N	TP		COD	NH3-N	TP	TN
JC	Flood Control Scheduling Period	0.37	0.44	0.40	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0.93	1.00
	Aquatic Ecological Scheduling Period	1.00	1.00	1.00	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0.78	1.00
	Water Supply and Aquatic Ecological Scheduling Period	1.00	1.00	1.00	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0.97	0.69
FH1- XM1	Flood Control Scheduling Period	0.85	0.87	0.83	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0.40	1.00
	Aquatic Ecological Scheduling Period	1.00	1.00	1.00	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0.73	1.00
	Water Supply and Aquatic Ecological Scheduling Period	1.00	1.00	1.00	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0.45	0.39
FH1- XM2	Flood Control Scheduling Period	0.92	1.00	0.92	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0.40	1.00
	Aquatic Ecological Scheduling Period	1.00	1.00	1.00	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0.97	1.00
	Water Supply and Aquatic Ecological Scheduling Period	1.00	1.00	1.00	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0.70	1.00

.

Under the 1991-Type 100-Year Return Period Rainfall scenario, the sensitive indicators in the flood control objective domain of this scheme set include the drainage efficiency of key outflow hubs, the exceedance risk of guaranteed water level at flood control representative stations, and the regional outflow coefficient. Since there is no difference in the water level of Taihu Lake on April 1 among all schemes, the pre-discharge target satisfaction degree is a non-sensitive indicator. The differences in the drainage efficiency of key outflow hubs among the schemes are reflected in the flood control period: the values of this indicator for the JC, FH1-XM1, and FH1-XM2 schemes are 0.37, 0.85, and 0.92, respectively, while the regional outflow coefficients of the western lake area are 0.4, 0.83, and 0.92, respectively. These results indicate that the outflow volumes of the Xinmeng River Project and the western lake area under the FH1-XM1 and FH1-XM2 schemes are higher than those under the JC scheme. With the increase in the outflow volume of the western lake area, the exceedance risk of guaranteed water level at flood control representative stations for the FH1-XM1 and FH1-XM2 schemes increases from 0.44 (JC scheme) to 0.87 and 1, respectively.

The objective function values of the three schemes are 94.4, 97.7, and 98.8, respectively. During the flood control period, the objective function value of the FH1-XM2 scheme is higher than those of the JC and FH1-XM1 schemes, as shown in

Table 4. Decision Table for the Enhanced Discharge Schemes of the Xinmeng River Project.

Scheduling Period		JC Scheme	FH1-XM1 Scheme	FH1-XM2 Scheme
Jan. 3–Mar. 23	Water Supply and Aquatic Ecological Scheduling Period	95.6	100.0	100.0
Mar. 26–May 3	Flood Control Scheduling Period	95.6	100.0	100.0
May 4–May 8	Aquatic Ecological Scheduling Period	95.6	100.0	100.0
May 10–May 23	Aquatic Ecological Scheduling Period	95.6	100.0	100.0
May 24–Aug. 2	Flood Control Scheduling Period	92.0	96.6	97.1
Aug. 4–Aug. 7	Aquatic Ecological Scheduling Period	92.9	99.4	99.7
Aug. 8–Aug. 17	Flood Control Scheduling Period	91.8	97.2	99.1
Aug. 18–Aug. 25	Aquatic Ecological Scheduling Period	94.5	97.2	99.8
Aug. 27–Dec. 30	Water Supply and Aquatic Ecological Scheduling Period	94.7	95.9	98.6
Year		94.4	97.7	98.9

. The objective function values of each scheme and the main decision indicators in the flood control objective domain indicate that the FH1-XM2 scheme is the optimal scheme among the set.

3.3.3. Benefit Analysis

(1) Effect of Enhanced Discharge of the Xinmeng River

The enhanced discharge schemes of the Xinmeng River reduce the reference water level for drainage scheduling of the Xinmeng River Jiepai Hub during the flood season (when the Taihu Lake water level is above the flood control level). For the FH1-XM2 scheme, the number of drainage days of the Jiepai Hub during the flood season increases from 32 days (JC scheme) to 43 days—this extension of drainage duration effectively expands the floodwater discharge window, reducing the accumulation of floodwater in the western lake area and alleviating the pressure of continuous high water levels on upstream embankments and hydraulic structures. Data on the discharge volumes of the western lake area and the Xinmeng River Project during the flood season and peak flood period show that the discharge volume of the Xinmeng River to the Yangtze River and the inflow volume of the western lake area into the Yangtze River are both significantly higher than those under the JC scheme, while the inflow volumes of the western lake area into Taihu Lake and the Wuchengxiyu Area decrease accordingly.

During the flood season, compared with the JC scheme, the FH1-XM2 scheme increases the discharge volume of the Xinmeng River Jiepai Hub to the Yangtze River by 100 million m³ (a growth rate of 9.5%)—this additional discharge volume is equivalent to the flood storage capacity of a small reservoir, directly reducing the risk of waterlogging in the 1200 km² drainage area of the western lake area, increases the discharge volume of the western lake area to the Yangtze River by 0.40 × 100 million m³—effectively reducing the backwater impact on the upstream river network and improving the drainage capacity of the regional water system, and reduces the inflow volume of the western lake area into Taihu Lake by 0.30 × 100 million m³—alleviating the storage pressure of Taihu Lake and avoiding the need for emergency discharge measures that may affect downstream areas. During the peak flood period, the discharge volume of the Xinmeng River Jiepai Hub to the Yangtze River increases by 0.72 × 100 million m³ (a growth rate of 12.6%)—this targeted increase in peak discharge effectively cuts off the flood peak, reducing the probability of exceedance over the guaranteed water level at key stations such as Wangmuguan and Fangqian, the inflow volume of the Xinmeng River into Taihu Lake decreases slightly—avoiding excessive water supplement to Taihu Lake during the peak flood period and maintaining the lake’s flood control storage space, the discharge volume of the western lake area to the Yangtze River increases by 0.51 × 100 million m³—strengthening the rapid discharge of floodwater in the core flood-prone area, and the inflow volume of the western lake area into Taihu Lake decreases by 0.32 × 100 million m³—reducing the hydraulic connection pressure between the western lake area and Taihu Lake, and improving the stability of the overall water system operation. Details are shown in

Table 5. Water Volume Statistics of the Western Lake Area and Xinmeng River During the Flood Season and Peak Flood Period (During the Flood Control Period).

Statistical Period	Statistical Item	Water Volume Statistics (100 Million m3)		Water Volume Change (100 Million m3)	Variation Rate (%)
		JC	FH1-XM2
Flood Season	Discharge Volume of the Western Lake Area to the Yangtze River	15.35	15.75	0.40	2.6%
	Inflow Volume of the Western Lake Area into Taihu Lake	46.57	46.27	−0.30	−0.6%
	Inflow Volume of the Western Lake Area into the Wuchengxiyu Area	17.49	17.33	−0.16	−0.9%
	Discharge Volume of the Jiepai Hub to the Yangtze River	7.47	8.18	0.71	9.5%
	Inflow Volume of the Xinmeng River into Taihu Lake	11.02	10.95	−0.07	−0.6%
Peak Flood Period	Peak Flood Period	11.60	12.11	0.51	4.4%
	Inflow Volume of the Western Lake Area into Taihu Lake	17.87	17.55	−0.32	−1.8%
	Inflow Volume of the Western Lake Area into the Wuchengxiyu Area	5.25	5.10	−0.15	−2.8%
	Discharge Volume of the Jiepai Hub to the Yangtze River	5.72	6.44	0.72	12.6%
	Inflow Volume of the Xinmeng River into Taihu Lake	3.44	3.37	−0.07	−2.0%

.

(2) Regional Flood Control Benefits of the Basin

With the increase in the outflow volumes of the Xinmeng River Project and the western lake area, under the 1991-Type 100-Year Return Period Rainfall scenario, the maximum water levels at Wangmuguan, Fangqian, Jintan, Changzhou (III) and other stations under the FH1-XM2 scheme are significantly lower than those under the JC scheme. Specifically, the maximum water levels at Wangmuguan and Fangqian decrease by 5 cm, while those at Jintan and Changzhou (III) decrease by 4 cm. As the upstream outflow volume increases and the regional water level decreases, the maximum water level of Taihu Lake under the FH1-XM2 scheme is 1 cm lower than that under the JC scheme, as shown in

Table 6. Statistical Table of Water Level Characteristic Values for Taihu Lake and Regional Areas.

Stations	Annual Maximum Water Level (m)			Annual Duration of Exceeding the Guaranteed Water Level (d)
	JC	FH1-XM2	Variation	JC	FH1-XM2	Variation
Taihu Lake	4.49	4.48	−0.01	0	0	0
Wangmuguan	6.35	6.30	−0.05	10	10	0
Fangqian	5.73	5.68	−0.05	22	21	−1
Jintan	6.71	6.67	−0.04	7	7	0
Changzhou (III)	5.64	5.60	−0.04	19	19	0

.

3.3.4. Scheme Recommendation

Under the 1991-Type 100-Year Return Period Design Rainfall scenario, the number of drainage days of the Jiepai Hub during the flood season increases under the FH1-XM2 scheme. Compared with the JC scheme, the discharge volumes of the western lake area and the Xinmeng River Project to the Yangtze River are significantly higher during both the flood season and peak flood period, while the inflow volume of the western lake area into Taihu Lake decreases accordingly. The maximum water levels at regional stations decrease more significantly, and the water level of Taihu Lake is also reduced to a certain extent, thus reducing the regional flood control risk of the basin. Based on the decision results of the joint scheduling model, the FH1-XM2 scheme is recommended as the optimal scheme among the enhanced discharge schemes for the Xinmeng River Project.

3.4. Discussion

3.4.1. Analysis of Scheduling Results

Beyond the quantitative data presented earlier, the scheduling results reveal important intrinsic logic and practical implications worth further discussion. The optimal enhanced discharge scheme’s superior performance stems from the dynamic weighting strategy’s adaptive adjustment of objective priorities. Unlike the basic scheme with fixed weighting, this strategy flexibly allocates weights to flood control, water supply, and ecological indicators according to different hydrological scenarios. During the flood season, it prioritizes flood control needs to ensure rapid discharge while maintaining basic water supply security and ecological base flow, effectively addressing the limitations of fixed weighting schemes in responding to extreme hydrological events.

The optimal scheme also demonstrates strong spatial-temporal adaptability by fully considering the hydrological and hydrodynamic characteristics of the Taihu Lake Basin’s plain river network. In the western flood-prone region, it extends the drainage duration of key hubs to alleviate upstream waterlogging risks, while in the northern core water supply zone, it maintains stable water supply conditions, realizing coordinated optimization of multi-region and multi-objective demands. Temporally, the dynamic weighting mechanism enables adaptive adjustment across different scheduling periods—prioritizing flood discharge during the main flood season and shifting to balance water supply and ecological protection in non-flood seasons.

Compared with traditional empirical scheduling that relies on fixed thresholds, the optimal scheme integrates a basin water quantity-quality coupled model to fully capture the strong hydraulic coupling between the Xinmeng River Project and the lake network. This avoids the suboptimal discharge timing and intensity issues caused by ignoring system-level connections in traditional scheduling, leading to more comprehensive and reasonable scheduling effects that better align with the complex water network’s operational characteristics.

3.4.2. Practical Benefits for Practitioners

The research results provide multi-dimensional practical support for water resources practitioners, including basin management institutions, on-site scheduling engineers, and water conservancy operation and maintenance personnel. In decision-making, the established multi-objective indicator system and dynamic weighting framework convert traditionally subjective experience-based scheduling decisions into a quantitative analysis process. This enhances the scientificity and objectivity of decisions, especially when balancing conflicting objectives such as flood control, water supply, and ecological protection, providing clear priority judgment criteria for complex scheduling scenarios.

In operation and management, the specific operational rules of the optimal scheme can be directly integrated with the Taihu Lake Basin’s existing scheduling management system. This reduces the blindness of manual intervention, lowers operational risks and labor costs, and optimizes the operation parameters of water conservancy projects such as pumping stations. Referencing the application effects of similar intelligent scheduling systems, it contributes to the energy-saving operation of projects. For emergency response to extreme hydrological events, the pre-simulated optimal scheme serves as a “ready-to-use” emergency reference, eliminating the need for complex re-simulations and significantly shortening the emergency response preparation time—an advantage of great practical significance for the Taihu Lake Basin with its dense river network and narrow emergency window.

Additionally, the research outcomes provide targeted scheduling logic and parameter ranges for the newly commissioned Xinmeng River Project, effectively addressing the practical challenge of lacking mature operation and maintenance experience for new water conservancy projects and offering technical support for their standardized operation.

3.4.3. Application Paths and Operation Guidelines

To facilitate the practical application of research results by practitioners and simplify the handling of complex optimization problems, a phased implementation framework and lightweight operation strategies are proposed. In the short term, practitioners can directly adopt the scheduling logic and core parameters of the optimal scheme for daily scheduling and emergency response and activate pre-simulated engineering operation combinations for typical extreme rainfall scenarios.

In the medium term, the core modules of the dynamic weighting model and optimization algorithm can be integrated into a functional plug-in compatible with existing water resources scheduling systems. Relying on the basin’s established monitoring data platform, practitioners can input real-time data such as rainfall, water level, and water demand forecasts to automatically generate optimized scheduling schemes without the need to master complex algorithm principles or programming skills.

In the long term, parameters can be dynamically adjusted according to annual hydrological conditions and regional management requirements, with reference to relevant water resources scheduling management regulations, to achieve localized adaptation and continuous optimization of scheduling schemes.

To address the difficulty of non-research-oriented practitioners in handling complex optimization equations, the multi-objective functions and constraint conditions are encapsulated into a user-friendly visualization tool. Through a simplified process of “selecting hydrological scenarios—importing real-time monitoring data—generating scheduling schemes,” practitioners can obtain optimal operation suggestions without manual solution of complex mathematical equations. Meanwhile, multiple sets of pre-calibrated parameter templates for common hydrological scenarios in the Taihu Lake Basin are provided to reduce parameter setting difficulty and avoid errors caused by improper manual adjustments. Complementary technical support includes detailed operation manuals, online consultation services, and on-site training, comprehensively addressing practical issues such as abnormal data processing and system adaptation that may arise during application, ensuring the effective landing and practical effect of the research results.

4. Conclusions

This study focuses on the core demand of multi-objective coordinated scheduling in complex water networks, systematically constructing a complete technical system including indicator system, weighting strategy, model construction, and case verification. The main conclusions are as follows:

4.1. Construction of a Comprehensive Multi-Objective Indicator System

The established indicator system covers three key areas of flood control, water supply, and aquatic ecological environment, with 12 specific indicators such as drainage efficiency (DS), exceedance risk of guaranteed water level (CB), water supply efficiency (η), and ecological water level guarantee rate (PW). These indicators follow the principles of systematicness, conciseness, and independence, comprehensively reflecting the multi-dimensional scheduling needs of complex water networks and laying a foundation for quantitative coordination of conflicting objectives.

4.2. Effectiveness of the Dynamic Variable Weighting Strategy

By adopting the analytic hierarchy process (AHP) combined with dynamic weighting adjustment, the study realizes adaptive conversion of multi-objective problems under different hydrological scenarios (flood control period, water supply period, etc.). This method not only avoids subjective bias in traditional fixed weighting but also solves the incommensurability among indicators with different physical dimensions, significantly improving the scientificity and practical operability of scheduling decisions.

4.3. Optimal Scheduling Scheme Verified by Case Study

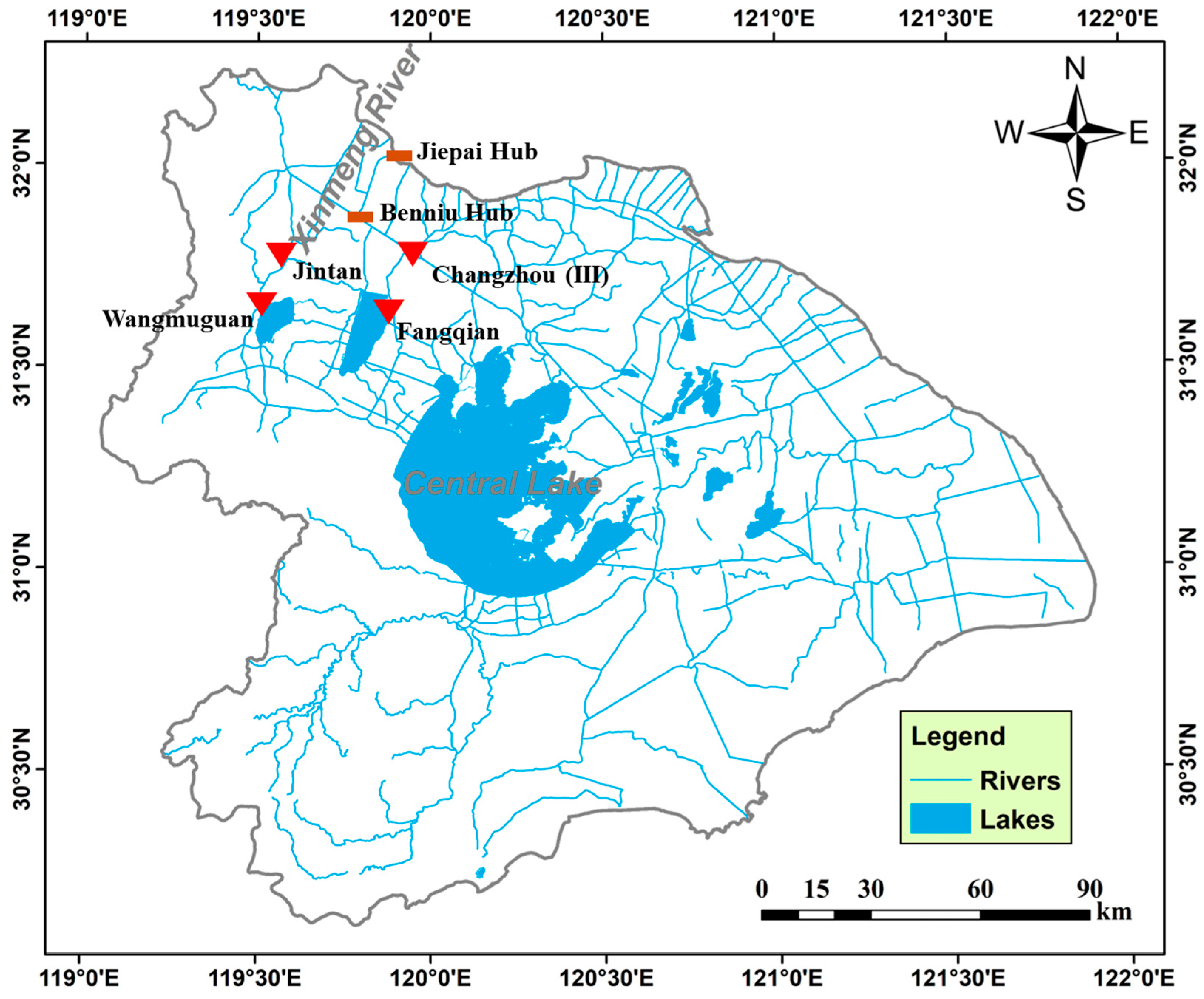
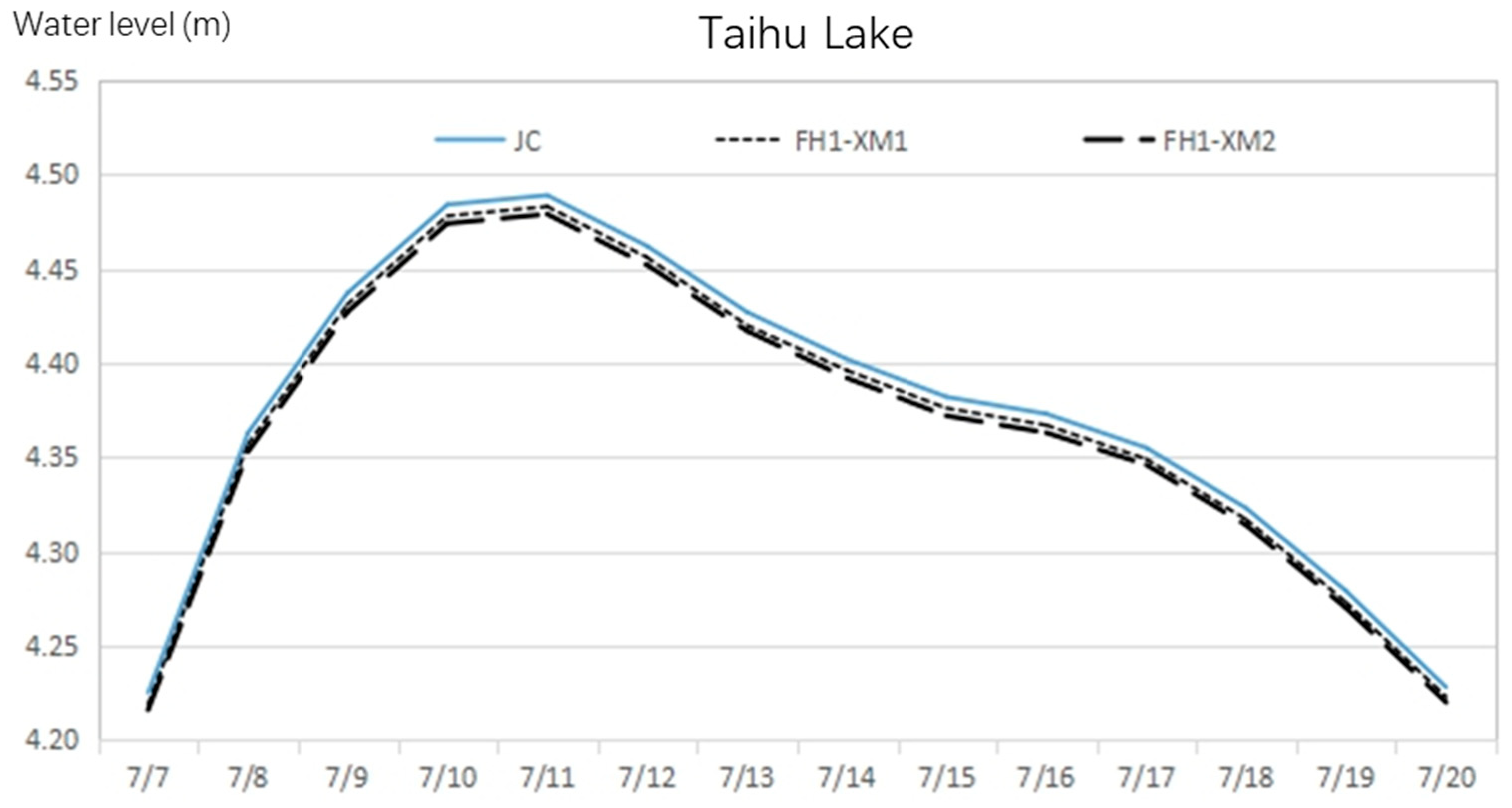
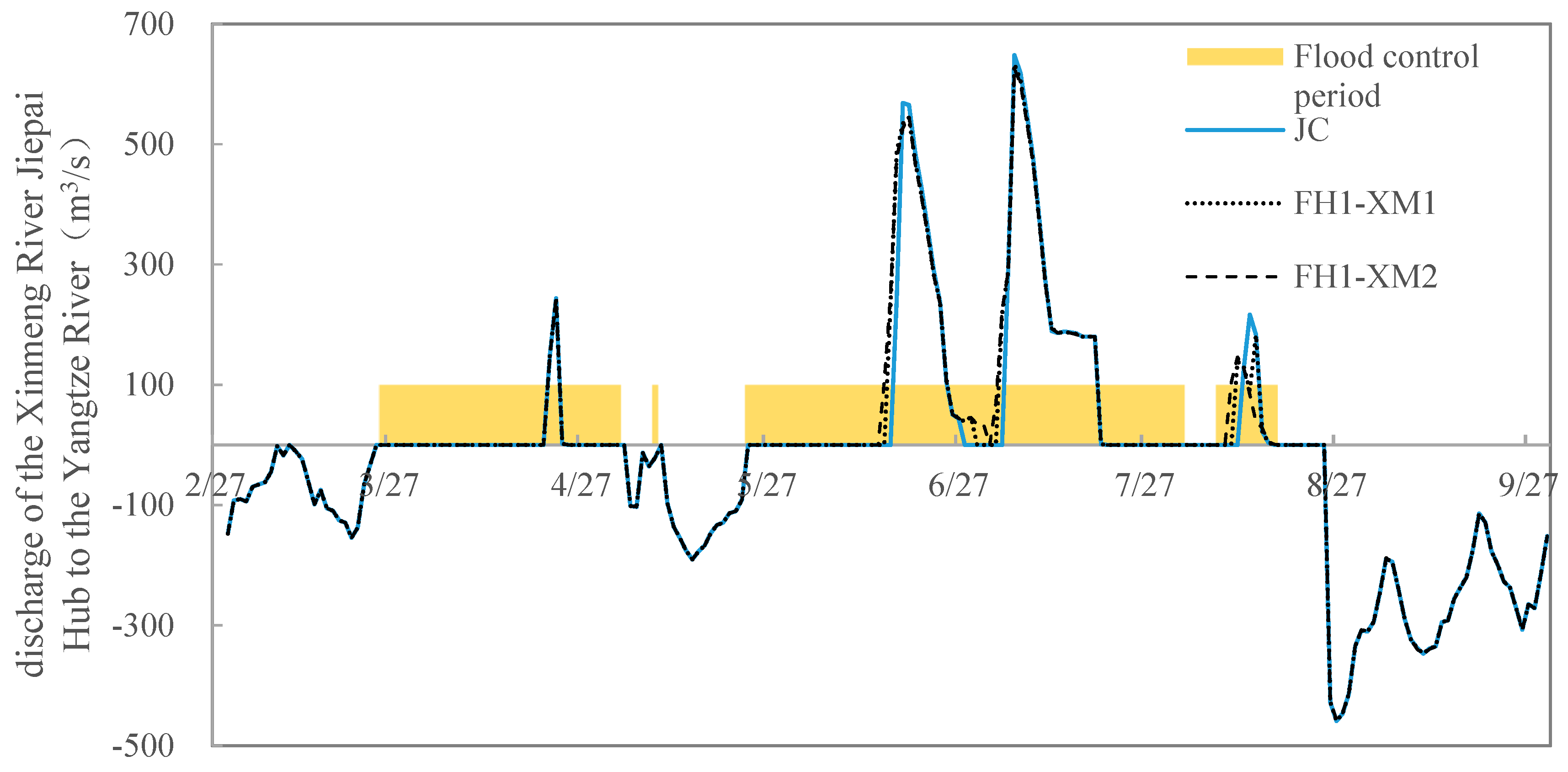
Under the 1991-Type 100-Year Return Period Rainfall scenario, the FH1-XM2 scheme is identified as the optimal enhanced discharge scheme. It effectively increases the drainage volume of the Xinmeng River Project and the western lake area (the flood season discharge volume to the Yangtze River increases by 0.71 × 100 million m³ and 0.40 × 100 million m³ respectively), reduces regional and Taihu Lake water levels, and lowers the basin’s flood control risk. The scheme’s advantages in key indicators such as drainage efficiency (0.92) and regional outflow coefficient (0.92) fully demonstrate the practical effect of the scheduling model.

4.4. Research Contributions and Prospects

This study breaks through technical bottlenecks in complex water network scheduling such as intricate hydraulic connections, numerous conflicting objectives, and heavy computational loads. The integrated technical process of “indicator system construction—dynamic weighting transformation—combined model solving” provides a new paradigm for multi-objective coordinated water resources scheduling, with its feasibility and effectiveness verified by the Taihu Lake Basin case study. However, this study is limited to the Taihu Lake Basin and the 1991-Type rainfall scenario; future research can expand to other complex water network basins, incorporate more extreme hydrological scenarios (e.g., extreme droughts), and optimize the algorithm to improve the model’s adaptability and solution efficiency. Additionally, integrating socio-economic factors such as water use costs and benefit allocation will further enhance the model’s practical application value.