Fractal Dimension as a Criterion for the Optimal Design and Operation of Water Distribution Systems
Abstract
1. Introduction
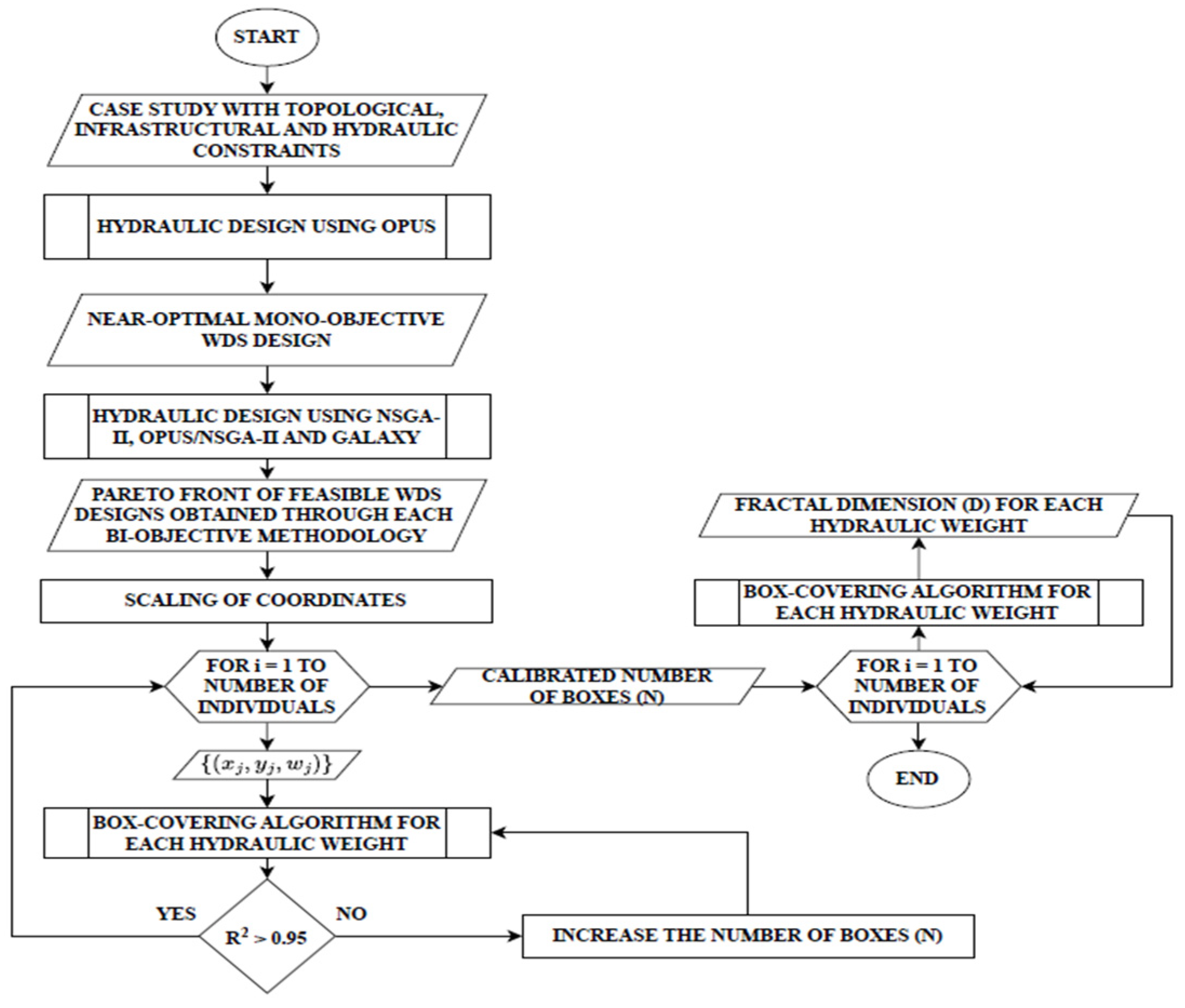
2. Methodology
2.1. Hydraulic Design
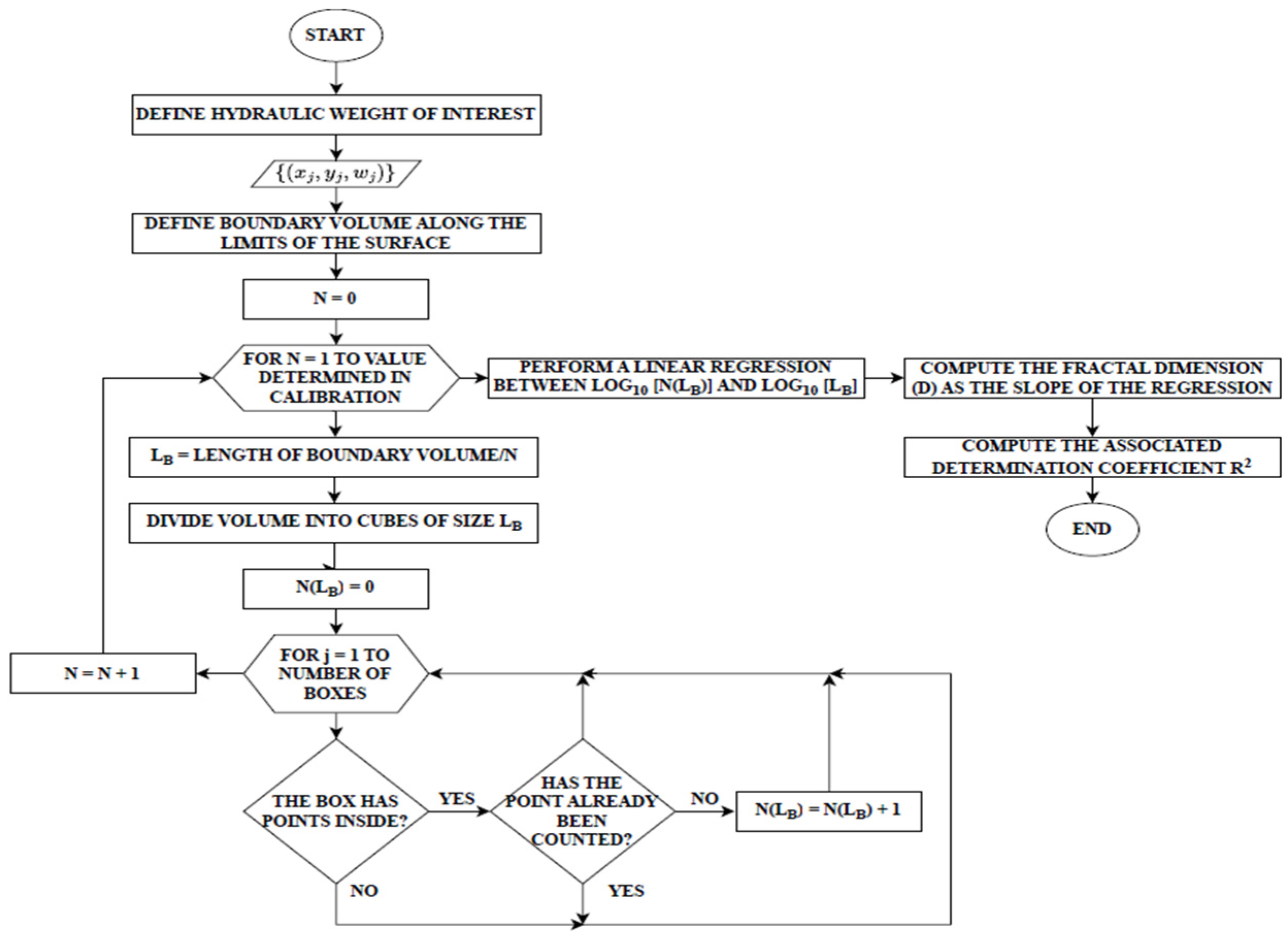
2.2. Fractal Analysis
2.3. Fractal Analysis of the Design Outcomes
2.4. Sensitivity Analysis
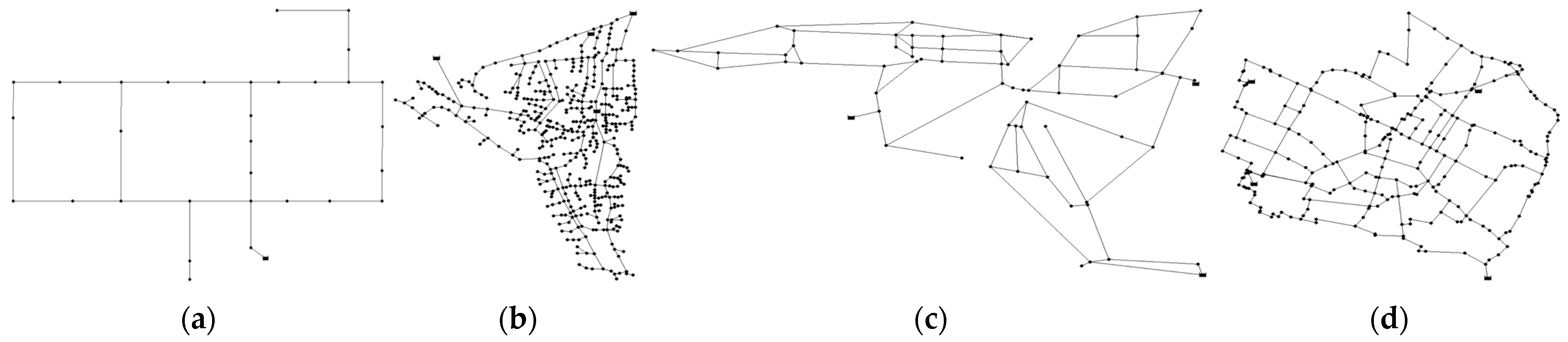
3. Case Studies
4. Results
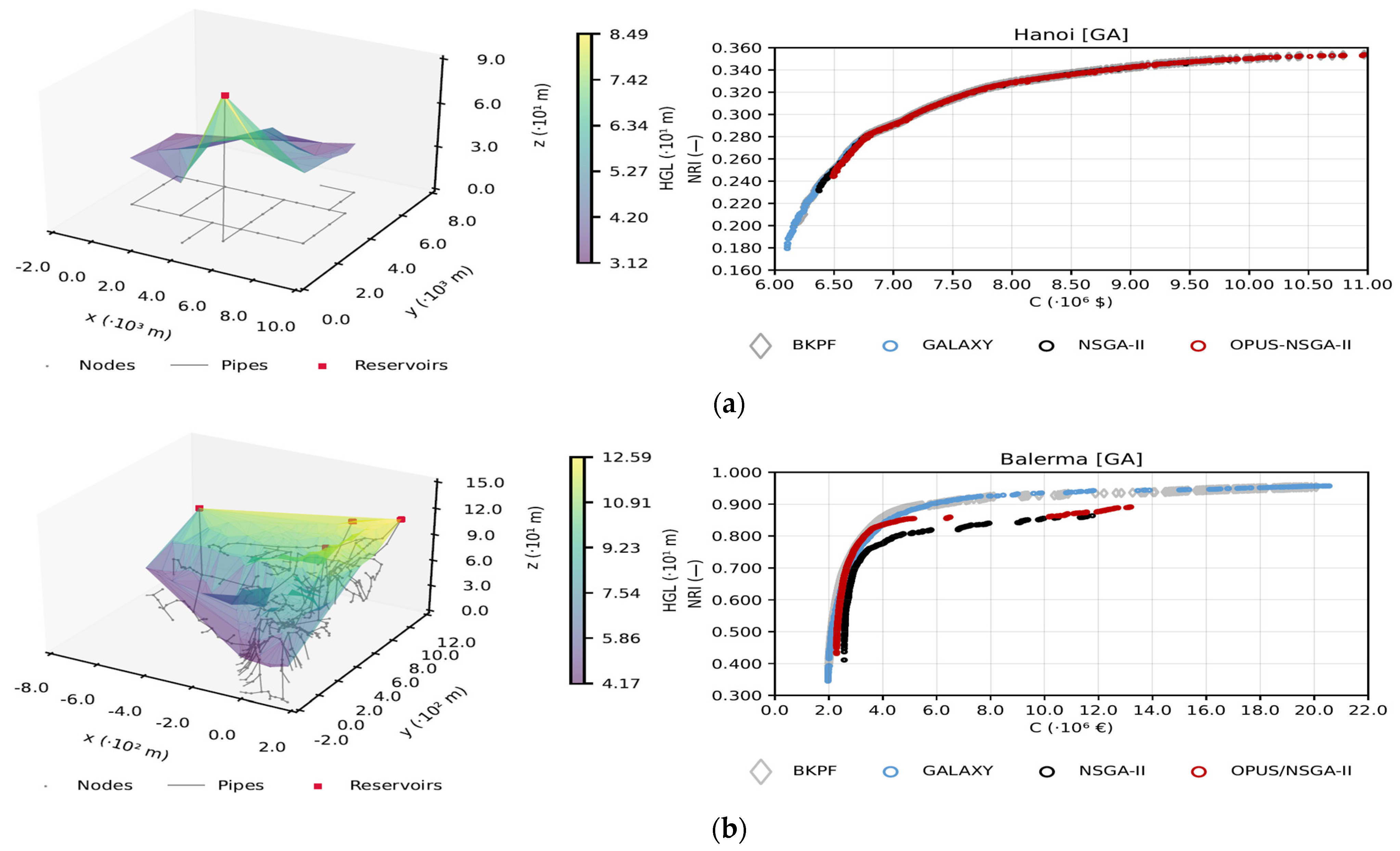
4.1. Optimal Designs
4.2. Fractal Analysis
4.3. Sensitivity Analysis
4.4. Computational Requirements
5. Analysis of Results
5.1. Fractal Behavior in WDS
5.2. D as an Indicator of Optimality
5.3. Significance of the Topology in D
6. Conclusions and Future Work
- WDS are self-similar fractal bodies.
- Fractal dimension (D) magnitudes are restricted by the underlying complexity of WDS.
- The fractal dimension (D) does not approach the fractal dimension of the OHGS in minimum cost designs.
- The fractal dimension (D) does not depend on the design cost (C) of the WDS.
- The fractal dimension (D) only depends on the topology.
- Fractal-based topologies inspired by natural drainage patterns can be used to redesign WDS. The fractal topologies can be used to subsequently perform the diameter (d) selection process using algorithms like NSGA-II to evaluate if fractal topologies improve the resulting cost (C) and resilience (NRI) of the design outcomes.
- D can guide the iterative definition of WDS layouts, aiming to replicate the structural properties of reference systems.
- D can function as an indicator of redundancy, with higher values reflecting increased pipe interconnections; this can support compliance with regulatory redundancy standards.
- Fractal analysis might be extended to operational aspects of WDS, helping to understand effects related to pipe roughness and nodal demand (Qd) increase.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- EPA. Drinking Water Infrastructure Needs Survey and Assessment; EPA: Washington, DC, USA, 2025.
- Wang, Q.; Guidolin, M.; Savic, D.; Kapelan, Z. Two-Objective Design of Benchmark Problems of a Water Distribution System via MOEAs: Towards the Best-Known Approximation of the True Pareto Front. J. Water Resour. Plan. Manag. 2015, 141, 04014060. [Google Scholar] [CrossRef]
- Yates, D.F.; Templeman, A.B.; Boffey, T.B. The Computational Complexity of the Problem of Determining Least Capital Cost Designs for Water Supply Networks. Eng. Optim. 1984, 7, 143–155. [Google Scholar] [CrossRef]
- Cunha, M.d.C.; Sousa, J. Water Distribution Network Design Optimization: Simulated Annealing Approach. J. Water Resour. Plan. Manag. 1999, 125, 215–221. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Saldarriaga, J.; Páez, D.; Salcedo, C.; Cuero, P.; López, L.L.; León, N.; Celeita, D. A Direct Approach for the Near-Optimal Design of Water Distribution Networks Based on Power Use. Water 2020, 12, 1037. [Google Scholar] [CrossRef]
- Sitzenfrei, R.; Wang, Q.; Kapelan, Z.; Savić, D. Using Complex Network Analysis for Optimization of Water Distribution Networks. Water Resour. Res. 2020, 56, e2020WR027929. [Google Scholar] [CrossRef]
- Hwang, H.; Lansey, K. Water Distribution System Classification Using System Characteristics and Graph-Theory Metrics. J. Water Resour. Plan. Manag. 2017, 143, 04017071. [Google Scholar] [CrossRef]
- Carvajal, J.; Ariza, A.; Saldarriaga, J. Advanced Geometrical Analysis of Water Distribution Networks (WDNs): A Comparison between Standard and Minimum Capital-Cost Designs. In Proceedings of the World Environmental and Water Resources Congress 2021, Virtual, 7–11 June 2021; American Society of Civil Engineers: Reston, VA, USA, 2021; pp. 914–924. [Google Scholar]
- Rana, S.M.M.; Boccelli, D.L.; Marchi, A.; Dandy, G.C. Drinking Water Distribution System Network Clustering Using Self-Organizing Map for Real-Time Demand Estimation. J. Water Resour. Plan. Manag. 2020, 146, 04020090. [Google Scholar] [CrossRef]
- Abokifa, A.A.; Sela, L. Identification of Spatial Patterns in Water Distribution Pipe Failure Data Using Spatial Autocorrelation Analysis. J. Water Resour. Plan. Manag. 2019, 145, 04019057. [Google Scholar] [CrossRef]
- Perelman, L.; Ostfeld, A. Topological Clustering for Water Distribution Systems Analysis. Environ. Model. Softw. 2011, 26, 969–972. [Google Scholar] [CrossRef]
- Qiu, M.; Ostfeld, A. Dynamic Clustering for Water Distribution System Water Quality Management. In Proceedings of the World Environmental and Water Resources Congress 2020, Henderson, NV, USA, 17–21 May 2020; American Society of Civil Engineers: Reston, VA, USA, 2020; pp. 318–328. [Google Scholar]
- Alvisi, S.; Franchini, M. Calibration and Sensitivity Analysis of the C-Town Pipe Network Model. In Proceedings of the Water Distribution Systems Analysis 2010, Tucson, AZ, USA, 12–15 September 2010; American Society of Civil Engineers: Reston, VA, USA, 2011; pp. 1573–1584. [Google Scholar]
- Diao, K.; Zhou, Y.; Li, J.; Liu, Z. Battle of the Water Calibration Networks (BWCN): A Component Status Changes Oriented Calibration Method for Zonal Management Water Distribution Networks. In Proceedings of the Water Distribution Systems Analysis 2010, Tucson, AZ, USA, 12–15 September 2010; American Society of Civil Engineers: Reston, VA, USA, 2011; pp. 1629–1644. [Google Scholar]
- Scibetta, M.; Boano, F.; Revelli, R.; Ridolfi, L. Community Detection as a Tool for District Metered Areas Identification. Procedia Eng. 2014, 70, 1518–1523. [Google Scholar] [CrossRef]
- Ferrari, G.; Savic, D.; Becciu, G. Graph-Theoretic Approach and Sound Engineering Principles for Design of District Metered Areas. J. Water Resour. Plan. Manag. 2014, 140, 04014036. [Google Scholar] [CrossRef]
- Buhl, C.; Gautrais, J.; Reeves, N.; Solé, R.V.; Valverde, S.; Kuntz, P.; Theraulaz, G. Topological Patterns in Street Networks of Self-Organized Urban Settlements. Eur. Phys. J. B-Condens. Matter Complex Syst. 2006, 49, 513–522. [Google Scholar] [CrossRef]
- Lämmer, S.; Gehlsen, B.; Helbing, D. Scaling Laws in the Spatial Structure of Urban Road Networks. Phys. A Stat. Mech. Its Appl. 2006, 363, 89–95. [Google Scholar] [CrossRef]
- Barthélemy, M.; Flammini, A. Co-Evolution of Density and Topology in a Simple Model of City Formation. Netw. Spat. Econ. 2009, 9, 401–425. [Google Scholar] [CrossRef]
- Yang, S.; Paik, K.; McGrath, G.S.; Urich, C.; Krueger, E.; Kumar, P.; Rao, P.S.C. Functional Topology of Evolving Urban Drainage Networks. Water Resour. Res. 2017, 53, 8966–8979. [Google Scholar] [CrossRef]
- Krueger, E.; Klinkhamer, C.; Urich, C.; Zhan, X.; Rao, P.S.C. Generic Patterns in the Evolution of Urban Water Networks: Evidence from a Large Asian City. Phys. Rev. E 2017, 95, 032312. [Google Scholar] [CrossRef]
- Zischg, J.; Reyes-Silva, J.D.; Klinkhamer, C.; Krueger, E.; Krebs, P.; Rao, P.S.C.; Sitzenfrei, R. Complex Network Analysis of Water Distribution Systems in Their Dual Representation Using Isolation Valve Information. In Proceedings of the World Environmental and Water Resources Congress 2019, Pittsburgh, PA, USA, 19–23 May 2019; American Society of Civil Engineers: Reston, VA, USA, 2019; pp. 484–497. [Google Scholar]
- Falconer, K. Fractal Geometry; Wiley: Hoboken, NJ, USA, 2003; ISBN 9780470848616. [Google Scholar]
- Diao, K.; Butler, D.; Ulanicki, B. Fractality in Water Distribution Networks: Application to Criticality Analysis and Optimal Rehabilitation. Urban. Water J. 2021, 18, 885–895. [Google Scholar] [CrossRef]
- Pentland, A.P. Fractal-Based Description of Natural Scenes. IEEE Trans. Pattern Anal. Mach. Intell. 1984, PAMI-6, 661–674. [Google Scholar] [CrossRef]
- Kowalski, D.; Kowalska, B.; Suchorab, P. A Proposal for the Application of Fractal Geometry in Describing the Geometrical Structures of Water Supply Networks. WIT Trans. Built Environ. 2014, 139, 75–87. [Google Scholar]
- Qi, S.; Ye, J.; Gao, J.; Wu, W.; Wang, J.; Zhang, Z.; Chen, L.; Shi, T.; Zhou, L. Fractal-Based Planning of Urban Water Distribution System in China. Procedia Eng. 2014, 89, 886–892. [Google Scholar] [CrossRef]
- Vargas, K.; Salcedo, C.; Saldarriaga, J. Dimensión Fractal e Identificación de Potenciales Sectores de Servicio En Redes de Distribución de Agua Potable Utilizando Criterios Hidráulicos. Rev. Recur. Hídricos 2019, 40, 27–38. [Google Scholar] [CrossRef]
- Kowalski, D.; Kowalska, B.; Kwietniewski, M. Monitoring of Water Distribution System Effectiveness Using Fractal Geometry. Bull. Pol. Acad. Sci. Tech. Sci. 2015, 63, 155–161. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Greco, R.; Santonastaso, G.F. Complex Network and Fractal Theory for the Assessment of Water Distribution Network Resilience to Pipe Failures. Water Supply 2018, 18, 767–777. [Google Scholar] [CrossRef]
- Kowalski, D.; Kowalska, B.; Bławucki, T.; Suchorab, P.; Gaska, K. Impact Assessment of Distribution Network Layout on the Reliability of Water Delivery. Water 2019, 11, 480. [Google Scholar] [CrossRef]
- Giudicianni, C.; Di Nardo, A.; Greco, R.; Scala, A. A Community-Structure-Based Method for Estimating the Fractal Dimension, and Its Application to Water Networks for the Assessment of Vulnerability to Disasters. Water Resour. Manag. 2021, 35, 1197–1210. [Google Scholar] [CrossRef]
- Liu, C.; Li, Y.; Yin, H.; Zhang, J.; Wang, W. A Stochastic Interpolation-Based Fractal Model for Vulnerability Diagnosis of Water Supply Networks Against Seismic Hazards. Sustainability 2020, 12, 2693. [Google Scholar] [CrossRef]
- Iwanek, M.; Kowalski, D.; Kowalska, B.; Suchorab, P. Fractal Geometry in Designing and Operating Water Networks. J. Ecol. Eng. 2020, 21, 229–236. [Google Scholar] [CrossRef]
- Jaramillo, A.; Saldarriaga, J. Fractal Analysis of the Optimal Hydraulic Gradient Surface in Water Distribution Networks. J. Water Resour. Plan. Manag. 2023, 149, 04022074. [Google Scholar] [CrossRef]
- Jaramillo, A.; Saldarriaga, J. Fractal-Based Analysis of the Optimal Hydraulic Gradient Surface in the Optimized Design of Water Distribution Networks. In Proceedings of the World Environmental and Water Resources Congress 2022, Atlanta, GA, USA, 5–8 June 2022; American Society of Civil Engineers: Reston, VA, USA, 2022; pp. 1000–1014. [Google Scholar]
- Saldarriaga, J.; Salcedo, C.; González, M.A.; Ortiz, C.; Wiesner, F.; Gómez, S. On the Evolution of the Optimal Design of WDS: Shifting towards the Use of a Fractal Criterion. Water 2022, 14, 3795. [Google Scholar] [CrossRef]
- Páez, D.; Salcedo, C.; Garzón, A.; González, M.A.; Saldarriaga, J. Use of Energy-Based Domain Knowledge as Feedback to Evolutionary Algorithms for the Optimization of Water Distribution Networks. Water 2020, 12, 3101. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Wang, Q.; Savić, D.A.; Kapelan, Z. GALAXY: A New Hybrid MOEA for the Optimal Design of Water Distribution Systems. Water Resour. Res. 2017, 53, 1997–2015. [Google Scholar] [CrossRef]
- Song, C.; Havlin, S.; Makse, H.A. Self-Similarity of Complex Networks. Nature 2005, 433, 392–395. [Google Scholar] [CrossRef]
- Song, C.; Havlin, S.; Makse, H.A. Origins of Fractality in the Growth of Complex Networks. Nat. Phys. 2006, 2, 275–281. [Google Scholar] [CrossRef]
- Song, C.; Gallos, L.K.; Havlin, S.; Makse, H.A. How to Calculate the Fractal Dimension of a Complex Network: The Box Covering Algorithm. J. Stat. Mech. Theory Exp. 2007, 2007, P03006. [Google Scholar] [CrossRef]
- Fujiwara, O.; Khang, D.B. A Two-Phase Decomposition Method for Optimal Design of Looped Water Distribution Networks. Water Resour. Res. 1990, 26, 539–549. [Google Scholar] [CrossRef]
- Reca, J.; Martínez, J. Genetic Algorithms for the Design of Looped Irrigation Water Distribution Networks. Water Resour. Res. 2006, 42, 1–9. [Google Scholar] [CrossRef]
- Bragalli, C.; D’Ambrosio, C.; Lee, J.; Lodi, A.; Toth, P. On the Optimal Design of Water Distribution Networks: A Practical MINLP Approach. Optim. Eng. 2012, 13, 219–246. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, L.; Huang, W.; Wang, Z.; Liu, S.; Savić, D.A. Parameterization of NSGA-II for the Optimal Design of Water Distribution Systems. Water 2019, 11, 971. [Google Scholar] [CrossRef]
- Yusoff, Y.; Ngadiman, M.S.; Zain, A.-M. Overview of NSGA-II for Optimizing Machining Process Parameters. Procedia Eng. 2011, 15, 3978–3983. [Google Scholar] [CrossRef]
- Saldarriaga, J.; Pulgarrn, L.; Cuero, P.; Duque, N. Pipeline Hydraulics Academic Software. SSRN Electron. J. 2017, 1, 1–8. [Google Scholar] [CrossRef]
- Todini, E. Looped Water Distribution Networks Design Using a Resilience Index Based Heuristic Approach. Urban Water 2000, 2, 115–122. [Google Scholar] [CrossRef]
- Atkinson, S.; Farmani, R.; Memon, F.A.; Butler, D. Reliability Indicators for Water Distribution System Design: Comparison. J. Water Resour. Plan. Manag. 2014, 140, 160–168. [Google Scholar] [CrossRef]
- Zhan, X.; Meng, F.; Liu, S.; Fu, G. Comparing Performance Indicators for Assessing and Building Resilient Water Distribution Systems. J. Water Resour. Plan. Manag. 2020, 146, 06020012. [Google Scholar] [CrossRef]
- Wen, T.; Cheong, K.H. The Fractal Dimension of Complex Networks: A Review. Inf. Fusion 2021, 73, 87–102. [Google Scholar] [CrossRef]
- Kim, J.S.; Goh, K.-I.; Salvi, G.; Oh, E.; Kahng, B.; Kim, D. Fractality in Complex Networks: Critical and Supercritical Skeletons. Phys. Rev. E 2007, 75, 016110. [Google Scholar] [CrossRef] [PubMed]
- Goh, K.-I.; Salvi, G.; Kahng, B.; Kim, D. Skeleton and Fractal Scaling in Complex Networks. Phys. Rev. Lett. 2006, 96, 018701. [Google Scholar] [CrossRef]
- Csányi, G.; Szendrői, B. Fractal–Small-World Dichotomy in Real-World Networks. Phys. Rev. E 2004, 70, 016122. [Google Scholar] [CrossRef]
- Jaramillo, A. Análisis de La Geometría Fractal de La Superficie Óptima de Presiones En El Diseño Optimizado de Redes de Distribución de Agua Potable; Universidad de los Andes: Bogotá, Colombia, 2020. [Google Scholar]
- Tolle, C.R.; McJunkin, T.R.; Gorsich, D.J. Suboptimal Minimum Cluster Volume Cover-Based Method for Measuring Fractal Dimension. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 32–41. [Google Scholar] [CrossRef]
- Zhou, G.; Lam, N.S.-N. A Comparison of Fractal Dimension Estimators Based on Multiple Surface Generation Algorithms. Comput. Geosci. 2005, 31, 1260–1269. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET 2 Users Manual; US Environmental Protection Agency: Cincinnati, OH, USA, 2000.
- Eliades, D.G.; Kyriakou, M.; Vrachimis, S.; Polycarpou, M.M. EPANET-MATLAB Toolkit: An Open-Source Software for Interfacing EPANET with MATLAB. In Proceedings of the 14th International Conference on Computing and Control for the Water Industry (CCWI), Amsterdam, The Netherlands, 7–9 November 2016. [Google Scholar]
- Klise, K.A.; Bynum, M.; Moriarty, D.; Murray, R. A Software Framework for Assessing the Resilience of Drinking Water Systems to Disasters with an Example Earthquake Case Study. Environ. Model. Softw. 2017, 95, 420–431. [Google Scholar] [CrossRef] [PubMed]
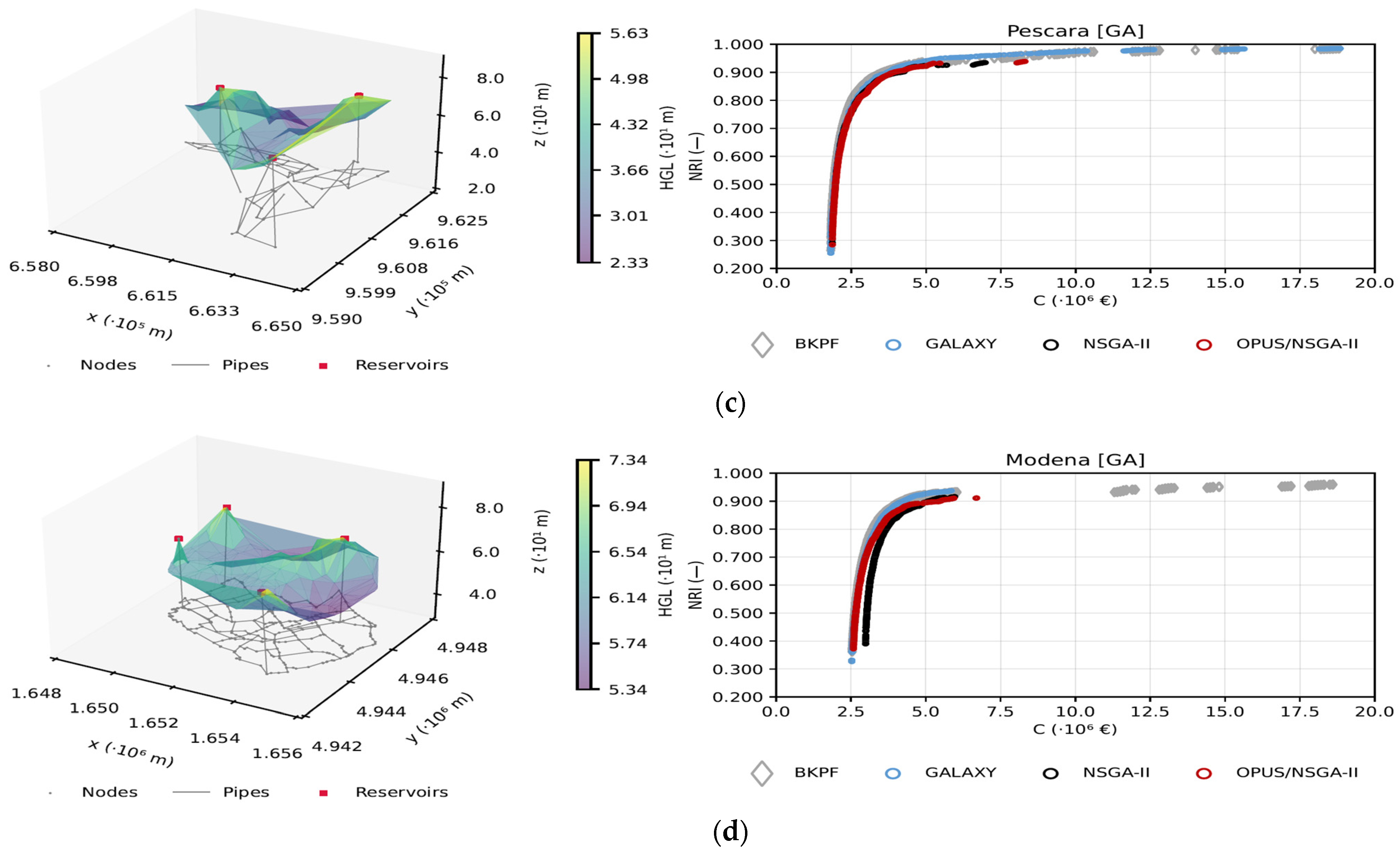
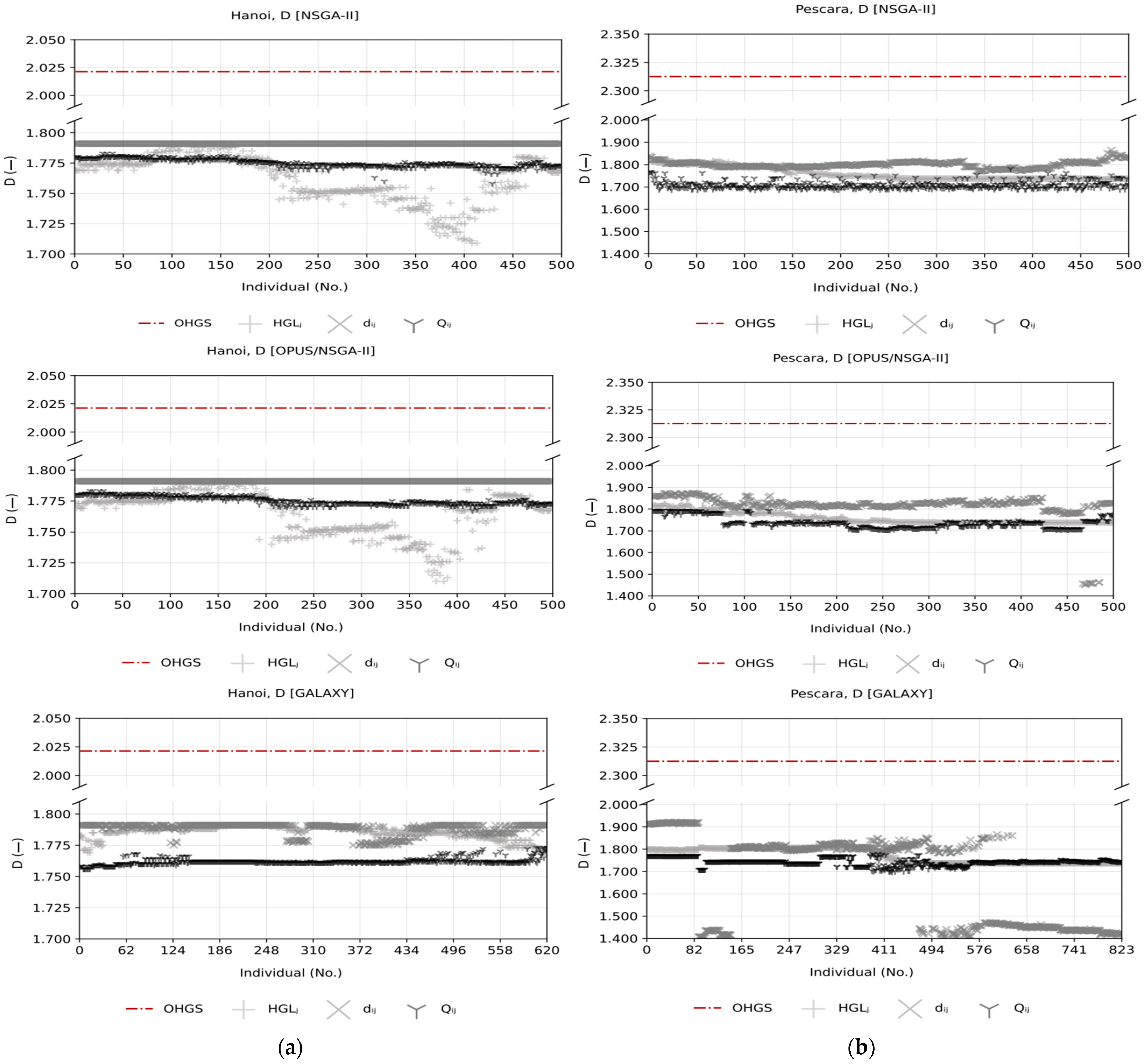
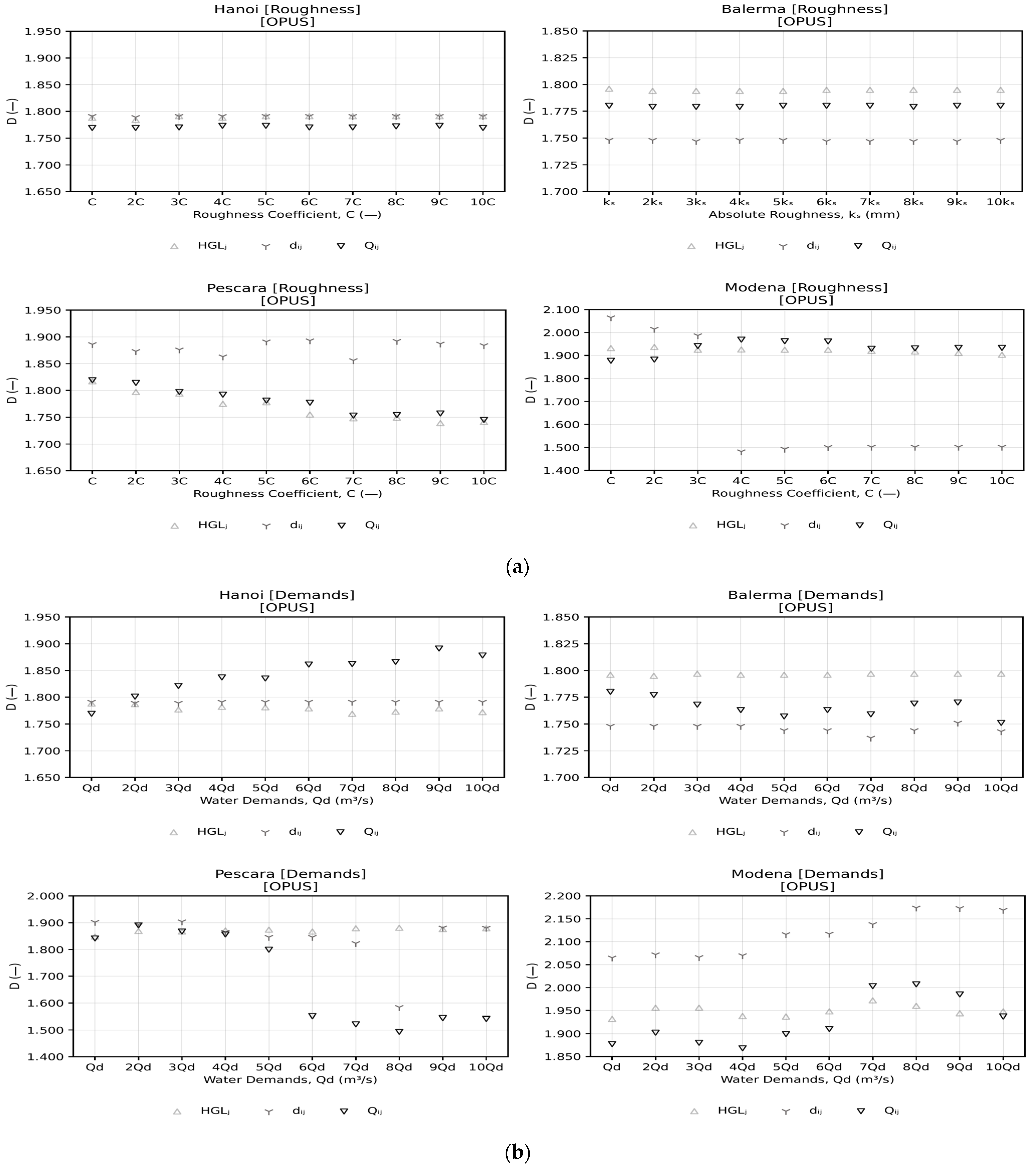
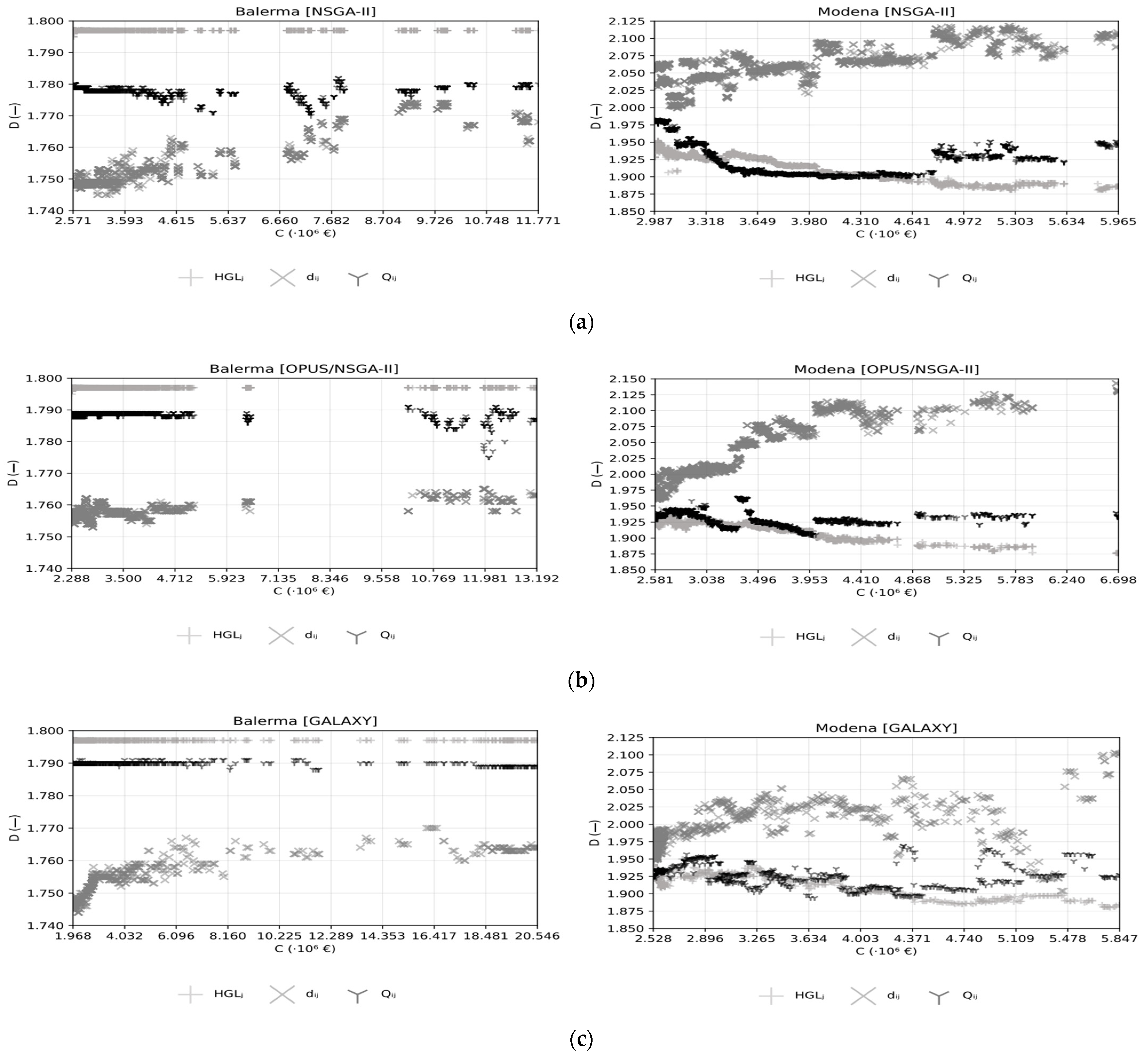
| Network | Hydraulic Equation | Roughness | C | Nodes | Pipes | Reservoirs | Pressure Constraints | Velocity Constraints | Search Space [2] | Problem Size [2] | OHGS [36] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Hanoi [45] | Hazen − Williams | C 130 | USD 43.315d1.500/m | 31 | 34 | 1 | pmin 30 m | No | 2.87 × 1026 | Medium | 2.0214 |
| Balerma [46] | Darcy − Weisbach | ks 2.500 × 10−6 m | EUR 0.040d2.0618/m | 443 | 454 | 4 | pmin 20 m | No | 1.00 × 10455 | Large | 2.2982 |
| Pescara [47] | Hazen − Williams | C 130 | EUR 72.800d1.270/m | 68 | 99 | 3 | pmin 20 m pmax variable | vmax 2 m/s | 1.91 × 10110 | Intermediate | 2.3125 |
| Modena [47] | Hazen − Williams | C 130 | EUR 72.800d1.270/m | 268 | 317 | 4 | pmin 20 m pmax variable | vmax 2 m/s | 1.32 × 10353 | Large | 2.3204 |
| Biobjective Approach | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OPUS | NSGA-II and OPUS/NSGA-II | GALAXY | ||||||||||
| Network | F | F and B/C | b | Arrangement Criterion | Individuals | Generations | Mutation Distribution Index | Crossover Distribution Index | Retrofitted Frequency | Population Size | Function Evaluations | Pdcm |
| Hanoi | 0.25 | Highest Pressure and Highest Relation | 2.6 | H/L | 500 | 500 | 20 | 3 | 5 | 100 | 50,000 | 0.7 |
| Balerma | 0.25 | 2000 | 4500 | 100 | 2 | 10 | 200 | 400,000 | 0.7 | |||
| Pescara | 0.10 | 500 | 2000 | 100 | 10 | 20 | 100 | 100,000 | ||||
| Modena | 0.20 | 2000 | 4000 | 20 | 7 | 50 | 200 | 40,000 | ||||
| Hanoi | Balerma | Pescara | Modena | ||
|---|---|---|---|---|---|
| OHGS [36] | 2.0214 | 2.2982 | 2.3125 | 2.3204 | |
| D | HGLj | 1.788 (11.547%), R2 = 0.999 | 1.796 (21.852%), R2 = 0.999 | 1.817 (21.427%), R2 = 0.998 | 1.932 (16.739%), R2 = 0.998 |
| Σidij | 1.791 (11.398%), R2 = 0.999 | 1.748 (23.941%), R2 = 1.000 | 1.886 (18.443%), R2 = 0.999 | 2.065 (11.007%), R2 = 0.996 | |
| ΣiQij | 1.769 (12.486%), R2 = 0.999 | 1.781 (22.505%), R2 = 1.000 | 1.819 (21.341%), R2 = 0.999 | 1.769 (23.763%), R2 = 0.999 | |
| wj = HGLj | wj = Σidij | wj = ΣiQij | |||||
|---|---|---|---|---|---|---|---|
| DHGLⱼ | R2 | Ddᵢⱼ | R2 | DQᵢⱼ | R2 | ||
| NSGA-II | Hanoi | [1.709, 1.791] | [0.997, 0.999] | 1.791 | [0.990, 1.000] | [1.758, 1.783] | [0.996, 1.000] |
| Balerma | [1.795, 1.797] | [1.745, 1.774] | [1.770, 1.782] | ||||
| Pescara | [1.734, 1.820] | [1.771, 1.865] | [1.686, 1.781] | ||||
| Modena | [1.881, 1.952] | [1.999, 2.118] | [1.900, 1.983] | ||||
| OPUS/NSGA-II | Hanoi | [1.710, 1.791] | [0.997, 1.000] | 1.791 | [0.971, 1.000] | [1.767, 1.783] | [0.997, 1.000] |
| Balerma | [1.795, 1.797] | [1.753, 1.765] | [1.775, 1.791] | ||||
| Pescara | [1.737, 1.824] | [1.452, 1.874] | [1.700, 1.793] | ||||
| Modena | [1.876, 1.941] | [1.944, 2.143] | [1.905, 1.963] | ||||
| GALAXY | Hanoi | [1.769, 1.791] | [0.997, 1.000] | [1.775, 1.791] | [0.952, 1.000] | [1.756, 1.773] | [0.996, 0.999] |
| Balerma | 1.797 | [1.744, 1.770] | [1.788, 1.791] | ||||
| Pescara | [1.735, 1.811] | [1.400, 1.922] | [1.697, 1.780] | ||||
| Modena | [1.880, 1.950] | [1.904, 2.103] | [1.894, 1.969] | ||||
| wj | DMono-objective | DBiobjective | DMaterial | DDemands | D | |
|---|---|---|---|---|---|---|
| Hanoi | HGLj | 1.788 | 1.772 (σ = 0.019) | 1.790 (σ = 0.002) | 1.779 (σ = 0.006) | 1.778 (σ = 0.015) |
| Σidij | 1.791 | 1.790 (σ = 0.003) | 1.791 (σ = 0.001) | 1.791 (σ = 0.001) | ||
| ΣiQij | 1.769 | 1.770 (σ = 0.007) | 1.771 (σ = 0.002) | 1.842 (σ = 0.037) | ||
| Balerma | HGLj | 1.796 | 1.797 (σ = 0.000) | 1.795 (σ = 0.001) | 1.796 (σ = 0.001) | 1.779 (σ = 0.019) |
| Σidij | 1.748 | 1.754 (σ = 0.006) | 1.748 (σ = 0.001) | 1.746 (σ = 0.004) | ||
| ΣiQij | 1.781 | 1.785 (σ = 0.005) | 1.780 (σ = 0.001) | 1.766 (σ = 0.009) | ||
| Pescara | HGLj | 1.817 | 1.765 (σ = 0.031) | 1.769 (σ = 0.027) | 1.871 (σ = 0.010) | 1.744 (σ = 0.104) |
| Σidij | 1.886 | 1.723 (σ = 0.175) | 1.880 (σ = 0.013) | 1.842 (σ = 0.095) | ||
| ΣiQij | 1.819 | 1.741 (σ = 0.021) | 1.779 (σ = 0.026) | 1.690 (σ = 0.171) | ||
| Modena | HGLj | 1.932 | 1.917 (σ = 0.016) | 1.922 (σ = 0.010) | 1.949 (σ = 0.012) | 1.923 (σ = 0.023) |
| Σidij | 2.065 | 2.039 (σ = 0.042) | 1.655 (σ = 0.254) | 2.116 (σ = 0.046) | ||
| ΣiQij | 1.769 | 1.930 (σ = 0.020) | 1.932 (σ = 0.031) | 1.927 (σ = 0.053) |
| wj | DMono-objective | DBiobjective | |
|---|---|---|---|
| Hanoi | HGLj | 1.211 (%E = 32.287%) | [1.200, 1.211] (%E = 32.291%, %E = 31.676%) |
| Σidij | 1.221 (%E = 31.837%) | [1.214, 1.227] (%E = 32.168%, %E = 31.430%) | |
| ΣiQij | 1.070 (%E = 39.525%) | [1.061, 1.079] (%E = 40.085%, %E = 39.017%) | |
| Balerma | HGLj | 0.588 (%E = 67.277%) | [0.582, 0.588] (%E = 67.635%, %E = 67.295%) |
| Σidij | 0.579 (%E = 66.894%) | [0.574, 0.582] (%E = 67.252%, %E = 66.842%) | |
| ΣiQij | 0.571 (%E = 67.928%) | [0.570, 0.573] (%E = 68.090%, %E = 67.910%) | |
| Pescara | HGLj | 0.611 (%E = 66.401%) | [0.596, 0.611] (%E = 66.255%, %E = 65.411%) |
| Σidij | 0.887 (%E = 52.985%) | [0.854, 0.995] (%E = 50.435%, %E = 42.258%) | |
| ΣiQij | 0.925 (%E = 49.137%) | [0.925, 1.035] (%E = 46.858%, %E = 40.528%) | |
| Modena | HGLj | 1.249 (%E = 35.357%) | [1.232, 1.260] (%E = 35.722%, %E = 34.293%) |
| Σidij | 1.268 (%E = 38.615%) | [1.217, 1.268] (%E = 40.324%, %E = 37.832%) | |
| ΣiQij | 1.209 (%E = 31.685%) | [1.192, 1.228] (%E = 38.259%, %E = 36.358%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez, S.; Salcedo, C.; González, L.; Saldarriaga, J. Fractal Dimension as a Criterion for the Optimal Design and Operation of Water Distribution Systems. Water 2025, 17, 1318. https://doi.org/10.3390/w17091318
Gómez S, Salcedo C, González L, Saldarriaga J. Fractal Dimension as a Criterion for the Optimal Design and Operation of Water Distribution Systems. Water. 2025; 17(9):1318. https://doi.org/10.3390/w17091318
Chicago/Turabian StyleGómez, Santiago, Camilo Salcedo, Laura González, and Juan Saldarriaga. 2025. "Fractal Dimension as a Criterion for the Optimal Design and Operation of Water Distribution Systems" Water 17, no. 9: 1318. https://doi.org/10.3390/w17091318
APA StyleGómez, S., Salcedo, C., González, L., & Saldarriaga, J. (2025). Fractal Dimension as a Criterion for the Optimal Design and Operation of Water Distribution Systems. Water, 17(9), 1318. https://doi.org/10.3390/w17091318










