Abstract
The adsorption of Fe(III) onto the surface of microplastics (MPs) enhances their toxicity and mobility in aquatic environments, posing a serious threat to human health and ecosystem balance. This study investigated the adsorption mechanism and influencing factors of Fe(III) on three types of MPs with varying particle sizes and aging degrees using batch experiments in freshwater and saltwater. Machine learning (ML) techniques were employed to predict the adsorption capacity and conduct attribution analysis. The results showed that Fe(III) adsorption in both freshwater and saltwater followed Pseudo-First-Order kinetics and Langmuir isotherms, indicating a monolayer homogeneous physical reaction driven by oxygen-containing functional groups, hydrogen bonds and aromatic rings on the MP surface. The adsorption capacity of MPs for Fe(III) was higher in freshwater than in saltwater, and was positively correlated with the aging degree and pH value, but negatively correlated with the particle size. Among the tested ML models, the Random Forest and Gaussian Process Regression models with Bayesian Optimization performed well in predicting adsorption capacity, with pH value and aging degree identified as key factors based on SHAP analysis. This study conducted a comprehensive investigation of the adsorption behavior between MPs and Fe(III) in water, providing valuable insights for the risk assessment and prevention of MP and Fe(III) pollution in aquatic environments.
1. Introduction
Globally, over 70 million tons of plastic waste are generated annually [1]. This waste gradually degrades into microplastics (MPs) with diameters < 5 mm via weathering, fragmentation, biodegradation, and so on [2]. MPs are widely distributed in aquatic environments such as rivers, lakes, oceans, and wetlands, particularly in industrialized areas and densely populated urban regions [3,4,5]. MPs not only contaminate water and soil [6], but also induce hepatic dysfunction, systemic inflammation, and respiratory decline in humans when they enter the human body through the food chain [7]. Fe3+ ions (Fe(III)) are also prevalent contaminants in both surface water and groundwater in these regions [8,9]. MPs can transport heavy metal ions to migrate in the aquatic environment, thereby enhancing their toxicity and accelerating their dispersion in water, soil, and sediments [10,11,12]. The physicochemical interactions between MPs and various heavy metal species in aquatic systems demonstrate distinct behavioral differences [13], while the interaction mechanism between MPs and Fe(III) remains unclear.
The adsorption mechanisms of MPs and heavy metal ions in aquatic environments primarily involve electrostatic interactions, van der Waals forces, and surface complexation [14,15,16]. In aquatic environments, electrostatic interactions dominate the adsorption processes of Pb, Cu, Cr, and Cd onto polypropylene (PP), polystyrene (PS), and polyvinyl chloride (PVC) MPs [17]. Van der Waals forces exert a significant influence on the adsorption of Cr4+ by PP, PS, and polyamide (PA) MPs [18]. Surface complexation is the predominant mechanism for the adsorption of Cu2+, Ni2+, and Zn2+ by nylon MPs [19]. However, current research has paid limited attention to Fe-MP interactions in aquatic environments, particularly regarding their adsorption behaviors. The intensity and mechanisms of adsorption are closely related to the structure and properties of MPs [20]. Smaller MPs have a greater specific surface area, which enhances their capacity for heavy metal adsorption [21]. Highly crystalline polyethylene (PE) MPs adsorb more lead ions (Pb2+) than polypropylene (PP) and polyethylene terephthalate (PET) [22]. Aging MPs exhibit an enhanced capacity for heavy metal adsorption due to an increased specific surface area, elevated oxygen-containing functional groups, and a greater surface negative charge [16]. Aquatic physicochemical properties also significantly influence the adsorption interactions between MPs and heavy metal ions in aquatic environments. Godoy et al. demonstrated that elevated pH promoted the precipitation of Cr and Pb ions, while saline ions (e.g., Na+) and heavy metal ions competed for the adsorption sites on MPs [23]. Higher water temperatures inhibit chemisorption, currently resulting in a reduced Cu2+ adsorption capacity of MPs [24].
Adsorption kinetic models are employed to characterize the time-dependent uptake behavior of heavy metal ions on MPs in water, while isotherm adsorption models are used to quantify the saturated adsorption capacity of MPs under specific equilibrium conditions [25,26]. In aquatic environmental studies, several isothermal adsorption models are commonly employed, including the Henry, Langmuir, Freundlich, and Temkin models [27]. Some of them (e.g., Temkin, Dubinin–Radushkevich models, etc.) require strict thermodynamic conditions and specialized physical assumptions, severely limiting their practical application in complex environmental systems [28]. While the Langmuir and Freundlich models are not constrained by rigorous physical assumptions, their parameters can respond dynamically to aqueous-phase environmental variations, making them better aligned with real-water environments [28,29]. Consequently, the Langmuir and Freundlich models demonstrate the broadest applicability for characterizing the adsorption behavior of diverse contaminants, including heavy metals, organic compounds, and pharmaceutical residues [23,30,31]. Distinct adsorption mechanisms govern the interactions between MPs and heavy metal ions in aquatic environments. For instance, Pb2+ adsorption onto polypropylene (PP) and polystyrene (PS) MPs follows Pseudo-First-Order kinetics (PFO) and the Langmuir adsorption isotherm model [24]. In contrast, Cu2+ adsorption onto PP/PS MPs and Cr2+ adsorption onto PP MPs are better fitted to Pseudo-Second-Order kinetics (PSO) and the Freundlich adsorption isotherm model [24,32].
Machine learning (ML) techniques have gained increasing attention and application in environmental science research. ML methods can simultaneously account for the nonlinear relationships among multiple variables. This capability enables the accurate prediction and comprehensive analysis of complex dependencies that traditional methods often fail to capture. In recent years, ML methods have been employed to analyze the key pollutants influencing water quality indices across different seasons [33], to elucidate the effects and interactions of various factors on soil heavy metal pollution [34], and to identify the critical determinants affecting the efficiency of heavy metal adsorption [35]. For example, Guo and Wang developed an Artificial Neural Network (ANN) model to predict the adsorption capacity of MPs for Pb and Cd ions [36]. Bi et al. combined the meta-analysis and Random Forest (RF) model to conclude that the concentrations of MPs and heavy metals, as well as pH values, were the key factors in predicting adsorption capacity [6]. However, most prior studies on the influencing factors of MPs adsorption have primarily relied on linear regression-based correlation analysis. This type of approach often falls short in capturing the complex nonlinear relationships among these factors, thereby compromising the accuracy of the results [37,38].
In this study, polypropylene (PP), polyethylene terephthalate (PET), and polystyrene (PS) MPs with different sizes and aging degrees were chosen to conduct Fe(III) adsorption experiments in both freshwater and saline water using an Fe(III) solution. The main goal was to uncover the interaction mechanisms and influencing factors of Fe(III) adsorption onto these MPs. Furthermore, machine learning techniques were used to predict the adsorption capacity of MPs for Fe(III) ions in aquatic environments, with SHAP analysis employed to identify the key factors affecting the capacity. The results provide a theoretical foundation for the control and risk management of MPs and Fe(III) pollution in aquatic environments.
2. Materials and Methodology
2.1. Materials
2.1.1. Microplastics
The polypropylene (PP), polyethylene terephthalate (PET), and polystyrene (PS) MPs used in this study were purchased from Fengtai Polymer Material Company in Beijing, China. The three types of MPs were classified into three sizes, including 15 μm (S), 150 μm (M), and 300 μm (L). The three types of MPs were placed in a closed UV aging chamber and irradiated continuously for 10 days and 30 days, respectively, with a UV lamp with a constant power of 40 W, to obtain the aged MPs. The aging degree of the different MPs is labeled by the subscript of the radiation time, for example, the PS MPs irradiated for 10 days are indicated as PS10.
A scanning electron microscope (Car Zeiss EVO LS1, Carl Zeiss, Hertfordshire, UK) was employed to analyze the micro-morphological changes in MPs before and after aging, as shown in Figure 1. The spherical surface of unaged PS was smooth without cracks and depressions (Figure 1a), while unaged PP and PET displayed irregular granularity with subtle wrinkles on the surface (Figure 1d,g). In contrast, the surfaces of PS, PP, and PET MPs aged for 10 days showed wrinkles, increasing the specific surface area and porosity of MPs (Figure 1b,e,h). As the aging degrees increased, more cracks and pits were exhibited on the surface of the three types of MPs (Figure 1c,f,i).

Figure 1.
SEM images of PS, PP, and PET MPs with different aging degrees.
2.1.2. Reaction Solutions
The reaction solutions for the adsorption experiments consisted of Fe(III) solutions of varying salinities and pH values. Dissolved iron concentrations in global surface water systems spanned approximately 0.00018–84.2 mg/L [39], with particularly elevated levels (up to 33.40 mg/L) observed in the groundwater systems of the Pearl River Delta [40]. In order to observe the concentration-dependent adsorption behavior, the heavy metal ion (e.g., Pb2+, Cu2+) concentrations of the MP adsorption experiments were in the range of 1–20 mg/L in previous studies [41,42]. Consequently, this study employed an Fe(III) concentration range of 3–30 mg/L to systematically evaluate concentration-dependent adsorption behavior while ensuring both environmental relevance and methodological consistency. Fe(III) freshwater in concentrations of 3, 5, 10, 15, 20, 25, and 30 mg/L were prepared by dissolving ferric nitrate nonahydrate reagent (AR, McLean’s Reagent) in ultrapure water. NaCl (AR, Damao Chemical Reagent Factory, Tianjin, China) was used to prepare salt Fe(III) solutions with a salinity of 3 g/L.
When a solution’s pH > 6, heavy metal ions tend to precipitate [24]. This phenomenon could interfere with the accurate assessment of adsorption mechanisms. Conversely, the high concentration of H+ ions in the solution of pH < 4 may neutralize the negatively charged surfaces of MPs [41], significantly suppressing the electrostatic adsorption of Fe(III). Therefore, this study selected pH 4, 5, and 6 as experimental conditions to ensure optimal adsorption performance while enabling the precise investigation of Fe(III) adsorption mechanisms by MPs. The pH values of Fe(III) freshwater and saltwater were adjusted to 4, 5, and 6 using HNO3 (AR, Guangzhou Chemical Reagent Factory, Guangzhou, China) and NaOH solutions (AR, Damao Chemical Reagent Factory, Tianjin, China). The pH-adjusted Fe(III) solutions were prepared using a controlled titration method. For the preparation of the pH 6 solution, 500 mL of Fe(III) solution was placed in a glass beaker under constant magnetic stirring. The initial pH adjustment was performed by the dropwise addition of 1 mol/L NaOH solution until pH 5.5 was reached. The pH was fine-tuned to 6.0 by sequential dropwise titration with 0.1 mol/L NaOH and HNO3 solutions. During the adjustment process, the solution’s pH was continuously monitored in real-time by a calibrated multi-parameter analyzer (DZS-706-A, INESA Analytical Instrument Co., Ltd., Shanghai, China) with a resolution of ±0.01 pH units. Fe(III) solutions at pH 4 and 5 were prepared following an identical procedure. All chemicals used in this study were of an analytical grade. Ultrapure water was produced in-house using a laboratory ultrapure water purification system (Milli-Q Advantage A10, Millipore Corporation, Billerica, MA, USA).
2.2. Adsorption Experiments
Most adsorption experimental studies employ a solid-to-liquid ratio range of 1:1000 for MP–heavy metal systems based on adsorption site availability considerations [24,41,43]. This study maintained the same solid-to-liquid ratio, achieved by adding 10 mg of MP to 10 mL Fe(III) solution. A total of 10 mg of PP, PET, and PS particles with different sizes and aging degrees were mixed with 10 mL of Fe(III) freshwater and saltwater with different pH values in clear glass vials, and adsorption experiments were conducted on a constant temperature shaker (26 °C, 150 rpm). In the kinetic adsorption experiment, sampling intervals were set at 5, 20, 30, 60, 300, 720, 1440, and 1800 min. The oscillation duration for the isothermal adsorption experiments was 1440 min. During the experiment, the absorbance of the Fe(III) solution was measured using an atomic absorption spectrophotometer (ICE-3500, Thermo Fisher Scientific, Waltham, MA, USA), and the concentration of Fe(III) was calculated based on the standard curve. The equilibrium adsorption capacity of Fe(III) onto MPs was calculated using Equation (1) [44]:
where is the equilibrium adsorption amount of Fe(III), is the mass of MP particles, () is the initial concentration of Fe(III) in the reaction solution, is the concentration of Fe(III) when the adsorption equilibrium is reached, and is the total volume of solution. Before and after the adsorption experiments, the functional groups of the reactive PP, PET, and PS MPs were tested by Fourier transform infrared spectroscopy (Nicolet 670, Thermo Fisher Scientific, Waltham, MA, USA).
2.3. Analytical Methods
2.3.1. Adsorption Kinetics and Isotherm Models
The adsorption experimental data were fitted to adsorption kinetics and isothermal adsorption models, respectively. The adsorption kinetic models were categorized into Pseudo-First-Order (PFO, Equation (2)) and Pseudo-Second-Order (PSO, Equation (3)) models. The PFO model indicates a proportional relationship between the adsorption rate and the number of unoccupied sites, relying on physical interactions. The PSO model reflects the chemical interactions between MPs and Fe(III) [45].
Extensive studies have demonstrated that the Langmuir and Freundlich models yield optimal fitting results for heavy metal adsorption on MPs [46]. With assumptions of monolayer adsorption and energetically homogeneous surface sites, the Langmuir model provides optimal fitting for adsorption systems where MPs demonstrate uniform surface site distribution [17,47]. The Freundlich model utilizes empirical parameters to characterize multilayer adsorption phenomena on the heterogeneous surfaces of MPs, thereby effectively describing the nonlinear adsorption isotherms resulting from concentration-dependent binding intensity variations [46,48]. Given their demonstrated accuracy and widespread applicability, this study employs both the Langmuir and Freundlich models to systematically investigate Fe(III) adsorption behavior on MPs. This dual-model approach enables a comprehensive interpretation of adsorption mechanisms, combining the theoretical rigor of Langmuir analysis (Equation (4)) with the practical flexibility of Freundlich modeling (Equation (5)). The equations for the PFO, PSO, Langmuir, and Freundlich models are as follows [44]:
where is the adsorption capacity of MPs for Fe(III) at time t(h); is the saturated adsorption capacity; and are the adsorption rate constants for the PFO and PSO models, respectively; is the Langmuir’s constant; and is the Freundlich’s constant, where represents the adsorption intensity (dimensionless).
2.3.2. Spearman’s Correlation Analysis
Spearman’s correlation analysis is a valuable statistical tool for assessing the nonlinear monotonic relationship between diverse variables through Spearman’s rank correlation coefficients (), and significance coefficients () [49,50]. A positive Spearman’s rank correlation coefficient (> 0) indicated a monotonic positive relationship, while a negative value ( < 0) signified an inverse correlation [51]. A p value of less than 0.05 was considered statistically significant, indicating a significant correlation [52]. In this study, the values of and between the Fe(III) adsorption capacity () and the reactive properties, including the aging degrees of MPs, the sizes of MPs, and the pH of the solution, were calculated to analyze the factors influencing the adsorption of Fe(III) onto PP, PET, and PS MPs.
2.3.3. Machine Learning Techniques
This study focused on exploring the adsorption capacity of MPs for Fe(III), as well as analyzing the influence of different environmental conditions and MP properties on the adsorption behavior. In view of the complex nonlinear relationships and multivariable interactions involved in this issue, five mainstream machine learning methods were selected, along with the Bayesian Optimization (BO) algorithm for optimizing the machine learning models. On this basis, the best performing models were further selected and combined with the SHAP method to carry out feature importance analysis. The application of this series of methods aimed to comprehensively evaluate the fitting and interpretive capabilities of different models for the adsorption behavior of Fe(III) by MPs, especially under the conditions of a limited sample size and complex nonlinear relationships among variables.
- (1)
- Gaussian Process Regression (GPR)
Gaussian Process Regression (GPR) is an advanced machine learning technique specifically designed for nonlinear regression problems. Due to its exceptional performance, GPR has been widely applied in modeling and predicting complex system behaviors [53]. A Gaussian process can be viewed as a probability distribution over functions, enabling it to effectively utilize existing data information and prior knowledge of the relationship between data and functions to directly predict new data without additional validation steps. This unique advantage allows the GPR model to efficiently derive predictive distributions corresponding to new test inputs, thereby providing robust support for complex system prediction tasks [54]. A Gaussian process is characterized by its mean and covariance functions , and, given a training dataset with N samples, denoted as , it is denoted as follows:
where represents the n-dimensional influence factor and is the amount of MPs adsorption.
- (2)
- Support Vector Machine (SVM)
Support Vector Machine (SVM) is a supervised learning method grounded in statistical learning theory [55]. The fundamental concept involves employing the kernel trick to map nonlinear data into a high-dimensional feature space, facilitating the construction of an optimal hyperplane for classification or regression tasks. By selecting appropriate kernel functions, SVM effectively handles high-dimensional data, demonstrating successful applications across various domains, particularly excelling with small- to medium-sized datasets [56]. The incorporation of insensitive loss functions and regularization parameters allows for precise control over model complexity, thereby enhancing predictive stability on unseen data. In the context of MP adsorption capacity prediction, SVM utilizes training datasets to identify the optimal hyperplane that maximizes the margin between classes. This hyperplane is defined by a weight vector and bias, with the decision boundary determined by the insensitive loss function.
- (3)
- Random Forest (RF)
The Random Forest (RF) model is an ensemble learning algorithm based on decision trees. By constructing multiple decision trees and leveraging their collective decision-making ability, RF demonstrates significant advantages in classification, regression, and feature selection tasks [57]. In the context of predicting MPs adsorption capacity, the RF model does not require any assumptions regarding the specific distribution of the data; it can automatically evaluate the importance of features that affect adsorption capacity and enhance predictive stability through its ensemble learning mechanism. Additionally, RF effectively reduces the risk of overfitting and improves the generalization ability of type through random feature selection, sample sampling, and the regulation of regularization parameters, combined with ensemble learning mechanisms (e.g., voting or averaging) [58].
- (4)
- Neural Network (NN)
Neural Networks (NNs) are computational models inspired by the human nervous system, designed to simulate the complex information processing and response mechanisms of biological neural systems [59]. A typical NN model consists of three primary layers: the input layer, hidden layers, and the output layer. The input layer, positioned at the front end of the network, is responsible for receiving external data and decomposing it into independent feature variables, thereby enabling the network to effectively capture the key attributes of the input data. The hidden layers, located between the input and output layers, serve as the core processing units of the network, performing complex nonlinear transformations and feature extractions on the input data. A hidden layer can comprise one or more sublayers, each containing multiple neurons that are interconnected through weights. These weights are continuously adjusted during the training process using learning algorithms to optimize the network’s ability to process the input data. The output layer, situated at the end of the network, generates the final predictions or results for adsorption capacity based on the raw MP adsorption data and the processed outcomes from the hidden layers.
- (5)
- Decision Tree (DT)
Decision Tree (DT) is a tree-based supervised learning model that generates intuitive and interpretable decision rules by recursively dividing the dataset [60]. Its basic structure is composed of nodes and branches, with different types of nodes playing different roles in processing data. The root node of the decision tree contains the complete training dataset, and is divided recursively according to specific criteria to gradually build a tree structure. In the top-down greedy algorithm, a feature is selected to partition the node data at each step, and the process is guided by the information gain criterion. The information gain criterion determines the optimal splitting feature and split point by evaluating the degree of improvement of data homogeneity in the child node after the split. The splitting operation continues until it reaches a leaf node, where the preset purity condition or stopping rule is satisfied, and the leaf node represents the final decision result. Pruning methods prevent the tree from overfitting the training dataset by removing subtrees that increase complexity and decrease generalization accuracy [61]. DT has broad applicability to datasets with mixed data type characteristics and missing data or outliers.
- (6)
- Bayesian Optimization (BO)
Bayesian Optimization (BO) is a hyper parameter optimization method based on probabilistic models. Based on Bayesian inference, BO dynamically updates the posterior distribution by integrating prior knowledge with observed data. During the optimization process, BO continuously refines the prior distribution using new observational data, constructs a probabilistic model of the objective function, and efficiently explores the hyper parameter space to identify the optimal combination that best satisfies the objective function, thereby yielding more robust results [62]. Furthermore, BO determines the optimal strategy for subsequent evaluations by analyzing the predictive distribution of the trained model on the training data. This approach can substantially reduce the number of computations required during the parameter search, thereby lowering the overall computational cost. BO is particularly well suited for addressing expensive and complex black-box optimization problems, such as hyper parameter tuning in machine learning and deep learning [63].
2.3.4. Shapley Additive Explanations (SHAP)
Shapley Additive Explanations (SHAP) is a feature importance explanation method based on the Shapley values of game theory, and it has been widely applied in the interpretability analysis of machine learning models. SHAP calculates the marginal contribution of each input feature to the model’s output, offering a fair and consistent approach to quantifying feature importance. It treats each feature as a critical factor influencing the model’s predictions, and by integrating optimal credit allocation with the principle of local interpretability, characterizes the attribution effects of features in individual samples, as detailed in Equation (7) [64]. It should be noted that the dataset used in this study included a categorical variable, “type”. To meet the input requirements of the algorithms and avoid misleading the model with any ordinal assumptions regarding this categorical variable, One-Hot Encoding was employed to transform each category of “type” into an independent binary vector. For example, the categories “PET”, “PS”, and “PP” were encoded as the features “type_PET”, “type_PS”, and “type_PP”, respectively. When computing the SHAP values for “type” and interpreting its contribution, each of these One-Hot Encoded features were analyzed individually to ensure the accuracy and interpretability of the results.
where is the contribution of the m-th feature, L is the feature subset, is the complete feature set, M is the total number of features, is the predicted value of the model after adding M to feature set L, and is the predicted value when only L is included.
3. Results and Discussion
3.1. Adsorption Mechanisms
3.1.1. Adsorption Kinetics
The adsorption kinetic curves for Fe(III) onto PS, PP, and PET MPs in freshwater and saltwater environments at pH 5 are shown in Figure 2. The equilibrium adsorption amounts of Fe(III) by PS MPs (Figure 2a–c) were higher than those by PP and PET MPs (Figure 2d–i), due to the larger surface area ratio and lower negative surface potential of PS MPs [65]. The equilibrium adsorption amounts of Fe(III) by the three types of MPs were higher in freshwater than those in saltwater, similar to the adsorption of Pb2+ by MPs [66]. The adsorption of Fe(III) by PS, PP, and PET MPs exhibited an evident logarithmic growth relationship with the contact time, which can be categorized into three stages in Figure 2: the fast adsorption stage (0~5 h), slow adsorption stage (5~15 h), and equilibrium adsorption stage (15~30 h). During the first stage, abundant active sites were available on the MP surfaces for Fe(III) [45]. As adsorption progressed, Fe(III) gradually occupied available surface sites on the MPs until reaching saturation, ultimately achieving adsorption equilibrium. Notably, 80% of the total Fe(III) adsorption occurred during the first stage, demonstrating exceptionally fast adsorption kinetics of Fe(III) onto MPs [44].

Figure 2.
Adsorption kinetics profiles for Fe(III) onto PS, PP, and PET MPs in freshwater and saltwater (pH = 5; S, M, and L represent the different sizes of MPs; f and s represent freshwater and saltwater, respectively).
The adsorption processes of Fe(III) onto PS, PP, and PET were fitted using PFO and PSO kinetic models (fitting results in Tables S1 and S2), as shown in Figure 2. The results demonstrated that the PFO model exhibited superior accuracy in describing the adsorption behavior of Fe(III) onto MPs in both freshwater and saltwater (R2 = 0.966). This suggests that physical interactions, such as van der Waals forces and electrostatic attraction, primarily govern the adsorption process [67]. The PSO model fitted the adsorption curves (R2 = 0.948), indicating that the surface complexation of metal ions influenced the adsorption process [68]. The second-order adsorption rate constant k2 was relatively small (0.001–0.029), suggesting that the chemisorption rate was proportional to the number of unoccupied active sites [45].
3.1.2. Adsorption Isotherms
The isothermal adsorption process of Fe(III) on PS, PP, and PET MPs is shown in Figure 3. The adsorption capacities of MPs for Fe(III) were lower in saltwater compared to freshwater, and increased with rising initial Fe(III) concentrations. However, the adsorption rate gradually decreased as the adsorption sites on the MP surfaces became progressively occupied by Fe(III) [68]. The Langmuir and Freundlich models were employed to elucidate the adsorption mechanisms, with the corresponding model fitting parameters summarized in Tables S3 and S4. The Langmuir model showed higher accuracy in describing the adsorption isotherm processes of the three types of MPs for Fe(III) adsorption in both freshwater and saltwater (R2 = 0.974). The adsorption processes of Fe(III) on PS, PP, and PET MPs were predominantly monolayer and homogeneous, similar to those of Pb2+ [69,70].
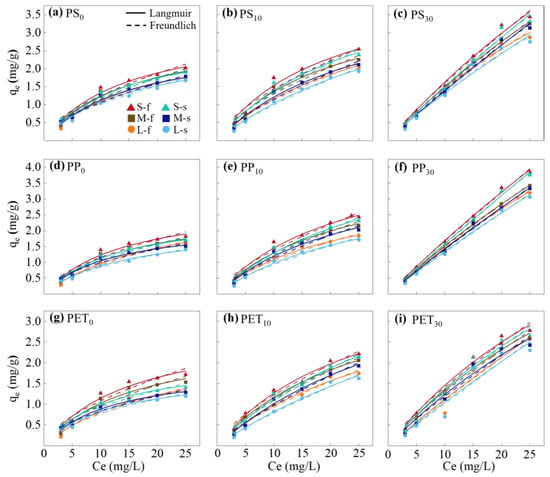
Figure 3.
The isothermal adsorption curves of Fe(III) adsorbed onto PS, PP, and PET MPs in freshwater and saltwater (pH = 5; S, M, and L represent the different sizes of MPs; f and s represent freshwater and saltwater, respectively).
3.1.3. Interaction Mechanism
According to the results of the adsorption experiments, the adsorption behaviors and mechanism of Fe(III) onto PS, PP, and PET MPs were similar between freshwater and saltwater. The FTIR spectra profiles of PS, PP, and PET MPs before and after the adsorption of Fe(III) in freshwater are shown in Figure 4. Before Fe(III) adsorption, the surfaces of PS, PP, and PET MPs contained oxygen-containing and aromatic ring functional groups. After adsorbing Fe(III), the characteristic peak intensity at 863 cm−1 (C-H bond) of all three types of MPs weakened (Figure 4). The peak intensity at 1554 cm−1 (aromatic C-C bond) significantly decreased for PS and PET (Figure 4a,c), while it increased for PP (Figure 4b). The peak intensity at 1739 cm−1 (oxygen-containing functional group C=O) decreased for both PP and PS (Figure 4a,b), while the peak intensity at 3440 cm−1 (O-H bond) for PET weakened (Figure 4c).

Figure 4.
FTIR spectra profiles of PS, PP, and PET MPs before (in dashed lines) and after (solid lines) adsorption of Fe(III) in freshwater.
However, the characteristic peaks of the three types of MPs at 3440 cm−1 (O-H stretching) showed no shift after adsorption, indicating the absence of complexation between the MPs and Fe(III) [14]. In addition, the characteristic peak range of Fe (700–1000 cm−1) did not change before and after adsorption [71], indicating that the PS, PP, and PET MPs adsorbed Fe(III) primarily through physical electrostatic interactions and van der Waals forces [17,32]. Similar results were obtained in studies of Pb, Cd, and As adsorption on MPs in water [17,72]. Consequently, the adsorption behavior of Fe(III) onto MPs was primarily governed by oxygen-containing functional groups, aromatic ring structures, and hydrogen-bonding interactions.
3.2. Analysis of Influencing Factors
3.2.1. Analysis of the Role of Influencing Factors
Figure 5 summarizes the Fe(III) adsorption capacities of PS, PP, and PET MPs in both freshwater and saltwater. The results showed that the adsorption capacity of Fe(III) onto PS, PP, and PET MPs increased with an increasing pH in the aquatic environment. When the pH decreased, the increased concentration of H+ in the solution competed with Fe(III) for adsorption sites on the MPs’ surfaces, leading to a reduction in the negative surface charge of the MPs [69]. Meanwhile, the Fe(III) adsorption capacities of all MPs progressively increased with advancing aging degrees, which can be attributed to the increased surface area and elevated oxygen-containing functional groups in aged MPs [24,73]. The aged MPs developed distinct wrinkles and grooves on their surfaces, creating additional adsorption sites for heavy metal ions [74]. The Fe(III) adsorption capacity, in descending order for unaged MPs, was PS, PP, and PET (Figure 5a,d,g), but changed to PP, PS, and PET for MPS aged for 30 days (Figure 5c,f,i). The reason was that under identical aging conditions, the pore size distribution range was unchanged for PS and PET MPs, but decreased significantly for PP MPs [75].
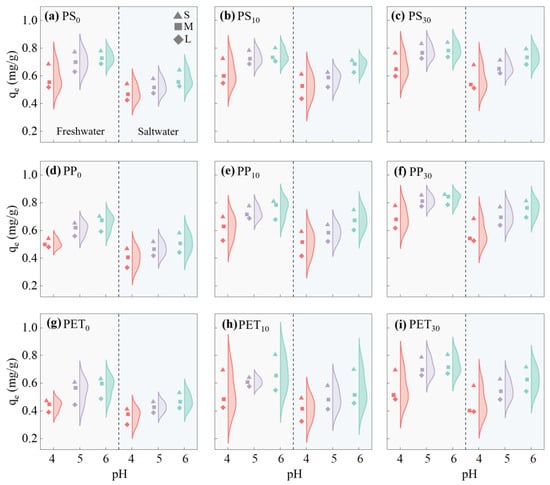
Figure 5.
Fe(III) adsorption capacities of PS, PP, and PET MPs in freshwater and saltwater (S, M, and L represent the different sizes of MPs).
In both freshwater and saltwater, the Fe(III) adsorption capacity exhibited an inverse correlation with particle size across all types of MPs (Figure 5). This is because smaller MPs have larger specific surface areas, providing more available adsorption sites and consequently stronger adsorption capacities [76,77]. However, the Fe(III) adsorption capacities in saltwater were lower than those in freshwater, with correspondingly slower increase rates, likely due to the competitive occupation of adsorption sites on MPs by Na+ ions in saltwater [41]. Since salinity-enhanced aggregation reduced the contact area of MPs with Fe(III) in saltwater, the effect of MP size on adsorption capacity was less pronounced compared to in freshwater [78].
3.2.2. Correlation Analysis of Influencing Factors
Figure 6 presents Spearman’s correlation analysis results between the Fe(III) adsorption capacities of PS, PP, and PET MPs with various experimental factors, including the aging degrees of MPs, sizes of MPs, and pH values of the freshwater and saltwater. The results indicated that the Fe(III) adsorption capacities of three types of MPs were significantly negatively correlated with their size, while positively correlated with aging degree and pH. For PS MPs, the positive correlation coefficients between pH and Fe(III) adsorption capacity were greater than those for aging degree, with this difference being more pronounced in freshwater. However, for PP MPs, the influence of aging degree outweighed that of pH, which was more pronounced in saltwater. For PET MPs, the influence of aging degree predominated over pH in freshwater, while the relationship was reversed in saltwater. Overall, the effects of pH and size were more pronounced in freshwater, whereas the influence of MP aging degree was enhanced in saltwater. As the salinity-induced neutralization of surface negative charges diminished the effects of pH and size in saltwater, PS MPs exhibited the lowest aging-dependent variation in Fe(III) adsorption capacity in freshwater [78].
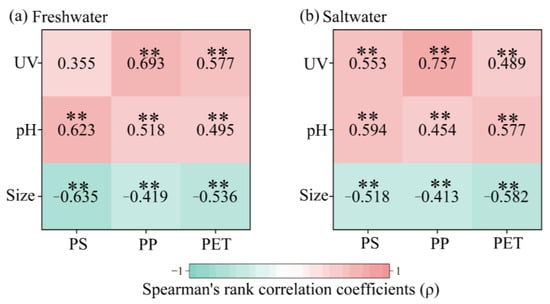
Figure 6.
Spearman’s correlation coefficients between the Fe(III) adsorption capacities of MPs and their aging degree, size, and pH of the solution. ** p <= 0.01.
3.3. Machine Learning-Based Analysis
In this study, five regression models, namely GPR, SVM, NN, DT, and RF, along with their Bayesian Optimization (BO)-enhanced versions, were employed to train and predict the MPs adsorption dataset for Fe(III) ions in both freshwater and saline environments. The results are presented in Figure 7 and Figure 8, respectively. Overall, Bayesian Optimization significantly improved the predictive performance of several models. For example, in the freshwater environment, the BO-enhanced RF model performed most notably, with its R2 increasing dramatically from 0.74 to 0.94, indicating a substantial enhancement in the model’s explanatory power. Additionally, the MAE, MSE, and RMSE of this model decreased by 50% (Figure 7a,b). In the saline environment, the BO-enhanced GPR model demonstrated the best performance (Figure 8a,b), achieving an R2 of 0.97 and MAE, MSE, and RMSE values of 0.015, 0.0004, and 0.02, respectively, reflecting its excellent fitting capability and extremely low prediction error. In contrast, the predictive accuracies of the SVM, NN, and DT models were lower in both environments. This may be attributed to the suboptimal kernel function selection in the SVM model, the inadequate network structure in the NN, and the DT model’s difficulty in capturing deep associations within complex data. These models require further optimization to enhance their predictive performance.

Figure 7.
Freshwater environment: performance metrics and computational efficiency plots for each model (a) without and (b) with Bayesian Optimization (BO); (c) SHAP analysis results.

Figure 8.
Saltwater environment: performance metrics and computational efficiency plots for each model (a) without and (b) with Bayesian Optimization (BO); (c) SHAP analysis results.
Based on the optimal models (RF and GPR) established for freshwater and saline environments, this study employed the SHAP algorithm to quantify feature importance and elucidate the influence of various characteristics on the MPs adsorption of Fe(III), as illustrated in Figure 7c and Figure 8c. In both aquatic environments, pH, UV irradiation, and MPs size demonstrated significant impacts on Fe(III) adsorption, consistent with the results of Spearman’s correlation analysis. However, the hierarchical importance of these parameters differed between the environments: pH exhibited the highest contribution in freshwater systems, followed by UV and particle size, whereas UV emerged as the predominant factor in saline environments, succeeded by pH and size. Further analysis of data point distributions revealed that higher pH and UV levels (denoted by blue scatters) were predominantly clustered in regions with positive SHAP values, whereas lower values (red scatters) were concentrated in regions with negative SHAP values. This indicated that a higher pH and UV enhanced their predictive contribution to the adsorption capacity. Conversely, larger MPs sizes (blue scatters) exhibited pronounced aggregation in regions with negative SHAP values, revealing a statistically significant negative correlation with adsorption predictions.
For the One-Hot Encoded categorical features (type_PET, type_PS, type_PP), most of their SHAP values displayed minimal magnitudes and clustered near the region of the zero line, confirming their limited explanatory power in the model. Specifically, the scatter for the PET class was concentrated in regions with negative SHAP values, indicating a slight negative impact on predictions. In contrast, the PS and PP categories had a slight positive effect on the prediction results, but both of their effects were extremely low. Furthermore, these results indicated that when studying the behavior and mechanisms of heavy metal adsorption by MPs, it is necessary to focus on the chemical environmental conditions of the water rather than the physical and chemical properties of the MPs themselves.
4. Conclusions
This study focused on the adsorption mechanisms, influencing factors, and adsorption capacities of Fe(III) onto three types of MPs (PS, PP, PET) in both freshwater and saltwater. The results indicated that the adsorption processes of Fe(III) onto MPs followed the PFO and Langmuir models. The Fe(III) adsorption capacity of MPs in freshwater exceeded that in saltwater due to the salinity-promoted aggregation of MPs and competitive Na+ adsorption. The results based on the ML methods showed that the GPR, NN, and RF models demonstrated robust predictive performance for the Fe(III) adsorption capacities of the three types of MPs, with the RF model exhibiting superior accuracy. Moreover, SHAP analysis indicated that, in both freshwater and saline environments, pH, ultraviolet (UV) irradiation intensity, and MP particle sizes were the key variables in the optimal models for predicting Fe(III) adsorption capacity. Specifically, pH and UV showed a positive promoting effect on the adsorption capacity, while larger MP particle sizes tended to reduce it. In freshwater, the influences of pH and size were more significant, whereas the effect of the aging degree was enhanced in saltwater.
While this study has provided fundamental insights into MP-Fe(III) interactions, several limitations should be acknowledged. First, our investigation focused on three prevalent MP types (PS, PP, PET; 15–300 μm), which limits the generalizability of our findings to other polymer classes (e.g., PVC, PE) that may exhibit distinct Fe(III) adsorption behaviors. Second, the single-factor UV irradiation used in our study may not fully capture the synergistic effects of multiple environmental aging processes. Finally, the controlled laboratory conditions may differ substantially from complex aquatic systems where DOM, biofilms, and multiple contaminants coexist. Therefore, future research could prioritize the following directions: (1) conducting systematic screening across a diverse range of MPs to establish structure–activity relationships for Fe(III) adsorption; (2) performing multi-factor aging experiments using field-collected MPs to better simulate real-world conditions; and (3) investigating ternary interactions involving organic matter and microbial communities in environmentally relevant studies.
Overall, this paper provides a theoretical basis for assessing the interaction between MPs and Fe(III) in aquatic environments and their associated ecological risks. Additionally, the contributions of controllable factors (MP properties and experimental conditions) for predicting Fe(III) adsorption by MPs were systematically analyzed through the integration of RF and GPR models with the SHAP algorithm, and the importance of each feature was quantified. Through systematic experimental characterization and theoretical modeling, this study provides fundamental insights into the adsorption mechanisms of Fe(III) onto MPs in aquatic environments. The predictive framework developed, which was validated by high correlation coefficients across diverse environmental conditions, significantly advanced our understanding of MP–heavy metal co-pollution systems. Moreover, the machine learning-based SHAP analysis quantitatively elucidated the relative importance of key environmental parameters. These findings not only clarify the molecular-scale processes underlying MP–metal interactions but also establish a transferable methodology for assessing contaminant behavior in complex aquatic systems, with important implications for environmental risk assessment and remediation strategy development.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/w17091316/s1, Table S1: Kinetics parameters for the adsorption of Fe(III) ions onto MPs in freshwater environments; Table S2: Kinetics parameters for the adsorption of Fe(III) ions onto MPs in saltwater environments; Table S3: Isotherm parameters for the adsorption of Fe(III) ions onto MPs in freshwater environments; Table S4: Isotherm parameters for the adsorption of Fe(III) ions onto MPs in saltwater environments.
Author Contributions
Conceptualization, X.G. and Q.Z.; methodology, X.G. and Q.Z.; software, S.L. and Y.Y.; validation, X.G., Q.Z., S.L. and Y.Y.; formal analysis, X.G., S.L. and Y.Y.; writing—original draft preparation, X.G., S.L. and Y.Y.; writing—review and editing, X.G. and Q.Z.; visualization, S.L. and Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 42002249), the Guangdong Basic and Applied Basic Research Foundation (Grant No. 2023A1515030126 and 2024A1515011791), Special Project for Research and Development in Key areas of Guangdong Province (Grant No. 2019B110207001), the National Key Research and Development Program of China (Grant No. 2023-3.1), and the Joint Fund Program of Natural Science Foundation of Hunan Province, China (Grant No. 2025JJ80030).
Data Availability Statement
All data used during this study appear in the submitted article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, D.; Wang, P.; Liu, S.; Wang, R.; Wu, Y.; Zhu, A.X.; Deng, C. Global patterns of lake microplastic pollution: Insights from regional human development levels. Sci. Total Environ. 2024, 954, 176620. [Google Scholar] [CrossRef] [PubMed]
- Thompson, R.C.; Olsen, Y.; Mitchell, R.P.; Davis, A.; Rowland, S.J.; John, A.W.G.; McGonigle, D.; Russell, A.E. Lost at sea: Where is all the plastic? Science 2004, 304, 838. [Google Scholar] [CrossRef]
- Dalvand, M.; Hamidian, A.H. Occurrence and distribution of microplastics in wetlands. Sci. Total Environ. 2023, 862, 160740. [Google Scholar] [CrossRef]
- Pothiraj, C.; Amutha Gokul, T.; Ramesh Kumar, K.; Ramasubramanian, A.; Palanichamy, A.; Venkatachalam, K.; Pastorino, P.; Barcelò, D.; Balaji, P.; Faggio, C. Vulnerability of microplastics on marine environment: A review. Ecol. Indic. 2023, 155, 111058. [Google Scholar] [CrossRef]
- Chanda, M.; Bathi, J.R.; Khan, E.; Katyal, D.; Danquah, M. Microplastics in ecosystems: Critical review of occurrence, distribution, toxicity, fate, transport, and advances in experimental and computational studies in surface and subsurface water. J. Environ. Manag. 2024, 370, 122492. [Google Scholar] [CrossRef]
- Bi, S.; Liu, S.; Liu, E.; Xiong, J.; Xu, Y.; Wu, R.; Liu, X.; Xu, J. Adsorption behavior and mechanism of heavy metals onto microplastics: A meta-analysis assisted by machine learning. Environ. Pollut. 2024, 360, 124634. [Google Scholar] [CrossRef]
- Mozafarjalali, M.; Hamidian, A.H.; Sayadi, M.H. Microplastics as carriers of iron and copper nanoparticles in aqueous solution. Chemosphere 2023, 324, 138332. [Google Scholar] [CrossRef]
- Roshan, A.; Polya, D.A.; Kumar, A.; Ghosh, A.; Glenny, A.-M.; Sedighi, M.; Reichman, S.M.; Arora, M.; Richards, L.A. Comparison of the distribution of groundwater remediation units and contaminant (arsenic, iron, fluoride) distribution in Bihar, India for improved water security and management. J. Environ. Manag. 2024, 372, 123157. [Google Scholar] [CrossRef]
- Sherif, Z.N.; Anitha, K. Efficacious sensing and elimination of iron ions from aqueous medium by polyethylenimine functionalized carbon dot. J. Environ. Chem. Eng. 2024, 12, 113595. [Google Scholar] [CrossRef]
- Fang, S.; Hua, C.; Yang, J.; Liu, F.; Wang, L.; Wu, D.; Ren, L. Combined pollution of soil by heavy metals, microplastics, and pesticides: Mechanisms and anthropogenic drivers. J. Hazard. Mater. 2025, 485, 136812. [Google Scholar] [CrossRef]
- Khalid, N.; Aqeel, M.; Noman, A.; Khan, S.M.; Akhter, N. Interactions and effects of microplastics with heavy metals in aquatic and terrestrial environments. Environ. Pollut. 2021, 290, 118104. [Google Scholar] [CrossRef]
- Ling, X.; Yan, Z.; Lu, G. Vertical transport and retention behavior of polystyrene nanoplastics in simulated hyporheic zone. Water Res. 2022, 219, 118609. [Google Scholar] [CrossRef]
- Shi, M.; Xie, Q.; Li, Z.L.; Pan, Y.F.; Yuan, Z.; Lin, L.; Xu, X.-R.; Li, H.X. Adsorption of heavy metals on biodegradable and conventional microplastics in the pearl river estuary, China. Environ. Pollut. 2023, 322, 121158. [Google Scholar] [CrossRef]
- Dong, Y.; Gao, M.; Song, Z.; Qiu, W. As (III) adsorption onto different-sized polystyrene microplastic particles and its mechanism. Chemosphere 2020, 239, 124792. [Google Scholar] [CrossRef]
- Fu, Q.; Tan, X.; Ye, S.; Ma, L.; Gu, Y.; Zhang, P.; Chen, Q.; Yang, Y.; Tang, Y. Mechanism analysis of heavy metal lead captured by natural-aged microplastics. Chemosphere 2021, 270, 128624. [Google Scholar] [CrossRef]
- Shi, C.; Niu, F.; Xie, Y.; Zhang, Z.; Geng, J.; Wang, C. Mechanism of dynamic interaction between aging microplastics and heavy metal ions under different hydrodynamic environments. J. Water Process Eng. 2025, 71, 107232. [Google Scholar] [CrossRef]
- Liu, Q.; Wu, H.; Chen, J.; Guo, B.; Zhao, X.; Lin, H.; Li, W.; Zhao, X.; Lv, S.; Huang, C. Adsorption mechanism of trace heavy metals on microplastics and simulating their effect on microalgae in river. Environ. Res. 2022, 214, 113777. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Su, F.; Wang, Y.; Peng, L.; Liu, D. Adsorption behaviour of microplastics on the heavy metal Cr(VI) before and after ageing. Chemosphere 2022, 302, 134865. [Google Scholar] [CrossRef]
- Liu, S.; Huang, J.; Zhang, W.; Shi, L.; Yi, K.; Zhang, C.; Pang, H.; Li, J.; Li, S. Investigation of the adsorption behavior of Pb(II) onto natural-aged microplastics as affected by salt ions. J. Hazard. Mater. 2022, 431, 128643. [Google Scholar] [CrossRef]
- Chen, C.C.; Zhu, X.; Xu, H.; Chen, F.; Ma, J.; Pan, K. Copper adsorption to microplastics and natural particles in seawater: A comparison of kinetics, isotherms, and bioavailability. Environ. Sci. Technol. 2021, 55, 13923–13931. [Google Scholar] [CrossRef]
- Shi, Y.; Chen, W.; Yang, S.; Fan, Y.; Lu, L. Freshwater microplastics governance and sustainable development: Pollution status, interactions, policies, and prospective studies. Desalination Water Treat. 2024, 320, 100704. [Google Scholar] [CrossRef]
- Han, X.; Wang, S.; Yu, X.; Vogt, R.D.; Feng, J.; Zhai, L.; Ma, W.; Zhu, L.; Lu, X. Kinetics and size effects on adsorption of CU(II), CR(III), and PB(II) onto polyethylene, polypropylene, and polyethylene terephthalate microplastic particles. Front. Mar. Sci. 2021, 8, 785146. [Google Scholar] [CrossRef]
- Godoy, V.; Blázquez, G.; Calero, M.; Quesada, L.; Martín-Lara, M.A. The potential of microplastics as carriers of metals. Environ. Pollut. 2019, 255, 113363. [Google Scholar] [CrossRef]
- Muthuraja, R.; Ou, B.; Thangavelu, M.; Narhayanan, T.N.; Chittamart, N.; Janjaroen, D. Effects of particle size and aging on heavy metal adsorption by polypropylene and polystyrene microplastics under varying environmental conditions. Chemosphere 2024, 369, 143843. [Google Scholar] [CrossRef]
- Cao, G.; Sun, J.; Chen, M.; Sun, H.; Zhang, G. Co-transport of ball-milled biochar and Cd2+ in saturated porous media. J. Hazard. Mater. 2021, 416, 125725. [Google Scholar] [CrossRef]
- Qiu, Y.; Li, Z.; Zhang, T.; Zhang, P. Predicting aqueous sorption of organic pollutants on microplastics with machine learning. Water Res. 2023, 244, 120503. [Google Scholar] [CrossRef]
- Fu, H.; He, H.; Usman, M.; Chen, Q.; Laipan, M.; Yang, Y.; Zhu, R.; Cai, L. Facile synthesis of Al/Fe bimetallic (oxyhydr)oxide-coated magnetite for efficient removal of fluoride from water. Environ. Technol. 2020, 41, 2625–2636. [Google Scholar] [CrossRef]
- Al Ghouti, M.A.; Da’ana, D.A. Guidelines for the use and interpretation of adsorption isotherm models: A review. J. Hazard. Mater. 2020, 393, 122383. [Google Scholar] [CrossRef]
- Chung, H.K.; Kim, W.H.; Park, J.; Cho, J.; Jeong, T.Y.; Park, P.K. Application of Langmuir and Freundlich isotherms to predict adsorbate removal efficiency or required amount of adsorbent. J. Ind. Eng. Chem. 2015, 28, 241–246. [Google Scholar] [CrossRef]
- Kalaronis, D.; Evgenidou, E.; Kyzas, G.Z.; Bikiaris, D.N.; Lambropoulou, D.A. Investigation on the adsorption mechanism of a mixture of seven pharmaceutical compounds on virgin and aged biodegradable microplastics. Colloid Surf. A 2024, 702, 135019. [Google Scholar] [CrossRef]
- Shahi, N.K.; Kim, J.Y.; Dockko, S. Process analysis of microplastic aging during the photochemical oxidation process and its effect on the adsorption behavior of dissolved organic matter. Chemosphere 2023, 341, 139980. [Google Scholar] [CrossRef]
- Tenea, A.G.; Dinu, C.; Rus, P.A.; Ionescu, I.A.; Gheorghe, S.; Iancu, V.I.; Vasile, G.G.; Pascu, L.F.; Chiriac, F.L. Exploring adsorption dynamics of heavy metals onto varied commercial microplastic substrates: Isothermal models and kinetics analysis. Heliyon 2024, 10, e35364. [Google Scholar] [CrossRef]
- Xu, Y.; Li, P.; Zhang, M.; Xiao, L.; Wang, B.; Zhang, X.; Wang, Y.; Shi, P. Quantifying Seasonal Variations in Pollution Sources with Machine Learning-Enhanced Positive Matrix Factorization. Ecol. Indic. 2024, 166, 112543. [Google Scholar] [CrossRef]
- Yan, Y.; Yang, Y. Revealing the Synergistic Spatial Effects in Soil Heavy Metal Pollution with Explainable Machine Learning Models. J. Hazard. Mater. 2025, 482, 136578. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, J.; Du, J.; Peng, S.; Tan, S.; Zhang, W.; Yan, X.; Wang, H.; Lin, Z. Machine Learning Predicts Heavy Metal Adsorption on Iron (Oxyhydr)Oxides: A Combined Insight into the Adsorption Efficiency and Binding Configuration. Sci. Total Environ. 2024, 950, 175370. [Google Scholar] [CrossRef]
- Guo, X.; Wang, J. Projecting the sorption capacity of heavy metal ions onto microplastics in global aquatic environments using Artificial Neural Networks. J. Hazard. Mater. 2021, 402, 123709. [Google Scholar] [CrossRef]
- Bai, Y.; Zeng, B.; Li, C.; Zhang, J. An ensemble long short-term memory neural network for hourly PM2.5 concentration forecasting. Chemosphere 2019, 222, 286–294. [Google Scholar] [CrossRef]
- Bahrami, M.; Amiri, M.J.; Rajabi, S.; Mahmoudi, M. The removal of methylene blue from aqueous solutions by polyethylene microplastics: Modeling batch adsorption using random forest regression. Alex. Eng. J. 2024, 95, 101–113. [Google Scholar] [CrossRef]
- Tong, S.; Li, H.; Tudi, M.; Yuan, X.; Yang, L. Comparison of characteristics, water quality and health risk assessment of trace elements in surface water and groundwater in China. Ecotoxicol. Environ. Saf. 2021, 219, 112283. [Google Scholar] [CrossRef]
- Yi, H.; Cui, J.; Sun, J.; Zhou, X.; Ye, T.; Gan, S.; Chen, J.; Yang, Y.; Liang, W.; Guo, P.; et al. Key drivers regulating arsenic enrichment in shallow groundwater of the Pearl River Delta: Comprehensive analyses of iron, competitive anions, and dissolved organic matter. Appl. Geochem. 2023, 151, 105602. [Google Scholar] [CrossRef]
- Wang, L.; Guo, C.; Qian, Q.; Lang, D.; Wu, R.; Abliz, S.; Wang, W.; Wang, J. Adsorption behavior of UV aged microplastics on the heavy metals Pb(II) and Cu(II) in aqueous solutions. Chemosphere 2023, 313, 137439. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Sun, Y.; Wang, Y.; Yu, F.; Ma, J. Adsorption behavior of Cu(II) and Cr(VI) on aged microplastics in antibiotics-heavy metals coexisting system. Chemosphere 2022, 291, 132794. [Google Scholar] [CrossRef]
- Tang, S.; Ma, S.; Lin, L.; Ding, Y.; Zhang, X.; Wu, X.; Zhang, Q.; Pervez Md, N.; Cao, C.; Zhao, Y. Carrier effects of face mask-derived microplastics on metal ions: Enhanced adsorption by photoaging combined with biofilms, exemplified with Pb(II). J. Hazard. Mater. 2024, 477, 135311. [Google Scholar] [CrossRef] [PubMed]
- Ma, M.; Han, R.; Han, R.; Xu, D.; Li, F. Binding between Cu2+/Zn2+ and aged polyethylene and polyethylene terephthalate microplastics in swine wastewaters: Adsorption behavior, and mechanism insights. Environ. Pollut. 2024, 360, 124685. [Google Scholar] [CrossRef]
- Zhao, Y.; Wan, S.; Xu, M.; Wu, G.; Wang, D.; Yi, C.; Cui, L. Effect of aging on the properties of microplastics and their adsorption behavior of norfloxacin. J. Water Process Eng. 2025, 70, 107021. [Google Scholar] [CrossRef]
- Gao, X.; Hassan, I.; Peng, Y.; Huo, S.; Ling, L. Behaviors and influencing factors of the heavy metals adsorption onto microplastics: A review. J. Clean. Prod. 2021, 319, 128777. [Google Scholar] [CrossRef]
- Lei, C.; Chengkai, M.; Shanning, Y.; Xianjuan, P.; Huanhuan, L.; Xiangyu, C.; Haiyang, S.; Minghong, W. Comparison of aging behavior and adsorption processes of biodegradable and conventional microplastics. Chem. Eng. J. 2024, 502, 157915. [Google Scholar] [CrossRef]
- Chen, X.; Hossain, M.F.; Duan, C.; Lu, J.; Tsang, Y.F.; Islam, M.S.; Zhou, Y. Isotherm models for adsorption of heavy metals from water—A review. Chemosphere 2022, 307, 135545. [Google Scholar] [CrossRef]
- Haritwal, D.K.; Singh, P.; Ramana, G.V.; Datta, M. Advanced characterisation of groundwater contamination at a dumpsite: Methodology and assessment—Case study of a municipal solid waste dumpsite in India. Sci. Total Environ. 2024, 957, 177642. [Google Scholar] [CrossRef]
- Jin, Z.; Chen, K.; Zhu, Q.; Hu, X.; Tian, S.; Xiang, A.; Sun, Y.; Yuan, M.; Yao, H. Non-degradable microplastic promote microbial colonization: A meta-analysis comparing the effects of microplastic properties and environmental factors. Environ. Res. 2025, 270, 121053. [Google Scholar] [CrossRef]
- Morshed, S.R.; Fattah, M.A.; Kafy, A.A.; Alsulamy, S.; Almulhim, A.I.; Shohan, A.A.A.; Khedher, K.M. Decoding seasonal variability of air pollutants with climate factors: A geostatistical approach using multimodal regression models for informed climate change mitigation. Environ. Pollut. 2024, 345, 123463. [Google Scholar] [CrossRef] [PubMed]
- Ozabor, F.; Onyemenam, P.I.; Wekpe, V.O.; Obisesan, A. Determinants of housing demands and residential rent costs in an emerging city in southern Nigeria. Urban Gov. 2024, 4, 232–244. [Google Scholar] [CrossRef]
- Lyu, C.; Liu, X.; Mihaylova, L. Review of recent advances in gaussian process regression methods. In Advances in Computational Intelligence Systems Contributions Presented at the 21st UK Workshop on Computational Intelligence, September 7–9, 2022, Sheffield, UK; Panoutsos, G., Mahfouf, M., Mihaylova, L.S., Eds.; Springer International Publishing Ag: Cham, Switzerland, 2024; Volume 1454, pp. 226–237. [Google Scholar]
- Wang, J. An intuitive tutorial to Gaussian Process Regression. Comput. Sci. Eng. 2023, 25, 4–11. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Cervantes, J.; Garcia-Lamont, F.; Rodriguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Halabaku, E.; Bytyçi, E. Overfitting in machine learning: A comparative analysis of decision trees and random forests. Intell. Autom. Soft Comput. 2024, 39, 987–1006. [Google Scholar] [CrossRef]
- Kohonen, T. An introduction to neural computing. Neural Netw. 1988, 1, 3–16. [Google Scholar] [CrossRef]
- Mienye, I.D.; Jere, N. A Survey of Decision Trees: Concepts, Algorithms, and Applications. IEEE Access 2024, 12, 86716–86727. [Google Scholar] [CrossRef]
- Furnkranz, J. Pruning Algorithms for Rule Learning. Mach. Learn. 1997, 27, 139–171. [Google Scholar] [CrossRef]
- Khan, M.E.; Nielsen, D. Fast yet simple natural-gradient descent for variational inference in complex models. In Proceedings of the 2018 International Symposium on Information Theory and Its Applications (ISITA), Singapore, 28–31 October 2018; IEEE: New York, NY, USA, 2018; pp. 31–35. [Google Scholar]
- Turner, R.; Eriksson, D.; McCourt, M.; Kiili, J.; Laaksonen, E.; Xu, Z.; Guyon, I. Bayesian optimization is superior to random search for machine learning hyperparameter tuning: Analysis of the black-box optimization challenge 2020. In Proceedings of the NeurIPS 2020 Competition and Demonstration Track, Vancouver, BC, Canada, 6–12 December 2020; Escalante, H.J., Hofmann, K., Eds.; JMLR-Journal Machine Learning Research: Cambridge, MA, USA, 2020; Volume 133, pp. 3–26. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Duan, L.; Qin, Y.; Meng, X.; Liu, Y.; Zhang, T.; Chen, W. Sulfide and UV-induced aging differentially affect contaminant-binding properties of microplastics derived from commercial plastic products. Sci. Total Environ. 2023, 869, 161800. [Google Scholar] [CrossRef] [PubMed]
- Tang, S.; Yang, X.; Zhang, T.; Qin, Y.; Cao, C.; Shi, H.; Zhao, Y. Adsorption mechanisms of metal ions (Pb, Cd, Cu) onto polyamide 6 microplastics: New insight into environmental risks in comparison with natural media in different water matrices. Gondwana Res. 2022, 110, 214–225. [Google Scholar] [CrossRef]
- Tang, S.; Sun, P.; Ma, S.; Jin, W.; Zhao, Y. The interfacial behaviors of different arsenic species on polyethylene mulching film microplastics: Roles of the plastic additives. J. Hazard. Mater. 2023, 442, 130037. [Google Scholar] [CrossRef]
- Fan, X.; Zou, Y.; Geng, N.; Liu, J.; Hou, J.; Li, D.; Yang, C.; Li, Y. Investigation on the adsorption and desorption behaviors of antibiotics by degradable MPs with or without UV ageing process. J. Hazard. Mater. 2021, 401, 123363. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Huang, J.; Shi, L.; He, W.; Zhang, W.; Li, E.; Zhang, C.; Pang, H.; Tan, X. Interaction of Pb(II) with Microplastic-Sediment complexes: Critical effect of surfactant. Environ. Pollut. 2024, 361, 124815. [Google Scholar] [CrossRef]
- Tang, S.; Lin, L.; Wang, X.; Feng, A.; Yu, A. Pb(II) uptake onto nylon microplastics: Interaction Mechanism and Adsorption Performance. J. Hazard. Mater. 2020, 386, 121960. [Google Scholar] [CrossRef]
- Niraimathee, V.A.; Subha, V.; Ravindran, R.S.E.; Renganathan, S. Green synthesis of iron oxide nanoparticles from mimosa pudica root extract. Int. J. Environ. Sustain. Dev. 2016, 15, 227–240. [Google Scholar] [CrossRef]
- Dong, Y.; Gao, M.; Song, Z.; Qiu, W. Adsorption mechanism of As(III) on polytetrafluoroethylene particles of different size. Environ. Pollut. 2019, 254, 112950. [Google Scholar] [CrossRef]
- Tang, S.; Lin, L.; Wang, X.; Yu, A.; Sun, X. Interfacial interactions between collected nylon microplastics and three divalent metal ions (Cu(II), Ni(II), Zn(II)) in aqueous solutions. J. Hazard. Mater. 2021, 403, 123548. [Google Scholar] [CrossRef]
- Chen, P.W.; Hsiao, M.N.; Xiao, L.W.; Liu, Z.S. Adsorption behavior of heavy metals onto microplastics derived from conventional and biodegradable commercial plastic products. Sci. Total Environ. 2024, 951, 175537. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, J.; Zhu, J.; Lei, M.; Huang, C.; Xu, H.; Liu, Z.; Wang, P. The interfacial interaction between typical microplastics and Pb2+ and their combined toxicity to Chlorella pyrenoidosa. Sci. Total Environ. 2024, 918, 170591. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.B.; Ho, T.B.C.; Huang, C.P.; Chen, C.W.; Chen, W.H.; Hsieh, S.; Hsieh, S.L.; Dong, C.D. Adsorption of lead(II) onto PE microplastics as a function of particle size: Influencing factors and adsorption mechanism. Chemosphere 2022, 304, 135276. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Xie, N.; Yuan, S.; Shao, H. Adsorption mechanism of hexavalent chromium on electron beam-irradiated aged microplastics: Novel aging processes and environmental factors. Chemosphere 2024, 363, 142741. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Shen, Z.; Wu, J.; Su, M.; Zheng, L.; Xie, M.; Hong, H.; Huang, X.; Lu, H. High salinity restrains microplastic transport and increases the risk of pollution in coastal wetlands. Water Res. 2024, 267, 122463. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).