Abstract
Cyanobacteria harmful blooms (Cyano-HABs) have become a globally critical environmental issue, threatening freshwater ecosystems by degrading water quality and posing risks to human and aquatic life. Chlorophyll-a (Chl-a), a key biomarker of bloom intensity, offers crucial insights into algal bloom dynamics. However, predicting Chl-a concentrations remains challenging due to the complex interactions between various environmental factors. This study utilizes machine learning (ML) models to predict Chl-a concentrations, focusing on Lake Taihu in China, a large eutrophic lake that serves as an example of numerous freshwater lakes suffering from Cyano-HABs. The research leverages nine critical water quality parameters—water temperature, pH, dissolved oxygen, turbidity, electrical conductivity permanganate index, ammonia nitrogen, total phosphorus, and total nitrogen—to develop an ensemble ML model using XGBoost, known for its ability to handle nonlinear relationships and integrate multiple variables. The XGBoost model achieved superior predictive accuracy with an R2 value of 0.78 and RMSE of 8.97 mg/m3 on the test set, outperforming traditional models like linear regression, decision trees, multi-layer perceptrons, support vector regression, and random forests. Feature importance analysis identified electrical conductivity, turbidity, and water temperature as the most significant predictors of Chl-a levels. This study further enhances model interpretability through Pearson correlation analysis, which quantifies the relationships between Chl-a concentrations and other water quality factors. Additionally, we employed principal component analysis (PCA), mutual information, Spearman rank correlation coefficients, and SHAP models to analyze feature importance and model interpretability in ML. The model’s robustness was tested across multiple monitoring sites in Lake Taihu, demonstrating its potential for broader application in other eutrophic lakes facing similar environmental challenges. By providing a reliable tool for forecasting Chl-a concentrations, this research contributes to the development of early warning systems that can help mitigate the impacts of Cyano-HABs, aiding in more effective water resource management.
1. Introduction
Cyanobacteria harmful blooms (Cyano-HABs) present significant challenges to inland aquatic ecosystems, particularly in lakes, by releasing high concentrations of toxic compounds into the water column. These toxic events degrade water quality and trigger a cascade of adverse health impacts on both human populations and aquatic life. The scale and urgency of the issue have been escalating in recent years, making it a critical environmental concern [1,2]. For instance, a recent cyanobacterial bloom in freshwater lakes led to a severe drinking water crisis, underlining the potentially devastating consequences of these phenomena [3]. This pressing challenge demands a better understanding of algal bloom dynamics to inform more effective mitigation strategies.
Among the various biomarkers of algal bloom activity, chlorophyll-a (Chl-a) is a critical indicator of both the development and intensity of blooms [4,5,6]. Monitoring Chl-a concentrations provides insights into the health of aquatic ecosystems, as its fluctuations are influenced by a myriad of environmental and water quality factors [7,8]. In the case of Lake Taihu, for example, despite significant reductions in chemical oxygen demand (COD) and ammonia nitrogen (NH3-N) in recent years, total phosphorus (TP) levels remain high [9]. This persistent elevation of TP has been a driving force behind the proliferation of cyanobacteria blooms, complicating efforts to control their growth. The persistence of high TP concentrations is a cause for concern, as it continues to exacerbate the occurrence of these harmful blooms.
Chl-a is a pigment essential for photosynthesis in freshwater algae and serves as a reliable metric for assessing the spatial distribution of plankton. It also correlates with key water quality parameters such as water temperature (WT), dissolved oxygen (DO), TP, total nitrogen (TN) [10], turbidity, electrical conductivity (EC) [7], and total organic carbon (TOC) [8]. This correlation is crucial for developing predictive models for bloom dynamics, as Chl-a concentrations fluctuate based on these environmental inputs. Effective Chl-a monitoring is therefore critical to ecosystem health assessments and for improving predictive models that support environmental management.
Currently, prediction methods for Chl-a concentrations and Cyano-HABs are generally categorized into two types [2]: process-based (PB) methods [11,12,13] and data-driven (DD) methods [10,14,15,16,17,18,19,20]. PB models typically use mathematical formulations to simulate the interaction between algal growth and environmental factors. Han et al. [21] developed a PB model for Jordan Lake, concluding that nutrient variations had a more significant impact on Chl-a concentrations than temperature or light. However, while valuable, the broader application of PB models is hindered by the need to calibrate numerous environmental parameters, many of which are difficult to measure accurately, limiting the usability of these models [22].
In contrast, DD methods, particularly those utilizing machine learning (ML) and deep learning (DL) algorithms, have recently gained traction due to their ability to model nonlinear relationships between water quality variables and Chl-a concentrations. ML models are particularly adept at handling complex, nonlinear data, making them well-suited for predicting algal bloom dynamics. Techniques such as multi-layer perceptrons (MLP), support vector regression (SVR), random forests (RFs), long short-term memory (LSTM) networks, and convolutional neural networks (CNNs) [23,24,25,26] have been successfully applied to predict Chl-a concentrations in a variety of aquatic environments. For example, Rousso et al. [2] have summarized 151 articles using artificial neural network (ANN) models to predict the concentrations of Chl-a from 2008 to 2019. Additionally, Park et al. [16,17,27] demonstrated the efficacy of SVM and ANN models in predicting cyanobacterial bloom intensity by integrating water quality and meteorological data, while Yu et al. applied LSTM models to predict Chl-a concentrations in Dianchi Lake with encouraging results [14]. DL models have demonstrated remarkable improvements in predictive accuracy [15,18]. However, DL models often require large datasets for training, which can be costly and time-consuming to acquire. This presents a significant limitation for studies with smaller datasets, where traditional methods like multiple linear regression (MLR) may suffer from overfitting and suboptimal performance [16].
Although ensemble learning techniques, such as XGBoost [28], have demonstrated strong predictive capabilities in river systems—successfully addressing some limitations of traditional ML methods by integrating multiple environmental variables and optimizing model complexity to capture unique hydrological characteristics—applying these models to lake environments presents distinct challenges [7]. Lakes, such as Lake Taihu, are characterized by slow-moving or static water, leading to longer retention times for nutrients and pollutants, which facilitates persistent algal blooms, especially in eutrophic systems. Moreover, lakes operate as time-varying systems where fluctuations in nutrient loads and environmental conditions occur over longer timescales compared to rivers. Consequently, it remains unclear how well existing ML models designed for rivers can be adapted to predict Chl-a concentrations in lake ecosystems. Additionally, critical water quality parameters, such as the permanganate index (CODMn), are often excluded from existing ML models, further highlighting the need for lake-specific studies. Furthermore, most existing models suffer from insufficient complexity and rely on traditional statistical methods or simple ML approaches, such as linear regression (LR) and SVM, which struggle to capture the nonlinear relationships and multivariate interactions inherent in complex ecosystems like Lake Taihu. Compounding these issues is the lack of model interpretability and explainability. While some studies have developed high-accuracy predictive models, they often fail to provide in-depth insights into the key environmental drivers of Chl-a concentrations or identify critical factors through feature importance analysis. These limitations hinder the practical application of such models in water management and policymaking.
This research aims to fill these gaps by focusing on Lake Taihu as the study area and developing a predictive model based on XGBoost. The model will utilize nine key water quality indicators: WT, pH, dissolved oxygen (DO), turbidity, EC, ammonia nitrogen (NH3-N), TP, TN, and CODMn. The research unfolds in two primary phases. First, we will develop a robust predictive model for Chl-a concentrations using ML algorithms, with XGBoost chosen for its ability to handle nonlinear relationships and integrate multiple variables. Second, to enhance the model’s interpretability, we plan to apply Pearson correlation analysis (PCA), mutual information (MI), and Spearman rank correlation coefficient (SRCC) to quantify the relationships between water quality parameters and Chl-a concentrations. This process is essential for understanding the influence of specific environmental variables on Chl-a dynamics and improving the transparency of the model for water resource managers. Furthermore, the study will evaluate the model’s generalizability across different monitoring sites within Lake Taihu, thereby enhancing its predictive accuracy and providing deeper insights into the factors governing Chl-a distribution. By addressing the current research gaps, this study not only aims to improve the accuracy of Chl-a concentration predictions but also seeks to provide a robust decision-support tool for lake management, promoting sustainable water resource management and conservation.
2. Materials and Methods
2.1. Study Area
Lake Taihu, located in the core area of the Yangtze River Delta, has experienced increasing eutrophication and frequent algal blooms in recent years, severely affecting the water quality of inflowing rivers, urban river ecosystems, and residents’ daily lives [15]. Lake Taihu is taken as the study area, with a latitude range of 30°55′ to 31°33′, and a longitude range of 119°53′ to 120°38′. The shape of Lake Taihu is irregular, extending from southwest to northeast, about 70 km long, about 50 km wide, with an area of about 2338 square kilometers, of which the water area is 2316 square kilometers, and the land area is 22 square kilometers.
Three monitoring sites were selected in this study for the Chl-a concentrations: S1–S3 (Hexi, (119°58′, 31°03′), Changxing (119°59′, 31°02′), and Yangjiapu (120°01′, 31°01′) monitoring sites) as shown in Figure 1. The primary data for this study were collected from these sites and cover the period from 1 January to 31 December in 2022.
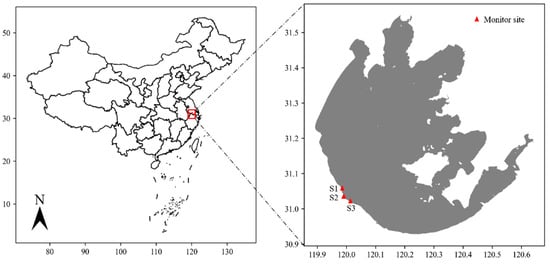
Figure 1.
Location of Lake Taihu in China and monitor sites in Lake Taihu. S1, S2, and S3 represent the Hexi, Changxing, and Yangjiapu sites.
2.2. Data Preprocessing
2.2.1. Data Introduction
Water quality datasets in this study were based on daily observations from 1 January 2022 to 31 December 2022 (https://szzdjc.cnemc.cn:8070/GJZ/Business/Publish/Main.html, accessed on 10 May 2024). Datasets encompass nine parameters: WT, pH, DO, NTU, EC, CODMn, NH3-N, TP, and TN. Table 1 presents the statistics for water quality data, with varying degrees of missing entries across datasets. Datasets 1 to 3 are consistent with the algal data, corresponding to the algal data of S1, S2, and S3 in 2022, respectively. Datasets 1 to 3 have varying degrees of missing data. For example, in dataset 1, WT, pH, DO, NTU, and EC have 334 days of data, and the CODMn has 363 days of data. The concentrations of Chl-a are closely related to water quality data, with literature reporting that WT, the ratio of TN to TP in water quality, and trace elements can directly affect the occurrence of algal blooms. Therefore, this paper will statistically analyze the water quality information and select water quality information related to Chl-a as representative input features for constructing the ML model.

Table 1.
Statistical count of water quality days at Lake Taihu at S1, S2, and S3. For details, please refer to the Supplementary Information (Tables S2–S4).
2.2.2. Data Preprocessing Steps
Query and remove missing or duplicate data entries. Due to the consecutive nature of the missing data, imputing with means or medians might affect the model’s performance, hence the decision to exclude them. Merge Chl-a data with water quality data by time, aligning input feature variables (WT, pH, DO, NTU, EC, CODMn, NH3-N, TP, TN) with the Chl-a. Split the dataset into training (80%) and testing (20%) sets.
2.3. Machine Learning Model
2.3.1. Feature Analysis Methods
The feature analysis methods used include linear analysis and nonlinear analysis:
- (a)
- Pearson correlation coefficient (PCC) and principal component analysis (PCA)
Before constructing the ML model, the correlation between water quality data and Chl-a is first analyzed, and the correlation is analyzed by calculating the PCC [29]. The formula for calculating the PCC used is as follows:
where the covariance between and is , here and σ represents the standard deviation, , describes the linear relationship between and . When is greater than 0, it indicates a positive correlation. when is less than 0, it indicates a negative correlation. If equals 0, it indicates that the two variables are not correlated. In addition, to gain a more intuitive understanding of the data structure and distribution, PCA is also employed for dimensionality reduction and visualization of the data. PCA identifies the directions of maximum variance in the data, allowing it to extract the main features while reducing dimensionality. We project the nine water quality parameters into two primary dimensions for analysis.
- (b)
- Mutual information (MI) and Spearman rank correlation coefficients (SRCCs)
MI is used to measure the statistical dependence between two random variables. It quantifies the amount of information obtained about one variable through the other. MI is widely applied in feature selection, ML, image processing, and other fields, particularly for capturing nonlinear relationships in high-dimensional data [30]. For two discrete random variables X and Y, the MI is defined as
X represents the water quality features, Y represents the Chl-a concentration, represents the joint distribution, and are the corresponding marginal distributions. The SRCC is a measure of the strength and direction of monotonic relationships between two variables. It is widely used in data analysis and statistical studies. To calculate it, first, sort two groups of data in ascending or descending order. Then, for each pair of ordered observations, compute the squared difference in ranks. The SRCC ρ is obtained by
where denotes the differences between ranks.
- (c)
- SHAP model
The SHapley Additive exPlan (SHAP) model, grounded in the computation of Shapley values, quantifies the influence of individual features on model predictions [31]. These values serve as a metric for feature importance. The advent of SHAP has unlocked significant potential in deciphering the inner workings of machine learning models, facilitating breakthroughs in feature attribution. Mathematical formulation is delineated as follows:
In this equation, g represents the interpretative model, M denotes the total number of features, z indicates the presence (0 or 1) of each feature, and signifies the corresponding Shapley value for each feature. This formulation allows for a transparent and additive interpretation of model predictions, enhancing the comprehensibility of complex ML algorithms.
2.3.2. ML Model Construction
A variety of ML algorithms are used for prediction, such as LR [32], decision tree (DT) [33], SVR, MLP, RF [34], and XGBoost [28]. The ML models and related data processing codes used in this study are implemented using python3. The ML algorithms are implemented using the scikit-learn ML module version 1.3.1 [35] and the XGBoost module version 2.0.3.
- (a)
- Linear Regression
LR is a statistical method used to analyze the linear relationship between two or more independent variables (explanatory variables) and a dependent variable. It is widely applied in economics, biostatistics, and environmental science [32,36], and can be represented by a linear combination as follows:
X is a set of nine-dimensional vectors encompassing water quality parameters such as WT and DO, represents the predicted Chl-a concentrations, and are the model parameters that need to be learned.
- (b)
- Decision Tree
The DT model is a widely used predictive and classification tool in data science and statistics [33]. It predicts the value of the target variable by simulating the decision-making process and is commonly used for classification and regression problems. The decision tree recursively divides the dataset into smaller subsets through a series of binary decision rules until a termination condition is met, such as reaching a subset with high purity or meeting the minimum sample size requirement.
- (c)
- Support Vector Regression
The SVR [37] model adeptly encapsulates the intrinsic nonlinear dynamics of data through the employment of a hyperplane within an augmented-dimensional space. This hyperplane is optimally aligned with the data whilst rigorously confining margin deviations to hyper-parameters: cost (C), epsilon (ε), and gamma (γ) [8,38]. The SVR’s objective is to meticulously delineate a mapping that correlates input vectors to their corresponding output vectors. In this study, the input variables consist of a range of water quality information, with the output variable being the concentrations of Chl-a.
- (d)
- Multi-Layer Perceptrons
The MLP constitutes a quintessential example of an artificial neural network, comprising a hierarchical structure of nodes that include an input layer, multiple hidden layers, and an output layer. The nodes within the hidden layers are characteristically activated through nonlinear functions. By employing a supervised learning algorithm termed backpropagation [39], the MLP is trained to reduce the difference between its output and the designated target values through the optimization of its interstitial weights and biases. The MLP has been extensively applied across diverse fields, ranging from financial analytics to medical diagnostics, as well as in image and speech recognition tasks [40]. Its utility spans across various problem types, including but not limited to classification, regression, and pattern recognition. The present study employs the MLP as a regression tool specifically aimed at predicting the concentrations of Chl-a.
- (e)
- Random Forest
The RF algorithm is an ensemble ML algorithm that improves the accuracy and stability of the model by constructing multiple decision trees and combining their prediction results. The basic principle is to randomly extract X samples (X is usually less than the size of the training set) from the training set, denoted as the sample set. For each extracted sample set, train a DT using a random subset of L features (L is usually less than the total number of features). When new prediction data are input into all decision trees, each decision tree outputs a prediction value, and then the average of all prediction values is taken as the final prediction result. The prediction result can be expressed as
where is the result, is the regression result of the j-th tree, and m is the number of decision trees. In this study, the RF algorithm was used to predict the concentrations of Chl-a by inputting water quality information.
- (f)
- XGBoost
XGBoost is an efficient implementation of the gradient boosting tree (GBDT) algorithm, and its core idea is ensemble learning; that is, to construct a strong learner by combining multiple weak learners [28]. Unlike the RF algorithm, it uses the gradient boosting framework to train decision tree models and update the model according to gradient information. In addition, it can introduce regularization terms to prevent overfitting. Its objective function can be expressed as
where is the loss function, is the training loss, is the true value of the i-th sample, is the predicted value, and is the regularization term. XGBoost has the characteristics of high accuracy, strong robustness, easy interpretation, and support for various objective functions. In this study, we used the XGBoost model to predict the concentrations of Chl-a and sorted the importance of various features.
2.3.3. Evaluation Indicators
The optimization of ML model parameters is essential for model construction, significantly improving accuracy and generalization ability. In this study, we used cross-validation methods to determine the best combination of hyper-parameters for the proposed models. For example, the number of trees for random forest RF and extreme gradient boosting XGBoost, the number of neurons and the number of hidden layers for neural networks, among others. We also used determination coefficient R2 and the root mean square error (RMSE) as evaluation metrics to assess the predicted Chl-a concentrations [27].
In this context, represents the actual observed Chl-a concentrations at the monitoring site, denotes the Chl-a concentrations values predicted by the model, signifies the average observed Chl-a concentrations at the site, and N is the total number of samples.
3. Results
3.1. The Spatial and Temporal Distribution Features of Algal and Water Quality Datasets
3.1.1. The Spatio-Temporal Distribution of Chl-a Concentrations
Initially, a statistical analysis was conducted on the Chl-a concentrations data. For instance, the statistical results for S1 are presented in Table 2: After merging Chl-a concentrations data from 2022, there were a total of 332 data points. The maximum Chl-a concentrations recorded is 290.51, with the minimum at 2.25, and the mean at 24.76. The variance for Chl-a is 35.41. Additionally, the lower quartile (25%), median, and upper quartile (75%), are 8.79, 13.62, and 23.12, respectively.

Table 2.
Statistical information of machine learning data at S1.
The Chl-a concentrations at sites S1, S2, and S3 exhibited similar temporal distribution patterns, characterized by pronounced increasing trends with recurrent prominent peaks during the latter half of the year (Figure 2). The elevation of Chl-a showed a strong correlation with cyanobacterial blooms. Among the five algal groups analyzed, including cyanobacteria, all demonstrated minimal fluctuations in the first half of the year, with concentrations consistently below 50 μg/L. However, from July onward, cyanobacteria exhibited marked increases and multiple significant peaks, particularly at sites S2 and S3. At S2, peak concentrations exceeded 200 μg/L, while at S3, two distinct peaks surpassed 300 μg/L, indicating a eutrophic state at this site likely influenced by persistent agricultural runoff or domestic wastewater discharge. The cyanobacterial proliferation displayed marked seasonality (summer dominance) and spatial heterogeneity (S3 > S2 > S1), highlighting the necessity for focused monitoring and control of algal blooms during high-temperature periods at sites S2 and S3.
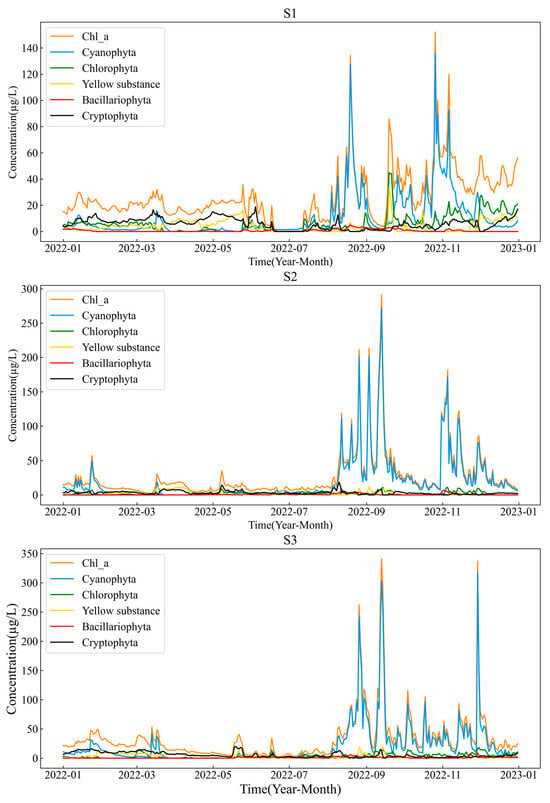
Figure 2.
Temporal variations of Chl-a and algal concentration at S1, S2, and S3.
3.1.2. Correlation Analysis of Algal Information and Chl-a
To systematically evaluate the relationships between algal communities, water quality parameters, and Chl-a concentrations, we performed Pearson correlation heatmap analysis on five algal groups and Chl-a data, following established interpretation thresholds where coefficients >0.6 and >0.8 denote strong and very strong correlations, respectively [41,42]. The analysis revealed distinct spatial patterns in algal-Chl-a associations across sampling sites (Figure 3, Supplementary Information).
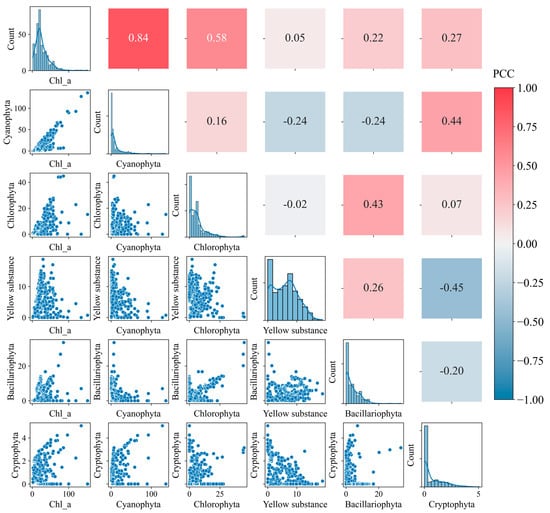
Figure 3.
Heatmap of correlation analysis between algal concentration and Chl-a at S1. The lower-left triangle of the figure consists of scatter plots, while the diagonal represents the histogram statistics of algal concentration. The upper-right triangle displays the PCC coefficients between different algal concentrations, with darker red indicating stronger positive correlation and darker blue indicating stronger negative correlation.
At S1, cyanobacteria exhibited a very strong positive correlation with Chl-a (r = 0.84), with other algal groups demonstrating negligible associations (r < 0.6). Notably, S2 displayed an exceptional cyanobacteria–Chl-a correlation (r = 0.99), whereas S3 demonstrated an equally strong cyanobacteria–Chl-a relationship (r = 0.99). Across all sites, cyanobacteria consistently showed the strongest Chl-a correlations (r > 0.8), with S2 and S3 reaching near-perfect linear associations (r = 0.99). The visualized correlation patterns in the heatmaps not only quantify algal–Chl-a interactions but also identify critical bioindicators for water quality monitoring, establishing a robust foundation for developing ML models to predict Chl-a concentrations based on algal community composition. The exceptional correlations (r = 0.99) at S2–S3 particularly highlight the potential for using dominant algal groups as proxy indicators in predictive frameworks. In some eutrophic water bodies, the high correlation between cyanobacteria and Chl-a concentration (Figure 3, Supplementary Information Figures S2 and S3) provides data support for Chl-a as an early warning indicator of cyanobacterial blooms.
3.1.3. Analysis of Water Quality Information and Chl-a
Water quality information is closely related to Chl-a concentrations. In this study, nine water quality information variables, including WT, pH, DO, turbidity, EC, CODMn, NH3-N, TP, and TN, were used as inputs to predict Chl-a concentrations. Each variable was recorded with 332 data points, providing mean, Std, min, Q1 (25%), median (50%), Q3 (75%), and max. The EC shows the highest mean level and its variance fluctuation, while TP presents the lowest mean level and the most stable variance (in Table 2).
Figure 4 shows that the correlation coefficients between the nine types of water quality information and Chl-a were calculated as −0.24, −0.03, −0.08, 0.37, 0.40, 0.38, 0.25, 0.30, and 0.02, respectively. The top three in terms of correlation were EC, CODMn, and NTU. For the data of S2 and S3, the top three are CODMn, EC, and WT; NTU, CODMn, and TP. Although the water quality information strongly correlated with Chl-a varied slightly in different datasets from different stations and times, the strong correlation of information such as EC, CODMn, and NTU with Chl-a concentrations are universal and consistent.
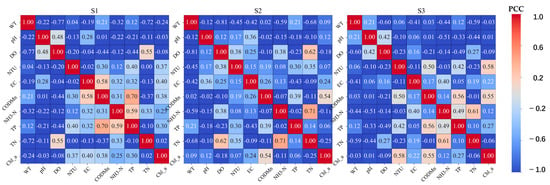
Figure 4.
Heatmap of correlation analysis between water quality information and Chl-a. The figure shows the PCC coefficients between different water quality parameters and Chl-a concentrations at the three sites.
To further visualize the analysis, the PCA dimensionality reduction technique is employed to compress the nine-dimensional sample space into a 2D space. It reveals that the points with lower Chl-a concentrations (represented in blue) are numerous and concentrated within the regions of low PC1 and PC2 values. In contrast, points with higher Chl-a concentrations are more sparsely distributed along the edges of PC1 and PC2. This may lead to difficulties for ML models in predicting peaks of high Chl-a concentrations (Figure 5).
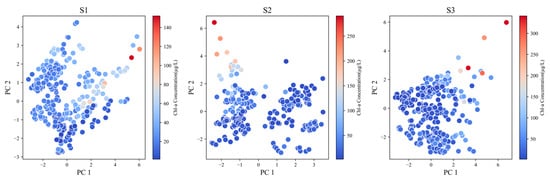
Figure 5.
PCA was conducted between water quality information and Chl-a. The figure illustrates how the nine-dimensional water quality information is mapped onto the two-dimensional space of PC1 and PC2.
Additionally, we computed MI and SRCC to analyze the nonlinear relationships between Chl-a concentrations and water quality information. The MI values ranked the features for each dataset S1, S2, S3 as follows: WT, EC, and TN for S1; WT, TN, and EC for S2; and WT, EC, and NTU for S3. Similarly, the SRCCs for S1, S2, S3 were ranked as EC, WT, and CODMn for S1; EC, CODMn, and WT for S2; and EC, CODMn, and NTU for S3. WT, EC, and CODMn are highly important features (Figure 6).
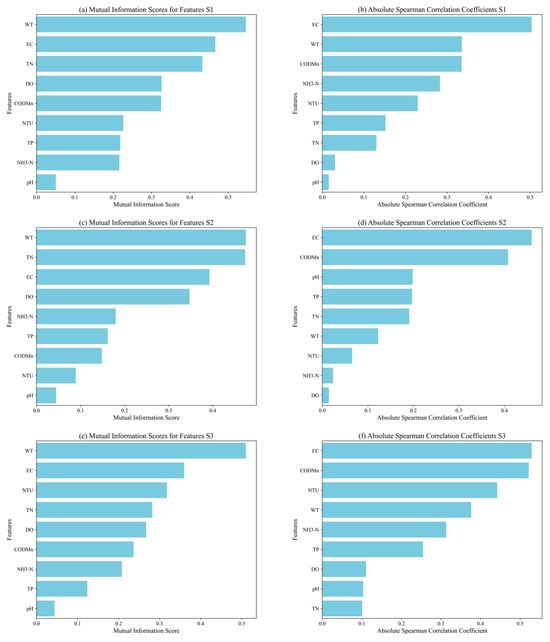
Figure 6.
Analysis using MI and SRCC between water quality and Chl-a.
3.2. Machine Learning Prediction of Chl-a Concentration
3.2.1. Model Accuracy
In this study, six different ML models, including linear LR, DT, SVR, MLP RF, and XGBoost model, were used to predict Chl-a concentration. Figure 7 shows that for the training set, the R2 of LR, DT, SVR, MLP, RF, and XGBoost models were 0.45, 0.81, 0.64, 0.71, 0.95, and 1.0, respectively; the RMSE were 13.46, 8.0, 10.87, 9.86, 4.06, and 0, respectively. To test the generalization and robustness of the models, the results for the test set were R2 of 0.3, 0.54, 0.46, 0.58, 0.65, and 0.78; RMSE of 16.23,13.08,14.23, 12.46, 11.59, and 8.97, respectively (Table 3).
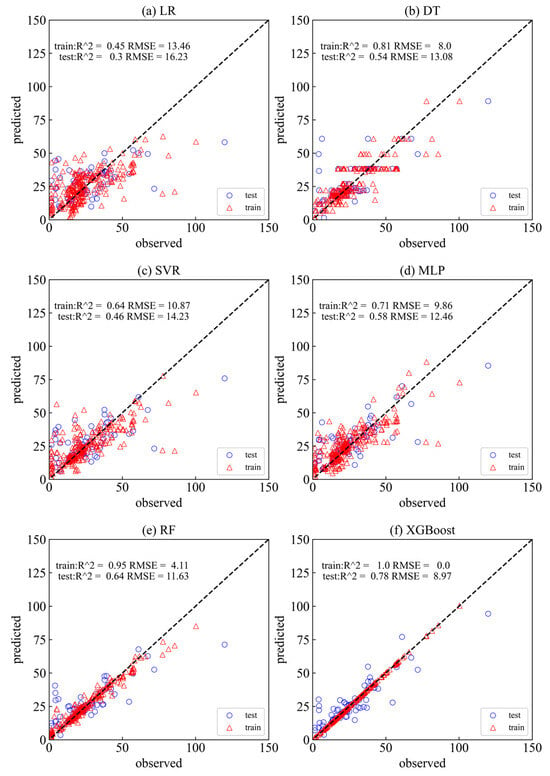
Figure 7.
Comparison of Evaluation Metrics Across Different ML Models. The red triangle represents the training set and the blue circle represents the test set.

Table 3.
Model hyper-parameters and performance comparison. The best indicators for different models have been highlighted in bold.
The XGBoost model demonstrated the highest accuracy across several monitoring points compared to five other ML models, including the RF model (Figure 7, Table 3), which is consistent with previous studies by Yang et al. [7]. This superior performance is partly attributed to the incorporation of regularization terms within the objective function of the XGBoost model, which aids in controlling model complexity and mitigates the risk of overfitting. Consequently, the XGBoost model was selected as the optimal ML predictive model for Chl-a. The XGBoost model in the test set exhibited an R2 value of 0.78, surpassing the 0.52 of the RF by Yajima at Lake Shinji, the 0.63 of the LSTM by Yu et al. at Dianchi Lake [14], as well as the 0.747 of Kim and Ahn along the Han River. In our study, there were the same input variables for different models, which is consistent with previous studies by Park et al. [38] and Shin et al. [43]. The R2 for SVR was 0.46 and for the MLP it was 0.58. These results are consistent with Kim’s findings [8] but are in stark contrast to Park et al. [38]. Such discrepancies may be related to differences in the combination of input variables and the settings of hyper-parameters, among other factors.
To more intuitively describe the predictive ability of the models, Figure 8 shows the prediction of Chl-a concentration data at S1. As shown in Figure 8, the DT and XGBoost model can predict the trend of changes in Chl-a concentration for most data more accurately, and there is room for improvement in predicting the intensity of some peaks. The XGBoost model is smoother and more refined than the DT model, and the prediction of the peaks and troughs of Chl-a concentration is also more accurate. More prediction figures can be seen in the Supplementary Materials.
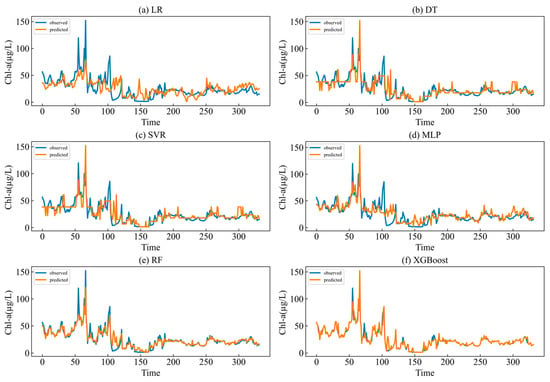
Figure 8.
Prediction of Chl-a concentration by the LR, DT, SVR, MLP, RF, and XGBoost model at S1.
3.2.2. Feature Important Explanation
The input variables exert variegated influences upon the model’s outcome, with each variable’s impact articulated through the quantification of Feature Importance. This is a direct measure of the response variance engendered by the variable in question. Global Feature Importance attenuates sequentially for the input variables as follows (Figure 9): EC SHAP value is 5.28, WT is 4.99, CODMn is 2.47, NTU is 1.98, TN is 1.58, DO is 1.46, NH3-N is 0.91, TP is 0.9, and PH is 0.07.
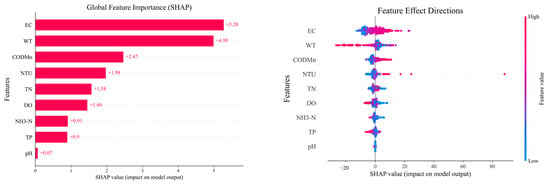
Figure 9.
SHAP explains the feature contributions in the XGBoost model.
Although the RF algorithm and XGBoost algorithm have differences in the methods and scores for calculating feature importance, the relative ranking of input variables is relatively consistent. For example, Figure 9 shows the feature importance ranking of the XGBoost model, which is EC, WT, CODMn, NTU, TN, DO, NH3-N, TP, and pH, while the RF model is EC, NTU, WT, CODMn, TN, DO, NH3-N, TP, and pH (see Figure S4 in Supplementary Materials). We use nonlinear analysis and MI calculation to determine the feature importance rankings. According to our analysis, the top three features are WT, EC, and TN, while for ASCC, the top features are EC, WT, and CODMn (Figure 6). Therefore, in different models, the relative ranking of feature importance is more important than the feature importance score [8]. Therefore, whether RF or XGBoost models are used to predict Chl-a concentration, water quality features such as EC, WT, CODMn, and NTU are considered the most important features, while pH is the least important feature.
We selected seven pieces of literature and conducted a comparative analysis with the XGBoost model proposed in this paper, thereby identifying the first three key input variables (see Table 4). The XGBoost model recognized EC as the primary water quality factor affecting the concentration of Chl-a (see Figure 9). According to research by Beretta-Blanco et al. [44], EC can serve as a surrogate indicator of nutrient concentration in water bodies, exhibiting a significant positive correlation with Chl-a concentration and substantially influencing the growth of aquatic organisms, such as cyanobacteria. In the Nakdong River, EC was the second most influential factor. In the XGBoost model, the second most important variable is NTU, which is consistent with previous studies on Lake Shinji, where Yajima and Derot in 2018 considered NTU as one of the most influential variables affecting Chl-a concentration. Similarly, Han et al. in 2021 listed NTU as one of the seven important variables affecting Chl-a concentration.
WT, as a necessary condition for the growth of algae, ranks third in model importance assessments. Numerous previous studies have indicated that WT is a key environmental factor for the growth and reproduction of algae and is an indispensable input variable for predicting Chl-a concentration [8,45,46]. CODMn, as an important indicator for assessing the level of organic pollution in water bodies [14], has been applied in various ML models for predicting Chl-a concentration, and in this study, it ranks fourth in importance.


Table 4.
Relative importance rank of input variables.
Table 4.
Relative importance rank of input variables.
| Rank | Ref [38] | Ref [43] | Ref [46] | Ref [47] | Ref [21] | Ref [45] | Ref [8] | This Study | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Juam reservoir | Yeongsan reservoir | Nakdong river | Nakdong river | Lake Shinji | Lake Jordan | Imha reservoir | Lacustrine zone | Han river | Lake Taihu | |
| Model | SVM | SVM | RF | ANN | RF | Mechanistic model | SVM | SVM | RF | XGBoost |
| 1 | PO4–P | NH3–N | PO4–P | Wind velocity | NTU | Limiting nutrient | WT | WT | TOC | EC |
| 2 | NO3–N | NO3–N | DO | EC | CODMn | TN | TSS a | Prep b | TN | WT |
| 3 | Wind speed | Solar radiation | NH3–N | Alkalinity | SS c | TP | DO | BOD | pH | CODMn |
Notes: a TSS: Total suspended solid. b Prep.: Precipitation [46]. c SS: Suspended solid.
The fifth, sixth, seventh, eighth, and ninth most important variables are NH3-N, TP, TN, DO, and pH value, respectively. These water quality information variables are also key factors in predicting Chl-a concentration. Discussions on the nitrogen and phosphorus nutrients and their ratios in water bodies are frequently encountered [38]. However, when predicting Chl-a concentration in actual lakes, rivers, and reservoirs, some variables may encounter challenges. This is because there is a complex nonlinear relationship between Chl-a concentration and water quality information. The data used to construct the ML model in the water quality information space is often sparse, which may lead to insufficient generalization capability of the model. For the XGBoost model constructed in this study, it is expected that the accuracy and generalization ability of the model will be further improved after introducing more new variables and obtaining more data from single sites. The application of variable importance measures within XGBoost is crucial for gaining a deeper understanding of the water quality variables that influence Chl-a concentrations.
4. Discussion
4.1. Model Performance and Feature Analysis
This study used an XGBoost model to predict Chl-a concentrations, achieving an R2 of 0.78 on the test set, a significant improvement over models like LSTM (Dianchi Lake, R2 = 0.63) from the literature [14]. This advantage stems from XGBoost’s integrated regularization terms (L1/L2), which curb overfitting, especially when handling high-variance features (e.g., EC, WT), reducing noise sensitivity. Compared to traditional linear models (LR, R2 = 0.30) and single-tree models (DT, R2 = 0.54), XGBoost better captures nonlinear relationships through gradient boosting and ensemble strategies. Feature importance analysis revealed that EC (SHAP = 5.28), WT (4.99), and CODMn (2.47) contributed the most to model output (Figure 9). This aligns with the three-stage correlation analysis: Pearson analysis showed the strongest linear correlation between EC (r = 0.40) and Chl-a, while SRCC and MI further uncovered nonlinear association strengths. PCA results indicated that high-Chl-a samples exhibited marginal discrete distributions in the PC1-PC2 space (Figure 5), implying nonlinear response characteristics. Notably, cross-validation across multiple groups found a strong linear relationship between cyanobacterial biomass and Chl-a (r = 0.99 at S2–S3 sites), underpinning the early-warning application of cyanobacteria as a biomarker (Figure 3). Longitudinal comparisons with existing studies show significant regional applicability in feature weight rankings: EC was the second most important in Nakdong River studies [46], while NTU dominated in Lake Shinji cases [47] (Table 4). These differences likely arise from hydrological environmental heterogeneity, making EC more representative of composite pollution. Thus, feature engineering optimization should incorporate watershed pollution characteristics during cross-watershed model transfer.
4.2. Model Generalization Performance
While NH3-N, TP, TN, DO, and pH ranked lower in model variable analysis, these water quality variables are also critical for predicting Chl-a concentrations in practical applications. The importance of variables can vary across different scenarios (e.g., lakes, rivers, reservoirs) due to the complex nonlinear relationships between Chl-a concentrations and water quality/meteorological information. The sparsity of water quality data used to build ML models can lead to insufficient generalization and accuracy. Another limitation is the synergistic effects of multi-dimensional water quality parameters. For instance, though pH (r = −0.03) showed no significant correlation with Chl-a in single-factor analysis, alkaline conditions often indirectly affect algal growth by promoting phosphate desorption in eutrophic waters like Lake Taihu. These higher-order interaction effects are not fully captured by current linear feature processing. Additionally, PCA results show sparse distributions of high-Chl-a samples in reduced-dimensional spaces (Figure 5), causing systematic prediction biases for algal bloom peaks (Figure 8). For the XGBoost model developed in this study, introducing more variables (e.g., satellite and hyperspectral data) and collecting data from diverse sites is expected to further enhance accuracy and generalization.
5. Conclusions
This study aims to predict Chl-a concentrations in Lake Taihu using machine learning models to address the environmental challenges posed by Cyano-HABs. By analyzing nine key water quality parameters, an ensemble machine learning model based on XGBoost was developed. The model achieved an R2 value of 0.78 and an RMSE of 8.97 mg/m3 on the test set, outperforming traditional models such as linear regression, decision trees, multi-layer perceptrons, support vector regression, and random forests. Feature importance analysis identified electrical conductivity, turbidity, and water temperature as the most significant predictors for predicting Chl-a levels. This research not only enhances the accuracy of Chl-a forecasting but also improves model interpretability through various methods, providing a scientific basis for the development of water quality management and Cyano-HABs early warning systems in other eutrophic lakes.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/w17081219/s1, Supplementary Information to this article can be found at SI.docx. Figure S1. Heatmap of Correlation Analysis between Algal Concentration and Chlorophyll-a at S2 in 2022. Figure S2. Heatmap of Correlation Analysis between Algal Concentration and Chlorophyll-a at S3 in 2022. Figure S3. Visualization of the First Three Layers of a Decision Tree Model. Figure S4. Ranking the Importance of Various Water Quality Features on Chl-a Concentration in an RF Model. Figure S5. Prediction of Chl-a concentration by the DT and XGBoost model at S2. Figure S6. Prediction of Chl-a concentration by the DT and XGBoost model at S3. Table S1. Statistical Table of Algal Datasets at Lake Taihu Sites. Table S2. Water quality information dataset of S1. Table S3. Water quality information dataset of S2. Table S4. Water quality information dataset of S3.
Author Contributions
Conceptualization, X.C.; Methodology, X.C.; Validation, W.Z.; Formal analysis, C.W.; Resources, X.Q.; Data curation, G.S.; Writing—original draft, X.C.; Writing—review & editing, Y.H.; Supervision, P.X.; Project administration, Y.S. and Y.H.; Funding acquisition, G.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key Research and Development Program of China (2022YFE0128600), the Nanxun scholars’ program of ZJWEU (RC2023010975), and X.C. would like to acknowledge the Startup Funds of the Institute of Zhejiang University-Quzhou (No. IZQ2021RCZX030).
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Abbreviations
| ANN | Artificial neural network |
| Chl-a | Chlorophyll-a |
| CNN | Convolutional neural network |
| CODMn | Permanganate index |
| DD | Data-driven |
| DL | Deep learning |
| DO | Dissolved oxygen |
| DT | Decision tree |
| EC | Electrical conductivity |
| Cyano-HABs | Cyanobacteria harmful blooms |
| LR | Linear regression |
| LSTM | Long short-term memory |
| ML | Machine learning |
| MLP | Multi-layer perceptron |
| NH3-N | Ammonia nitrogen |
| NTU | Nephelometric turbidity units |
| PB | Process-based |
| PCA | Principal component analysis |
| PCC | Pearson correlation coefficient |
| R2 | Coefficient of determination |
| RF | Random forest |
| RMSE | Root mean square error |
| SRCC | Spearman rank correlation coefficient |
| SVR | Support vector regression |
| TP | Total phosphorus |
| TN | Total nitrogen |
| WT | Water temperature |
| XGBoost | eXtreme Gradient Boosting |
References
- Lévesque, B.; Gervais, M.C.; Chevalier, P.; Gauvin, D.; Anassour-Laouan-Sidi, E.; Gingras, S.; Fortin, N.; Brisson, G.; Greer, C.; Bird, D. Prospective study of acute health effects in relation to exposure to cyanobacteria. Sci. Total Environ. 2014, 466, 397–403. [Google Scholar] [CrossRef] [PubMed]
- Rousso, B.Z.; Bertone, E.; Stewart, R.; Hamilton, D.P. A systematic literature review of forecasting and predictive models for cyanobacteria blooms in freshwater lakes. Water Res. 2020, 182, 115959. [Google Scholar] [CrossRef] [PubMed]
- Guo, L. Doing battle with the green monster of Taihu Lake. Science 2007, 317, 1166. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, R.; Zhang, J.; Ni, L.; Shen, H.; Xie, P. A Novel and Convenient Method for Early Warning of Algal Cell Density by Chlorophyll Fluorescence Parameters and Its Application in a Highland Lake. Front. Plant Sci. 2018, 9, 869. [Google Scholar] [CrossRef]
- Recknagel, F. Current scope, case studies and future directions of ecological informatics. J. Environ. Inform. 2013, 21, 3–11. [Google Scholar] [CrossRef]
- Boyer, J.N.; Kelble, C.R.; Ortner, P.B.; Rudnick, D.T. Phytoplankton bloom status: Chlorophyll a biomass as an indicator of water quality condition in the southern estuaries of Florida, USA. Ecol. Indic. 2009, 9, S56–S67. [Google Scholar] [CrossRef]
- Yang, J.; Zheng, Y.; Zhang, W.; Zhou, Y.; Zhang, Y. Comparative analysis of machine learning methods for prediction of chlorophyll-a in a river with different hydrology characteristics: A case study in Fuchun River, China. J. Environ. Manag. 2024, 364, 121386. [Google Scholar] [CrossRef]
- Kim, K.-M.; Ahn, J.-H. Machine learning predictions of chlorophyll-a in the Han river basin, Korea. J. Environ. Manag. 2022, 318, 115636. [Google Scholar] [CrossRef]
- Qin, B.; Paerl, H.W.; Brookes, J.D.; Liu, J.; Jeppesen, E.; Zhu, G.; Zhang, Y.; Xu, H.; Shi, K.; Deng, J. Why Lake Taihu continues to be plagued with cyanobacterial blooms through 10 years (2007–2017) efforts. Sci. Bull. 2019, 64, 7–9. [Google Scholar] [CrossRef]
- Shin, Y.; Kim, T.; Hong, S.; Lee, S.; Lee, E.; Hong, S.; Lee, C.; Kim, T.; Park, M.S.; Park, J.; et al. Prediction of Chlorophyll-a Concentrations in the Nakdong River Using Machine Learning Methods. Water 2020, 12, 1822. [Google Scholar] [CrossRef]
- Fadel, A.; Lemaire, B.J.; Vinçon-Leite, B.; Atoui, A.; Slim, K.; Tassin, B. On the successful use of a simplified model to simulate the succession of toxic cyanobacteria in a hypereutrophic reservoir with a highly fluctuating water level. Environ. Sci. Pollut. Res. Int. 2017, 24, 20934–20948. [Google Scholar] [CrossRef]
- Elliott, J.A. Is the future blue-green? A review of the current model predictions of how climate change could affect pelagic freshwater cyanobacteria. Water Res. 2012, 46, 1364–1371. [Google Scholar] [CrossRef]
- Pätynen, A.; Elliott, J.A.; Kiuru, P.; Sarvala, J.; Ventelä, A.M.; Jones, R.I. Modelling the impact of higher temperature on the phytoplankton of a boreal lake. Boreal Environ. Res. 2014, 19, 66–78. [Google Scholar]
- Yu, Z.; Yang, K.; Luo, Y.; Shang, C. Spatial-temporal process simulation and prediction of chlorophyll-a concentration in Dianchi Lake based on wavelet analysis and long-short term memory network. J. Hydrol. 2020, 582, 124488. [Google Scholar] [CrossRef]
- Weijuan, K.; Ronghua, M.A.; Hongtao, D. The neural network model for estimation of chlorophyll-a with water temperature in Lake Taihu. J. Lake Sci. 2009, 21, 193–198. [Google Scholar] [CrossRef]
- Yi, H.S.; Park, S.; An, K.G.; Kwak, K.C. Algal Bloom Prediction Using Extreme Learning Machine Models at Artificial Weirs in the Nakdong River, Korea. Int. J. Environ. Res. Public Health 2018, 15, 2078. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Lee, H.K.; Shin, J.K.; Chon, K.; Kim, S.; Cho, K.H.; Kim, J.H.; Baek, S.S. A machine learning approach for early warning of cyanobacterial bloom outbreaks in a freshwater reservoir. J. Environ. Manag. 2021, 288, 112415. [Google Scholar] [CrossRef]
- Zhang, T.L.; He, M.X. A Method to Retrieve the Oceanic Chlorophyll-a Concentrations in Case I Water Based on Artificial Neural Network. Natl. Remote Sens. Bull. 2002, 1, 44–48. [Google Scholar]
- Ly, Q.V.; Nguyen, X.C.; Lê, N.C.; Truong, T.D.; Hoang, T.H.; Park, T.J.; Maqbool, T.; Pyo, J.; Cho, K.H.; Lee, K.S.; et al. Application of Machine Learning for eutrophication analysis and algal bloom prediction in an urban river: A 10-year study of the Han River, South Korea. Sci. Total Environ. 2021, 797, 149040. [Google Scholar] [CrossRef]
- Soranno, P. Factors affecting the timing of surface scums and epilimnetic blooms of blue-green algae in a eutrophic lake. Can. J. Fish. Aquat. Sci. 1997, 54, 1965–1975. [Google Scholar]
- Han, Y.; Aziz, T.N.; Del Giudice, D.; Hall, N.S.; Obenour, D.R. Exploring nutrient and light limitation of algal production in a shallow turbid reservoir. Environ. Pollut. 2021, 269, 116210. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Recknagel, F.; Bartkow, M. Spatially-explicit forecasting of cyanobacteria assemblages in freshwater lakes by multi-objective hybrid evolutionary algorithms. Ecol. Model. 2016, 342, 97–112. [Google Scholar] [CrossRef]
- Liu, J.-Y.; Zeng, L.-H.; Ren, Z.-H. The application of spectroscopy technology in the monitoring of microalgae cells concentration. Appl. Spectrosc. Rev. 2020, 56, 171–192. [Google Scholar] [CrossRef]
- Liu, J.Y.; Zeng, L.H.; Ren, Z.H.; Du, T.M.; Liu, X. Rapid in situ measurements of algal cell concentrations using an artificial neural network and single-excitation fluorescence spectrometry. Algal Res. 2020, 45, 101739. [Google Scholar] [CrossRef]
- Chen, Y.; Song, L.; Liu, Y.; Yang, L.; Li, D. A Review of the Artificial Neural Network Models for Water Quality Prediction. Appl. Sci. 2020, 10, 5776. [Google Scholar] [CrossRef]
- Yang, H.; Kong, J.; Hu, H.; Du, Y.; Gao, M.; Chen, F. A Review of Remote Sensing for Water Quality Retrieval: Progress and Challenges. Remote Sens. 2022, 14, 1770. [Google Scholar] [CrossRef]
- Lucas, H.R.; Fernandez, R.D. Navigating the dynamic landscape of alpha-synuclein morphology: A review of the physiologically relevant tetrameric conformation. Neural Regen. Res. 2020, 15, 407–415. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J. Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Cover, T.M. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Lubo-Robles, D.; Devegowda, D.; Jayaram, V.; Bedle, H.; Marfurt, K.J.; Pranter, M.J. Machine learning model interpretability using SHAP values: Application to a seismic facies classification task. In Proceedings of the SEG International Exposition and Annual Meeting, Virtual Event, 12–16 October 2020. [Google Scholar]
- Seber, G.A.F.; Lee, A.J. Linear Regression Analysis, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Quinlan, J.R. Induction of decision trees. Machine Learning. In Proceedings of the 24th Annual ACM Symposium on the Theory of Computing, Berkeley, CA, USA, 28–30 May 1986. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Andrews, D.F. A Robust Method for Multiple Linear Regression. Technometrics 1974, 16, 523–531. [Google Scholar] [CrossRef]
- Vapnik, V.; Golowich, S.; Smola, A. Support vector method for function approximation, regression estimation and signal processing. Adv. Neural Inf. Process. Syst. 1996, 9, 281–287. [Google Scholar]
- Park, Y.; Cho, K.H.; Park, J.; Cha, S.M.; Kim, J.H. Development of early-warning protocol for predicting chlorophyll-a concentration using machine learning models in freshwater and estuarine reservoirs, Korea. Sci. Total Environ. 2015, 502, 31–41. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Wei, B.; Sugiura, N.; Maekawa, T. Use of artificial neural network in the prediction of algal blooms. Water Res. 2001, 35, 2022–2028. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Routledge: London, UK, 2013. [Google Scholar]
- Shin, Y.; Lee, H.; Lee, Y.J.; Seo, D.K.; Jeong, B.; Hong, S.; Kim, J.; Kim, T.; Lee, J.K.; Heo, T.Y. The prediction of diatom abundance by comparison of various machine learning methods. Math. Probl. Eng. 2019, 2019, 5749746. [Google Scholar] [CrossRef]
- Beretta-Blanco, A.; Carrasco-Letelier, L. Relevant factors in the eutrophication of the Uruguay River and the Río Negro. Sci. Total Environ. 2021, 761, 143299. [Google Scholar] [CrossRef]
- Mamun, M.; Kim, J.J.; Alam, M.A.; An, K.G. Prediction of algal chlorophyll-a and water clarity in monsoon-region reservoir using machine learning approaches. Water 2019, 12, 30. [Google Scholar] [CrossRef]
- Kim, H.G.; Hong, S.; Jeong, K.S.; Kim, D.K.; Joo, G.J. Determination of sensitive variables regardless of hydrological alteration in artificial neural network model of chlorophyll a: Case study of Nakdong River. Ecol. Model. 2019, 398, 67–76. [Google Scholar] [CrossRef]
- Yajima, H.; Derot, J. Application of the Random Forest model for chlorophyll-a forecasts in fresh and brackish water bodies in Japan, using multivariate long-term databases. J. Hydroinformatics 2018, 20, 206–220. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).