Comprehensive Assessment of Water Resource Carrying Capacity Based on Improved Matter–Element Extension Modeling
Abstract
1. Introduction
2. Literature Review
2.1. Connotations of Water Resource Carrying Capacity
2.2. Water Resource Carrying Capacity Evaluation Indicators
2.3. Water Resource Carrying Capacity Evaluation Methods
2.4. Literature Review and Critique
3. Data Sources and Model Construction
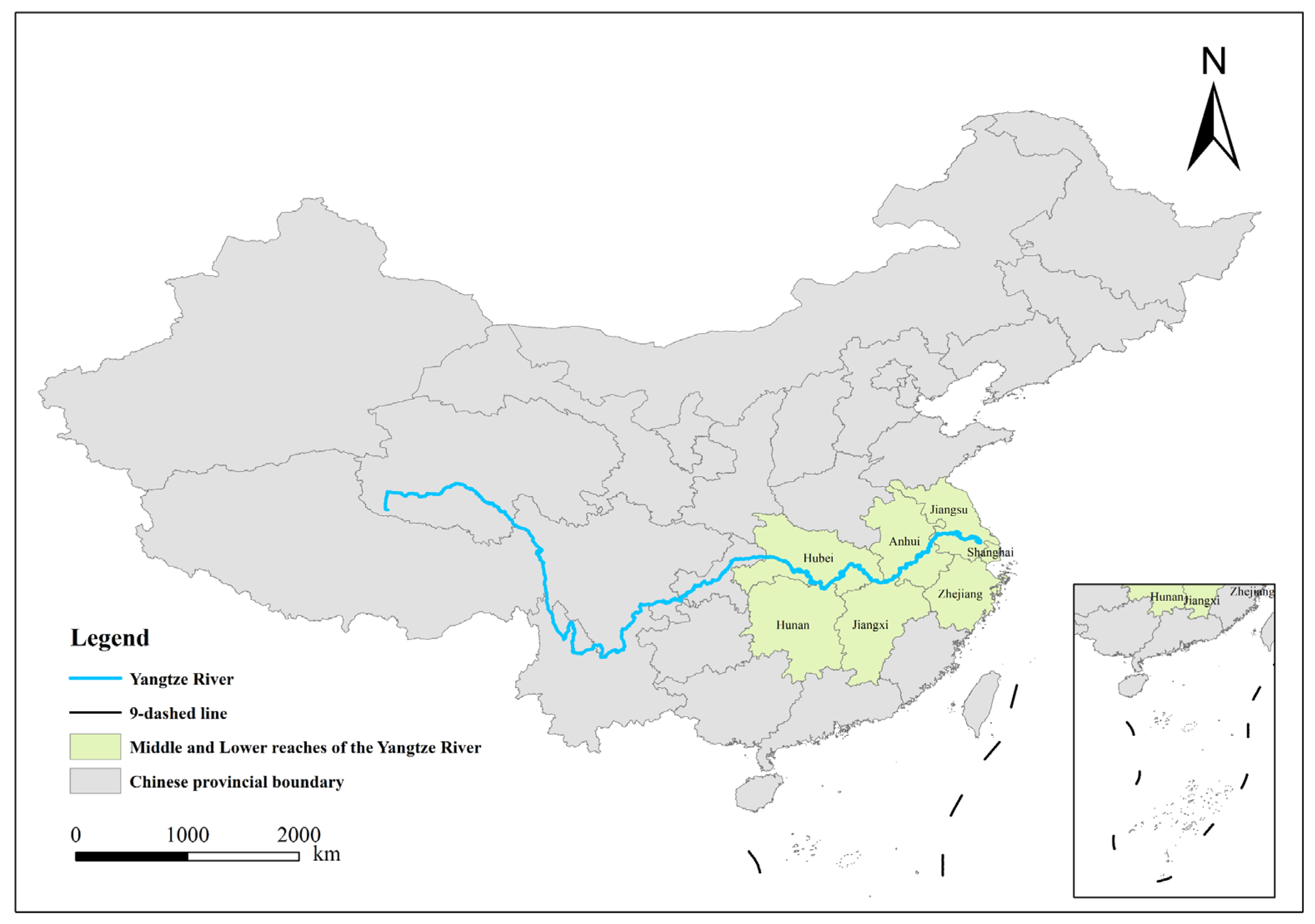
3.1. Overview of the Study Area
3.2. Data Sources
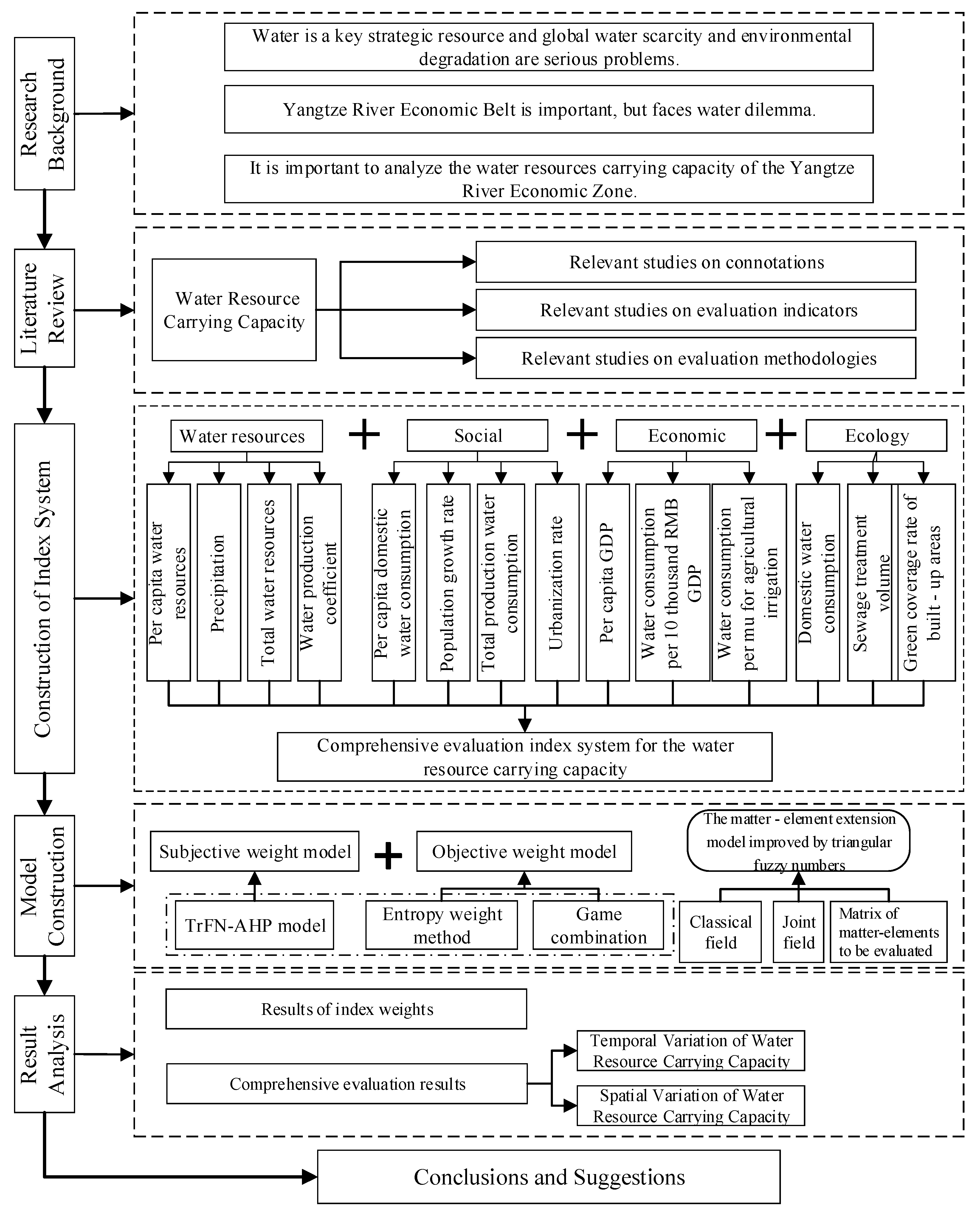
3.3. Research Framework
3.4. Indicator System Construction
3.5. Model Construction
3.5.1. Indicator Weighting Model
Triangular Fuzzy Analytic Hierarchy Process (TrFN-AHP)
Entropy Weight Method
Determination of Portfolio Weights
3.5.2. Indicator Weighting Model
Determining the Classical Domain
Determining the Sectional Domain
Determining the Extension Matrix of the Evaluated Object
Standardization
Calculating the Distance Between the Levels and the Classic Domain
Calculating the Proximity Degree
Level Assessment
3.5.3. Determining the Classic Domain of WRCC Indicators
4. Results
4.1. Indicator Weight Results
4.1.1. Subjective Weight Results
4.1.2. Objective Weight Results
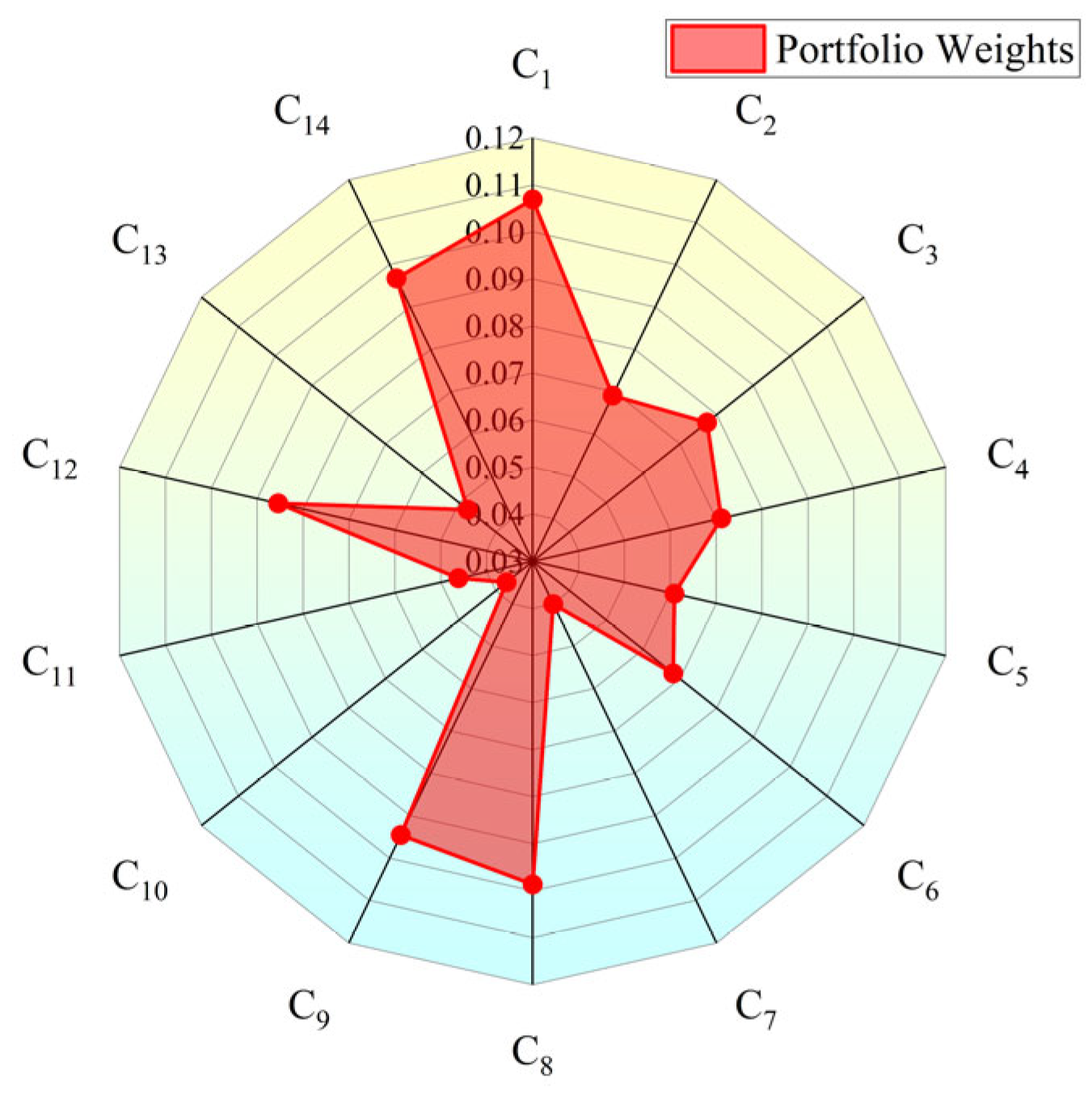
4.1.3. Portfolio Weight Results
4.2. Comprehensive Evaluation Results
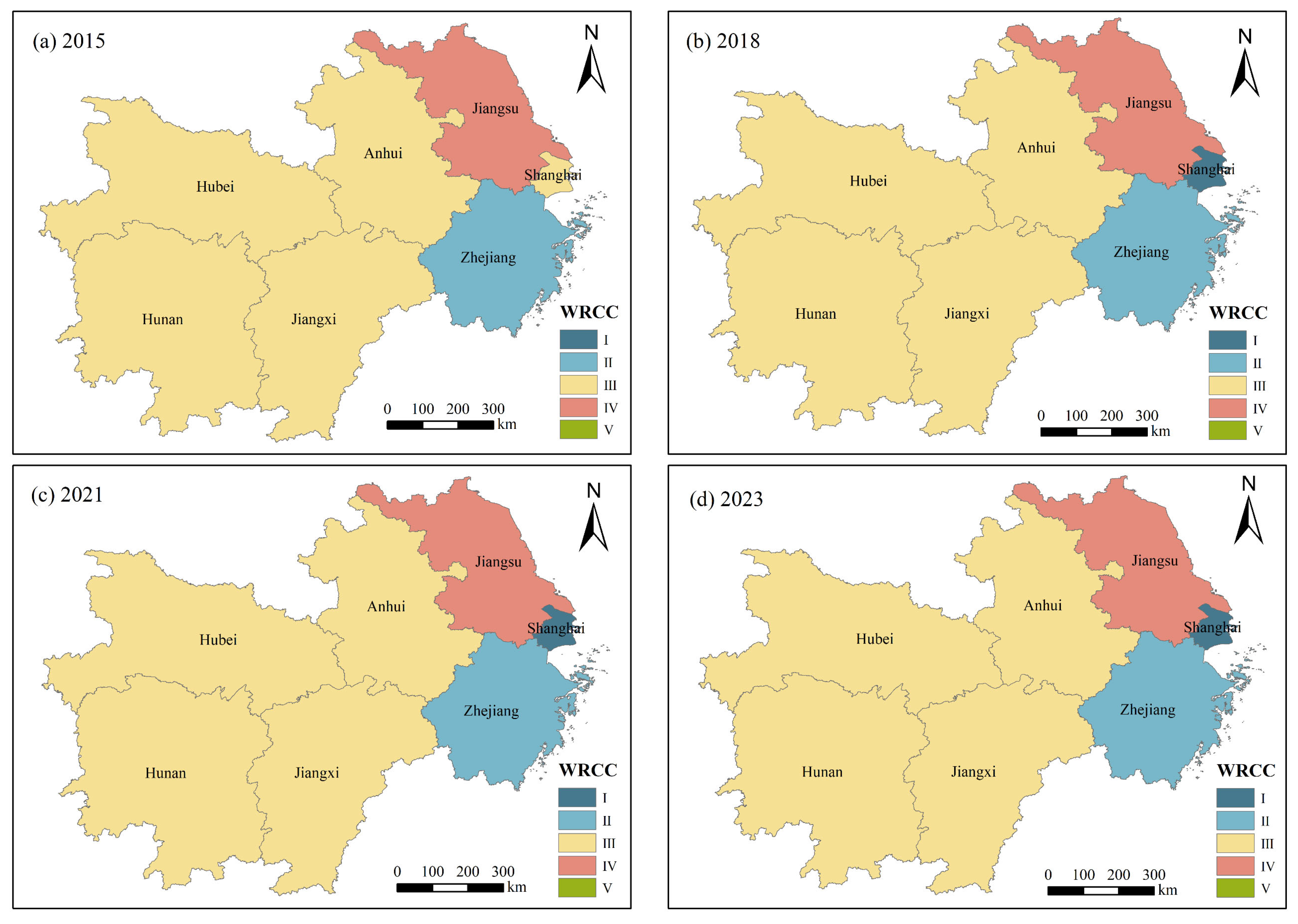
4.2.1. Temporal Changes in WRCC
4.2.2. Spatial Changes in WRCC
5. Discussion
5.1. Distribution of and Changes in Subsystems
5.2. Analysis of Influencing Factors
5.3. Comparative Analysis with Existing Studies
5.4. Study Limitations
6. Conclusions
- (1)
- From 2015 to 2023, the WRCC evaluation grades in seven provinces (municipalities) within the study area demonstrated consistent improvement. Shanghai exhibited the most significant enhancement, advancing from Grade III to Grade I. Zhejiang maintained stable Grade II performance, while Hubei and Hunan remained at Grade III but displayed positive developmental trends. Jiangsu’s WRCC showed notable fluctuations during this period.
- (2)
- Subsystem evaluation values across the region revealed distinct patterns. The water resource subsystem maintained relative stability in most areas, while the social subsystem displayed a gradual decline. Conversely, both the economic and ecological subsystems showed positive development, indicating the successful implementation of economic and environmental protection measures across the region.
- (3)
- Impact analysis identified the water resource subsystem as the most significant contributor to overall WRCC. At the indicator level, four key factors emerged as primary influencers: per capita water resources (C1), the urbanization rate (C8), the green coverage rate in built-up areas (C14), and per capita GDP (C9). These indicators collectively represent the most substantial determinants of WRCC in the middle and lower Yangtze River regions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peng, Q.L.; He, W.J.; Kong, Y.; Shen, J.Q.; Yuan, L.; Ramsey, T.S. Spatio-temporal analysis of water sustainability of cities in the Yangtze River Economic Belt based on the perspectives of quantity-quality-benefit. Ecol. Indic. 2024, 160, 17. [Google Scholar] [CrossRef]
- He, G.; Xia, Y.; Qin, Y.; Zhu, Y.; Wang, W. Evaluation of Water Resources Carrying Capacity of the Yangtze River Economic Belt and Timing and Spatial Dynamic Changes. Soil Water Conserv. Res. 2019, 26, 287–292+300. [Google Scholar] [CrossRef]
- Suvigya, K.; Lalita, S.; Gopinadhan, K. Membranes for desalination and dye separation: Are 2D materials better than polymers? A critical comparison. Sep. Purif. Technol. 2023, 325, 12. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, J.; Wang, H.; Zhou, L.; Yang, R. Characteristics of spatial and temporal changes of water environment carrying capacity in the Yangtze River economic belt. South North Water Divers. Water Sci. Technol. 2022, 20, 714–723. [Google Scholar] [CrossRef]
- He, W.; Chen, S.; Qiu, L. Comprehensive Evaluation and Spatial and Temporal Evolution of Water Resource Carrying Capacity in the Three Gorges Ecological and Economic Corridor of the Yangtze River Area. Yangtze River Basin Resour. Environ. 2022, 31, 1208–1219. [Google Scholar]
- Yuan, L.; Liu, C.Y.; Wu, X.; He, W.J.; Kong, Y.; Degefu, D.M.; Ramsey, T.S. A Set Pair Analysis Method for Assessing and Forecasting Water Conflict Risk in Transboundary River Basins. Water Resour. Manag. 2024, 38, 775–791. [Google Scholar] [CrossRef]
- Chi, C.; Shen, J.; Gao, X.; Hu, P.; Yi, P. Horizontal ecological compensation standards based on ecosystem services flow. Ecol. Indic. 2024, 163, 112081. [Google Scholar] [CrossRef]
- Chi, C.; Shen, J.; Gao, X.; Li, Z.; Sun, F. Spatiotemporal changes of ecosystem services value and cross regional ecological compensation in the Yangtze River Basin. Environ. Dev. Sustain. 2024, 35, 1–35. [Google Scholar] [CrossRef]
- Wang, B.; Yang, H.; Zhu, Y. Study on Comprehensive Evaluation of Water Resources Carrying Capacity of Yangtze River Economic Belt. Resour. Ind. 2020, 22, 1–11. [Google Scholar] [CrossRef]
- Milano, M.; Ruelland, D.; Dezetter, A.; Fabre, J.; Ardoin-Bardin, S.; Servat, E. Modeling the current and future capacity of water resources to meet water demands in the Ebro basin. J. Hydrol. 2013, 500, 114–126. [Google Scholar] [CrossRef]
- Xu, Y. Study on Comprehensive Evaluation of Water Resources Carrying Capacity in Arid Zones—Taking the Hetian River Basin in Xinjiang as an Example. J. Nat. Resour. 1993, 3, 229–237. [Google Scholar]
- Li, L.; Gan, H. Pilot study on the relationship between the concept of rational allocation and carrying capacity of water resources and sustainable development. Prog. Water Sci. 2000, 3, 307–313. [Google Scholar] [CrossRef]
- Huang, X.; Zhou, Y. An overview of research methods on the carrying capacity of resources and the environment. China Environ. Manag. 2018, 10, 36–42+54. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, D.; Xiao, W.; Chen, Y.; Hu, P. Exploring the Theoretical Basis of Water Resources Carrying Capacity: Definitional Connotation and Scientific Issues. J. Water Resour. 2017, 48, 1399–1409. [Google Scholar] [CrossRef]
- Liu, Y.L.; Luo, Y.Q.; Zhang, W.J.; Wu, Y.Y.; Wang, Q. The construction of urban water resources carrying capacity evaluation system based on PSR model. Environ. Pollut. Control 2016, 38, 100–104. [Google Scholar] [CrossRef]
- Ren, L.; Gao, J.; Song, S.; Li, Z.; Ni, J. Evaluation of Water Resources Carrying Capacity in Guiyang City. Water 2021, 13, 2155. [Google Scholar] [CrossRef]
- Zhai, Z.; Sang, X.; Li, H. Study on index system and judgment criterion of water resources carrying capacity. Shuili Xuebao J. Hydraul. Eng. 2017, 48, 1023–1029. [Google Scholar] [CrossRef]
- Li, F.; Niu, K. Evaluation of water resources carrying capacity in Changzhi City Based on Analytic Hierarchy Process. IOP Conf. Ser. Earth Environ. Sci. 2021, 692, 042077. [Google Scholar] [CrossRef]
- Xi-Yin, Z.; Kun, L.; Wei, M.; Soon-Thiam, K.; Jian, Z.; Mingna, W.; Junfeng, Y. Space–time approach to water environment carrying capacity calculation. J. Clean. Prod. 2017, 149, 302–312. [Google Scholar] [CrossRef]
- Dan, D.; Mingdong, S.; Xubo, L.; Juxiang, H.; Hua, Z.; Xiangqin, X.; Kun, L. Comprehensive assessment of the water environment carrying capacity based on the spatial system dynamics model, a case study of Yongding River Basin in North China. J. Clean. Prod. 2022, 344, 131137. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, X.; Wang, X.; Jin, Z.; Chen, F. Multi-Level Fuzzy Comprehensive Evaluation for Water Resources Carrying Capacity in Xuzhou City, China. Sustainability 2023, 15, 11369. [Google Scholar] [CrossRef]
- Wu, F.; Zhuang, Z.; Liu, H.-L.; Shiau, Y.-C. Evaluation of Water Resources Carrying Capacity Using Principal Component Analysis: An Empirical Study in Huai’an, Jiangsu, China. Water 2021, 13, 2587. [Google Scholar] [CrossRef]
- Deng, L.; Yin, J.; Tian, J.; Li, Q.; Guo, S. Comprehensive Evaluation of Water Resources Carrying Capacity in the Han River Basin. Water 2021, 13, 249. [Google Scholar] [CrossRef]
- Wang, Q.; Li, S.; Li, R. Evaluating water resource sustainability in Beijing, China: Combining PSR model and matter-element extension method. J. Clean. Prod. 2019, 206, 171–179. [Google Scholar] [CrossRef]
- Wang, Y.; Ji, Z. Evaluation of Water Resource Carrying Capacity Based on Fuzzy Matter-element Model. IOP Conf. Ser. Earth Environ. Sci. 2021, 706, 012003. [Google Scholar] [CrossRef]
- Wu, Y.; Zhongyu, M.; Li, X.; Sun, L.; Sun, S.; Jia, R. Assessment of water resources carrying capacity based on fuzzy comprehensive evaluation—Case study of Jinan, China. Water Supply 2020, 21, 513–524. [Google Scholar] [CrossRef]
- Gül, S. Usage of Entropy-Based Objective Weighting in Neutrosophic Multiple Attribute Decision-Making. In Multiple Criteria Decision Making: Beyond the Information Age; Topcu, Y.I., Özaydın, Ö., Kabak, Ö., Önsel Ekici, Ş., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 343–367. [Google Scholar]
- Peng, T.; Jin, Z.; Xiao, L. Assessment on water resources carrying capacity in karst areas under a novel multi-dimensional cloud model—A case study. Arab. J. Geosci. 2023, 16, 267. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Song, Y. Comprehensive comparison and assessment of three models evaluating water resource carrying capacity in Beijing, China. Ecol. Indic. 2022, 143, 109305. [Google Scholar] [CrossRef]
- Lv, P.; Liu, D.; Zhao, F.F. Comprehensive Evaluation of Water Resources Carrying Capacity in Jiansanjiang Branch Bureau. Adv. Mater. Res. 2011, 204–210, 834–837. [Google Scholar] [CrossRef]
- Lv, B.; Liu, C.; Li, T.; Meng, F.; Fu, Q.; Ji, Y.; Hou, R. Evaluation of the water resource carrying capacity in Heilongjiang, eastern China, based on the improved TOPSIS model. Ecol. Indic. 2023, 150, 110208. [Google Scholar] [CrossRef]
- Li, S.; Shen, J.; Sun, F. A study on the water resource assets management audit for outgoing officials considering asset elements. J. Clean. Prod. 2025, 494, 144931. [Google Scholar] [CrossRef]
- Li, S.; Shen, J.; Wu, Y.; Huang, X.; Sun, F. An integrated accounting system of the economic-social-ecological framework for assessing the value of intensive land use: A case study of the Taihu Lake governance project. Ecol. Indic. 2024, 158, 111506. [Google Scholar] [CrossRef]
- Wu, C.G.; Zhou, L.Y.; Jin, J.L.; Ning, S.W.; Zhang, Z.X.; Bai, L. Regional water resource carrying capacity evaluation based on multi-dimensional precondition cloud and risk matrix coupling model. Sci. Total Environ. 2020, 710, 136324. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Xiao, C.L.; Qi, Z.W.; Meng, F.A.; Liang, X.J. Development tendency analysis for the water resource carrying capacity based on system dynamics model and the improved fuzzy comprehensive evaluation method in the Changchun city, China. Ecol. Indic. 2021, 122, 107232. [Google Scholar] [CrossRef]
- Meng, L.H.; Chen, Y.N.; Li, W.H.; Zhao, R.F. Fuzzy comprehensive evaluation model for water resources carrying capacity in Tarim River Basin, Xinjiang, China. Chin. Geogr. Sci. 2009, 19, 89–95. [Google Scholar] [CrossRef]
- Kong, Y.; He, W.; Gao, X.; Yuan, L.; Peng, Q.; Li, S.; Zhang, Z.; Degefu, D.M. Dynamic assessment and influencing factors analysis of water environmental carrying capacity in the Yangtze River Economic Belt, China. Ecol. Indic. 2022, 142, 109214. [Google Scholar] [CrossRef]
- Huang, X.; Shen, J.Q.; Sun, F.H.; Wang, L.Y.; Zhang, P.C.; Wan, Y. Study on the Spatial and Temporal Distribution of the High-Quality Development of Urbanization and Water Resource Coupling in the Yellow River Basin. Sustainability 2023, 15, 12270. [Google Scholar] [CrossRef]
- Huang, X.; Shen, J.; Li, S.; Chi, C.; Guo, P.; Hu, P. Sustainable flood control strategies under extreme rainfall: Allocation of flood drainage rights in the middle and lower reaches of the yellow river based on a new decision-making framework. J. Environ. Manag. 2024, 367, 122020. [Google Scholar] [CrossRef]
- Wang, B.; Xie, H.-L.; Ren, H.-Y.; Li, X.; Chen, L.; Wu, B.-C. Application of AHP, TOPSIS, and TFNs to plant selection for phytoremediation of petroleum-contaminated soils in shale gas and oil fields. J. Clean. Prod. 2019, 233, 13–22. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Janitza, S.; Tutz, G.; Boulesteix, A.-L. Random forest for ordinal responses: Prediction and variable selection. Comput. Stat. Data Anal. 2016, 96, 57–73. [Google Scholar] [CrossRef]
- Wang, H. Comprehensive Evaluation of Water Resource Carrying Capacity of Yangtze River Economic Belt Based on Entropy Weight TOPSIS-Coupling Coordination Degree-Gray Correlation Degree. J. Wuhan Univ. Eng. Ed. 2023, 56, 532–541. [Google Scholar] [CrossRef]




| Guideline Layer | Indicator Layer [Unit] (Symbols) | Attributes | Sources |
|---|---|---|---|
| Water resources | Water resources per capita [m3] (C1) | + | [31] |
| Precipitation [108 m3] (C2) | + | [32] | |
| Total water resources [108 m3] (C3) | + | [33] | |
| Coefficient of water supply [/] (C4) | + | [34] | |
| Society | Per capita domestic water consumption [m3] (C5) | − | [35] |
| Population growth rate [%] (C6) | + | [36] | |
| Total water consumption for production [108 m3] (C7) | − | [37] | |
| Urbanization Rate [%] (C8) | + | [31] | |
| Economy | GDP per capita [CHY] (C9) | + | [38] |
| Water consumption per 10,000 CHY of GDP [m3] (C10) | − | [31] | |
| Water consumption per mu of irrigated agriculture [m3] (C11) | − | [34] | |
| Ecology | Ecological water consumption [108 m3] (C12) | + | [34] |
| Daily sewage treatment capacity [108 m3] (C13) | + | [39] | |
| Greening coverage of built-up area [%] (C14) | + | [39] |
| Importance Level | AHP Scale | TrFN-AHP Scale |
|---|---|---|
| Equally important | 1 | (1, 1, 3) |
| Slightly more important | 3 | (1, 3, 5) |
| Important | 5 | (3, 5, 7) |
| Very important | 7 | (5, 7, 9) |
| Extremely important | 9 | (7, 9, 10) |
| Between | 2,4,6,8 |
| , | |
| Indicators | I | II | III | IV | V |
|---|---|---|---|---|---|
| C1 | (4500,2500] | (2500,1700] | (1700,1000] | (1000,500] | (500,0] |
| C2 | (3500,1200] | (1200,800] | (800,600] | (600,400] | (400,0] |
| C3 | (3500,2800] | (2800,2100] | (2100,1400] | (1400,700] | (700,0] |
| C4 | (1,0.6] | (0.6,0.55] | (0.55,0.5] | (0.5,0.4] | (0.4,0] |
| C5 | (45,0] | (50,45] | (55,50] | (60,55] | (80,60] |
| C6 | (7,4] | (4.3] | (3,2] | (2,1] | (1,0] |
| C7 | (100.0] | (200,100] | (300,200] | (400,300] | (500,400] |
| C8 | (100,70] | (70,60] | (60,50] | (50,30] | (30,0] |
| C9 | (20000,145200] | (145200,91011.36] | (91011.36,29373.96] | (29373.96,7521.36] | (7514.1,0] |
| C10 | (60,0] | (70,60] | (80,60] | (100,80] | (150,100] |
| C11 | (550,500] | (500,450] | (450,380] | (380,300] | (300,0] |
| C12 | (30,24] | (24,18] | (18,12] | (12,6] | (6,0] |
| C13 | (55,45] | (45,35] | (35,25] | (25,15] | (15,0] |
| C14 | (100,40] | (40,35] | (35,31] | (31,29] | (29,0] |
| Guideline Layer | Indicator | Importance (%) | Overall Ranking |
|---|---|---|---|
| Water resources (37.3977%) [9.3494%] | C1 | 16.9542 | 1 |
| C2 | 6.7821 | 7 | |
| C3 | 7.6360 | 6 | |
| C4 | 6.0254 | 8 | |
| Society (22.8275%) [5.7069%] | C5 | 3.2654 | 12 |
| C6 | 5.1843 | 9 | |
| C7 | 2.9513 | 13 | |
| C8 | 11.4265 | 2 | |
| Economy (15.716%) [5.2387%] | C9 | 10.0251 | 4 |
| C10 | 3.8462 | 11 | |
| C11 | 1.8447 | 14 | |
| Ecology (24.0588%) [8.0196%] | C12 | 8.2546 | 5 |
| C13 | 4.9218 | 10 | |
| C14 | 10.8824 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, J.; Nie, Y.; Huang, X.; Ma, M. Comprehensive Assessment of Water Resource Carrying Capacity Based on Improved Matter–Element Extension Modeling. Water 2025, 17, 1197. https://doi.org/10.3390/w17081197
Shen J, Nie Y, Huang X, Ma M. Comprehensive Assessment of Water Resource Carrying Capacity Based on Improved Matter–Element Extension Modeling. Water. 2025; 17(8):1197. https://doi.org/10.3390/w17081197
Chicago/Turabian StyleShen, Juqin, Yong Nie, Xin Huang, and Meijing Ma. 2025. "Comprehensive Assessment of Water Resource Carrying Capacity Based on Improved Matter–Element Extension Modeling" Water 17, no. 8: 1197. https://doi.org/10.3390/w17081197
APA StyleShen, J., Nie, Y., Huang, X., & Ma, M. (2025). Comprehensive Assessment of Water Resource Carrying Capacity Based on Improved Matter–Element Extension Modeling. Water, 17(8), 1197. https://doi.org/10.3390/w17081197






