Research on Flood Forecasting in the Pa River Basin Based on the Xin’anjiang Model
Abstract
1. Introduction
2. Methodology
2.1. Hydrological Model Setup and Parameter Constraints
2.2. Performance Evaluation Metrics
- (1)
- Deterministic Accuracy Metrics
- (2)
- Hydrograph Fit Metrics
2.3. Calibration Procedure Using SCE-UA
2.3.1. Calibration Execution for Each Event
2.3.2. Algorithm Configuration and Execution Details
- Parameter Space Definition: Eleven model parameters were subject to calibration. Their initial ranges were set according to the regional hydrological conditions and prior studies.
- Population Initialization: 100 parameter sets were generated using Latin hypercube sampling to ensure broad coverage of the feasible space. Each set represented an 11-dimensional vector.
- Complex Structure: The population was divided into 5 complexes (subpopulations) of 20 parameter sets each, enabling exploration of different solution regions in parallel.
- Evolution and Recombination: Within each complex, 3–5 evolution steps were performed using competitive evolution strategies. Poor-performing members were replaced by new candidates extrapolated from the best performers.
- Shuffling Mechanism: Every 5 iterations, all complexes were merged and globally re-ranked. The updated population was then re-divided into new complexes. This shuffling promoted information exchange and prevented stagnation.
- Convergence Criteria: The calibration for each event continued until either (a) a maximum of 5000 model evaluations was reached or (b) improvement in the best NSE was less than 0.001 over two consecutive shuffling intervals.
2.3.3. Input Parameter Settings and Initialization
- n: Number of decision variables (model parameters) = 11.
- p: Number of complexes = 5 (subpopulations).
- m: Number of points per complex = 20.
- Initial population size: 100 This initial population was generated by Latin hypercube sampling within the specified parameter ranges, ensuring a well-spread and diverse set of trial solutions. Each parameter set is essentially an 11-dimensional vector containing one value for each model parameter (WM, WUM, …, KG, etc.).
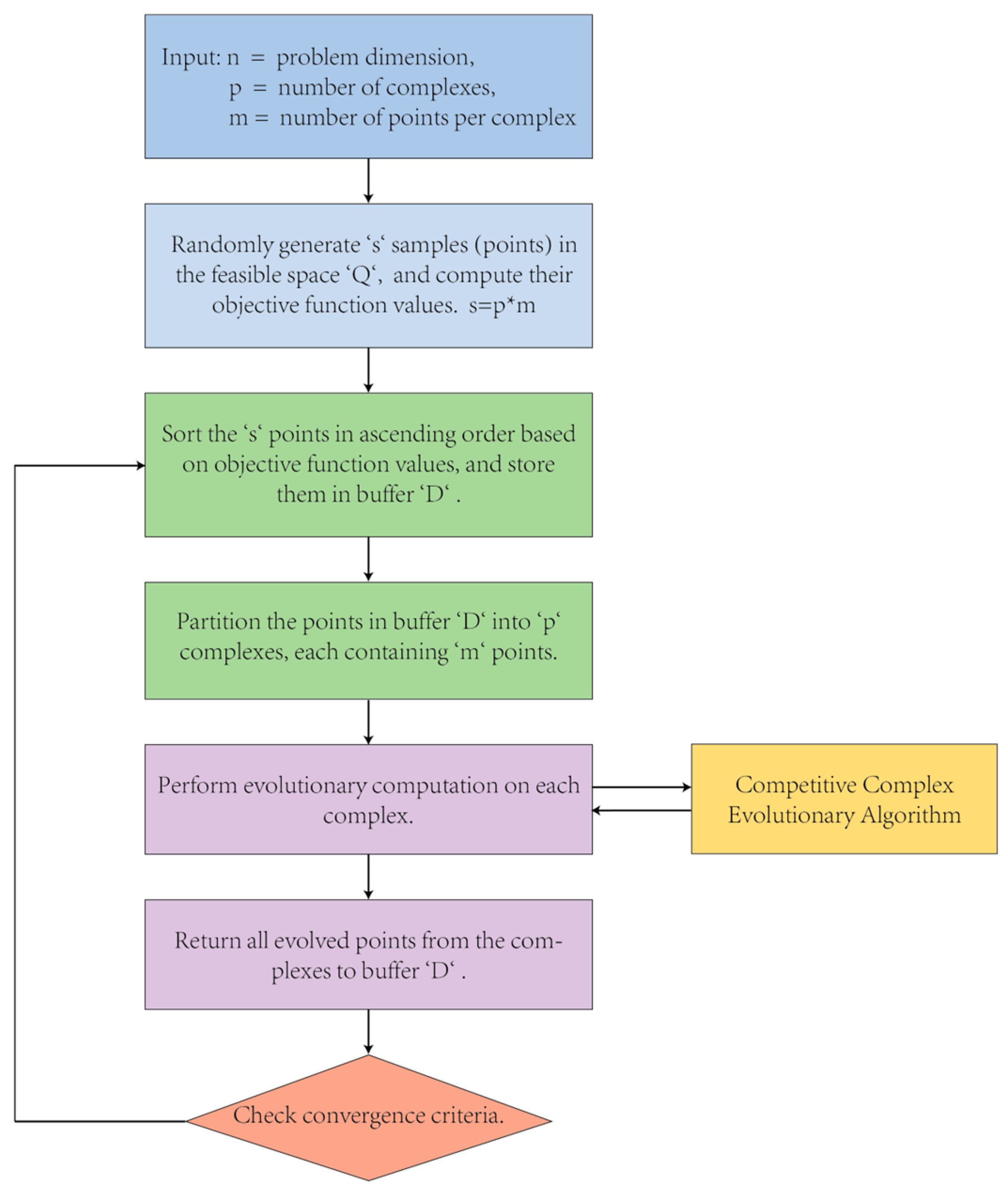
2.3.4. Stepwise Calibration
- Step 1: Random Sampling
- Step 2: Sorting and Buffer Initialization
- Step 3: Complex Partitioning
- Step 4: Evolutionary Computation
- Step 5: Buffer Update
- Step 6: Convergence Check
3. Study Area Description and Data Preparation
3.1. Study Area
3.2. Data Collection and Preprocessing
4. Results and Discussion
4.1. Parameter Calibration Outcomes
4.2. Simulation Results and Model Applicability Assessment
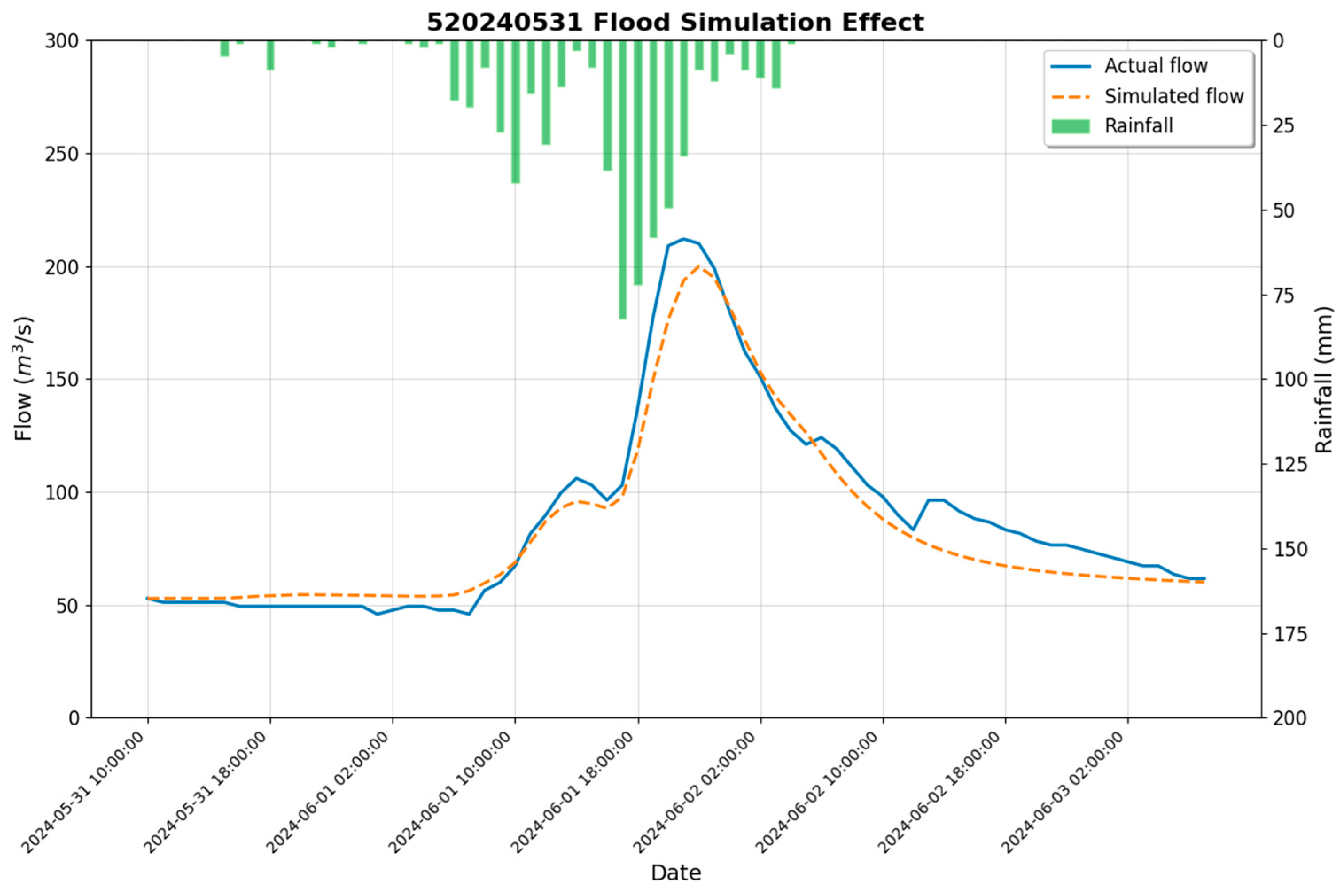
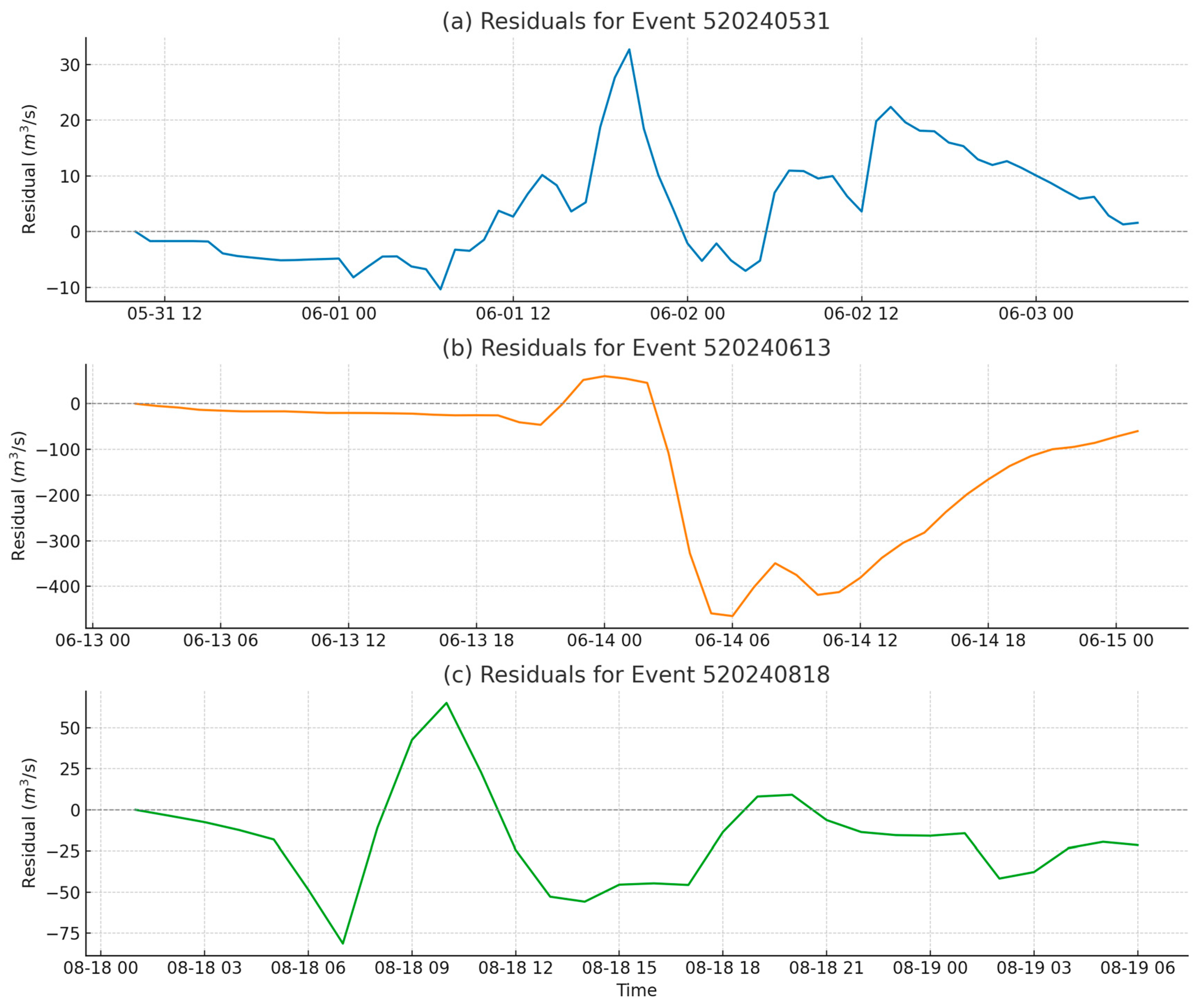
4.2.1. Simulation Results
4.2.2. Applicability Assessment
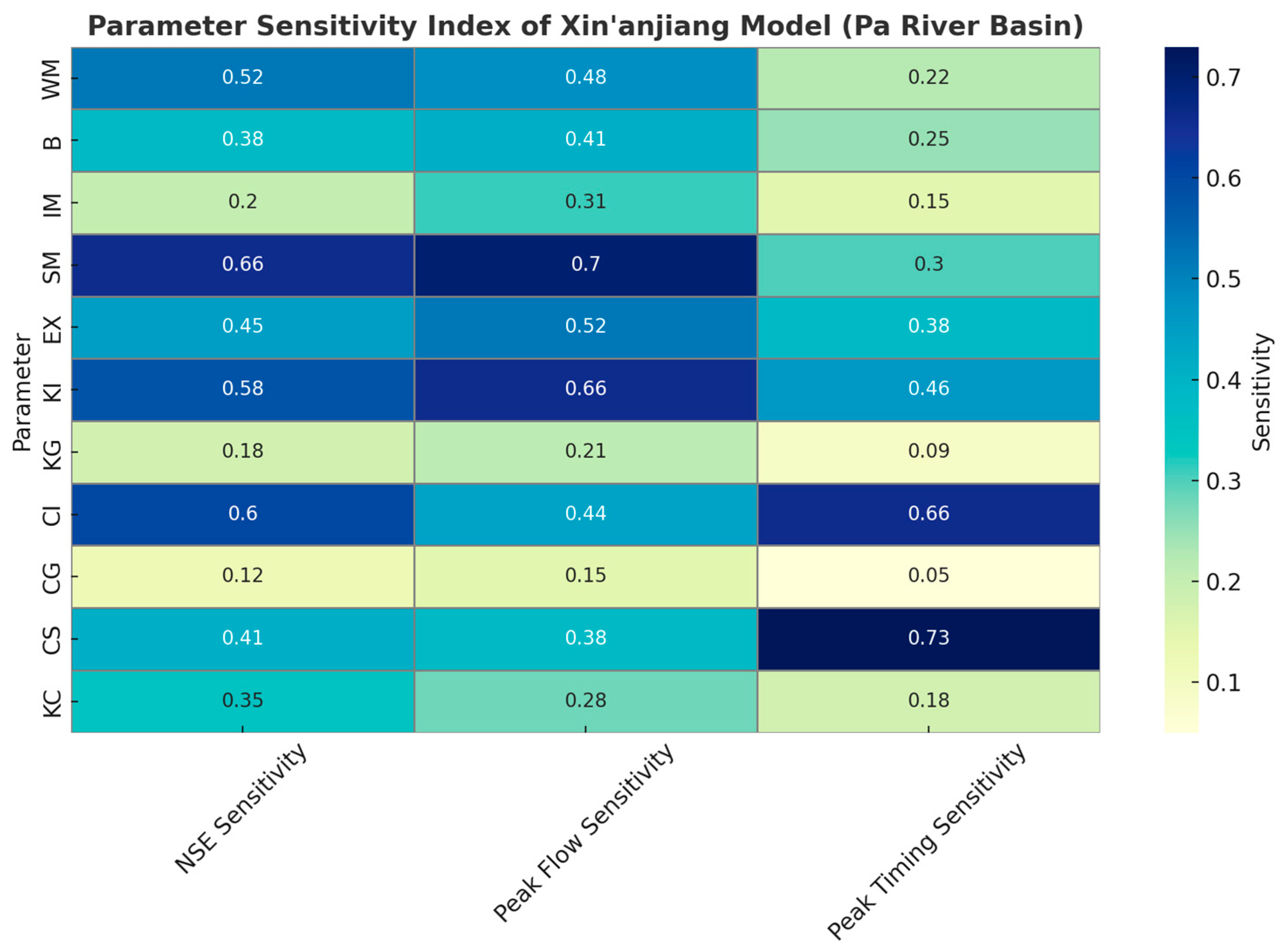
4.3. Parameter Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fornarelli, R.; Galelli, S.; Castelletti, A.; Antenucci, J.P.; Marti, C.L. An Empirical Modeling Approach to Predict and Understand Phytoplankton Dynamics in a Reservoir Affected by Interbasin Water Transfers. Water Resour. Res. 2013, 49, 3626–3641. [Google Scholar] [CrossRef]
- Ewen, J.; O’Connell, E.; Bathurst, J.; Birkinshaw, S.J.; Kilsby, C.; Parkin, G.; O’Donnell, G. Physically-Based Modelling, Uncertainty, and Pragmatism Comment on: ‘Systeme Hydrologique Europeen (She): Review and Perspectives After 30 Years Development in Distributed Physically-Based Hydrological Modelling’ by Jens Christian Refsgaard, Borge Storm and Thomas Clausen. Hydrol. Res. 2012, 43, 945–947. [Google Scholar] [CrossRef][Green Version]
- Beven, K. Towards an Alternative Blueprint for a Physically Based Digitally Simulated Hydrologic Response Modelling System. Hydrol. Process. 2002, 16, 189–206. [Google Scholar] [CrossRef]
- Efstratiadis, A.; Koutsoyiannis, D. One Decade of Multi-Objective Calibration Approaches in Hydrological Modelling: A Review. Hydrol. Sci. J. 2010, 55, 58–78. [Google Scholar] [CrossRef]
- Zhang, L.; Meng, X.; Wang, H.; Yang, M.; Cai, S. Investigate the Applicability of CMADS and CFSR Reanalysis in Northeast China. Water 2020, 12, 996. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep Learning and Process Understanding for Data-Driven Earth System Science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Chen, E.; Andersen, M.S.; Chandra, R. Deep Learning Framework with Bayesian Data Imputation for Modelling and Forecasting Groundwater Levels. Environ. Model. Softw. 2024, 178, 106072. [Google Scholar] [CrossRef]
- Vrugt, J.A. Distribution-Based Model Evaluation and Diagnostics: Elicitability, Propriety, and Scoring Rules for Hydrograph Functionals. Water Resour. Res. 2024, 60, e2023WR036710. [Google Scholar] [CrossRef]
- Mix, K.; Lopes, V.L.; Rast, W. A Systems Approach to Understanding the Evolution of the Agro-Social-Ecological System of the Upper Rio Grande-San Luis Valley, Colorado. Water Resour. Manag. 2015, 29, 233–251. [Google Scholar] [CrossRef]
- Seong, C.; Her, Y.; Benham, B.L. Automatic Calibration Tool for Hydrologic Simulation Program-FORTRAN Using a Shuffled Complex Evolution Algorithm. Water 2015, 7, 503–527. [Google Scholar] [CrossRef]
- Naeini, M.R.; Analui, B.; Gupta, H.V.; Duan, Q.; Sorooshian, S. Three Decades of the Shuffled Complex Evolution (SCE-UA) Optimization Algorithm: Review and Applications. Sci. Iran. 2019, 26, 2015–2031. [Google Scholar]
- Vrugt, J.A.; Gupta, H.V.; Bastidas, L.A.; Bouten, W.; Sorooshian, S. Effective and Efficient Algorithm for Multiobjective Optimization of Hydrologic Models. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Lee, S.; Kang, T. Analysis of Constrained Optimization Problems by the SCE-UA with an Adaptive Penalty Function. J. Comput. Civ. Eng. 2016, 30, 04015035. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, C.; Yu, Q.; Zhao, C.; Quan, L.; Hu, C. Study on a Hybrid Hydrological Forecasting Model SCE-GUH by Coupling SCE-UA Optimization Algorithm and General Unit Hydrograph. Water 2023, 15, 2783. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, X.; Liu, C.; Ren, L.; Cai, X.; Li, K. Hydrological Simulation and Parameter Optimization Based on the Distributed Xin’anjiang Model and the Particle Swarm Optimization Algorithm: A Case Study of Xunhe Watershed in Shandong, China. Water 2024, 16, 3168. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, L.; Li, D. Research on Simpliffied Evaluation Method for Soil-Rock Mixed Slope Stability Under Dam-Break Flood Impact. Bull. Eng. Geol. Environ. 2025, 84, 46. [Google Scholar] [CrossRef]
- Xu, H.; Zhao, Y.; Dajun, Z.; Duan, Y.; Xu, X. Exploring the Typhoon Intensity Forecasting Through Integrating AI Weather Forecasting with Regional Numerical Weather Model. NPJ Clim. Atmos. Sci. 2025, 8, 38. [Google Scholar] [CrossRef]
- Ikeuchi, K.; Kakinuma, D.; Nakamura, Y.; Numata, S.; Mochizuki, T.; Kubota, K.; Yasukawa, M.; Nemoto, T.; Koike, T. Development of Flash Flood Forecasting System for Small and Medium-Sized Rivers. J. Flood Risk Manag. 2025, 18, e70026. [Google Scholar] [CrossRef]
- Wu, M.; Gao, Y.; Liu, Y.; Xu, L.; Gao, L. Application and Effect Evaluation of Different Optimization Algorithms in Distributed Hydrological Model. J. Hydrol. Reg. Stud. 2025, 58, 102207. [Google Scholar] [CrossRef]
- Kan, G.; He, X.; Ding, L.; Li, J.; Liang, K.; Hong, Y. A Heterogeneous Computing Accelerated SCE-UA Global Optimization Method Using OpenMP, OpenCL, CUDA, and OpenACC. Water Sci. Technol. 2017, 76, 1640–1651. [Google Scholar] [CrossRef]
- Kan, G.; Liang, K.; Li, J.; Ding, L.; He, X.; Hu, Y.; Amo-Boateng, M. Accelerating the SCE-UA Global Optimization Method Based on Multi-Core CPU and Many-Core GPU. Adv. Meteorol. 2016, 2016, 8483728. [Google Scholar] [CrossRef]
- Borga, M.; Anagnostou, E.N.; Bloeschl, G.; Creutin, J.D. Flash Flood Forecasting, Warning and Risk Management: The Hydrate Project. Environ. Sci. Policy 2011, 14, 834–844. [Google Scholar] [CrossRef]
- Dore, J.; Lebel, L.; Molle, F. A Framework for Analysing Transboundary Water Governance Complexes, Illustrated in the Mekong Region. J. Hydrol. 2012, 466, 23–36. [Google Scholar] [CrossRef]
- Yuan, F.; Ren, L.-L.; Yu, Z.-B.; Xu, J. Computation of Potential Evapotranspiration Using a Two-Source Method for the Xin’anjiang Hydrological Model. J. Hydrol. Eng. 2008, 13, 305–316. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, J.; Huang, Y.; Yu, L.; Liu, S.; Ma, G. A New Xin’anjiang and Sacramento Combined Rainfall-Runoff Model and Its Application. Hydrol. Res. 2021, 52, 1173–1183. [Google Scholar] [CrossRef]
- Jahanshahi, A.; Booij, M.J.; Patil, S.D. Dependence of Rainfall-Runoff Model Performance on Calibration Conditions Under Changing Climatic Conditions. Hydrol. Sci. J. 2025, 70, 581–596. [Google Scholar] [CrossRef]
- Xu, C.; Zhong, P.-a.; Zhu, F.; Xu, B.; Wang, Y.; Yang, L.; Wang, S.; Xu, S. A Hybrid Model Coupling Process-Driven and Data-Driven Models for Improved Real-Time Flood Forecasting. J. Hydrol. 2024, 638, 131494. [Google Scholar] [CrossRef]
- Wang, A.; Pianosi, F.; Wagener, T. Technical Report-Methods: A Diagnostic Approach to Analyze the Direction of Change in Model Outputs Based on Global Variations in the Model Inputs. Water Resour. Res. 2020, 56, e2020WR027153. [Google Scholar] [CrossRef]
- Syvitski, J.P.M.; Vörösmarty, C.J.; Kettner, A.J.; Green, P. Impact of Humans on the Flux of Terrestrial Sediment to the Global Coastal Ocean. Science 2005, 308, 376–380. [Google Scholar] [CrossRef]
- Walling, D.E. Human Impact on Land-Ocean Sediment Transfer by the World’s Rivers. Geomorphology 2006, 79, 192–216. [Google Scholar] [CrossRef]
- Cheng, Y.; Sang, Y.; Wang, Z.; Guo, Y.; Tang, Y. Effects of Rainfall and Underlying Surface on Flood Recession-The Upper Huaihe River Basin Case. Int. J. Disaster Risk Sci. 2021, 12, 111–120. [Google Scholar] [CrossRef]
- Fischer, S.; Buehler, P.; Schumann, A. Impact of Flood Types on Superposition of Flood Waves and Flood Statistics Downstream. J. Hydrol. Eng. 2021, 26, 04021024. [Google Scholar] [CrossRef]
- Ashok, K.; Saji, N.H. On the Impacts of ENSO and Indian Ocean Dipole Events on Sub-Regional Indian Summer Monsoon Rainfall. Nat. Hazards 2007, 42, 273–285. [Google Scholar] [CrossRef]
- Zhou, T.J.; Yu, R.C. Atmospheric Water Vapor Transport Associated with Typical Anomalous Summer Rainfall Patterns in China. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Jin, D.; Guan, Z.; Huo, L.; Wang, X. Possible Impacts of Spring Sea Surface Temperature Anomalies over South Indian Ocean on Summer Rainfall in Guangdong-Guangxi Region of China. Clim. Dyn. 2017, 49, 3075–3090. [Google Scholar] [CrossRef]
- Ding, Y.H.; Chan, J.C.L. The East Asian Summer Monsoon: An Overview. Meteorol. Atmos. Phys. 2005, 89, 117–142. [Google Scholar] [CrossRef]
- Schutte, C.; van der Laan, M.; van der Merwe, B. Leveraging Historic Streamflow and Weather Data with Deep Learning for Enhanced Streamflow Predictions. J. Hydroinform. 2024, 26, 835–852. [Google Scholar] [CrossRef]
- GB/T 22482-2008; Standard for Hydrological Information and Hydrological Forecasting. China Standards Press: Beijing, China, 2008.
- Paradis, D.; Gloaguen, E.; Lefebvre, R.; Giroux, B. A Field Proof-of-Concept of Tomographic Slug Tests in an Anisotropic Littoral Aquifer. J. Hydrol. 2016, 536, 61–73. [Google Scholar] [CrossRef]
- Ronen-Eliraz, G.; Ginat, H.; Dody, A.; Blumberg, D.; Dahan, O. Flood Hydrograph Reconstruction from the Peak Flow Value in Ephemeral Streams Using a Simplified Robust Single-Parameter Model. Hydrol. Process. 2016, 30, 3004–3013. [Google Scholar] [CrossRef]
- Anwar, H.; Khan, A.U.; Ullah, B.; Taha, A.T.B.; Najeh, T.; Badshah, M.U.; Ghanim, A.A.J.; Irfan, M. Intercomparison of Deep Learning Models in Predicting Streamflow Patterns: Insight from CMIP6. Sci. Rep. 2024, 14, 17468. [Google Scholar] [CrossRef]
- Fischer, S.; Schumann, A.; Buehler, P. Timescale-Based Flood Typing to Estimate Temporal Changes in Flood Frequencies. Hydrol. Sci. J. 2019, 64, 1867–1892. [Google Scholar] [CrossRef]
- Jeon, J.-H.; Park, C.-G.; Engel, B.A. Comparison of Performance Between Genetic Algorithm and SCE-UA for Calibration of SCS-CN Surface Runoff Simulation. Water 2014, 6, 3433–3456. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, N.; Bao, X.; Wu, J.; Cui, X. Spatio-Temporal Deep Learning Model for Accurate Streamflow Prediction with Multi-source Data Fusion. Environ. Model. Softw. 2024, 178, 106091. [Google Scholar] [CrossRef]
- He, J.B. Analysis of the “2020.6 Extreme Storm Flood in the Panjiang River”. Water Resour. Sci. Cold Zone Eng. 2022, 5, 63–65. [Google Scholar]
- Yang, J.; Wen, L.; Guo, J.; Chen, Y.; Zhu, Y.; Wang, Y.; Ma, M. A Cooperative Search Algorithm-Based Flood Forecasting Framework: Application Across Diverse Chinese Catchments. Front. Earth Sci. 2025, 13, 1538235. [Google Scholar] [CrossRef]

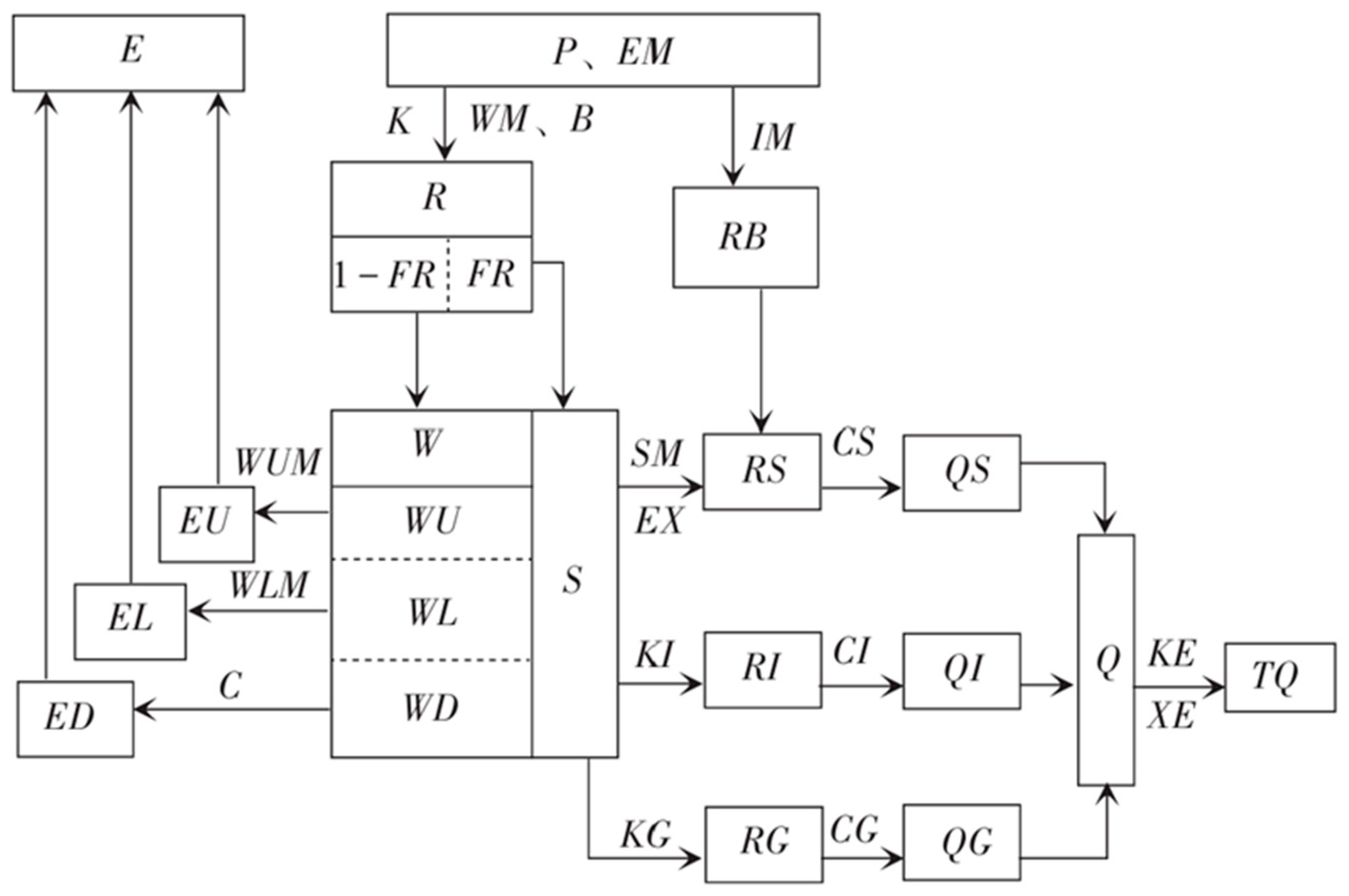




| Abbreviation | Full Name | Description | Abbreviation | Full Name | Description |
|---|---|---|---|---|---|
| P | Precipitation | Volume of water falling on the land surface per unit area and time. | IM | Impervious Area Ratio | Fraction of the basin that is impervious, affecting direct runoff. |
| EM | Water Surface Evaporation | Evaporation rate from open water surfaces. | SM | Free Water Storage Capacity | Capacity of the surface soil layer to store free water before surface runoff occurs. |
| E | Evapotranspiration | Combined water loss through soil evaporation and plant transpiration. | EX | Exponent of the Free Water Storage Capacity Curve | Influences how free water storage varies across the basin. |
| R | Runoff from Permeable Areas | Surface flow generated in permeable zones. | KI | Interflow Runoff Coefficient | Regulates the proportion of quick subsurface flow (interflow) contributing to total runoff. |
| FR | Runoff-Generating Area Ratio | Proportion of basin area contributing to direct runoff. | KG | Groundwater Runoff Coefficient | Determines the fraction of slow baseflow (groundwater flow) contributing to total runoff. |
| RB | Runoff from Impervious Areas | Surface flow generated in urbanized or impervious zones. | CI | Recession Constant of the Interflow Reservoir | Affects the depletion rate of interflow storage, influencing the recession limb of the hydrograph. |
| EU/EL/ED | Upper/Lower/Deep-Layer Evapotranspiration | Partitioned evapotranspiration components from soil layers. | CG | Recession Constant of the Groundwater Reservoir | Influences the depletion rate of groundwater storage, affecting baseflow recession. |
| W | Total Capillary Water Storage | Sum of water held in soil capillary pores. | CS | Recession Constant of the River Network Storage | Controls the attenuation and lag of flow through the river network, impacting flood peak timing and magnitude. |
| WU/WL/WD | Upper/Lower/Deep-Layer Capillary Water | Water storage in specific soil horizons. | KC | Evapotranspiration Correction Coefficient | Adjusts the potential evapotranspiration rates to better match observed conditions. |
| S | Surface Free Water Storage | Temporary ponding water before becoming runoff. | KE | Coefficient of Evapotranspiration | Modifies the rate of evapotranspiration, affecting water loss estimates. |
| RS/RI/RG | Surface Runoff/Interflow/Groundwater Runoff | Three-component runoff generation mechanism. | C | Deep-Layer Evaporation Coefficient | Adjusts evaporation from deeper soil layers, influencing soil moisture dynamics. |
| B | Exponent of the Tension Water Capacity Curve | Determines the spatial distribution of the tension water capacity. | N | Manning’s Roughness Coefficient | Represents the roughness of the river channel, affecting flow velocity and routing. |
| Parameter | Original Range | Adjusted Range for Pa River | Adjustment Basis |
|---|---|---|---|
| WM | 100–300 | 100–200 | The Pa River basin features alluvial plains and weathered sedimentary soils with moderate water-holding capacity. |
| B | 0.1–0.7 | 0.2–0.6 | The basin exhibits heterogeneous soil types and moderate spatial variability in field capacity. |
| IM | 0–0.05 | 0–0.03 | The basin’s substantial forest coverage and limited urbanization result in a low impervious area ratio. |
| SM | 10–50 | 10–40 | The presence of thin soil layers in certain regions leads to reduced water storage capacity. |
| EX | 0.1–1.5 | 0.1–1.3 | The topographic relief and uneven infiltration capacity in the Pa River basin. |
| KI | 0.0–1.0 | 0.1–1.0 | The basin’s permeable soil layers and steep upper catchments facilitate interflow, necessitating a moderately high KI range. |
| KG | 0.0–1.0 | 0.1–0.8 | The fractured bedrock and shallow groundwater table support slow baseflow contribution, reflected in a constrained but active KG range. |
| CI | 0.0–1.0 | 0.1–0.7 | The slope-driven quick response and flash-flood characteristics in the upper basin require tighter control over interflow depletion. |
| CG | 0.0–1.0 | 0.1–1 | Groundwater storage recession is relatively slow. |
| CS | 0.0–1.0 | 0.01–0.2 | Steep flood hydrographs indicate rapid recession, characteristic of the basin’s hydrological response. |
| KC | 0.5–1.5 | 0.7–1.3 | The adjustment reflects the region’s subtropical monsoon climate with high seasonal evapotranspiration variability. |
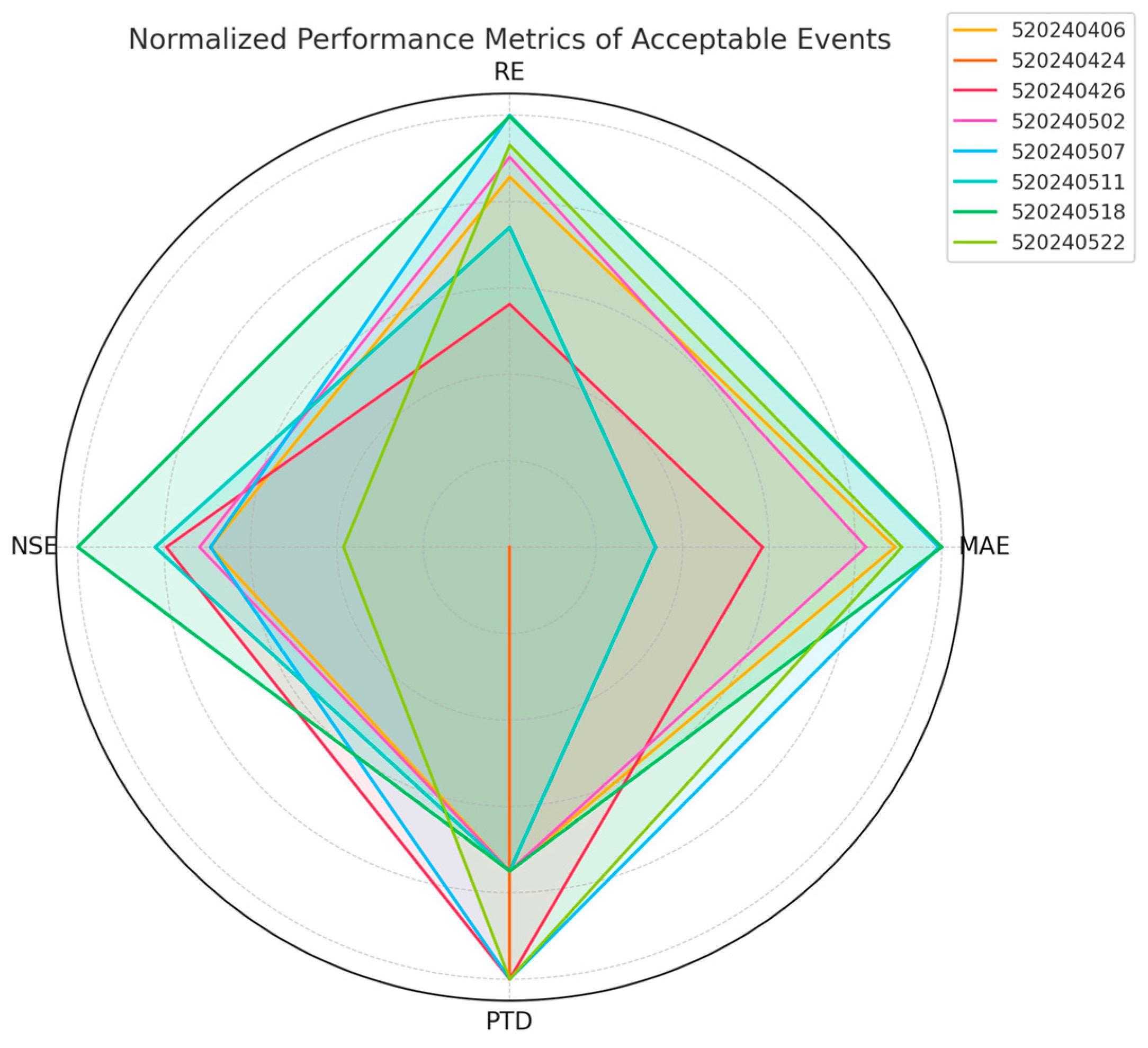
| Event ID | Observed Peak Discharge (m3/s) | Simulated Peak Discharge (m3/s) | Absolute Error (MAE) | Relative Error (%) (RE) | NSE | Peak Timing Discrepancy (h) (PTD) | Simulation Tier |
|---|---|---|---|---|---|---|---|
| 520240405 | 482 | 337.8 | −144.2 | −29.92 | 0.70 | 4 | Noncompliant |
| 520240406 | 382 | 357 | −6.54 | −6.54 | 0.86 | 1 | optimal |
| 520240419 | 1010 | 968.3 | −4.13 | −4.13 | 0.84 | −3 | Noncompliant |
| 520240424 | 515 | 326.5 | −36.60 | −36.60 | 0.59 | 0 | optimal |
| 520240426 | 915 | 760.6 | −16.87 | −16.87 | 0.90 | 0 | Moderate |
| 520240502 | 179 | 187.8 | 8.8 | 4.92 | 0.87 | −1 | optimal |
| 520240507 | 205 | 208.11 | 3.11 | 1.52 | 0.86 | 0 | optimal |
| 520240511 | 237 | 211.78 | −25.22 | −10.64 | 0.91 | 1 | Moderate |
| 520240518 | 179 | 176.1 | −2.9 | −1.62 | 0.98 | 1 | optimal |
| 520240522 | 152 | 146 | −6 | −3.95 | 0.74 | 0 | Moderate |
| 520240525 | 108 | 108.4 | 0.4 | 0.37 | 0.52 | 1 | Noncompliant |
| 520240607 | 151 | 117.72 | −33.28 | −22.04 | 0.65 | 1 | Noncompliant |
| Phase | Parameter Symbol | Final Calibrated Value |
|---|---|---|
| Evapotranspiration | K | 0.898 |
| WUM | 26.994 | |
| WLM | 61.473 | |
| C | 0.180 | |
| Runoff Yield | WM | 120.000 |
| B | 0.300 | |
| IM | 0.010 | |
| Flow Component Separation | SM | 22.479 |
| EX | 1.220 | |
| KI | 0.370 | |
| KG | 0.277 | |
| CS | 0.008 | |
| CG | 0.971 | |
| CI | 0.191 | |
| Flow Routing | CR | 0.478 |
| L | 0.000 | |
| KE | 2.791 | |
| XE | 0.328 |
| Parameter | NSE Sensitivity | Peak Flow Sensitivity | Peak Timing Sensitivity |
|---|---|---|---|
| WM | 0.52 | 0.48 | 0.22 |
| B | 0.38 | 0.41 | 0.25 |
| IM | 0.20 | 0.31 | 0.15 |
| SM | 0.66 | 0.70 | 0.30 |
| EX | 0.45 | 0.52 | 0.38 |
| KI | 0.58 | 0.66 | 0.46 |
| KG | 0.18 | 0.21 | 0.09 |
| CI | 0.60 | 0.44 | 0.66 |
| CG | 0.12 | 0.15 | 0.05 |
| CS | 0.41 | 0.38 | 0.73 |
| KC | 0.35 | 0.28 | 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Liu, S.; Tu, C.; Zhou, H. Research on Flood Forecasting in the Pa River Basin Based on the Xin’anjiang Model. Water 2025, 17, 1154. https://doi.org/10.3390/w17081154
Huang Z, Liu S, Tu C, Zhou H. Research on Flood Forecasting in the Pa River Basin Based on the Xin’anjiang Model. Water. 2025; 17(8):1154. https://doi.org/10.3390/w17081154
Chicago/Turabian StyleHuang, Zeguang, Shuai Liu, Chunxi Tu, and Haolan Zhou. 2025. "Research on Flood Forecasting in the Pa River Basin Based on the Xin’anjiang Model" Water 17, no. 8: 1154. https://doi.org/10.3390/w17081154
APA StyleHuang, Z., Liu, S., Tu, C., & Zhou, H. (2025). Research on Flood Forecasting in the Pa River Basin Based on the Xin’anjiang Model. Water, 17(8), 1154. https://doi.org/10.3390/w17081154





