Interfacial Behavior of Janus Nanorods: A Dissipative Particle Dynamics (DPD) Study on Water–Oil Systems and Nanoconfinement
Abstract
1. Introduction
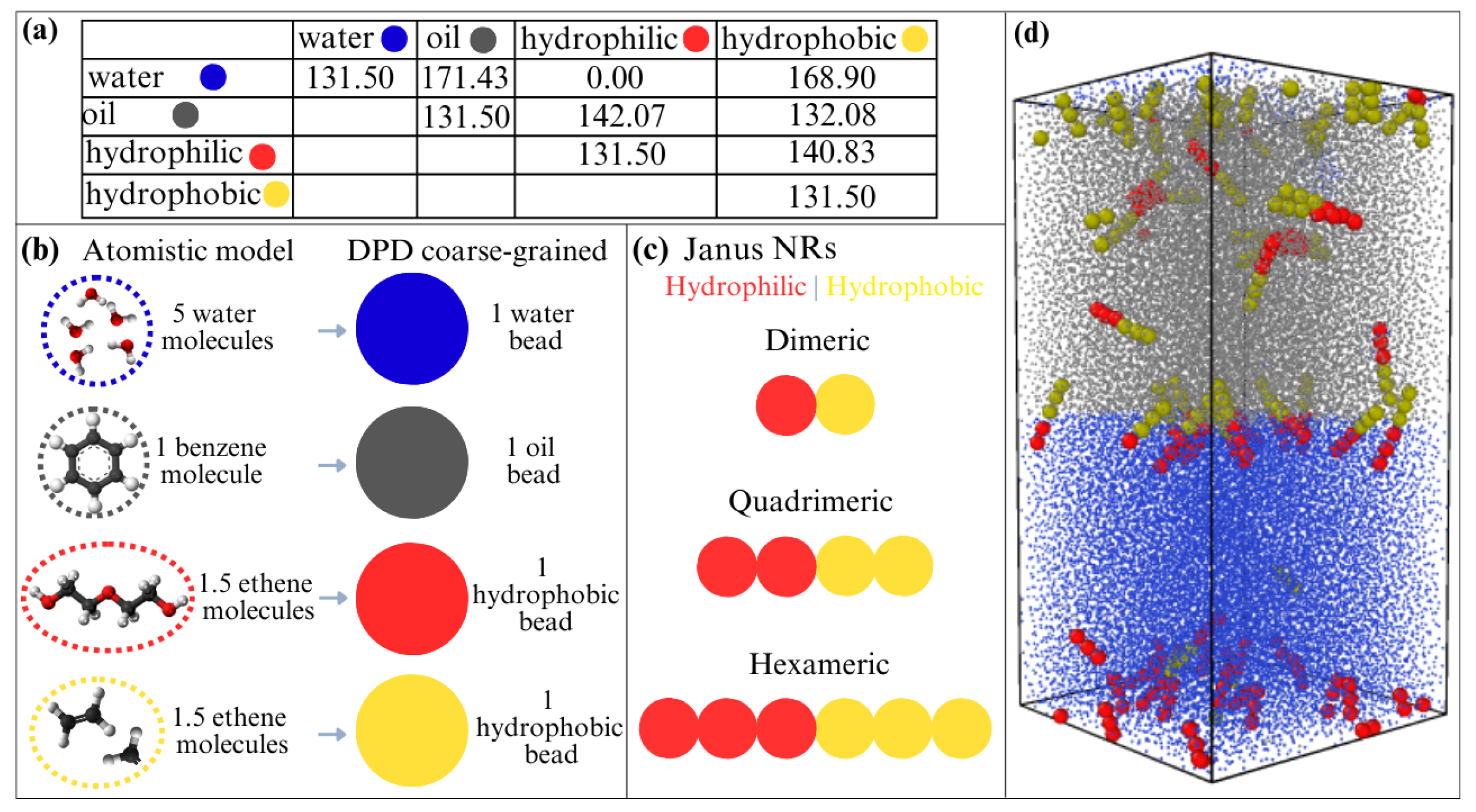
2. The Method and the Models
2.1. Dissipative Particle Dynamics
2.2. The Model and System Details
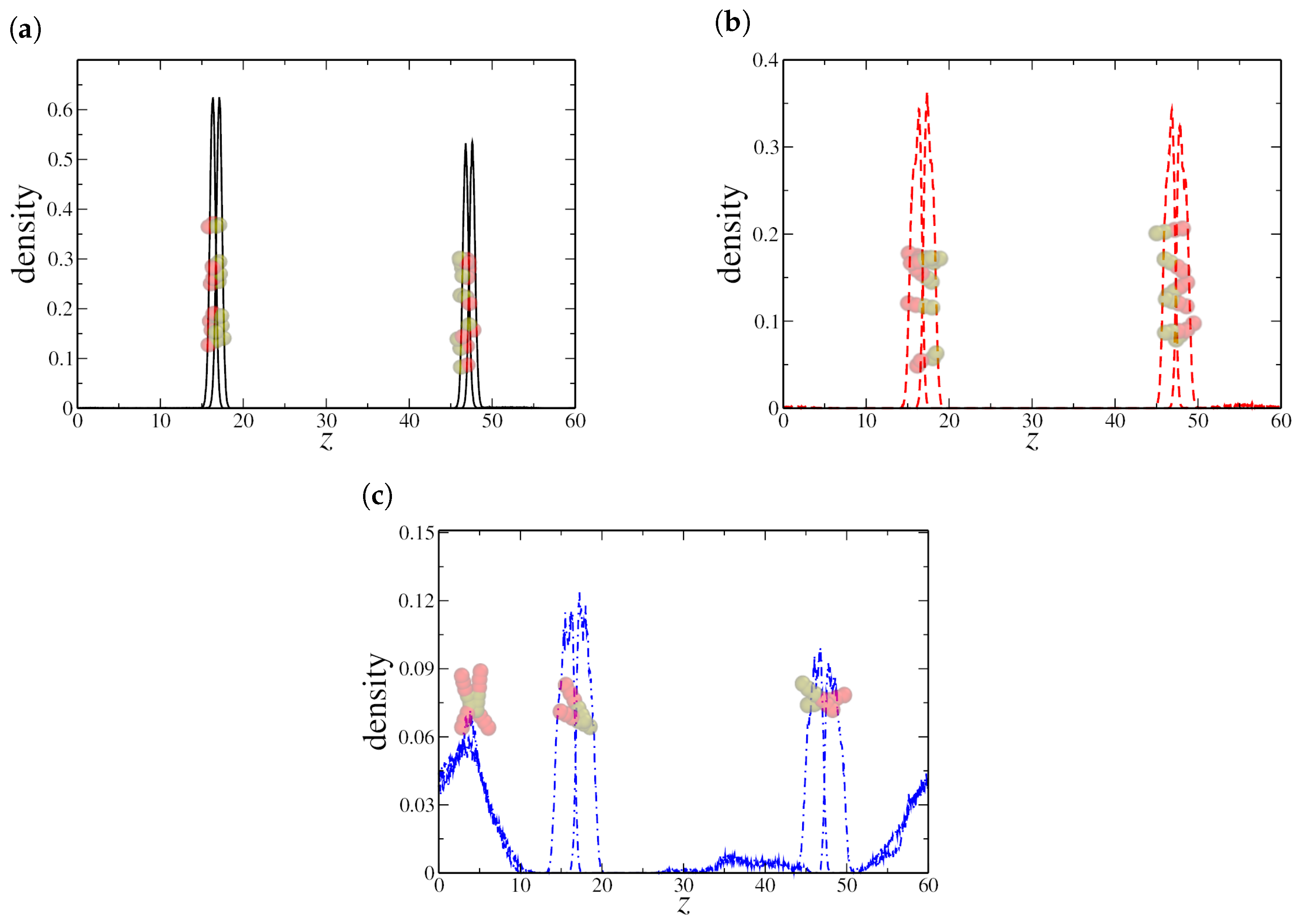
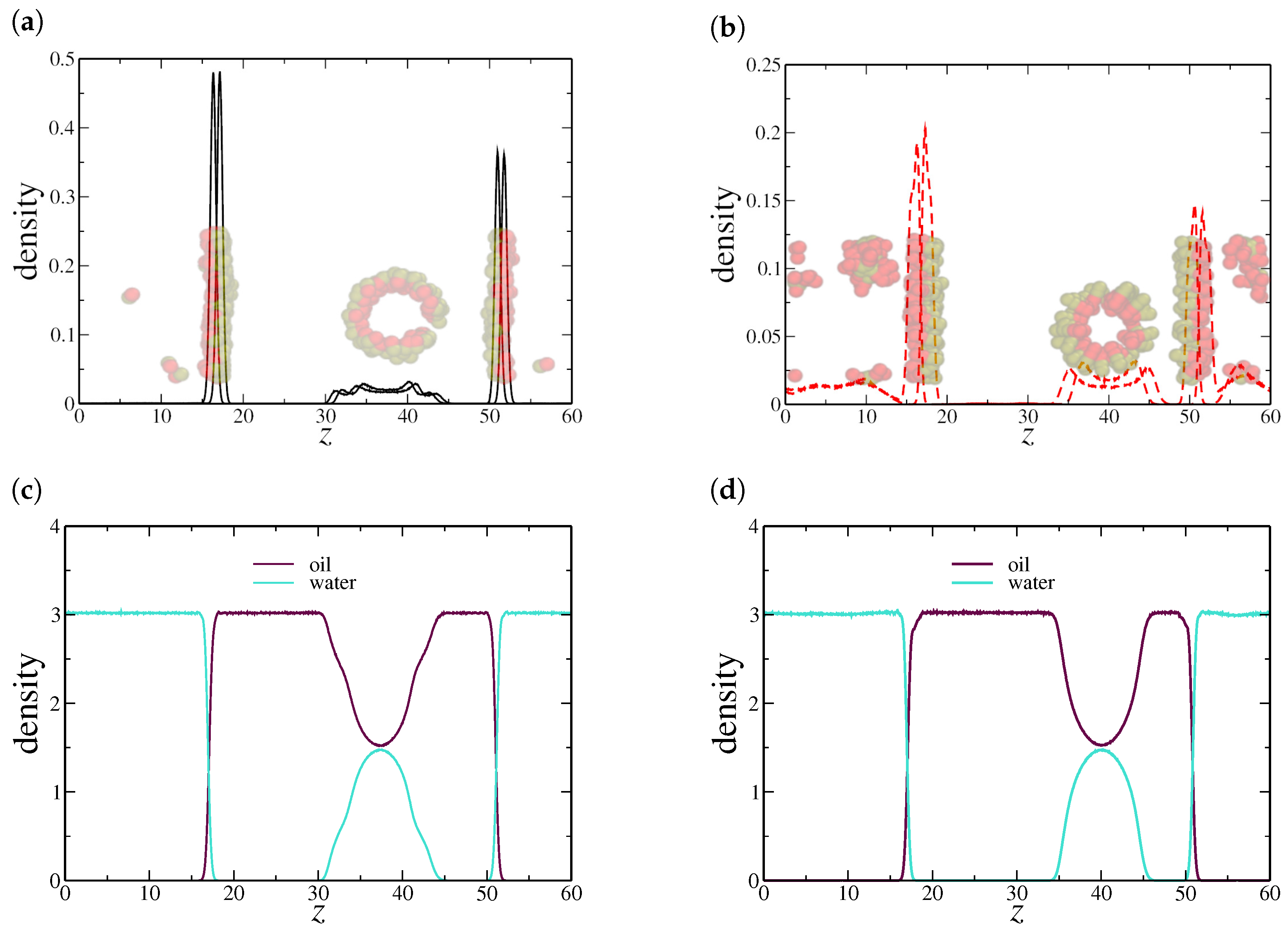
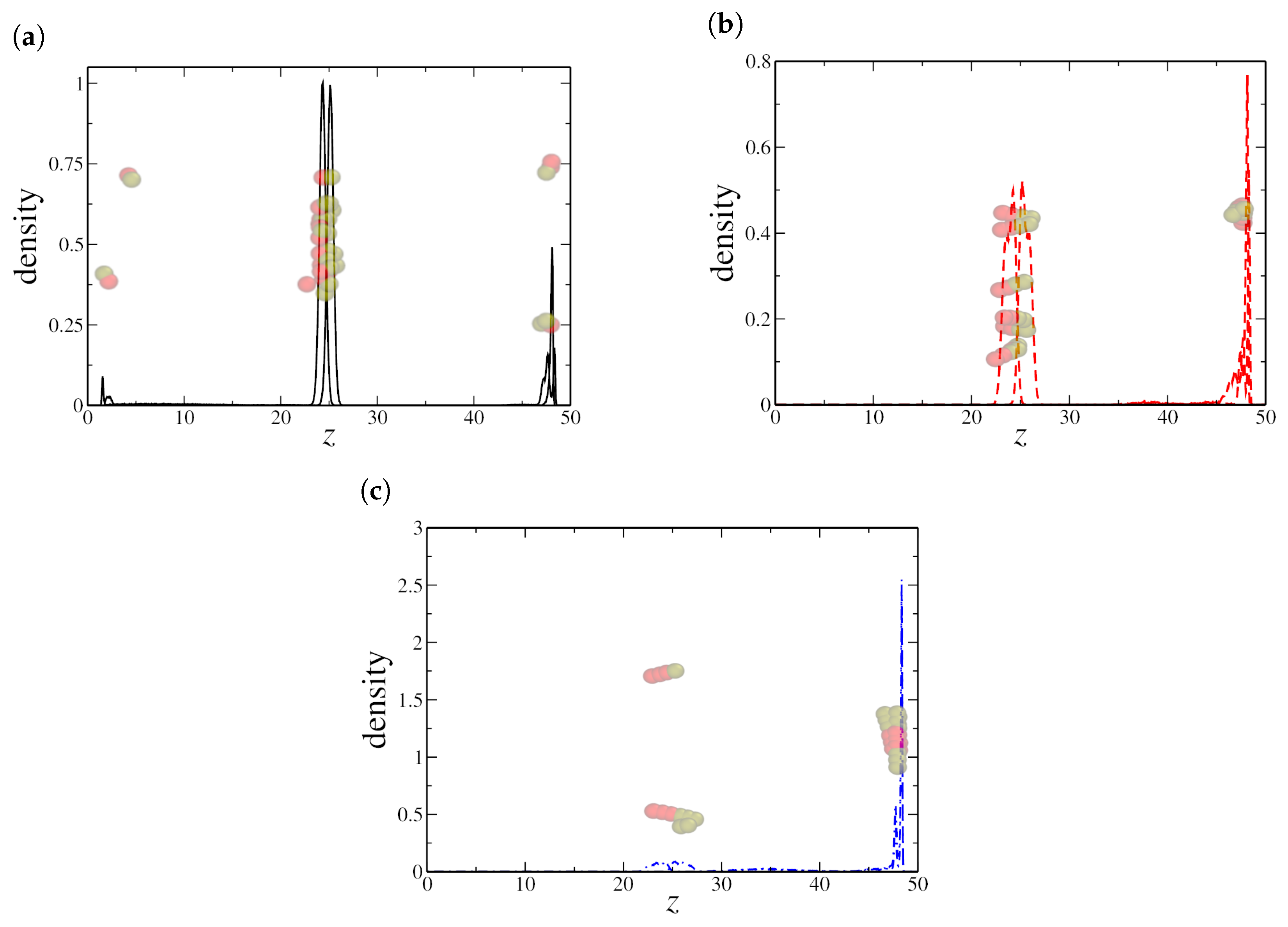
3. Results and Discussion
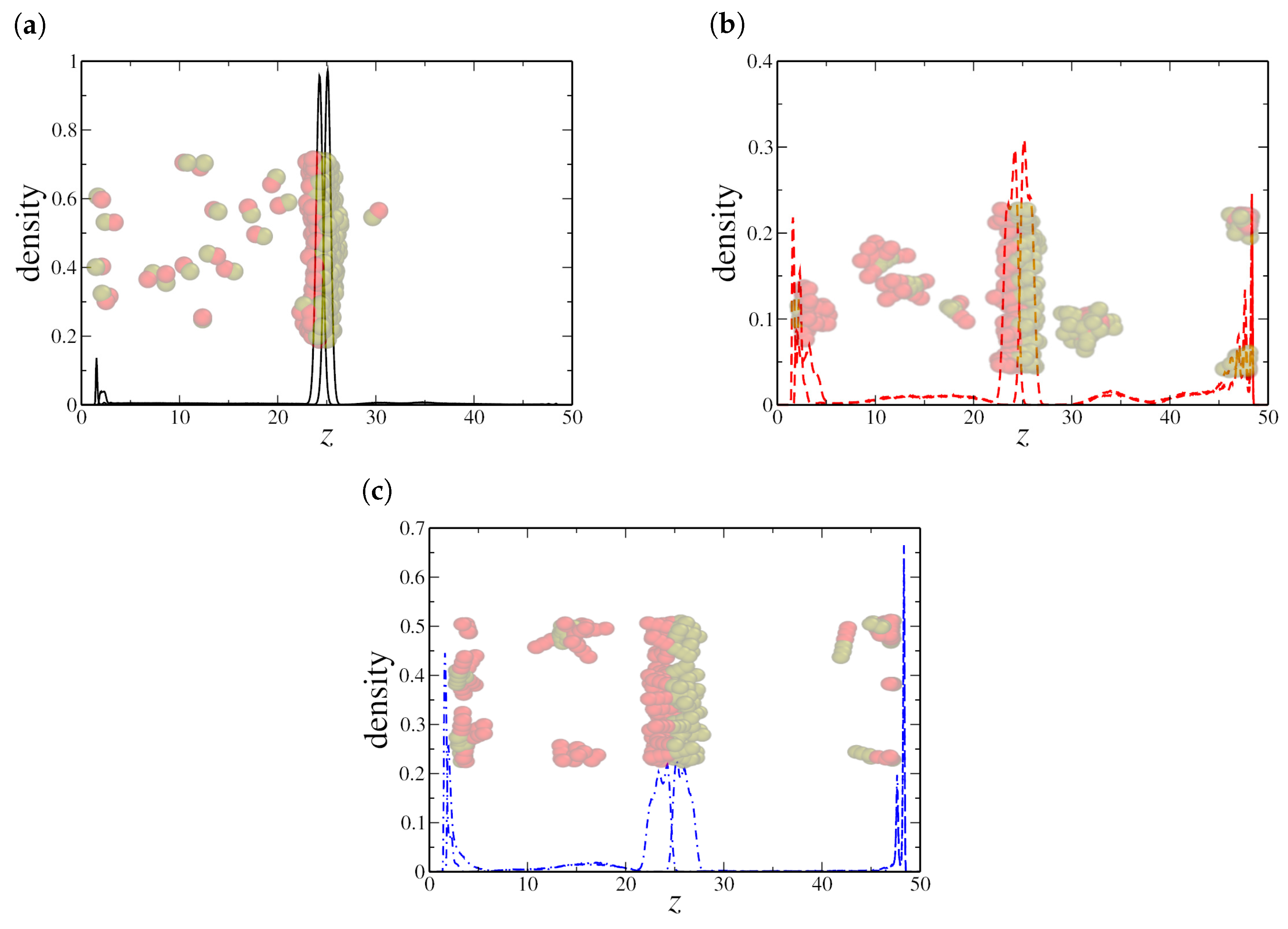
3.1. Water–Oil Thin Films
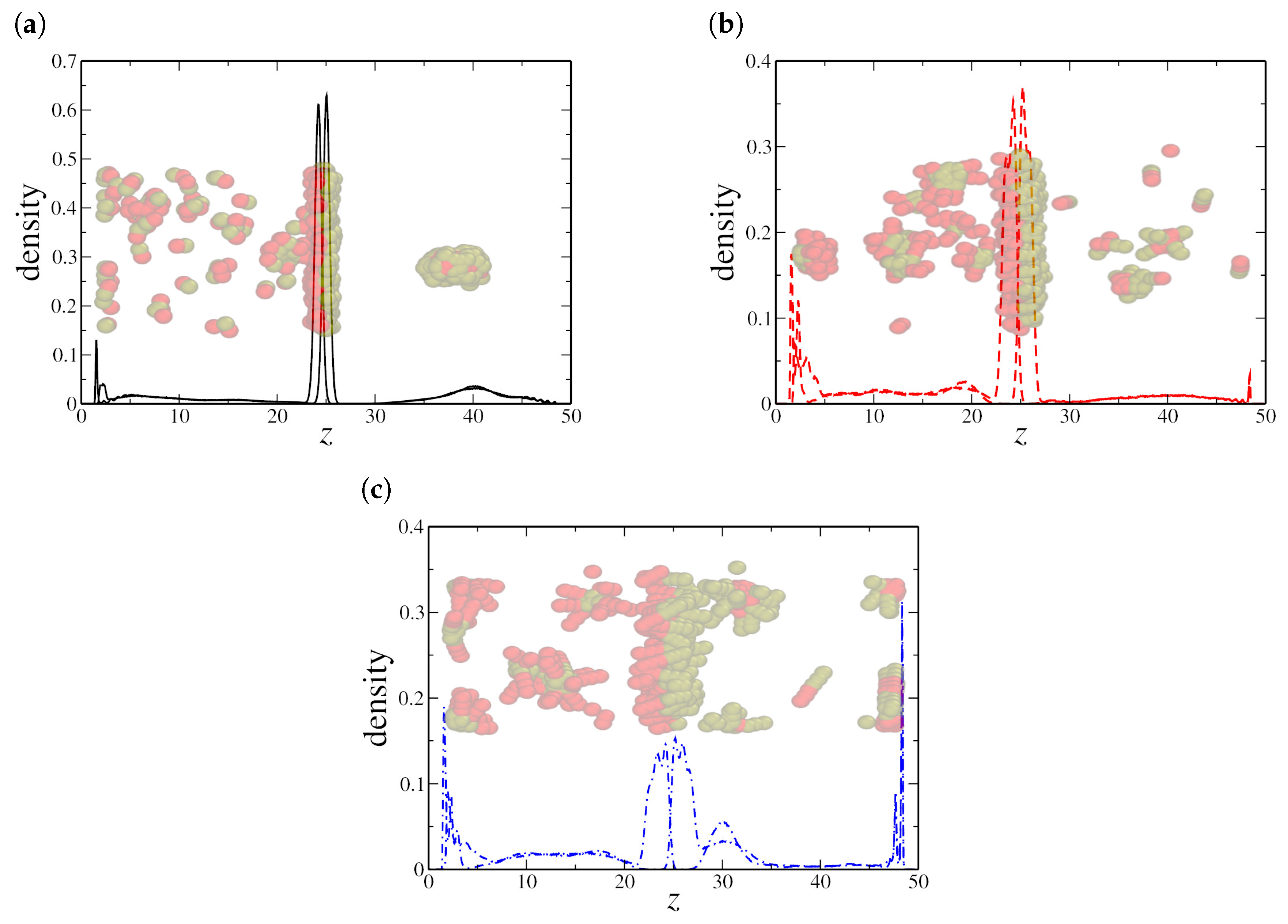
3.2. Nanoconfined Oil–Water
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Programme, United Nations World Water Development. The United Nations World Water Development Report 2023: Partnerships and Cooperation for Water; United Nations Educational, Scientific and Cultural Organization: London, UK, 2023. [Google Scholar]
- Méndez, C.; Simpson, N.P.; Johnson, F.X.; Birt, A. Climate Change 2023: Synthesis Report (Full Volume) Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2023. [Google Scholar]
- Zhao, Y.; Chang, C.; Ji, H.; Li, Z. Challenges of petroleum wastewater treatment and development trends of advanced treatment technologies: A review. J. Environ. Chem. Eng. 2024, 12, 113767. [Google Scholar] [CrossRef]
- Adetunji1, A.I.; Olaniran, A.O. Treatment of industrial oily wastewater by advanced technologies: A review. Appl. Water Sci. 2021, 11, 98. [Google Scholar] [CrossRef]
- Zheng, W.; Huang, J.; Li, S.; Ge, M.; Teng, L.; Chen, Z.; Lai, Y. Advanced Materials with Special Wettability toward Intelligent Oily Wastewater Remediation. ACS Appl. Mater. Interfaces 2021, 13, 67–87. [Google Scholar] [CrossRef] [PubMed]
- Lim, M.W.; Lau, E.V.; Poh, P.E. A comprehensive guide of remediation technologies for oil contaminated soil — Present works and future directions. Mar. Pollut. Bull. 2016, 109, 14–45. [Google Scholar] [CrossRef]
- Truskewycz, A.; Gundry, T.D.; Khudur, L.S.; Kolobaric, A.; Taha, M.; Aburto-Medina, A.; Ball, A.S.; Shahsavari, E. Petroleum Hydrocarbon Contamination in Terrestrial Ecosystems—Fate and Microbial Responses. Molecules 2019, 24, 3400. [Google Scholar] [CrossRef] [PubMed]
- Adipah, S. Introduction of Petroleum Hydrocarbons Contaminants and its Human Effects. J. Environ. Sci. Public Health 2018, 3, 1–9. [Google Scholar] [CrossRef]
- Han, M.; Zhang, J.; Chu, W.; Chen, J.; Zhou, G. Research Progress and Prospects of Marine Oily Wastewater Treatment: A Review. Water 2019, 11, 2517. [Google Scholar] [CrossRef]
- Labud, V.; Garcia, C.; Hernandez, T. Effect of hydrocarbon pollution on the microbial properties of a sandy and a clay soil. Chemosphere 2007, 66, 1863–1871. [Google Scholar] [CrossRef]
- Jamaly, S.; Giwa, A.; Hasan, S.W. Recent improvements in oily wastewater treatment: Progress, challenges, and future opportunities. J. Environ. Sci. 2015, 37, 15–30. [Google Scholar] [CrossRef]
- Laffon, B.; Pássaro, E.; Valdiglesias, V. Effects of exposure to oil spills on human health: Updated review. J. Toxicol. Environ. Heal. Part B 2016, 19, 105–128. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Han, M.; He, F. A review of treating oily wastewater. Arab. J. Chem. 2017, 10, S1913–S1922. [Google Scholar] [CrossRef]
- Akizuki, Y.; Bressers, A.; Couse, J.; Healy, C.; Mackey, P.; Martin, D.; Messing, J.; Thomson, J.; Canu, J.; Rosa, L.F.; et al. Oil 2023: Analysis and Forecast to 2028; International Energy Agency—OECD Publishing: Paris, France, 2023. [Google Scholar]
- OILS & FATS International. Vegetable Oil Production in 2023/24 Expected to Be Up on Previous Year; OILS & FATS International: Surrey, UK, 2023. [Google Scholar]
- Arellano, P.; Tansey, K.; Balzter, H.; Boyd, D.S. Detecting the effects of hydrocarbon pollution in the Amazon forest using hyperspectral satellite images. Environ. Pollut. 2015, 205, 225–239. [Google Scholar] [CrossRef]
- Zahri, K.N.M.; Zulkharnain, A.; Sabri, S.; Gomez-Fuentes, C.; Ahmad, S.A. Research Trends of Biodegradation of Cooking Oil in Antarctica from 2001 to 2021: A Bibliometric Analysis Based on the Scopus Database. Int. J. Environ. Res. Public Health 2021, 18, 2050. [Google Scholar] [CrossRef]
- Stark, J.S. Effects of lubricant oil and diesel on macrofaunal communities in marine sediments: A five year field experiment in Antarctica. Environ. Pollut. 2022, 311, 119885. [Google Scholar] [CrossRef]
- Foo, W.H.; Koay, S.S.N.; Chia, S.R.; Chia, W.Y.; Tang, D.Y.Y.; Nomanbhay, S.; Chew, K.W. Recent advances in the conversion of waste cooking oil into value-added products: A review. Fuel 2022, 324, 124539. [Google Scholar] [CrossRef]
- Foo, W.H.; Chia, W.Y.; Tang, D.Y.Y.; Koay, S.S.N.; Lim, S.S.; Chew, K.W. The conundrum of waste cooking oil: Transforming hazard into energy. J. Hazard. Mater. 2021, 417, 126129. [Google Scholar] [CrossRef] [PubMed]
- Tamothran, A.M.; Bhubalan, K.; Anuar, S.T.; Curtis, J.M. The degradation and toxicity of commercially traded vegetable oils following spills in aquatic environment. Environ. Res. 2022, 214, 113985. [Google Scholar] [CrossRef]
- Fingas, M. Vegetable Oil Spills. In Handbook of Oil Spill Science and Technology; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014; Chapter 4; pp. 79–91. [Google Scholar] [CrossRef]
- Feng, Y.; Hou, J.; Yang, Y.; Wang, S.; Wang, D.; Cheng, T.; You, Z. Morphology of MoS2 nanosheets and its influence on water/oil interfacial tension: A molecular dynamics study. Fuel 2022, 312, 122938. [Google Scholar] [CrossRef]
- Nowrouzi, I.; Manshad, A.K.; Mohammadi, A.H. Effects of dissolved binary ionic compounds and different densities of brine on interfacial tension (IFT), wettability alteration, and contact angle in smart water and carbonated smart water injection processes in carbonate oil reservoirs. J. Mol. Liq. 2018, 254, 83–92. [Google Scholar] [CrossRef]
- Moradi, S.; Isari, A.A.; Bachari, Z.; Mahmoodi, H. Combination of a new natural surfactant and smart water injection for enhanced oil recovery in carbonate rock: Synergic impacts of active ions and natural surfactant concentration. J. Pet. Sci. Eng. 2019, 176, 1–10. [Google Scholar] [CrossRef]
- Mehrabianfar, P.; Bahraminejad, H.; Manshad, A.K. An introductory investigation of a polymeric surfactant from a new natural source in chemical enhanced oil recovery (CEOR). J. Pet. Sci. Eng. 2021, 198, 108172. [Google Scholar] [CrossRef]
- Nowrouzi, I.; Khaksar Manshad, A.; Mohammadi, A.H. Effects of MgO, γ-Al2O3, and TiO2 Nanoparticles at Low Concentrations on Interfacial Tension (IFT), Rock Wettability, and Oil Recovery by Spontaneous Imbibition in the Process of Smart Nanofluid Injection into Carbonate Reservoirs. ACS Omega 2022, 7, 22161–22172. [Google Scholar] [CrossRef]
- Horstmann, R.; Hecht, L.; Kloth, S.; Vogel, M. Structural and Dynamical Properties of Liquids in Confinements: A Review of Molecular Dynamics Simulation Studies. Langmuir 2022, 38, 6506–6522. [Google Scholar] [CrossRef] [PubMed]
- Krott, L.B.; Gavazzoni, C.; Bordin, J.R. Anomalous diffusion and diffusion anomaly in confined Janus dumbbells. J. Chem. Phys. 2016, 145, 244906. [Google Scholar] [CrossRef] [PubMed]
- Bordin, J.R.; Krott, L.B. Confinement effects on the properties of Janus dimers. Phys. Chem. Chem. Phys. 2016, 18, 28740–28746. [Google Scholar] [CrossRef] [PubMed]
- Bordin, J.R.; Krott, L.B. How Competitive Interactions Affect the Self-Assembly of Confined Janus Dumbbells. J. Phys. Chem. B 2017, 121, 4308–4317. [Google Scholar] [CrossRef]
- Hoang, A.T.; Nguyen, X.P.; Duong, X.Q.; Huynh, T.T. Sorbent-based devices for the removal of spilled oil from water: A review. Environ. Sci. Pollut. Res. 2021, 28, 28876–28910. [Google Scholar] [CrossRef]
- Lusweti, E.; Kanda, E.K.; Obando, J.; Makokha, M. Effects of oil exploration on surface water quality—A review. Water Pract. Technol. 2022, 17, 2171–2185. [Google Scholar] [CrossRef]
- Doshi, B.; Sillanpää, M.; Kalliola, S. A review of bio-based materials for oil spill treatment. Water Res. 2018, 135, 262–277. [Google Scholar] [CrossRef]
- Kalla, S. Use of membrane distillation for oily wastewater treatment—A review. J. Environ. Chem. Eng. 2021, 9, 104641. [Google Scholar] [CrossRef]
- Leão, M.B.; Bordin, J.R.; de Matos, C.F. Specific Surface Area Versus Adsorptive Capacity: An Application View of 3D Graphene-Based Materials for the Removal of Emerging Water Pollutants. Water Air Soil Pollut. 2023, 234, 136. [Google Scholar] [CrossRef]
- Bordin, J.R.; Ferreira de Matos Jauris, C.; Côrtes, P.R.B.; Araújo, W.S.; Moreira, L.S.; Pereira dos Santos, A.; Bitencourt Leão, M.; Moraes, E.E.; Piotrowski, M.J.; Köhler, M.H. Computational condensed matter science contributions to addressing water emerging contaminant pollution: A comprehensive review. J. Phys. Condens. Matter 2025, 37, 113004. [Google Scholar] [CrossRef]
- Gong, J.; Xiang, B.; Sun, Y.; Li, J. Janus smart materials with asymmetrical wettability for on-demand oil/water separation: A comprehensive review. J. Mater. Chem. A 2023, 11, 25093–25114. [Google Scholar] [CrossRef]
- Paiva, F.L.; Secchi, A.R.; Calado, V.; Maia, J.; Khani, S. Slip and momentum transfer mechanisms mediated by Janus rods at polymer interfaces. Soft Matter 2020, 16, 6662–6672. [Google Scholar] [CrossRef] [PubMed]
- Hossain, M.T.; Gates, I.D.; Natale, G. Dynamics of Brownian Janus rods at a liquid–liquid interface. Phys. Fluids 2022, 34, 012117. [Google Scholar] [CrossRef]
- Naidu, K.C.B.; Kumar, N.S.; Banerjee, P.; Reddy, B.V.S. A review on the origin of nanofibers/nanorods structures and applications. J. Mater. Sci. Mater. Med. 2021, 32, 68. [Google Scholar] [CrossRef]
- Rafael Bordin, J. Distinct self-assembly aggregation patters of nanorods with decorated ends: A simple model study. Fluid Phase Equilibria 2019, 499, 112251. [Google Scholar] [CrossRef]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. A review on the mechanics of nanostructures. Int. J. Eng. Sci. 2018, 133, 231–263. [Google Scholar] [CrossRef]
- Gupta, D.; Varghese, B.S.; Meera Suresh, C.P.; Gupta, T.K. Nanoarchitectonics: Functional nanomaterials and nanostructures—A review. J. Nanoparticle Res. 2022, 24, 196. [Google Scholar] [CrossRef]
- Bai, L.; Wang, X.; Sun, X.; Li, J.; Huang, L.; Sun, H.; Gao, X. Enhanced superhydrophobicity of electrospun carbon nanofiber membranes by hydrothermal growth of ZnO nanorods for oil–water separation. Arab. J. Chem. 2023, 16, 104523. [Google Scholar] [CrossRef]
- Yan, F.; Tong, L.; Qin, H.; Guo, W.; Liu, J.; Xie, W.; Gao, P.; Xiao, H. Preparation of superhydrophilic-underwater superoleophobic silica nanorods modified fiber membrane for efficient oil-in-water emulsion separation. Ceram. Int. 2023, 49, 23317–23325. [Google Scholar] [CrossRef]
- Yin, X.; Yu, S.; Wang, L.; Wang, J.; Wang, B.; Li, H.; Chen, Z. Dual-functional underliquid superhydrophobic and superoleophobic stainless steel mesh decorated with Ni3S2 nanorods for continuous oil/water separation. Surf. Coatings Technol. 2022, 434, 128177. [Google Scholar] [CrossRef]
- Zhao, X.; Cheng, L.; Jia, N.; Wang, R.; Liu, L.; Gao, C. Polyphenol-metal manipulated nanohybridization of CNT membranes with FeOOH nanorods for high-flux, antifouling and self-cleaning oil/water separation. J. Membr. Sci. 2020, 600, 117857. [Google Scholar] [CrossRef]
- Yin, X.; Yu, S.; Wang, L.; Li, H.; Xiong, W. Design and preparation of superhydrophobic NiS nanorods on Ni mesh for oil-water separation. Sep. Purif. Technol. 2020, 234, 116126. [Google Scholar] [CrossRef]
- Ahmed, F.U.; Upadhaya, D.; Dhar Purkayastha, D.; Krishna, M.G. Stable hydrophilic and underwater superoleophobic ZnO nanorod decorated nanofibrous membrane and its application in wastewater treatment. J. Membr. Sci. 2022, 659, 120803. [Google Scholar] [CrossRef]
- He, H.; Li, Z.; Ouyang, L.; Liang, Y.; Yuan, S. Hierarchical WO3@Cu(OH)2 nanorod arrays grown on copper mesh with superwetting and self-cleaning properties for high-performance oil/water separation. J. Alloy. Compd. 2021, 855, 157421. [Google Scholar] [CrossRef]
- Español, P.; Warren, P.B. Perspective: Dissipative particle dynamics. J. Chem. Phys. 2017, 146, 150901. [Google Scholar] [CrossRef]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics. Europhys. Lett. 1992, 19, 155. [Google Scholar] [CrossRef]
- Español, P.; Warren, P. Statistical Mechanics of Dissipative Particle Dynamics. Europhys. Lett. 1995, 30, 191. [Google Scholar] [CrossRef]
- Limbach, H.; Arnold, A.; Mann, B.; Holm, C. ESPResSo—An extensible simulation package for research on soft matter systems. Comput. Phys. Commun. 2006, 174, 704–727. [Google Scholar] [CrossRef]
- Arnold, A.; Lenz, O.; Kesselheim, S.; Weeber, R.; Fahrenberger, F.; Roehm, D.; Košovan, P.; Holm, C. ESPResSo 3.1: Molecular Dynamics Software for Coarse-Grained Models. In Proceedings of the Meshfree Methods for Partial Differential Equations VI; Griebel, M., Schweitzer, M.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–23. [Google Scholar]
- Moeendarbary, E.; Ng, T.; Zangeneh, M. Dissipative particle dynamics: Introduction, methodology and complex fluid applications—A review. Int. J. Appl. Mech. 2009, 1, 737–763. [Google Scholar] [CrossRef]
- Khedr, A.; Striolo, A. DPD Parameters Estimation for Simultaneously Simulating Water–Oil Interfaces and Aqueous Nonionic Surfactants. J. Chem. Theory Comput. 2018, 14, 6460–6471. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Liu, X.; Liang, C.; Wang, Z.; Jia, Y. Dissipative particle dynamics to study asphaltenes and surfactants interactions at the oil–water interface. J. Mol. Liq. 2023, 381, 121802. [Google Scholar] [CrossRef]
- Parsons, J.D. Nematic ordering in a system of rods. Phys. Rev. A 1979, 19, 1225–1230. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira dos Santos, A.; Ferreira de Matos Jauris, C.; Bordin, J.R. Interfacial Behavior of Janus Nanorods: A Dissipative Particle Dynamics (DPD) Study on Water–Oil Systems and Nanoconfinement. Water 2025, 17, 1128. https://doi.org/10.3390/w17081128
Pereira dos Santos A, Ferreira de Matos Jauris C, Bordin JR. Interfacial Behavior of Janus Nanorods: A Dissipative Particle Dynamics (DPD) Study on Water–Oil Systems and Nanoconfinement. Water. 2025; 17(8):1128. https://doi.org/10.3390/w17081128
Chicago/Turabian StylePereira dos Santos, Alexsandra, Carolina Ferreira de Matos Jauris, and José Rafael Bordin. 2025. "Interfacial Behavior of Janus Nanorods: A Dissipative Particle Dynamics (DPD) Study on Water–Oil Systems and Nanoconfinement" Water 17, no. 8: 1128. https://doi.org/10.3390/w17081128
APA StylePereira dos Santos, A., Ferreira de Matos Jauris, C., & Bordin, J. R. (2025). Interfacial Behavior of Janus Nanorods: A Dissipative Particle Dynamics (DPD) Study on Water–Oil Systems and Nanoconfinement. Water, 17(8), 1128. https://doi.org/10.3390/w17081128





