Accumulation Patterns and Numerical Simulation of Nitrate-N in Layered Soils of the Vadose Zone in Cotton Fields
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview of the Test Area
2.2. Test Design
2.2.1. Field Test Layout Scheme
2.2.2. Indoor Test Items and Methods
3. Establishment of HYDRUS-1D Model
3.1. Model Description
3.2. Basic Equation
3.2.1. Soil Water Movement Equation
3.2.2. Basic Equation of Soil Solute Transport
3.3. Initial and Boundary Conditions
3.3.1. Initial and Boundary Conditions of Soil Water Movement
3.3.2. Initial and Boundary Conditions of Soil Solute Transport
3.4. Model Parameters
3.5. Unit Division and Time Step
4. Results and Analysis
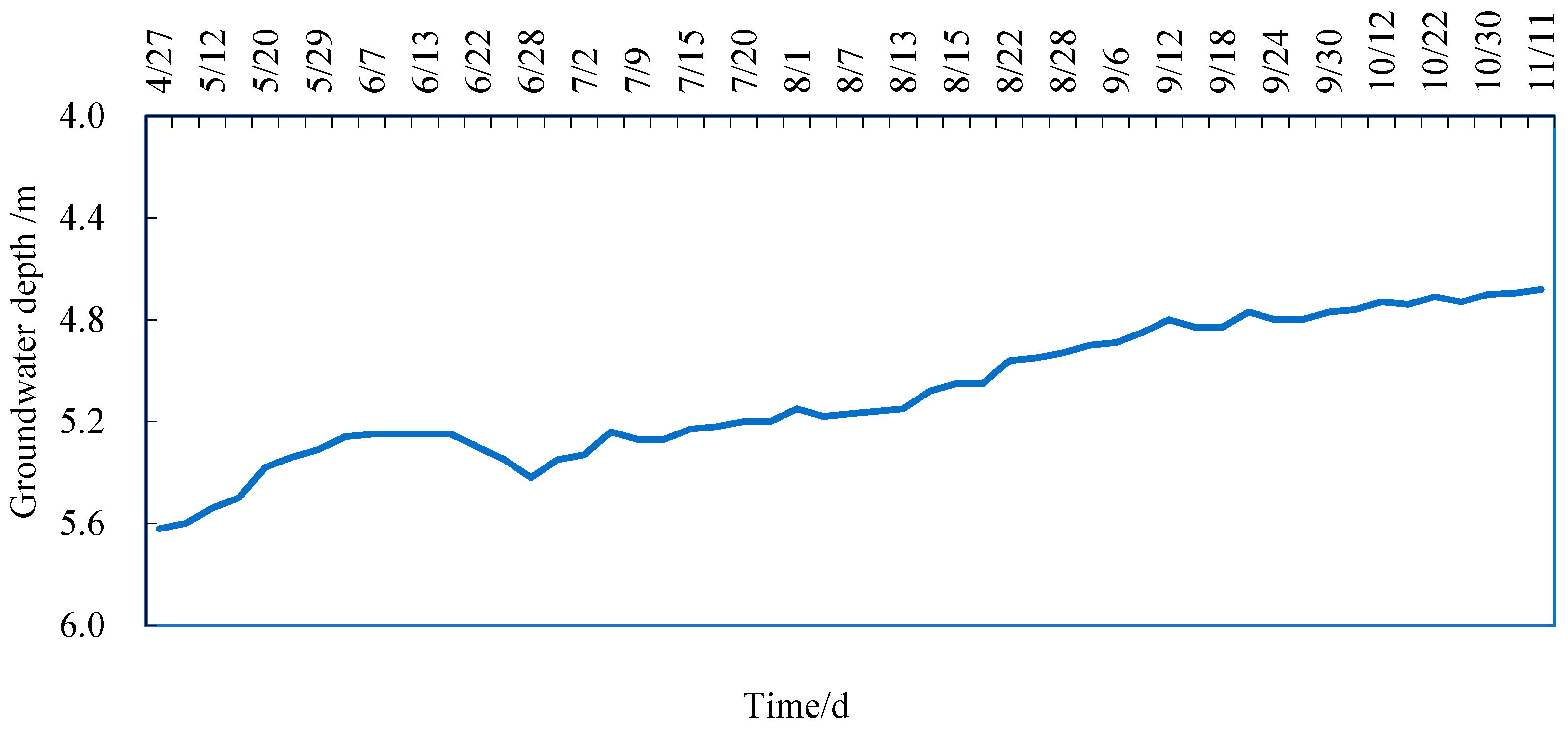
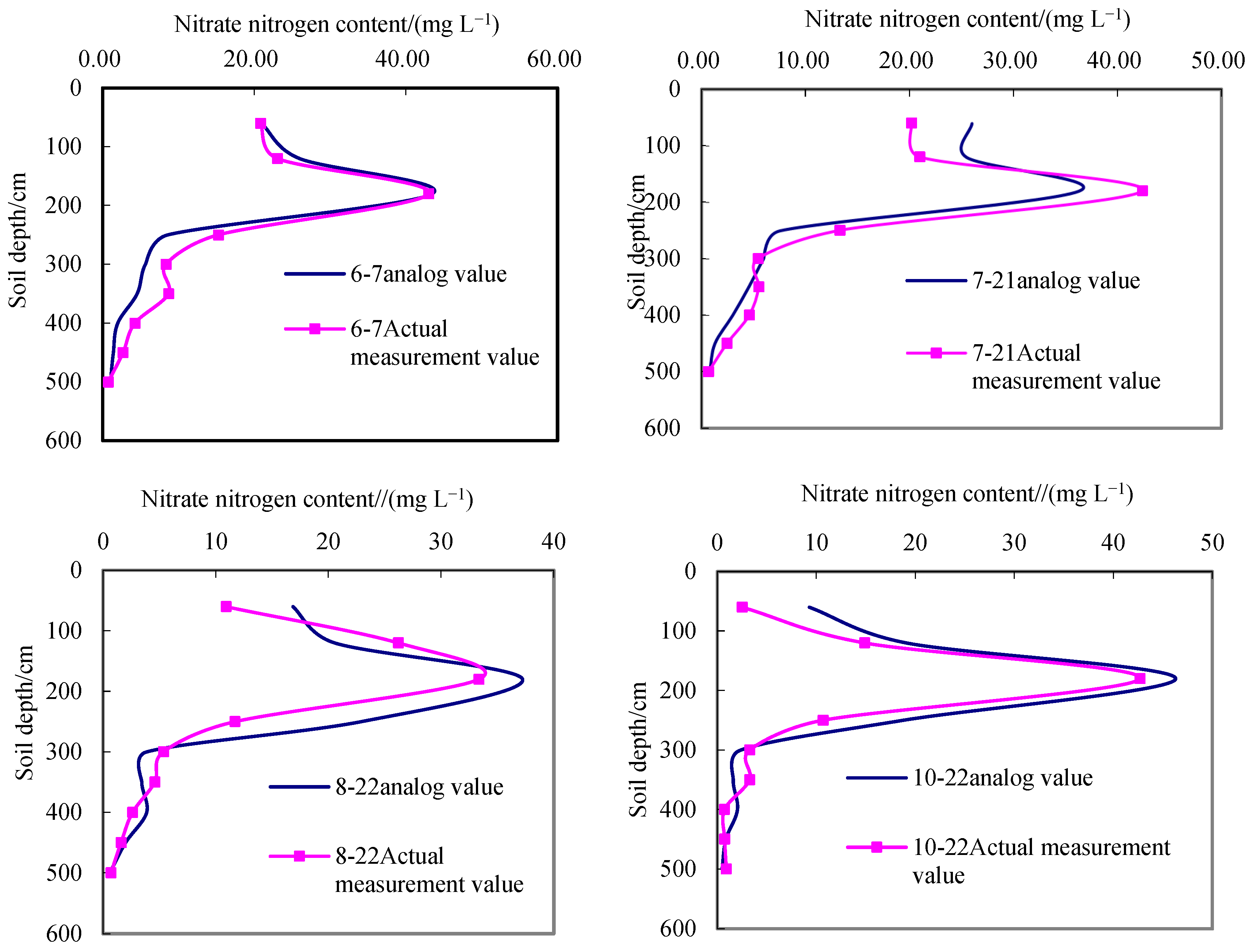
4.1. Model Validation
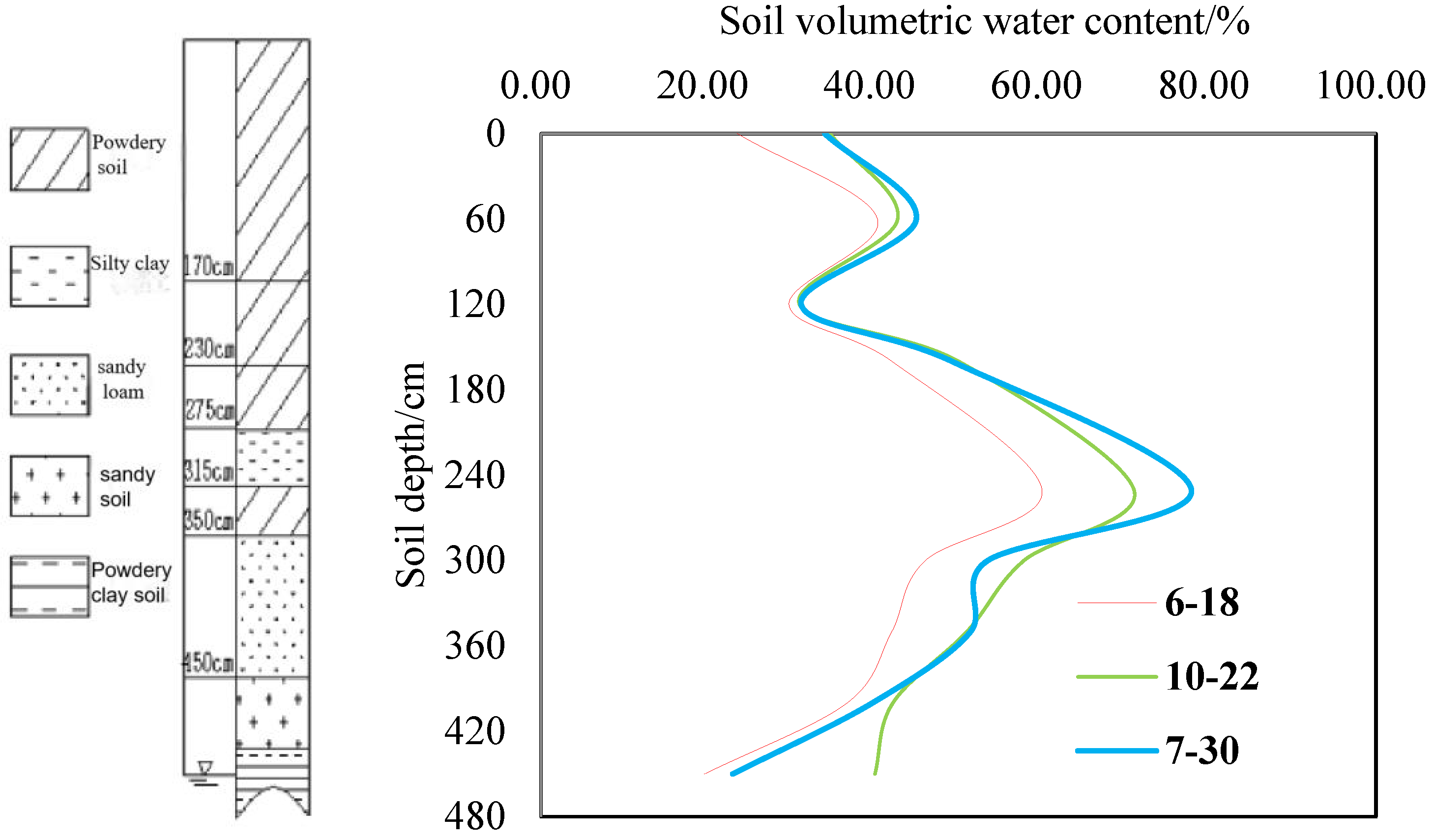
4.2. Basic Physicochemical Properties of Soil in the Vadose Zone
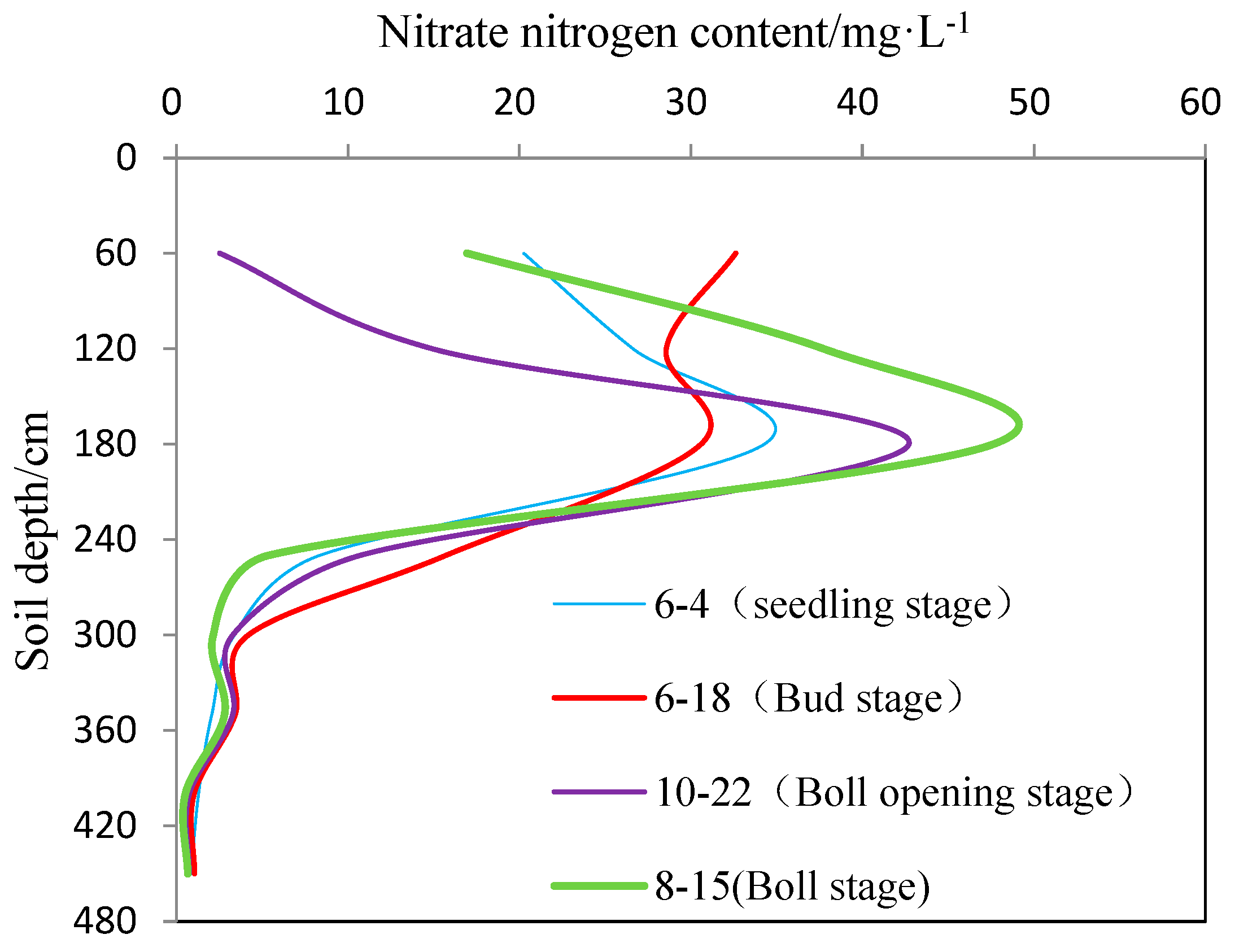
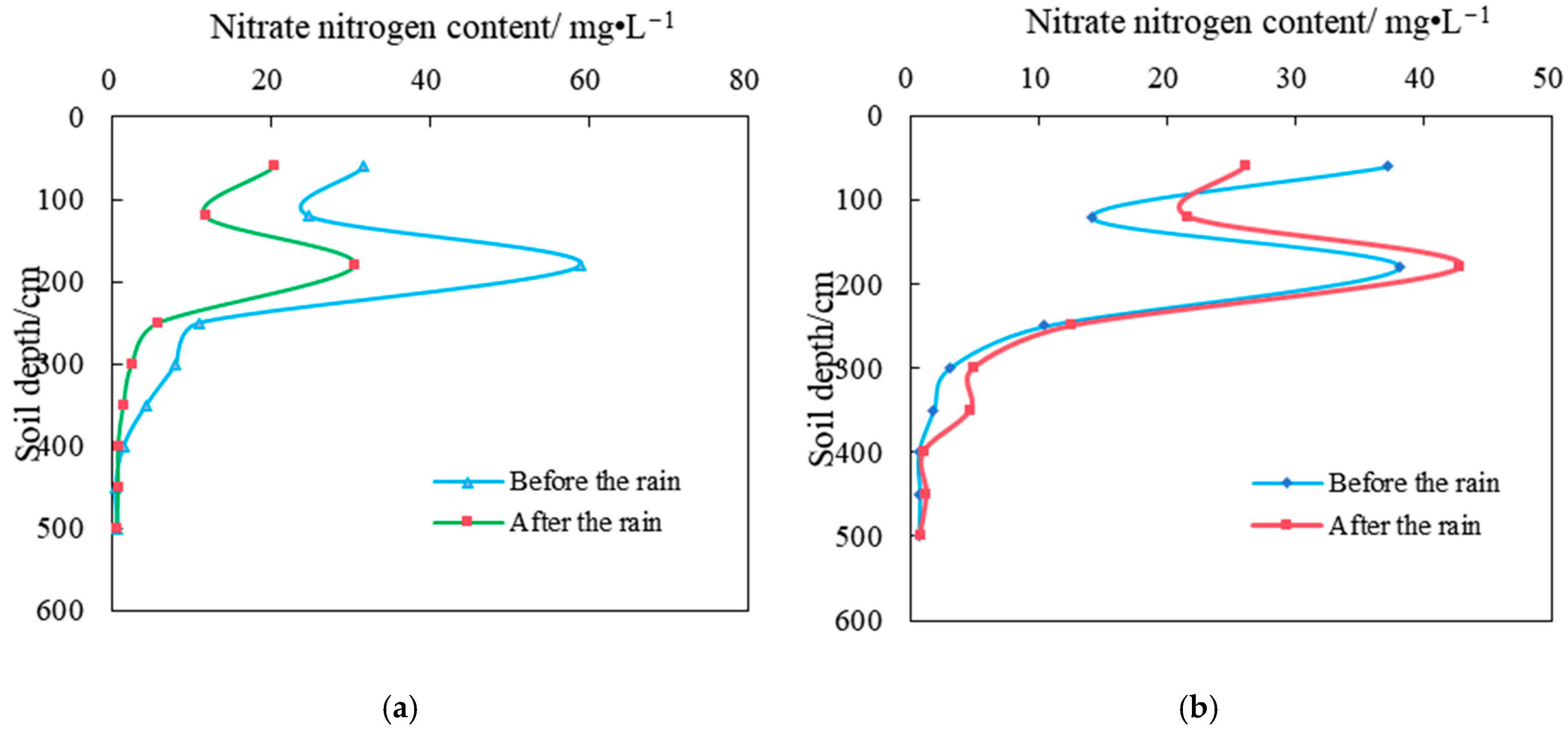
4.3. Accumulation and Migration Characteristics of Nitrate-N in Stratified Soil Profiles
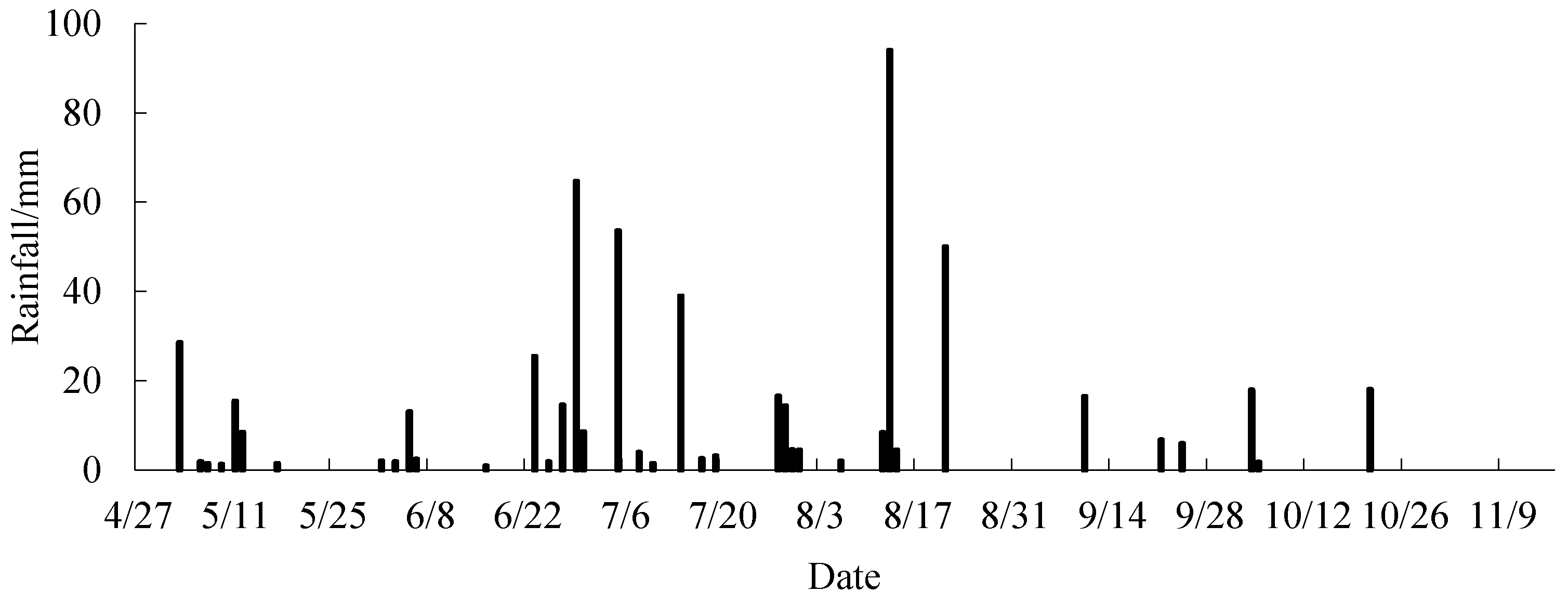
4.4. Vertical Distribution Pattern of Nitrate-N in the Soil Vadose Zone Under the Influence of Short-Term Precipitation
4.5. Accumulation Characteristics of Nitrate-N Below the Cotton Root System Layer
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ascott, M.J.; Gooddy, D.C.; Wang, L.; Stuart, M.E.; Lewis, M.A.; Ward, R.S.; Binley, A.M. Global patterns of nitrate storage in the vadose zone. Nat. Commun. 2017, 8, 153–226. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Gu, B.; Schlesinger, W.H.; Ju, X. Significant accumulation of nitrate in Chinese semi-humid croplands. Sci. Rep. 2016, 6, 25088. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.H.; Tang, L. Progress in Research on Influencing Factors and Control Measures of Nitrate-Nitrogen Leaching Losses in Farmland. J. North China Univ. Water Conserv. Electr. Power 2020, 41, 58–64. [Google Scholar]
- Lu, B.; Zhang, X.P.; Liang, A.Z.; Jia, S.X.; Chen, X.W.; Chen, S.L.; Liu, S.Y. Overview of N2O Emission Processes and Nitrate Leaching Losses in Agricultural Soils. Soil Crop Sci. 2015, 4, 168–175. [Google Scholar]
- Zhang, Q.Z.; Chen, X.; Shen, S.M. Progress in research on nitrate accumulation and leaching in farmland soil. Chin. J. Appl. Ecol. 2002, 13, 233–238. [Google Scholar]
- Yuan, X.M.; Tong, Y.A.; Yang, X.Y.; Li, X.L.; Zhang, F.S. Impact of irrigation and precipitation on soil NO3−-N accumulation. J. Soil Water Conserv. 2000, 14, 71–74. [Google Scholar]
- Zhang, X.J.; Zhao, G.F.; Zhu, W.Q.; Chen, X.Q.; Wang, L.M.; Wu, L.S.; Hu, C.X. Advances in research on nitrogen leaching loss in vegetable field soil and its control measures. Ecol. Environ. 2004, 13, 105–108. [Google Scholar]
- Zhang, X.K.; BaiJ, Y.; Yan, H.X. Impact of irrigation volume and nitrogen application rate on nitrate transport in different types of soils. Water-Sav. Irrig. 2020, 2, 83–87. [Google Scholar]
- He, Y.P.; Zhang, Z.Y.; Xu, J.Z.; Yang, S.H.; Hong, D.L. Control of groundwater level to reduce nitrogen leaching loss in water-saving irrigated paddy fields. J. Chin. Soc. Agric. Eng. 2014, 30, 121–127. [Google Scholar]
- Liu, M.; Min, L.; Wu, L.; Pei, H.; Shen, Y. Evaluating nitrate transport and accumulation in the deep vadose zone of the intensive agricultural region, North China Plain. Sci. Total Environ. 2022, 825, 153894. [Google Scholar] [CrossRef]
- de Graaf, I.E.; Gleeson, T.; Van Beek, L.P.H.; Sutanudjaja, E.H.; Bierkens, M.F. Environmental flow limits to global groundwater pumping. Nature 2019, 574, 90–94. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wu, G.; Ma, B.; Wu, T.; Wang, X.; Wu, Q. Revealing climatic and groundwater impacts on the spatiotemporal variations in vegetation coverage in marine sedimentary basins of the North China Plain, China. Sci. Rep. 2024, 14, 10085. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Shen, Y. Estimation of agricultural water consumption from meteorological and yield data: A case study of Hebei, North China. PLoS ONE 2013, 8, e58685. [Google Scholar] [CrossRef]
- Han, M.; Zhao, C.; Šimůnek, J.; Feng, G. Evaluating the impact of groundwater on cotton growth and root zone water balance using Hydrus-1D coupled with a crop growth model. Agric. Water Manag. 2015, 160, 64–75. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Twarakavi, N.K.C.; Šimůnek, J.; Seo, S. Evaluating interactions between groundwater and vadose zone using the HYDRUS-based flow package for MODFLOW. Vadose Zone J. 2008, 7, 757–768. [Google Scholar] [CrossRef]
- Radcliffde, D.E.; Simunek, J. Soil Physics with HYDRUS: Modeling and Applications; CRC Press: Bocs Raton, FL, USA, 2010. [Google Scholar]
- Zhang, S.; Li, B.; Wang, X.H.; Sun, N.N. Study on solute transport in Va-dose zone based on Hydrus-1D model. Arid Environ. Monit. 2021, 35, 97–102. [Google Scholar]
- Fan, Y.W.; Huang, N.; Ma, X.Y.; Bi, G.Q.; Zhao, W.J. Simulation of infiltration characteristics in soil with sand interlayer using HYDRUS-1D. Soils 2016, 48, 193–200. [Google Scholar]
- Li, B.B.; Wang, Y.Q.; Li, Z. Applicability of HYDRUS-1D model for simulating soil moisture in deep profiles of Weibei dryland. Chin. J. Appl. Ecol. 2019, 30, 398–404. [Google Scholar]
- Jin, Y.; Xia, J.; Zhang, Z. Comparative analysis on the treatment of ammonia nitrogen in industrial wastewater. Ind. Water Treat. 2013, 33, 5–10. (In Chinese) [Google Scholar]
- Simunek, J.; Van Genuchten, M.T.; Sejna, M. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media; University of California Riverside: Riverside, CA, USA, 2005; Volume 3, pp. 1–240. [Google Scholar]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Development and applications of the HYDRUS and STANMOD software packages and related codes. Vadose Zone J. 2008, 7, 587–600. [Google Scholar] [CrossRef]
- Shouse, P.J.; Ayars, J.E.; Šimůnek, J. Simulating root water uptake from a shallow saline groundwater resource. Agric. Water Manag. 2011, 98, 784–790. [Google Scholar] [CrossRef]
- Šimůnek, J.; Angulo-Jaramillo, R.; Schaap, M.G.; Vandervaere, J.-P.; Van Genuchten, M.T. Using an inverse method to estimate the hydraulic properties of crusted soils from tension-disc infiltrometer data. Geoderma 1998, 86, 61–81. [Google Scholar] [CrossRef]
- Meng, J.L. Simulation Study on Water-Salt and Drainage Systems. Master’s Thesis, Xinjiang Agricultural University, Ürümqi, China, 2004; pp. 34–37. [Google Scholar]
- Myrold, D.D.; Tiedje, J.M. Simultaneous estimation of several nitrogen cycle rates using 15’N: Theory and application. Soil Biol. Bioehem. 1956, 15, 559–568. [Google Scholar]
- Stenger, R.; Priesack, E.; Beese, F. Rates of nitrogen mineralization in disturbed and undlsturbed soils. Plant Soil 1995, 171, 323–332. [Google Scholar] [CrossRef]
- Kersebaum, K.C.; Richter, J. Modelling nitrogen dynamics in a Plant-soil system with a simple model for advisory purposes. Nutr. Cycl. Agroecosyst. 1991, 27, 273–281. [Google Scholar]
- Hu, K.L.; Li, B.G.; Chen, D.L.; White, R.E. Spatial variability of soil moisture and salinity in farmland and their collaborative Kriging estimation. Adv. Water Sci. 2001, 12, 460–466. [Google Scholar]
- Hu, K.L.; Li, B.G.; Lin, Q.M.; Li, G.T.; Chen, D.L. Spatial variability characteristics of soil nutrients in farmland. J. Chin. Soc. Agric. Eng. 1999, 15, 33–38. [Google Scholar]
- Cao, Q.H.; Gong, Y.S. Simulation and analysis of water and nitrogen transport characteristics in winter wheat fields using the Hydrus-Id model. J. Plant Nutr. Fertil. Sci. 2003, 9, 139–145. [Google Scholar]
- Jones, C.A. CERES-Maize: A Simulation Model of Maize Growth and Development; TEXAS A and M university Press: College Station, TX, USA, 1986; pp. 79–90. [Google Scholar]
- Chiew, F.H.S.; Kamaladasa, N.N.; Malano, H.M.; McMahon, T.A. Penman-Monteith, FAO-24 reference crop evapotranspiration and class-A pan data in Australia. Agric. Water Manag. 1995, 28, 9–21. [Google Scholar] [CrossRef]
- Wang, G.S.; Shi, H.B.; Li, X.Y.; Yan, J.W.; Miao, Q.F.; Chen, N.; Wang, W.G. Simulation and evaluation of water and salt transport in desert oases based on the HYDRUS-1D model. J. Chin. Soc. Agric. Eng. 2021, 37, 87–98. [Google Scholar]
- Ma, Y.; Feng, S.; Song, X. Evaluation of optimal irrigation scheduling and groundwater recharge at representative sites in the North China Plain with SWAP model and field experiments. Comput. Electron. Agric. 2015, 116, 125–136. [Google Scholar] [CrossRef]
- Wang, W.; Lu, Y. Analysis of the mean absolute error (MAE)and the root mean square error (RMSE) in assessing rounding model. IOP Conf. Ser. Mater. Sci. Eng. 2018, 324, 012049. [Google Scholar] [CrossRef]
- Liang, H.Y.; Wang, S.Q.; Wei, S.C. Distribution and accumulation patterns of nitrate-N in typical thick vadose zones of the piedmont plain in North China. Soil 2017, 49, 1179–1186. [Google Scholar]
- Zhu, Z.; Chen, D. Nitrogen fertilizer use in China—Contributions to food production, impacts on the environment and best management strategies. Nutr. Cycl. Agroecosyst. 2002, 63, 117–127. [Google Scholar] [CrossRef]



| Soil Depth/cm | Sand Content/% | Silt Content/% | Clay Content/% | Soil Texture |
|---|---|---|---|---|
| 0–170 | 12 | 66 | 22 | Silty soil |
| 170–230 | 35 | 56 | 9 | Silty soil |
| 230–250 | 7 | 78 | 15 | Silty soil |
| 250–315 | 1 | 55 | 44 | Silty clay |
| 315–350 | 14 | 67 | 19 | Silty clay |
| 350–450 | 65 | 28 | 7 | Sandy loam |
| 450–500 | 86 | 10 | 4 | Sandy soil |
| 500–540 | 6 | 60 | 34 | Silty clayey soil |
| 540–590 | 3 | 68 | 29 | Silty clayey soil |
| 590–600 | 35 | 56 | 10 | Silty clay |
| Soil Layer/cm | Qr (10−2) | Qs (10−2) | a (10−2) | n | Ks |
|---|---|---|---|---|---|
| 0–170 | 7.56 | 44.88 | 0.55 | 1.62 | 10.26 |
| 170–230 | 4.52 | 41.50 | 0.52 | 1.65 | 42.00 |
| 230–275 | 6.81 | 50.33 | 0.59 | 1.65 | 10.15 |
| 275–315 | 10.40 | 55.25 | 1.25 | 1.40 | 2.55 |
| 315–350 | 7.04 | 44.35 | 0.50 | 1.65 | 10.23 |
| 350–450 | 3.62 | 39.00 | 3.16 | 1.41 | 45.02 |
| 450–500 | 4.33 | 38.38 | 3.94 | 2.08 | 119.22 |
| 500–540 | 9.17 | 48.07 | 0.87 | 1.50 | 10.08 |
| Soil Layer/cm | /g·cm−3 | DW/cm2·d−1 | D | /10−2mg·kg−1·d−1 | /10−2 d−1 | /10−2 d−1 |
|---|---|---|---|---|---|---|
| 0–170 | 1.40 | 2.14 | 4.50 | 100.00 | 2.00 | 0.50 |
| 170–230 | 1.37 | 2.14 | 4.00 | 50.00 | 1.00 | 0.30 |
| 230–275 | 1.50 | 2.14 | 3.00 | 0.05 | 0.50 | 0.50 |
| 275–315 | 1.60 | 2.14 | 2.70 | 0.03 | 0.40 | 1.00 |
| 315–350 | 1.50 | 2.14 | 3.50 | 0.03 | 0.40 | 1.00 |
| 350–450 | 1.33 | 2.14 | 4.50 | 0.02 | 0.20 | 0.80 |
| 450–500 | 1.20 | 2.14 | 5.20 | 0.02 | 0.20 | 0.80 |
| 500–540 | 1.50 | 2.14 | 3.60 | 0.01 | 0.10 | 0.60 |
| Date Calibration | Evaluation | ||
|---|---|---|---|
| R2 | RMSE | MAE | |
| 6.7 | 0.73 | 0.05 | 0.04 |
| 6.30 | 0.72 | 0.05 | 0.05 |
| 7.30 | 0.71 | 0.05 | 0.04 |
| 8.31 | 0.86 | 0.06 | 0.05 |
| Date Calibration | Evaluation | ||
|---|---|---|---|
| R2 | RMSE | MAE | |
| 7 June | 0.97 | 3.10 | 2.30 |
| 21 July | 0.91 | 3.80 | 3.00 |
| 22 August | 0.85 | 4.60 | 3.00 |
| 22 October | 0.95 | 4.10 | 3.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Yang, S.; Jiao, X.; Jiang, Z. Accumulation Patterns and Numerical Simulation of Nitrate-N in Layered Soils of the Vadose Zone in Cotton Fields. Water 2025, 17, 1117. https://doi.org/10.3390/w17081117
Li F, Yang S, Jiao X, Jiang Z. Accumulation Patterns and Numerical Simulation of Nitrate-N in Layered Soils of the Vadose Zone in Cotton Fields. Water. 2025; 17(8):1117. https://doi.org/10.3390/w17081117
Chicago/Turabian StyleLi, Feng, Shihong Yang, Xiyun Jiao, and Zewei Jiang. 2025. "Accumulation Patterns and Numerical Simulation of Nitrate-N in Layered Soils of the Vadose Zone in Cotton Fields" Water 17, no. 8: 1117. https://doi.org/10.3390/w17081117
APA StyleLi, F., Yang, S., Jiao, X., & Jiang, Z. (2025). Accumulation Patterns and Numerical Simulation of Nitrate-N in Layered Soils of the Vadose Zone in Cotton Fields. Water, 17(8), 1117. https://doi.org/10.3390/w17081117








