A Sediment Process Simulation on the Steep Area of the Upper Yangtze River Basin Using a Hybrid Distributed Soil Erosion Model
Abstract
1. Introduction
2. Study Area and Dataset
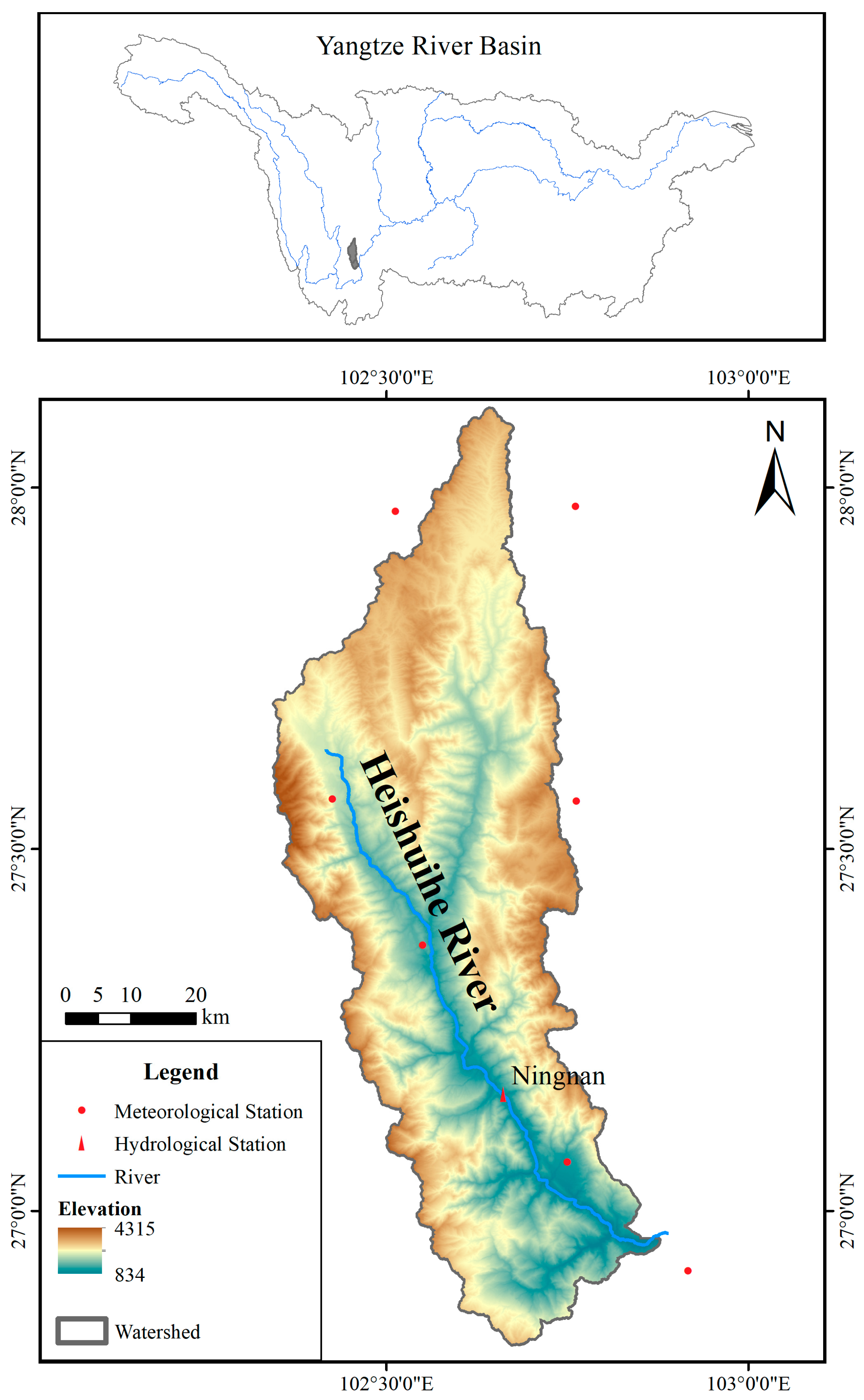
2.1. Study Area
2.2. Dataset
3. Methodology
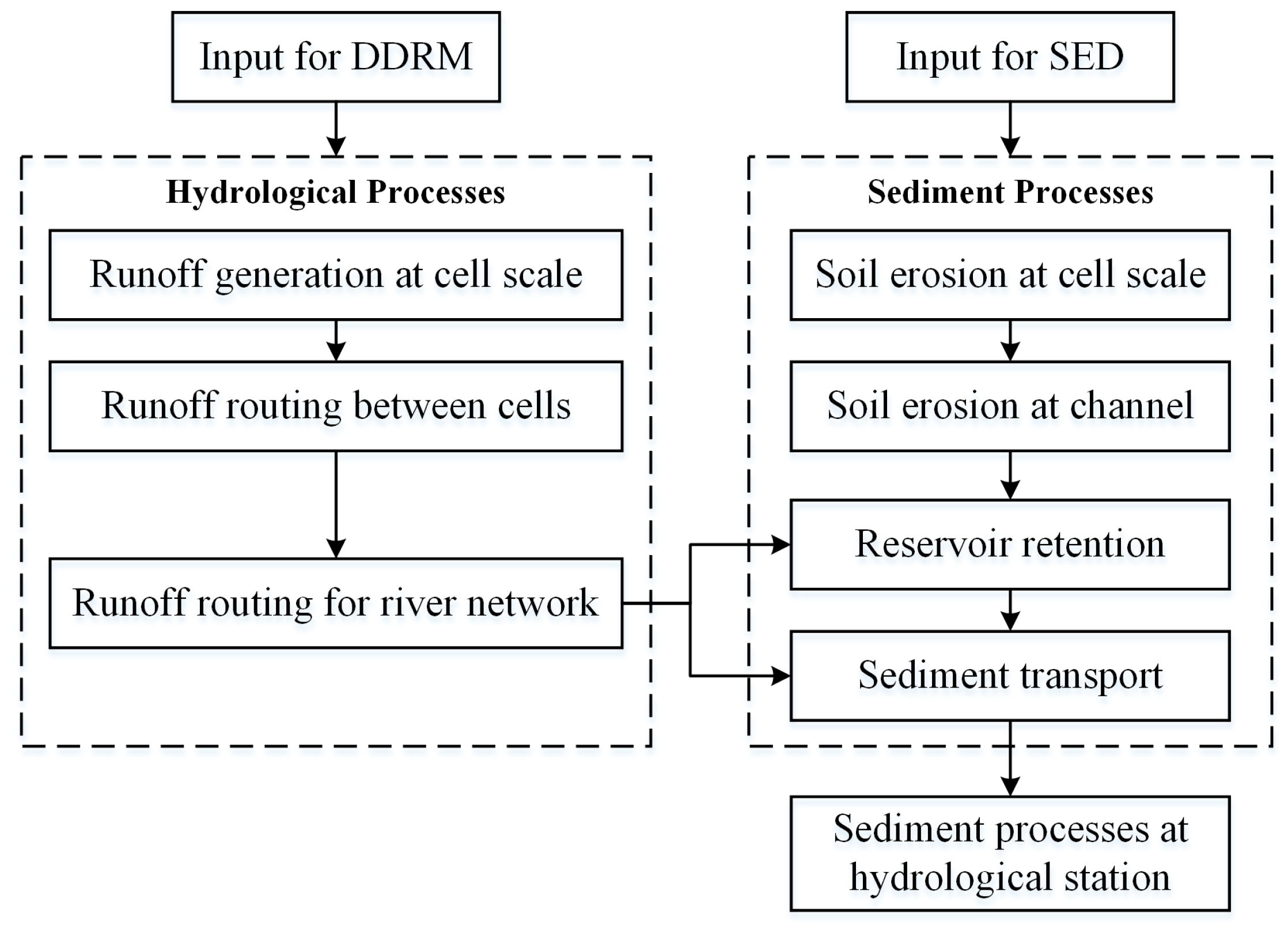
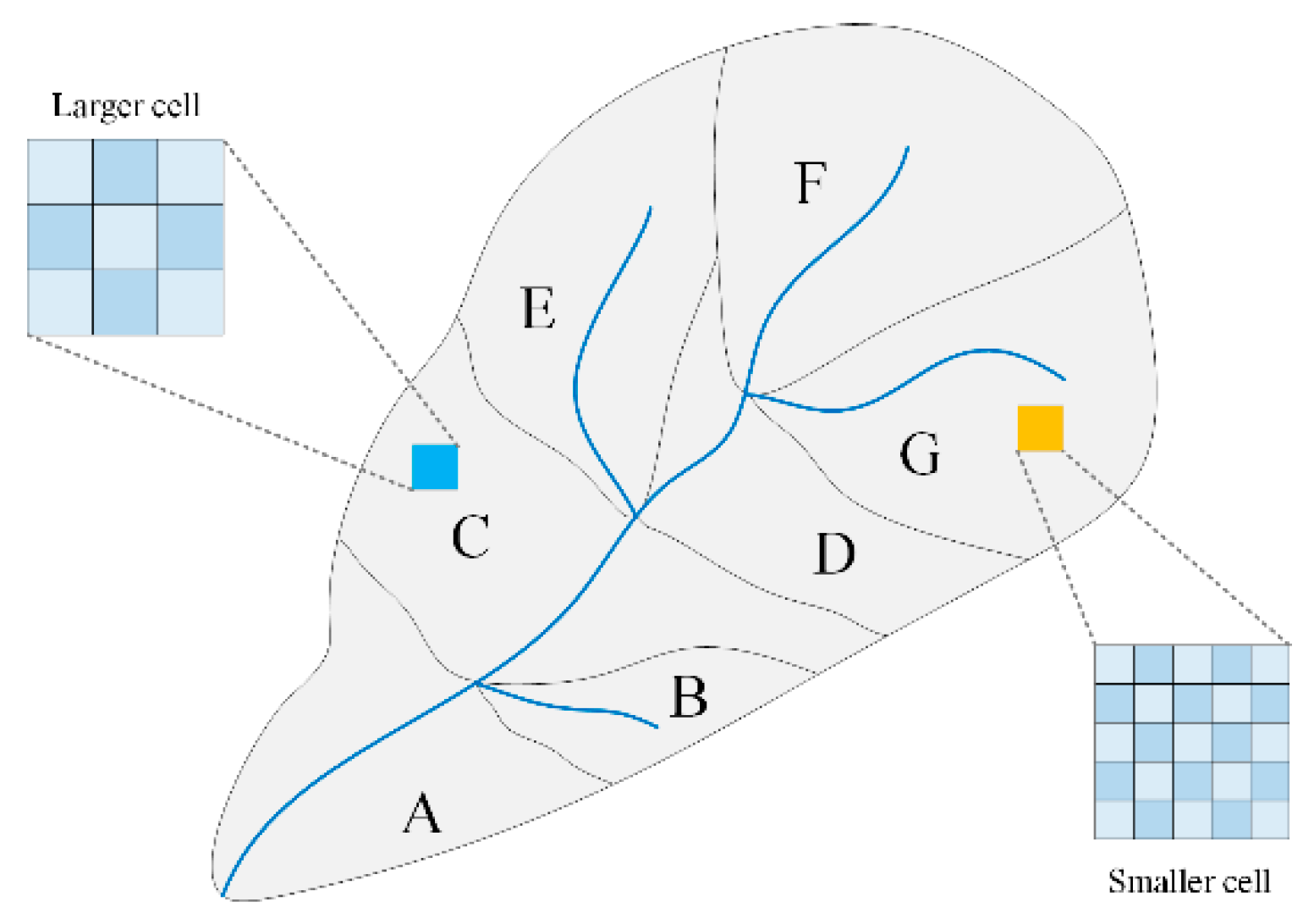
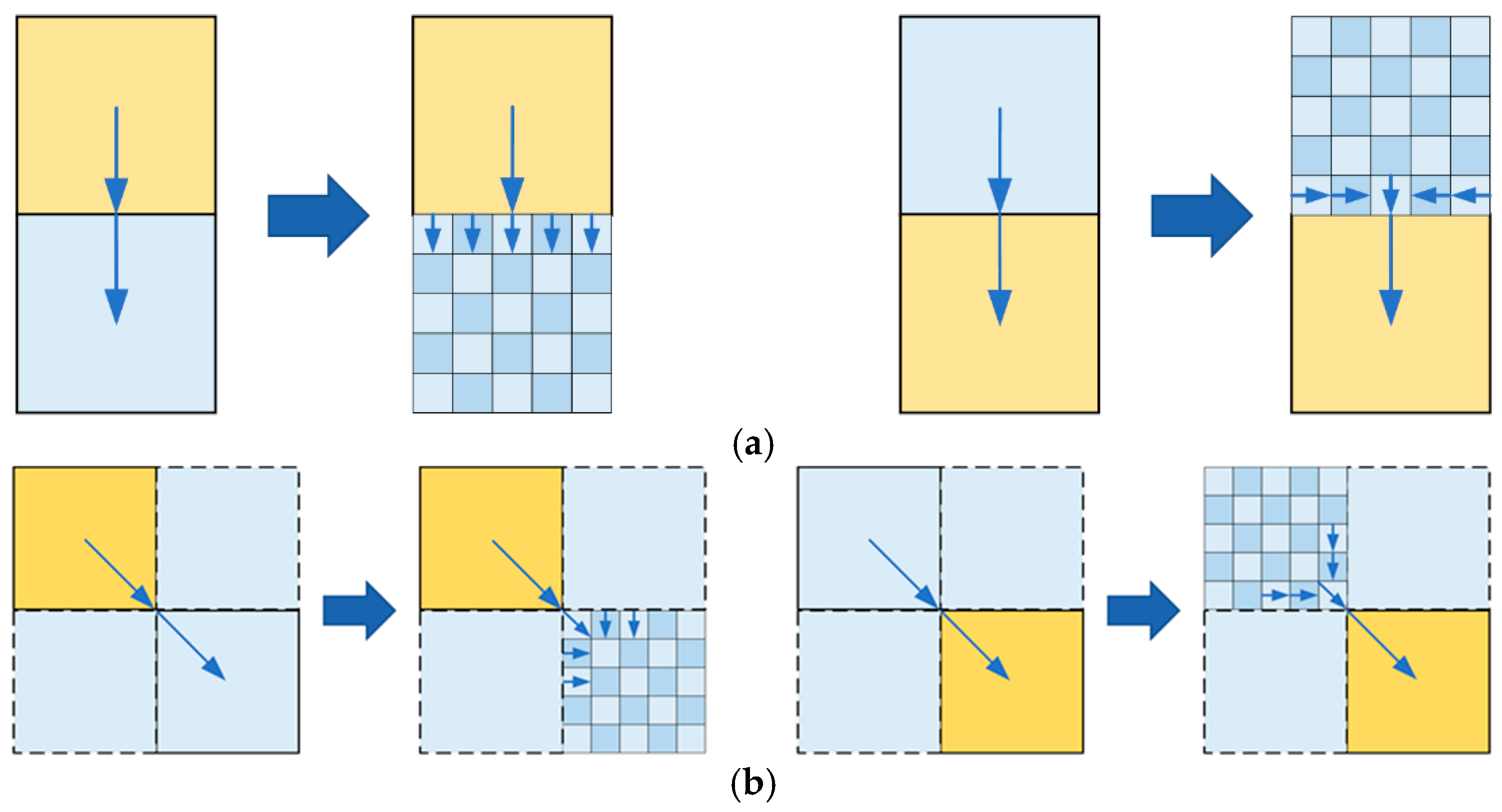
3.1. The DEM-Based Distributed Rainfall-Runoff Model
3.2. Model Modification for Sediment Simulation
3.2.1. Soil Erosion Calculation at Cell Scale
3.2.2. Soil Erosion and Transport Calculation at River Channel
3.2.3. Reservoir Retention
3.3. Model Setup
3.4. Model Calibration and Evaluation
4. Results
4.1. Basin Characteristics and Dataset Analysis
4.2. Model Performance of the DDRM-SED Model
4.3. Comparison of Simulation Performance from Multi-Model
5. Conclusions
- (1)
- The modified version of the DDRM model (i.e., DDRM-SED) shows a good simulation performance in terms of flow and sediment processes. The DDRM-SED model with multi-spatial resolution shows a better simulation performance than the model with constant spatial resolution.
- (2)
- A spatial discretization method for basins based on multiple spatial resolutions is proposed in this study, which is able to accurately describe topography (e.g., slope length and slope gradient) and take into account its influence on soil process simulation. However, the simulation and validation using only the data from Ningnan Station cannot reflect the spatial and temporal variations of the model.
- (3)
- The research proposes a modification of the DDRM model, showing the performance in simulating flow and sediment processes, and by applying the modified model, a better simulation of flow and sediment processes can be obtained. It provides technical support and a theoretical basis for the simulation of the water–sediment transport process. In future studies, coupling multi-source water–sediment data and sub-basin refinement measurements can enable accurate simulation and validation of basin water–sediment processes with multiple spatial resolutions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Poesen, J. Soil erosion in the Anthropocene: Research needs. Earth Surf. Process. Landf. J. Br. Geomorphol. Res. Group 2018, 43, 64–84. [Google Scholar] [CrossRef]
- Cheng, Y.; Xia, J.; Zhou, M.; Deng, S. Improved formula of sediment transport capacity and its application in the lower Yellow River. J. Hydrol. 2024, 631, 130812. [Google Scholar] [CrossRef]
- Khalid, M.A.; Ghumman, A.R.; Pasha, G.A. A Comparative Analysis of Sediment Concentration Using Artificial Intelligence and Empirical Equations. Hydrology 2024, 11, 63. [Google Scholar] [CrossRef]
- Xu, J. Erosion caused by hyperconcentrated flow on the Loess Plateau of China. Catena 1999, 36, 1–19. [Google Scholar]
- Liu, W.L.; Deng, Y.L.; Li, C.Y.; Guo, Z.Y.; Zhang, L. Progress of soil erosion forecasting modeling in the middle and upper reaches of the Yangtze River. Technol. Soil Water Conserv. 2006, 3, 29–32. [Google Scholar]
- Prajapati, P.; Meena, G.K.; Swarnkar, S.; Jha, S.K. Impact of Indira Sagar Dam on Water Discharge and Sediment Flow Regimes of the Narmada Basin. J. Hydrol. Eng. 2025, 30, 05025002. [Google Scholar] [CrossRef]
- Dong, L.; Fu, S.; Liu, B. Effects of Rock Fragment Cover on the Sediment Transport Capacity of Overland Flow. Water Resour. Res. 2025, 61, e2024WR038621. [Google Scholar] [CrossRef]
- Mostafazadeh, R.; Azizi, E. Determination of river flow and sediment regime changes in response to construction of regulating dams: An indicator-based approach. Environ. Earth Sci. 2025, 84, 36. [Google Scholar] [CrossRef]
- Chen, X.Y.; He, B.H.; Miu, C.Y.; Wu, Y. Study on Application of WEPP Model for Sloping Surface Erosion Prediction in Purple Soil. J. Soil Water Conserv. 2003, 17, 43–44, 47. [Google Scholar]
- Li, Q.X. Study on the Trend of Water and Sediment and the Model of Sediment Transport in Typical Drainage Area of Three Gorges Reservoir Area; Changjiang River Scientific Research Institute: Wuhan, China, 2018. [Google Scholar]
- Niu, Z.M.; Xie, M.S.; Sun, G.; Mcnulty, S.G. Applying ANSWERS2000 to Simulate Soil Erosion Process on Two Watersheds of Three Gorges Area. J. Soil Water Conserv. 2001, 15, 57–60. [Google Scholar]
- Wang, H.; Cai, Q.G.; Zhu, Y.D. Evaluation of the EUROSEM Model for predicting water erosion on steep slopeland in the Three Gorges Reservoir Area, China. Geogarhical Res. 2003, 22, 579–589. [Google Scholar]
- Liang, Y.Z.; Xia, Z.Y.; Niu, P.H.; Xu, W.N.; Chen, Y. Rainfall Infiltration and Characteristics of Runoff and Sediment Yield in Small Watershed of Three Gorges Reservoir Area. J. Yangtze River Sci. Res. Inst. 2016, 33, 28–32. [Google Scholar]
- Lu, X.P. Simulation Study on Rainfall Erosivity of Hilly area of Purple Soil; Southwest University: Chongqing, China, 2006. [Google Scholar]
- Zhang, R.Z.; Ran, Q.L. Sand production modeling and erosive force distribution in small and medium-sized watersheds in the upper reaches of the Yangtze River. J. Hydraul. Eng. 1992, 000, 51–56. [Google Scholar]
- Liu, J.G.; Zhang, P.C.; Ren, H.Y. Evolution of Soil Erosion Prediction Models in Yangtze River Basin. J. Yangtze River Sci. Res. Inst. 2007, 24, 12–14. [Google Scholar]
- Yang, H.F.; Yang, S.L.; Xu, K.H.; Milliman, J.D.; Wang, H.; Yang, Z.; Chen, Z.; Zhang, C.Y. Human impacts on sediment in the Yangtze River: A review and new perspectives. Glob. Planet. Change 2018, 162, 8–17. [Google Scholar] [CrossRef]
- Liu, B.Y.; Nearing, M.A.; Risse, L.M. Slope Gradient Effects on Soil Loss for Steep Slopes. Trans. ASAE 1994, 37, 1835–1840. [Google Scholar] [CrossRef]
- Bieger, K.; Hörmann, G.; Fohrer, N. Simulation of streamflow and sediment with the soil and water assessment tool in a data scarce catchment in the three gorges region, China. J. Environ. Qual. 2014, 43, 37–45. [Google Scholar] [CrossRef]
- Demirci, A.; Karaburun, A. Estimation of soil erosion using RUSLE in a GIS framework: A case study in the Buyukcekmece Lake watershed, northwest Turkey. Environ. Earth Sci. 2011, 66, 903–913. [Google Scholar] [CrossRef]
- Kebede, Y.S.; Endalamaw, T.; Sinshaw, B.G.; Atinkut, H.B. Modeling soil erosion using RUSLE and GIS at watershed level in the upper beles, Ethiopia. Environ. Chall. 2021, 1, 100009. [Google Scholar] [CrossRef]
- Koirala, P.; Thakuri, S.; Joshi, S.; Chauhan, R. Estimation of Soil Erosion in Nepal Using a RUSLE Modeling and Geospatial Tool. Geosciences 2019, 9, 147. [Google Scholar] [CrossRef]
- Konz, M.; Chiari, M.; Rimkus, S.; Turowski, J.M.; Molnar, P.; Rickenmann, D.; Burlando, P. Sediment transport modelling in a distributed physically based hydrological catchment model. Hydrol. Earth Syst. Sci. 2011, 15, 2821–2837. [Google Scholar]
- Wang, J.; Zhang, Z.; Greimann, B.; Huang, V.J.E.M. Application and evaluation of the HEC-RAS—Riparian vegetation simulation module to the Sacramento River. Ecol. Model. 2018, 368, 158–168. [Google Scholar] [CrossRef]
- Montaseri, H.; Tavakoli, K.; Evangelista, S.; Omidvar, P. Sediment transport and bed evolution in a 180 curved channel with lateral intake: Numerical simulations using Eulerian and Discrete Phase models. Int. J. Mod. Phys. C 2020, 31, 2050113. [Google Scholar]
- Warren, S.D.; Mitasova, H.; Hohmann, M.G.; Landsberger, S.; Iskander, F.Y.; Ruzycki, T.S.; Senseman, G.M. Validation of a 3-D enhancement of the Universal Soil Loss Equation for prediction of soil erosion and sediment deposition. Catena 2005, 64, 281–296. [Google Scholar]
- Ansarifard, S.; Eyvazi, M.; Kalantari, M.; Mohseni, B.; Ghorbanifard, M.; Moghaddam, H.J.; Nouri, M. Simulation of floods under the influence of effective factors in hydraulic and hydrological models using HEC-RAS and MIKE 21. Discov. Water 2024, 4, 92. [Google Scholar]
- Xia, Y.H.; Zhang, P.C. Study on Watershed Soil Erosion Models Based on Erosion Mechanics Mechanism—Taking Yangtze Rive Three Gorges Reservoir Area as an Example. J. Soil Water Conserv. 2003, 17, 152–154. [Google Scholar]
- Du, J.; Shi, C.X.; Zhou, Y.Y. Sediment Yield Pattern and Its Contralling Factors in the Upper Yangtze River. J. Mt. Sci. 2010, 6, 660–667. [Google Scholar]
- Wang, A.J.; Li, Z.G.; Liu, F. Spatiotemporal Distribution of Rainfall Erosivity for Water Erosion District in Upper Reaches of Yangtze River. Bull. Soil Water Conserv. 2013, 31, 9–11. [Google Scholar]
- Chen, S.; Xiong, L.; Zeng, L.; Kim, J.-S.; Zhang, Q.; Jiang, C. Distributed rainfall-runoff simulation for a large-scale karst catchment by incorporating landform and topography into the DDRM model parameters. J. Hydrol. 2022, 610, 127853. [Google Scholar]
- Xiong, L.; Zeng, L. Impacts of Introducing Remote Sensing Soil Moisture in Calibrating a Distributed Hydrological Model for Streamflow Simulation. Water 2019, 11, 666. [Google Scholar] [CrossRef]
- Shi, D.M.; Lu, X.P.; Jiang, G.Y. Simulation on simple algorithm of rainfall erosivity in purple hilly area. Trans. CSAE 2010, 26, 117–122. [Google Scholar]
- Bao, W.M. A Conceptual Modelling Study for Small Basin Sediment Yields in Loss Regions. Adv. Water Sci. 1993, 4, 45–50. [Google Scholar]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]


| Data Type | Spatial Resolution | Temporal Resolution | Period |
|---|---|---|---|
| Precipitation | station | daily | 2011–2020 |
| Temperature | station | daily | 2011–2020 |
| Runoff | station | daily | 2011–2020 |
| Sediment | station | daily | 2011–2020 |
| DEM | 30 m and 300 m | / | / |
| Land use | 1 km | / | / |
| NDVI | 1 km | monthly | 2011–2020 |
| Soil texture | 1 km | / | / |
| soil organic carbon content | 1 km | / | / |
| Area | Cell Size | Percentage of Area in Terrain with Different Slopes | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0–5° | 5–10° | 10–15° | 15–20° | 20–25° | 25–30° | 30–35° | 35–40° | 40–45° | >45° | ||
| Above Ningnan Station | 300 m | 6.96% | 18.08% | 24.64% | 23.10% | 15.35% | 8.03% | 3.09% | 0.69% | 0.06% | 0.00% |
| 30 m | 3.51% | 7.27% | 13.94% | 18.77% | 18.51% | 15.13% | 11.12% | 6.73% | 3.08% | 1.94% | |
| Period | Flood No. | Flood Peak Flow (m3/s) | Peak Occurrence Time Error (d) | Flood Volume (108 m3) | NSE | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Measured | Simulated | Relative Error | Measured | Simulated | Relative Error | |||||
| Calibration period | 2010 | 20100710 | 309 | 286 | −7.4% | 0 | 0.09 | 0.08 | −11.1% | 0.76 |
| 2011 | 20110623 | 311 | 269 | −13.5% | 0 | 0.12 | 0.13 | 8.3% | 0.71 | |
| 2012 | 20120705 | 667 | 589 | −11.7% | 0 | 0.21 | 0.24 | 14.3% | 0.79 | |
| 2013 | 20130912 | 520 | 495 | −4.8% | 0 | 0.27 | 0.23 | −14.8% | 0.71 | |
| 2014 | 20140818 | 511 | 434 | −15.1% | 0 | 0.16 | 0.18 | 12.5% | 0.68 | |
| 2015 | 20150715 | 424 | 372 | −12.3% | 0 | 0.09 | 0.08 | −13.3% | 0.83 | |
| 2016 | 20160628 | 656 | 598 | −8.8% | 0 | 0.44 | 0.38 | −13.6% | 0.73 | |
| 2017 | 20170625 | 431 | 382 | −11.4% | 0 | 0.29 | 0.26 | −10.3% | 0.72 | |
| Validation period | 2019 | 20190713 | 330 | 288 | −12.7% | 0 | 0.13 | 0.14 | 7.7% | 0.79 |
| 2020 | 20200917 | 583 | 548 | −6.0% | 0 | 0.42 | 0.38 | −9.5% | 0.77 | |
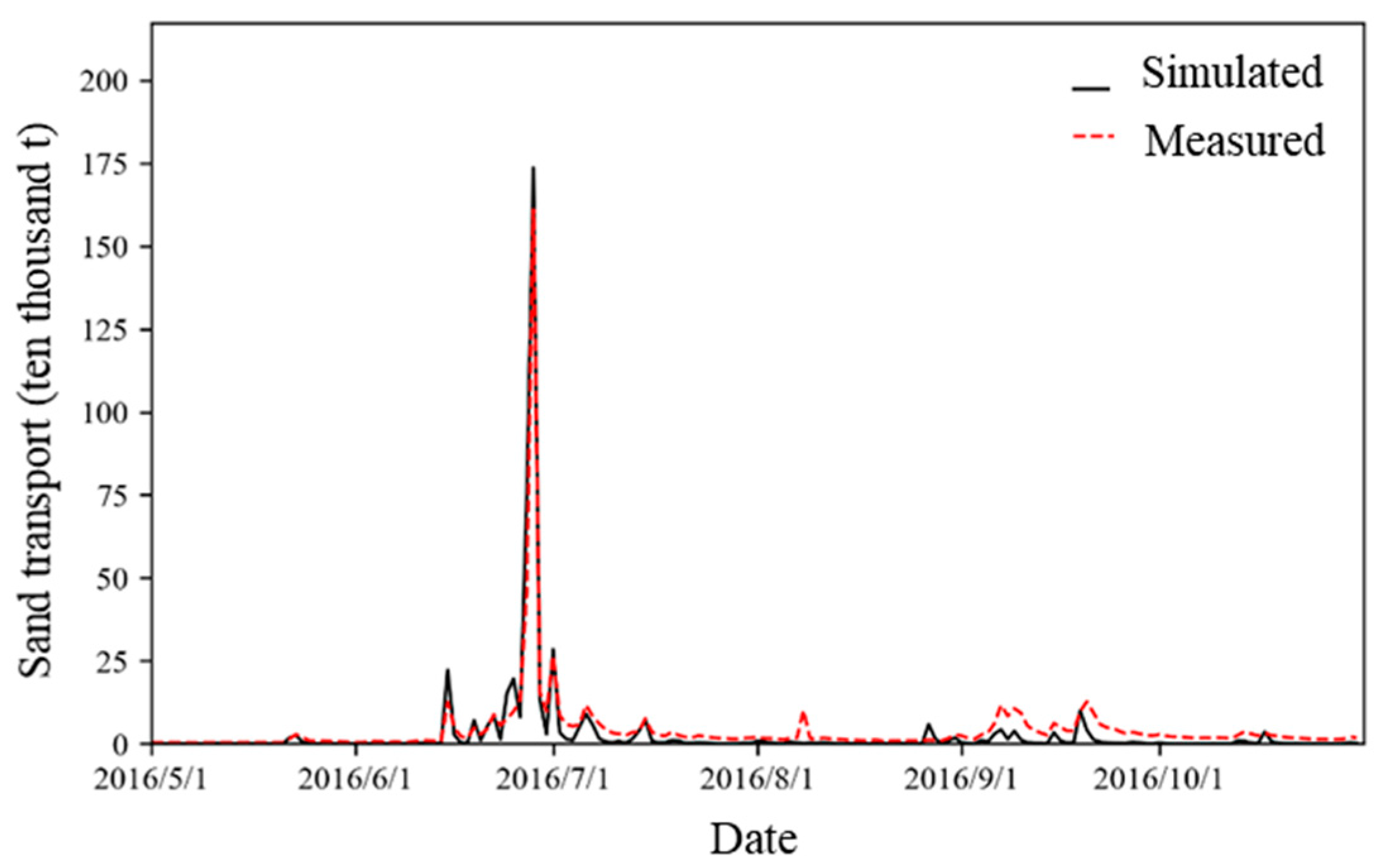
| Period | Flood No. | Sediment Peak Volume (104 t) | Peak Occurrence Time Error (d) | Sediment Transport Volume (104 t) | NSE | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Measured | Simulated | Relative Standard Deviation | Measured | Simulated | Relative Standard Deviation | |||||
| Calibration period | 2010 | 20100710 | 34.91 | 31.23 | −10.5% | 0 | 102.72 | 97.54 | −5.0% | 0.73 |
| 2011 | 20110623 | 51.15 | 48.83 | −4.5% | 0 | 70.65 | 67.44 | −4.5% | 0.79 | |
| 2012 | 20120705 | 71.63 | 69.55 | −2.9% | 0 | 146.27 | 129.33 | −11.6% | 0.83 | |
| 2013 | 20130912 | 38.36 | 42.52 | 10.8% | 0 | 69.16 | 71.32 | 3.1% | 0.76 | |
| 2014 | 20140818 | 57.45 | 55.19 | −3.9% | 0 | 75.62 | 79.31 | 4.9% | 0.77 | |
| 2015 | 20150715 | 46.89 | 43.5 | −7.2% | 0 | 50.15 | 47.27 | −5.7% | 0.73 | |
| 2016 | 20160628 | 173.66 | 161.02 | −7.3% | 0 | 373.88 | 359.18 | −3.9% | 0.86 | |
| 2017 | 20170625 | 108.86 | 115.61 | 6.2% | 0 | 298.27 | 277.45 | −7.0% | 0.71 | |
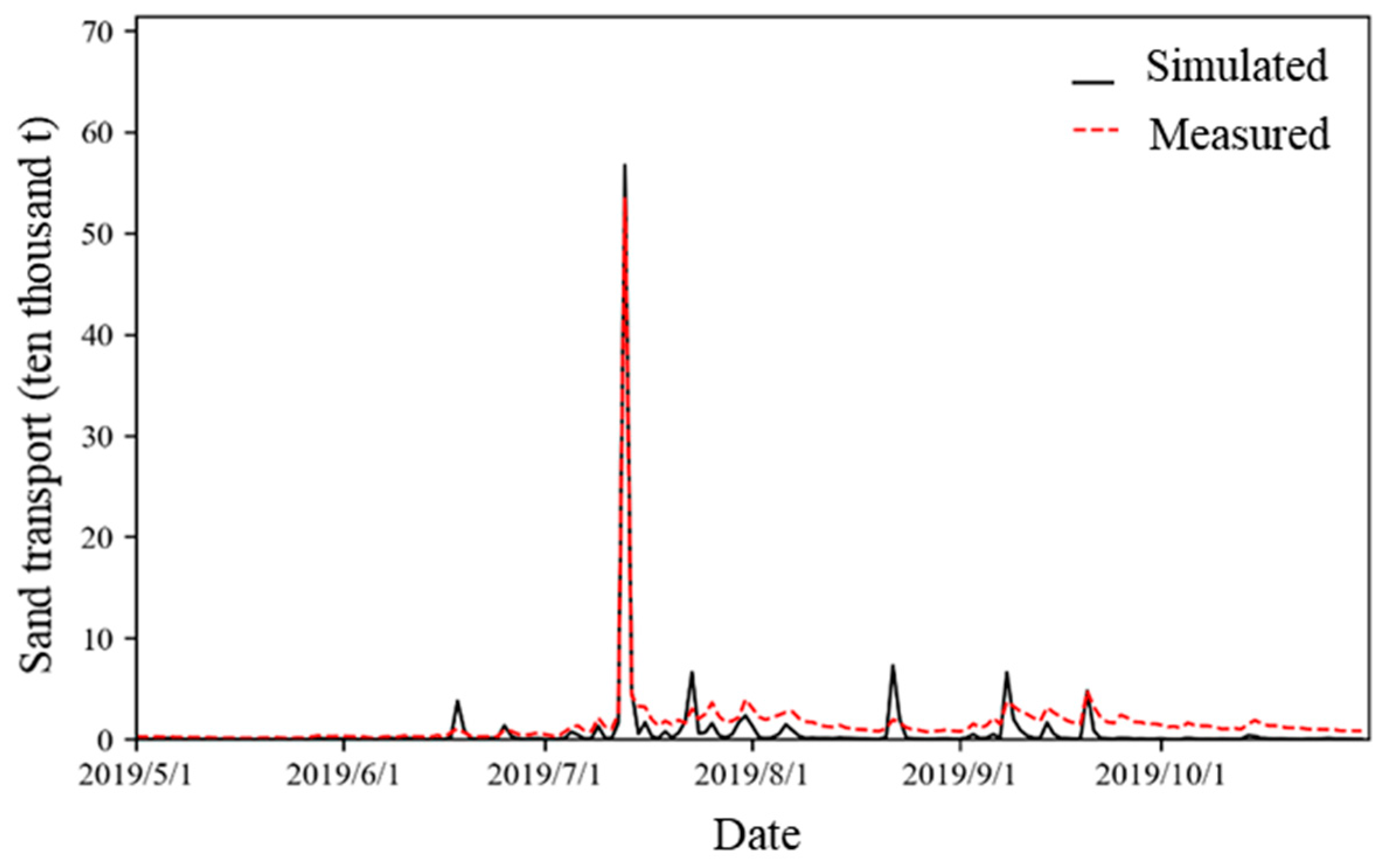
| Validation period | 2019 | 20190713 | 56.74 | 53.41 | −5.9% | 0 | 65.32 | 68.74 | 5.2% | 0.78 |
| 2020 | 20200917 | 39.89 | 41.51 | 4.1% | 0 | 163.13 | 171.31 | 5.0% | 0.75 | |
| Models | Evaluation Indicators | Calibration Period | Validation Period |
|---|---|---|---|
| Revised Universal Soil Loss Equation RUSLE(Centralized model and distributed model) | Relative error of multi-year average erosion sediment yield | 18.9% | −13.2% |
| Distributed water–sediment yield and transportation model (Equal-size cell) | Nash efficiency factor | 0.74 | 0.79 |
| Relative error of sediment peak | 7.7% | 5.3% | |
| Relative error of multi-year sediment transport | 21.3% | −9.9% | |
| Distributed water–sediment yield and transportation model (Multi-size cell) | Nash efficiency factor | 0.79 | 0.84 |
| Relative error of sediment peak | 7.9% | −8.1% | |
| Relative error of multi-year sediment transport | 17.0% | 7.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Jin, Y.; Bi, H.; Ren, Y. A Sediment Process Simulation on the Steep Area of the Upper Yangtze River Basin Using a Hybrid Distributed Soil Erosion Model. Water 2025, 17, 996. https://doi.org/10.3390/w17070996
Wang Y, Jin Y, Bi H, Ren Y. A Sediment Process Simulation on the Steep Area of the Upper Yangtze River Basin Using a Hybrid Distributed Soil Erosion Model. Water. 2025; 17(7):996. https://doi.org/10.3390/w17070996
Chicago/Turabian StyleWang, Yibo, Ye Jin, Hongwei Bi, and Yufeng Ren. 2025. "A Sediment Process Simulation on the Steep Area of the Upper Yangtze River Basin Using a Hybrid Distributed Soil Erosion Model" Water 17, no. 7: 996. https://doi.org/10.3390/w17070996
APA StyleWang, Y., Jin, Y., Bi, H., & Ren, Y. (2025). A Sediment Process Simulation on the Steep Area of the Upper Yangtze River Basin Using a Hybrid Distributed Soil Erosion Model. Water, 17(7), 996. https://doi.org/10.3390/w17070996








