The Investigation of Two-Phase Fluid Flow Structure Within Rock Fracture Evolution in Terms of Flow Velocity: The Role of Fracture Surface Roughness and Shear Displacement
Abstract
1. Introduction
2. Research Methodology
2.1. Governing Equations
2.2. Rough Fracture Geometry Model Generation
2.3. Numerical Solution Scheme, Boundary Conditions, and Physical Parameters
- (1)
- Construction of a suitable geometric model;
- (2)
- Define the physical parameters and variables in the model;
- (3)
- Introduce the control equations into the corresponding model to define the model boundary conditions and initial conditions;
- (4)
- Select appropriate mesh parameters for meshing;
- (5)
- Select the solver to solve the model;
- (6)
- Post-processing of the simulation results.
3. Results and Analysis
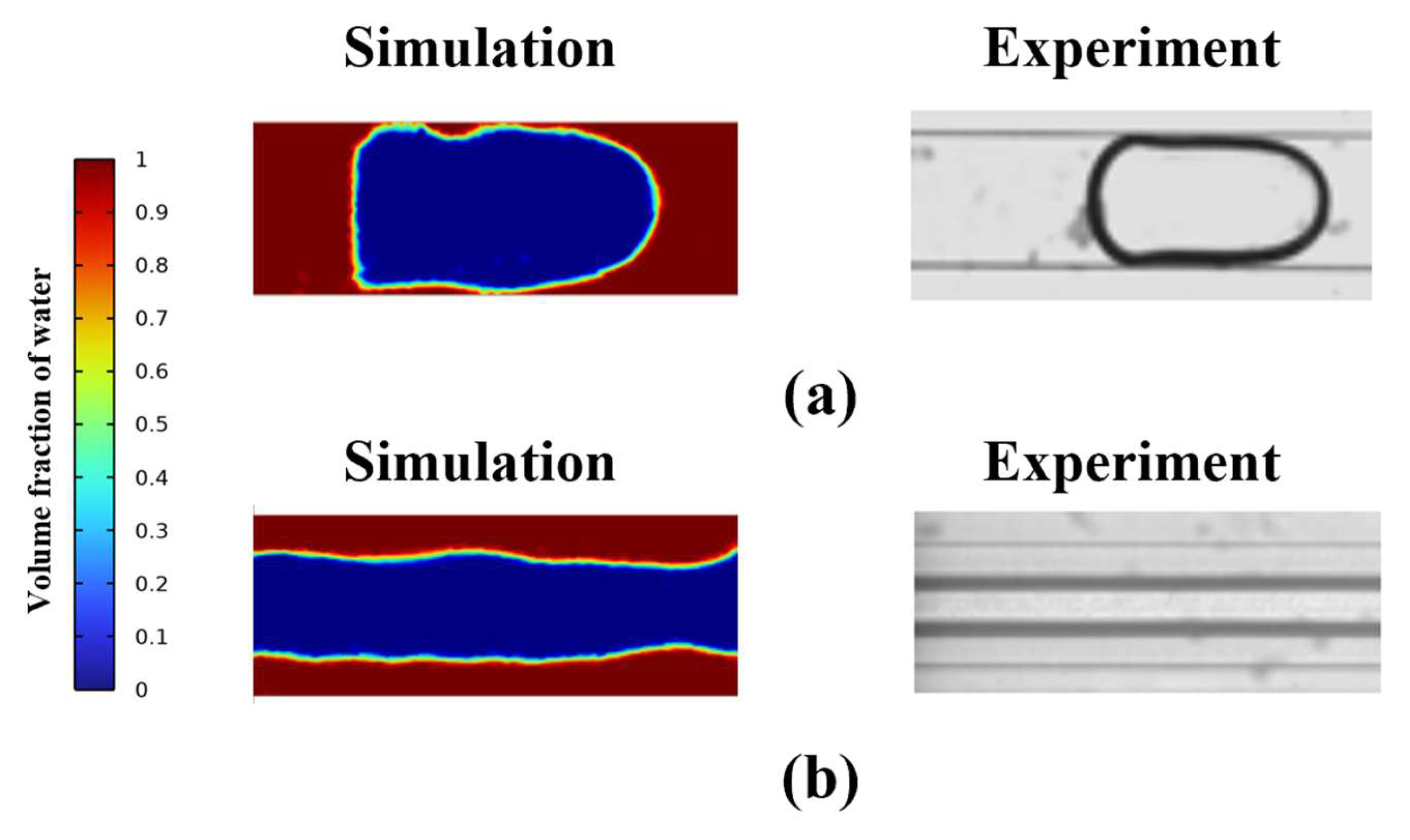
3.1. Validation of the Numerical Simulation Methods
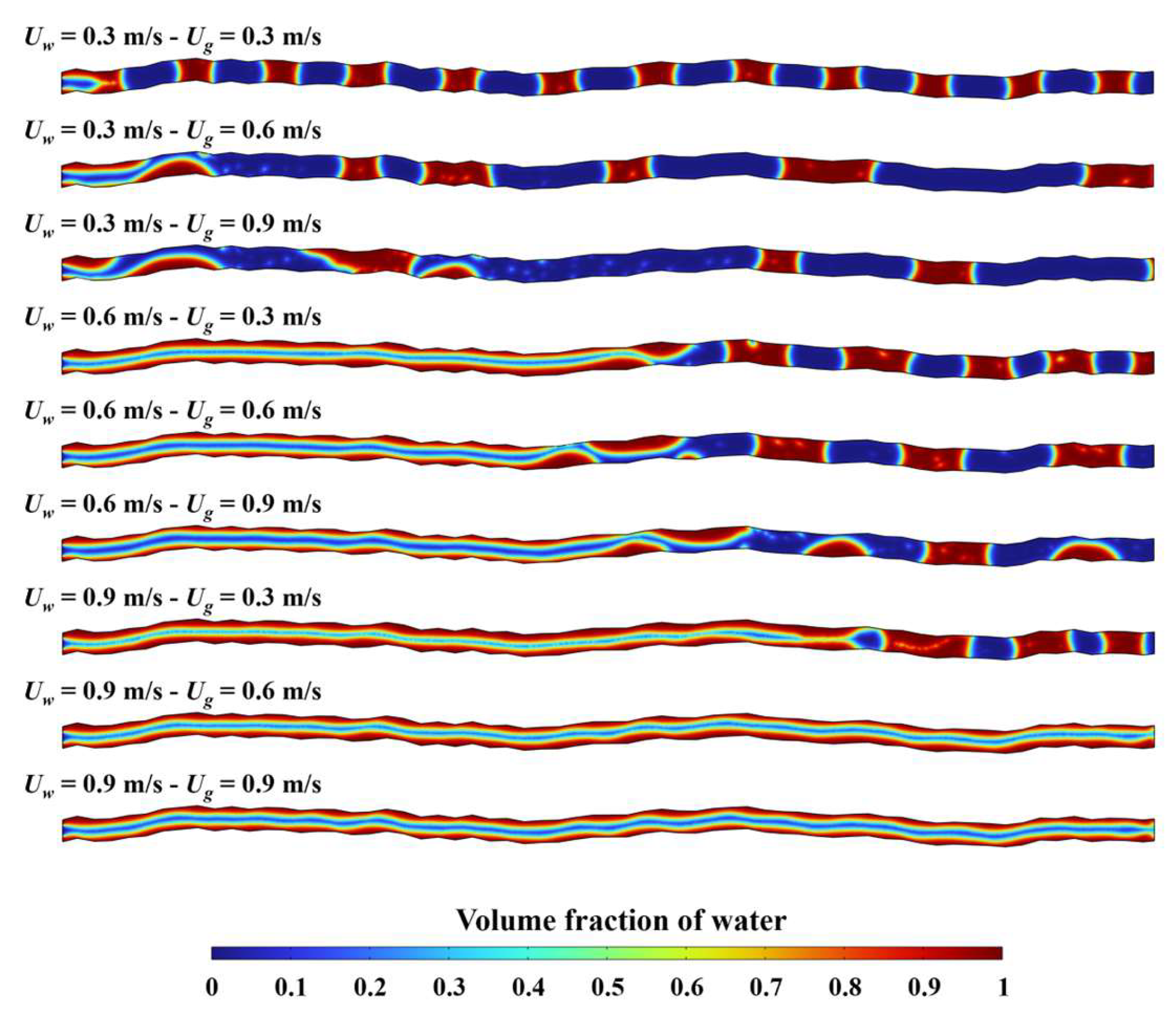
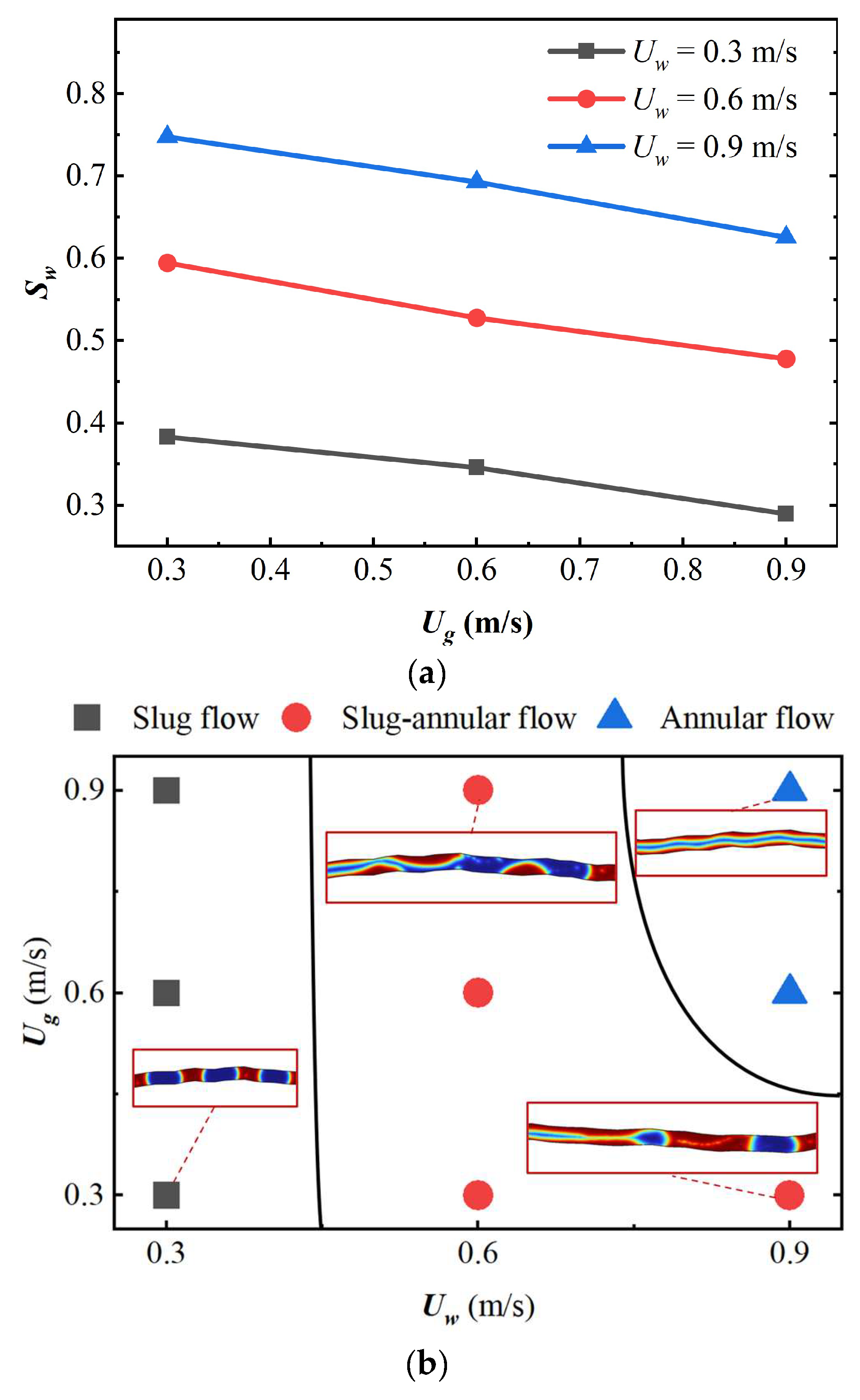
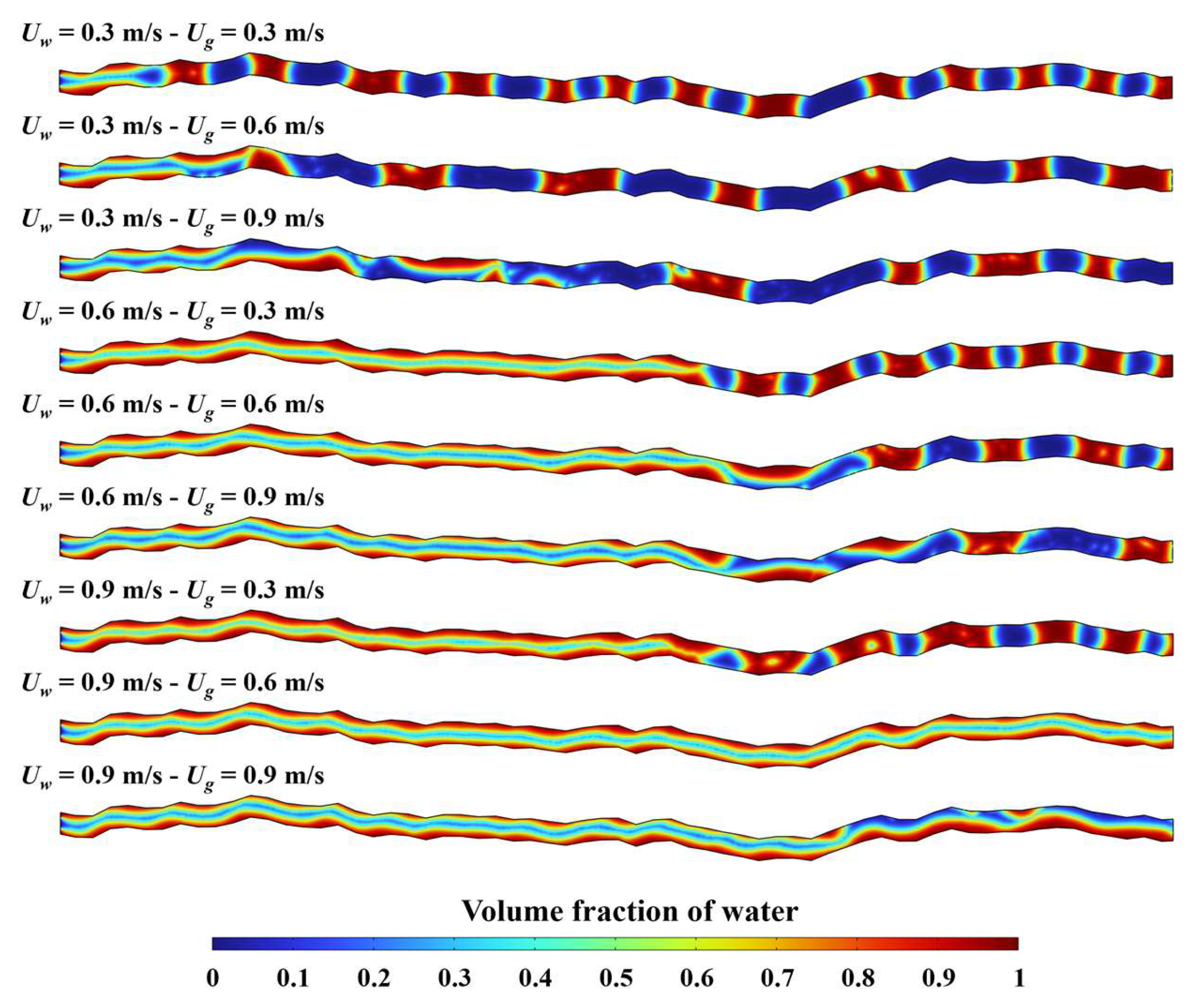
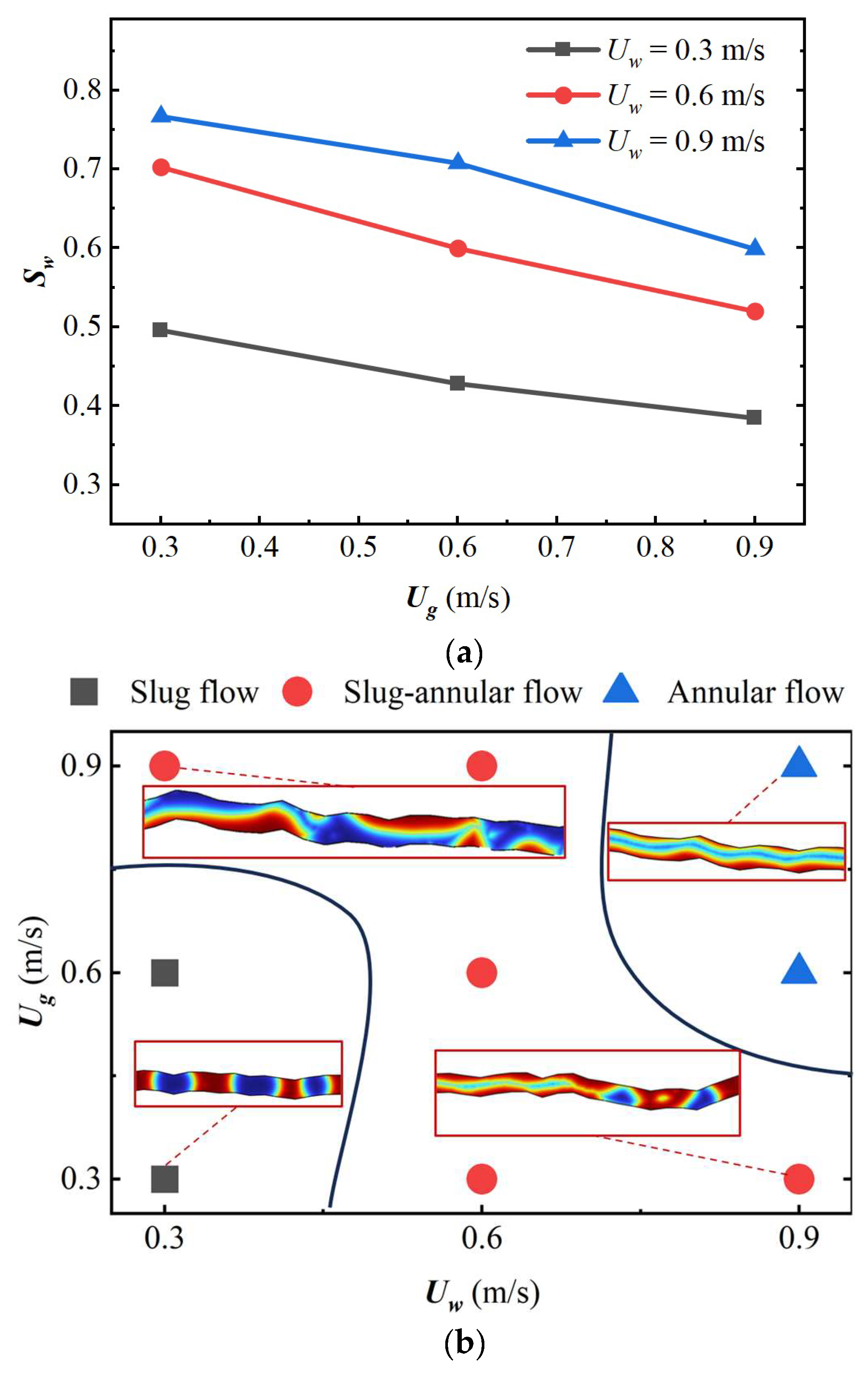
3.2. Effect of Flow Rate on the Structure of Two-Phase Fluid Flow
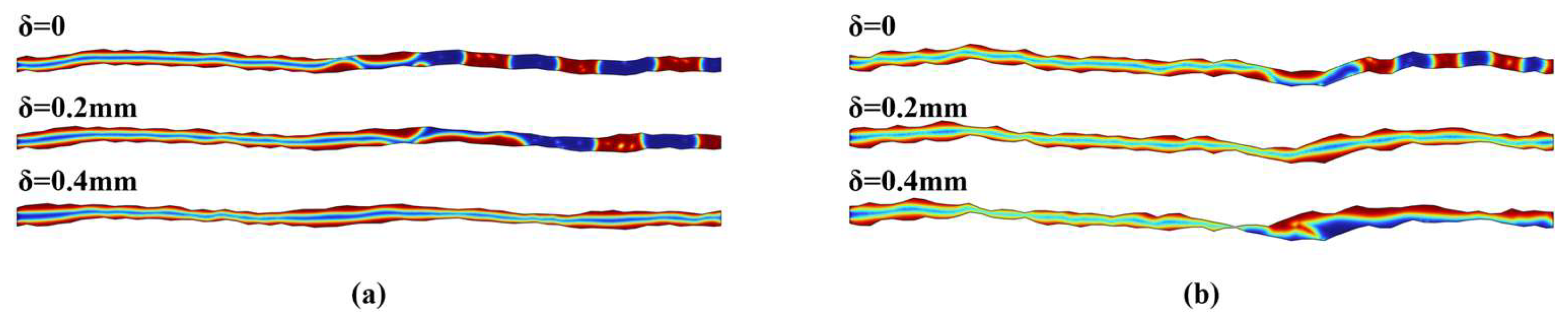
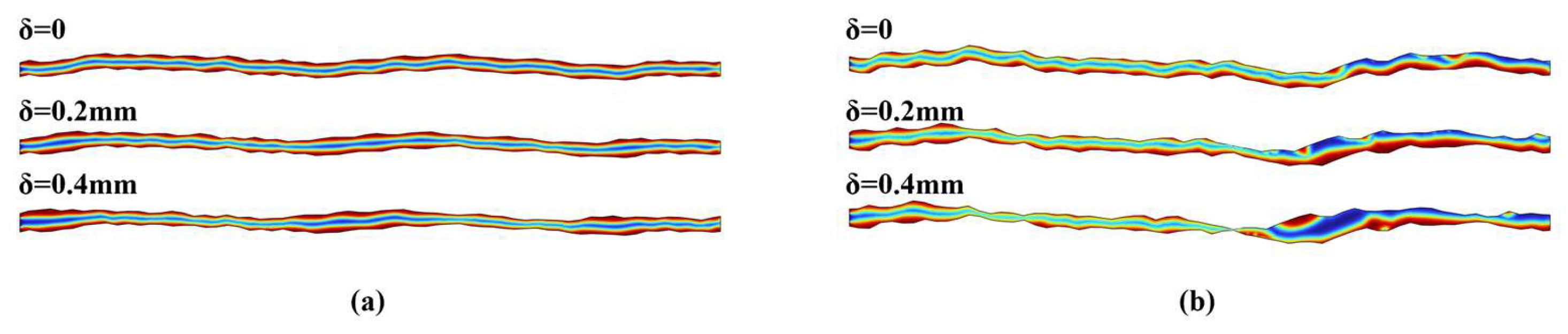
3.3. Effect of Surface Roughness on the Structure of Two-Phase Fluid Flow
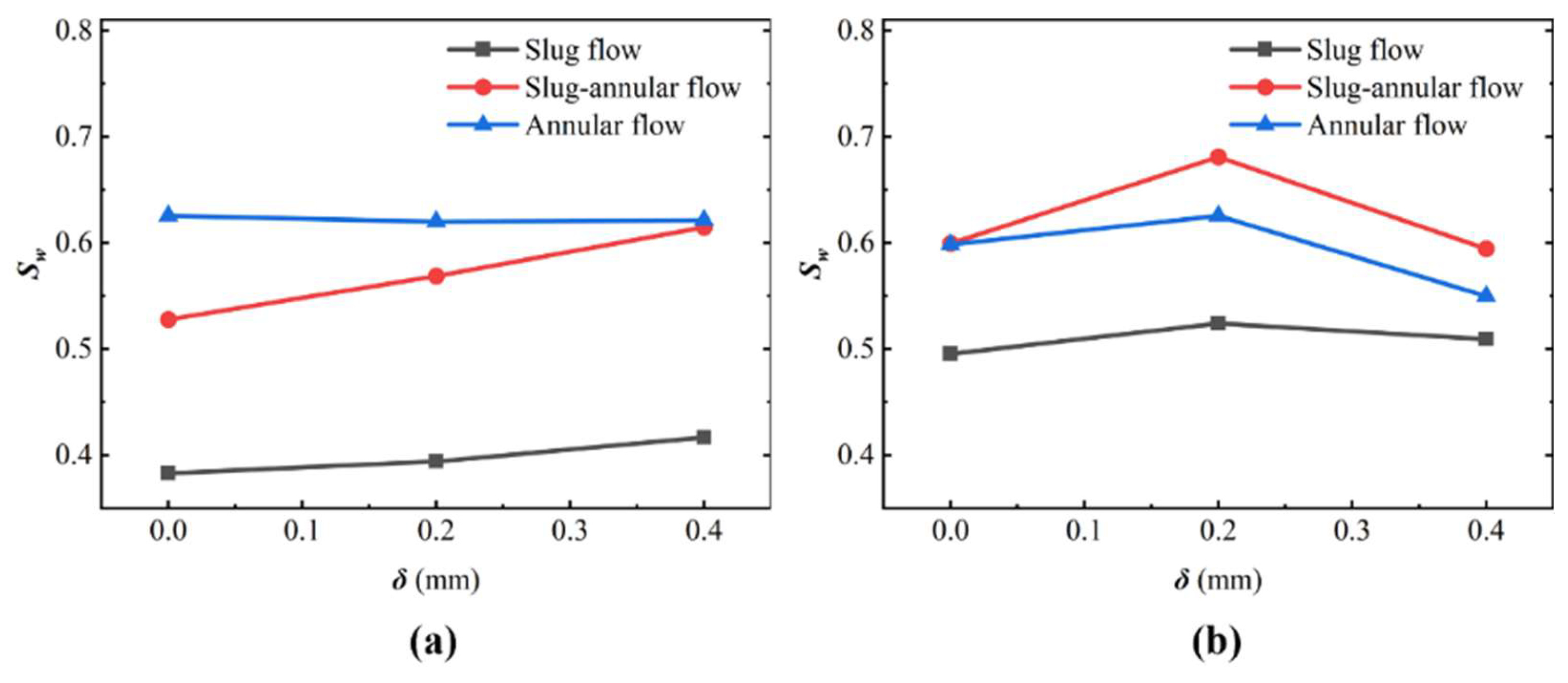
3.4. Effect of Dislocations on the Structure of Two-Phase Fluid Flow
4. Conclusions
- (1)
- Impact of Two-Phase Fluid Flow Rate
- (2)
- Effect of Surface Roughness
- (3)
- Effect of Dislocation
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| F | Other external forces in the system |
| Fg | Gravity |
| Fst | Surface tension |
| H | Hurst index |
| I | Unit matrix |
| K | Current permeability |
| M | The molar mass of the gas |
| R | The gas constant |
| T | The gas phase temperature |
| Ug | The velocity of the gas |
| Uw | The velocity of the water |
| p | Fluid pressure |
| r | Arbitrary constant |
| u | Velocity vector |
| Greek letter | |
| ρ | Fluid density |
| σ | Surface tension coefficient |
| μ | Dynamic viscosity |
| Interface curvature | |
| Dirac delta function | |
| φ | The level set function |
| ρw | Density of water |
| ρg | Density of gas |
| μw | Dynamic viscosity of water |
| μg | Dynamic viscosity of gas |
| ε | Model mesh size parameters |
| γ | Model velocity field parameters |
References
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Karra, S.; Makedonska, N.; Viswanathan, H.S.; Painter, S.L.; Hyman, J.D. Effect of advective flow in fractures and matrix diffusion on natural gas production. Water Resour. Res. 2015, 51, 8646–8657. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, C.; Dowd, P.; Xiong, F.; Wang, H. A nonlinear version of the reynolds equation for flow in rock fractures with complex void geometries. Water Resour. Res. 2020, 56, e2019WR026149. [Google Scholar] [CrossRef]
- Cao, M.; Hirose, S.; Sharma, M.M. Factors controlling the formation of complex fracture networks in naturally fractured geothermal reservoirs. J. Pet. Sci. Eng. 2022, 208, 109642. [Google Scholar] [CrossRef]
- Zhu, W.; Chen, Z.; Yang, Y.; Gong, W.; Wang, M. Impacts of t-type intersections on the connectivity and flow in complex two-dimensional fracture networks. Eng. Geol. 2023, 320, 107122. [Google Scholar] [CrossRef]
- Xue, K.; Zhang, Z.; Han, X.; Guang, W. A fractal model for estimating the permeability of tortuous fracture networks with correlated fracture length and aperture. Phys. Fluids 2023, 35, 043615. [Google Scholar] [CrossRef]
- Harp, D.R.; Ortiz, J.P.; Pandey, S.; Karra, S.; Anderson, D.; Bradley, C.; Viswanathan, H.; Stauffer, P.H. Immobile pore-water storage enhancement and retardation of gas transport in fractured rock. Transp. Porous Media 2018, 124, 369–394. [Google Scholar] [CrossRef]
- Pritchett, J. Dry-steam wellhead discharges from liquid-dominated geothermal reservoirs: A result of coupled nonequilibriurn multiphase fluid and heat flow through fractured rock. Dyn. Fluids Transp. Fract. Rock 2005, 162, 175. [Google Scholar] [CrossRef]
- Li, T.; Tang, C.; Rutqvist, J.; Hu, M. TOUGH-RFPA: Coupled thermal-hydraulic-mechanical rock failure process analysis with application to deep geothermal wells. Int. J. Rock Mech. Min. Sci. 2021, 142, 104726. [Google Scholar] [CrossRef]
- Azim, R.A. Finite element model to simulate two-phase fluid flow in naturally fractured oil reservoirs: Part I. ACS Omega 2022, 7, 27278–27290. [Google Scholar] [CrossRef]
- Zheng, J.; Jin, Y.; Dong, J.; Liu, S.; Zhang, Q.; Song, H.; Huang, P. Reexamination of the permeability-aperture relationship for rough fractures with mismatched self-affine surfaces. J. Hydrol. 2022, 609, 127727. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Cao, H.; Wu, J.; Wang, F.; Wang, Y. The Crack Propagation Behaviour of CO2 Fracturing Fluid in Unconventional Low Permeability Reservoirs: Factor Analysis and Mechanism Revelation. Processes 2025, 13, 159. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Wu, J.; Li, X.; Li, H.; Cheng, Y. Wellhead Stability During Development Process of Hydrate Reservoir in the Northern South China Sea: Evolution and Mechanism. Processes 2025, 13, 40. [Google Scholar] [CrossRef]
- Shen, W.; Ma, T.; Li, X.; Sun, B.; Hu, Y.; Xu, J. Fully coupled modeling of two-phase fluid flow and geomechanics in ultra-deep natural gas reservoirs. Phys. Fluids 2022, 34, 043101. [Google Scholar] [CrossRef]
- Khudayarov, B.A.; Komilova, K.M. Vibration and dynamic stability of composite pipelines conveying a two-phase fluid flows. Eng. Fail. Anal. 2019, 104, 500–512. [Google Scholar] [CrossRef]
- Cheng, L.; Xia, G. Flow patterns and flow pattern maps for adiabatic and diabatic gas liquid two phase flow in microchannels: Fundamentals, mechanisms and applications. Exp. Therm. Fluid Sci. 2023, 148, 110988. [Google Scholar] [CrossRef]
- Khoei, A.R.; Mortazavi, S.M.S. Thermo-hydro-mechanical modeling of fracturing porous media with two-phase fluid flow using X-FEM technique. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 2430–2472. [Google Scholar] [CrossRef]
- Momen, A.M.; Sherif, S.A.; Lear, W.E. Modeling of two-phase gas-liquid slug flows in microchannels. Comput. Therm. Sci. 2024, 16, 113–128. [Google Scholar] [CrossRef]
- Guiltinan, E.J.; Santos, J.E.; Cardenas, M.B.; Espinoza, D.N.; Kang, Q. Two-phase fluid flow properties of rough fractures with heterogeneous wettability: Analysis with lattice boltzmann simulations. Water Resour. Res. 2020, 57, e2020WR027943. [Google Scholar] [CrossRef]
- Gao, Z.; Qu, Z.; Cai, Q.; Hou, L.; Liu, M.; Yuan, T. A deep branch-aggregation network for recognition of gas–liquid two-phase flow structure. IEEE Trans. Instrum. Meas. 2021, 70, 5000408. [Google Scholar] [CrossRef]
- Huang, J.; Lu, Y.; Jia, L. Experimental study on the two-phase flow structure in a supercritical water-fluidized bed. Ind. Eng. Chem. Res. 2019, 58, 20099–20108. [Google Scholar] [CrossRef]
- Krzaczek, M.; Nitka, M.; Tejchman, J. Effect of gas content in macropores on hydraulic fracturing in rocks using a fully coupled DEM/CFD approach. Int. J. Numer. Anal. Methods Geomech. 2020, 45, 234–264. [Google Scholar] [CrossRef]
- Gong, Y.; Sedghi, M.; Piri, M. Two-phase relative permeability of rough-walled fractures: A dynamic pore-scale modeling of the effects of aperture geometry. Water Resour. Res. 2021, 57, e2021WR030104. [Google Scholar] [CrossRef]
- Wong, T.N.; Che, Z.; Nguyen, N.T. Flow field, heat transfer and mixing in segmented plug flow in microchannels. In Proceedings of the 7th International Multidisciplinary Conference on Optofluidics, Singapore, 25–28 July 2017. [Google Scholar] [CrossRef]
- Muzychka, Y.S.; Walsh, E.J.; Walsh, P. Heat transfer enhancement using laminar gas-liquid segmented plug flows. J. Heat Transf. 2011, 133, 041902. [Google Scholar] [CrossRef]
- Chen, G. Structural, solvent quality changes and flow regulation through PEO-grafted gold nanopore. Macromolecules 2024, 57, 4855–4866. [Google Scholar] [CrossRef]
- Wang, Q.; Hu, J.; Song, M.; Shen, H.; Zhou, Y.; Li, D.; Xie, F. Study on the transient flow characteristics of a hump water pipeline based on the random distribution of bubbles. Water 2023, 15, 3831. [Google Scholar] [CrossRef]
- Ahammad, M.J.; Rahman, M.A.; Zheng, L.; Alam, J.M.; Butt, S. Numerical investigation of two-phase fluid flow in a perforation tunnel. J. Nat. Gas. Sci. Eng. 2018, 55, 606. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Ranjith, P.G.; Han, X. Flow structure transition and identification of two-phase fluid flow through rough rock fractures. Eur. Phys. J. Plus 2023, 138, 376. [Google Scholar] [CrossRef]
- Chen, C.Y.; Horne, R.N. Two-phase flow in rough-walled fractures: Experiments and a flow structure model. Water Resour. Res. 2006, 42, W03430.1–W03430.17. [Google Scholar] [CrossRef]
- Zhao, J.; Kang, Q.; Yao, J.; Viswanathan, H.; Pawar, R.; Zhang, L.; Sun, H. The effect of wettability heterogeneity on relative permeability of two-phase flow in porous media: A lattice Boltzmann study. Water Resour. Res. 2018, 54, 1295–1311. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L.; Zhang, R.; Chen, X.; Zhao, Y.; Yuan, S. Numerical simulation of gas-liquid two-phase flow in the micro-fracture networks in fractured reservoirs. J. Nat. Gas Sci. Eng. 2021, 94, 104101. [Google Scholar] [CrossRef]
- Liu, D.; Pu, H.; Xue, K.; Ni, H. Numerical Simulation of Gas–Water Two-Phase Flow Patterns in Fracture: Implication for Enhancing Natural Gas Production. Water 2024, 16, 2860. [Google Scholar] [CrossRef]
- Hu, R.; Zhou, C.; Wu, D.; Yang, Z.; Chen, Y. Roughness control on multiphase flow in rock fractures. Geophys. Res. Lett. 2019, 46, 12002–12011. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar]
- Xue, K.; Zhang, Z.; Jiang, Y.; Luo, Y. Estimating the permeability of fractured rocks using topological characteristics of fracture network. Comput. Geotech. 2023, 157, 105337. [Google Scholar] [CrossRef]
- Shabelansky, A.H.; Nihei, K.T.; Fradelizio, G.; Tracey, S.; Bevc, D. Efficient fully coupled 3d poroelastic modeling of geomechanical deformation during depletion and reinjection: An asymptotic transformation of biot’s poroelasticity from a dynamic to a quasistatic response. Geophysics 2023, 88, M201–M212. [Google Scholar] [CrossRef]
- Wang, P.; Fu, Y.; Liu, C.; Zhou, X.; Cai, M. Directional fracture patterns of excavated jointed rock mass within rough discrete fractures. Eng. Fract. Mech. 2024, 309, 110419. [Google Scholar] [CrossRef]
- Zhang, A.; Yang, J.; Cheng, L.; Ma, C. A simulation study on stress-seepage characteristics of 3d rough single fracture based on fluid-structure interaction. J. Pet. Sci. Eng. 2022, 211, 110215. [Google Scholar] [CrossRef]
- Barton, N. Review of a new shear-strength criterion for rock joints. Eng. Geol. 1973, 7, 287–332. [Google Scholar] [CrossRef]
- Sur, A.; Yang, L.; Liu, D. Experimental and numerical investigation of two-phase patterns in a cross-junction microfluidic chip. In Proceedings of the 8th International Conference on Nanochannels, Mi-Crochannels and Minichannels, Montreal, QC, Canada, 1–5 August 2010. [Google Scholar] [CrossRef]
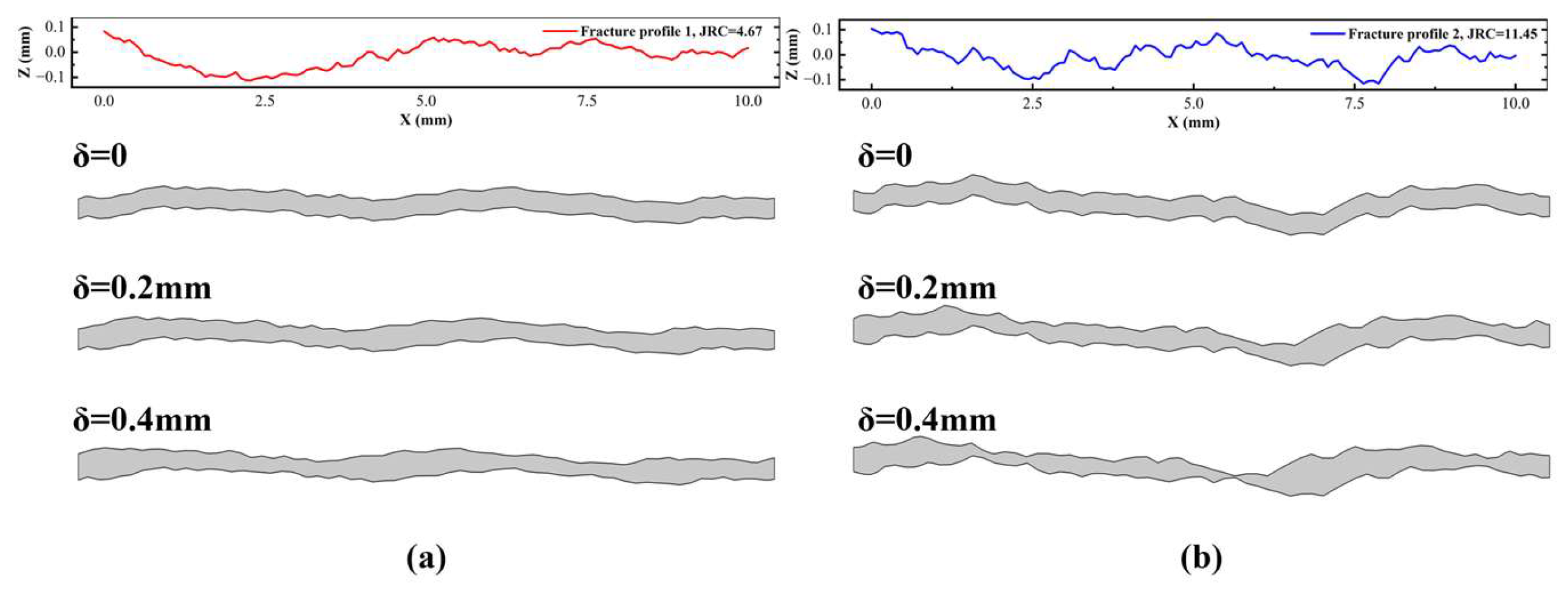

| Fracture (δ = 0) | Length (mm) | H | Z2 | JRC |
|---|---|---|---|---|
| No. 1 | 10 | 0.33 | 0.14 | 4.67 |
| No. 2 | 10 | 0.27 | 0.23 | 11.46 |
| Temperature (K) | Density (kg/m3) | Viscosity (Pa·s) | |
|---|---|---|---|
| Nitrogen | 293.15 | 1.184 | 1.79 × 10−5 |
| Water | 293.15 | 1000 | 1.12 × 10−3 |
| Method | Fluid | Density (kg/m3) | Velocity (m/s) | Flow Structure | |
|---|---|---|---|---|---|
| 1 | Experiment [41] | Air | 1.16 | 0.2 | Slug flow |
| Water | 997 | 0.29 | |||
| Numerical | Air | 1.16 | 0.2 | Slug flow | |
| Water | 1000 | 0.29 | |||
| 2 | Experiment [41] | Air | 1.16 | 4.74 | Annular flow |
| Water | 997 | 0.07 | |||
| Numerical | Air | 1.16 | 4.74 | Annular flow | |
| Water | 1000 | 0.07 |
| Fracture | δ (mm) | Uw (m/s) | Ug (m/s) |
|---|---|---|---|
| No. 1, No. 2 | 0.2, 0.4 | 0.3, 0.6, 0.9 | 0.3, 0.6, 0.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Ren, S.; Li, X.; Liu, M.; Long, K.; Liu, Y. The Investigation of Two-Phase Fluid Flow Structure Within Rock Fracture Evolution in Terms of Flow Velocity: The Role of Fracture Surface Roughness and Shear Displacement. Water 2025, 17, 973. https://doi.org/10.3390/w17070973
Chen L, Ren S, Li X, Liu M, Long K, Liu Y. The Investigation of Two-Phase Fluid Flow Structure Within Rock Fracture Evolution in Terms of Flow Velocity: The Role of Fracture Surface Roughness and Shear Displacement. Water. 2025; 17(7):973. https://doi.org/10.3390/w17070973
Chicago/Turabian StyleChen, Lichuan, Shicong Ren, Xiujun Li, Mengjiao Liu, Kun Long, and Yuanjie Liu. 2025. "The Investigation of Two-Phase Fluid Flow Structure Within Rock Fracture Evolution in Terms of Flow Velocity: The Role of Fracture Surface Roughness and Shear Displacement" Water 17, no. 7: 973. https://doi.org/10.3390/w17070973
APA StyleChen, L., Ren, S., Li, X., Liu, M., Long, K., & Liu, Y. (2025). The Investigation of Two-Phase Fluid Flow Structure Within Rock Fracture Evolution in Terms of Flow Velocity: The Role of Fracture Surface Roughness and Shear Displacement. Water, 17(7), 973. https://doi.org/10.3390/w17070973





