Bivariate and Partial Wavelet Coherence for Revealing the Remote Impacts of Large-Scale Ocean-Atmosphere Oscillations on Drought Variations in Xinjiang, China

Abstract

Xinjiang, an arid area located in the central part of the Eurasian continent with high evaporation and low precipitation, experiences frequent droughts. This study builds on previous research by incorporating five key ocean-atmosphere oscillations and using the one-month SPEI as a meteorological drought indicator. Monthly time series of precipitation and temperature from 53 meteorological stations are utilized to calculate the monthly SPEI time series, and the seasonal Kendall test analyzes trends. Despite increased precipitation, the drought conditions in Xinjiang worsened due to increased temperatures, especially in the south, during 1961–2017. The 53 monthly SPEI time series are clustered using the agglomerative hierarchical method, basically reflecting Xinjiang’s topographical and climatic diversity. However, classical correlation methods show a weak or negligible overall correlation between the SPEI and large-scale ocean-atmosphere oscillators. Therefore, the partial wavelet coherence (PWC) method was used to detect the scale-specific correlations. Both bivariate wavelet coherence (BWC) and PWC detected significant correlations between the SPEI and the ocean-atmosphere oscillators at some specific time scales. Our analyses indicate that southern Xinjiang droughts are more influenced by Pacific or Indian Ocean oscillators, while northern droughts are affected by Atlantic or Arctic climate variations.

1. Introduction

A drought is a widespread and complex natural phenomenon due to long-term insufficient precipitation, exacerbated by the combined effects of increased evapotranspiration [1,2,3,4]. Wilhite and Glantz [5] categorized droughts into four types: meteorological drought, hydrological drought, agricultural drought, and socioeconomic drought. These four types of droughts have different implications. Meteorological drought stems from prolonged precipitation deficits; hydrological drought involves reduced surface and groundwater availability; agricultural drought occurs when soil moisture is insufficient to sustain crops or livestock; and socioeconomic drought emerges when water scarcity disrupts supply and demand, exacerbating access inequities or conflict risks [6,7,8]. The definition of meteorological drought is based on the deficiency of precipitation in a specific period, which affects the overall water availability in the atmosphere [9]. It is usually considered as the precursor to other three types of droughts.

Meteorological drought indices are often used to detect drought trends in climate science [10,11,12].

Table 1. Summaries of a few commonly applied drought indices.

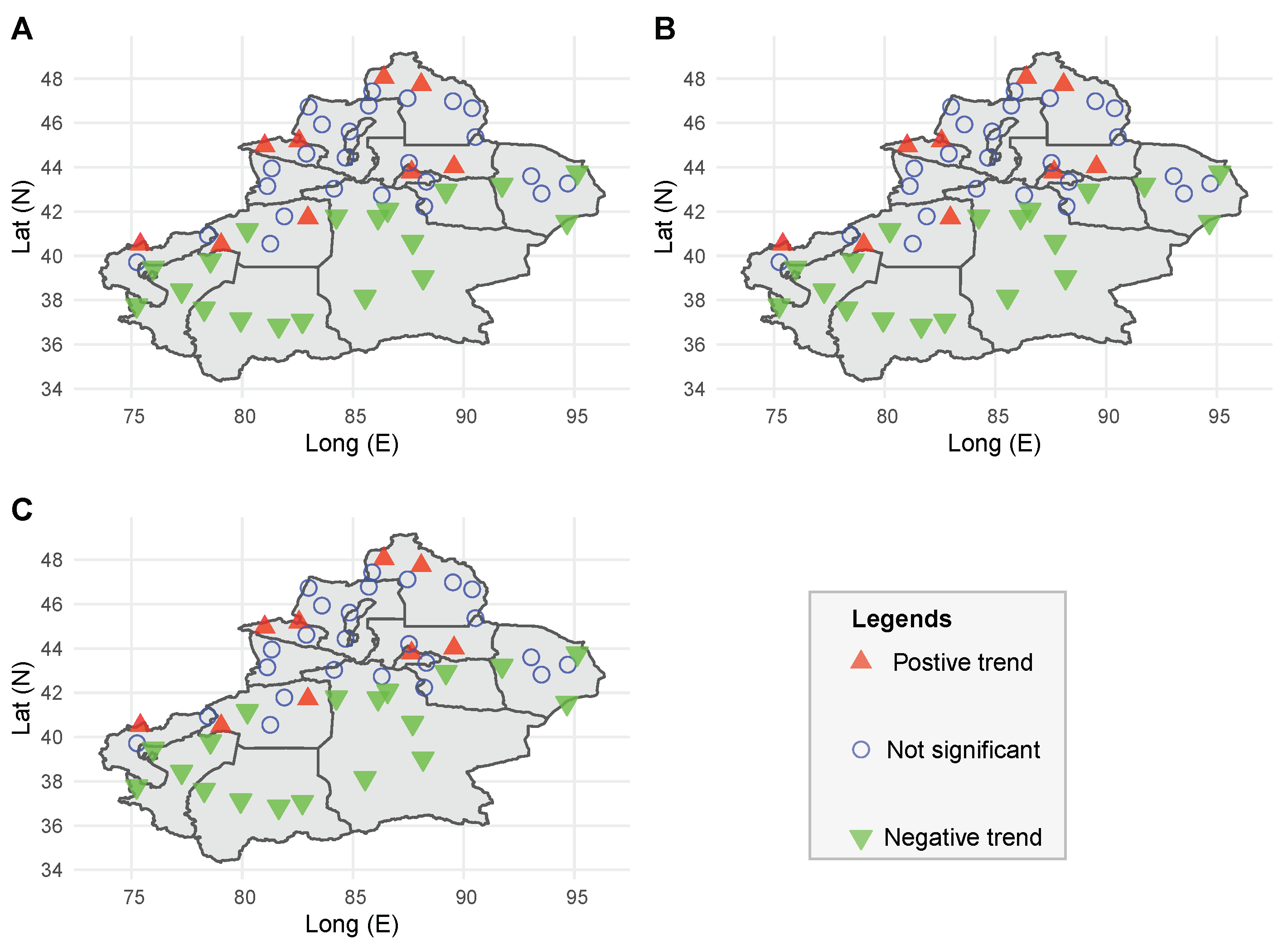
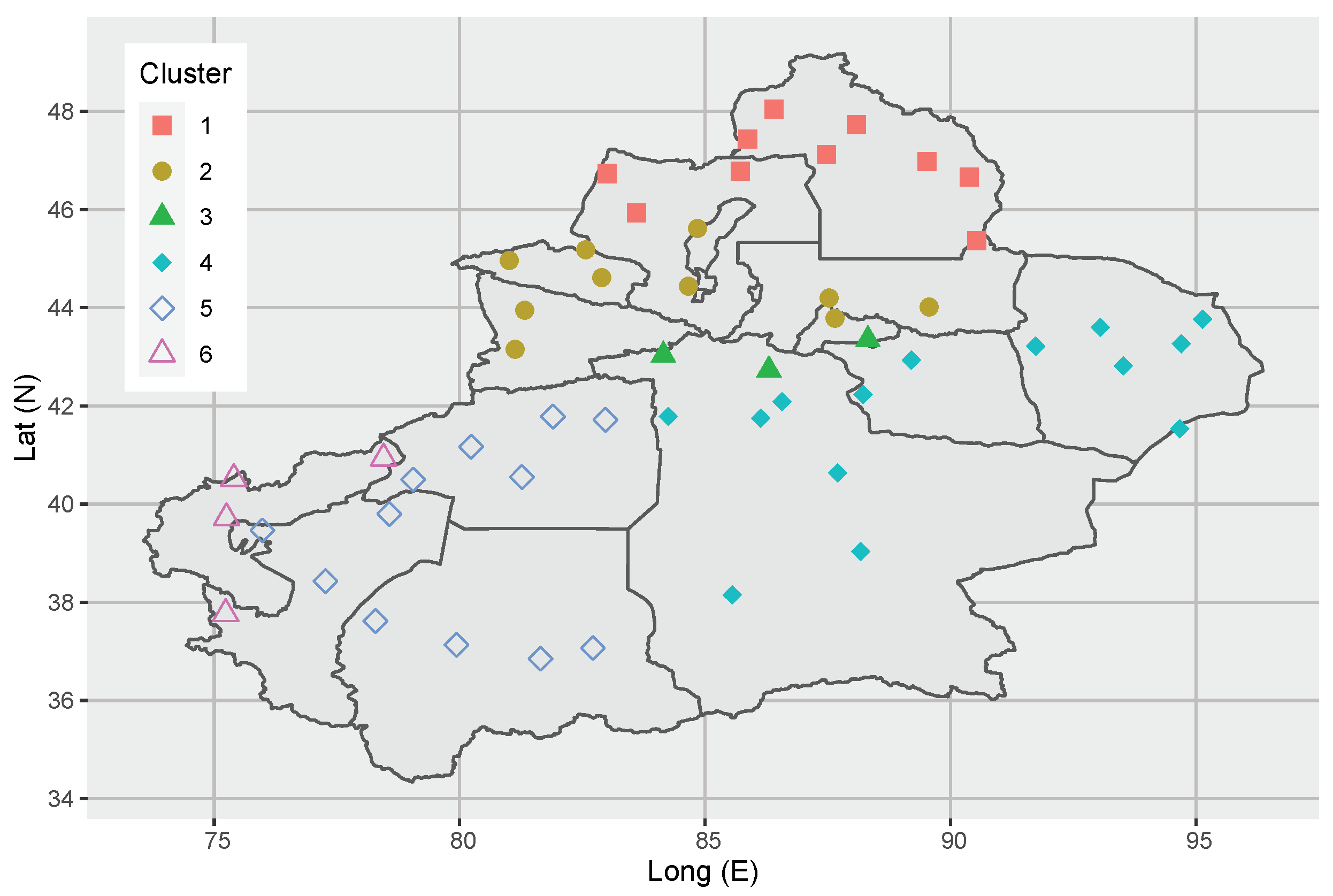
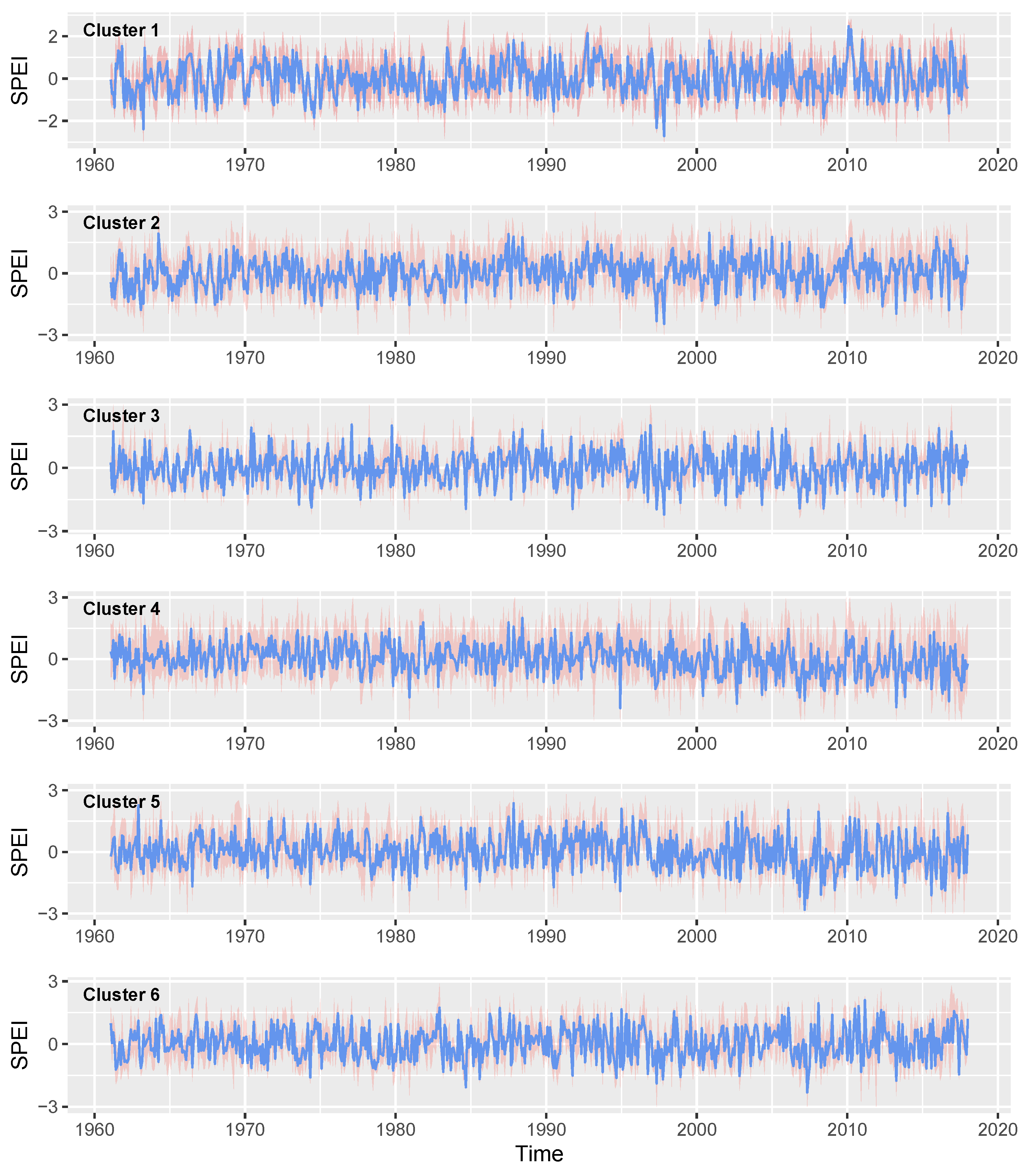
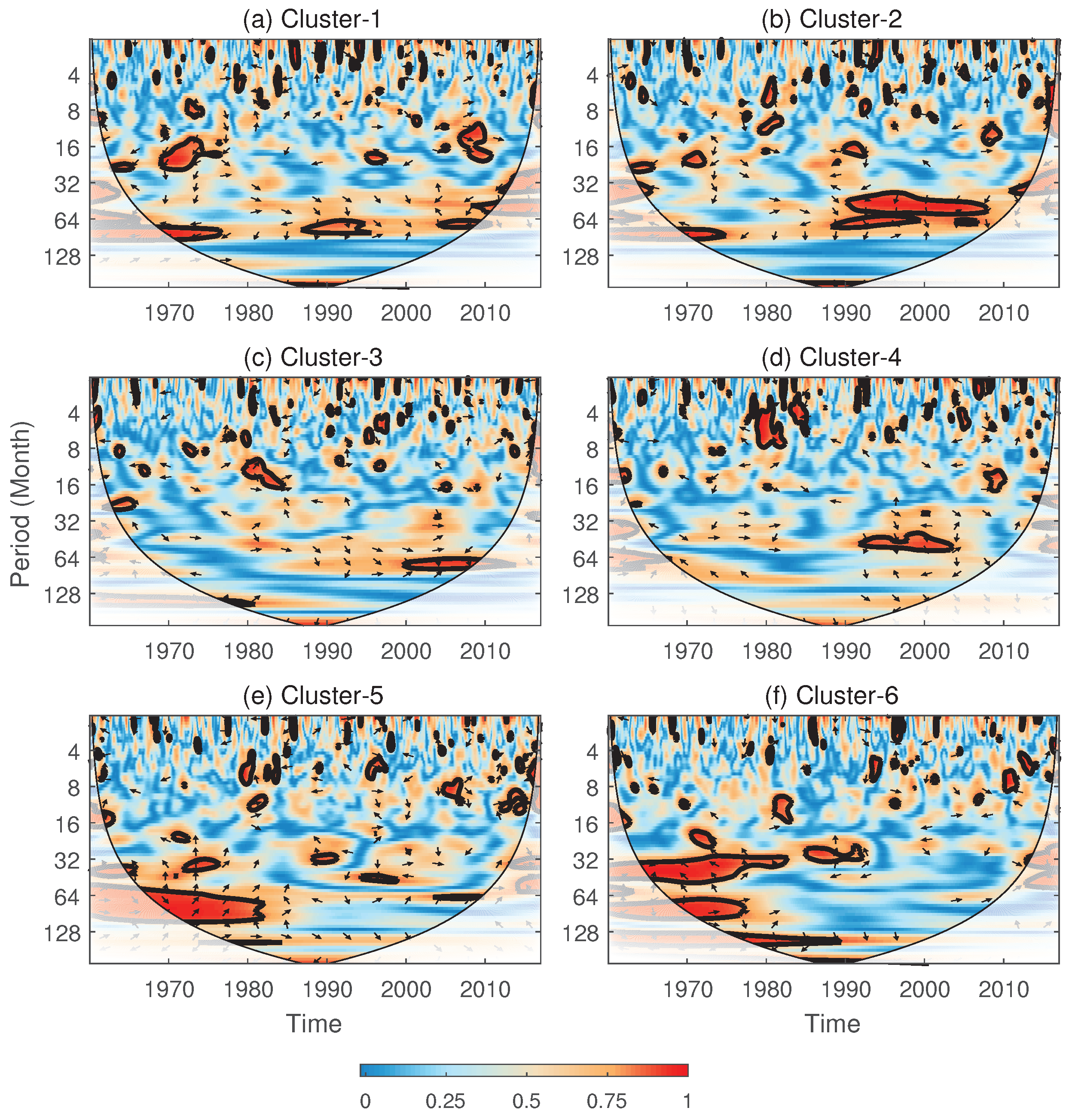
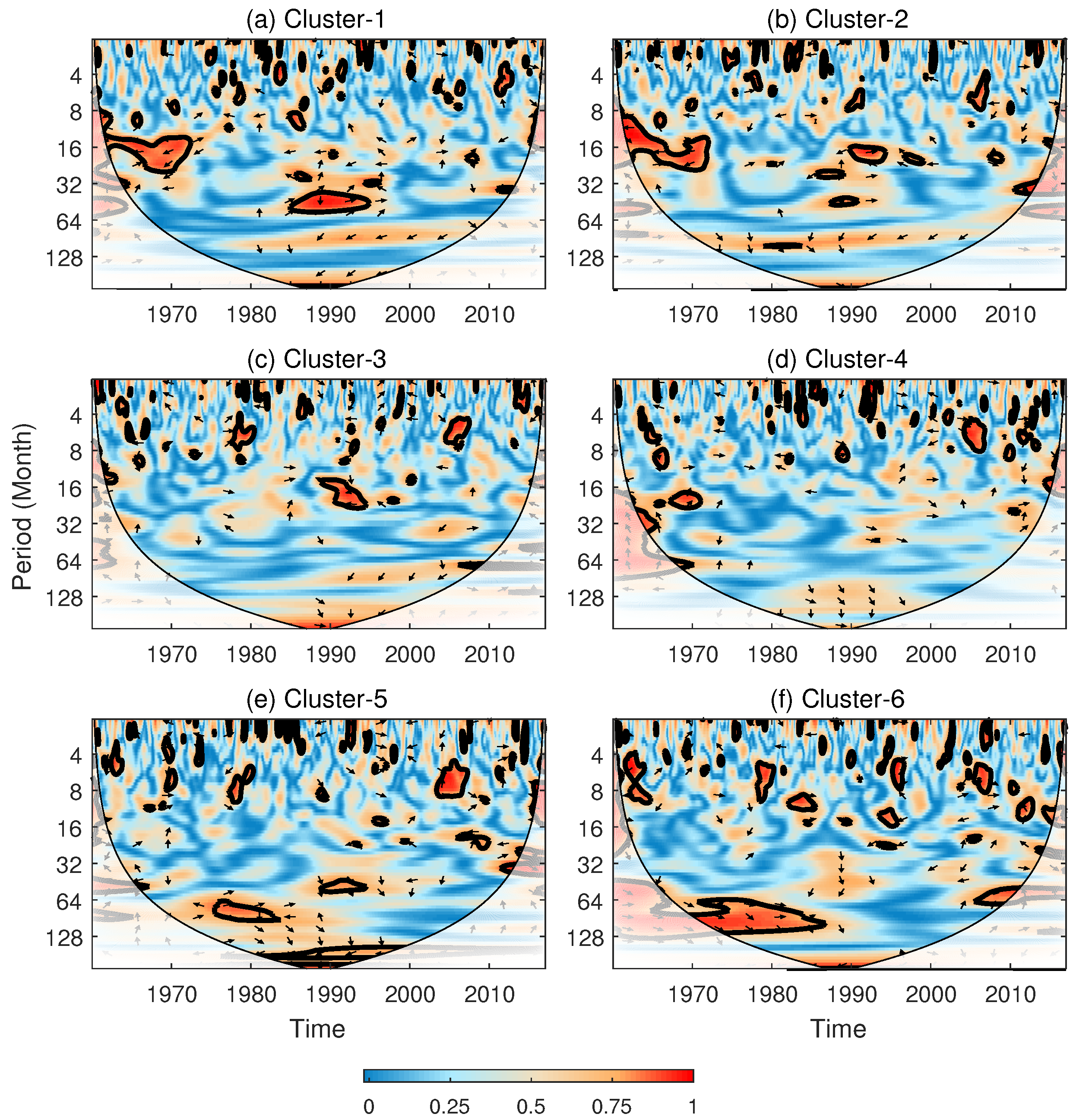
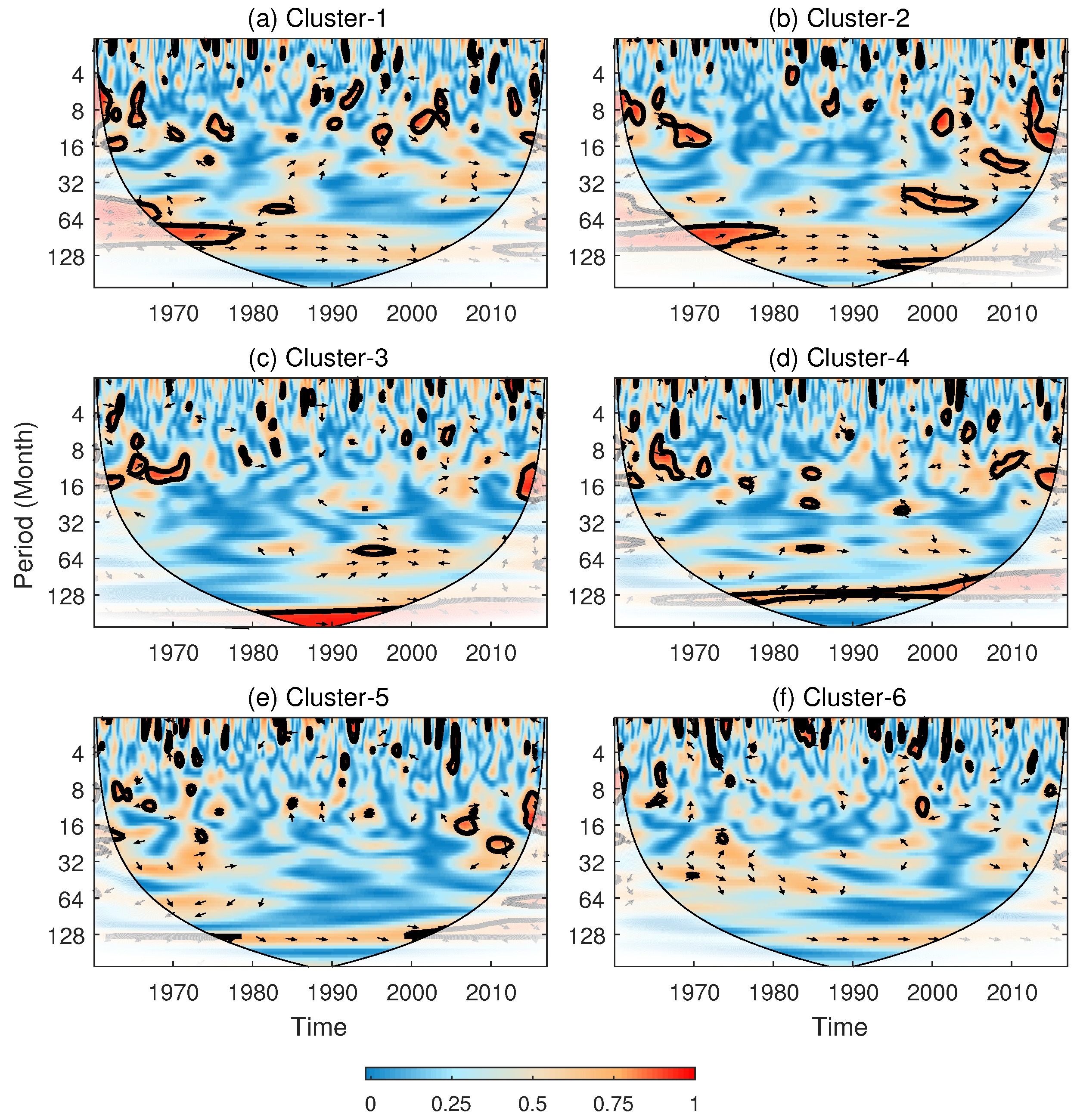
Index Name	Core Variables	Timescale	Applicable Scenarios
Moisture Index (MI) [26]	Precipitation, potential evapotranspiration	Monthly or longer	Agricultural drought monitoring, crop water stress assessment
Weighted Anomaly Standardized Precipitation (WASP) [27]	Precipitation	1–12 months	Rapid assessment of precipitation deficits
Rainfall Deciles (RDs) [28]	Precipitation	Monthly or longer	Assess the current precipitation patterns
Palmer Drought Severity Index (PDSI) [29]	Precipitation, temperature, soil moisture	Long-term (annual or multi-year)	Drought severity and duration
Standardized Precipitation Index (SPI) [30]	Precipitation	Multiple scales (1–48 months)	Meteorological and hydrological drought monitoring
Standardized Precipitation Evapotranspiration Index (SPEI) [13]	Precipitation, potential evapotranspiration	Multiple scales (1–48 months)	Meteorological drought in temperature-sensitive regions
Modified PDSI [31]	Precipitation, temperature, potential evapotranspiration	Long-term (annual or multi-year)	Cumulative drought impact assessment

summarizes a few commonly applied drought indices. The SPEI integrates both precipitation and potential evapotranspiration data so that the balance between water supply and demand can be captured by this index [13,14]. Previous studies have shown that the SPEI was superior to other drought indices such as the SPI and PDSI, because the SPEI can be used to assess drought across multiple time scales [15,16,17]. Furthermore, the SPEI can also be used to evaluate the impacts of global climate change on drought occurrence [13,18]. Recently, there have been many studies reporting the application of the SPEI to investigate the spatiotemporal distribution pattern and changing trends of meteorological droughts in various regions worldwide [19,20,21,22,23,24]. Ma et al. [25] used the SPEI to identify a meteorological drought event, which is indicated when the SPEI values are lower than −0.5 for at least 30 days. Wang et al. [17] analyzed the spatial patterns of drought using the SPEI as the metric in China during 1960–2018. Consequently, for this study, we select the SPEI with a one-month time scale as the meteorological drought index.

In water-scarce regions, it is essential to understand the dynamical causes of drought variations, especially from the perspective large-scale climate variability [32]. Natural climate variability usually plays an important role in shaping regional extreme climatic events such as the frequent drought occurrences [33]. Typically, droughts are driven by extreme natural variations in the global climate system, which are influenced by the interactions between oceans and the atmosphere and even the land surface [34]. It has been confirmed that large-scale oceanic–atmospheric oscillations are tightly related to droughts variations in numerous areas on the Earth [35]. In recent years, various statistical models have been employed to link climate drought indices with several circulation indices, thereby uncovering the remote influences of large-scale oceanic–atmospheric oscillations on drought conditions. Yang et al. [36] analyzed the correlations between three large-scale circulation indices and the SPEI index in Xinjiang, China, utilizing both correlation and partial correlation analysis methods. Gao et al. [4] employed the t-test method to compare the differences in SPEI patterns across East Asia, where the ocean SSTs are linked to the SPEI by complex networks. Additional studies have confirmed that the remote effects of large-scale climate dynamics on drought exhibit temporal variability [35]. Traditional statistical methods such as correlation analysis and the t-test can not reveal the time-varying relationship between large-scale climate dynamics and drought. Bivariate wavelet coherence (BWC) has emerged as a prevalent tool for elucidating scale-specific and localized relationships within transient processes, especially in domains like geophysics [37]. Nevertheless, the BWC method is confined to the analysis of two variables, whereas droughts are often multifaceted and may be influenced by more than just two climate factors. To address this limitation, the multiple wavelet coherence (MWC) method, which builds upon BWC, has been developed. MWC is capable of depicting the combined effects among multiple variables across multiple time scales while preserving the advantages of BWC [38]. Wang et al. [17] utilized the MWC method to identify the primary oscillations that influence the drought pattern in China. The application of MWC has demonstrated that an increased number of predictor variables does not necessarily account for more variations in the response variable, partly due to the common cross-correlation among predictor variables [38]. Mihanoviæ et al. [39] extended BWC to partial wavelet coherence (PWC), where the effect of one other variable is eliminated, like in partial correlation analysis. Recently, Hu and Si [40] developed a modified PWC method considering more than one excluding variable and also providing phase information. This method is effective in revealing the scale-specific and localized bivariate relationships after removing the effects of other variables in geosciences.

The primary aim of this research is to investigate the remote impacts of large-scale ocean-atmosphere oscillations on meteorological drought in Xinjiang by employing the refined PWC method. The meteorological drought is represented by the SPEI. We examine five large-scale oscillation indices: (1) the Southern Oscillation Index (SOI), which reflects temperature fluctuations in the Pacific Ocean, specifically the El Niño–Southern Oscillation (ENSO); (2) the Pacific Decadal Oscillation (PDO) index, representing the first principal component of sea surface temperature anomalies in the North Pacific; (3) the Dipole Mode Index (DMI), quantifying the strength and direction of the Indian Ocean Dipole (IOD); (4) the Arctic Oscillation (AO) index, serving as an indicator of the general circulation of the atmosphere and mass distribution between the poles; and (5) the North Atlantic Oscillation (NAO), characterized by opposite changes in air pressure between the Azores High and the Icelandic Low, which significantly impacts the climate of North America and Europe. The results of the PWC analysis are also compared with those of the BWC method.

The remainder of this paper is organized as follows. The data and statistical methods used in this study are presented in Section 2. The results and discussions are presented in Section 3 and Section 4, respectively. Finally, the main findings of this study are summarized in Section 5.

2. Materials and Methods

2.1. Study Area

Xinjiang is the largest provincial administrative region in terms of land area in Northwest China. It is located in the central part of the Eurasian continent (Figure 1). Xinjiang occupies approximately one-sixth of the country’s total landmass. The nearest ocean to Xinjiang is more than 2500 km away, making it one of the most inland regions in the world [41]. Xinjiang’s topography is characterized by mountains, basins, and deserts. The Tianshan Mountains, stretching across the region, serve as a natural divide between northern and southern Xinjiang [42]. The Tarim Basin and Junggar Basin are two of the largest inland basins in China. Meanwhile, the Taklimakan Desert, the largest mobile desert in China, and the Gurbantunggut Desert add to the region’s unique desert landscape. Xinjiang’s climate is characterized by a temperate continental climate with pronounced seasonal variations [43]. The winters are long, cold, and dry, while the summers are hot and dry. Precipitation is relatively scarce, with the majority occurring in spring and summer. Winter precipitation mainly falls as snow, which accumulates in the mountains and serves as a vital water resource for the region [44]. Since the moist marine air seldom reaches the inland areas [45], Xinjiang is considered one of the driest regions globally [46]. This arid climate results in a unique water cycle in the region [47]. Due to the scarcity of precipitation, Xinjiang is characterized by a lack of water resources and usually suffers from frequent droughts [48].

2.2. Data

The monthly precipitation and mean air temperature time series are utilized to compute the SPEI (Standardized Precipitation Evapotranspiration Index) time series. The original daily meteorological dataset was sourced from the Climate Data Center of the China Meteorological Administration (CMA), with data quality assurance provided by the National Meteorological Information Center (NMIC) [49]. The dataset encompasses 53 meteorological stations with relatively complete time series in Xinjiang, spanning the period from 1961 to 2017 (Figure 1). The official website of the CMA is http://data.cma.cn/ and only open to registered users (accessed on 15 May 2020). All the five large-scale oscillation indices available on the NOAA’s website can be directly accessed at https://www.ncei.noaa.gov/access (accessed on 10 May 2024).

2.3. Methods

2.3.1. SPEI

The SPEI (Standardized Precipitation Evapotranspiration Index) offers a quantitative assessment of drought severity and duration, taking into account both water supply (precipitation) and water demand (evapotranspiration) [13]. In this research, the calculation of the SPEI is based on the climatic water balance on a monthly time scale, specifically the difference between precipitation (P) and potential evapotranspiration (ET0). Subsequently, a probability distribution is fitted to the cumulative water balance series. Then, these cumulative values are transformed into the standard normal distribution to derive the SPEI values. Both the pre-processing of the precipitation and temperature data and the calculation of SPEI values are carried out using the R package “SPEI” [50]. Furthermore, the SPEI can be categorized into distinct classes based on various thresholds. The specific classification criteria are outlined in

Table 2. Drought classification based on the SPEI [13].

SPEI Value	Category
SPEI $\ge 2$	extreme wet
$1.5\le$ SPEI $<2$	severe wet
$1\le$ SPEI $<1.5$	moderate wet
$0.5\le$ SPEI $<1$	slight wet
$-0.5\le$ SPEI $<0.5$	near normal
$-1\le$ SPEI $<-0.5$	slight dry
$-1.5\le$ SPEI $<-1$	moderate dry
$-2\le$ SPEI $<-1.5$	severe dry
SPEI $\le -2$	extreme dry

.

2.3.2. Seasonal Kendall Test and Hierarchical Clustering

The Mann–Kendall (M-K) test is a commonly used statistical approach to detect whether there is a significant positive (increasing) or negative (decreasing) trend within a time series. It is a non-parametric method that does not assume a specific distribution. The M-K test has found widespread application in fields such as climate diagnosis, hydrology, and environmental monitoring. The classical M-K test is not directly applicable to the monthly time series of precipitation, temperature, and the SPEI due to seasonality. Instead, the seasonal Kendall test is employed. Unlike the standard M-K test, the seasonal Kendall test is specifically designed for data exhibiting seasonal patterns, such as monthly or quarterly observations spanning multiple years. By comparing differences between seasonal data points, this test can identify trends that may be obscured by the inherent variability and seasonality of the data. For further details on this method, please refer to [51]. The seasonal Kendall test is implemented using the R package “Kendall” [52].

Spatially closer SPEI time series typically exhibit similar characteristics; thus, in practical applications, it is unnecessary to correlate all SPEI time series with oscillation indices. In this study, the 53 meteorological stations are spatially clustered into distinct groups using the agglomerative hierarchical clustering method, based on the characteristics of the SPEI [53]. Subsequently, the SPEI time series within each cluster are averaged for further analysis. The hierarchical clustering is implemented using the R package “cluster” [54].

2.3.3. Correlation Analysis and Partial Correlation Analysis

Correlation analysis and partial correlation analysis are two basic statistical methods used to study the relationships between the response variable and the predictor variable [55]. Correlation analysis is a statistical approach to investigate whether there is a statistical link between two or more variables. It focuses on the strength and direction of the relationship, which can be positive, negative, or zero. The Pearson correlation coefficient is commonly used to measure the linear relationship between the response variable Y and the predictor variable X, ranging from $-1$ to 1. The mathematical formula used for calculating Pearson correlation coefficient is as follows:

$$r_{xy}={\displaystyle \frac{n\sum x_t{y}_t-(\sum x_t)(\sum y_t)}{[\sqrt{n\sum x_t^2-{(\sum x_t)}^2][n\sum y_t^2-{(\sum y_t)}^2]}}}$$

(1)

where $x_t$ and $y_t$ are the corresponding time series of random variables X and Y, respectively. Partial correlation analysis goes further by measuring the correlation between two variables while controlling for the influence of other variables. This method provides a deeper understanding of the relationship between variables by eliminating the interference of the control variables [56]. For example, the mathematical formula of the partial correlation coefficient between X and Y, excluding the influence of the controlling variable Z, can be calculated using

$$r_{xy·z}={\displaystyle \frac{r_{xy}-r_{xz}{r}_{yz}}{\sqrt{(1-r_{xz}^2)(1-r_{yz}^2)}}}$$

(2)

where $r_{xy}$, $r_{yz}$, and $r_{xz}$ are simple correlation coefficients. The statistical significance of correlation and partial correlation analyses are both determined through a t-test, and the significance level is set to be $\alpha =0.05$. Both correlation and partial correlations are calculated using the R package “ppcor” [57].

2.3.4. A Brief Review of Wavelet Coherence Analysis

Before computing BWC and PWC, the continuous wavelet transform (CWT) needs to be calculated. Given a time series $X=\{x_i,i=1,2,\cdots ,N\}$ with a constant sampling interval $\delta t$, the CWT $W_i\left(s\right)$ at scale s and time $t_i=i\delta t$ can be considered as an enhanced version of the discrete Fourier transform $F\left(\omega \right)={\sum }_j{x}_{j}exp\left(i\omega t_j\right)$. Here, the periodic exponential function $exp\left(i\omega t_j\right)$ of the Fourier transformation is substituted by a special wavelet function $\psi (t_j-t_i,s)$ [37]. The wavelet function can be translated by varying the localized time t, and contracted and stretched by changing the scale s. By introducing wavelet basis functions with adjustable time–frequency windows, the CWT achieves high time resolution at high frequencies and high frequency resolution at low frequencies. This transform decomposes a signal into a linear combination of wavelet functions through scaling and translation along the time axis. Specifically, the time series can be decomposed as follows:

$$W_i^X\left(s\right)=\sum _{j=0}^{N-1}{x}_j\sqrt{{\displaystyle \frac{\delta t}{s}}}{\psi }_0^{*}\left({\displaystyle \frac{t_j-t_i}{s}}\right)$$

(3)

where * denotes the complex conjugate, $\sqrt{{\displaystyle \frac{\delta t}{s}}}$ denotes the normalization factor (so that $\psi$ has units of energy), and the wavelet power is defined as $|W_i^X{\left(s\right)|}^2$. A variety of mother wavelets can be utilized for the wavelet transform, with the Morlet wavelet standing out as it offers an excellent balance between location and scale localization, being composed of a complex exponential multiplied by a Gaussian window. In this study, the Morlet wavelet, a nonorthogonal function,

$${\psi }_0\left(\eta \right)={\pi }^{-1/4}{e}^{i{\omega }_0\eta }{e}^{-{\displaystyle \frac{1}{2}}{\eta }^2}$$

(4)

is adopted. Here, $\eta$ is the dimensionless time and ${\omega }_0$ is the dimensionless frequency. The cone of influence (COI) represents the region within the wavelet power spectrum where edge effects cannot be disregarded, as the wavelet is not fully localized in time. The statistical significance of wavelet power is evaluated in comparison to red noise. The CWT is particularly advantageous for analyzing non-stationary signals, enabling feature extraction and the identification of crucial signal characteristics. For further insights into the CWT method, please refer to [37].

Wavelet coefficients and their complex conjugates serve to compute auto-wavelet power spectra and cross-wavelet power spectra. The BWC is determined by dividing the smoothed cross-wavelet power spectrum of two variables by the product of their respective auto-wavelet power spectra [37]. For time series X and Y with the wavelet transform $W_i^X\left(s\right)$ and $W_i^Y\left(s\right)$, the wavelet transform coherence can be defined as follows [58]:

$$R_i^2={\displaystyle \frac{|S\left(s^{-1}{W}_i^{XY}\left(s\right)\right){|}^2}{S\left(s^{-1}{\left|W_i^X\left(s\right)\right|}^2\right)·S\left(s^{-1}{\left|W_i^Y\left(s\right)\right|}^2\right)}}$$

(5)

where S denotes the smoothing operator and

$$W_i^{XY}\left(s\right)=W_i^X\left(s\right)·W_i^{Y*}\left(s\right)$$

(6)

where the symbol * denotes the complex conjugate. The value of $R_i^2$ ranges between 0 and 1, where 0 signifies no correlation between the two time series, and 1 indicates a perfect correlation between them.

Similarly to BWC, PWC is calculated from auto- and cross-wavelet power spectra for the response variable Y, predictor variable X, and excluding variables Z ($Z=\{Z_1,Z_2,\cdots ,Z_q\}$). Koopmans [59] formulated the multivariate complex PWC in the frequency (or scale) domain. Hu and Si [40] extended Koopmans’ method from the frequency (or scale) domain to the time–frequency (or location–scale) domain. Therefore, the complex PWC between Y and X, after excluding variables Z at scale s and location t, can be denoted as follows:

$${\gamma }_{Y,X·Z}={\displaystyle \frac{\left(1-R_{Y,X,·Z}^2(s,t)\right){\gamma }_{Y,X}(s,t)}{\sqrt{\left(1-R_{Y,Z}^2(s,t)\right)\left(1-R_{X,Z}^2(s,t)\right)}}}$$

(7)

where the symbol “·” is the notation for excluding variables. More details about the calculations of $R_{Y,X,·Z}^2(s,t)$, $R_{Y,Z}^2(s,t)$, and $R_{X,Z}^2(s,t)$ can be found in [38]. Moreover, the wavelet phase between the response variable Y and the predictor variable X can also be computed. A zero phase difference indicates that the examined time series move in unison. An arrow pointing to the right or left signifies that the time series are in-phase or anti-phase, respectively, whereas an arrow pointing upwards reveals a ${90}^{\circ }$ lag of the predictor variable behind the response variable. The Monte Carlo method is employed to determine the $95\%$ statistical significance of BWC, MWC, and PWC [37,38,40]. The ability of the predictor variables to elucidate the variations in the response variable across different scales can be evaluated through the average BWC or PWC and the percent area of significant coherence (PASC) in relation to the scale-location region, as outlined in [38]. A higher PASC accompanied by a larger PWC indicates that the variations in the response variable are more accurately explained by a specific predictor variable. The wavelet coherence analysis is implemented using the matlab package “pwc” [60].

3. Results

The Pearson correlations among these five indices are depicted in Figure 2. SOI is negatively correlated with the PDO and DMI, but positively correlated with the AO. The PDO, in turn, is negatively correlated with the AO. Additionally, the AO displays a positive correlation with the NAO. In conducting wavelet coherence analysis, it is crucial to take into account the statistically significant cross-correlations among these oscillation indices. These cross-correlations are incorporated in the following partial correlation analysis and partial wavelet coherence analysis.

The seasonal Kendall method was employed to analyze the evolving trends in precipitation, temperature, and the SPEI index at 53 stations from 1961 to 2017. The trend graph is depicted in Figure 3. The results revealed that precipitation increased during the period 1961–2017 at most stations, with the exceptions being a few stations located in southern Xinjiang. Furthermore, the mean temperature also rose, aligning with global warming trends. However, only a limited number of stations in northern Xinjiang exhibited positive trends in the SPEI series, while a greater number of stations in southern Xinjiang showed negative trends. This means droughts in southern Xinjing became severer, while northern Xinjiang became wetter.

The 53 monthly SPEI time series were grouped employing the agglomerative hierarchical clustering method. The optimal number of clusters was determined based on the disparity between the average correlation between groups and the average correlation within groups. The spatial distribution of the six clusters is illustrated in Figure 4, while the average SPEI time series for each cluster is depicted in Figure 5. Cluster 1 comprises 10 stations situated on the northern side of Xinjiang, while Cluster-2 also includes 10 stations primarily located at the northern foothills of the Tianshan Mountains. The stations in Cluster 3 are found in the high-latitude regions of the Tianshan Mountains. Stations in Cluster 4 are distributed across an area ranging from the Taklimakan Desert to southeast Xinjiang. The 12 stations in Cluster 5 are scattered along the edge of the Taklimakan Desert. Finally, the four stations in Cluster 6 are located in the high-latitude area of the western end of the Kunlun Mountains. The differences in the SPEI time series among the six clusters are not readily apparent and can be further examined using a multi-scale analysis method.

The average SPEI time series correlations and partial correlations with large-scale oscillators for six clusters are illustrated in Figure 6. Correlation analysis indicates that Clusters 4 and 5 have positive correlations with the PDO time series but negative correlations with the DMI time series. Cluster 6, on the other hand, positively correlates with the AO. Additionally, Clusters 2, 3, and 5 positively correlate with the NAO. The results of the partial correlation analysis largely align with those of the correlation analysis. Specifically, the SPEI time series across all clusters, except Cluster 6, positively correlates with the PDO when other variables (SOI, DMI, and AO) are held constant. Furthermore, Cluster 6’s SPEI time series also negatively correlates with the DMI. The SPEI time series in Clusters 1 and 4 are negatively correlated with the AO. Notably, the partial correlation analysis confirms that all clusters except Cluster 6 positively correlate with the NAO when the other oscillator AO is controlled for.

The squared wavelet coherence of the SPEI in the six clusters, along with the SOI, is depicted in Figure 7. The bivariate wavelet coherence analyses reveal a weak teleconnection between large-scale circulation and the SPEI in Xinjiang. Notably, this teleconnection exhibited variation not only among the clusters but also across diverse time scales and periods, despite the sparse distribution of areas with significant common power. For example, the SPEI in Cluster 4 shows a positive correlation with the SOI for periods spanning 16 to 65 months (1985–1995). This was indicated by the small arrows in this region pointing to the left, suggesting an anti-phase (negatively correlated) relationship between the SPEI and SOI. The significant common power period detected in the WTC plots, ranging from 16 to 64 months, basically coincides with the ENSO period. Figure 8 presents the PWC between the SPEI and SOI, after excluding the influences of the PDO, DMI, and AO.

Table 3. Average bivariate wavelet coherence (BWC) between the SPEI and individual circulation oscillator time series. The percentages in the round brackets are the corresponding PACS values.

	SOI	PDO	DMI	AO	NAO
Cluster 1	0.33 (5.46%)	0.34 (6.45%)	0.34 (2.88%)	0.38 (9.46%)	0.34 (5.67%)
Cluster 2	0.34 (6.58%)	0.35 (6.79%)	0.29 (4.43%)	0.37 (10.32%)	0.35 (10.1%)
Cluster 3	0.31 (3.31%)	0.32 (4.72%)	0.30 (4.15%)	0.35 (7.76%)	0.33 (7.22%)
Cluster 4	0.35 (6.8%)	0.35 (8.63%)	0.30 (4.02%)	0.37 (8.49%)	0.36 (6.22%)
Cluster 5	0.34 (5.3%)	0.33 (6.72%)	0.34 (5.81%)	0.33 (5.84%)	0.33 (5.91%)
Cluster 6	0.35 (8.13%)	0.33 (5.62%)	0.35 (8.47%)	0.32 (5.52%)	0.33 (6.33%)

and

Table 4. Average partial wavelet coherence (PWC) between the SPEI and individual circulation oscillator after excluding other indicators. The percentages in the round brackets are the corresponding PACS values.

	SOI−(PDO, DMI, AO)	PDO−(SOI, AO)	DMI−(SOI)	AO−(SOI, PDO, NAO)	NAO−(AO)
Cluster 1	0.43 (4.64%)	0.4 (6.28%)	0.34 (6.08%)	0.46 (7.2%)	0.39 (5.78%)
Cluster 2	0.44 (6.84%)	0.4 (5.39%)	0.36 (7.82%)	0.43 (4.13%)	0.4 (6.97%)
Cluster 3	0.41 (3.75%)	0.38 (3.53%)	0.33 (4.15%)	0.44 (7.99%)	0.36 (5.15%)
Cluster 4	0.42 (4.17%)	0.38 (3.89%)	0.35 (4.47%)	0.43 (4.74%)	0.37 (5.32%)
Cluster 5	0.45 (6.03%)	0.41 (4.45%)	0.38 (6.09%)	0.4 (5.72%)	0.34 (3.42%)
Cluster 6	0.43 (7.44%)	0.41 (7.26%)	0.35 (3.29%)	0.41 (6.24%)	0.35 (2.8%)

showcase the averages of BWC and PWC, as well as the corresponding PACS. When compared to the bivariate wavelet coherence (BWC), the averages of PWC are higher, indicating stronger relationships. Furthermore, a larger area with higher PWC values suggests tighter correlations between the SPEI in Xinjiang and the SOI (Figure 8). For instance, the PWC detected a closer relationship between drought in Clusters 5 and 6 and the ENSO of longer periods (32–128) during 1965–1985. However, it is important to note that both the correlation analysis and partial correlation analysis, as shown in Figure 6, indicate that the SPEI time series are not statistically correlated with the SOI when considering all time scales. Despite this, BWC and PWC still detect significant correlations between the SPEI and SOI at specific time scales and periods. This suggests that the relationship between the SPEI and SOI may be more complex and scale-dependent than previously thought.

The squared wavelet coherence between the six SPEI time series and PDO time series is displayed in Figure 9. Figure 10 presents the PWC between the SPEI and PDO, after excluding the influences of the SOI, and AO. Table 3 and Table 4 present the averages of BWC and PWC values, as well as the PACS for bivariate wavelet coherence analyses and partial wavelet coherence analyses. The bivariate wavelet coherence analyses reveal a weak teleconnection between the decadal oceanic oscillation, the PDO, and the SPEI in Xinjiang. The spatial patterns of higher BWC values and higher PWC values are largely similar, particularly in the period range of 16–64 months. Most arrows in the significant power area point to the right, indicating a positive correlation between the SPEI and PDO. This finding is consistent with the results of both the correlation and partial correlation analyses. For instance, the correlation analysis shows that the SPEI and PDO are positively correlated for Cluster 4, but this correlation becomes nonsignificant in the partial correlation analysis. The BWC analysis indicates that the SPEI in Cluster 4 was positively correlated with PDO occurrence periods of 80–128 months (1980–2000) (Figure 9d). However, this correlation was not detected by the PWC analysis (Figure 10d). This suggests that while there may be a relationship between the SPEI and PDO at certain time scales and periods, other factors may also influence this relationship, leading to differences in the detection of correlations by different methods.

In the Supplementary Materials, the results of BWC and PWC for the SPEI versus the DMI and AO are given in Figures S1–S4, respectively. The partial correlation analysis reveals that the SPEI in Clusters 4 and 5 exhibits a negative correlation with the DMI (Figure S2). This negative correlation is partially mirrored in the PWC, where arrows in the significant power areas point to the left. Despite the overall weak correlation between the SPEI in Xinjiang and the DMI, the influence of large-scale oscillations on drought can still be discerned through BWC and PWC analyses (Figures S1 and S2). The PWC analysis further indicates that drought during the 64–128 month periods between 1970 and 1990 is negatively correlated with the AO in Xinjiang, after excluding the influences of the SOI, PDO and NAO. Figure 11 and Figure 12 showcase the results of BWC and PWC analyses for the SPEI versus NAO. The BWC analysis suggests that drought in Xinjiang is positively correlated with the NAO at periods of 128 months or longer, particularly in Clusters 2 and 3. In the PWC analysis, the influence of the AO has been excluded. Additionally, the PWC analysis indicates that the SPEI in Cluster 3 is positively correlated with the NAO at a period of 140 months. Moreover, the positive correlation between the SPEI and NAO in Clusters 1 and 2 is more pronounced during the 64–128 month periods throughout the entire study period (Figure 11a,b).

4. Discussion

In this study, we selected Xinjiang, an extremely dry area in China, as the study area. Meteorological drought is predominantly influenced by a multitude of climate factors, and is usually correlated with large-scale climate variations [35]. Under the background of global climate change, the relationship between large-scale climate oscillations and regional climate variations might also change. Consequently, regional climate change may alter the evaporation rate, the precipitation frequency and intensity, and finally change the drought [61].

Previous studies reported that the annual mean temperature in Xinjiang increased by 0.30–0.40 °C/decade from 1961 to 2015, exceeding the global average [62,63]. Numerous other studies have also indicated that the climate in Northwest China, including Xinjiang, has progressively become wetter since the 1960s amidst the backdrop of global warming [64,65]. In this paper, the trends of both monthly precipitation and temperature time series have been observed to increase during the period from 1961 to 2017. This aligns with the findings reported in a previous study [42,66]. The increase in precipitation is attributable to enhanced westerly moisture transport due to the Atlantic Oscillation [67]. Zhang et al. [68] discovered that the severity of drought across Xinjiang is decreasing overall, yet there are regional variations. Specifically, northern Xinjiang has seen a decline in drought severity, while southern Xinjiang has experienced a slight increase. Additionally, Li et al. [69] also noted a decrease in drought severity during the period from 1961 to 2012. The meteorological drought index utilized in this study is the widely recognized SPEI [13]. The trends in SPEI values at most stations in southern Xinjiang indicate a downward direction, while in northern Xinjiang, the trends are nonsignificant. This suggests that drought conditions in southern Xinjiang worsened during the period from 1961 to 2017. Zhang et al. [70] discovered that the wintertime SPEI time series in Xinjiang exhibited upward trends, whereas the springtime, summertime, and autumntime SPEI time series demonstrated downward trends. The findings about the trends in the SPEI in this study are basically consistent with those in [70]. Wang et al. [34], on the other hand, utilized a different drought index, the Palmer Drought Severity Index (PDSI), to analyze changing trends. They observed a significant increase in the PDSI in most regions of Xinjiang, suggesting a trend towards wetter conditions. This apparent inconsistency can be explained as follows. The PDSI is based on the concept of water supply and demand. It considers both current and historical moisture conditions, incorporating factors such as precipitation, temperature, soil properties, and land use that affect evapotranspiration and soil moisture changes [29]. When applying the M-K test to analyze trends in drought indices, the differences in sensitivity and data requirements between the PDSI and SPEI can lead to different results. The PDSI’s lower sensitivity to evapotranspiration changes may result in smoother trends that are less affected by short-term climatic fluctuations. In contrast, the SPEI’s higher sensitivity may capture more nuanced trends related to changes in both precipitation and evapotranspiration.

Large-scale atmospheric circulation patterns reflect the natural variations in the Earth’s climate system, and then directly influence the transportation of vapor from ocean to land and shape the regional drought conditions around the world [35,71,72]. For instance, atmospheric circulations patterns around the Pacific are often linked to large-scale ocean–atmospheric oscillations, such as the ENSO and PDO. Situated in the transitional zone between the mid-latitude westerlies, Xinjiang’s climate exhibits a high degree of sensitivity to changes in the westerly jet stream. Due to global warming, Arctic Amplification has induced a poleward displacement of the westerly jet, while the subtropical high’s northward expansion has modified the moisture transport routes on the Euro-Asian continent [73]. For the Central Asian continent, the decrease in winter moisture originating from the Atlantic and Mediterranean via the westerlies stands in contrast to the increase in summer moisture from the periphery of the South Asian monsoon [74]. Therefore, the investigation of drought variations should be linked to these large-scale climate oscillations, including their interactions with ocean–atmospheric oscillations, and is indispensable for understanding the mechanisms that underlie meteorological drought. In this study, the monthly SPEI time series for 53 meteorological stations were computed using monthly precipitation and mean temperature datasets. Given Xinjiang’s complex topography and vast territory, there is considerable spatial variability in both precipitation and temperature. Consequently, the hierarchical clustering method was employed to categorize the 53 stations into distinct homogeneous subregions (clusters). As a result, the SPEI time series within the same cluster exhibit similar characteristics. The clustering process has been widely applied in previous studies [35,49,75]. Wang et al. [17] investigated the temporal and spatial patterns of drought in China, dividing the entire study area into nine river basins. However, we noticed that this division may not be appropriate for meteorological drought in this study, as a single river basin often encompasses a diverse range of climate types. Besides the clustering method, the spatial variability of drought can also be considered by using the empirical orthogonal function (EOF), rotated empirical orthogonal function (REOF) [34], and spatial interpolation [36]. Since our primary goal is to examine the relationship between drought and large-scale ocean-atmosphere oscillators employing the wavelet coherence analysis method, it is logical to correlate a consolidated SPEI time series with climate time series. Hence, we utilized the hierarchical clustering method and computed the average SPEI time series for each cluster, designating it as the consolidated SPEI time series. The spatial arrangement of these clusters broadly mirrors the spatial variations in climate and topography.

The ENSO represents the complex ocean-atmosphere interactions in the tropical Pacific region, with the ENSO-PDO relationship being one of the most extensively studied coupling effects [4,76]. Previous research has thoroughly examined the impact of the ENSO on the global climate system, with numerous articles delving into its varied effects on temperature, precipitation, and other climatic factors [77,78,79]. The ENSO was previously considered the primary trigger for numerous episodic droughts globally; the remote impact of the PDO and ENSO on Xinjiang’s climate has also been reported [36]. Previous studies have indicated that a positive phase of the PDO tends to promote precipitation in Xinjiang and a negative phase might cause dryness, aligning with the influence of the ENSO pattern on the region’s drought variations [36]. In addition to the PDO and ENSO originating in the Pacific, another significant climate variation, the Indian Ocean Dipole (IOD), plays an important role in affecting the regional climates around the Indian Ocean and even further regions. The IOD represents the oscillations of the difference in sea surface temperatures (SSTs) between the of the IOD are intricate and sometimes interact with the ENSO that occurs in the Pacific Ocean [80,81]. In this study, the intensify of the IOD is presented as a simple climate indictor, the DMI. The reason why the third climate indictor, AO, is selected is because the AO is an important atmospheric circulation mode affecting the climate variability in the Northern Hemisphere [17,34]. It was reported that the negative phase of the AO might increase cold air incursions, but this effect was offset by the weakening Siberian High, leading to fewer extreme cold events in Xinjiang [82]. The last climate indictor is the NAO, which can strongly influence the large-scale atmospheric circulation patterns in the Atlantic region. Then, the NAO can subsequently affect the flow of moisture and temperature across Eurasia. During a positive NAO phase, stronger westerly winds may usher in warmer and wetter air to Central Asia, whereas during a negative phase, colder and drier air may prevail [83]. Xinjiang is situated in the heartland of Eurasia, remote from any ocean on Earth. Consequently, we chose five representative ocean-atmosphere oscillations for this study. Our classical correlation analysis revealed that the time series of these five oscillations exhibit either positive or negative correlations.

The subsequent correlation analysis between the large-scale oscillators and SPEI was conducted using partial correlation or partial wavelet coherence analysis, respectively. Partial correlation is a simpler method that looks at the direct relationship between two variables, while partial wavelet coherence analysis provides a more detailed view of how these relationships change over time and across different frequency components. For the ENSO, both classical correlation and partial correlation analyses showed that there is no statistically significant correlations between SPEI time series and SOI time series. However, both BWC and PWC still detect significant correlations between the SPEI and SOI at some specific time scales and periods [17,34]. This finding indicated that the relationship between the SPEI and SOI may be more complex and scale-dependent. Moreover, the statistical analyses also indicated that droughts in Clusters 4, 5, and 6 exhibit a stronger correlation with the SOI, PDO, and DMI time series. Despite Xinjiang’s remote location from the ocean, southern Xinjiang occasionally receives moisture from the Indian monsoon (southwest monsoon) and East Asian monsoon (southeast monsoon) under specific meteorological conditions [84,85]. Additionally, Xinjiang primarily receives moisture from westerly winds that transport moisture from the Atlantic Ocean, Mediterranean Sea, and adjacent water bodies [86]. This moisture is generally obstructed by the Tianshan Mountains, causing it to rise and result in condensation and precipitation in northern Xinjiang. Consequently, our findings revealed that droughts in Xinjiang tend to correlate with the NAO. Even though Xinjiang is situated far from any ocean, the signatures of large-scale ocean-atmosphere oscillations can still be identified through classical correlation analysis or wavelet coherence analysis methods.

5. Conclusions

Xinjiang is located in the arid region of Central Asia, characterized by high evaporation rates and highly variable precipitation patterns both spatially and temporally, leading to frequent droughts in the area. This study builds upon previous research conducted in Xinjiang by incorporating five key ocean-atmosphere oscillations. In this study, the one-month SPEI is utilized as a meteorological drought indicator, which takes into account both precipitation and evapotranspiration. Monthly precipitation and mean temperature time series from 53 meteorological stations located in Xinjiang were used to calculate the monthly SPEI time series. Subsequently, the seasonal Kendall test was applied to analyze trends in precipitation, temperature, and the SPEI, respectively. The combined effect of increased precipitation and temperature has led to a decrease in SPEI values, indicating a worsening of meteorological drought conditions in Xinjiang, particularly in its southern region.

The 53 monthly SPEI time series were categorized using the agglomerative hierarchical clustering method. The spatial arrangement of these clusters broadly mirrors the topographical and climatic diversity of Xinjiang, with the SPEI time series within each cluster displaying comparable characteristics. The overall correlation between the SPEI time series and large-scale ocean-atmosphere oscillator time series, as revealed by classical correlation or partial correlation methods, is either weak or negligible. Given the cross-correlations among these large-scale ocean-atmosphere oscillators, the partial wavelet coherence (PWC) method was employed to uncover scale-specific and localized bivariate relationships, after accounting for the influences of other variables. Both the bivariate wavelet coherence (BWC) and PWC methods were able to detect significant correlations between the SPEI and the ocean-atmosphere oscillators at certain specific time scales and periods. Our statistical analyses indicate that droughts in southern Xinjiang are more susceptible to the influence of ocean-atmosphere oscillators originating in the Pacific or Indian Oceans, whereas droughts in northern Xinjiang tend to be affected by climate variations stemming from the Atlantic or Arctic Oceans.