Evaluation of ICESat-2 Laser Altimetry for Inland Water Level Monitoring: A Case Study of Canadian Lakes
Abstract
:1. Introduction
2. Materials and Methods
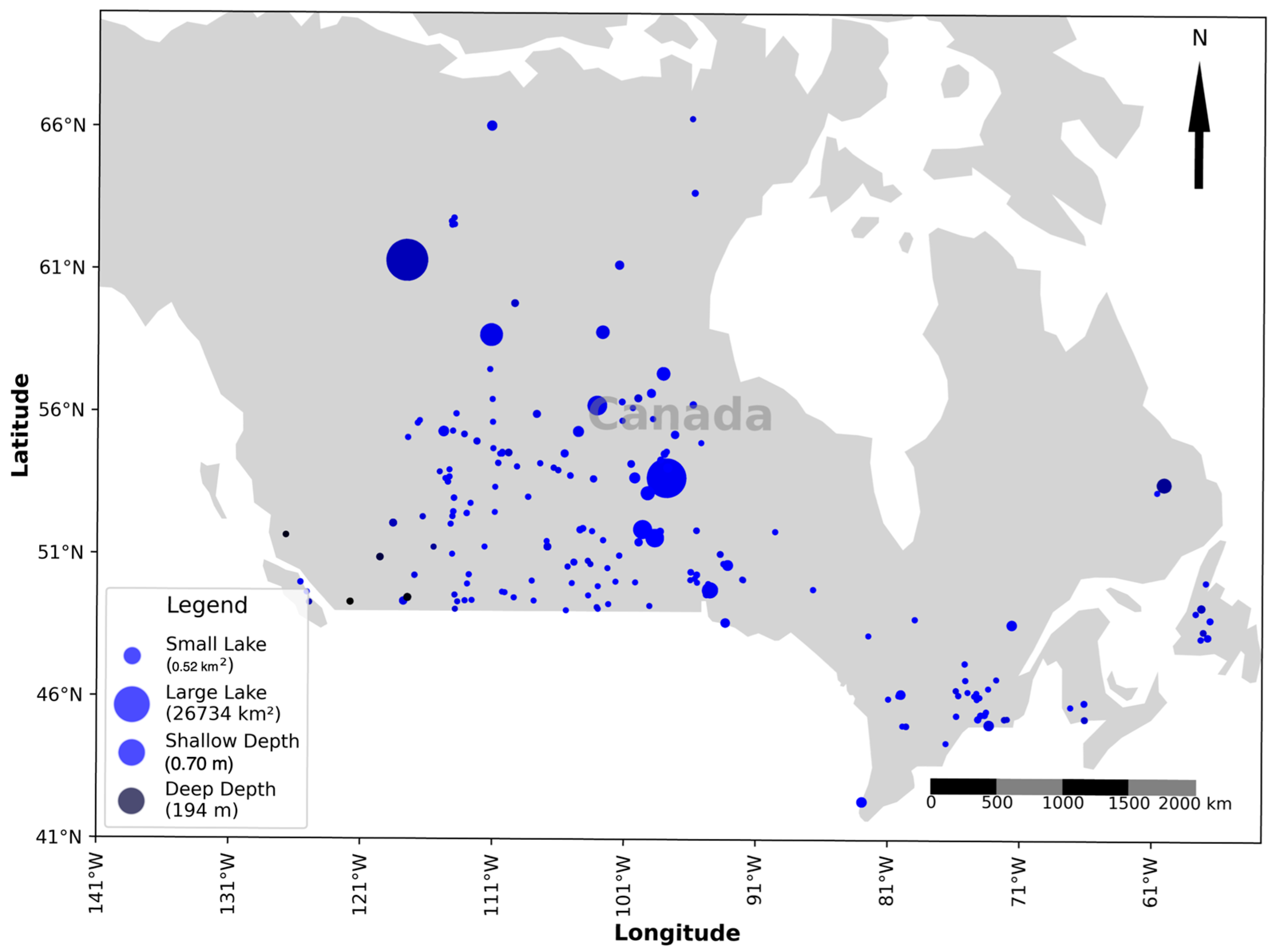
2.1. Geographical Scope of the Study
2.2. Data
2.2.1. ICESat-2 ATL13
2.2.2. HydroLAKES
2.2.3. Gauge Station Data
2.3. Methodology
2.3.1. Data Preprocessing and Lake Selection
- Presence of a Gauge Station: To facilitate validation, a hydrometric gauge station had to be associated with the lake. Each station location was cross-referenced with HydroLAKES polygons, and only lakes with corresponding in situ measurements were selected.
- Inclusion in HydroLAKES: Only lakes identified in HydroLAKES (≥10 ha surface area) were considered to ensure data consistency and compatibility with established lake classifications.
- Sufficient ICESat-2 Observations: The lake needed to have at least 10 days of ICESat-2 ATL13 measurements to enable a meaningful temporal analysis.
2.3.2. Outlier Removal
2.3.3. Water Level Extraction
2.3.4. Advanced Statistical Analysis: Refined Hydrological Assessment
3. Results and Discussions
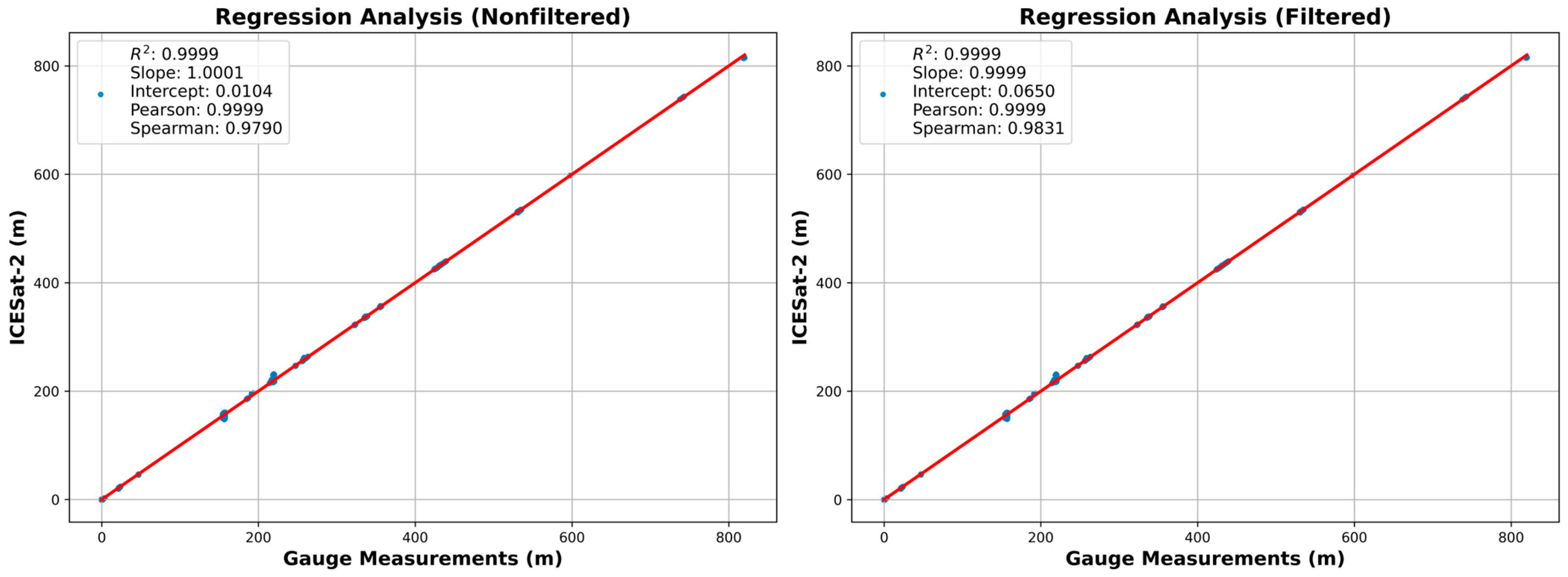
3.1. Error Metric Evaluation and Filtering Effects on ICESat-2 Water Level Estimates
3.2. Regression and Correlation Analysis
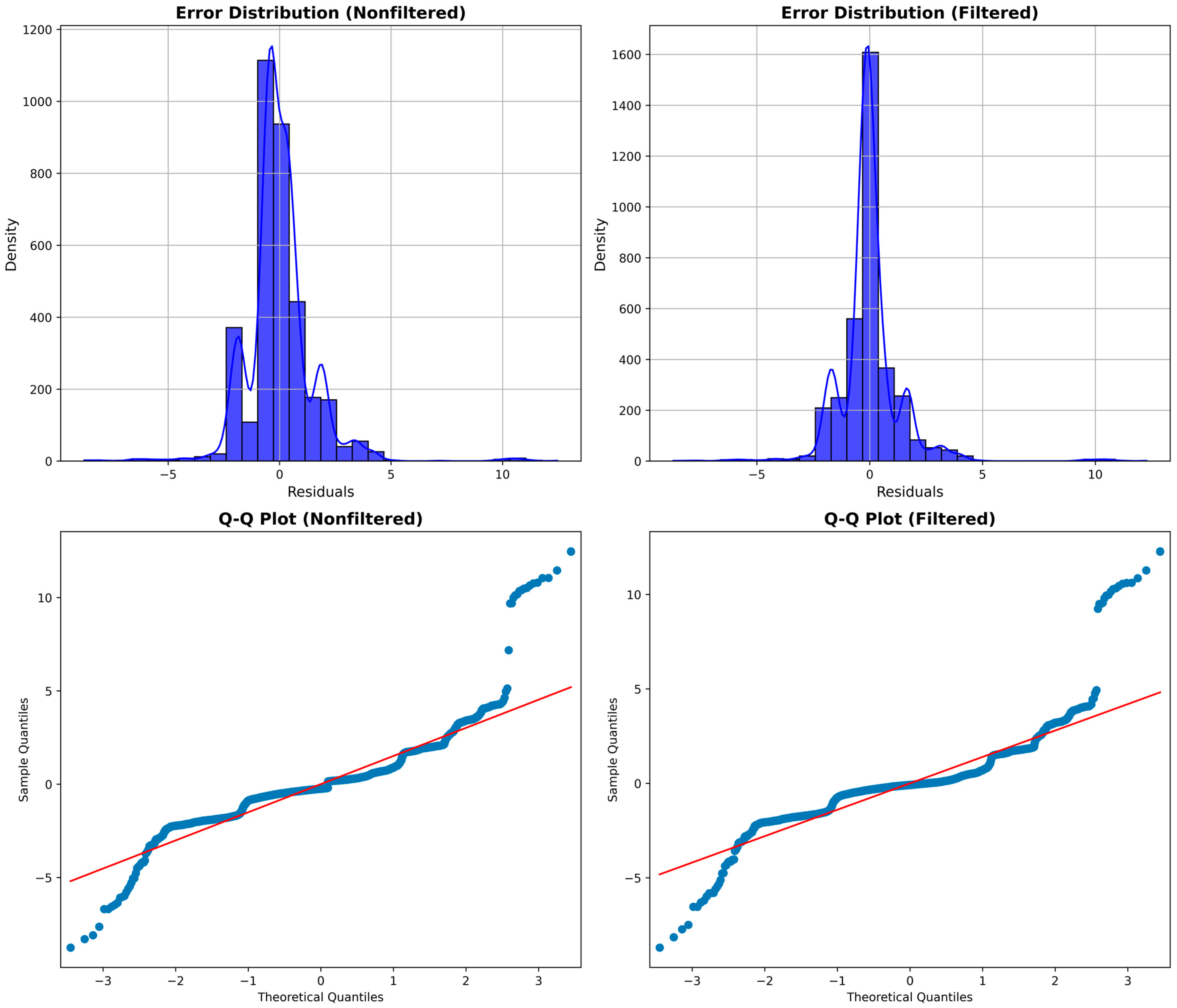
3.3. Error Distribution Characteristics
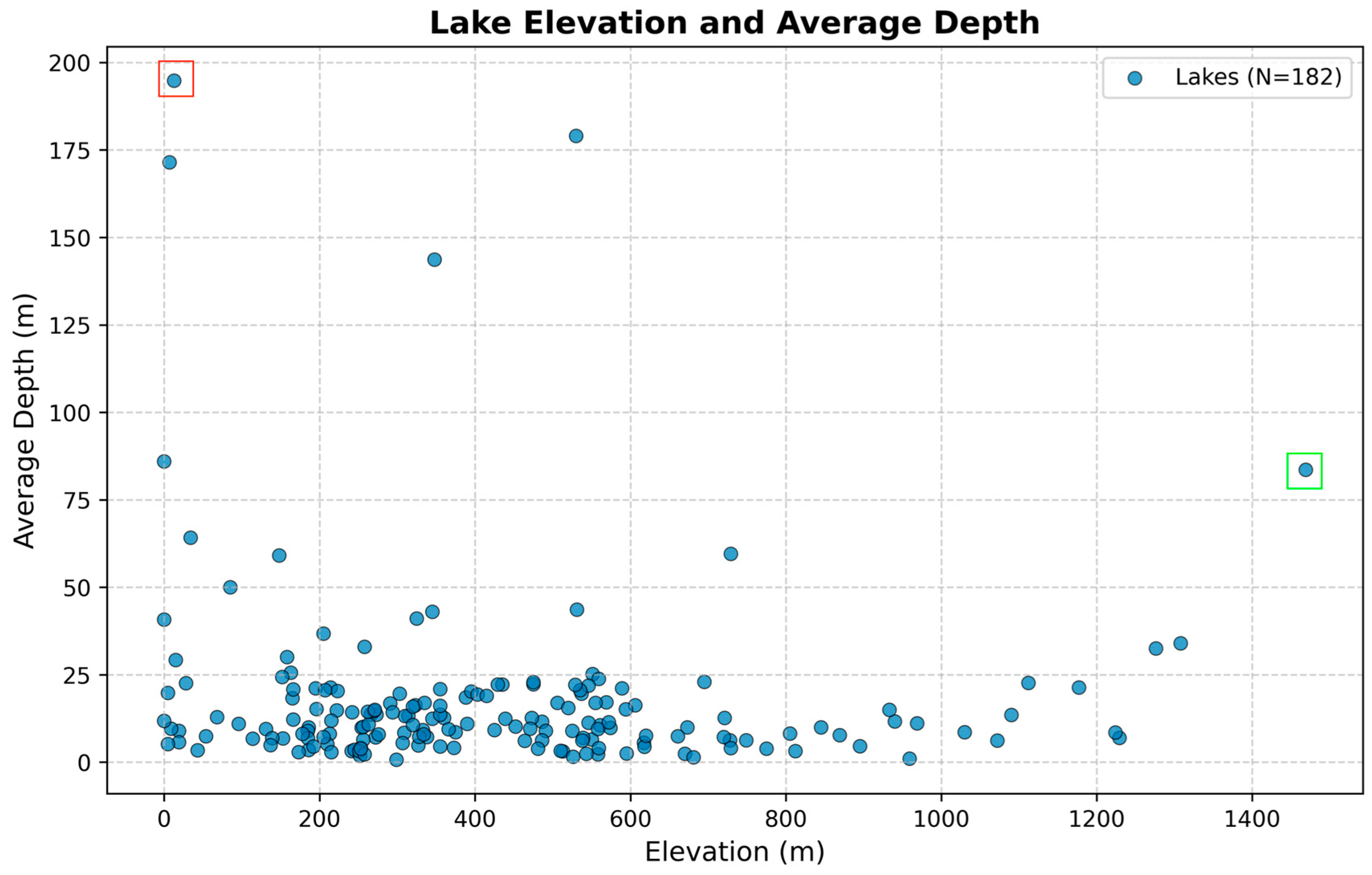
3.4. Spatial Variability of Errors
3.5. Effect of Lidar Point Density on Accuracy
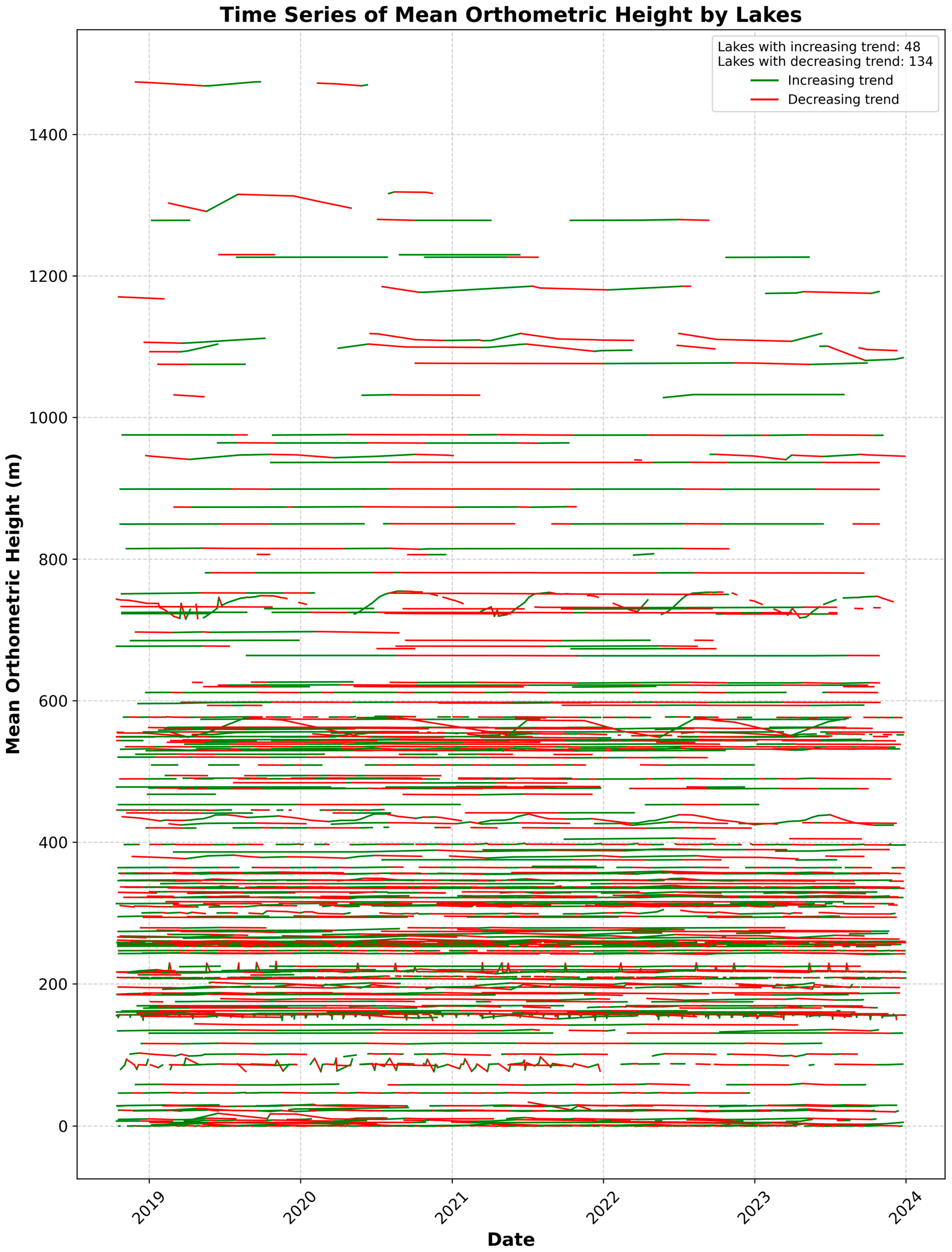
3.6. Temporal Variability of Water Levels
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Whitehead, P.G.; Wilby, R.L.; Battarbee, R.W.; Kernan, M.; Wade, A.J. A review of the potential impacts of climate change on surface water quality. Hydrol. Sci. J. 2009, 54, 101–123. [Google Scholar] [CrossRef]
- Hao, H.; Yao, J.; Chen, Y.; Xu, J.; Li, Z.; Duan, W.; Ismail, S.; Wang, G. Ecological transitions in Xinjiang, China: Unraveling the impact of climate change on vegetation dynamics (1990–2020). J. Geogr. Sci. 2024, 34, 1039–1064. [Google Scholar] [CrossRef]
- Williamson, C.E.; Saros, J.E.; Vincent, W.F.; Smol, J.P. Lakes and reservoirs as sentinels, integrators, and regulators of climate change. Limnol. Oceanogr. 2009, 54, 2273–2282. [Google Scholar] [CrossRef]
- Heino, J.; Alahuhta, J.; Bini, L.M.; Cai, Y.; Heiskanen, A.S.; Hellsten, S.; Angeler, D.G. Lakes in the era of global change: Moving beyond single-lake thinking in maintaining biodiversity and ecosystem services. Biol. Rev. 2021, 96, 89–106. [Google Scholar] [CrossRef]
- Xiao, Q.; Xu, X.; Qi, T.; Luo, J.; Lee, X.; Duan, H. Lakes shifted from a carbon dioxide source to a sink over past two decades in China. Sci. Bull. 2024, 69, 1857–1861. [Google Scholar] [CrossRef]
- Wu, C.; Wu, X.; Lu, C.; Sun, Q.; He, X.; Yan, L.; Qin, T. Characteristics and driving factors of lake level variations by climatic factors and groundwater level. J. Hydrol. 2022, 608, 127654. [Google Scholar] [CrossRef]
- Raihan, A. A review of the global climate change impacts, adaptation strategies, and mitigation options in the socio-economic and environmental sectors. J. Environ. Sci. Econ. 2023, 2, 36–58. [Google Scholar]
- Adebisi, N.; Balogun, A.L.; Min, T.H.; Tella, A. Advances in estimating sea level rise: A review of tide gauge, satellite altimetry and spatial data science approaches. Ocean Coast. Manag. 2021, 208, 105632. [Google Scholar] [CrossRef]
- Ren, H.; Cromwell, E.; Kravitz, B.; Chen, X. Using long short-term memory models to fill data gaps in hydrological monitoring networks. Hydrol. Earth Syst. Sci. 2022, 26, 1727–1743. [Google Scholar] [CrossRef]
- Fassoni-Andrade, A.C.; Fleischmann, A.S.; Papa, F.; Paiva, R.C.D.D.; Wongchuig, S.; Melack, J.M.; Pellet, V. Amazon hydrology from space: Scientific advances and future challenges. Rev. Geophys. 2021, 59, e2020RG000728. [Google Scholar] [CrossRef]
- Huang, Z.; Sun, R.; Wang, H.; Wu, X. Trends and innovations in surface water monitoring via satellite altimetry: A 34-year bibliometric review. Remote Sens. 2024, 16, 2886. [Google Scholar] [CrossRef]
- Frappart, F.; Blarel, F.; Fayad, I.; Bergé-Nguyen, M.; Crétaux, J.F.; Shu, S.; Baghdadi, N. Evaluation of the performances of radar and lidar altimetry missions for water level retrievals in mountainous environment: The case of the Swiss lakes. Remote Sens. 2021, 13, 2196. [Google Scholar] [CrossRef]
- Kossieris, S.; Tsiakos, V.; Tsimiklis, G.; Amditis, A. Inland water level monitoring from satellite observations: A scoping review of current advances and future opportunities. Remote Sens. 2024, 16, 1181. [Google Scholar] [CrossRef]
- Ross, N.; Rostami, A.; Lee, H.; Chang, C.H.; Hossain, F.; Milillo, P.; Towashiraporn, P. Monitoring reservoir water elevation changes using Jason-2/3 altimetry satellite missions: Exploring the capabilities of JASTER (Jason-2/3 Altimetry Stand-Alone Tool for Enhanced Research). Int. J. Digit. Earth 2024, 17, 2406387. [Google Scholar]
- Moreau, T.; Cadier, E.; Boy, F.; Aublanc, J.; Rieu, P.; Raynal, M.; Mavrocordatos, C. High-performance altimeter Doppler processing for measuring sea level height under varying sea state conditions. Adv. Space Res. 2021, 67, 1870–1886. [Google Scholar]
- Kwok, R.; Cunningham, G.F.; Zwally, H.J.; Yi, D. Ice, Cloud, and land Elevation Satellite (ICESat) over Arctic sea ice: Retrieval of freeboard. J. Geophys. Res. Ocean. 2007, 112, C12013. [Google Scholar] [CrossRef]
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; DiMarzio, J.P. Overview of the ICESat mission. Geophys. Res. Lett. 2005, 32, 21. [Google Scholar]
- Urban, T.J.; Schutz, B.E.; Neuenschwander, A.L. A survey of ICESat coastal altimetry applications: Continental coast, open ocean island, and inland river. Terr. Atmos. Ocean. Sci. 2008, 19, 1–19. [Google Scholar]
- Shu, L.; Jiang, Q.; Zhang, X.; Zhao, K. Potential and limitations of satellite laser altimetry for monitoring water surface dynamics: ICESat for US lakes. Int. J. Agric. Biol. Eng. 2017, 10, 154–165. [Google Scholar] [CrossRef]
- Martino, A.J.; Neumann, T.A.; Kurtz, N.T.; McLennan, D. ICESat-2 mission overview and early performance. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XXIII, Strasbourg, France, 9–12 September 2019; Volume 11151, pp. 68–77. [Google Scholar]
- Smith, B.; Fricker, H.A.; Holschuh, N.; Gardner, A.S.; Adusumilli, S.; Brunt, K.M.; Siegfried, M.R. Land ice height-retrieval algorithm for NASA’s ICESat-2 photon-counting laser altimeter. Remote Sens. Environ. 2019, 233, 111352. [Google Scholar]
- Ryan, J.C.; Smith, L.C.; Cooley, S.W.; Pitcher, L.H.; Pavelsky, T.M. Global characterization of inland water reservoirs using ICESat-2 altimetry and climate reanalysis. Geophys. Res. Lett. 2020, 47, e2020GL088543. [Google Scholar] [CrossRef]
- Yuan, C.; Gong, P.; Bai, Y. Performance assessment of ICESat-2 laser altimeter data for water-level measurement over lakes and reservoirs in China. Remote Sens. 2020, 12, 770. [Google Scholar] [CrossRef]
- Narin, O.G.; Abdikan, S. Multi-temporal analysis of inland water level change using ICESat-2 ATL-13 data in lakes and dams. Environ. Sci. Pollut. Res. 2023, 30, 15364–15376. [Google Scholar]
- Chen, T.; Song, C.; Luo, S.; Ke, L.; Liu, K.; Zhu, J. Monitoring global reservoirs using ICESat-2: Assessment on spatial coverage and application potential. J. Hydrol. 2022, 604, 127257. [Google Scholar]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Zwally, J. The Ice, Cloud, and Land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar]
- Dietrich, J.T.; Magruder, L.A.; Holwill, M. Monitoring coastal waves with ICESat-2. J. Mar. Sci. Eng. 2023, 11, 2082. [Google Scholar] [CrossRef]
- Kui, M.; Xu, Y.; Wang, J.; Cheng, F. Research on the adaptability of typical denoising algorithms based on ICESat-2 data. Remote Sens. 2023, 15, 3884. [Google Scholar] [CrossRef]
- Xie, J.; Li, B.; Jiao, H.; Zhou, Q.; Mei, Y.; Xie, D.; Fu, Y. Water level change monitoring based on a new denoising algorithm using data from Landsat and ICESat-2: A case study of Miyun Reservoir in Beijing. Remote Sens. 2022, 14, 4344. [Google Scholar] [CrossRef]
- Han, K.; Kim, S.; Mehrotra, R.; Sharma, A. Enhanced water level monitoring for small and complex inland water bodies using multi-satellite remote sensing. Environ. Model. Softw. 2024, 180, 106169. [Google Scholar]
- Messager, M.L.; Lehner, B.; Grill, G.; Nedeva, I.; Schmitt, O. Estimating the volume and age of water stored in global lakes using a geo-statistical approach. Nat. Commun. 2016, 7, 13603. [Google Scholar]
- Han, W.; Huang, C.; Gu, J.; Hou, J.; Zhang, Y.; Wang, W. Water level change of Qinghai Lake from ICESat and ICESat-2 laser altimetry. Remote Sens. 2022, 14, 6212. [Google Scholar] [CrossRef]
- Liu, C.; Hu, R.; Wang, Y.; Lin, H.; Zeng, H.; Wu, D.; Shao, C. Monitoring water level and volume changes of lakes and reservoirs in the Yellow River Basin using ICESat-2 laser altimetry and Google Earth Engine. J. Hydro-Environ. Res. 2022, 44, 53–64. [Google Scholar]
- Braun, A.; Cheng, K.C.; Csatho, B.; Shum, C.K. ICESat laser altimetry in the Great Lakes. In Proceedings of the 60th Annual Meeting of the Institute of Navigation, Dayton, OH, USA, 7–9 June 2004; pp. 409–416. [Google Scholar]
- Xiang, J.; Li, H.; Zhao, J.; Cai, X.; Li, P. Inland water level measurement from spaceborne laser altimetry: Validation and comparison of three missions over the Great Lakes and lower Mississippi River. J. Hydrol. 2021, 597, 126312. [Google Scholar]
- Balsamo, G.; Agusti-Panareda, A.; Albergel, C.; Arduini, G.; Beljaars, A.; Bidlot, J.; Blyth, E.; Bousserez, N.; Boussetta, S.; Brown, A.; et al. Satellite and In Situ Observations for Advancing Global Earth Surface Modelling: A Review. Remote Sens. 2018, 10, 2038. [Google Scholar] [CrossRef]
- Du, J.; Watts, J.D.; Jiang, L.; Lu, H.; Cheng, X.; Duguay, C.; Farina, M.; Qiu, Y.; Kim, Y.; Kimball, J.S.; et al. Remote sensing of environmental changes in cold regions: Methods, achievements and challenges. Remote Sens. 2019, 11, 1952. [Google Scholar] [CrossRef]
- Erler, A.R. High Resolution Hydro-Climatological Projections for Western Canada; University of Toronto: Toronto, ON, Canada, 2015. [Google Scholar]
- Curran, J.H.; Biles, F.E. Identification of seasonal streamflow regimes and streamflow drivers for daily and peak flows in Alaska. Water Resour. Res. 2021, 57, e2020WR028425. [Google Scholar]
- Rawson, D.S. The bottom fauna of Great Slave Lake. J. Fish. Board Can. 1953, 10, 486–520. [Google Scholar]
- Stewardship, M.W. State of Lake Winnipeg: 1999 to 2007; Environment Canada and Manitoba Water Stewardship: Winnipeg, MB, Canada, 2011. [Google Scholar]
- Desloges, J.R.; Gilbert, R. Sedimentary record of Harrison Lake: Implications for deglaciation in southwestern British Columbia. Can. J. Earth Sci. 1991, 28, 800–815. [Google Scholar]
- Landals, A.J. The Lake Minnewanka Site: Patterns in Late Pleistocene Use of the Albarta Rocky Mountains; University of Calgary: Calgary, AB, USA, 2008. [Google Scholar]
- Quartly, G.D.; Rinne, E.; Passaro, M.; Andersen, O.B.; Dinardo, S.; Fleury, S.; Guillot, A.; Hendricks, S.; Kurekin, A.A.; Müller, F.L.; et al. Retrieving sea level and freeboard in the Arctic: A review of current radar altimetry methodologies and future perspectives. Remote Sens. 2019, 11, 881. [Google Scholar] [CrossRef]
- Neumann, T.A.; Brenner, A.; Hancock, D.; Robbins, J.; Saba, J.; Harbeck, K.; Gibbons, A.; Lee, J.; Luthcke, S.B.; Rebold, T.; et al. ATLAS/ICESat-2 L2A Global Geolocated Photon Data, Version 3; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2021. [Google Scholar]
- Lehner, B.; Grill, G. Global river hydrography and network routing: Baseline data and new approaches to study the world’s large river systems. Hydrol. Process. 2013, 27, 2171–2186. [Google Scholar]
- Pietroniro, A.; Peters, D.L.; Yang, D.; Fiset, J.M.; Saint-Jean, R.; Fortin, V.; Leconte, R.; Bergeron, J.; Siles, G.L.; Trudel, M.; et al. Canada’s Contributions to the SWOT Mission-Terrestrial Hydrology (SWOT-C TH). Can. J. Remote Sens. 2019, 45, 116–138. [Google Scholar] [CrossRef]
- National Water Data Archive, Water Level and Flow. Water Office of Canada. Available online: https://wateroffice.ec.gc.ca (accessed on 7 February 2025).
- Singh, V.P.; Singh, R.; Paul, P.K.; Bisht, D.S.; Gaur, S. Hydrological Processes Modelling and Data Analysis; Water Science and Technology Library; Springer: Singapore, 2024; Volume 127. [Google Scholar]
- Wan, X.; Wang, W.; Liu, J.; Tong, T. Estimating the sample mean and standard deviation from the sample size, median, range and/or interquartile range. BMC Med. Res. Methodol. 2014, 14, 135. [Google Scholar] [CrossRef] [PubMed]
- Chapaneri, R.; Shah, S. Multi-level Gaussian mixture modeling for detection of malicious network traffic. J. Supercomput. 2021, 77, 4618–4638. [Google Scholar] [CrossRef]
- Shen, W.; Chen, S.; Xu, J.; Zhang, Y.; Liang, X.; Zhang, Y. Enhancing Extreme Precipitation Forecasts through Machine Learning Quality Control of Precipitable Water Data from Satellite FengYun-2E: A Comparative Study of Minimum Covariance Determinant and Isolation Forest Methods. Remote Sens. 2024, 16, 3104. [Google Scholar] [CrossRef]
- Helsel, D.R. Less than obvious-statistical treatment of data below the detection limit. Environ. Sci. Technol. 1990, 24, 1766–1774. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE). Geosci. Model Dev. Discuss. 2014, 7, 1525–1534. [Google Scholar]
- Hu, X.; Xie, Z.; Liu, F. Assessment of speckle pattern quality in digital image correlation from the perspective of mean bias error. Measurement 2021, 173, 108618. [Google Scholar] [CrossRef]
- Aalen, O.O. A linear regression model for the analysis of life times. Stat. Med. 1989, 8, 907–925. [Google Scholar] [CrossRef]
- De Winter, J.C.; Gosling, S.D.; Potter, J. Comparing the Pearson and Spearman correlation coefficients across distributions and sample sizes: A tutorial using simulations and empirical data. Psychol. Methods 2016, 21, 273. [Google Scholar] [CrossRef]
- Zonn, I.S.; Glantz, M.; Kosarev, A.N.; Kostianoy, A.G. The Aral Sea Encyclopedia; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Woolway, R.I.; Kraemer, B.M.; Lenters, J.D.; Merchant, C.J.; O’Reilly, C.M.; Sharma, S. Global lake responses to climate change. Nat. Rev. Earth Environ. 2020, 1, 388–403. [Google Scholar] [CrossRef]
- Geris, J.; Comte, J.C.; Franchi, F.; Petros, A.K.; Tirivarombo, S.; Selepeng, A.T.; Villholth, K.G. Surface water-groundwater interactions and local land use control water quality impacts of extreme rainfall and flooding in a vulnerable semi-arid region of Sub-Saharan Africa. J. Hydrol. 2022, 609, 127834. [Google Scholar]
- Ji, P.; Su, R.; Wu, G.; Xue, L.; Zhang, Z.; Fang, H.; Gao, R.; Zhang, W.; Zhang, D. Projecting Future Wetland Dynamics Under Climate Change and Land Use Pressure: A Machine Learning Approach Using Remote Sensing and Markov Chain Modeling. Remote Sens. 2025, 17, 1089. [Google Scholar] [CrossRef]
- Pielke Sr, R.A.; Pitman, A.; Niyogi, D.; Mahmood, R.; McAlpine, C.; Hossain, F.; Goldewijk, K.K.; Nair, U.; Betts, R.; Fall, S.; et al. Land use/land cover changes and climate: Modeling analysis and observational evidence. Wiley Interdiscip. Rev. Clim. Change 2011, 2, 828–850. [Google Scholar] [CrossRef]
- Fatichi, S.; Vivoni, E.R.; Ogden, F.L.; Ivanov, V.Y.; Mirus, B.; Gochis, D.; Downer, C.W.; Camporese, M.; Davison, J.H.; Ebel, B.; et al. An overview of current applications, challenges, and future trends in distributed process-based models in hydrology. J. Hydrol. 2016, 537, 45–60. [Google Scholar]



| Analysis Type | Description | Metrics/Tests Used | Reference |
|---|---|---|---|
| Error Metrics | Quantifies discrepancies between satellite and gauge levels | RMSE (Equation (3)), MAE (Equation (4)), MBE (Equation (5)) | [54,55] |
| Regression Analysis | Models the relationship between ICESat-2 and gauge data | β1 (Slope), β0 (Intercept), R2 (Equation (6)) | [56] |
| Correlation Analysis | Measures the strength of the association between datasets | Pearson’s r (Equation (7)), Spearman’s ρ | [57] |
| Error Distribution Analysis | Examines the nature and normality of error distributions | Histogram, KDE, Shapiro–Wilk Test | |
| Temporal and Spatial Stratification | Evaluates error variation across different conditions | Daily boxplots, Lake-specific groupings | |
| Lidar Point Density Analysis | Assesses the relationship between point density and error metrics | RMSE, MAE comparison based on photon density |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaya, Y. Evaluation of ICESat-2 Laser Altimetry for Inland Water Level Monitoring: A Case Study of Canadian Lakes. Water 2025, 17, 1098. https://doi.org/10.3390/w17071098
Kaya Y. Evaluation of ICESat-2 Laser Altimetry for Inland Water Level Monitoring: A Case Study of Canadian Lakes. Water. 2025; 17(7):1098. https://doi.org/10.3390/w17071098
Chicago/Turabian StyleKaya, Yunus. 2025. "Evaluation of ICESat-2 Laser Altimetry for Inland Water Level Monitoring: A Case Study of Canadian Lakes" Water 17, no. 7: 1098. https://doi.org/10.3390/w17071098
APA StyleKaya, Y. (2025). Evaluation of ICESat-2 Laser Altimetry for Inland Water Level Monitoring: A Case Study of Canadian Lakes. Water, 17(7), 1098. https://doi.org/10.3390/w17071098







