Abstract
Enhancing the performance of aged water distribution networks (WDNs) has become a significant global challenge. Many of these networks face issues such as deteriorated pipes, insufficient pumping heads, and increased water demands. Upgrading existing WDNs is often performed using optimization techniques, characterized by numerous decision variables, resulting in computationally intensive and time-consuming simulations. This paper proposes a novel optimal upgrading methodology for WDNs, leveraging clustering principles from graph theory. The proposed methodology involves adding a new storage tank and rehabilitating selected pipes of an existing WDN. The methodology begins with dividing the WDN into smaller subsystems based on its communication properties. The parameter ranges for adding a new storage tank are determined using a sensitivity analysis, assessing their values and impact on network resilience and water quality. Critical pipes that directly impact the WDN performance are identified and replaced for rehabilitation through three proposed scenarios, each with a distinct selection criterion. The problem is formulated as a multi-objective problem, aiming to minimize total annual costs while maximizing network resilience. The proposed methodology has proven effective in reducing the search space size and computational effort, outperforming the traditional full search space optimization approach.
1. Introduction
The increasing demand for drinking water, coupled with the deterioration and insufficiency of infrastructure, poses significant challenges for existing water distribution networks (WDNs) in pre-developed and developing nations [1]. These challenges often result in substandard water provision that fails to meet pressure and water quality requirements or increases the running costs due to higher operating expenditures or water losses. Financial constraints further complicate significant upgrades, including strengthening, rehabilitation, or expansion [2].
Consequently, an effective strategy for a full or partial WDN upgrade must be developed. The strategy should include appropriate upgrade options tailored to the current requirements of the distribution system, ensuring efficient and reliable operation. The strategy must be economically and computationally feasible while maintaining essential WDN performance metrics (e.g., water quality and hydraulic efficiency) within acceptable limits under both current and future conditions [3,4].
Upgrading existing WDNs is complex, yet numerous methods for upgrading strategies for WDNs have been developed by various researchers and practitioners in recent decades [5]. In recent decades, advances in computational modeling tools and processing technology have led to significant interest in optimization models for developing effective upgrading techniques [6]. The primary benefit of employing optimization models is in their capacity to accommodate several independent variables and to effectively explore alternative combinations for WDN upgrading solutions [7]. These techniques incorporate a wide range of decision variables. Examples include optimal pipe rehabilitation models [8,9,10,11], tank sizing and siting [12,13], and pump operation scheduling [14,15,16]. Typically, the problem is framed as multi-objective optimization with objectives such as minimizing total capital and operational costs, reducing leakage, and maximizing system reliability [17,18,19].
In such optimization problems, the trade-off between conflicting objectives is addressed using multi-objective evolutionary algorithms (MOEAs), yielding a Pareto front of non-dominated solutions. Each solution on the front represents a unique upgrading strategy with specific objective values. Identifying the optimal Pareto front for a WDN with numerous candidate pipes requiring an upgrade poses a considerable challenge due to the vastness of the decision space [20].
Diverse approaches have been employed to alleviate the complexity and computational requirements of optimal upgrading techniques. These approaches include the path method [21], global sensitivity assessment [22], and sequential multistage MOEAs [23].
Furthermore, cluster-based analysis is an effective method for simplifying the assessment of WDNs. It partitions a network into multiple subnetworks (i.e., clusters), each consisting of vertices and edges [24]. The resulting cluster design identifies network configuration, thus providing a clearer understanding of the network topology and connections among its components. Various clustering techniques have been applied to WDNs [24]. A graph-based algorithm was employed to integrate depth-first and breadth-first methodologies for the analysis of WDNs [25,26]. Perelman and Ostfeld [27] employed similar approaches to partition WDNs into strongly and poorly connected subgraphs based on flow directions in pipes. Deuerlein [28] introduced a graph decomposition method that simplifies networks into two primary components: forests (tree structures) and cores (loop structures). Deuerlein et al. [29] further enhanced this model by distinguishing the tree structure from the looping structure, significantly diminishing the system’s nonlinearity. Diao et al. [30] employed a modularity-based technique [31,32] for segmenting WDNs. Giustolisi and Ridolfi [33] enhanced the modularity-based technique by developing a novel modularity index, which was employed in multi-objective optimization, to produce diverse decomposition solutions for WDNs.
A key application of cluster-based decomposition is the development of district metered areas (DMAs) [30,34,35,36]. Swamee and Sharma [37,38] developed a method for deconstructing a multi-source WDN, through examining the influencing regions of different water sources. The method identifies single-supplier subsystems for separate design and subsequent integration into the system. Zheng et al. [39] presented an effective dual-stage multi-objective optimization technique utilizing network decomposition, in which each independent subsystem is optimized individually prior to integration for a holistic system evaluation. Diao et al. [40] proposed a twin-hierarchy decomposition method to restructure the WDN optimization into two levels: supplying mains and local neighborhoods, allowing independent community-level design.
The discretization process of WDNs into a set of DMAs consists of two main stages. The first stage utilizes graph theory to convert the network into an undirected graph, where reservoirs, nodes, and storage tanks are represented by vertices, while pipes, pumps, and valves are represented by edges [27]. The second stage involves partitioning the WDN graph into DMAs using a clustering algorithm while ensuring that the internal connection within each DMA is stronger than the external connection. Various clustering algorithms exist in the literature, but the most commonly used ones are the community structure algorithm [41], modularity-based algorithm [42], multilevel graph partitioning [43], and spectral graph algorithm [44].
Additionally, sensitivity analysis improves network design by minimizing search space size, directing the optimization process toward addressing the key decision variables relevant to system performance, and pinpointing critical sources of uncertainty in stochastic design scenarios [45]. Fu, Kapelan, and Reed [45] conducted a sensitivity analysis on a WDN to simplify complex optimization procedures and evaluate several performance indicators affecting the distribution system. Fiorini et al. [46] employed a sensitivity analysis to assess WDN performance utilizing a pressure-driven analytical method and a classification strategy using an artificial neural network. Izquierdo et al. [47] developed a methodology to assess the relative importance of pipes by analyzing uncertainty in WDN data using sensitivity analysis. Jensen and Jerez [48] performed sensitivity analyses for large WDNs with high uncertainty, integrating factors such as storage tank head, pipe roughness, and nodal demand with a probabilistic model. Guangtao, Kapelan, and Reed [22] used sensitivity analysis to reduce the computational budget required for optimizing WDN design and operation. The study identified the ineffective decision variables and directed the problem to the effective variables, thus reducing problem complexity and computational demands.
Developing a comprehensive and effective rehabilitation plan for existing WDNs is a challenging task due to the large number of decision variables, uncertainties in the available data, and the complexity of determining whether to add new elements to the network, especially in the absence of supercomputing facilities [23]. The search space size for WDN optimization problems is determined by the WDN scale along with the number of decision variables and their associated options, such as the pipe diameters available in the local market [21]. Therefore, many researchers have focused on developing methods to reduce the search space size in the different optimization processes of WDNs. Kadu Mahendra et al. [21] modified the genetic algorithm and introduced a methodology to reduce the search space based on the critical path method for network pipes. Reca et al. [49] developed a new approach to efficiently determine the optimal design of WDNs by limiting the search space through specifying a predefined diameter range for the pipes in the network.
This current study introduces an innovative methodology for optimal WDN upgrading through rehabilitating selected pipes and adding a new storage tank, leveraging graph clustering and decomposition concepts proposed by Schaeffer [24] and Fortunato [50]. By integrating hydraulic insights from each subsystem, the proposed methodology aims to significantly reduce the number of decision variables before conducting network optimization. This work serves as a framework to assess and compare the effectiveness of different graph-based optimization approaches. The following sections outline the suggested technique and its application to a case study, followed by the presentation and analysis of the results. Finally, the main findings are summarized, and recommendations for future work are provided.
2. Study Area
In this work, the WDN for Al-Hashimiya city, located in the Babylon Governorate in central Iraq, was studied. The network suffers from deterioration due to aging infrastructure, poor maintenance, and random expansions. These issues have led to a decline in the network’s overall efficiency and an increase in the required maintenance rate. Variations in node pressures, insufficient water supply to meet demand, and fluctuations in disinfectant concentrations significantly reduce end-user satisfaction.
The Al-Hashimiya WDN serves five residential neighborhoods located in the center of the city. Considering that the estimated city population was 23,535 capita according to the 2010 population census and according to the city’s population growth rate (2.5%), the current population is estimated at 33,254 capita, as reported by the Iraqi Ministry of Planning/Central Bureau of Statistics. The Al-Hashimiya WDN consists of three main components: a drinking water treatment plant, a pump station, and a pipe network. Figure 1 shows all the details of the Al-Hashimiya WDN. For more details about the network and its location, please refer to the Supplementary Information (Supplementary Figures S1 and S2).
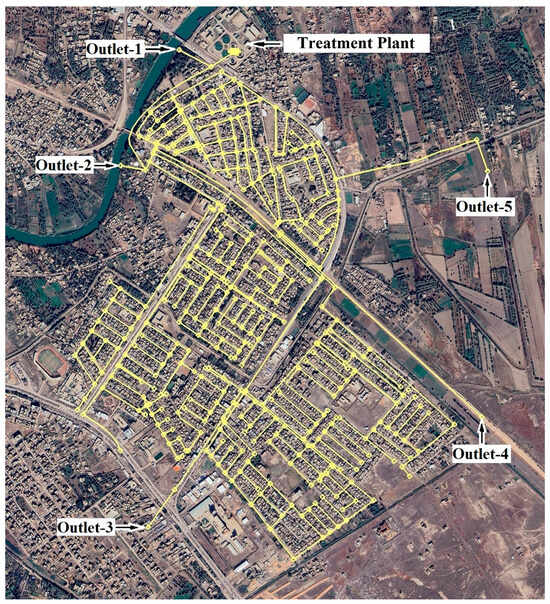
Figure 1.
Al-Hashimiya WDN details.
The drinking water treatment plant is located in the northwestern part of the WDN along the Shatt al-Hilla River. The station operates with a production capacity estimated at 6000 m3/h. It takes raw water from Shatt al-Hilla and supplies treated water to four WDNs. The share of the Al-Hashimiya WDN is 700 m3/h of the total treated water.
The pumping station consists of two parallel fixed-speed pumps that operate alternately to supply the Al-Hashimiya WDN with potable water. Water is conveyed to the network through a 600 mm diameter and 720 m long pipeline. Each pump operates with a power of 80 kW, delivering a discharge of 700 m3/h and a head of 42 m.
The network consists of 434 pipes and 383 nodes, with pipe diameters ranging from 75 mm to 600 mm, made from different materials such as plastic, asbestos, and ductile iron. The network has five water outlets with different discharges: outlet #1 (150 m3/h), outlet #2 (100 m3/h), outlet #3 (50 m3/h), outlet #4 (30 m3/h), and outlet #5 (15 m3/h). These outlets supply smaller networks near the Al-Hashimiya WDN.
The Al-Hashimiya WDN currently meets 90% of end-users’ demand during normal conditions but fails during peak demand times, which amounts to 1.4 of the base demand. Figure 2 shows the daily demand pattern for any junction within the network. To enhance network efficiency and fulfill design requirements for the next 20 years, the addition of a new storage tank and the replacement of selected critical pipes have been recommended. The pressure of the network must be maintained between 10 m and 50 m, chlorine concentrations are between 0.2 mg/L and 0.5 mg/L, and flow velocity in pipes should not exceed 2.3 m/s. All the new pipes are made from PVC with a Hazen–Williams coefficient of 140, and information about the pipes available in the local market is shown in Table 1. To conduct this study, an EPANET input file for the Al-Hashimiya WDN was obtained from the official authorities of the Al-Hashimiya Water Centre.
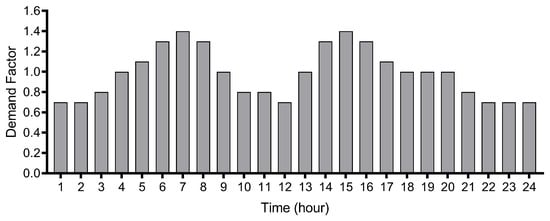
Figure 2.
Daily demand pattern for the Al-Hashimiya WDN.

Table 1.
Details of pipes available in local markets.
3. Methodology
The methodology is mainly based on the clustering concept and incorporates two distinct features: first, determining the best parameter range for a new storage tank added to the existing WDN based on sensitivity analysis; and second, identifying critical pipes that negatively impact the network performance. The recommended tank parameter ranges, along with the selected pipes, were incorporated into the optimization process as decision variables for rehabilitating the existing WDN.
The methodology consisted of four steps:
- Network Clustering: The network is divided into smaller subnetworks, pre-defined based on the characteristics of the connection between them, in line with the clustering concept.
- Tank Parameter Ranges Identification: Decision variables for the new storage tank are identified, imposing a range of recommended values. The optimal ranges are determined after conducting a sensitivity analysis based on network performance.
- Critical Pipe Identification: Pipes that negatively impact network performance are identified and included as decision variables in the optimal rehabilitation process. This step proposes three rehabilitation scenarios, each with a specific set of pipe-decision variables selected using a distinct approach.
- Network Optimization: The optimization process for upgrading the WDN is carried out using two approaches: (1) Guided optimization: This approach utilizes the best tank location and decision variable ranges identified through sensitivity analysis. The pipe replacement decision variables are then identified based on the three rehabilitation scenarios. (2) Full search space optimization: This approach serves as a benchmark for the comparison and verification of the proposed methodology. It explores all possible tank locations and ranges of tank decision variables, while randomly selecting the replaced pipe and their number.
The following subsections provide a detailed description of these steps.
3.1. Clustering the Al-Hashimiya WDN into DMAs
Several methods and approaches for clustering WDNs are available, primarily based on graph theory and clustering algorithms [24,51,52]. Partitioning a WDN into district metered areas (DMAs) facilitates identifying service failure locations and allows the isolation of the affected part of the network without disrupting service across the entire system, thus improving WDN management [30]. Moreover, conducting such an analysis simplifies control and operation, particularly for large and complex networks [2].
In this study, the modularity-based clustering algorithm [31,52] was used due to its efficiency in analyzing large-scale systems. The algorithm maximizes the modularity index (M, which can be expressed as follows:
where , in which
me is the number of edges in the graph, Aνω denotes the elements inside the adjacency matrix of the network, kν and kω are the summation of edges connected to vertices ν and ω, respectively. cν and cω are two different clusters (communities) that include vertices and respectively, δ(cν, cω) is a function that depends on communities (equals 1 when cν = cω and 0 otherwise). Further details about this method and clustering design concepts can be found in [30,31].
The Al-Hashimiya WDN was partitioned into DMAs using the previous clustering analysis. Trial and error analysis was performed during the implementation of the clustering algorithm to establish five DMAs, each representing a neighborhood within the Al-Hashimiya WDN, as shown in Figure 3. Subsequently, five potential locations were identified for the proposed storage tank, one for each DMA, with the goal of selecting the best location that effectively serves all five DMAs. Priority was given to areas with significant pressure deficiency or high water demand within the DMAs.
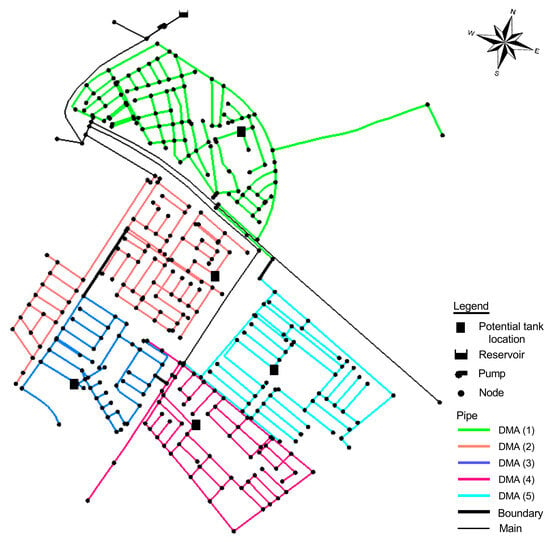
Figure 3.
DMAs of the Al-Hashimiya WDN and potential storage tank locations.
3.2. Storage Tank Parameters
The optimization of WDNs when adding a new storage tank should first involve leveraging engineering experience to define the relevant tank parameters and establish reasonable ranges for them. The closer the optimization decision variables align with engineering considerations, the more efficient the resulting solutions will be. On this basis, the storage tank parameters in this study were classified into independent variables (decision variables) and dependent variables (derived variables). The decision variables for adding a new storage tank to the Al-Hashimiya WDN can be summarized as tank location, tank elevation (Et), tank diameter (Dt), riser diameter (Dr), and initial water volume (Vi). The tank riser is the pipe responsible for both supplying water to the tank and draining it.
Selecting appropriate values for these parameters is crucial, as it directly impacts the solutions quality in terms of applicability, cost, and computational efficiency. Appropriate values of these parameters reduce the search space size, leading to more effective optimized solutions.
Therefore, a sensitivity analysis was conducted to identify the best values for the storage tank parameters. The individual impact of each parameter on the network resilience (Re) and average water age (AWA) was evaluated, considering the addition of only one new storage tank.
Although several widespread formulas for calculating Re are widely discussed in the literature, the Todini [53] formula was used in this study for its simplicity. This formula indicates the network’s ability to maintain operation within the required pressure constraints during failure events. Re evaluates network resilience by predicting the surplus energy available for all network junctions, as shown in the following equation:
where Nj is the number of junctions in the network, is the demand of junction m, is the actual piezometric head of junction m, is the minimum required piezometric head of junction m, Nr is the number of reservoirs in the network, Qr is the reservoir outflow, Hr is the reservoir water elevation, Nps is the number of pumps in the network, and γ is the unit weight of water. Re ranges from 0.0 to 1.0, with the best value being close to 1.0, indicating a highly resilient system.
AWA is calculated by averaging the water age at all nodes during the simulation time [54], and is given by
where WAm is the water age of node m at time t (h). The best AWA value is when it approaches 0.0.
A preliminary analysis of the Al-Hashimiya WDN was conducted to determine reasonable ranges for the new tank’s independent variables. After several attempts based on network characteristics, the following base values were assumed: 20 m for Et, 150 mm for Dr, 13 m for Dt, and 943 m3 for Vi. Ranges of independent variables were selected as follows: 22–40 m with an increment of 2 m for Et, 140–50 mm with a decrease of 10 mm for Dr, 14.3–26 m with an increment of 1.3 m for Dt, and 1037–1886 m3 with an increment of 94.3 m3 for Vi. According to this practice, the number of scenarios was 41 for each potential storage tank location, resulting in a total number of 205 scenarios.
The simulation time of the network was assumed to be four days with a time step of 0.25 h. Re and AWA were evaluated on the fourth day of the simulation to ensure a steady periodic reading of water age and pressure patterns. Re was calculated at 3:00 pm on the fourth day, corresponding to the time of maximum daily demand. All the analyses were conducted using EPANET v2.2 [55].
After conducting the analysis, the tank parameters yielding the highest Re and the shortest AWA were adopted. Figure 4 shows the results of the sensitivity analysis, revealing that the best tank location was location 4. Taking Dt as an example, it was found that Re decreased with increasing Dt, while AWA increased, suggesting that minimizing Dt improves network performance.
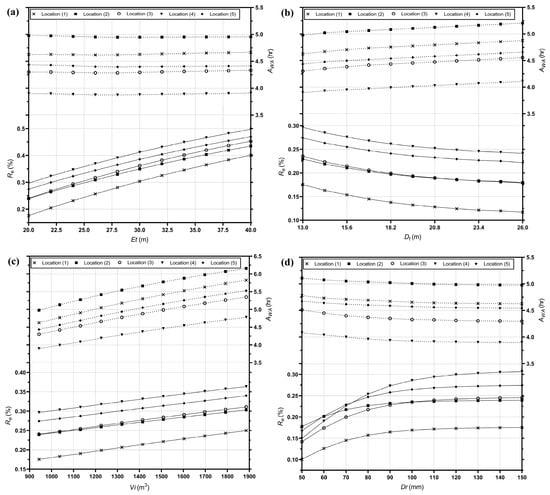
Figure 4.
Variation in Re and AWA with respect to tank parameters: (a)—Et, (b)—Dt, (c)—Vi, (d)—Dr.
On this basis, the best tank location and recommended values of the tank parameters were determined based on sensitivity analysis results as follows: The potential storage tank was located in DMA #4, Et range was 20 to 40 m, Dt range was 13 to 18.2 m, Vi range was 943 to 1131 m3, and Dr was 150 mm or above.
3.3. Critical Pipes Identification
Rehabilitating the studied WDN was optimized by replacing pipes that directly impact network performance. The pipes affecting the network performance can be classified into three types. First, high head loss pipes, where significant losses occur due to insufficient diameter, i.e., due to increased demand or high roughness resulting from network aging. Second, boundary pipes, which serve as water conveyors between the different DMAs. Third, the group of pipes along the feeding path, i.e., the shortest path of flowing water from the source to the DMAs.
Accordingly, three scenarios were proposed for selecting pipes that will be replaced within the optimal rehabilitation process. These scenarios can be summarized as follows:
Scenario 1: Rehabilitation of pipes along the feeding path
In this scenario, the rehabilitation focuses only on the pipes located along the shortest path between the water source and the DMAs. The number of pipes along the feeding path for each DMA is illustrated in Table 2. Here, it was assumed that these pipes were the main cause of pressure deficiency at the network nodes. This pressure deficiency is often due to high head loss or inadequate diameters of these pipes. Rehabilitating a limited number of pipes could effectively solve the pressure deficiency at a relatively low cost.

Table 2.
Properties of DMAs and pipes considered as decision variables for Scenarios 1 and 2.
Scenario 2: Pipe rehabilitation within DMAs
This scenario focuses on rehabilitating the pipes within each DMA that experience pressure deficiencies. These deficiencies are assumed to be a result of high head loss in certain pipes, primarily caused by insufficient diameters due to increased demand and high friction due to network aging. Therefore, priority is given to the rehabilitation of pipes with high roughness, characterized by a Hazen–Williams coefficient of less than 90, as well as pipes with large head loss gradient values, defined as gradients greater than 8 m/km.
On the other hand, part of the pressure deficiency was attributed to insufficient water supply to the DMAs, often due to the undersized or aging of boundary pipes between DMAs. Rehabilitating these pipes will alleviate pressure deficiency at the network nodes.
On this basis, the Al-Hashimiya WDN had 40 pipes with a Hazen–Williams coefficient of less than 90, 28 pipes with a head loss gradient of more than 8 m/km, and 7 boundary pipes. After excluding 13 common pipes, the total number of pipes that were included in the optimization process as decision variables in this scenario was 62.
Scenario 3: Combined Rehabilitation Approach
In this scenario, both Scenario 1 and Scenario 2 were integrated. This meant considering the critical pipes within the DMAs as well as the pipes connecting the DMAs to the water source. Although this combined scenario may have the largest search space, it encompasses all the potential pipes that could be significant for consideration during rehabilitation.
Since pipe replacement was the only option considered for rehabilitation, the decision variables for optimizing network rehabilitation were the diameters of the replaced pipe. Eleven pipe diameters were available in the Al-Hashimiya WDN for replacement, resulting in a full search space size of 11434 = 9.213 × 10451. In total, 35 pipes were identified as decision variables for Scenario 1, and 62 pipes in Scenario 2, resulting in corresponding search space sizes of 2.81 × 1036 and 3.684 × 1064, respectively. After deducting 23 pipes common to both Scenarios 1 and 2, the number of decision variables for Scenario 3 was 74, leading to a search space size of 1.156 × 1077. All these scenarios are illustrated in Figure 5. The diameters of the replaced pipes for Scenarios 1, 2 and 3 are provided in Supplementary Figures S3–S5. Table 2 summarizes the hydraulic properties and pipes considered as decision variables of the DMAs for the different proposed scenarios.
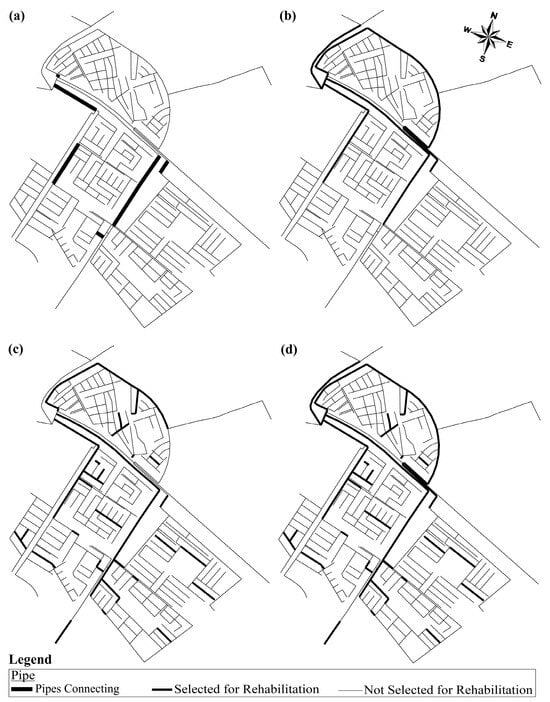
Figure 5.
Pipes considered decision variables for rehabilitation: (a)—boundary pipes, (b)—Scenario 1, (c)—Scenario 2, (d)—Scenario 3.
3.4. Network Optimization Procedures
3.4.1. Problem Formulation
The main scope of this work was to optimize the upgrading of the studied WDN. The optimal solutions should eliminate the nodal pressure deficit and increase the performance of the distribution system while considering prespecified pressure and velocity constraints. The upgrading process of the studied WDN included two main features: (1) adding a new storage tank, and (2) rehabilitating selected pipes according to three proposed scenarios. Two-objective functions were targeted for optimizing the WDN upgrading process: (1) minimizing the total annual costs (TAC), and (2) maximizing Re. The total annual cost (TAC) is a function of three components: annual replaced pipes cost (APC), annual storage tank cost (ATC), and annual pumping energy cost (AEC) as follows:
in which
where Np is the number of pipes, Cp is the unit cost of replaced pipes (including excavation, backfilling, and finishing works), Lp is the pipe length, Cr is the capital recovery factor, ∀ is the tank balancing volume (m3), Et is the tank elevation (m), I is the interest rate (0.09), Pp is the pumping power (kW), EUC is the energy unit cost (USD/kW·h), and N is the expected WDN lifetime (20 years), where the estimated population of the city after 20 years is 54,491 people, according to a growth rate of 2.5%.
Todini’s formula [53], as mentioned in Equation (2), was used to evaluate Re during the optimization process.
In addition to the budget and performance embedded in the studied objective functions, the optimization process must meet specific operational constraints. These included maintaining nodal pressure within the range of 10 m to 50 m, and ensuring the flow velocity in pipes did not exceed 2.3 m/s. On the other hand, the objective functions were normalized to a consistent scale during the optimization process. Once the optimization was complete, the values of the objective functions were converted back to their original scale for displaying the results.
Decision variables were categorized into two groups: The first group was the decision variables specified for adding a new storage tank, which included tank location (Lt), tank elevation (Et), tank diameter (Dt), riser diameter (Dr), and initial volume (Vi). The best range of values for the decision variables was obtained from the sensitivity analysis conducted as outlined earlier in Section 3.2. Pump power was also included as a decision variable, with a range of 100 kW to 200 kW. This range was assumed and validated through trial runs to ensure periodic operation of the storage tank levels, preventing the tank from filling continuously throughout the operation period or experiencing insufficient filling. The pumping power value can be directly used in EPANET by specifying a constant pumping power in the pump properties window. The second group was the rehabilitation decision variables, which were the diameters of the replaced pipes. Three proposed scenarios determined the selection of pipes to be replaced, with 35, 62, and 74 pipes designated for Scenarios 1, 2, and 3, respectively, as described in Section 3.3.
3.4.2. Optimization Process
The optimization process of WDNs is usually based on linking a specific optimization algorithm to a WDN hydraulic simulator. The hydraulic simulation of the WDN in this work was conducted using EPANET v2.2 [55]. The Non-dominated Sorting Genetic Algorithm III (NSGA-III) [56] was employed to reach a set of feasible non-dominated solutions that satisfied the pressure and velocity constraints throughout the simulation time.
Although NSGA-III in multi-objective optimization requires more computational effort than its counterpart, NSGA-II, the studied problem necessitates maintaining a diverse set of solutions throughout the optimization process. The complexity of this problem arises from the combination of continuous and discrete decision variables, which can lead to irregularities or discontinuities in the generated Pareto front. Unlike NSGA-II, which relies on crowding distance, NSGA-III employs a reference point-based selection mechanism to ensure well-distributed Pareto-optimal solutions, guiding the search toward more diverse and near-continuous solutions while reducing the risk of convergence to local optima. This advantage is particularly relevant for small population sizes, provided that the population size is greater than the number of reference points [57].
Deb and Jain [58] also mentioned that decision-making in multi-objective and many-objective optimization problems typically requires only a limited number of tradeoff solutions. They also demonstrated that NSGA-III effectively identifies a small set of Pareto-optimal solutions even with a reduced population size, thereby reducing the required computational budget.
On the other hand, selecting the appropriate population size and number of runs remains a challenging task, especially when optimizing scenarios with varied search space sizes. Generally, a larger population size is preferred over a smaller one, assuming all other factors are equal. A larger population size allows for more global search and may lead to faster convergence, while maintaining greater diversity. However, it may encounter difficulties with local optima in noisy environments and requires a larger computational budget. Therefore, to balance the benefits of a larger population while minimizing its drawbacks, it is important to choose a reasonable population size and increase the number of runs. This approach can lead to more diverse exploration, faster convergence, and a reduced computational budget. Nevertheless, a large population size with a larger number of runs remains preferable. Given the constraint of a limited computational budget and the decision to increase the number of runs, a smaller population size was chosen for all the studied scenarios. This size should satisfy the NSGA-III condition, where the population size must be a multiple of four and greater than or equal to the number of reference points [58].
The optimization process for upgrading the Al-Hashimiya WDN was carried out using two approaches: (1) Guided optimization: This optimization applied the best tank location and decision variables ranges obtained from the sensitivity analysis. Then, the decision variables for replacing the pipes were applied according to the three proposed scenarios. (2) Full search space optimization: This optimization was used for comparison and verification of the proposed methodology. All possible tank locations and wider ranges of tank decision variables were used, and the replaced pipes and their numbers were randomly determined. Table 3 summarizes the decision variables and their values used in the two optimization approaches.

Table 3.
Decision variables of optimization processes.
The NSGA-III parameter values were selected as shown in Table 4. The assumed values for NSGA-III parameters were 10 for the number of divisions (Nd), 0.5 for the crossover percentage (Cp), 0.5 for the mutation percentage (Mp), and 0.02 for the mutation rate (Mr). For the population size (Ps), function evaluations (Fe), and maximum number of iterations (Ni), their values were set to 40, 75,000, and 1875, respectively. Although the used NSGA-III population size may be considered relatively small, using the same population size ensured that each scenario was tested under the same limited computational conditions, providing a fair evaluation of performance without interference from population size. Studying the effect of different population sizes or number of iterations on the optimization results is beyond the scope of this study.

Table 4.
Parameter values of NSGA-III used in optimization processes.
The number of parents (Np), number of mutants (Nm), and mutation step size (Ms) were calculated using the following formulas:
where Uv and Lv are the upper and lower bounds of variables, respectively. Np and Nm are rounded to the nearest one.
For the guided optimization, 10 runs were conducted for each scenario to obtain 10 Pareto fronts, which were then accumulated to extract the best Pareto front corresponding to each scenario. The full search space optimization problem was analyzed in the same manner. Finally, decision-makers selected the most suitable solution after considering the available budget and required network performance.
4. Results and Discussion
4.1. Pareto Optimal Solutions
The NSGA-III algorithm was used to perform the optimization and generate Pareto optimal solutions, where the optimization was repeated 10 times for each scenario, including the full search space scenario. The optimization goal was to reach the best rehabilitation scenario among the studied scenarios. To establish a comparison between different scenarios based on using the same computational budget, the convergence metric (Cv) of each scenario’s solutions was assessed. This metric computed the average Euclidean distance between all the Pareto front solutions and a reference point. The reference point was assumed to be at TAC = $0.0 and Re = 1.0. The Cv formula can be written as follows:
where ni is the number of Pareto optimal solutions and Ci is the Euclidean distance between each Pareto front solution and the reference point.
A comparison was conducted using the mean and standard deviation of convergence across scenarios 1, 2, 3, and the full search space scenario. A lower mean convergence value indicates that the Pareto front is closer to the optimal solution, while a lower standard deviation suggests that the solutions are more tightly clustered around the mean value, leading to larger consistency in the optimization results.
Figure 6 shows the differences between the objective function values for all the runs of scenarios 1, 2, and 3, along with the full search space scenario, while Table 5 presents the mean and standard deviation of the convergence metrics computed from 10 runs of each scenario. The Pareto front resulted from each run is illustrated in Supplementary Figures S6–S9. The results in Table 5 indicate that Scenario 2 exhibited the best convergence performance. The relative difference in the mean and standard deviation for each scenario compared to the full search space expresses the extent of improvement in results compared to the full search space.
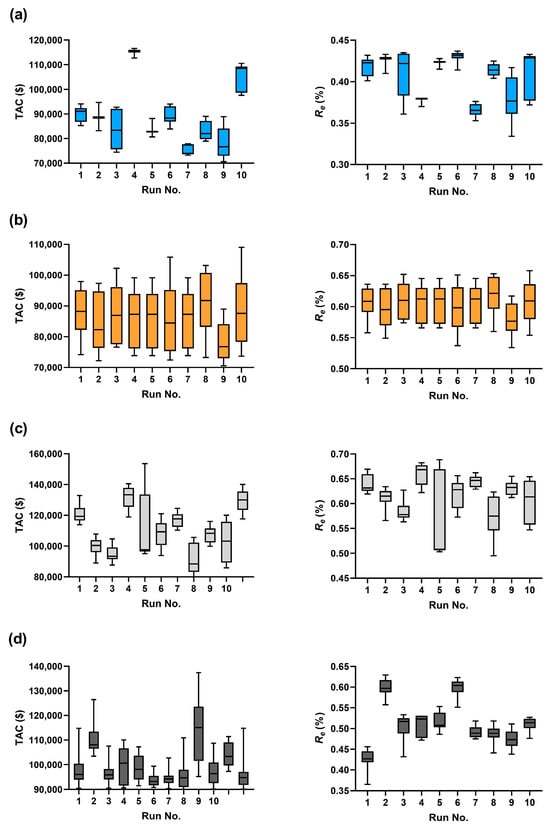
Figure 6.
Box and whiskers plot for TAC and Re values ((a)—scenario 1, (b)—scenario 2, (c)—scenario 3, and (d)—full search space).

Table 5.
Mean and standard deviation of the convergence metrics of the Pareto optimal solutions.
4.2. Guided Optimization Results
In this optimization, the best storage tank location and recommended ranges for the tank decision variables obtained from the sensitivity analysis were adopted. Moreover, the decision variables for the replaced pipes were applied according to the proposed scenarios 1, 2, and 3. The optimization analysis was conducted with 10 runs for each scenario to generate 10 Pareto fronts, which were then accumulated to extract the cumulative Pareto front. Figure 7 shows the cumulative Pareto front between TAC and Re for the final optimization result of the Al-Hashimiya WDN under each scenario. All solutions shown in Figure 7 satisfied the operational constraints. The cumulative Pareto front for Scenario 1 consisted of 42 solutions, with Re values ranging from 0.353 to 0.437 and TAC values between $73,234 and $93,920. For Scenario 2, the cumulative Pareto front consisted of 65 solutions, with Re values ranging from 0.534 to 0.658 and TAC values between $70,592 and $108,966. Scenario 3 resulted in a cumulative Pareto front consisting of 59 solutions, with Re values ranging from 0.495 to 0.669 and TAC values between $79,580 and $132,742.
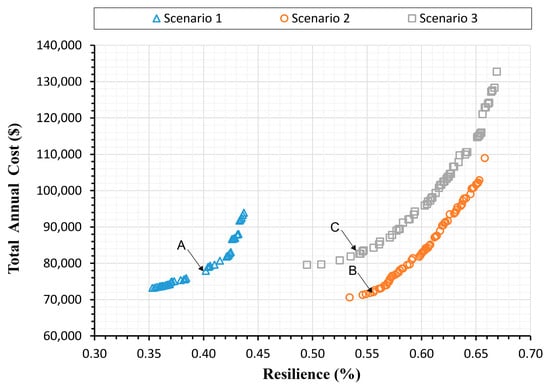
Figure 7.
Cumulative Pareto front of Scenarios 1, 2, and 3.
The analysis results showed that all solutions in the cumulative Pareto front of Scenario 2 dominated those of Scenarios 1 and 3. Table 6 provides key characteristics of all the cumulative Pareto fronts, facilitating an approximate comparison of results. The average TAC for the cumulative Pareto front of Scenario 2 was 4.076% higher than that of Scenario 1 and 16.873% lower than that of Scenario 3. Also, the average Re for the cumulative Pareto front of Scenario 2 was 34.868% and 0.978% higher than Scenarios 1 and 3, respectively. The convergence value for the cumulative Pareto front of Scenario 2 was approximately 11.785% and 9.744% lower than Scenarios 1 and 3, respectively.

Table 6.
Characteristics of the cumulative Pareto front of Scenarios 1, 2, and 3.
On the other hand, solutions A, B, and C on the cumulative Pareto fronts of Scenarios 1, 2, and 3, respectively, were identified as the closest solutions to the reference point (i.e., the solutions having the lowest Euclidean distance). The TAC value of solution B was 7.497% and 12.803% lower than that of solution A and solution C, while the Re value of solution B was 27.698% and 2.158% higher than solution A and solution C, respectively.
From the above analysis, Scenario 2 proved to be more efficient than Scenarios 1 and 3. This indicated that the replaced pipes in Scenario 2 have the most significant impact on the Al-Hashimiya WDN and are the primary contributors to system operational problems.
Differences in objective function results during the optimization process arose from variations in the decision variables. Although the storage tank parameters varied across solutions, the difference in objective function results was largely attributed to the rehabilitation decision variables, specifically the selected set of replaced pipes, which significantly varied in their impact on the distribution system from one scenario to another. More effective optimization outcomes can be achieved when the algorithm prioritizes replacing a larger number of pipes that have a high impact on the system. However, including pipes with minimal impact on the system leads to suboptimal results in terms of the rehabilitation cost. Therefore, merely increasing the number of replaced pipes is not a reliable criterion for system optimization. Instead, the key to better optimization lies in replacing pipes that significantly impact the system’s performance.
For instance, this concept can be mathematically demonstrated by calculating the average percentage increase in the diameters of the replaced pipes and the average percentage decrease in the head loss gradient for the pipes shared between solutions B and C. Solution C consisted of 74 pipes as a decision variable, 62 of which were also present in solution B, as shown in Figure 8 and Table 7. Figure 8 shows the common pipes’ IDs between solutions B and C.
Figure 8.
IDs of shared pipes between solutions B and C.

Table 7.
Relative improvement in shared pipes between solutions B and C in terms of pipe diameter and head loss gradient.
In Table 7, d, S, Id, and IS represent the pipe diameter, head loss gradient, percentage increase in the pipe diameter, and percentage decrease in the head loss gradient, respectively. The table shows that the average values of Id and IS were 41.123% and −61.046% for solution B and 66.402% and −54.557% for solution C, respectively.
Although the average percentage increase in the pipe diameters was lower in solution B compared to solution C, the average percentage decrease in the head loss gradient was greater in solution B. This suggests that solution B achieved a more effective reduction in the head loss gradient with smaller changes in the pipe diameters compared to solution C. Since solutions B and C shared the same conditions in all respects except for the inclusion of the feeding pipes from Scenario 1 in Scenario 3, it is likely that these additional pipes contributed to the observed deficiency in solution C. This can be attributed to the relatively minimal effect of rehabilitating these pipes on the studied system’s resilience, despite their significant impact on the rehabilitation costs.
4.3. Full Search Space Optimization Results
This optimization was conducted for comparison and verification of the proposed methodology in this study. Wider ranges of tank decision variables were considered, and the algorithm included determining the number of replaced pipes and their location as additional decision variables. The optimization analysis was performed in the same manner as the previous optimizations, with 10 runs to obtain 10 Pareto fronts, which were then accumulated to extract the cumulative Pareto front. Figure 9 shows the cumulative Pareto front between TAC and Re for the full search space problem. All the Pareto front solutions differed in terms of the number of replaced pipes and their locations. The cumulative Pareto front for the full search space problem consisted of 31 solutions, with Re values ranging from 0.477 to 0.629 and TAC values ranging from $91,002 to $126,492. The cumulative Pareto front of Scenario 2 was 19.936% lower in average TAC than the full search space problem and 6.250% higher in average Re than the full search space problem.
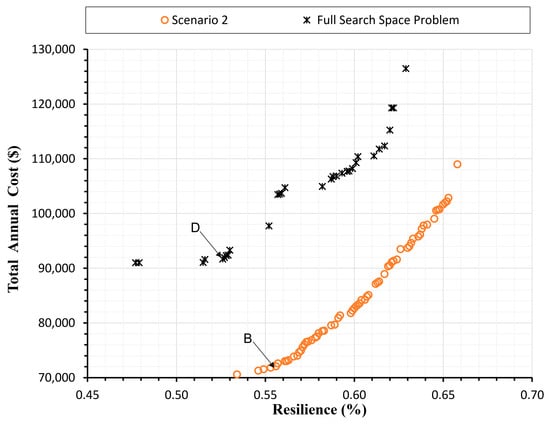
Figure 9.
Cumulative Pareto fronts of Scenario 2 and the full search space scenario.
Solution D represented the solution having the shortest Euclidean distance from the reference point. Table 8 presents the number of replaced pipes for solutions of the cumulative Pareto front, where solution D corresponds to solution #5, and subsequent solutions are listed in order.

Table 8.
Number of replaced pipes for Pareto front solutions of full search space scenario.
A comparison between the cumulative Pareto front for Scenario 2 and the cumulative Pareto for the full search space is made in Table 9. The results showed that Scenario 2 yielded 65 solutions, while the full search space front had 31 solutions, resulting in a 109.68% increase in the number of solutions for Scenario 2. This led to a wider range of applicable solutions when using Scenario 2, despite the search space size of Scenario 2 occupying only 14.28% of the full search space size. Furthermore, the TAC value for solution B was 21.398% lower than solution D, while its Re value was 5.396% higher than solution D.

Table 9.
Characteristics of the cumulative Pareto front of Scenario 2 and the full search space problem.
Convergence was measured for both the cumulative Pareto fronts of Scenario 2 and the full search space, using the reference point of TAC = $0 and Re = 1. The results showed that the average convergence of the front of Scenario 2 was 16.176% better than that of the full search space.
Scenario 2 demonstrated superiority over the full search space problem, especially in such a limited computational budget, due to the systematic selection of decision variables included in the optimization process. In Scenario 2, the critical pipes were carefully selected based on their hydraulic characteristics, ensuring a reduced and more reliable search space. In contrast, the full search space problem included all the pipes of the network, which significantly increased the computational complexity and time required to reach the best solutions.
These results demonstrated that the proposed methodology using Scenario 2 is more efficient in identifying the optimal solutions for upgrading existing WDNs. It achieves this by significantly reducing computational effort and narrowing the size of the search space, all while ensuring optimal performance and cost-effectiveness.
5. Conclusions and Recommendations
A new methodology for incorporating an additional storage tank and rehabilitating existing WDNs was proposed, leveraging graph theory clustering and the NSGA-III optimization algorithm. Using graph theory principles, the methodology was applied to upgrade the Al-Hashimiya WDN in Iraq, where the network was clustered into a predetermined number of subnetworks, DMAs. The problem is formulated as a multi-objective optimization problem, aiming to minimize annual total costs and maximize network resilience.
The decision variables were categorized into two groups. The first group pertains to a newly added tank, including its location, elevation, diameter, initial water volume, and riser diameter, while the second group concerns the diameters of the replaced pipes for rehabilitation purposes. Sensitivity analysis was conducted to determine the best tank location and optimal ranges for the rest of the tank parameters based on their impact on network resilience and water quality. Three scenarios were considered to determine the number and location of the replaced pipes, where Scenario 1 is concerned with rehabilitation of pipes along the shortest path from the feeding source for each DMA, Scenario 2 targets pipes having relatively higher head losses within DMAs along with the boundary pipes between the different DMAs, and Scenario 3 is a combination of Scenarios 1 and 2. Additionally, a full search space optimization was performed for the purposes of comparison between the different studied rehabilitation scenarios and verification of the proposed tank design methodology. The main conclusions reported in the current work are listed as follows:
- The proposed methodology for adding a new storage tank and rehabilitating critical pipes, mainly based on using graph theory clustering and sensitivity analysis, strikes an effective balance between total annual costs and network resilience;
- The optimization scenario focusing on rehabilitating high head-loss pipes within DMAs and boundary pipes (Scenario 2) produced a cumulative Pareto front that dominated those of other proposed scenarios relying on rehabilitating pipes along the feeding path of water (Scenarios 1 and 3). Furthermore, Scenario 2 outperformed the full search space optimization;
- These findings highlight the significance of using graph theory clustering in limiting both rehabilitation costs and operational issues in district-metered areas (DMAs) within water distribution networks (WDNs). The importance of using graph theory clustering is emphasized as it reduces the search space for locating the new storage tank, identifies and isolates low-pressure areas, and facilitates the hydraulic analysis process through sensitivity analysis;
- The recommended tank location and tank parameters ranges, derived from sensitivity analysis, can guide future optimizations of the Al-Hashimiya WDN. The sensitivity analysis helps in bridging the gap between engineering expertise and mathematical considerations, especially while choosing the values of the different decision variables;
- The developed approach streamlines the optimization process by simplifying the problem, reducing the search space size, and identifying optimal and practical solutions. Decision-makers can choose any solution located on the cumulative Pareto front of Scenario 2 to achieve optimal performance and cost-effective operation of the network.
In general, similar studies can be conducted for any existing WDNs to incorporate a storage tank, rehabilitate network pipes, or address both aspects, keeping in mind that the tank’s location and water elevation are both crucial for network resilience and water quality. Future work will focus on extending the developed methodology to more complex networks, incorporating multiple storage tanks and pumping stations.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/w17071072/s1, Figure S1: Al-Hashimiya City Location; Figure S2: Details of Al-Hashimiya WDN; Figure S3: Pipe diameters selected for rehabilitation, Scenario 1; Figure S4: Pipe diameters selected for rehabilitation, Scenario 2; Figure S5: Pipe diameters selected for rehabilitation, Scenario 3; Figure S6: Pareto optimal solutions of Scenarios 1; Figure S7: Pareto optimal solutions of Scenarios 2; Figure S8: Pareto optimal solutions of scenarios 3; Figure S9: Pareto optimal solutions of the full search space problem.
Author Contributions
Conceptualization, M.H.D., M.R.T. and E.G.; Data curation, M.H.D.; Formal analysis, M.H.D. and M.R.T.; Investigation, M.H.D.; Methodology, M.R.T.; Resources, M.H.D.; Software, M.H.D. and M.R.T.; Supervision, E.G.; Validation, E.G.; Writing—original draft, M.H.D. and M.R.T.; Writing—review and editing, E.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are openly available in 4TU.ResearchData at https://doi.org/10.4121/49badc7f-096a-4f2d-bdf9-c9a6057d8576.v2. Raw data were obtained from https://mop.gov.iq/en (accessed on 12 February 2024.) and https://mofa.gov.iq/newyork/?page_id=6745&lang=en (accessed on 12 February 2024.).
Acknowledgments
The authors would like to thank the three anonymous reviewers for the time and effort they spent in reviewing the manuscript, which helped improve its overall quality.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Alsanad, A.H.; Bin Mahmoud, A.A.; Aljadhai, S.I. An Optimal Upgrading Framework for Water Distribution Systems Operation. Water 2024, 16, 1737. [Google Scholar] [CrossRef]
- Muhammed, K.; Farmani, R.; Behzadian, K.; Diao, K.; Butler, D. Optimal rehabilitation of water distribution systems using a cluster-based technique. J. Water Resour. Plan. Manag. 2017, 143, 04017022. [Google Scholar] [CrossRef]
- Zaman, D.; Gupta, A.K.; Uddameri, V.; Tiwari, M.K.; Ghosal, P.S. Hydraulic performance benchmarking for effective management of water distribution networks: An innovative composite index-based approach. J. Environ. Manag. 2021, 299, 113603. [Google Scholar] [CrossRef] [PubMed]
- Minaei, A.; Creaco, E.; Sitzenfrei, R. A multi-utility and dynamic approach for the upgrade of an aged water distribution network. IOP Conf. Ser. Earth Environ. Sci. 2023, 1136, 012041. [Google Scholar] [CrossRef]
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in optimisation of water distribution systems? A literature review of system operation. Environ. Model. Softw. 2017, 93, 209–254. [Google Scholar] [CrossRef]
- Marques, J.; Cunha, M. Upgrading water distribution networks to work under uncertain conditions. Water Supply 2020, 20, 878–888. [Google Scholar] [CrossRef]
- Savić, D.A.; Bicik, J.; Morley, M.S. A DSS generator for multiobjective optimisation of spreadsheet-based models. Environ. Model. Softw. 2011, 26, 551–561. [Google Scholar] [CrossRef]
- Kim Joong, H.; Mays Larry, W. Optimal Rehabilitation Model for Water-Distribution Systems. J. Water Resour. Plan. Manag. 1994, 120, 674–692. [Google Scholar] [CrossRef]
- Giustolisi, O.; Laucelli, D.; Savic†, D.A. Development of rehabilitation plans for water mains replacement considering risk and cost-benefit assessment. Civ. Eng. Environ. Syst. 2006, 23, 175–190. [Google Scholar] [CrossRef]
- Elshaboury, N.; Marzouk, M. Prioritizing water distribution pipelines rehabilitation using machine learning algorithms. Soft Comput. 2022, 26, 5179–5193. [Google Scholar] [CrossRef]
- Farouk, A.M.; Rahman, R.A.; Romali, N.S. Economic analysis of rehabilitation approaches for water distribution networks: Comparative study between Egypt and Malaysia. J. Eng. Des. Technol. 2023, 21, 130–149. [Google Scholar] [CrossRef]
- Farmani, R.; Savic, D.A.; Walters, G.A. Evolutionary multi-objective optimization in water distribution network design. Eng. Optim. 2005, 37, 167–183. [Google Scholar] [CrossRef]
- Prasad, T.D. Design of pumped water distribution networks with storage. J. Water Resour. Plan. Manag. 2010, 136, 129–132. [Google Scholar] [CrossRef]
- Stokes, C.S.; Maier, H.R.; Simpson, A.R. Effect of Storage Tank Size on the Minimization of Water Distribution System Cost and Greenhouse Gas Emissions While Considering Time-Dependent Emissions Factors. J. Water Resour. Plan. Manag. 2016, 142, 04015052. [Google Scholar] [CrossRef]
- Jowitt Paul, W.; Germanopoulos, G. Optimal Pump Scheduling in Water-Supply Networks. J. Water Resour. Plan. Manag. 1992, 118, 406–422. [Google Scholar] [CrossRef]
- Cantu-Funes, R.; Coelho, L.C. Simulation-based optimization of pump scheduling for drinking water distribution systems. Eng. Optim. 2023, 55, 841–855. [Google Scholar] [CrossRef]
- Wang, Q.; Guidolin, M.; Savic, D.; Kapelan, Z. Two-Objective Design of Benchmark Problems of a Water Distribution System via MOEAs: Towards the Best-Known Approximation of the True Pareto Front. J. Water Resour. Plan. Manag. 2015, 141, 04014060. [Google Scholar] [CrossRef]
- Price, E.; Ostfeld, A. Successive Linear Programming Approach Applied to BBLAWN. J. Water Resour. Plan. Manag. 2016, 142, C4015001. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, H.; Pei, S.; Zhao, M.; Zhou, H. Multi-objective operational optimization toward improved resilience in water distribution systems. AQUA Water Infrastruct. Ecosyst. Soc. 2022, 71, 593–607. [Google Scholar] [CrossRef]
- Gupta, R.; Kakwani, N.; Ormsbee, L. Optimal Upgrading of Water Distribution Network Redundancy. J. Water Resour. Plan. Manag. 2015, 141, 04014043. [Google Scholar] [CrossRef]
- Kadu, M.S.; Gupta, R.; Bhave Pramod, R. Optimal Design of Water Networks Using a Modified Genetic Algorithm with Reduction in Search Space. J. Water Resour. Plan. Manag. 2008, 134, 147–160. [Google Scholar] [CrossRef]
- Guangtao, F.; Kapelan, Z.; Reed, P. Reducing the Complexity of Multiobjective Water Distribution System Optimization through Global Sensitivity Analysis. J. Water Resour. Plan. Manag. 2012, 138, 196–207. [Google Scholar] [CrossRef]
- Rahmani, F.; Behzadian, K.; Ardeshir, A. Rehabilitation of a Water Distribution System Using Sequential Multiobjective Optimization Models. J. Water Resour. Plan. Manag. 2016, 142, C4015003. [Google Scholar] [CrossRef]
- Schaeffer, S.E. Graph clustering. Comput. Sci. Rev. 2007, 1, 27–64. [Google Scholar] [CrossRef]
- Louati, M.H.; Benabdallah, S.; Lebdi, F.; Milutin, D. Application of a Genetic Algorithm for the Optimization of a Complex Reservoir System in Tunisia. Water Resour. Manag. 2011, 25, 2387–2404. [Google Scholar] [CrossRef]
- Tzatchkov, V.G.; Alcocer-Yamanaka, V.H.; Bourguett Ortíz, V. Graph Theory Based Algorithms for Water Distribution Network Sectorization Projects. In Proceedings of the Water Distribution Systems Analysis Symposium 2006, Cincinnati, OH, USA, 27–30 August 2006; pp. 1–15. [Google Scholar]
- Perelman, L.; Ostfeld, A. Topological clustering for water distribution systems analysis. Environ. Model. Softw. 2011, 26, 969–972. [Google Scholar] [CrossRef]
- Deuerlein, J.W. Decomposition Model of a General Water Supply Network Graph. J. Hydraul. Eng. 2008, 134, 822–832. [Google Scholar] [CrossRef]
- Deuerlein, J.; Elhay, S.; Simpson, A.R. Fast Graph Matrix Partitioning Algorithm for Solving the Water Distribution System Equations. J. Water Resour. Plan. Manag. 2016, 142, 04015037. [Google Scholar] [CrossRef]
- Diao, K.; Zhou, Y.; Rauch, W. Automated creation of district metered area boundaries in water distribution systems. J. Water Resour. Plan. Manag. 2013, 139, 184–190. [Google Scholar] [CrossRef]
- Clauset, A.; Newman, M.E.; Moore, C. Finding community structure in very large networks. Phys. Rev. E 2004, 70, 066111. [Google Scholar] [CrossRef]
- Newman, M.E.J. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef] [PubMed]
- Giustolisi, O.; Ridolfi, L. New Modularity-Based Approach to Segmentation of Water Distribution Networks. J. Hydraul. Eng. 2014, 140, 04014049. [Google Scholar] [CrossRef]
- Herrera, M. Improving Water Network Management by Efficient Division into Supply Clusters. Ph.D. Thesis, Universitat Politecnica De Valencia, Valencia, Spain, 2011. [Google Scholar]
- Ferrari, G.; Savic, D.; Becciu, G. Graph-Theoretic Approach and Sound Engineering Principles for Design of District Metered Areas. J. Water Resour. Plan. Manag. 2014, 140, 04014036. [Google Scholar] [CrossRef]
- Yu, T.; Zhang, X.; Long, Z.; Zhou, H.; Liu, X. Optimal design of district metered areas based on improved particle swarm optimization method for water distribution systems. Water Supply 2022, 22, 7930–7944. [Google Scholar] [CrossRef]
- Swamee, P.K.; Sharma, A.K. Decomposition of Large Water Distribution Systems. J. Environ. Eng. 1990, 116, 269–283. [Google Scholar] [CrossRef]
- Swamee, P.K.; Sharma, A.K. Design of Water Supply Pipe Networks; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Zheng, F.; Simpson, A.R.; Zecchin, A.C.; Deuerlein, J.W. A graph decomposition-based approach for water distribution network optimization. Water Resour. Res. 2013, 49, 2093–2109. [Google Scholar] [CrossRef]
- Diao, K.; Fu, G.; Farmani, R.; Guidolin, M.; Butler, D. Twin-Hierarchy Decomposition for Optimal Design of Water Distribution Systems. J. Water Resour. Plan. Manag. 2016, 142, C4015008. [Google Scholar] [CrossRef]
- Ciaponi, C.; Murari, E.; Todeschini, S. Modularity-Based Procedure for Partitioning Water Distribution Systems into Independent Districts. Water Resour. Manag. 2016, 30, 2021–2036. [Google Scholar] [CrossRef]
- Bruno, B.; Enrique, C.; Goulart, T.; Manzi, D.; Meirelles, G.; Herrera, M.; Izquierdo, J.; Luvizotto, E. Social Network Community Detection and Hybrid Optimization for Dividing Water Supply into District Metered Areas. J. Water Resour. Plan. Manag. 2018, 144, 04018020. [Google Scholar] [CrossRef]
- Alvisi, S. A New Procedure for Optimal Design of District Metered Areas Based on the Multilevel Balancing and Refinement Algorithm. Water Resour. Manag. 2015, 29, 4397–4409. [Google Scholar] [CrossRef]
- Di Nardo, A.; Giudicianni, C.; Greco, R.; Herrera, M.; Santonastaso, G.F. Applications of Graph Spectral Techniques to Water Distribution Network Management. Water 2018, 10, 45. [Google Scholar] [CrossRef]
- Fu, G.; Kapelan, Z.; Reed, P. Sensitivity Analysis to Improve Water Distribution System Optimisation. In Water Distribution Systems Analysis 2010; ASCE Press: New York, NY, USA, 2010; pp. 799–809. [Google Scholar]
- Fiorini, M.A.; Shaffiee Haghshenas, S.; Shaffiee Haghshenas, S.; Choi, D.Y.; Geem, Z.W. Sensitivity Analysis for Performance Evaluation of a Real Water Distribution System by a Pressure Driven Analysis Approach and Artificial Intelligence Method. Water 2021, 13, 1116. [Google Scholar] [CrossRef]
- Izquierdo, J.; Montalvo, I.; Pérez, R.; Herrera, M. Sensitivity analysis to assess the relative importance of pipes in water distribution networks. Math. Comput. Model. 2008, 48, 268–278. [Google Scholar] [CrossRef]
- Jensen, H.A.; Jerez, D.J. A Stochastic Framework for Reliability and Sensitivity Analysis of Large Scale Water Distribution Networks. Reliab. Eng. Syst. Saf. 2018, 176, 80–92. [Google Scholar] [CrossRef]
- Reca, J.; Martínez, J.; López, R. A Hybrid Water Distribution Networks Design Optimization Method Based on a Search Space Reduction Approach and a Genetic Algorithm. Water 2017, 9, 845. [Google Scholar] [CrossRef]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- Song, S.; Zhao, J. Survey of graph clustering algorithms using amazon reviews. In Proceedings of the 17th International Conference on World Wide Web, Beijing, China, 21–25 April 2008; pp. 21–25. [Google Scholar]
- Newman, M.E.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef]
- Todini, E. Looped water distribution networks design using a resilience index based heuristic approach. Urban Water 2000, 2, 115–122. [Google Scholar] [CrossRef]
- Farmani, R.; Walters, G.; Savic, D. Evolutionary multi-objective optimization of the design and operation of water distribution network: Total cost vs. reliability vs. water quality. J. Hydroinform. 2006, 8, 165–179. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET 2: Users Manual; Bibliogov. 2000. Available online: https://pdamciamis.co.id/uploads/ebuku/Buku_Manual_Program_EPANET.pdf (accessed on 5 March 2024).
- Jain, H.; Deb, K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: Handling constraints and extending to an adaptive approach. IEEE Trans. Evol. Comput. 2013, 18, 602–622. [Google Scholar] [CrossRef]
- Seada, H.; Deb, K. U-NSGA-III: A unified evolutionary algorithm for single, multiple, and many-objective optimization. COIN Rep. 2014, 9019, 34–49. [Google Scholar]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).