Influence Mechanism of Spatial Variability of Permeability Coefficient on Seepage Characteristics of High Core Rockfill Dams: Insights from Numerical Simulations
Abstract
1. Introduction
2. Methodology
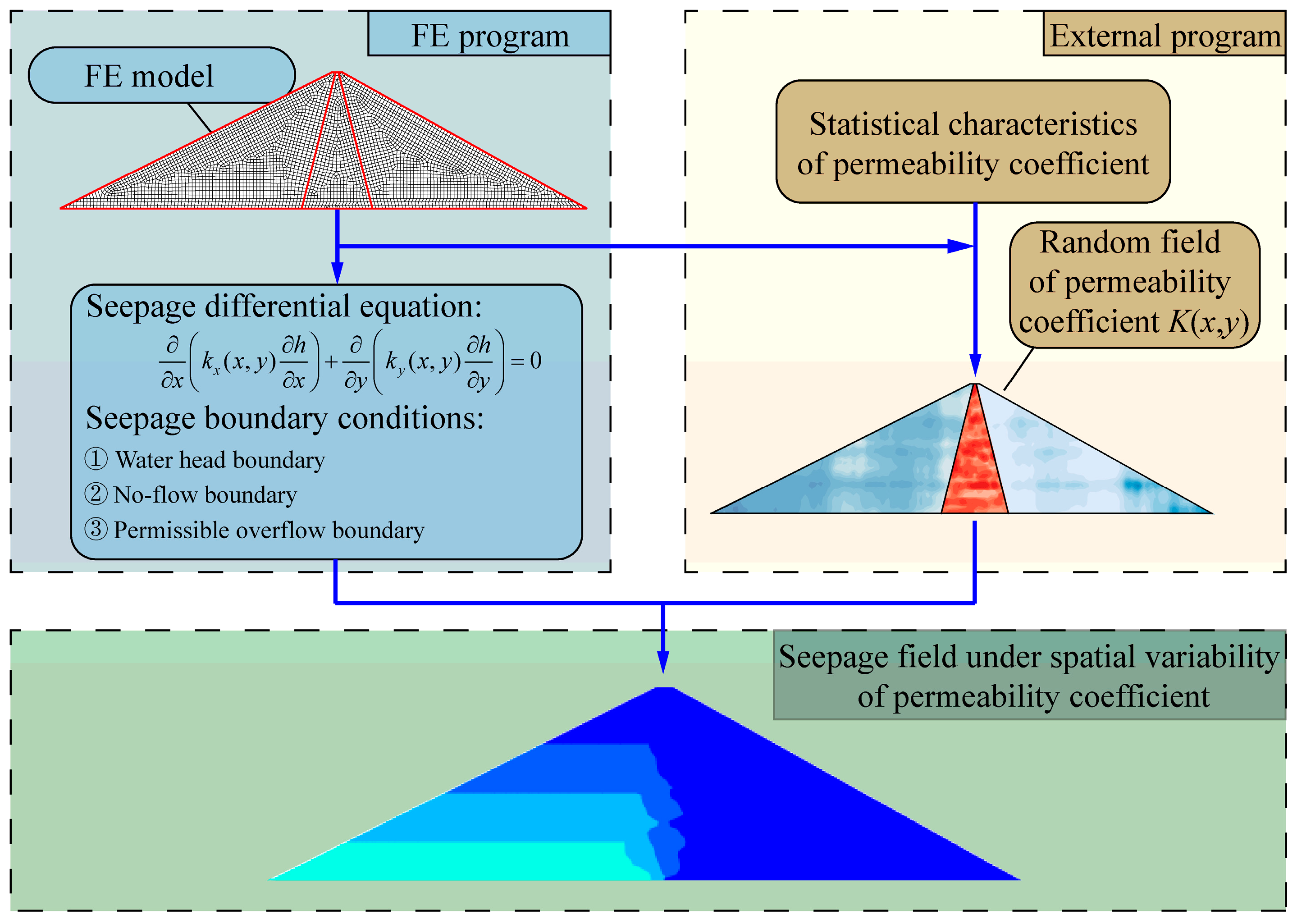
2.1. Random Field Simulation Techniques for the Spatial Variability of Permeability Coefficient
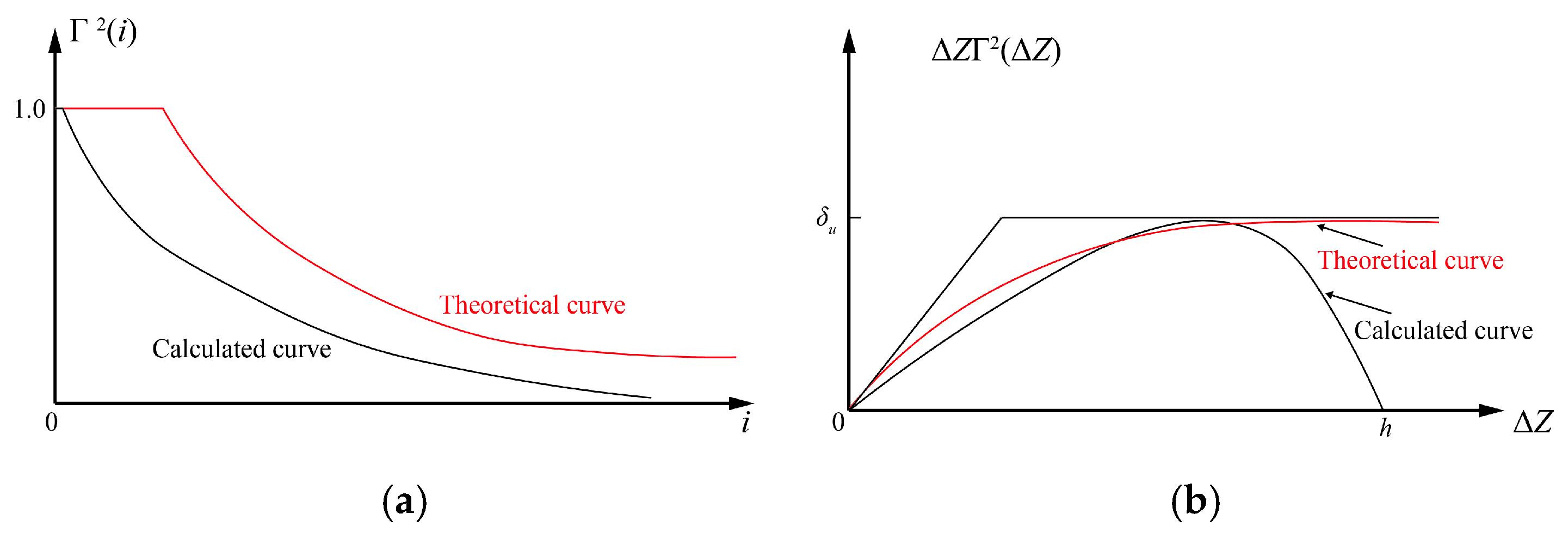
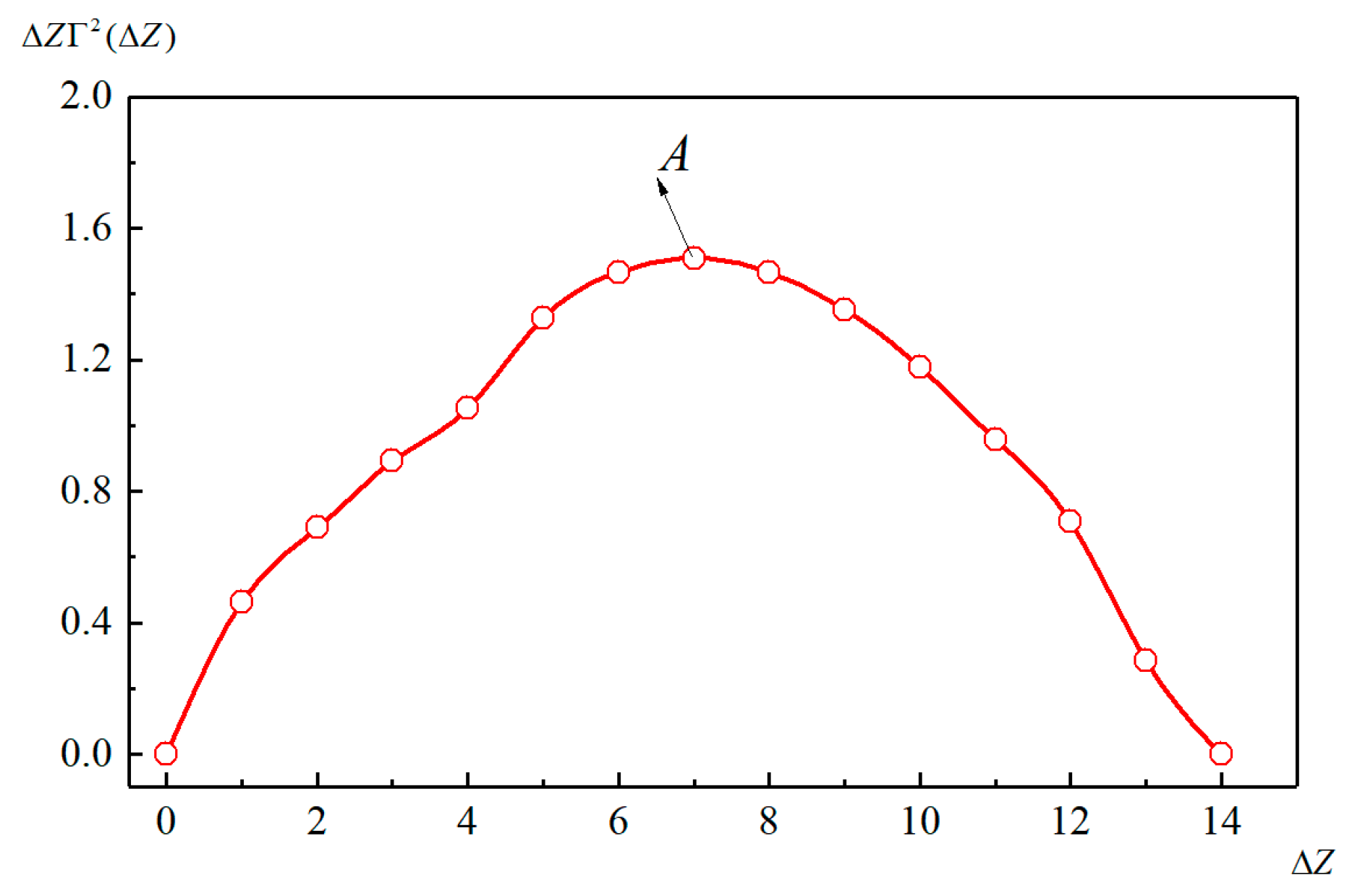
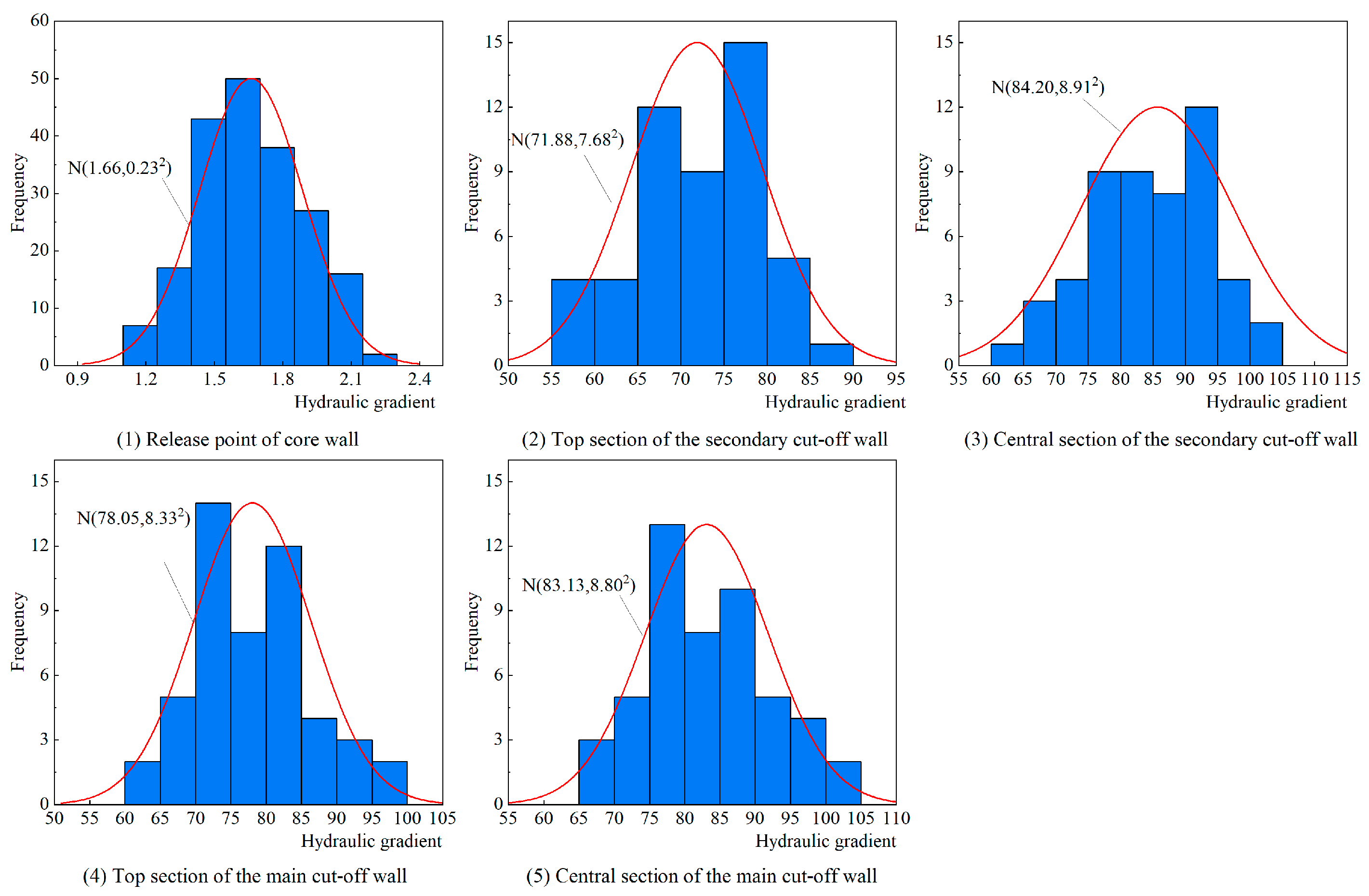
2.2. Estimation Method for Autocorrelation Distance
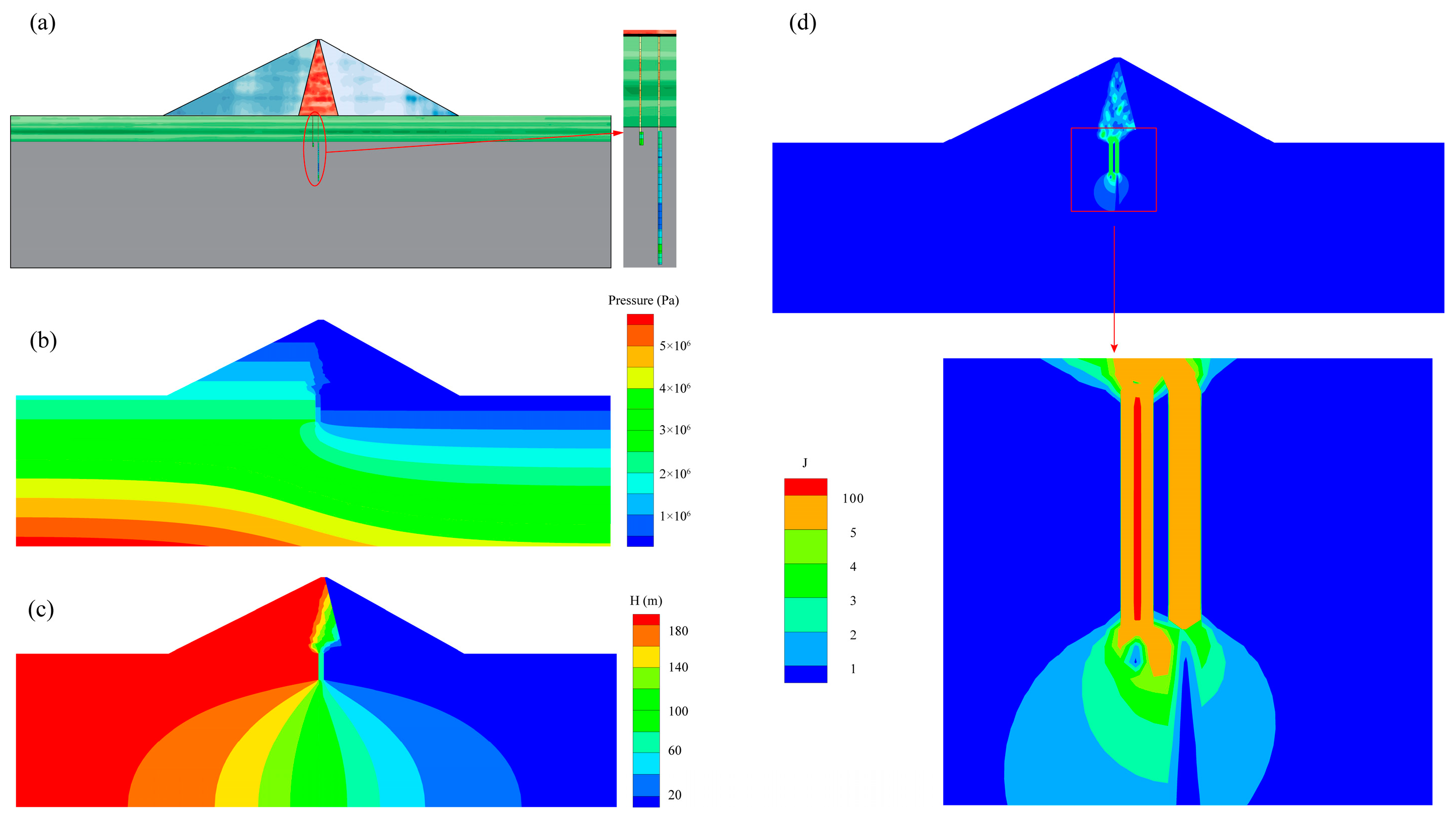
2.3. Seepage Numerical Simulation
3. Analysis and Results
3.1. Model and Parameters
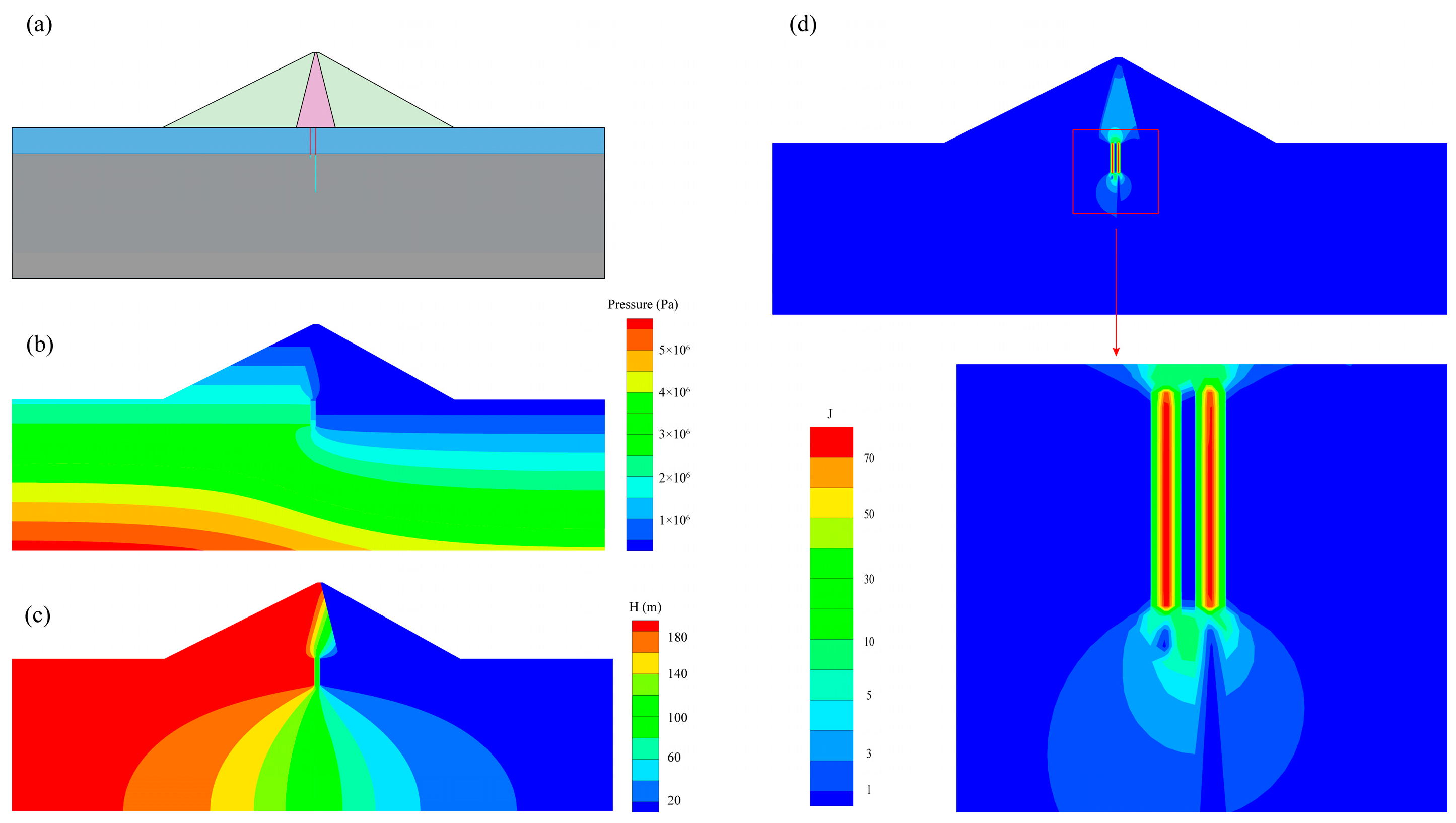
3.1.1. Finite Element Model
3.1.2. Material Parameters
3.2. Numerical Experiment Design
3.3. Effect of the Spatial Variability of Permeability Coefficient on the Seepage Characteristics
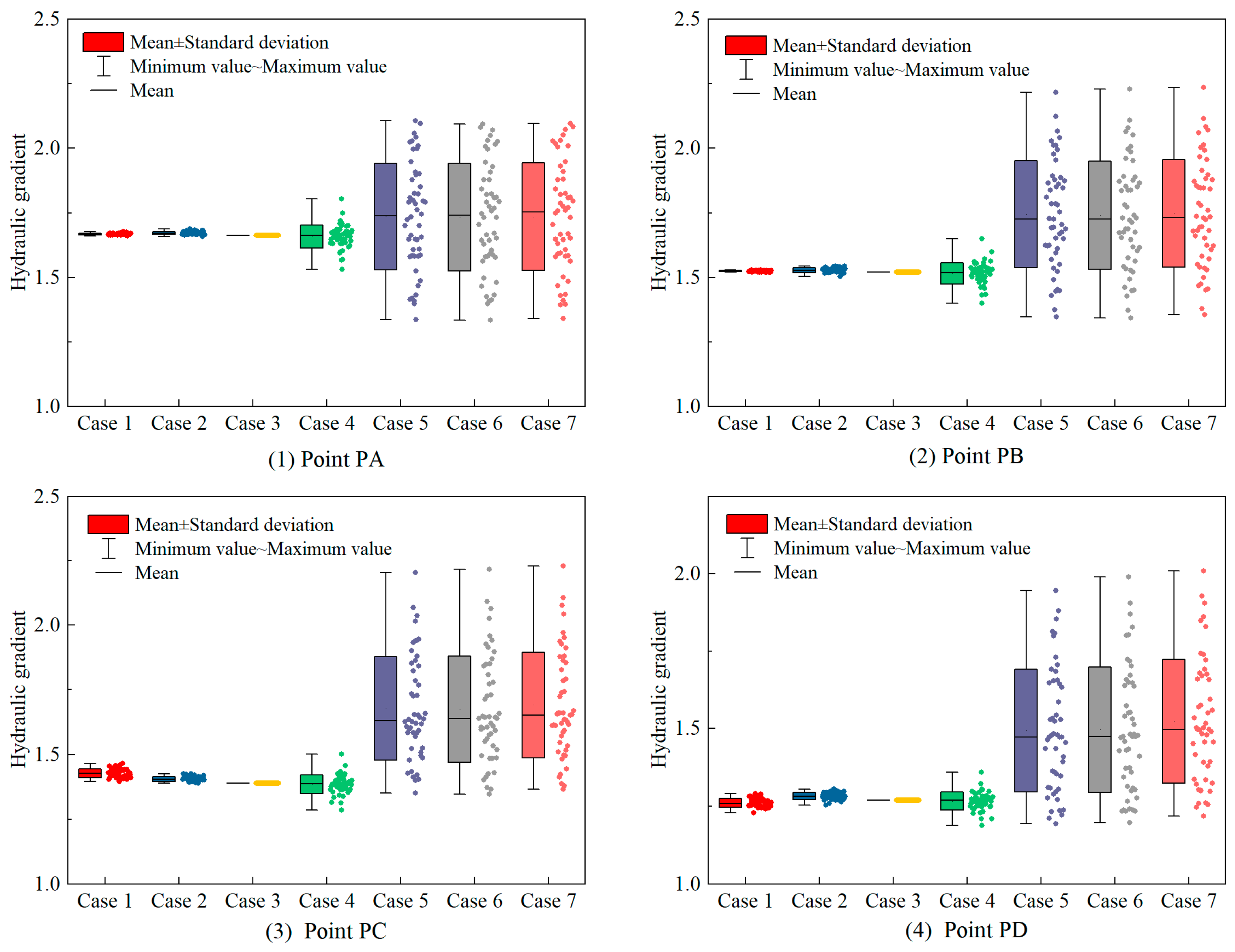
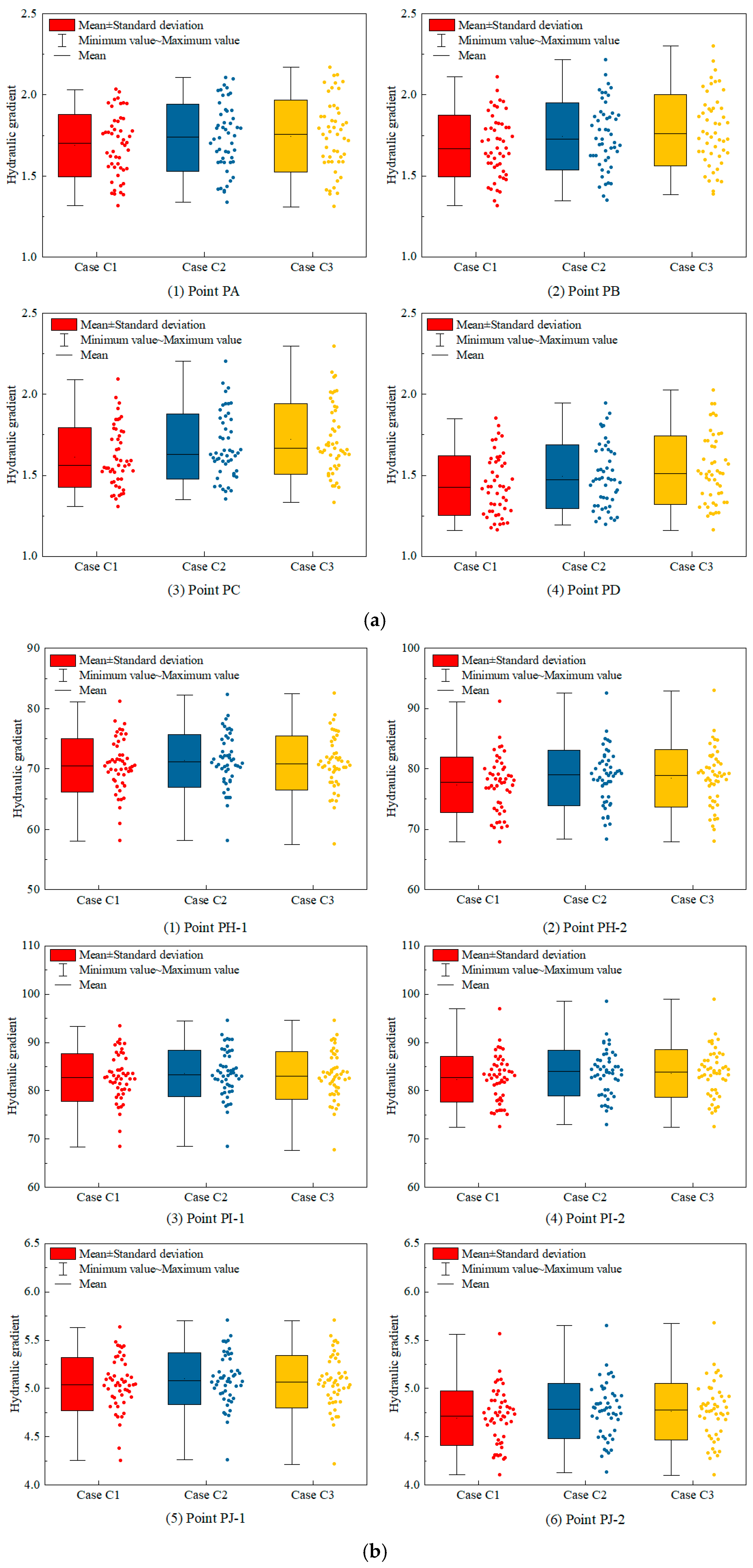
3.4. Effect of the Spatial Variability of Permeability Coefficient on the Hydraulic Gradient
4. Discussions
5. Conclusions
- (1)
- The spatial variability of permeability coefficients in the rockfill, the overburden, and the curtain shows relatively minor impacts on the seepage.
- (2)
- The spatial variability of permeability coefficients in the core wall and the cut-off walls significantly affects the seepage characteristics of the dam–foundation system, including the enhanced discreteness of the hydraulic gradient in the anti-seepage structures and an increased difference in the water head between the main and secondary cut-off walls, which is not conducive to the coordinated anti-seepage of the main and secondary cut-off walls.
- (3)
- Notably, the permeability characteristics of the core wall and the cut-off walls demonstrate distinct coupling behaviors, indicating their interdependent hydraulic relationship.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nourani, V.; Ojaghi, A.; Zhang, Y. Saturated and unsaturated seepage analysis of earth-fill dams using fractal hydraulic conductivity function and its verification. J. Hydrol. 2022, 612, 128302. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, H.; Mao, J.; Guan, G. Numerical simulation of the bubbling phenomenon ahead of the dam using a two-phase seepage free surface model. Comput. Geotech. 2023, 155, 105239. [Google Scholar] [CrossRef]
- Nan, S.; Ren, J.; Ma, Z.; Kang, J.; Sui, J. Inversion of the seepage parameters of earth/rockfill dams considering the coupling effect of seepage and thermal transfer. Comput. Geotech. 2024, 165, 105882. [Google Scholar]
- Wang, R.; Zhao, Y.; Qi, Y.; Sun, Z. Study on the changing law of three-dimensional electric field during the evolution of seepage field in earth and rock embankment dams. Measurement 2025, 239, 115483. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.; Wong, H.; Jiang, T.; Dong, J. Modeling dam deformation in the early stage of internal seepage erosion—Application to the Teton Dam, Idaho, before the 1976 incident. J. Hydrol. 2022, 605, 127378. [Google Scholar] [CrossRef]
- Yang, X.; Xu, Z.; Chai, J.; Qin, Y.; Cao, J. Numerical investigation of the seepage mechanism and characteristics of soil-structure interface by CFD-DEM coupling method. Comput. Geotech. 2023, 159, 105430. [Google Scholar]
- Guo, X.; Dias, D.; Carvajal, C.; Peyras, L.; Breul, P. Modelling and comparison of different types of random fields: Case of a real earth dam. Eng. Comput. 2022, 38, 4529–4543. [Google Scholar]
- Li, Y.; Liu, H.; Wen, L.; Xu, Z.; Zhang, Y. Reliability analysis of high core rockfill dam against seepage failure considering spatial variability of hydraulic parameters. Acta. Geotech. 2024, 19, 4091–4106. [Google Scholar] [CrossRef]
- Yu, X.; Li, Z.; Wang, Y.; Pang, R.; Lv, X.; Fu, M. Stress-deformation analysis of concrete anti-seepage structure in earth-rock dam on overburden considering spatial variability of geomechanical parameter. Probabilistic Eng. Mech. 2023, 79, 103725. [Google Scholar] [CrossRef]
- Guo, X.; Dias, D.; Pan, Q. Probabilistic stability analysis of an embankment dam considering soil spatial variability. Comput. Geotech. 2019, 113, 103093. [Google Scholar] [CrossRef]
- Li, J.; Wu, Z.; Chen, J.; Lu, X.; Li, Z. FEM-Bayesian Kriging method for deformation field estimation of earth dams with limited monitoring data. Comput. Geotech. 2022, 148, 104782. [Google Scholar]
- Ran, L.; Yang, J.; Zhang, P.; Wang, J.; Ma, C.; Cui, C.; Cheng, L.; Wang, J.; Zhou, M. A hybrid monitoring model of rockfill dams considering the spatial variability of rockfill materials and a method for determining the monitoring indexes. J. Civ. Struct. Health Monit. 2022, 12, 817–832. [Google Scholar]
- Li, Y.; Hicks, M.; Vardon, P. Uncertainty reduction and sampling efficiency in slope designs using 3D conditional random fields. Comput. Geotech. 2016, 79, 159–172. [Google Scholar]
- Yang, Z.; Ching, J. Simulation of three-dimensional random field conditioning on incomplete site data. Eng. Geol. 2021, 281, 105987. [Google Scholar]
- Wu, L. Preliminary analysis of elastic modulus stochastic field’s effect on concrete dam stress. Yunnan Water Power 2002, 18, 79–81. [Google Scholar]
- Chen, H.; Liu, D. Stochastic finite element analysis of rockfill dam considering spatial variability of dam material porosity. Eng. Comput. 2019, 36, 2929–2959. [Google Scholar]
- Chi, S.; Feng, W.; Jia, Y.; Zhang, Z. Stochastic finite-element analysis of earth-rockfill dams considering the spatial variability of soil parameters. Int. J. Geomech. 2022, 22, 04022224. [Google Scholar]
- Mouyeaux, A.; Carvajal, C.; Bressolette, P.; Peyras, L.; Breul, P.; Bacconnet, C. Probabilistic analysis of pore water pressures of an earth dam using a random finite element approach based on field data. Eng. Geol. 2019, 259, 105190. [Google Scholar] [CrossRef]
- Tan, X.; Wang, X.; Khoshnevisan, S.; Hou, X.; Zha, F. Seepage analysis of earth dams considering spatial variability of hydraulic parameters. Eng. Geol. 2017, 228, 260–269. [Google Scholar]
- Xu, M.; Pang, R.; Zhou, Y.; Xu, B. Seepage safety evaluation of high earth-rockfill dams considering spatial variability of hydraulic parameters via subset simulation. J. Hydrol. 2023, 626, 130261. [Google Scholar]
- Chi, F.; Breul, P.; Carvajal, C.; Peyras, L. Stochastic seepage analysis in embankment dams using different types of random fields. Comput. Geotech. 2023, 162, 105689. [Google Scholar]
- Li, J.; Chen, C.; Wu, Z.; Chen, J. Multi-source data-driven unsaturated seepage parameter inversion: Application to a high core rockfill dam. J. Hydrol. 2023, 617, 129171. [Google Scholar]
- Huang, Z.; Shen, Z.; Xu, L.; Sun, Y.; Li, H.; Liu, D. Seepage characteristics of core rockfill dam foundation with double cutoff walls in deep overburden: A case study. Case Stud. Constr. Mater. 2023, 21, e03576. [Google Scholar]
- Wu, Z.; Chen, C.; Zheng, Y.; Chen, J.; Bian, K.; Li, J. Analysis of seepage failure probability for high core rockfill dams during rapid drawdown of reservoir water level. J. Hydrol. 2024, 633, 131046. [Google Scholar] [CrossRef]
- Xu, M.; Zhou, Y.; Pang, R.; Xu, B.; Zhang, Y. A novel finite element limit equilibrium method and its application in instability analysis for 3-D high core rockfill dams. Structures 2024, 68, 107066. [Google Scholar]
- Xiang, Z.; Yu, S.; Wang, X. Modeling the hydraulic fracturing processes in shale formations using a meshless method. Water 2024, 16, 1855. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.; Seyed-Kolbadi, S.; Saouma, V.; Salamon, J.; Rajagopalan, B. Random finite element method for the seismic analysis of gravity dams. Eng. Struct. 2018, 171, 405–420. [Google Scholar]
- Lu, X.; Wu, Z.; Pei, L.; He, K.; Chen, J.; Li, Z.; Yang, Z. Effect of the spatial variability of strength parameters on the dynamic damage characteristics of gravity dams. Eng. Struct. 2019, 183, 281–289. [Google Scholar]
- Metya, S.; Bhattacharya, G. Accounting for 2D spatial variation in slope reliability analysis. Int. J. Geomech. 2020, 20, 04019190. [Google Scholar]
- Jiang, S.; Huang, J.; Griffiths, D.; Deng, Z.-P. Advances in reliability and risk analyses of slopes in spatially variable soils: A state-of-the-art review. Comput. Geotech. 2022, 141, 104498. [Google Scholar]
- Lu, X.; Pei, L.; Chen, J.; Wu, Z.; Li, Z. Comparison of homogenous and random fields of tensile strength effects on the nonlinear dynamical response of Guandi concrete gravity dams under strong earthquake waves. Struct. Infrastruct. Eng. 2021, 17, 1684–1697. [Google Scholar]
- Li, K.S.; Lumb, P. Probabilistic design of slopes. Can. Geotech. J. 1987, 24, 520–535. [Google Scholar]
- Li, Z.; Wu, Z.; Chen, J.; Pei, L.; Lu, X. Fuzzy seismic fragility analysis of gravity dams considering spatial variability of material parameters. Soil Dyn. Earthq. Eng. 2021, 140, 106439. [Google Scholar]
- Dang, V.; Ha Mac, V.; Huh, J.; Kwak, K.; Park, J.H. Response surface method-based efficient approach for the load and resistance factors calibration of breakwater foundation considering soil spatial variability. Appl. Ocean Res. 2024, 151, 104160. [Google Scholar]
- Jiang, S.; Hu, H.; Wang, Z. Improved Bayesian model updating of geomaterial parameters for slope reliability assessment considering spatial variability. Struct. Saf. 2025, 112, 102536. [Google Scholar] [CrossRef]
- Jiang, S.; Huang, J.; Yao, C.; Yang, J. Quantitative risk assessment of slope failure in 2-D spatially variable soils by limit equilibrium method. Appl. Math. Model. 2017, 47, 710–725. [Google Scholar]
- Vanmareke, E.H. Probability modeling of soil profile. J. Geotech. Eng. Div. 1977, 103, 1227–1245. [Google Scholar]
- Daneshkhah, A.; Remesan, R.; Chatrabgoun, O.; Holman, I.P. Probabilistic modeling of flood characterizations with parametric and minimum information pair-copula model. J. Hydrol. 2016, 540, 469–487. [Google Scholar] [CrossRef]
- Qi, W. ABAQUS 6.14 Super Learning Manual; Posts & Telecom Press: Beijing, China, 2016. [Google Scholar]
- Li, Z.; Wu, Z.; Chen, J.; Lu, X.; Pei, L.; Chen, C. Effect of correlated random fields on nonlinear dynamic responses of gravity dam. Nat. Hazards 2021, 106, 79–96. [Google Scholar]
- Hu, W.; Chen, X.; Lin, J.; Kuang, L. In-situ drilling tests of seepage in gravel soil core wall during the first impoundment in Pubugou hydropower station. Rock Soil Mech. 2013, 34, 1259–1263+1273. [Google Scholar]
- El-Ramly, H.; Morgenstern, N.R.; Cruden, D.M. Probabilistic stability analysis of a tailings dyke on presheared clay-shale. Can. Geotech. J. 2003, 40, 192–208. [Google Scholar]
- Phoon, K.K.; Kulhawy, F.H. Characterization of geotechnical variability. Can. Geotech. J. 1999, 36, 612–624. [Google Scholar]
- Ran, C.; Zhou, Z.; Pei, L.; Lu, X.; Gong, B.; He, K. A method for evaluating systematic risk in dams with random field theory. Appl. Sci. 2024, 14, 4349. [Google Scholar] [CrossRef]
- Jie, F. Spatial Variability of Streambed Hydraulic Conductivity in Yurungqash River. Master’s Thesis, Xinjiang University, Urumqi, China, 2018. [Google Scholar]
- Zhao, J. Spatial Variability of Streambed Hydraulic Conductivity in Golmud River. Master’s Thesis, Chang’an University, Xi’an, China, 2014. [Google Scholar]
- Zhou, Q. Anti-seepage treatment technology of lower reservoir dam foundation of Yangjiang Pumped Storage Power Station. Guangdong Water Resour. Hydropower 2023, 12, 63–68. [Google Scholar]
- Guo, Q. Method of Safety Risk Analysis for the Anti-Seepage System in High Core Rockfill Dams. Ph.D. Thesis, Sichuan University, Chengdu, China, 2020. [Google Scholar]
- Brunetti, G.; Maiolo, M.; Fallico, C.; Severino, G. Unraveling the complexities of a highly heterogeneous aquifer under convergent radial flow conditions. Eng. Comput. 2024, 40, 3115–3130. [Google Scholar] [CrossRef]
- Brunetti, G.; Bevacqua, M.; Maiolo, M.; Amisano, M. Optimizing the Reuse of Building Demolition Materials for Coastal Dunes Reestablishment. In Numerical Computations: Theory and Algorithms (NUMTA 2023); Sergeyev, Y.D., Kvasov, D.E., Astorino, A., Eds.; Springer: Cham, Switzerland, 2025; Lecture Notes in Computer Science; Volume 14477, pp. 184–191. [Google Scholar]




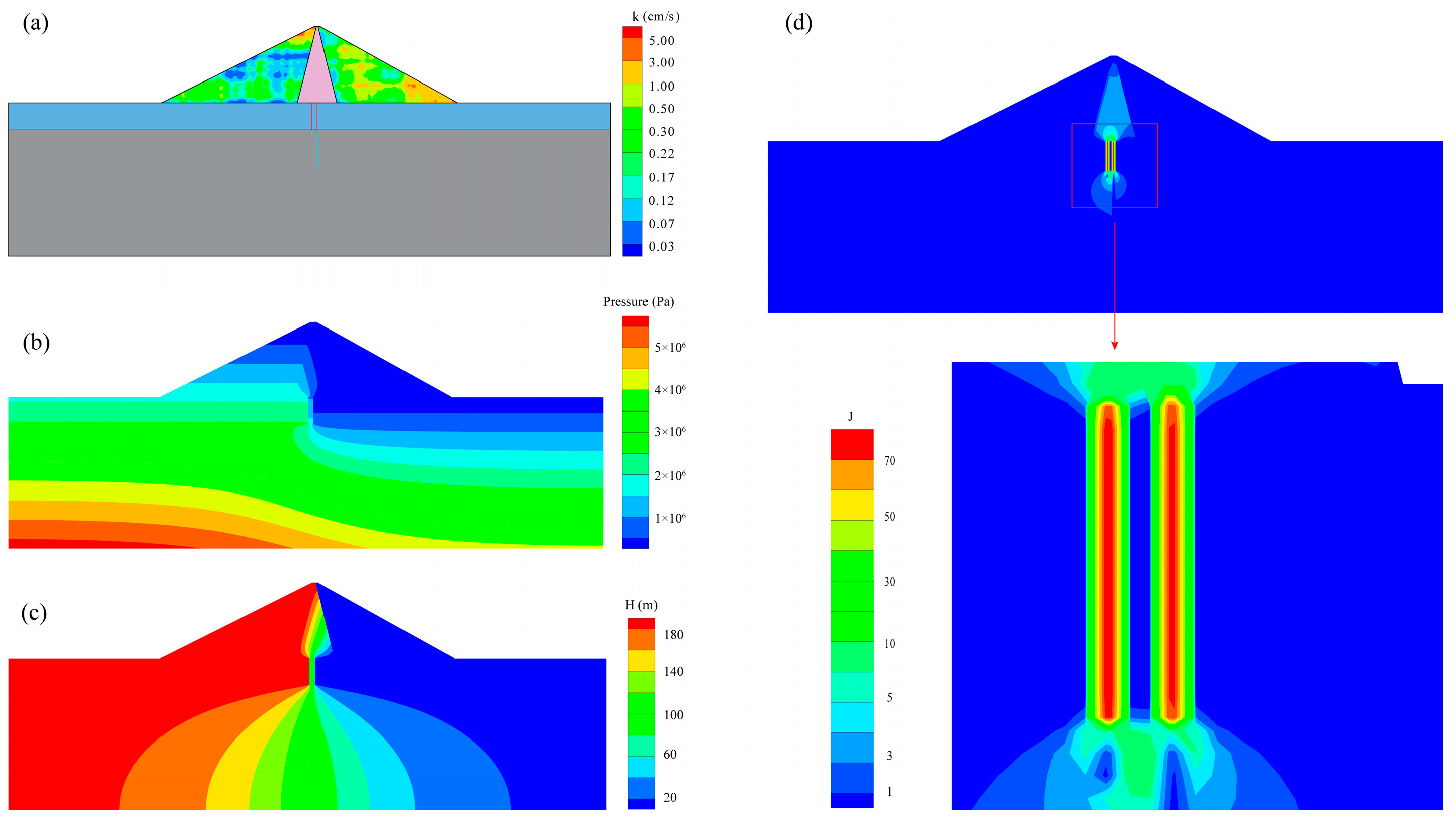

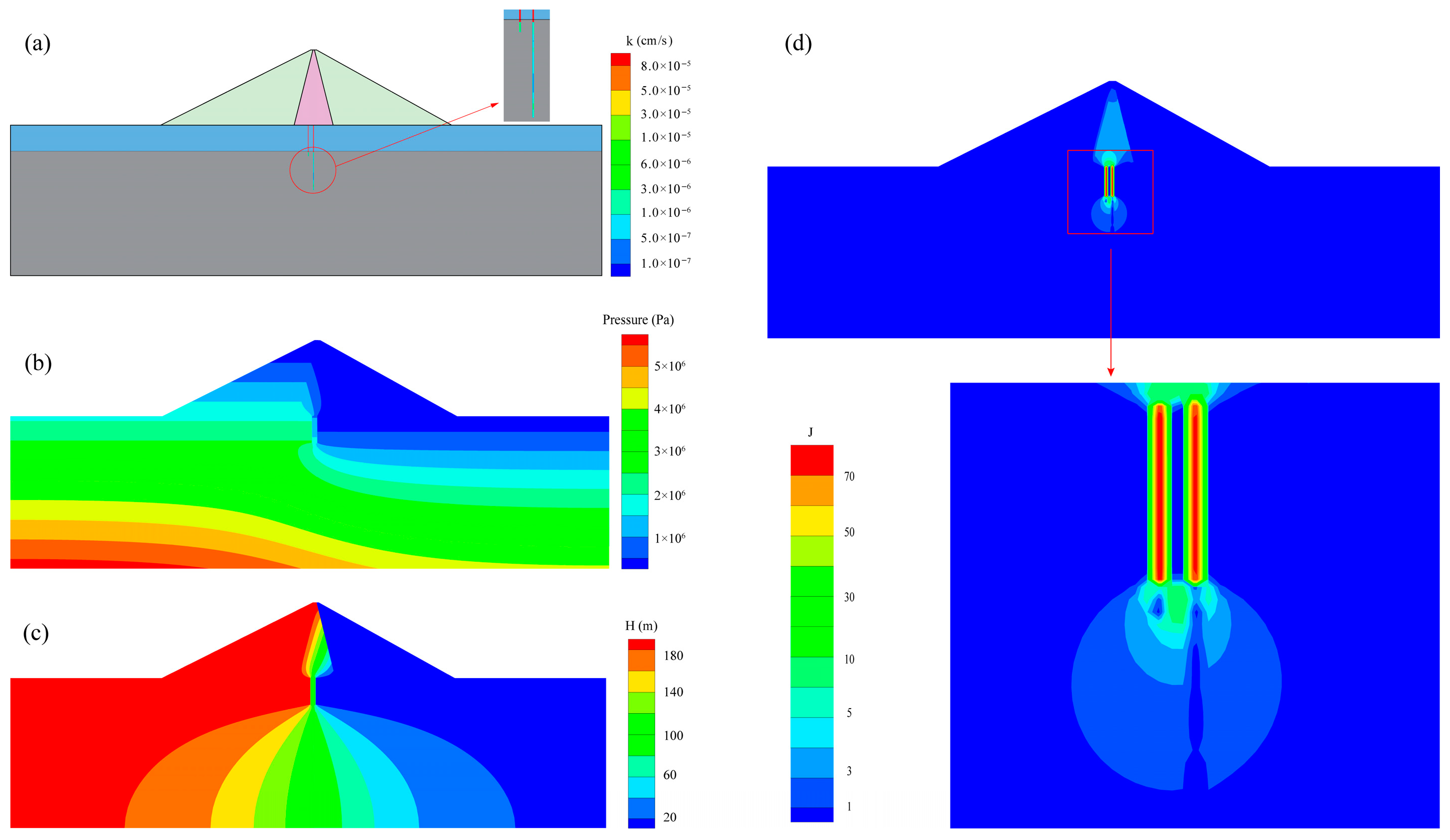
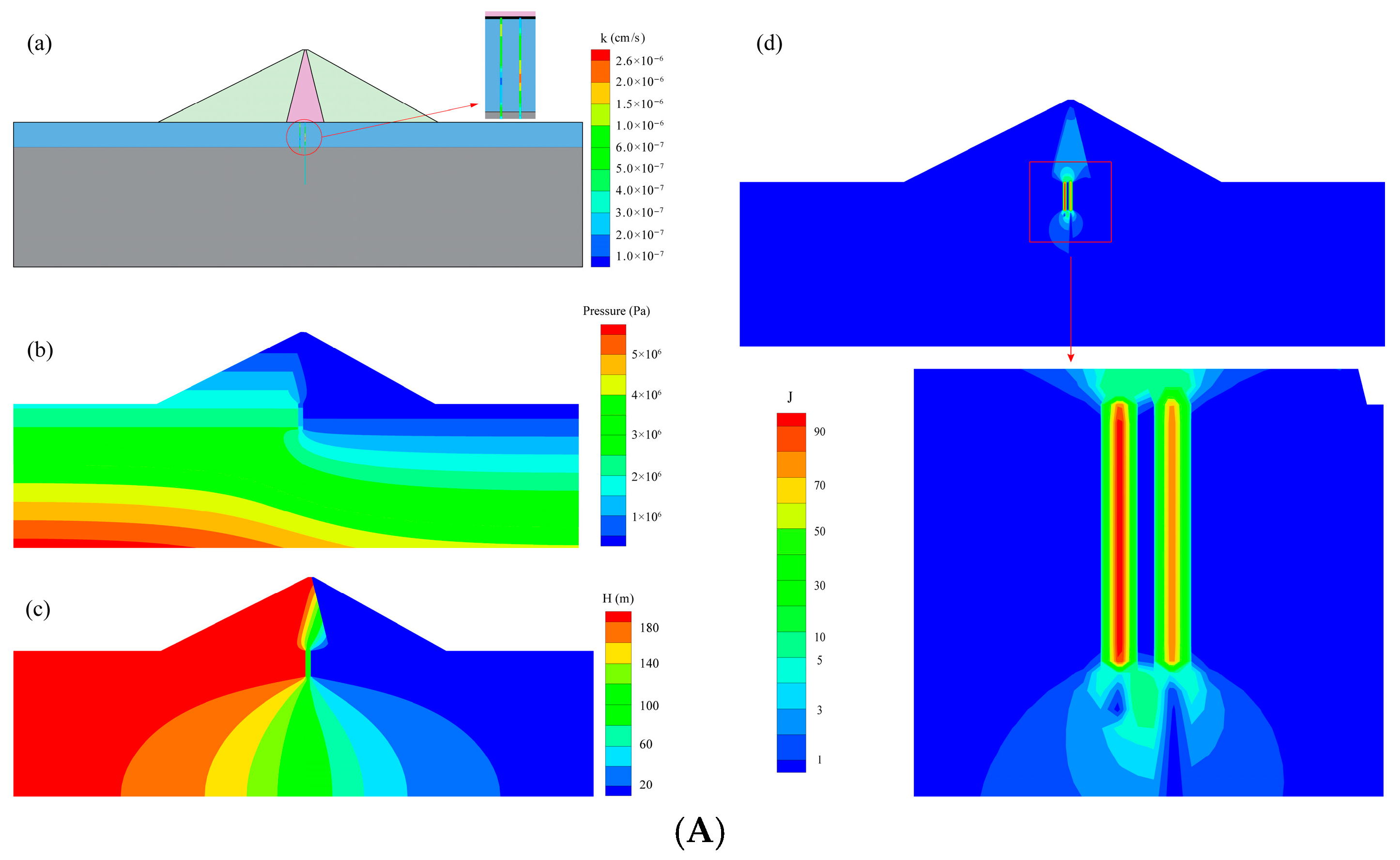
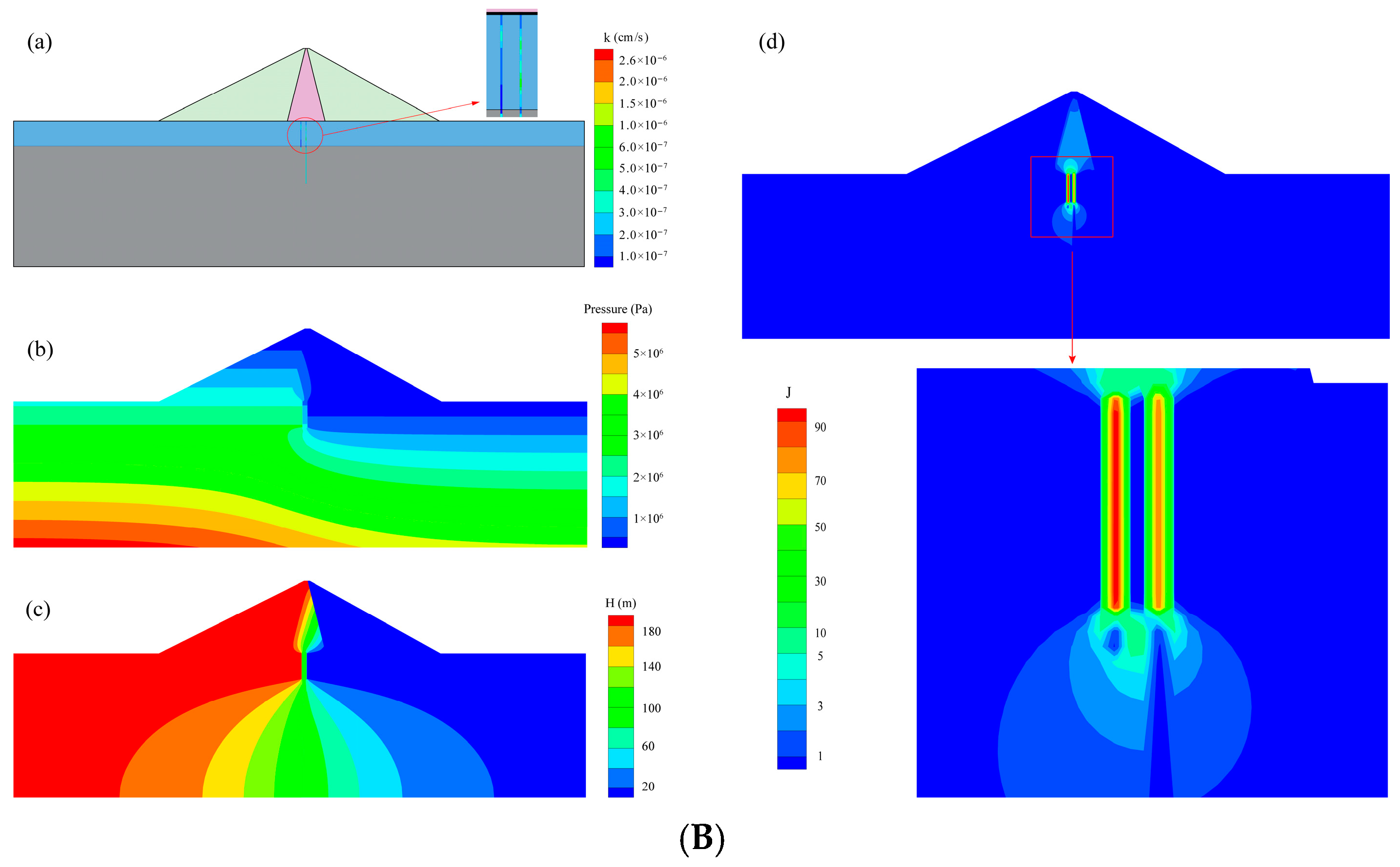




| Permeability Coefficients | Core Wall | Cut-Off Wall | Rockfill | Overburden | Curtain | Bedrock |
|---|---|---|---|---|---|---|
| Mean (cm/s) | ||||||
| Coefficient of variation | 1.72 | 0.86 | 0.92 | 1.48 | 0.98 | / |
| (m) | 45.0 | 1.2 | 120.0 | 1576 | 3.0 | / |
| (m) | 1.5 | 71.0 | 4.0 | 2.0 | 5.0 | / |
| Material Zoning | Rockfill | Overburden | Curtain | Cut-Off Wall | Core Wall | |
|---|---|---|---|---|---|---|
| Homogeneity scheme: Case 0 | 〇 | 〇 | 〇 | 〇 | 〇 | |
| Spatial variability scheme | Case 1 | √ | 〇 | 〇 | 〇 | 〇 |
| Case 2 | 〇 | √ | 〇 | 〇 | 〇 | |
| Case 3 | 〇 | 〇 | √ | 〇 | 〇 | |
| Case 4 | 〇 | 〇 | 〇 | √ | 〇 | |
| Case 5 | 〇 | 〇 | 〇 | 〇 | √ | |
| Case 6 | 〇 | 〇 | √ | √ | √ | |
| Case 7 | √ | √ | √ | √ | √ | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Lu, X.; Liu, X.; Chen, J. Influence Mechanism of Spatial Variability of Permeability Coefficient on Seepage Characteristics of High Core Rockfill Dams: Insights from Numerical Simulations. Water 2025, 17, 1064. https://doi.org/10.3390/w17071064
Guo Q, Lu X, Liu X, Chen J. Influence Mechanism of Spatial Variability of Permeability Coefficient on Seepage Characteristics of High Core Rockfill Dams: Insights from Numerical Simulations. Water. 2025; 17(7):1064. https://doi.org/10.3390/w17071064
Chicago/Turabian StyleGuo, Qinqin, Xiang Lu, Xiaolian Liu, and Jiankang Chen. 2025. "Influence Mechanism of Spatial Variability of Permeability Coefficient on Seepage Characteristics of High Core Rockfill Dams: Insights from Numerical Simulations" Water 17, no. 7: 1064. https://doi.org/10.3390/w17071064
APA StyleGuo, Q., Lu, X., Liu, X., & Chen, J. (2025). Influence Mechanism of Spatial Variability of Permeability Coefficient on Seepage Characteristics of High Core Rockfill Dams: Insights from Numerical Simulations. Water, 17(7), 1064. https://doi.org/10.3390/w17071064






