Analysis of Prediction Confidence in Water Quality Forecasting Employing LSTM
Abstract
1. Introduction
2. Methodology
2.1. Study Area
2.2. Data Sources
2.3. Model Development Based on LSTM Models
2.3.1. Principle of the Model
2.3.2. Model Training and Testing
2.3.3. Model Optimization
2.4. Confidence Analysis of LSTM Models
2.4.1. Model Accuracy Calculation
2.4.2. Confidence Analysis
3. Results and Discussion
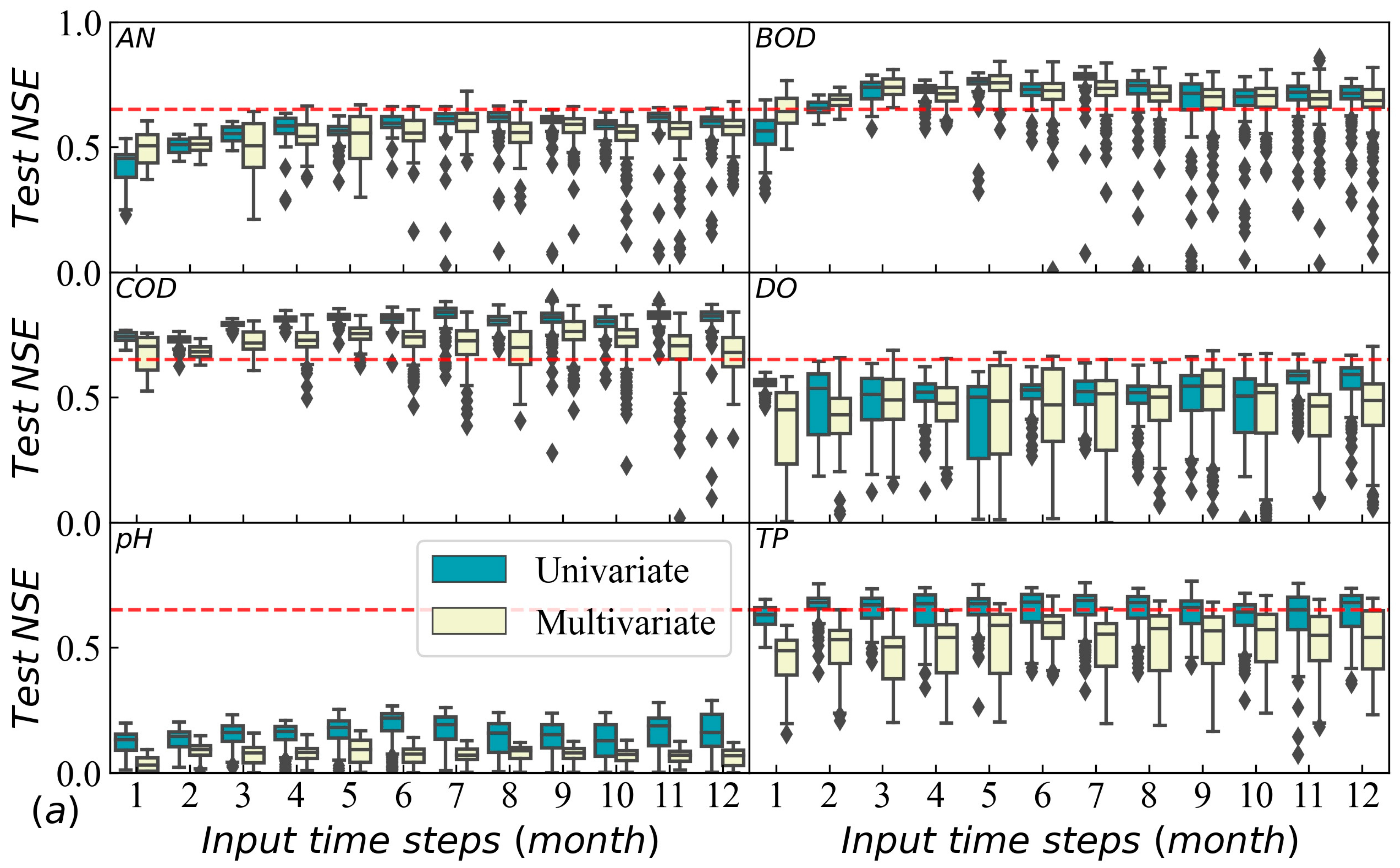
3.1. Model Accuracy Evaluation of Water Quality Prediction with Different Indexes
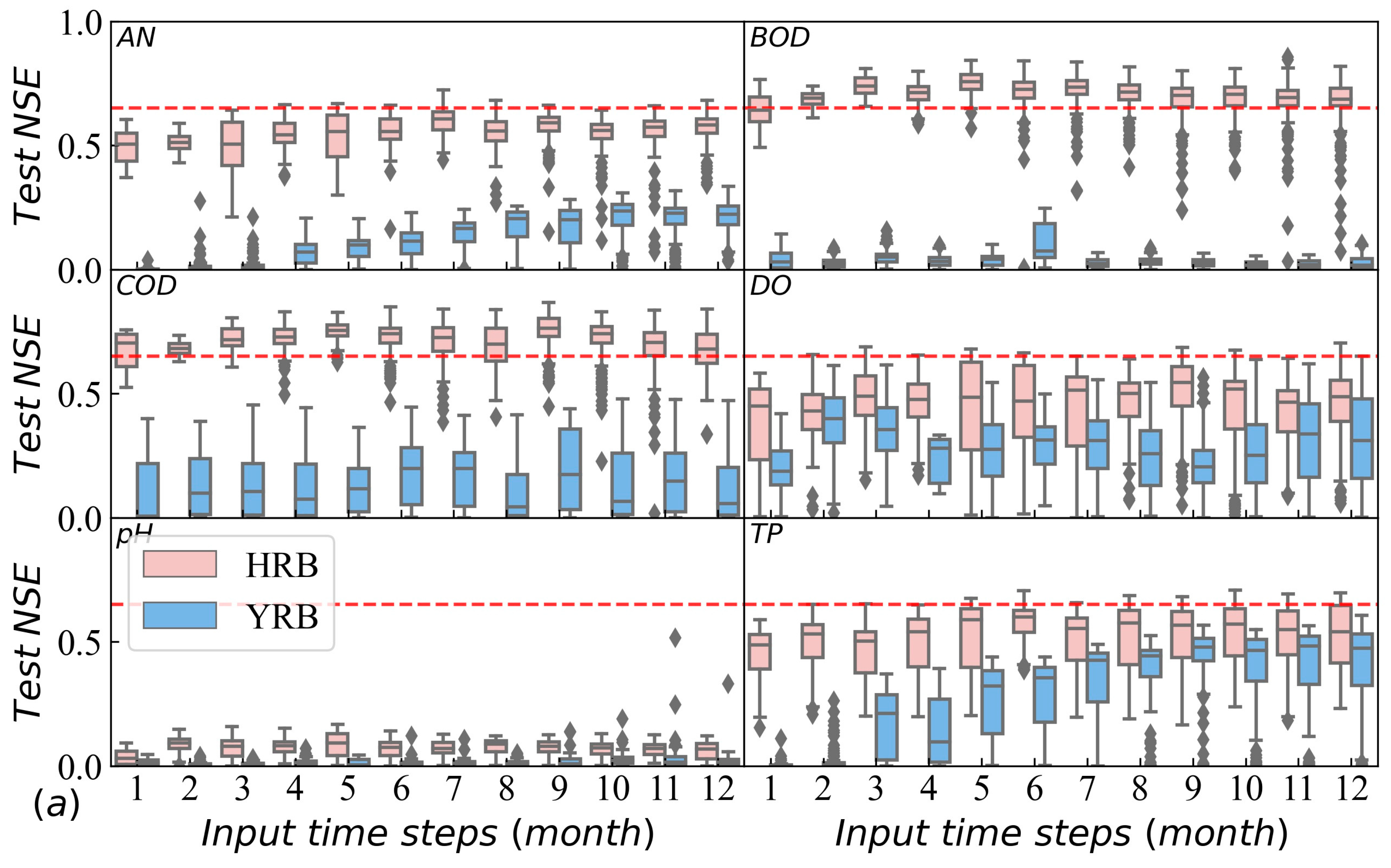
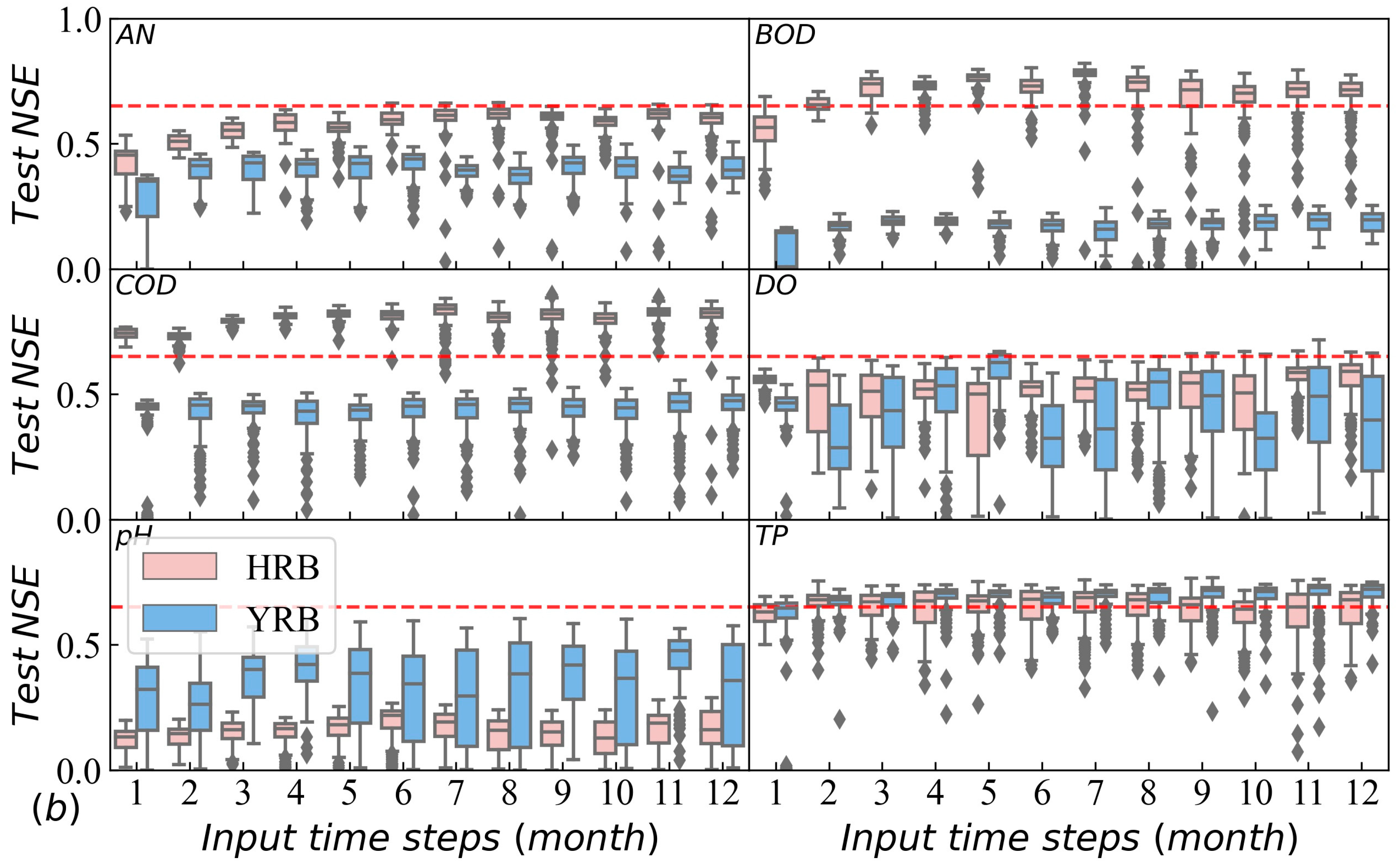
3.2. Confidence Analysis of LSTM for Water Quality Prediction in the Three Basins
3.3. Influencing Factors of Model Performance in Different Basins
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahmed, A.N.; Othman, F.B.; Afan, H.A.; Ibrahim, R.K.; Fai, C.M.; Hossain, M.S.; Ehteram, M.; Elshafie, A. Machine learning methods for better water quality prediction. J. Hydrol. 2019, 578, 124084. [Google Scholar] [CrossRef]
- Tung, T.M.; Yaseen, Z.M. A survey on river water quality modelling using artificial intelligence models: 2000–2020. J. Hydrol. 2020, 585, 124670. [Google Scholar] [CrossRef]
- Kim, H.G.; Hong, S.; Jeong, K.-S.; Kim, D.-K.; Joo, G.-J. Determination of sensitive variables regardless of hydrological alteration in artificial neural network model of chlorophyll a: Case study of Nakdong River. Ecol. Model. 2019, 398, 67–76. [Google Scholar] [CrossRef]
- Kim, S.E.; Seo, I.W. Artificial Neural Network ensemble modeling with conjunctive data clustering for water quality prediction in rivers. J. Hydro-Environ. Res. 2015, 9, 325–339. [Google Scholar] [CrossRef]
- Ahmed, A.A.M.; Shah, S.M.A. Application of adaptive neuro-fuzzy inference system (ANFIS) to estimate the biochemical oxygen demand (BOD) of Surma River. J. King Saud Univ.-Eng. Sci. 2017, 29, 237–243. [Google Scholar] [CrossRef]
- Mahmoodabadi, M.; Arshad, R.R. Long-term evaluation of water quality parameters of the Karoun River using a regression approach and the adaptive neuro-fuzzy inference system. Mar. Pollut. Bull. 2018, 126, 372–380. [Google Scholar] [CrossRef]
- Yi, H.-S.; Park, S.; An, K.-G.; Kwak, K.-C. Algal Bloom Prediction Using Extreme Learning Machine Models at Artificial Weirs in the Nakdong River, Korea. Int. J. Environ. Res. Public Health 2018, 15, 2078. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Li, M.; Guo, F.; Yan, Z.; Zheng, X.; Zhang, Y.; Xu, Z.; Wu, F. Priorization of River Restoration by Coupling Soil and Water Assessment Tool (SWAT) and Support Vector Machine (SVM) Models in the Taizi River Basin, Northern China. Int. J. Environ. Res. Public Health 2018, 15, 2090. [Google Scholar] [CrossRef] [PubMed]
- Ji, X.; Shang, X.; Dahlgren, R.A.; Zhang, M. Prediction of dissolved oxygen concentration in hypoxic river systems using support vector machine: A case study of Wen-Rui Tang River, China. Environ. Sci. Pollut. Res. 2017, 24, 16062–16076. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall-runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Antanasijević, D.; Pocajt, V.; Povrenović, D.; Perić-Grujić, A.; Ristić, M. Modelling of dissolved oxygen content using artificial neural networks: Danube River, North Serbia, case study. Environ. Sci. Pollut. Res. 2013, 20, 9006–9013. [Google Scholar] [CrossRef]
- Li, L.; Jiang, P.; Xu, H.; Lin, G.; Guo, D.; Wu, H. Water quality prediction based on recurrent neural network and improved evidence theory: A case study of Qiantang River, China. Environ. Sci. Pollut. Res. 2019, 26, 19879–19896. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, Y.; Xiao, F.; Wang, Y.; Sun, L. Water Quality Prediction Method Based on IGRA and LSTM. Water 2018, 10, 1148. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Short-term water quality variable prediction using a hybrid CNN-LSTM deep learning model. Stoch. Environ. Res. Risk Assess. 2020, 34, 415–433. [Google Scholar] [CrossRef]
- Liang, Z.; Zou, R.; Chen, X.; Ren, T.; Su, H.; Liu, Y. Simulate the forecast capacity of a complicated water quality model using the long short-term memory approach. J. Hydrol. 2020, 581, 124432. [Google Scholar] [CrossRef]
- Liu, P.; Wang, J.; Sangaiah, A.; Xie, Y.; Yin, X. Analysis and Prediction of Water Quality Using LSTM Deep Neural Networks in IoT Environment. Sustainability 2019, 11, 2058. [Google Scholar] [CrossRef]
- Song, C.; Yao, L.; Hua, C.; Ni, Q. A novel hybrid model for water quality prediction based on synchro squeezed wavelet transform technique and improved long short-term memory. J. Hydrol. 2021, 603, 126879. [Google Scholar] [CrossRef]
- Luo, Q.; Peng, D.; Shang, W. Water quality analysis based on LSTM and BP optimization with a transfer learning model. Environ. Sci. Pollut. Res. 2023, 30, 124341–124352. [Google Scholar] [CrossRef]
- Zou, Q.; Xiong, Q.; Li, Q.; Yi, H.; Yu, Y.; Wu, C. A water quality prediction method based on the multi-time scale bidirectional long short-term memory network. Environ. Sci. Pollut. Res. 2020, 27, 16853–16864. [Google Scholar] [CrossRef]
- Ueda, F.; Tanouchi, H.; Egusa, N.; Yoshihiro, T. A Transfer Learning Approach Based on Radar Rainfall for River Water-Level Prediction. Water 2024, 16, 607. [Google Scholar] [CrossRef]
- Chang, F.-J.; Tsai, Y.-H.; Chen, P.-A.; Coynel, A.; Vachaud, G. Modeling water quality in an urban river using hydrological factors—Data driven approaches. J. Environ. Manag. 2015, 151, 87–96. [Google Scholar] [CrossRef]
- Chen, K.; Chen, H.; Zhou, C.; Huang, Y.; Qi, X.; Shen, R.; Liu, F.; Zuo, M.; Zou, X.; Wang, J.; et al. Comparative analysis of surface water quality prediction performance and identification of key water parameters using different machine learning models based on big data. Water Res. 2020, 171, 115454. [Google Scholar] [CrossRef]
- Nemati, S.; Fazelifard, M.H.; Terzi, Ö.; Ghorbani, M.A. Estimation of dissolved oxygen using data-driven techniques in the Tai Po River, Hong Kong. Environ. Earth Sci. 2015, 74, 4065–4073. [Google Scholar] [CrossRef]
- Parmar, K.S.; Makkhan, S.J.S.; Kaushal, S. Neuro-fuzzy-wavelet hybrid approach to estimate the future trends of river water quality. Neural Comput. Appl. 2019, 31, 8463–8473. [Google Scholar] [CrossRef]
- Wang, C.; Shan, B.; Zhang, H.; Zhao, Y. Limitation of spatial distribution of ammonia-oxidizing microorganisms in the Haihe River, China, by heavy metals. J. Environ. Sci. 2014, 26, 502–511. [Google Scholar] [CrossRef]
- Zhu, S.; Luo, X.; Yuan, X.; Xu, Z. An improved long short-term memory network for streamflow forecasting in the upper Yangtze River. Stoch. Environ. Res. Risk Assess. 2020, 34, 1313–1329. [Google Scholar] [CrossRef]
- Zhu, Y.; Drake, S.; Lü, H.; Xia, J. Analysis of temporal and spatial differences in eco-environmental carrying capacity related to water in the Haihe river basins, China. Water Resour. Manag. 2010, 24, 1089–1105. [Google Scholar] [CrossRef]
- Xu, J.; Liu, R.; Ni, M.; Zhang, J.; Ji, Q.; Xiao, Z. Seasonal variations of water quality response to land use metrics at multi-spatial scales in the Yangtze River basin. Environ. Sci. Pollut. Res. 2021, 28, 37172–37181. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, X.; Chen, Y.; Zeng, W.; Zhao, Y. Pollution source identification and abatement for water quality sections in Huangshui River basin, China. J. Environ. Manag. 2023, 344, 118326. [Google Scholar] [CrossRef]
- Maguire, J.; Cusack, C.; Ruiz-Villarreal, M.; Silke, J.; McElligott, D.; Davidson, K. Applied simulations and integrated modelling for the understanding of toxic and harmful algal blooms (ASIMUTH): Integrated HAB forecast systems for Europe’s Atlantic Arc. Harmful Algae 2016, 53, 160–166. [Google Scholar] [CrossRef] [PubMed]
- Salacinska, K.; El Serafy, G.Y.; Los, F.J.; Blauw, A. Sensitivity analysis of the two dimensional application of the Generic Ecological Model (GEM) to algal bloom prediction in the North Sea. Ecol. Model. 2010, 221, 178–190. [Google Scholar] [CrossRef]
- Li, R. Water quality forecasting of Haihe River based on improved fuzzy time series model. Desalination Water Treat. 2018, 106, 285–291. [Google Scholar] [CrossRef]
- Liang, N.; Zou, Z.; Wei, Y. Regression models (SVR, EMD and FastICA) in forecasting water quality of the Haihe River of China. Desalination Water Treat. 2019, 154, 147–159. [Google Scholar] [CrossRef]
- Liu, X.B.; Peng, W.Q.; He, G.J.; Liu, J.L.; Wang, Y.C. A Coupled Model of Hydrodynamics and Water Quality for Yuqiao Reservoir in Haihe River Basin. J. Hydrodyn. 2008, 20, 574–582. [Google Scholar] [CrossRef]
- Zhang, L.; Zou, Z.H.; Zhao, Y.F. Application of chaotic prediction model based on wavelet transform on water quality prediction. IOP Conf. Ser. Earth Environ. Sci. 2016, 39, 012001. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, H.L.; Zhang, Y.Z. The Hybrid Method to Predict Biochemical Oxygen Demand of Haihe River in China. Adv. Mater. Res. 2012, 610–613, 1066–1069. [Google Scholar] [CrossRef]
- Chen, S.; Fang, G.; Huang, X.; Zhang, Y. Water Quality Prediction Model of a Water Diversion Project Based on the Improved Artificial Bee Colony–Backpropagation Neural Network. Water 2018, 10, 806. [Google Scholar] [CrossRef]
- Deng, W.; Wang, G.; Zhang, X. A novel hybrid water quality time series prediction method based on cloud model and fuzzy forecasting. Chemom. Intell. Lab. Syst. 2015, 149, 39–49. [Google Scholar] [CrossRef]
- Di, Z.; Chang, M.; Guo, P. Water Quality Evaluation of the Yangtze River in China Using Machine Learning Techniques and Data Monitoring on Different Time Scales. Water 2019, 11, 339. [Google Scholar] [CrossRef]
- Zhou, C.; Gao, L.; Gao, H.; Peng, C. Pattern Classification and Prediction of Water Quality by Neural Network with Particle Swarm Optimization. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; pp. 2864–2868. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, W.; Li, Y.; Wu, H.; Yang, N.; Hui, C. Dams shift microbial community assembly and imprint nitrogen transformation along the Yangtze River. Water Res. 2021, 189, 116579. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.; Liu, Y.; Zhang, Y.; Shen, H.; Yao, M.; Dahlgren, R.A.; Chen, D. Long-term (1980–2015) changes in net anthropogenic phosphorus inputs and riverine phosphorus export in the Yangtze River basin. Water Res. 2020, 177, 115779. [Google Scholar] [CrossRef]
- Liu, X.; Beusen, A.H.W.; Van Beek, L.P.H.; Mogollón, J.M.; Ran, X.; Bouwman, A.F. Exploring spatiotemporal changes of the Yangtze River (Changjiang) nitrogen and phosphorus sources, retention and export to the East China Sea and Yellow Sea. Water Res. 2018, 142, 246–255. [Google Scholar] [CrossRef] [PubMed]
- Dang, B.; Mao, D.; Xu, Y.; Luo, Y. Conjugative multi-resistant plasmids in Haihe River and their impacts on the abundance and spatial distribution of antibiotic resistance genes. Water Res. 2017, 111, 81–91. [Google Scholar] [CrossRef]
- Bao, Z.; Zhang, J.; Wang, G.; Fu, G.; He, R.; Yan, X.; Jin, J.; Liu, Y.; Zhang, A. Attribution for decreasing streamflow of the Haihe River basin, northern China: Climate variability or human activities? J. Hydrol. 2012, 460–461, 117–129. [Google Scholar] [CrossRef]
- Zheng, M.; Zheng, H.; Wu, Y.; Xiao, Y.; Du, Y.; Xu, W.; Lu, F.; Wang, X.; Ouyang, Z. Changes in nitrogen budget and potential risk to the environment over 20 years (1990–2010) in the agroecosystems of the Haihe Basin, China. J. Environ. Sci. 2015, 28, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhu, Y.; Zhang, X.; Ye, M.; Yang, J. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Panfeng, B.; Songlin, Z.; Hongyu, C.; Caiwei, L.; Pengtao, W.; Lichang, Q. Structural monitoring data repair based on a long short-term memory neural network. Sci. Rep. 2024, 14, 9974. [Google Scholar] [CrossRef]
- Bennett, N.D.; Croke, B.F.W.; Guariso, G.; Guillaume, J.H.A.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.H.; Norton, J.P.; Perrin, C.; et al. Characterising performance of environmental models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Sadiki, N.; Jang, D.W. Estimation of Hydraulic and Water Quality Parameters Using Long Short-Term Memory in Water Distribution Systems. Water 2024, 16, 3028. [Google Scholar] [CrossRef]
- Gachloo, M.; Liu, Q.; Song, Y.; Wang, G.; Zhang, S.; Hall, N. Using Machine Learning Models for Short-Term Prediction of Dissolved Oxygen in a Microtidal Estuary. Water 2024, 16, 1998. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Galelli, S.; Humphrey, G.B.; Maier, H.R.; Castelletti, A.; Dandy, G.C.; Gibbs, M.S. An evaluation framework for input variable selection algorithms for environmental data-driven models. Environ. Model. Softw. 2014, 62, 33–51. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]







| Basins | Indicators | Unit | Mean | Minimum | Maximum | SD | CV |
|---|---|---|---|---|---|---|---|
| YRB | AN | mg/L | 0.178 | 0.025 | 1.340 | 0.184 | 1.035 |
| BOD | mg/L | 1.100 | 0.500 | 2.500 | 0.400 | 0.300 | |
| COD | mg/L | 2.200 | 0.500 | 4.100 | 0.500 | 0.200 | |
| DO | mg/L | 8.530 | 4.400 | 13.10 | 1.510 | 0.180 | |
| pH | - | 7.970 | 6.930 | 8.920 | 0.330 | 0.040 | |
| TP | mg/L | 0.072 | 0.005 | 0.250 | 0.051 | 0.706 | |
| HRB | AN | mg/L | 8.104 | 0.012 | 122.00 | 14.554 | 1.796 |
| BOD | mg/L | 12.300 | 0.200 | 220.00 | 24.700 | 2.000 | |
| COD | mg/L | 11.000 | 0.600 | 127.00 | 16.00 | 1.400 | |
| DO | mg/L | 6.750 | 0.020 | 18.80 | 3.500 | 0.520 | |
| pH | - | 7.890 | 6.420 | 8.990 | 0.380 | 0.050 | |
| TP | mg/L | 0.730 | 0.005 | 8.880 | 1.243 | 1.703 | |
| HSB | AN | mg/L | 0.572 | 0.011 | 10.80 | 0.929 | 1.622 |
| BOD | mg/L | 2.100 | 0.200 | 24.00 | 1.700 | 0.800 | |
| COD | mg/L | 2.100 | 0.200 | 13.00 | 1.000 | 0.500 | |
| DO | mg/L | 8.190 | 3.220 | 12.700 | 1.200 | 0.150 | |
| pH | - | 8.220 | 6.490 | 9.290 | 0.310 | 0.040 | |
| TP | mg/L | 0.081 | 0.005 | 1.190 | 0.103 | 1.270 |
| Index | YRB | HRB | HSB | |||
|---|---|---|---|---|---|---|
| BOD | 0.060 | 0.038 | 0.773 | 0.070 | 0.523 | 0.167 |
| COD | 0.041 | 0.047 | 0.785 | 0.047 | 0.420 | 0.166 |
| DO | 0.375 | 0.174 | 0.623 | 0.055 | 0.074 | 0.110 |
| NH3-N | 0.233 | 0.038 | 0.631 | 0.082 | 0.706 | 0.043 |
| TP | 0.463 | 0.033 | 0.644 | 0.056 | 0.478 | 0.048 |
| Ph | 0.382 | 0.108 | 0.471 | 0.092 | 0.421 | 0.103 |
| Index | YRB | HSB | HRB | |||
|---|---|---|---|---|---|---|
| Ci | Ci | Ci | ||||
| BOD | [0.058, 0.062] | 0.071 | [0.769, 0.777] | 0.011 | [0.514, 0.532] | 0.035 |
| COD | [0.038, 0.044] | 0.123 | [0.782, 0.788] | 0.007 | [0.411, 0.429] | 0.043 |
| DO | [0.365, 0.385] | 0.053 | [0.620, 0.626] | 0.010 | [0.068, 0.080] | 0.156 |
| NH3-N | [0.231, 0.235] | 0.019 | [0.626, 0.636] | 0.015 | [0.704, 0.708] | 0.007 |
| TP | [0.461, 0.465] | 0.008 | [0.641, 0.647] | 0.010 | [0.475, 0.481] | 0.011 |
| Ph | [0.376, 0.388] | 0.033 | [0.465, 0.477] | 0.023 | [0.415, 0.427] | 0.028 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, P.; Wang, Y.; Zhao, Y.; Kang, J. Analysis of Prediction Confidence in Water Quality Forecasting Employing LSTM. Water 2025, 17, 1050. https://doi.org/10.3390/w17071050
Fang P, Wang Y, Zhao Y, Kang J. Analysis of Prediction Confidence in Water Quality Forecasting Employing LSTM. Water. 2025; 17(7):1050. https://doi.org/10.3390/w17071050
Chicago/Turabian StyleFang, Pan, Yonggui Wang, Yanxin Zhao, and Jin Kang. 2025. "Analysis of Prediction Confidence in Water Quality Forecasting Employing LSTM" Water 17, no. 7: 1050. https://doi.org/10.3390/w17071050
APA StyleFang, P., Wang, Y., Zhao, Y., & Kang, J. (2025). Analysis of Prediction Confidence in Water Quality Forecasting Employing LSTM. Water, 17(7), 1050. https://doi.org/10.3390/w17071050





