Simulation of Tidal Oscillations in the Pará River Estuary Using the MOHID-Land Hydrological Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Hydrological Model
2.3. Model Implementation
| Input Data | Scenario | Sources |
|---|---|---|
| Digital Elevation | All | USGS—GTOPO30 [48] |
| Roughness | All | Copernicus land-use maps [50] |
| Bathymetry | Reference, AtPmVg, FES2014 | LAPMAR bathymetry, with banks removed and smoothed |
| Bathymetry | Brazilian Sea Observatory [47] | |
| Vegetation and Land-Use | All | Annual Mapping Project of Land Use and Coverage (MapBiomas) [51] |
| Soil | All | SOTER-based soil parameter estimates (SOTWIS) [52] |
| Atmosphere | All | National Water Agency/Agência Nacional das Águas [53] |
| Discharge | All | National Water Agency/Agência Nacional das Águas [53] |
| Tidal elevation | Reference, AtPmVg, Bathymetry | TOPEX/POSEIDON tidal model (TPXO), Regional Amazon Shelf 1/60° model version [42] |
| FES2014 | Finite Element Solution—FES2014 |
2.3.1. TPXO Tide
2.3.2. FES Tide
2.4. Observed Tidal Data
2.5. Evaluation Metrics
3. Results
3.1. Tidal Boundary Conditions Analysis
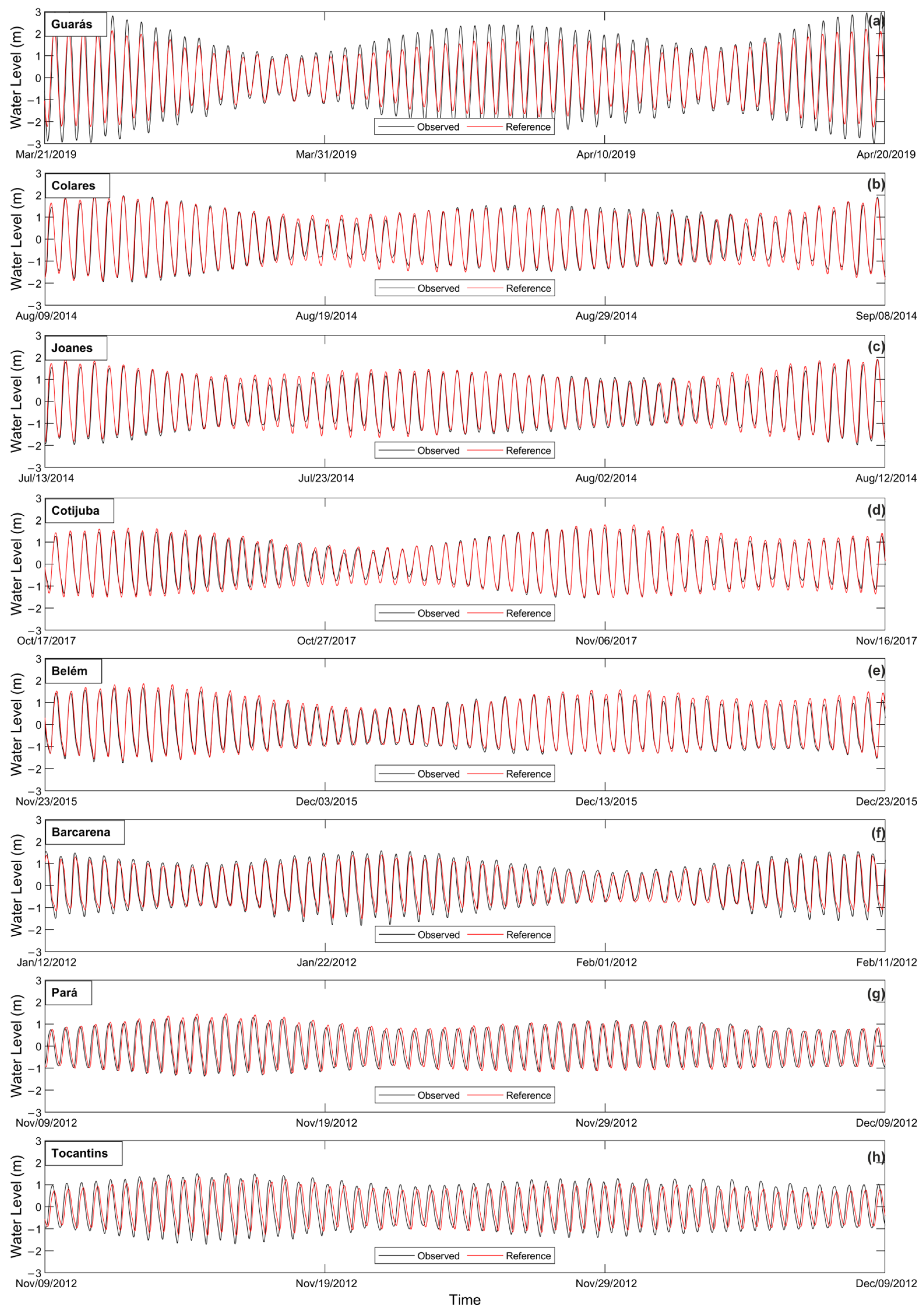
3.2. Reference Simulation
3.3. Scenario Performance
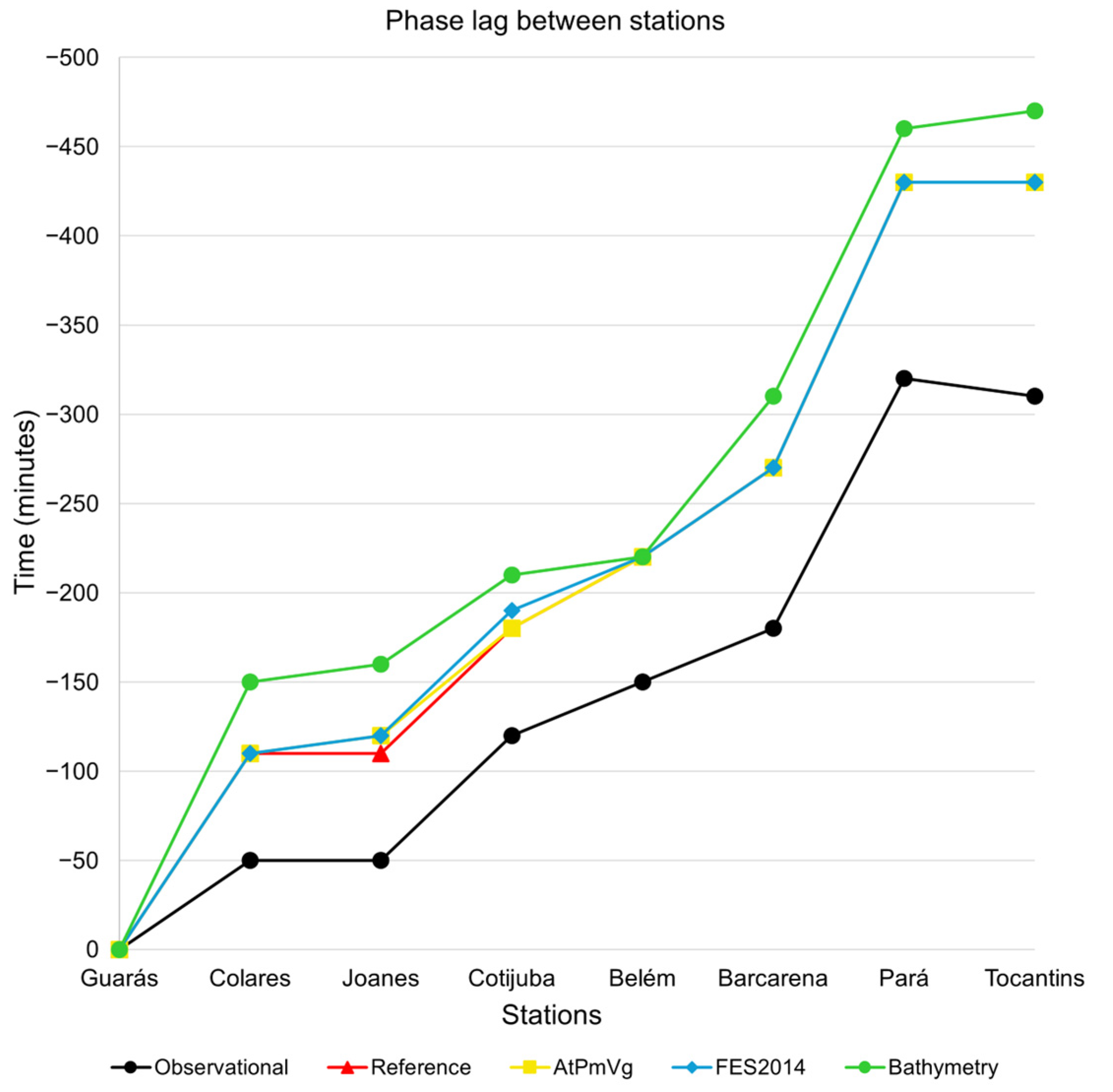
3.4. Tidal Wave Phase Lags
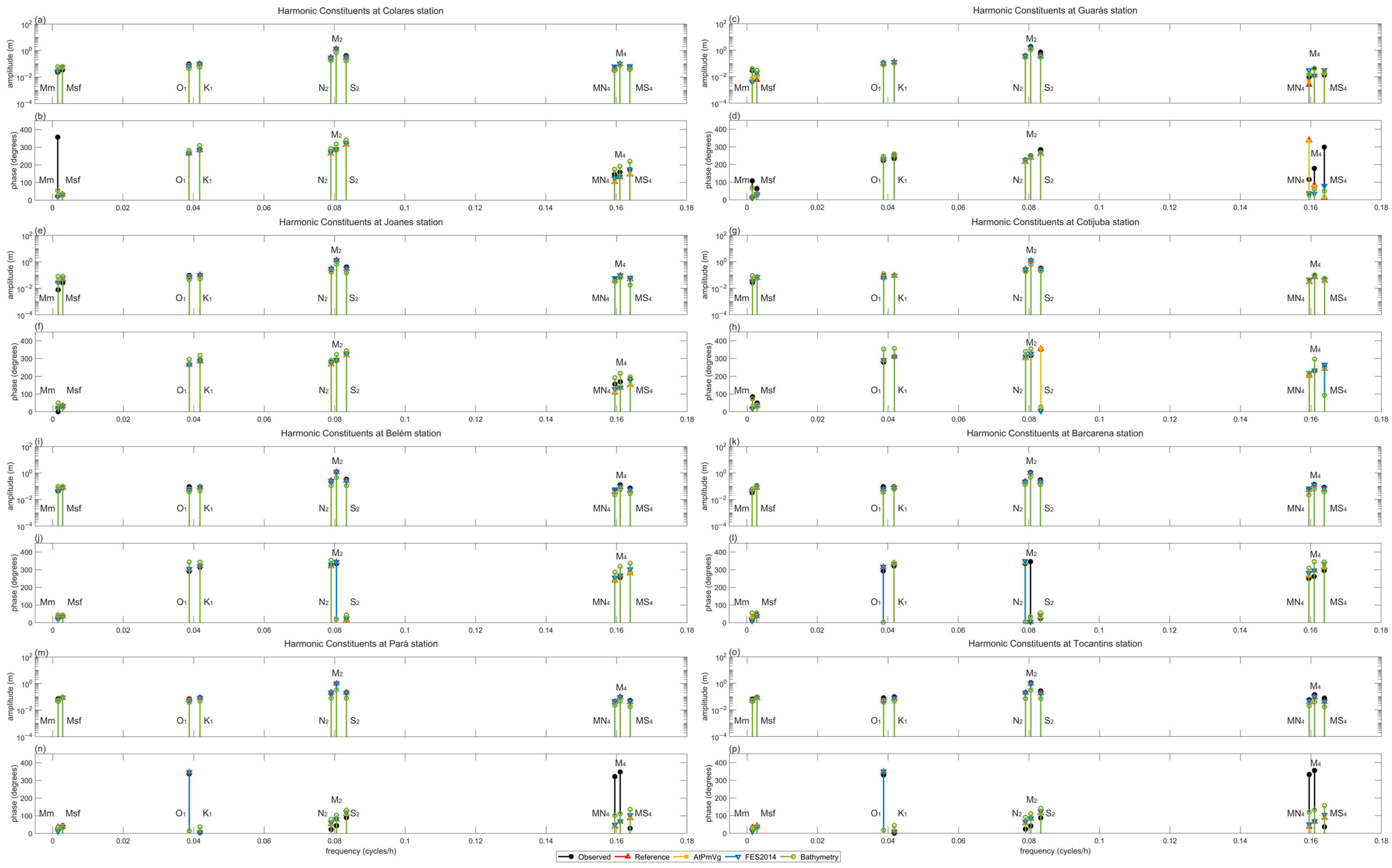
3.5. Harmonic Constituent Amplitude
3.6. Phases Lag in M2
4. Discussion
4.1. Boundary Conditions
4.2. Explicit Simulation of Vegetation and Porous Media
4.3. Bathymetry Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AtPmVg | Atmosphere, Porous Media, and Vegetation |
| LAPMAR | Research Laboratory for Marine Environmental Monitoring |
| OCA | Amazon Coastal Observatory |
| TPXO | TOPEX/POSEIDON tidal model |
| FES2014 | Finite Element Solution version 2014 |
| ANA | National Water Agency of Brazil |
| USDA | United States Department of Agriculture |
| USGS | United States Geological Survey |
| C | Clay |
| LS | Loamy sand |
| SL | Sandy loam |
| S | Sand |
| L | Loam |
| SCL | Sandy clay loam |
| SiCL | Silty clay loam |
References
- Spyrakos, E.; O’Donnell, R.; Hunter, P.D.; Miller, C.; Scott, M.; Simis, S.G.H.; Neil, C.; Barbosa, C.C.F.; Binding, C.E.; Bradt, S.; et al. Optical types of inland and coastal waters. Limnol. Oceanogr. 2018, 63, 846–870. [Google Scholar] [CrossRef]
- Cox, J.R.; Lingbeek, J.; Weisscher, S.A.H.; Kleinhans, M.G. Effects of Sea-Level Rise on Dredging and Dredged Estuary Morphology. J. Geophys. Res. Earth Surf. 2022, 127, e2022JF006790. [Google Scholar] [CrossRef]
- Schrijvershof, R.A.; van Maren, D.S.; Van der Wegen, M.; Hoitink, A.J.F. Land Reclamation Controls on Multi-Centennial Estuarine Evolution. Earth’s Future 2024, 12, e2024EF005080. [Google Scholar] [CrossRef]
- Wong, P.; Losada, I.; Gattuso, J.P.; Hinkel, J.; Khattabi, A.; McInnes, K.; Sallenger, A. Coastal Systems and Low-Lying Areas. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects; Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014; pp. 361–409. Available online: https://www.ipcc.ch/site/assets/uploads/2018/02/WGIIAR5-Chap5_FINAL.pdf (accessed on 4 February 2025).
- Guo, J.; Ma, Y.; Ding, C.; Zhao, H.; Cheng, Z.; Yan, G.; You, Z. Impacts of Tidal Oscillations on Coastal Groundwater System in Reclaimed Land. J. Mar. Sci. Eng. 2023, 11, 2019. [Google Scholar] [CrossRef]
- Abedin, M.A.; Habiba, U.; Shaw, R. Community Perception and Adaptation to Safe Drinking Water Scarcity: Salinity, Arsenic, and Drought Risks in Coastal Bangladesh. Int. J. Disaster Risk Sci. 2014, 5, 110–124. [Google Scholar] [CrossRef]
- Tully, K.; Gedan, K.; Epanchin-Niell, R.; Strong, A.; Bernhardt, E.S.; BenDor, T.; Weston, N.B. The Invisible Flood: The Chemistry, Ecology, and Social Implications of Coastal Saltwater Intrusion. BioScience 2019, 69, 368–378. [Google Scholar] [CrossRef]
- Kim, J.; Warnock, A.; Ivanov, V.Y.; Katopodes, N.D. Coupled modeling of hydrologic and hydrodynamic processes including overland and channel flow. Adv. Water Resour. 2012, 37, 104–126. [Google Scholar] [CrossRef]
- Siqueira, V.A.; Paiva, R.C.D.; Fleischmann, A.S.; Fan, F.M.; Ruhoff, A.L.; Pontes, P.R.M.; Paris, A.; Calmant, S.; Collischonn, W. Toward continental hydrologic–hydrodynamic modeling in South America. Hydrol. Earth Syst. Sci. 2018, 22, 4815–4842. [Google Scholar] [CrossRef]
- Beven, K. Causal models as multiple working hypotheses about environmental processes. Comptes Rendus Geosci. 2012, 344, 77–88. [Google Scholar] [CrossRef]
- Okiria, E.; Okazawa, H.; Noda, K.; Kobayashi, Y.; Suzuki, S.; Yamazaki, Y. A comparative evaluation of lumped and semi-distributed conceptual hydrological models: Does model complexity enhance hydrograph prediction? Hydrology 2022, 9, 89. [Google Scholar] [CrossRef]
- Devi, G.K.; Ganasri, B.P.; Dwarakish, G.S. A review on hydrological models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Suhana, M.P.; Nursyahnita, S.D.; Idris, F. Hydrodynamic model approach to study the pattern of sea surface currents around the Tanjungpinang City reclamation site. IOP Conf. Ser. Earth Environ. Sci. 2023, 1148, 012014. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, H.; Liang, Q. A coupled hydrological and hydrodynamic model for flood simulation. Hydrol. Res. 2019, 50, 589–606. [Google Scholar] [CrossRef]
- Mansanarez, V.; Thirel, G.; Delaigue, O.; Liquet, B. Development of a semi-distributed hydrological model on a tidal-affected river: Application to the Adour catchment, France. In Proceedings of the EGU General Assembly 2020, Online, 4–8 May 2020; Available online: https://meetingorganizer.copernicus.org/EGU2020/EGU2020-13582.html (accessed on 4 February 2025). [CrossRef]
- Lobligeois, F.; Andréassian, V.; Perrin, C.; Tabary, P.; Loumagne, C. When does higher spatial resolution rainfall information improve streamflow simulation? An evaluation using 3620 flood events. Hydrol. Earth Syst. Sci. 2014, 18, 575–594. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, W.; Sun, G.; Miao, G.; Noormets, A.; Emanuel, R.; King, J.S. Understanding coastal wetland hydrology with a new regional-scale, process-based hydrological model. Hydrol. Process. 2018, 32, 3158–3173. [Google Scholar] [CrossRef]
- Qu, Y.; Duffy, C.J. A semidiscrete finite volume formulation for multiprocess watershed simulation. Water Resour. Res. 2007, 43, 08419. [Google Scholar] [CrossRef]
- Brito, D.; Campuzano, F.J.; Sobrinho, J.; Fernandes, R.; Neves, R. Integrating operational watershed and coastal models for the Iberian Coast: Watershed model implementation—A first approach. Estuar. Coast. Shelf Sci. 2015, 167, 138–146. [Google Scholar] [CrossRef]
- Hascoet, T.; Pellet, V.; Aires, F.; Takiguchi, T. Learning Global Evapotranspiration Dataset Corrections from a Water Cycle Closure Supervision. Remote Sens. 2023, 16, 170. [Google Scholar] [CrossRef]
- Brouwer, C.; Goffeau, A.; Heibloem, M. Irrigation Water Management: Training Manual No. 1—Introduction to Irrigation; FAO—Food And Agriculture Organization of the United Nations: Rome, Italy, 1985; Available online: https://www.fao.org/4/r4082e/r4082e00.htm#Contents (accessed on 4 February 2025).
- Bot, A.; Benites, J. The Importance of Soil Organic Matter: Key to Drought-Resistant Soil and Sustained Food Production; FAO—Food And Agriculture Organization of the United Nations: Rome, Italy, 2005; Available online: https://www.fao.org/4/a0100e/a0100e00.htm#Contents (accessed on 4 February 2025).
- Gregg, D.E.; Penna, N.T.; Jones, C.; Maqueda, M.A.M. Accuracy assessment of recent global ocean tide models in coastal waters of the European North West Shelf. Ocean Model. 2024, 192, 102448. [Google Scholar] [CrossRef]
- Ray, R.D.; Egbert, G.D.; Erofeeva, S.Y. Tide Predictions in Shelf and Coastal Waters: Status and Prospects. In Coastal Altimetry Coastal Altimetry; Vignudelli, S., Kostianoy, A., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 191–216. [Google Scholar] [CrossRef]
- Steinigeweg, C.S.; Paul, M.; Kleyer, M.; Schröder, B. Conquering new frontiers: The effect of vegetation establishment and environmental interactions on the expansion of tidal marsh systems. Estuaries Coasts 2023, 46, 1515–1535. [Google Scholar]
- Allen, G.P.; Salomon, J.C.; Bassoullet, P.; Du Penhoat, Y.; de Grandpré, C. Effects of tides on mixing and suspended sediment transport in macrotidal estuaries. Sediment. Geol. 1980, 26, 69–90. [Google Scholar] [CrossRef]
- Moraes, B.C.; Costa, J.M.N.; Costa, A.C.L.; Costa, M.H. Variação Espacial e Temporal da Precipitação no Estado do Pará. Acta Amaz. 2005, 35, 207–214. [Google Scholar] [CrossRef]
- Gregório, A.M.D.S.; Mendes, A.C. Batimetria e Sedimentologia da Baía do Guajará, Belém, Estado do Pará, Brasil. Amaz. Ciênc. Desenvolv. 2009, 5, 53–72. Available online: https://repositorio.museu-goeldi.br/handle/mgoeldi/369 (accessed on 4 February 2025).
- Ministério do Meio Ambiente (MMA). Caderno da Região Hidrográfica do Tocantins-Araguaia. Brasilia, 132p. 2006. Available online: https://www.mma.gov.br/estruturas/161/_publicacao/161_publicacao02032011035943.pdf (accessed on 27 June 2022).
- Prestes, Y.O.; Borba, T.A.C.; Silva, A.C.; Rollnic, M. A Discharge Stationary Model for the Pará-Amazon Estuarine System. J. Hydrol. Reg. Stud. 2020, 28, 100668. [Google Scholar] [CrossRef]
- Barthem, R.B.; Schwassmann, H.O. Amazon River Influence on the Seasonal Displacement of the Salt Wedge in the Tocantins River Estuary, Brazil, 1983-1985. Bol. Mus. Para. Emílio Goeldi. Sér. Zool. 1994, 10, 19–130. Available online: https://repositorio.museu-goeldi.br/handle/mgoeldi/496 (accessed on 4 February 2025).
- Prestes, Y.O.; Silva, A.C.; Rollnic, M.; Rosário, R.P. The M2 and M4 Tides in the Pará River Estuary. Trop. Oceanogr. 2017, 45, 1679–3013. [Google Scholar] [CrossRef]
- Rollnic, M.; Rosário, R.P. Tide propagation in tidal courses of the Pará river estuary, Amazon Coast, Brazil. J. Coast. Res. 2013, 165, 1581–1586. [Google Scholar] [CrossRef]
- MOHID Wiki. Mohid Land. Available online: http://wiki.mohid.com/index.php?title=Mohid_Land (accessed on 27 June 2022).
- Oliveira, A.R.; Ramos, T.B.; Simionesei, L.; Pinto, L.; Neves, R. Sensitivity Analysis of the MOHID-Land Hydrological Model: A Case Study of the Ulla River Basin. Water 2020, 12, 3258. [Google Scholar] [CrossRef]
- Oliveira, A.R.; Ramos, T.B.; Pinto, L.; Neves, R. Direct integration of reservoirs’ operations in a hydrological model for streamflow estimation: Coupling a CLSTM model with MOHID-Land. Hydrol. Earth Syst. Sci. 2023, 27, 3875–3893. [Google Scholar] [CrossRef]
- Ramos, T.B.; Simionesei, L.; Jauch, E.; Almeida, C.; Neves, R. Modelling soil water and maize growth dynamics influenced by shallow groundwater conditions in the Sorraia Valley region, Portugal. Agric. Water Manag. 2017, 185, 27–42. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements. In FAO Irrigation & Drainage Paper 56; Food and Agriculture Organization (FAO): Rome, Italy, 1998. [Google Scholar]
- Ritchie, J.T. Model for predicting evaporation from a row crop with incomplete cover. Water Resour. Res. 1972, 8, 1204–1213. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Borba, T.A.C.; Rollnic, M. Runoff quantification on Amazonian Estuary based on hydrodynamic model. J. Coast. Res. 2016, 75, 43–47. [Google Scholar] [CrossRef]
- Rosário, R.P.; Borba, T.A.C.; Santos, A.S.; Rollnic, M. Variability of Salinity in Pará River Estuary: 2D Analysis with Flexible Mesh Model. J. Coast. Res. 2016, 75, 128–132. [Google Scholar] [CrossRef]
- Mendes, J.; Leitão, P.; Chambel Leitão, J.; Bartolomeu, S.; Rodrigues, J.; Dias, J.M. Improvement of an operational forecasting system for extreme tidal events in Santos Estuary (In Brazil). Geosciences 2019, 9, 511. [Google Scholar] [CrossRef]
- Cancio, N.C.; Pierini, J.O. Suspended sediment transport in Rio Colorado agricultural basin, Argentina. Front. Built Environ. 2023, 9, 1142671. [Google Scholar] [CrossRef]
- Brazilian Sea Observatory. AM_PA_2D. Available online: https://github.com/Brazilian-Sea-Observatory/AM_PA_2D (accessed on 21 May 2024).
- United States Geological Survey (USGS). Earth Explore. Available online: https://earthexplorer.usgs.gov/ (accessed on 1 October 2022).
- Marinha do Brasil. Cartas Raster. Available online: https://www.marinha.mil.br/chm/dados-do-segnav/cartas-raster (accessed on 27 March 2023).
- Copernicus European Eyes on Earth. Global Land Cover. Available online: https://lcviewer.vito.be/download (accessed on 23 July 2024).
- MapBiomas. Coleções MapBiomas. Available online: https://brasil.mapbiomas.org/colecoes-mapbiomas/ (accessed on 23 July 2024).
- Batjes, N.H. SOTER-Based Soil Parameter Estimates for Latin America and the Caribbean (Ver. 1.0). ISRIC–World Soil Information, Wageningen, 2005. Available online: https://isric.org/sites/default/files/isric_report_2005_02.pdf (accessed on 23 July 2024).
- Agência Nacional das Águas (ANA). HIDROWEB. Available online: https://www.snirh.gov.br/hidroweb/ (accessed on 25 May 2022).
- United States Department of Agriculture (USDA); Soil Science Division Staff. Soil Survey Manual. In USDA Handbook 18; Ditzler, C., Scheffe, K., Monger, H.C., Eds.; Government Printing Office: Washington, DC, USA, 2017. Available online: https://www.nrcs.usda.gov/resources/guides-and-instructions/soil-survey-manual (accessed on 23 July 2024).
- Handbook 60 (HB60). Rosetta, Estimate Unsaturated Soil Hydraulic Parameters from Soil Characterization Data. Available online: https://www.handbook60.org/rosetta/ (accessed on 23 July 2024).
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Single Levels from 1959 to Present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS) 2018. Available online: https://doi.org/10.24381/cds.adbb2d47 (accessed on 1 March 2023).
- Pereira, D.R.; Oliveira, A.R.; Costa, M.S.; Ramos, T.B.; Rollnic, M.; Neves, R.J. Evaluation of precipitation products in a Brazilian watershed: Tocantins-Araguaia watershed case study. Theor. Appl. Climatol. 2024, 155, 7845–7865. [Google Scholar] [CrossRef]
- Agência Nacional de Águas (ANA). Sistema Interligado Nacional, Bacia do rio Tocantins, Reservatórios. Available online: https://www.ana.gov.br/sar/sin/b_tocantins/# (accessed on 16 February 2023).
- Erofeeva, S.; Padman, L.; Howard, S.L. Tide Model Driver (TMD) Version 2.5, Toolbox for Matlab. GitHub 2020. Available online: https://www.github.com/EarthAndSpaceResearch/TMD_Matlab_Toolbox_v2.5 (accessed on 1 April 2023).
- Centre National d’Études Spatiales (CNES). Aviso-FES. Available online: https://github.com/CNES/aviso-fes/tree/main (accessed on 30 July 2024).
- Amazon Coastal Observatory (OCA). OCA Observational. Available online: https://oca.eco.br/en/banco-de-dados/oca-observa/ (accessed on 20 May 2022).
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Williams, J.J.; Esteves, L.S. Guidance on setup, calibration, and validation of hydrodynamic, wave, and sediment models for shelf seas and estuaries. Adv. Civ. Eng. 2017, 2017, 1–25. [Google Scholar] [CrossRef]
- Timko, P.G.; Timko, P.G.; Arbic, B.K.; Hyder, P.; Richman, J.G.; Zamudio, L.; O’Dea, E.; Wallcraft, A.J.; Shriver, J. F Assessment of shelf sea tides and tidal mixing fronts in a global ocean model. Ocean Model. 2019, 136, 66–84. [Google Scholar] [CrossRef]
- Byrne, D.; Horsburgh, K.; O’Neill, C.K. Sensitivity of AMM15-Surge to Varying Tidal Boundary Conditions and Bottom Friction Coefficients. Res. Consult. Rep. 2019, 71, 33. Available online: https://eprints.soton.ac.uk/434878/1/NOC_R_C_71_Final.pdf (accessed on 3 November 2023).
- Lee, J.C.; Lee, D.H. Accuracy assessment of recent global ocean tide models using tide gauge measurements from the East Sea of Korea. J. Coast. Res. 2022, 39, 354–359. [Google Scholar] [CrossRef]
- Fu, Y.; Feng, Y.; Zhou, D.; Zhou, X.; Li, J.; Tang, Q. Accuracy assessment of global ocean tide models in the South China Sea using satellite altimeter and tide gauge data. Acta Oceanol. Sin. 2020, 39, 1–10. [Google Scholar] [CrossRef]
- Ahn, J.E.; Ronan, A.D. Impact of discrepancies between global ocean tide models on tidal simulations in the Shinnecock Bay area. J. Waterw. Port Coast. Ocean Eng. 2019, 145, 04018042. [Google Scholar] [CrossRef]
- Ahsan, Q.; Blumberg, A.F.; Thuman, A.J.; Gallagher, T.W. Geomorphological and meteorological control of estuarine processes: A three-dimensional modeling analysis. J. Hydraul. Eng. 2005, 131, 259–272. [Google Scholar] [CrossRef]
- Cho, H.J. Effects of prevailing winds on turbidity of a shallow estuary. Int. J. Environ. Res. Public Health 2007, 4, 185–192. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, C.; Brett, M.T.; Nielsen, J.M. The importance of the wind-drag coefficient parameterization for hydrodynamic modeling of a large shallow lake. Ecol. Inform. 2020, 59, 101106. [Google Scholar] [CrossRef]
- Llebot, C.; Rueda, F.J.; Solé, J.; Artigas, M.L.; Estrada, M. Hydrodynamic states in a wind-driven microtidal estuary (Alfacs Bay). J. Sea Res. 2014, 85, 263–276. [Google Scholar] [CrossRef]
- Kjerfve, B.; Magill, K.E. Geographic and hydrodynamic characteristics of shallow coastal lagoons. Mar. Geol. 1989, 88, 187–199. [Google Scholar] [CrossRef]
- Wilson, A.M.; Gardner, L.R. Tidally driven groundwater flow and solute exchange in a marsh: Numerical simulations. Water Resour. Res. 2006, 42, W01405. [Google Scholar] [CrossRef]
- Wilson, A.M.; Morris, J.T. The influence of tidal forcing on groundwater flow and nutrient exchange in a salt marsh-dominated estuary. Biogeochemistry 2012, 108, 27–38. [Google Scholar] [CrossRef]
- Xin, P.; Yu, X.; Zhan, L.; Cheng, H.; Yuan, S. Surface water-groundwater interaction affects soil temperature distributions and variations in salt marshes. Adv. Water Resour. 2023, 172, 104366. [Google Scholar] [CrossRef]
- Cea, L.; French, J.R. Bathymetric error estimation for the calibration and validation of estuarine hydrodynamic models. Estuar. Coast. Shelf Sci. 2012, 100, 124–132. [Google Scholar] [CrossRef]
- Khanarmuei, M.; Suara, K.; Sumihar, J.; Brown, R.J. Hydrodynamic modelling and model sensitivities to bed roughness and bathymetry offset in a micro-tidal estuary. J. Hydroinform. 2020, 22, 1536–1553. [Google Scholar] [CrossRef]
- Knaapen, M.A. Sandbank occurrence on the Dutch continental shelf in the North Sea. Geo-Mar. Lett. 2009, 29, 17–24. [Google Scholar] [CrossRef]
- Pattiaratchi, C.; Collins, M. Mechanisms for linear sandbank formation and maintenance in relation to dynamical oceanographic observations. Prog. Oceanogr. 1987, 19, 117–176. [Google Scholar] [CrossRef]
- Sothmann, J.; Schuster, D.; Kappenberg, J.; Ohle, N. Efficiency of artificial sandbanks in the mouth of the Elbe estuary for damping the incoming tidal energy. In Proceedings of the 5th International Short Conference on Applied Coastal Research (SCACR 2011), Aachen, Germany, 6–9 June 2011. [Google Scholar]
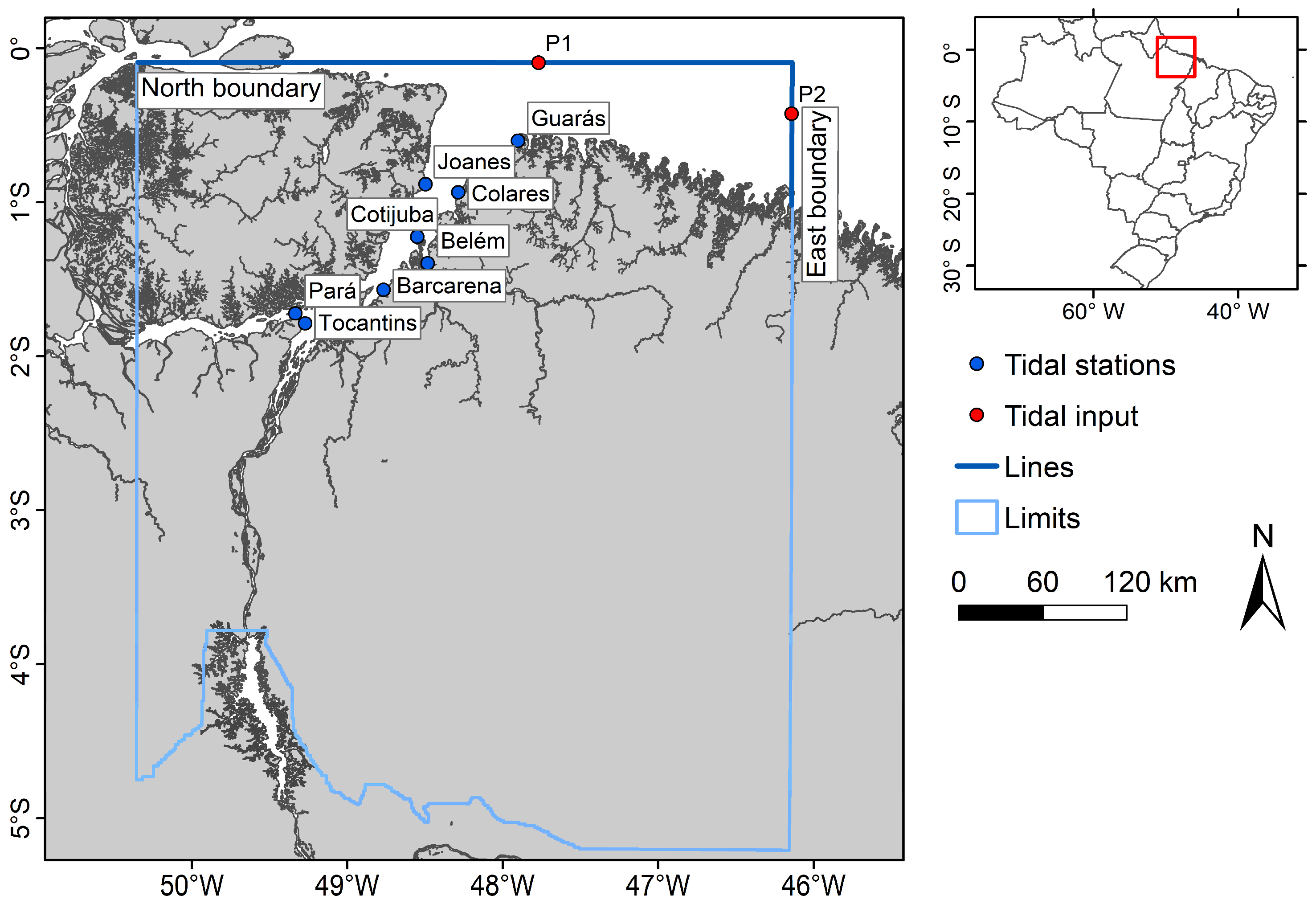



| Fluvial System | Town (Gauge Location) | Coordinates (Lat/Lon) | Years |
|---|---|---|---|
| Amazon | Óbidos | 1°55′9.12″ S/55°30′47.16″ W | 2005–2022 |
| Xingu | Altamira | 3°12′52.92″ S/52°12′43.92″ W | 2005–2020 |
| Tapajós | Burburé | 4°36′56.16″ S/56°19′30″ W | 2005–2022 |
| Station | Period Sampled | Institution |
|---|---|---|
| Colares | August 2014–June 2016 | Amazon Coastal Observatory (OCA) |
| Joanes | July 2014–June 2016 | |
| Belém | November 2015–June 2016 | |
| Barcarena | January 2019–March 2019 | |
| Rio Pará | November 2012–February 2013 | |
| Rio Tocantins | November 2012–March 2013 | |
| Cotijuba | October 2017–May 2018 | |
| Guarás | March 2019–April 2019 | Brazilian Navy |
| Metrics | Ideal Value | Very Good | Satisfactory |
|---|---|---|---|
| RMSE | 0 | - | ±0.1 m (river mouth); ±0.3 m (head) |
| RRMSE | 0 | - | 10% of the measured level (spring tide); ±15% (neap tide) |
| NSE | 1 | 0.7 | 0.5 |
| R2 | 1 | - | 0.6 |
| BIAS | 0 | - | <0.10 (coast); <0.20 (estuary) |
| Phase | 0 | - | ±15 min (river mouth); ±25 min (head) |
| Station | RMSE (m) | RRMSE (%) | R2 | NSE | Bias (m) |
|---|---|---|---|---|---|
| Guarás | 0.49 | 8.08 | 0.94 | 0.89 | 0.24 |
| Colares | 0.20 | 4.47 | 0.96 | 0.96 | 0.04 |
| Joanes | 0.19 | 4.43 | 0.96 | 0.96 | 0.04 |
| Cotijuba | 0.21 | 6.49 | 0.95 | 0.93 | 0.05 |
| Belém | 0.21 | 5.51 | 0.95 | 0.94 | 0.04 |
| Barcarena | 0.30 | 8.28 | 0.88 | 0.88 | 0.09 |
| Pará | 0.46 | 15.98 | 0.65 | 0.61 | 0.21 |
| Tocantins | 0.57 | 16.87 | 0.55 | 0.54 | 0.32 |
| Station | Simulation | RMSE (m) | RRMSE (%) | R2 | NSE | Bias (m) |
|---|---|---|---|---|---|---|
| Guarás | Reference | 0.49 | 8.07 | 0.94 | 0.89 | 0.24 |
| AtPmVg | 0.49 | 8.04 | 0.94 | 0.89 | 0.24 | |
| FES2014 | 0.43 | 6.99 | 0.96 | 0.92 | 0.18 | |
| Bathymetry | 0.66 | 10.88 | 0.97 | 0.81 | 0.44 | |
| Colares | Reference | 0.20 | 4.47 | 0.96 | 0.96 | 0.04 |
| AtPmVg | 0.20 | 4.53 | 0.96 | 0.96 | 0.04 | |
| FES2014 | 0.20 | 4.48 | 0.96 | 0.96 | 0.04 | |
| Bathymetry | 0.62 | 14.10 | 0.72 | 0.62 | 0.39 | |
| Joanes | Reference | 0.19 | 4.43 | 0.96 | 0.96 | 0.04 |
| AtPmVg | 0.19 | 4.45 | 0.96 | 0.96 | 0.04 | |
| FES2014 | 0.20 | 4.47 | 0.96 | 0.96 | 0.04 | |
| Bathymetry | 0.65 | 14.90 | 0.67 | 0.57 | 0.42 | |
| Cotijuba | Reference | 0.21 | 6.40 | 0.95 | 0.93 | 0.05 |
| AtPmVg | 0.22 | 6.63 | 0.95 | 0.93 | 0.05 | |
| FES2014 | 0.25 | 7.66 | 0.94 | 0.90 | 0.06 | |
| Bathymetry | 0.53 | 16.04 | 0.61 | 0.57 | 0.28 | |
| Belém | Reference | 0.21 | 5.50 | 0.95 | 0.94 | 0.04 |
| AtPmVg | 0.22 | 5.71 | 0.94 | 0.94 | 0.05 | |
| FES2014 | 0.24 | 6.18 | 0.94 | 0.93 | 0.06 | |
| Bathymetry | 0.69 | 18.20 | 0.49 | 0.39 | 0.48 | |
| Barcarena | Reference | 0.30 | 8.28 | 0.88 | 0.88 | 0.09 |
| AtPmVg | 0.30 | 8.51 | 0.87 | 0.87 | 0.09 | |
| FES2014 | 0.32 | 9.07 | 0.85 | 0.85 | 0.11 | |
| Bathymetry | 0.64 | 18.02 | 0.47 | 0.41 | 0.42 | |
| Pará | Reference | 0.46 | 15.98 | 0.65 | 0.61 | 0.21 |
| AtPmVg | 0.46 | 16.33 | 0.64 | 0.59 | 0.22 | |
| FES2014 | 0.48 | 16.87 | 0.62 | 0.56 | 0.23 | |
| Bathymetry | 0.64 | 22.39 | 0.24 | 0.23 | 0.41 | |
| Tocantins | Reference | 0.57 | 16.86 | 0.55 | 0.54 | 0.32 |
| AtPmVg | 0.58 | 17.22 | 0.53 | 0.52 | 0.34 | |
| FES2014 | 0.59 | 17.54 | 0.52 | 0.50 | 0.35 | |
| Bathymetry | 0.79 | 23.37 | 0.12 | 0.12 | 0.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, D.R.; Oliveira, A.R.; Costa, M.S.; Rollnic, M.; Neves, R. Simulation of Tidal Oscillations in the Pará River Estuary Using the MOHID-Land Hydrological Model. Water 2025, 17, 1048. https://doi.org/10.3390/w17071048
Pereira DR, Oliveira AR, Costa MS, Rollnic M, Neves R. Simulation of Tidal Oscillations in the Pará River Estuary Using the MOHID-Land Hydrological Model. Water. 2025; 17(7):1048. https://doi.org/10.3390/w17071048
Chicago/Turabian StylePereira, Débora R., Ana R. Oliveira, Mauricio S. Costa, Marcelo Rollnic, and Ramiro Neves. 2025. "Simulation of Tidal Oscillations in the Pará River Estuary Using the MOHID-Land Hydrological Model" Water 17, no. 7: 1048. https://doi.org/10.3390/w17071048
APA StylePereira, D. R., Oliveira, A. R., Costa, M. S., Rollnic, M., & Neves, R. (2025). Simulation of Tidal Oscillations in the Pará River Estuary Using the MOHID-Land Hydrological Model. Water, 17(7), 1048. https://doi.org/10.3390/w17071048







