Dynamic Changes in Both Summer Potential Evapotranspiration and Its Driving Factors in the Huai River Basin, China
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data
3. Methodology
3.1. Penman–Monteith Method
3.2. Sensitivity Analysis
3.3. Anomaly Contribution Analysis Method
- Step 1: Calculate the relative variations in meteorological factors xk and ETp against their multi–year average values:where θk,i(t) is the anomaly ratio of meteorological element k in year i during the study period; is the average of meteorological element k; ϕi(t) is the anomaly ratio of ETp in year i during the studying period; and is the average of ETp (t) during the studying period.
- Step 2: Calculate the contribution of each climate factor xk to the ETp:where γk,i is the contribution of xk to ETp at the ith year, and Sk,i is the sensitivity coefficient of ETp to the kth factor at the ith year.
- Step 3: Calculate the total contribution of all the climatic factors to the ETp:where ψi is the total contribution of all the climatic factors to the ETp at the ith year, and m is the number of meteorological elements considered.
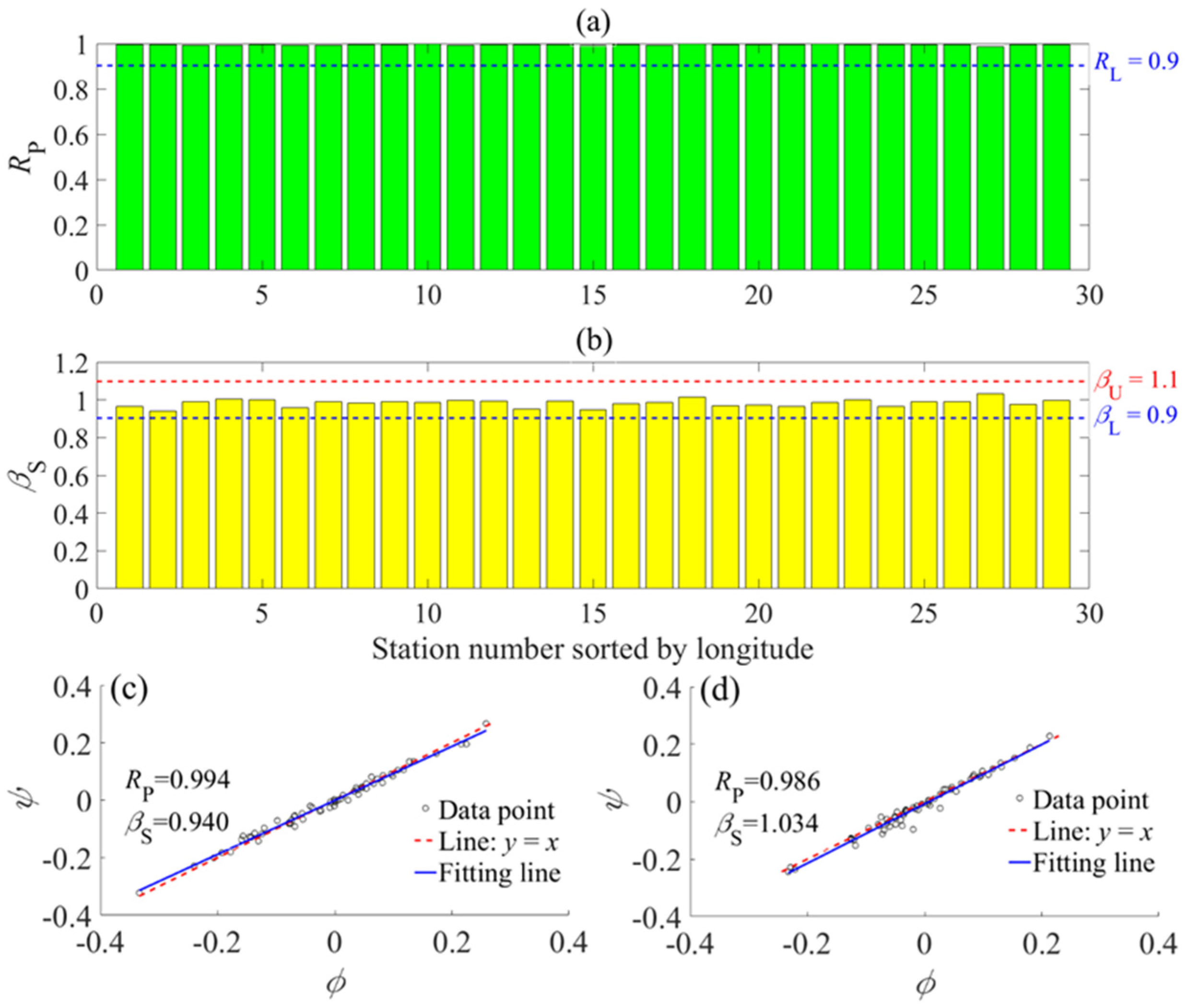
- Step 4: Determine the relationship between ϕi and ψi with the Pearson correlation coefficient and the Sen’s trend slope:where and are the averages of ϕi and ψi, respectively.
- Step 5: Calculate the relative contribution rate of a meteorological factor to the ETp:where Ck,i is the relative contribution rate of the kth meteorological factor to the ETp at the ith year, %. A positive (or negative) contribution rate indicates that the change of local climate factors improves (or reduces) ETp, while the absolute value of the contribution rate indicates the impact of the climate factors variations on ETp change. For the ETp, a climatic factor with the maximum |Ck,i| is called the dominant meteorological factor. More details can be found in Liu et al. (2023) [1].
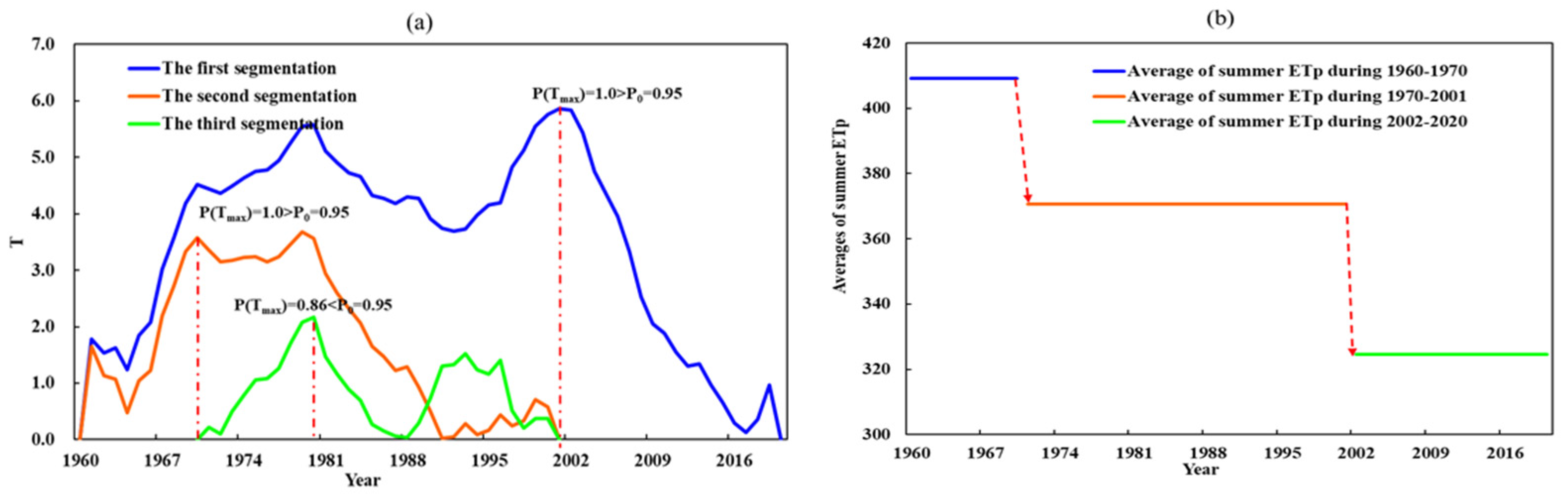
3.4. Trend Test and Change Point Identifying
4. Results
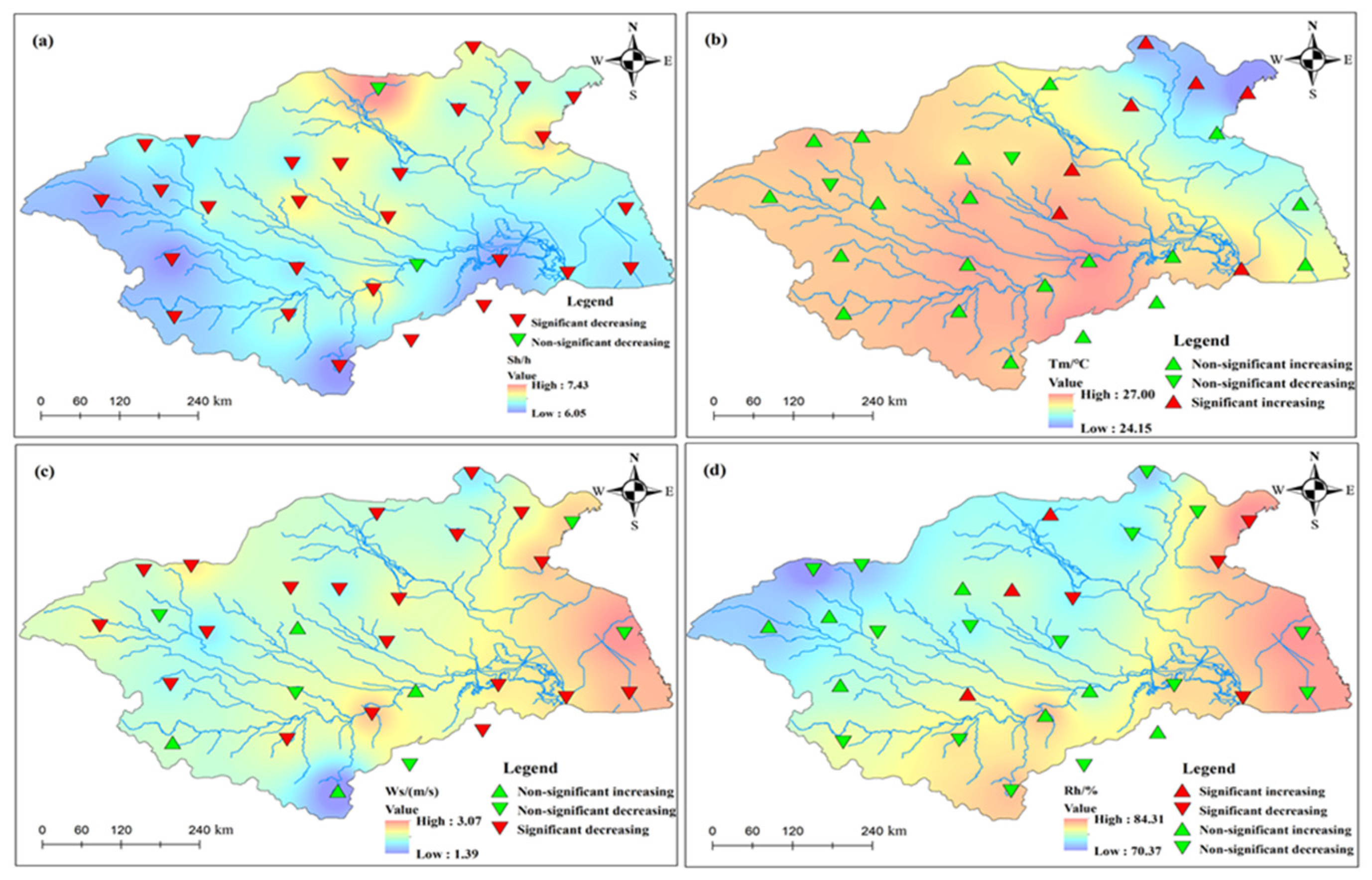
4.1. Trends of Summer Meteorological Factors
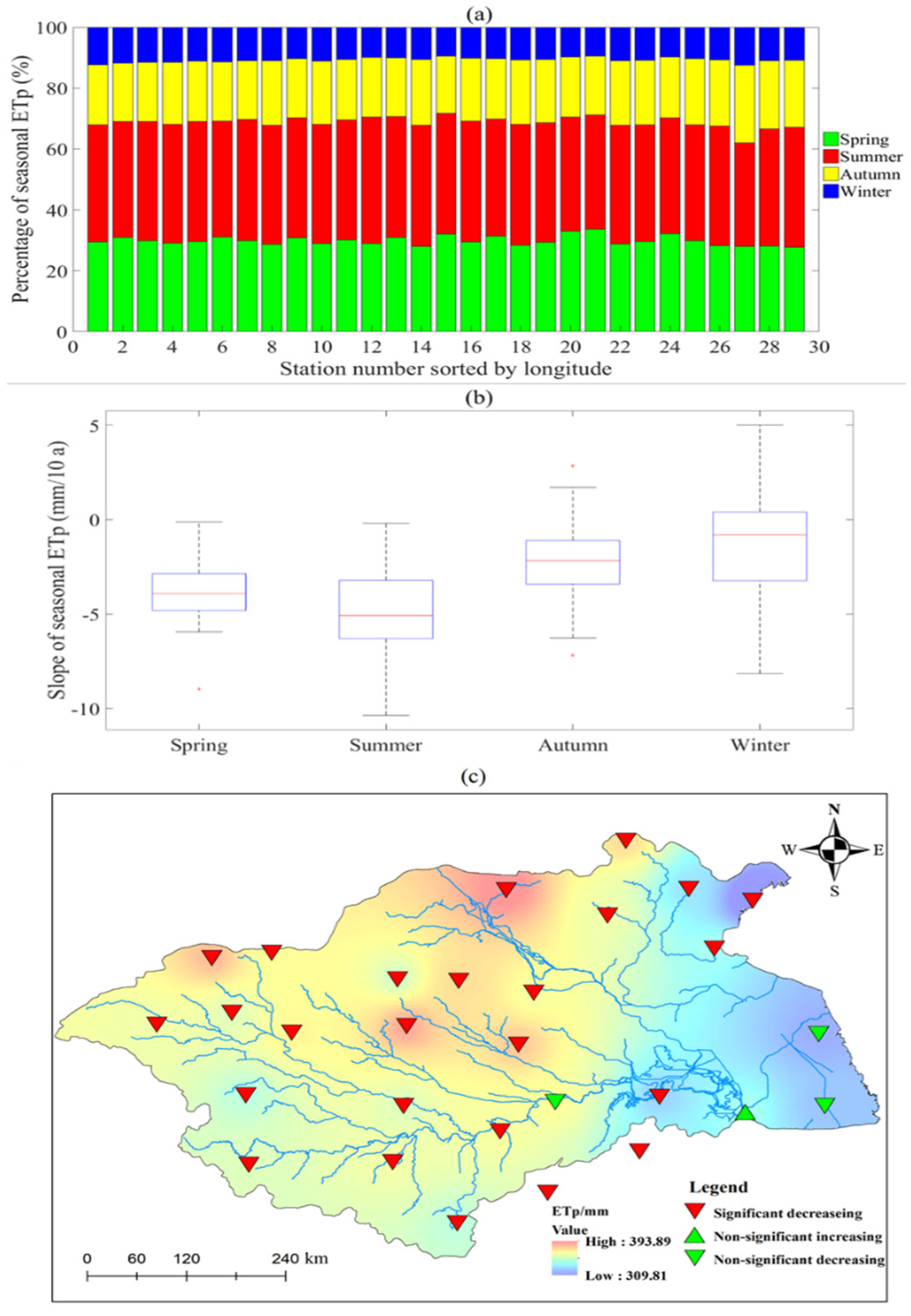
4.2. Changing Characteristics of Summer ETp
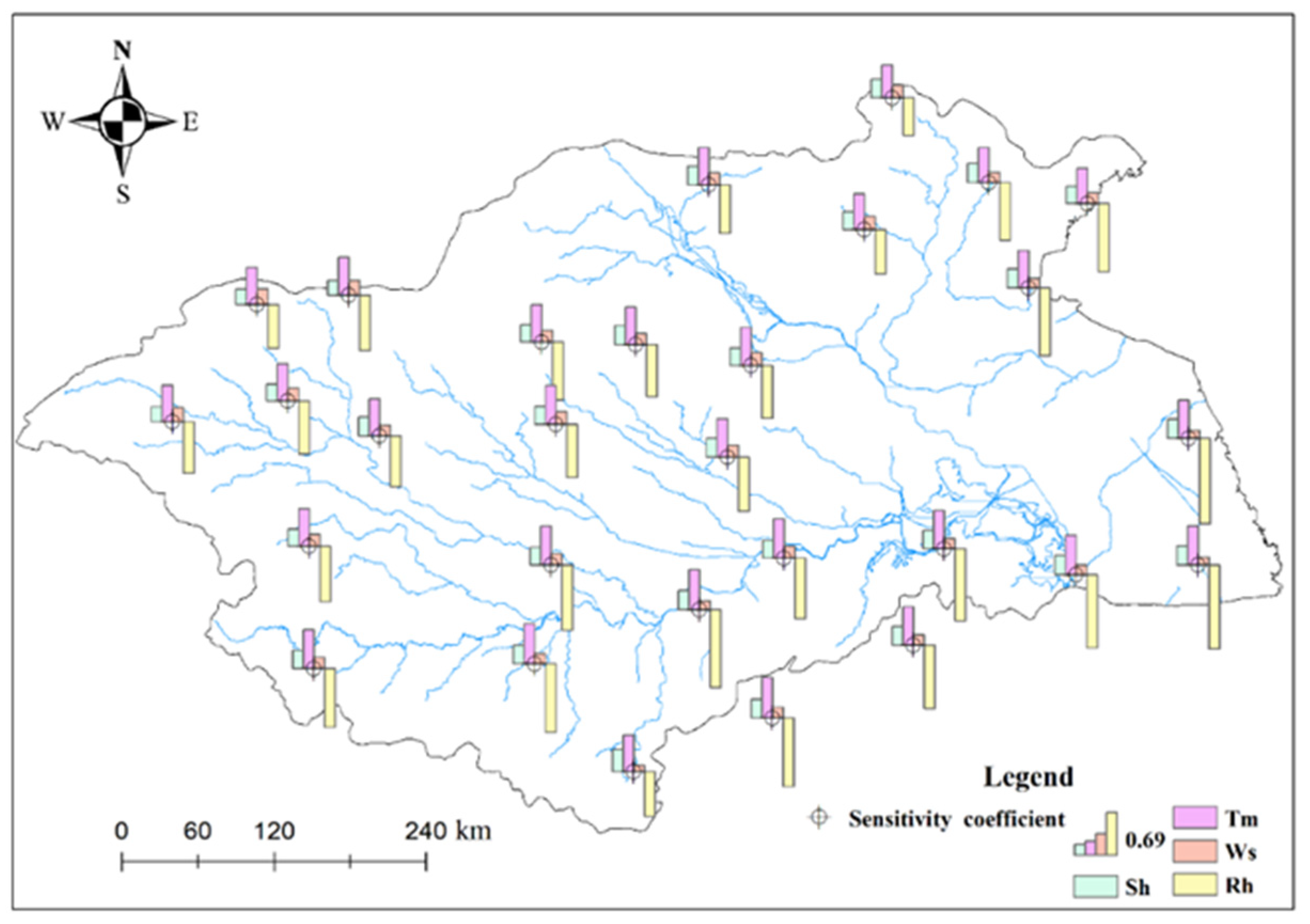
4.3. Sensitivity of ETp to Meteorological Factors in Summer
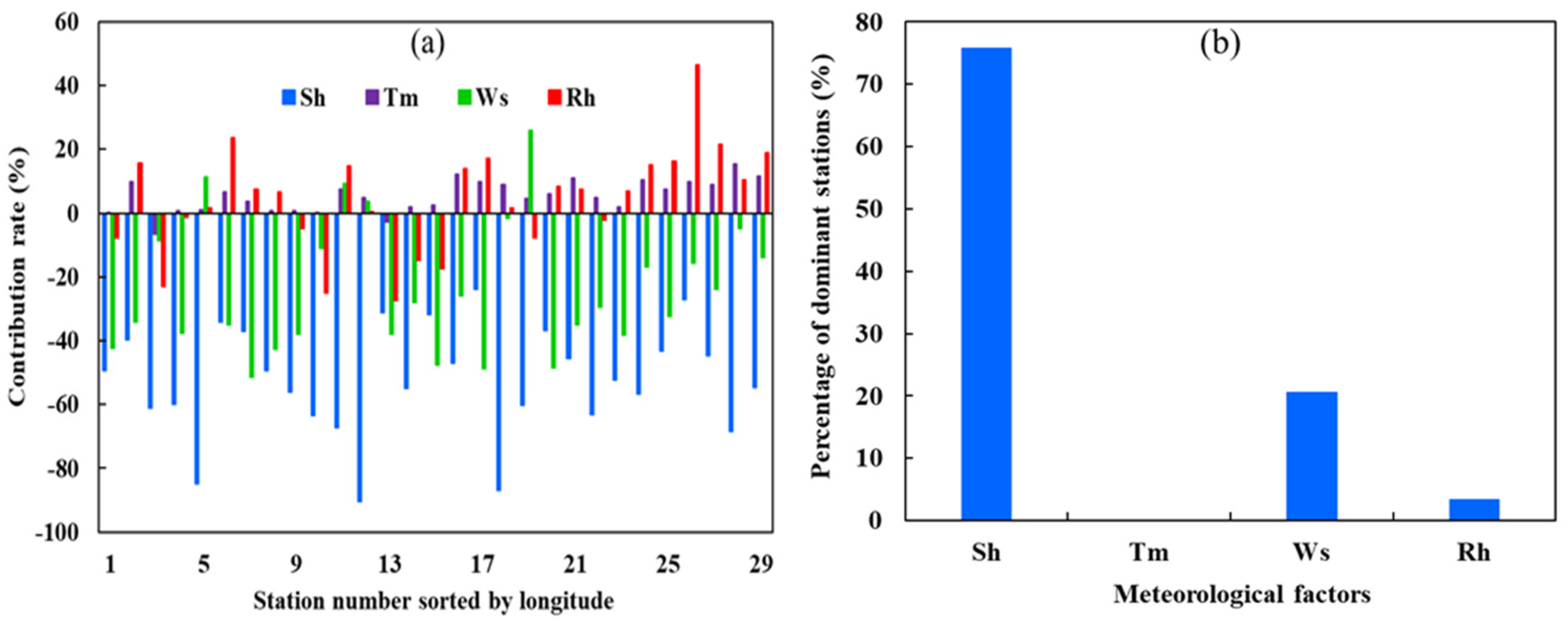
4.4. Contribution Patterns of Summer Meteorological Factors to Summer ETp
4.4.1. Contribution Analysis at Multi–Year Scale
4.4.2. Application of Anomaly Contribution Analysis
4.4.3. Contribution Analysis Based on the Anomaly Contribution Analysis
- (1)
- Spatiotemporal distributions of contributions
- (2)
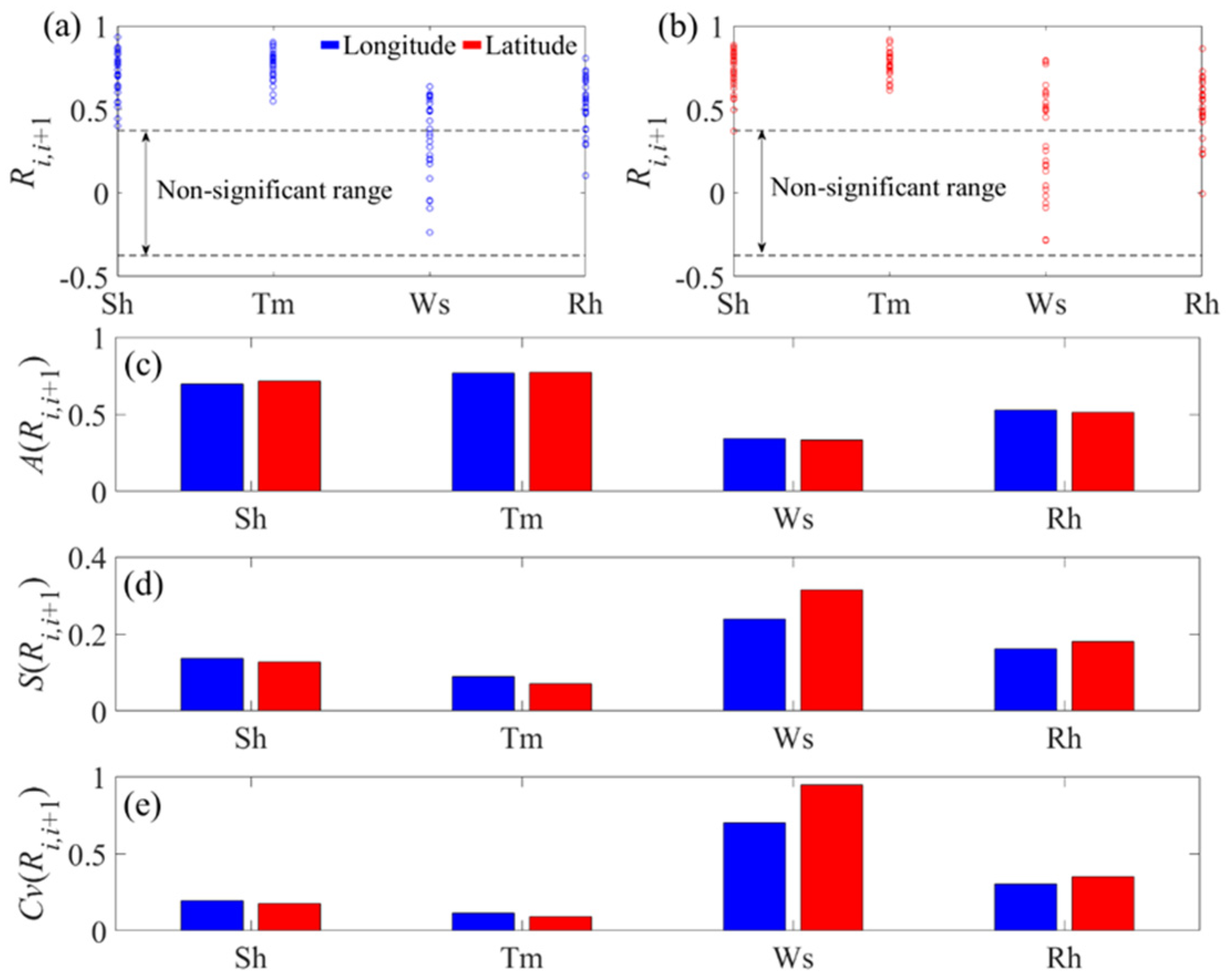
- Spatial correlations of contributions
- (3)
- Dominant meteorological factors
5. Discussion
5.1. Anachronistic Evaporation Paradox for Summer ETp
5.2. Simple Attribution Analysis for Summer ETp Changes
5.3. Anomaly Contribution Analysis for Summer ETp Changes
5.4. Differences in Dominant Meteorological Factors at Different Scales
6. Conclusions
- (1)
- There is a significant decreasing trend in the summer ETp but the trend in summer Tm is insignificant at most stations of the basin, suggesting the evaporation paradox might not be appropriate from the seasonal perspective. In addition, summer ETp experienced an abrupt change around the 1970s and 1980s because of the mutations in summer Sh and Ws, indicating the nonstationarity of the summer ETp series.
- (2)
- Sensitivity analysis demonstrates the sensitivity of summer ETp in the basin to meteorological factors can be ranked in descending order as Rh > Tm > Sh > Ws. However, the two most important dominant meteorological factors of summer ETp are summer Sh and Ws at the multi–year scale, while they are summer Sh and Rh at the seasonal scale, suggesting the dominant factors of ETp may be different at the multi–year and seasonal scales in the same region. Moreover, the dominant meteorological factors of summer ETp are also different at station and basin scales due to scale effects.
- (3)
- Dynamic changes in contribution rates show that summer Sh and Ws have significant step–shifts from positive to negative throughout the study period, while the contributions of summer Rh and Tm show clear positive–negative alterations. Except for summer Ws, the contributions of summer Sh, Tm, and Rh show good spatial homogeneity. Moreover, the contributions of summer Sh and Tm have better spatial homogeneity in the north–south direction, while the contributions of summer Ws and Rh have better spatial homogeneity in the east–west direction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, S.; Xie, Y.; Fang, H.; Xu, P.; Du, H. A method for identifying the dominant meteorological factors of atmospheric evaporative demand in mid-long term. Water Resour. Res. 2023, 59, e2022WR033321. [Google Scholar] [CrossRef]
- Gharbia, S.S.; Smullen, T.; Gill, L.; Johnston, P.; Pilla, F. Spatially distributed potential evapotranspiration modeling and climate projections. Sci. Total Environ. 2018, 633, 571–592. [Google Scholar] [CrossRef]
- Hamed, M.M.; Iqbal, Z.; Nashwan, M.S.; Kineber, A.F.; Shahid, S. Diminishing evapotranspiration paradox and its cause in the Middle East and North Africa. Atmos. Res. 2023, 289, 106760. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, X.; Wang, Q.; Yu, J.; Jiang, Q.; Jiang, W.; Li, L. Differences in reference evapotranspiration variation and climate-driven patterns in different altitudes of the Qinghai-Tibet Plateau (1961–2017). Water 2021, 13, 1749. [Google Scholar] [CrossRef]
- Wang, C.; Chen, J.; Gu, L.; Wu, G.; Tong, S.; Xiong, L.; Xu, C.-Y. A pathway analysis method for quantifying the contributions of precipitation and potential evapotranspiration anomalies to soil moisture drought. J. Hydrol. 2023, 621, 129570. [Google Scholar] [CrossRef]
- Hu, W.; She, D.; Xia, J.; He, B.; Hu, C. Dominant patterns of dryness/wetness variability in the Huang-Huai-Hai River Basin and its relationship with multiscale climate oscillations. Atmos. Res. 2021, 247, 105148. [Google Scholar] [CrossRef]
- Ma, T.; Liang, Y.; Lau, M.K.; Liu, B.; Wu, M.M.; He, H.S. Quantifying the relative importance of potential evapotranspiration and timescale selection in assessing extreme drought frequency in conterminous China. Atmos. Res. 2021, 263, 105797. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S.; Zhao, W.; Liu, Y. The increasing contribution of potential evapotranspiration to severe droughts in the Yellow River basin. J. Hydrol. 2022, 605, 127310. [Google Scholar] [CrossRef]
- Chen, X.; Yu, L.; Cui, N.; Cai, H.; Jiang, X.; Liu, C.; Shu, Z.; Wu, Z. Modeling maize evapotranspiration using three types of canopy resistance models coupled with single-source and dual-source hypotheses-A comparative study in a semi-humid and drought-prone region. J. Hydrol. 2022, 614, 128638. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, S.; Zhai, J.; He, G.; Zhao, Y.; Zhu, Y.; He, X.; Li, H.; Wang, L.; He, F.; et al. Effects of vegetation restoration on evapotranspiration water consumption in mountainous areas and assessment of its remaining restoration space. J. Hydrol. 2022, 605, 127259. [Google Scholar]
- Vogel, E.; Lerat, J.; Pipunic, R.; Frost, A.J.; Donnelly, C.; Griffiths, M.; Hudson, D.; Loh, S. Seasonal ensemble forecasts for soil moisture, evapotranspiration and runoff across Australia. J. Hydrol. 2021, 601, 126620. [Google Scholar] [CrossRef]
- Xu, L.; Sun, S.; Chen, H.; Chai, R.; Wang, J.; Zhou, Y.; Ma, Q.; Chotamonsak, C.; Wangpakapattanawong, P. Changes in the reference evapotranspiration and contributions of climate factors over the Indo-China Peninsula during 1961–2017. Int. J. Climatol. 2021, 41, 6511–6529. [Google Scholar] [CrossRef]
- Xiang, K.; Li, Y.; Hortaon, R.; Feng, H. Similarity and difference of potential evapotranspiration and reference crop evapotranspiration-a review. Agric. Water Manag. 2020, 232, 106043. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geog. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Estimation of potential evapotranspiration. J. Irrig. Drain. Eng. 1982, 108, 223–230. [Google Scholar]
- Hargreaves, G.H.; Samni, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Blaney, H.F.; Criddle, W.D. Determining Water Requirements in Irrigated Areas from Climatological Irrigation Data; Tech. Pap. 96; US Department of Agriculture, Soil Conservation Service: Washington, DC, USA, 1950; 48p.
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather. Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Makkink, G.F. Testing the Penman formula by means of lysimeters. J. Inst. Water Eng. 1957, 11, 277–288. [Google Scholar]
- Rohwer, C. Evaporation from free water surface. USDA Tech. Null. 1931, 217, 1–96. [Google Scholar]
- Albrecht, F. Die Methoden zur Bestimmung der Verdunstung der natürlichenErdoberfläche. Archiv. Für Meteorol. Geophys. Bioklimatol. Ser. B 1950, 2, 1–38. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Irrigation and Drainage Paper No 56.; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 1998. [Google Scholar]
- Wang, H.; Sun, F.; Wang, T.; Feng, Y.; Liu, F.; Liu, W. On the Pattern and Attribution of Pan Evaporation over China (1951–2021). J. Hydrometeorol. 2023, 24, 2023–2033. [Google Scholar] [CrossRef]
- Li, M.; Chu, R.; Shen, S.; Towfiqul Islam, A.R.M. Dynamic analysis of pan evaporation variations in the Huai River Basin, a climate transition zone in eastern China. Sci. Total Environ. 2018, 625, 496–509. [Google Scholar] [CrossRef] [PubMed]
- Chapman, R.A.; Midgley, G.F.; Smart, K. Diverse trends in observed pan evaporation in South Africa suggest multiple interacting drivers. S. Afr. J. Sci. 2021, 117, 80–86. [Google Scholar] [CrossRef]
- Jerin, J.N.; Islam, A.R.M.T.; Al Mamun, M.A.; Mozahid, M.N.; Ibrahim, S.M. Climate change effects on potential evapotranspiration in Bangladesh. Arab. J. Geosci. 2021, 14, 682. [Google Scholar] [CrossRef]
- Li, Y.; Qin, Y.; Rong, P. Evolution of potential evapotranspiration and its sensitivity to climate change based on the Thornthwaite, Hargreaves, and Penman-Monteith equation in environmental sensitive areas of China. Atmos. Res. 2022, 273, 106178. [Google Scholar] [CrossRef]
- Peterson, T.C.; Golubev, V.S.; Groisman, P.Y. Evaporation losing its strength. Nature 1995, 377, 687–688. [Google Scholar] [CrossRef]
- Roderick, M.L.; Farquhar, G.D. The cause of decreased pan evaporation over the past 50 years. Science 2002, 298, 1410–1411. [Google Scholar] [CrossRef]
- Ahmadi, A.; Daccache, A.; Snyder, R.L.; Suvocarev, K. Meteorological driving forces of reference evapotranspiration and their trends in California. Sci. Total Environ. 2022, 849, 157823. [Google Scholar] [CrossRef]
- Blyth, E.M.; Martinez-de la Torre, A.; Robinson, E.L. Trends in evapotranspiration and its drivers in Great Britain: 1961 to 2015. Prog. Phys. Geogr.-Earth Environ. 2019, 43, 666–693. [Google Scholar] [CrossRef]
- Li, Z.; Wang, S.; Li, J. Spatial variations and long-term trends of potential evaporation in Canada. Sci. Rep. 2020, 10, 22089. [Google Scholar] [CrossRef]
- Al-Hasani, A.A.J.; Shahid, S. Spatial distribution of the trends in potential evapotranspiration and its influencing climatic factors in Iraq. Theor. Appl. Climatol. 2022, 150, 677–696. [Google Scholar] [CrossRef]
- Du, Y.; Zhao, J.; Huang, Q. Quantitative driving analysis of climate on potential evapotranspiration in Loess Plateau incorporating synergistic effects. Ecol. Indic. 2022, 141, 109076. [Google Scholar] [CrossRef]
- Ding, Y.; Peng, S. Spatiotemporal change and attribution of potential evapotranspiration over China from 1901 to 2100. Theor. Appl. Climatol. 2021, 145, 79–94. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, D.; Feng, Y.; Wu, J.; Cui, W.; He, X.; Chen, A.; Zeng, Z. Decreasing relative humidity dominates a reversal of decreasing pan evaporation in mainland China after 1989. J. Hydrol. 2022, 608, 127641. [Google Scholar] [CrossRef]
- Nooni, I.K.; Ogou, F.K.; Lu, J.; Nakoty, F.M.; Chaibou, A.A.S.; Habtemicheal, B.A.; Sarpong, L.; Jin, Z. Temporal and spatial variations of potential and actual evapotranspiration and the driving mechanism over Equatorial Africa using satellite and reanalysis-based observation. Remote Sens. 2023, 15, 3201. [Google Scholar] [CrossRef]
- Solaraju-Murali, B.; Caron, L.P.; Gonzalez-Reviriego, N.; Doblas-Reyes, F.J. Multi-year prediction of European summer drought conditions for the agricultural sector. Environ. Res. Lett. 2019, 14, 124014. [Google Scholar] [CrossRef]
- Tomas-Burguera, M.; Beguería, S.; Vicente-Serrano, S.M. Climatology and trends of reference evapotranspiration in Spain. Int. J. Climatol. 2021, 41 (Suppl. S1), E1860–E1874. [Google Scholar] [CrossRef]
- Sabino, M.; de Souza, A.P. Global Sensitivity of Penman-Monteith Reference Evapotranspiration to Climatic Variables in Mato Grosso, Brazil. Earth 2023, 4, 714–727. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, S.; Fang, H.; Ding, M.; Liu, D. A study on the precipitation concentration in a Chinese region and its relationship with teleconnections indices. J. Hydrol. 2022, 612, 128203. [Google Scholar] [CrossRef]
- Wang, L.; Han, X.; Zhang, Y.; Zhang, Q.; Wan, X.; Liang, T.; Song, H.; Bolan, N.; Shaheen, S.M.; White, J.R.; et al. Impacts of land uses on spatio-temporal variations of seasonal water quality in a regulated river basin, Huai River, China. Sci. Total Environ. 2023, 857, 159584. [Google Scholar] [CrossRef]
- Ren, J.; Wang, W.; Wei, J.; Li, H.; Li, X.; Liu, G.; Chen, Y.; Ye, S. Evolution and prediction of drought-flood abrupt alternation events in Huang-Huai-Hai River Basin, China. Sci. Total Environ. 2023, 869, 161707. [Google Scholar] [CrossRef] [PubMed]
- Jerszurki, D.; de Souza, J.L.M.; de Carvalho Ramos Silva, L. Sensitivity of ASCE-Penman-Monteith reference evapotranspiration under different climate types in Brazil. Clim. Dyn. 2019, 53, 943–956. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, S.; Fang, H.; Wang, J. Global autocorrelation test based on the Monte Carlo method and impacts of eliminating nonstationary components on the global autocorrelation test. Stoch. Environ. Res. Risk Assess. 2020, 34, 1645–1658. [Google Scholar] [CrossRef]
- Liu, S.; Xie, Y.; Fang, H.; Du, H.; Xu, P. Trend test for hydrological and climatic time series considering the interaction of trend and autocorrelations. Water 2022, 14, 3006. [Google Scholar] [CrossRef]
- Liu, S.; Huang, S.; Xie, Y.; Huang, Q.; Wang, H.; Leng, G. Assessing the non-stationarity of low flows and their scale-dependent relationships with climate and human forcing. Sci. Total Environ. 2019, 687, 244–256. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Su, B.; Gao, M.; Tao, H.; Jiang, S.; Gong, Y.; Wang, Y.; Zhou, J.; Jiang, T. Will the ‘evapotranspiration paradox’ phenomenon exist across China in the future? Int. J. Climatol. 2023, 43, 7132–7151. [Google Scholar] [CrossRef]
- Zhou, F.; Zhao, Z.; Azorin-Molina, C.; Jia, X.; Zhang, G.; Chen, D.; Liu, J.; Guijarro, J.A.; Zhang, F.; Fang, K. Teleconnections between large-scale oceanic-atmospheric patterns and interannual surface wind speed variability across China: Regional and seasonal patterns. Sci. Total Environ. 2022, 838, 156023. [Google Scholar] [CrossRef]
- An, L.; Yao, Z.; Zhang, P.; Jia, S.; Zhao, J.; Gao, L.; Liu, Z. Regional characteristics and exploitation potential of atmospheric water resources in China. Int. J. Climatol. 2022, 42, 3225–3245. [Google Scholar] [CrossRef]
- Guo, X.J.; Wang, W.Z.; Li, C.X.; Wang, W.; Shi, J.S.; Miao, Y.; Hao, X.; Yuan, D. Temporal variations of reference evapotranspiration and controlling factors: Implications for climatic drought in karst areas. J. Groundw. Sci. Eng. 2022, 10, 267–284. [Google Scholar]
- Yan, Z.; Wang, S.; Ma, D.; Liu, B.; Lin, H.; Li, S. Meteorological factors affecting pan evaporation in the Haihe River Basin, China. Water 2019, 11, 317. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, R.; Song, Y.; Han, C.; Liu, J.; Liu, Z. Sensitivity of potential evapotranspiration to meteorological factors and their elevational gradients in the Qilian Mountains, northwestern China. J. Hydrol. 2019, 568, 147–159. [Google Scholar] [CrossRef]
- Ichiba, A.; Gires, A.; Tchiguirinskaia, I.; Schertzer, D.; Bompard, P.; Ten Veldhuis, M.C. Scale effect challenges in urban hydrology highlighted with a distributed hydrological model. Hydrol. Earth Syst. Sci. 2018, 22, 331–350. [Google Scholar] [CrossRef]
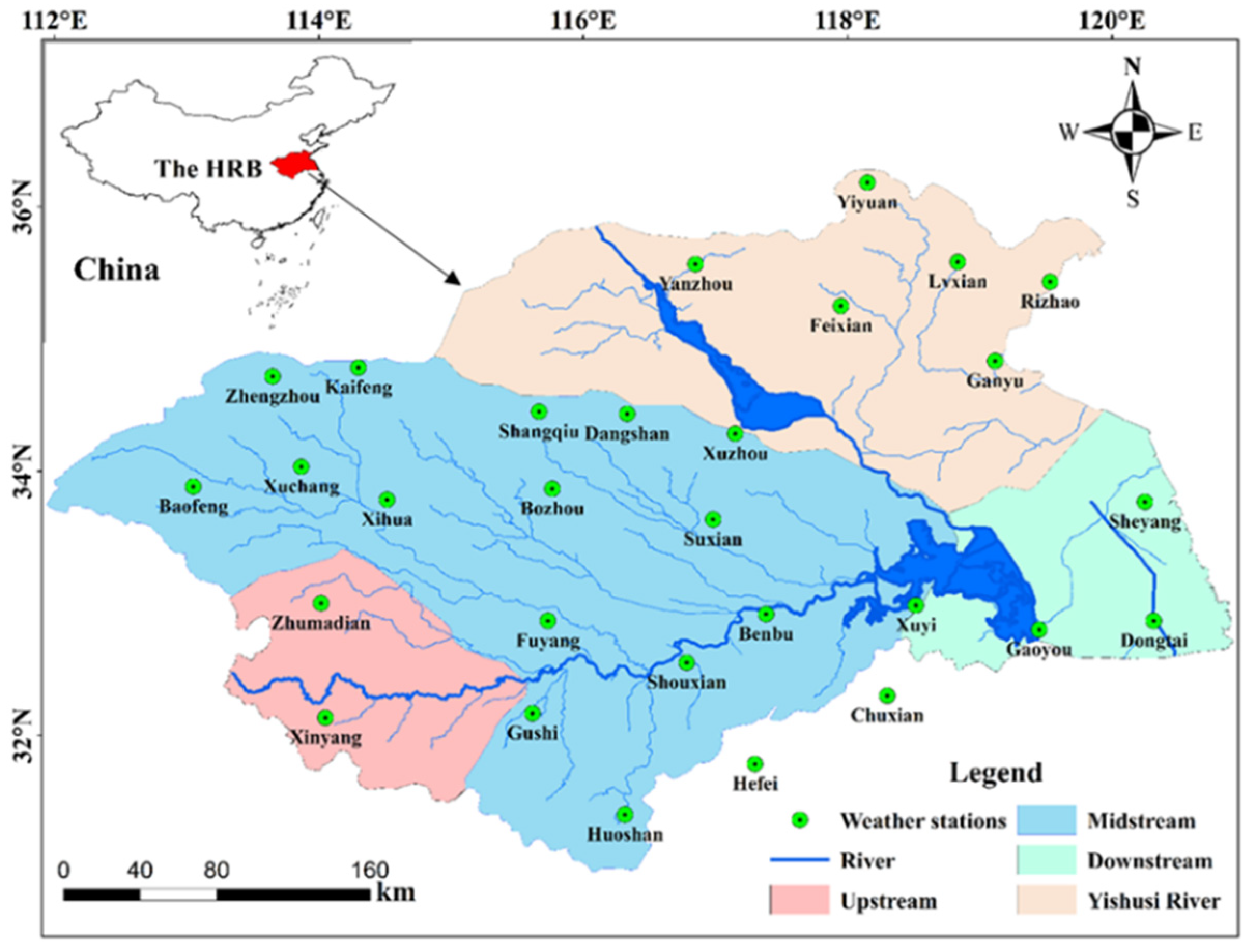



| No.1 a | Name | Latitude (°N) | Longitude (°E) | Elevation (m) |
|---|---|---|---|---|
| 1 | Baofeng | 33.88 | 113.05 | 136.40 |
| 2 | Zhengzhou | 34.72 | 113.65 | 110.40 |
| 3 | Xuchang | 34.03 | 113.87 | 66.80 |
| 4 | Zhumadian | 33.00 | 114.02 | 82.70 |
| 5 | Xinyang | 32.13 | 114.05 | 114.50 |
| 6 | Kaifeng | 34.78 | 114.30 | 73.70 |
| 7 | Xihua | 33.78 | 114.52 | 52.60 |
| 8 | Gushi | 32.17 | 115.62 | 42.90 |
| 9 | Shangqiu | 34.45 | 115.67 | 50.10 |
| 10 | Fuyang | 32.87 | 115.73 | 32.70 |
| 11 | Bozhou | 33.87 | 115.77 | 37.70 |
| 12 | Huoshan | 31.40 | 116.32 | 86.40 |
| 13 | Dangshan | 34.43 | 116.33 | 44.20 |
| 14 | Shouxian | 32.55 | 116.78 | 22.70 |
| 15 | Yanzhou | 35.57 | 116.85 | 51.70 |
| 16 | Suxian | 33.63 | 116.98 | 25.90 |
| 17 | Xuzhou | 34.28 | 117.15 | 41.20 |
| 18 | Hefei | 31.78 | 117.30 | 27.00 |
| 19 | Benbu | 32.92 | 117.38 | 21.90 |
| 20 | Feixian | 35.25 | 117.95 | 121.20 |
| 21 | Yiyuan | 36.18 | 118.15 | 305.10 |
| 22 | Chuxian | 32.30 | 118.30 | 27.50 |
| 23 | Xuyi | 32.98 | 118.52 | 40.80 |
| 24 | Lvxian | 35.58 | 118.83 | 107.40 |
| 25 | Ganyu | 34.83 | 119.12 | 3.30 |
| 26 | Gaoyou | 32.80 | 119.45 | 5.40 |
| 27 | Rizhao | 35.43 | 119.53 | 36.90 |
| 28 | Sheyang | 33.77 | 120.25 | 2.00 |
| 29 | Dongtai | 32.87 | 120.32 | 4.30 |
| No.1 | Stations | ETp | Sh | Tm | Ws | Rh |
|---|---|---|---|---|---|---|
| 1 | Baofeng | 1979 | 1980 | —— | 1977, 2006 | 1970 |
| 2 | Zhengzhou | 1975 | 1975, 1995 | 1970, 2008 | 1977 | 1970, 2008 |
| 3 | Xuchang | 1970 | 1970, 2002 | 1970 | 1982, 2006 | 1970 |
| 4 | Zhumadian | 1975 | 1980 | —— | 2002 | —— |
| 5 | Xinyang | 1979 | 1980, 2002 | —— | 1980, 2005 | —— |
| 6 | Kaifeng | 1970 | 1997 | 1970, 2008 | 1973 | 1970, 2004 |
| 7 | Xihua | 1979 | 1975, 2002 | —— | 1986 | —— |
| 8 | Gushi | 1980 | 1980, 2002 | —— | 1983, 2005 | —— |
| 9 | Shangqiu | 1979 | 1980 | —— | 1979, 1990 | —— |
| 10 | Fuyang | 1980 | 1980, 2002 | —— | 1971 | —— |
| 11 | Bozhou | 1971 | 1980 | —— | 1979, 2001 | 1970, 2009 |
| 12 | Huoshan | 1972 | 1979 | —— | 1973, 1989 | —— |
| 13 | Dangshan | 1970, 2001 | 1980 | —— | 2001 | 2002 |
| 14 | Shouxian | 1980 | 1980 | —— | 2005 | —— |
| 15 | Yanzhou | 1970 | 1979 | —— | 2003 | —— |
| 16 | Suxian | 1979 | 1980, 2002 | 1993 | 1979 | 2008 |
| 17 | Xuzhou | 1979 | 1979 | 2009 | 1986 | 2009 |
| 18 | Hefei | 1970 | 1970, 1992 | —— | 1972, 2006 | —— |
| 19 | Benbu | —— | 1980 | —— | 1978, 2001 | —— |
| 20 | Feixian | 1984 | 1993 | 2009 | 1979, 2003 | —— |
| 21 | Yiyuan | 1984 | 1988 | —— | 1979 | —— |
| 22 | Chuxian | 1972 | 1979 | —— | 1978, 2002 | —— |
| 23 | Xuyi | 1979 | 1979, 1990 | —— | 1970, 1990, 2003 | 2009 |
| 24 | Lvxian | 1970 | 1970, 1983, 1993 | —— | 1979 | —— |
| 25 | Ganyu | 1997 | 1981, 1997 | —— | 1992, 2003 | 1991 |
| 26 | Gaoyou | —— | 1979 | 2000 | 1985 | 1991, 2001 |
| 27 | Rizhao | 2005 | 2002 | 1993 | 1991, 2002 | 1992 |
| 28 | Sheyang | —— | 1970 | —— | —— | —— |
| 29 | Dongtai | —— | 1979 | 2003 | —— | 1993 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Gao, Z.; Xie, Y.; Sun, D.; Fang, H.; Du, H.; Xu, P. Dynamic Changes in Both Summer Potential Evapotranspiration and Its Driving Factors in the Huai River Basin, China. Water 2025, 17, 906. https://doi.org/10.3390/w17060906
Liu S, Gao Z, Xie Y, Sun D, Fang H, Du H, Xu P. Dynamic Changes in Both Summer Potential Evapotranspiration and Its Driving Factors in the Huai River Basin, China. Water. 2025; 17(6):906. https://doi.org/10.3390/w17060906
Chicago/Turabian StyleLiu, Saiyan, Zheng Gao, Yangyang Xie, Dongyong Sun, Hongyuan Fang, Huihua Du, and Pengcheng Xu. 2025. "Dynamic Changes in Both Summer Potential Evapotranspiration and Its Driving Factors in the Huai River Basin, China" Water 17, no. 6: 906. https://doi.org/10.3390/w17060906
APA StyleLiu, S., Gao, Z., Xie, Y., Sun, D., Fang, H., Du, H., & Xu, P. (2025). Dynamic Changes in Both Summer Potential Evapotranspiration and Its Driving Factors in the Huai River Basin, China. Water, 17(6), 906. https://doi.org/10.3390/w17060906





