A Fuzzy Logic Framework for Multi-Criteria Assessment of Rainwater Drainage Infrastructure

Abstract

Urban stormwater systems face escalating challenges due to climate change, aging infrastructure, and increasing impervious surfaces, necessitating holistic frameworks that integrate hydraulic, structural, and operational factors. This study proposes a fuzzy logic-based controller to evaluate the performance of stormwater drainage systems through three linguistic variables: Hydraulic Performance, Technical Condition, and Operational Condition. The model synthesizes expert knowledge into 125 inference rules, enabling a unified assessment of system reliability. Validated against empirical datasets from European and Chinese drainage networks, the framework demonstrates robust performance across diverse geospatial and operational contexts. Unlike traditional deterministic methods or single-criterion fuzzy systems, the controller addresses interdependencies between hydraulic efficiency, material degradation and external stressors. By translating multi-dimensional uncertainties into actionable maintenance priorities—from “Immediate Replacement” to “No Action Required”—the model enhances decision-making for utilities balancing flood resilience and infrastructure longevity.

1. Introduction

The rapid development of cities leads to the expansion of areas from which increasing amounts of rainwater must be drained. Additionally, the imperviousness of urban surfaces, the limited capacity of sewage networks, and the restricted capacity of stormwater receivers contribute to urban flooding. The design and operation of stormwater infrastructure systems in urban areas directly impact social and environmental challenges and are critically important for municipal governance. Proper urban stormwater system design has become essential due to the severe consequences of urban flooding, including economic losses and constrained budgets for renovating aging infrastructure. Climate change exacerbates these challenges by altering rainfall patterns, particularly increasing peak runoff intensities. A key aspect of stormwater system design is the optimal selection of sewer diameters, which must balance hydraulic capacity for rainwater conveyance with retention capabilities to mitigate receiver overflow risks.

Engineers’ interpretations of existing or proposed designs often involve subjectivity, leading to ambiguities in decision-making [1]. Uncertainty, imprecision, and vagueness are inherent in natural and engineered systems, motivating the use of fuzzy set theory and inference systems to formalize expert knowledge into robust decision rules [2]. This study aims to develop a fuzzy logic-based controller to evaluate stormwater pipe diameters and compare its performance with classical conditional approaches.

The first step in stormwater system design is rainfall-runoff modeling, which underpins flood forecasting, overflow design, water quality analysis, and urban planning [3]. Traditional modeling approaches require extensive computational resources, prompting researchers to explore fuzzy logic-based methods for simplification and efficiency. For instance, adaptive neuro-fuzzy inference systems (ANFIS) combined with principal component analysis (PCA) [4] or particle swarm optimization (PSO) [5] have improved runoff predictions using historical data. The versatility of ANFIS is further demonstrated in energy systems, where it outperforms conventional methods in maximum power point tracking for photovoltaic arrays by integrating fuzzy logic’s adaptability with neural network training efficiency [6]. Similarly, Takagi–Sugeno [7] and Mamdani-type [8] fuzzy systems have been applied to capture nonlinear rainfall-runoff relationships. Recent advances in real-time control (RTC) further demonstrate fuzzy logic’s potential: Mounce et al. [9] optimized flood mitigation in drainage networks using genetic algorithm-tuned fuzzy rules, achieving a 25% reduction in flood volumes. Similarly, Sun et al. [10] developed a predictive fuzzy-rule system for stormwater storage, enhancing peak flow control by up to 87% under uncertain rainfall forecasts. However, these studies primarily address specific aspects of stormwater management, such as flood mitigation or overflow control, without integrating hydraulic, structural, and operational factors into a cohesive framework.

Urban flooding arises from heavy rainfall, low surface permeability, and outdated infrastructure [11]. Effective stormwater drainage systems (SKD) must accommodate expanding catchment areas, changing land use, and pollutant loads while preventing channel overflow [12,13]. Multi-criteria decision-making (MCDM) frameworks, such as those combining GIS and fuzzy analytic hierarchy processes (FAHP) [14], have been employed to prioritize rehabilitation efforts. For example, Al Nasiri et al. [15] applied MCDM-AHP to optimize sewer treatment plant locations in Muscat, Oman, while Roghani et al. [16] integrated fuzzy logic into risk assessment models to evaluate structural failures in Tehran’s sewers, improving rehabilitation prioritization. Yet, these approaches often treat hydraulic performance, technical condition, and operational stressors as separate domains, neglecting their interdependencies.

The integration of fuzzy logic with GIS has also advanced urban planning. Di Martino and Cardone [17] partitioned urban systems into homogeneous zones using fuzzy rule-based classification of socioeconomic and environmental indicators, while Pleho and Avdagic [18] demonstrated how fuzzy-GIS frameworks manage imprecise spatial data for environmental quality evaluations. These approaches highlight fuzzy logic’s versatility in handling geospatial and hydraulic uncertainties.

Despite these advancements, real-time control and system optimization remain challenging. Vanrolleghem et al. [19] emphasized the need for integrated models to balance ecological and economic criteria in wastewater management, a concept extended by Regneri et al. [20], who used fuzzy decision-making for multi-criteria optimization of sewer networks. However, existing studies predominantly focus on isolated aspects of stormwater systems, such as flood mitigation [9], overflow control [10], or infrastructure siting [15], with limited integration of hydraulic, structural, and operational factors into a unified decision framework. While recent advances in fuzzy logic have enabled multi-criteria assessments—such as Roghani et al. [16], who evaluated structural failure risks, and He et al. [21], who analyzed network vulnerability—these approaches treat hydraulic performance, technical condition, and operational stressors as separate domains. This fragmentation overlooks the interdependencies between system components. For instance, a pipe with excellent hydraulic capacity (e.g., oversized diameter) may still fail due to poor technical condition (e.g., corrosion) or operational overload (e.g., upstream development), yet current models lack mechanisms to synthesize these dimensions.

Current evaluation methods rely on deterministic thresholds or single-criterion fuzzy systems, which oversimplify the complex interactions between hydraulic efficiency, material degradation, and real-world usage patterns. Studies like Hlavinek et al. [22] developed reliability models for sewer rehabilitation based on structural and environmental criteria, while Vanrolleghem et al. [19] optimized drainage networks using ecological-economic trade-offs. However, none incorporate the triad of hydraulic performance, technical condition, and operational risk into a single adaptive framework. This gap limits the ability of utilities to prioritize interventions that balance immediate flood risks with long-term infrastructure resilience.

Building upon previous fuzzy logic-based models, this study advances the field by integrating hydraulic performance, technical condition, and operational condition into a single, holistic framework. Unlike earlier approaches that focused on isolated criteria or treated system components independently, our model synthesizes these dimensions to capture their interdependencies. This enables a more comprehensive understanding of system reliability and supports scenario-based decision-making, where maintenance priorities are informed by the combined effects of hydraulic, structural, and operational factors.

This paper bridges this gap by proposing a fuzzy logic controller that holistically evaluates stormwater systems through three interconnected linguistic variables: Hydraulic Performance, Technical Condition, and Operational Condition. By translating expert knowledge into 125 inference rules, the model integrates diverse failure mechanisms—from hydraulic surcharge to material fatigue—into a unified consequence assessment. This approach extends previous GIS-fuzzy frameworks [17,18] by explicitly coupling spatial data with dynamic operational parameters, enabling scenario-based decision-making. For example, a system with “Fair” hydraulic performance and “Good” technical condition may still require “Major Rehabilitation” if operational risks (e.g., frequent roadworks) are “Very High”—a nuance absent in traditional single-variable models.

The proposed framework is validated against empirical datasets from European and Chinese drainage networks, demonstrating its robustness across varied geospatial and operational contexts. By addressing the interplay between hydraulic design, structural integrity, and usage patterns, this work advances fuzzy logic applications in urban water management beyond isolated diameter optimization [22] or risk indexing [16].

2. Materials and Methods

2.1. Fuzzy Logic and Fuzzy Sets

Fuzzy logic was introduced by Dr. Lotfi Zadeh in the 1960s as a formal framework to address the vagueness and imprecision inherent in many real-world systems [23]. In classical Boolean logic, propositions are evaluated strictly as true (1) or false (0); however, fuzzy logic extends this dichotomy by allowing truth values to span continuously between 0 and 1. This capability enables statements to be partially true and partially false, thereby capturing the nuances of uncertainty observed in natural phenomena [24].

A fuzzy inference system employs fuzzy set theory to convert input data into output decisions by utilizing linguistic terms and corresponding membership functions. By integrating expert knowledge through a collection of fuzzy rules, the FIS establishes a robust mechanism for decision-making under uncertain conditions. In the present study, the Mamdani fuzzy inference approach is implemented due to its intuitive rule-based structure and proven effectiveness in engineering applications [25,26,27].

Within the framework of fuzzy set theory, the traditional concept of set membership is generalized. Given a universal set U (often referred to as the possibility space), a fuzzy set A is defined as a collection of ordered pairs:

$$\mathrm{Ã}=(\mathrm{x},{\mathsf{\mu }}_{\mathrm{Ã}}(\mathrm{x}\left)\right|\mathrm{x}\in \mathrm{X})$$

(1)

In this formulation, $\begin{array}{c}\mathrm{\mu }\mathrm{A}\left(\mathrm{x}\right)\end{array}$ represents the membership function of the element $\mathrm{x}$ in the fuzzy set A, assigning each element a degree of membership that ranges continuously between 0 and 1. These contrasts sharply with the definition of a crisp (or sharpened) set, where membership is binary. For a crisp set, the membership function is given by:

$${\mathrm{X}}_{\mathrm{A}}\left(\mathrm{x}\right)=\mathrm{def}\left\{\begin{array}{c}1, \mathrm{if} \begin{array}{c}\mathrm{x}\end{array}\in \mathrm{A},\\ 0, \mathrm{if} \begin{array}{c}\mathrm{x}\end{array}\notin \mathrm{A},\end{array}\right.$$

(2)

Thus, while classical sets are characterized by clear, exclusive boundaries, fuzzy sets allow for partial membership. This feature provides a flexible and nuanced framework for modeling the imprecise boundaries that are often encountered in practical applications [2,28].

2.2. Linguistic Variables

A fuzzy inference system (FIS) relies on linguistic variables that transform numerical input data into qualitative categories using membership functions. These functions define the degree of belonging of a numerical value to a given linguistic category. In the developed fuzzy logic model, three input variables—Hydraulic Performance, Technical Condition, and Operational Condition—and one output variable—Consequence—are considered. Each variable is divided into five linguistic categories, which are mathematically formulated using membership functions.

To accurately capture the transitions between linguistic categories, three types of membership functions are utilized: Z-shaped (zmf), Pi-shaped (pimf), and S-shaped (smf). The Z-shaped membership function (3) is used for categories representing the lowest values within a variable domain. It ensures a smooth transition from full membership $\begin{array}{c}(\mathrm{\mu } (\mathrm{x})=1)\end{array}$ to non-membership $\begin{array}{c}(\mathrm{\mu } (\mathrm{x})=0)\end{array}$. The Pi-shaped membership function (4) is applied to intermediate categories, ensuring a gradual transition between neighboring linguistic terms. The S-shaped membership function (5) defines the highest categories, smoothly transitioning from non-membership $\begin{array}{c}(\mathrm{\mu } (\mathrm{x})=0)\end{array}$ to full membership $\begin{array}{c}(\mathrm{\mu } (\mathrm{x})=1)\end{array}$.

$${\mathsf{\mu }}_{\mathrm{z}\mathrm{m}\mathrm{f}}\left(\mathrm{x};\mathrm{a},\mathrm{b}\right)=\left\{\begin{array}{ll}1,& \mathrm{x}\le \mathrm{a}\\ 1-2{\left({\displaystyle \frac{\mathrm{x}-\mathrm{a}}{\mathrm{b}-\mathrm{a}}}\right)}^2,& \mathrm{a}\le \mathrm{x}\le {\displaystyle \frac{\mathrm{a}+\mathrm{b}}{2}}\\ 2{\left({\displaystyle \frac{\mathrm{x}-\mathrm{b}}{\mathrm{b}-\mathrm{a}}}\right)}^2,& {\displaystyle \frac{\mathrm{a}+\mathrm{b}}{2}}\le \mathrm{x}\le \mathrm{b}\\ 0,& \mathrm{x}\ge \mathrm{b}\end{array}\right.$$

(3)

$${\mathsf{\mu }}_{\mathrm{p}\mathrm{i}\mathrm{m}\mathrm{f}}\left(\mathrm{x};\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\right)=\left\{\begin{array}{cc}0,& \mathrm{x}\le \mathrm{a}\\ 2{\left({\displaystyle \frac{\mathrm{x}-\mathrm{a}}{\mathrm{b}-\mathrm{a}}}\right)}^2,& \mathrm{a}\le \mathrm{x}\le {\displaystyle \frac{\mathrm{a}+\mathrm{b}}{2}}\\ 1-2{\left({\displaystyle \frac{\mathrm{x}-\mathrm{b}}{\mathrm{b}-\mathrm{a}}}\right)}^2,& {\displaystyle \frac{\mathrm{a}+\mathrm{b}}{2}}\le \mathrm{x}\le \mathrm{b}\\ 1,& \mathrm{b}\le \mathrm{x}\le \mathrm{c}\\ 1-2{\left({\displaystyle \frac{\mathrm{x}-\mathrm{c}}{\mathrm{d}-\mathrm{c}}}\right)}^2,& {\displaystyle \frac{\mathrm{c}+\mathrm{d}}{2}}\le \mathrm{x}\le \mathrm{d}\\ 2{\left({\displaystyle \frac{\mathrm{x}-\mathrm{d}}{\mathrm{d}-\mathrm{c}}}\right)}^2,& {\displaystyle \frac{\mathrm{c}+\mathrm{d}}{2}}\le \mathrm{x}\le \mathrm{d}\\ 0,& \mathrm{x}\ge \mathrm{b}\end{array}\right.$$

(4)

$${\mathsf{\mu }}_{\mathrm{s}\mathrm{m}\mathrm{f}}\left(\mathrm{x};\mathrm{a},\mathrm{b}\right)=\left\{\begin{array}{cc}0,& \mathrm{x}\le \mathrm{a}\\ 2{\left({\displaystyle \frac{\mathrm{x}-\mathrm{a}}{\mathrm{b}-\mathrm{a}}}\right)}^2,& \mathrm{a}\le \mathrm{x}\le {\displaystyle \frac{\mathrm{a}+\mathrm{b}}{2}}\\ 1-2{\left({\displaystyle \frac{\mathrm{x}-\mathrm{b}}{\mathrm{b}-\mathrm{a}}}\right)}^2,& {\displaystyle \frac{\mathrm{a}+\mathrm{b}}{2}}\le \mathrm{x}\le \mathrm{b}\\ 1,& \mathrm{x}\ge \mathrm{b}\end{array}\right.$$

(5)

To accurately capture transitions between linguistic categories, three types of membership functions are used—Z-shaped (zmf), Pi-shaped (pimf), and S-shaped (smf)—defined by Equations (3)–(5). The Z-shaped function models the lowest range, the Pi-shaped function covers intermediate transitions, and the S-shaped function addresses the highest range of each variable.

Table 1. Classification of Hydraulic Performance using fuzzy membership functions.

Linguistic Variable	Category	Range	Fuzzy Set
Very Poor	0.00–0.30	zmf	a = 0.0, b = 0.3
Poor	0.10–0.50	pimf	a = 0.1, b = 0.3, c = 0.3, d = 0.5
Fair	0.30–0.70	pimf	a = 0.3, b = 0.5, c = 0.5, d = 0.7
Good	0.50–0.90	pimf	a = 0.5, b = 0.7, c = 0.7, d = 0.9
Excellent	0.70–1.00	smf	a = 0.7, b = 1.0

,

Table 2. Classification of Technical Condition using fuzzy membership functions.

Linguistic Variable	Category	Range	Fuzzy Set
Very Poor	0.00–0.30	zmf	a = 0.0, b = 0.3
Poor	0.10–0.50	pimf	a = 0.1, b = 0.3, c = 0.3, d = 0.5
Fair	0.30–0.70	pimf	a = 0.3, b = 0.5, c = 0.5, d = 0.7
Good	0.50–0.90	pimf	a = 0.5, b = 0.7, c = 0.7, d = 0.9
Excellent	0.70–1.00	smf	a = 0.7, b = 1.0

,

Table 3. Classification of Operational Condition using fuzzy membership functions.

Linguistic Variable	Category	Range	Fuzzy Set
Very Low	0.00–0.30	zmf	a = 0.0, b = 0.3
Low	0.10–0.50	pimf	a = 0.1, b = 0.3, c = 0.3, d = 0.5
Moderate	0.30–0.70	pimf	a = 0.3, b = 0.5, c = 0.5, d = 0.7
High	0.50–0.90	pimf	a = 0.5, b = 0.7, c = 0.7, d = 0.9
Very High	0.70–1.00	smf	a = 0.7, b = 1.0

and

Table 4. Classification of Consequence using fuzzy membership functions.

Linguistic Variable	Category	Range	Fuzzy Set
Immediate Replacement Required	0.00–0.30	zmf	a = 0.0, b = 0.3
Major Rehabilitation Recommended	0.10–0.50	pimf	a = 0.1, b = 0.3, c = 0.3, d = 0.5
Routine Maintenance Required	0.30–0.70	pimf	a = 0.3, b = 0.5, c = 0.5, d = 0.7
System Monitoring Only	0.50–0.90	pimf	a = 0.5, b = 0.7, c = 0.7, d = 0.9
No Action Required	0.70–1.00	smf	a = 0.7, b = 1.0

provide the numeric ranges and parameters for each linguistic categories visualized in Figure 1.

After aggregating the outputs of the activated fuzzy rules, the centroid method (6) is applied to convert the fuzzy output set into a crisp consequence value $\mathrm{C}\in \left[\mathrm{0.00,1.00}\right]$. In Equation (6), ${\mathsf{\mu }}_{\mathrm{i}}$ represents the membership degree of the output at discrete point ${\mathrm{x}}_{\mathrm{i}}$, and ${\mathrm{x}}_{\mathrm{i}}$ denotes the discrete positions across the output domain. The centroid is calculated as the weighted average of these values:

$$\mathrm{C}={\displaystyle \frac{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathsf{\mu }}_{\mathrm{i}}\cdot {\mathrm{x}}_{\mathrm{i}}}{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathsf{\mu }}_{\mathrm{i}}}}$$

(6)

This method ensures stable and interpretable defuzzification, even for asymmetric or overlapping membership functions [29].

2.3. Linguistic Variable Definitions and Their Gradation

The interpretation of linguistic variables is an integral part of the fuzzy inference framework, providing a basis for a systematic evaluation of system performance. The following sections describe each variable, its significance, and the criteria used for its categorization.

Hydraulic Performance is a fundamental variable assessing the efficiency of the stormwater drainage system in managing runoff. It considers the network’s design specifications and the degree of imperviousness in the contributing catchment. A five-tier classification provides a structured evaluation:

• Very Poor: The system is critically overwhelmed due to excessive runoff contributions from highly impervious catchments (>80%). Inadequate channel sizing prevents efficient stormwater conveyance, leading to recurrent urban flooding.
• Poor: The network exhibits limited hydraulic efficiency, frequently encountering surcharges under moderate to high loading conditions. Poor infiltration characteristics exacerbate flow instability.
• Fair: Hydraulic conditions remain generally stable; however, the system is vulnerable to peak discharges, where operational margins are significantly reduced.
• Good: The drainage network effectively accommodates stormwater, with rare instances of hydraulic stress. The system is primarily designed for mixed pervious-impervious catchments.
• Excellent: Hydraulic conditions are optimal, with substantial capacity margins ensuring effective runoff management across a range of hydrological scenarios, including extreme rainfall events.

Technical Condition characterizes the physical state of the drainage network, focusing on structural integrity, material resistance, and long-term durability. The classification follows the criteria established in DWA-A 143-2 [30] and EN 13508-2 [31], which define technical condition based on observed structural degradation. The five linguistic categories are assigned according to these guidelines to ensure consistency with engineering assessments.

• Very Poor: Severe structural damage, with extensive material failure and compromised load-bearing capacity; replacement or major reconstruction is required.
• Poor: Progressive material degradation, including corrosion, partial leaks, or structural weaknesses, requiring targeted reinforcement or repair.
• Fair: Moderate wear with no immediate performance risks, though periodic maintenance and structural assessments are recommended.
• Good: The system remains structurally stable, with minimal material fatigue, supporting reliable long-term operation.
• Excellent: The infrastructure is in pristine condition, either recently constructed or well-preserved, with no detectable structural defects.

Operational Condition describes the functional state of the drainage system, considering usage intensity, maintenance frequency, and failure risk. The classification of this variable was developed based on the criteria outlined in Maintenance of Drainage Features for Safety [31], Drainage System Condition Assessment [32], and EN 13508-2 [31].

• Very Low: Minimal usage with negligible hydraulic load; operational failures are highly unlikely, and maintenance requirements are virtually nonexistent.
• Low: Limited system utilization, requiring only occasional minor maintenance interventions; operational risk remains low.
• Moderate: The system undergoes moderate stress due to routine loading; planned maintenance is necessary to sustain reliability, particularly during peak events.
• High: Intensive usage and a large number of connections contribute to frequent performance challenges; maintenance activities are more frequent to mitigate failure risks.
• Very High: The system operates at or beyond its design capacity, leading to increased maintenance needs and a heightened risk of critical operational failures.

The Consequence variable provides a structured approach to determining necessary maintenance actions, ensuring system longevity and efficiency. It classifies intervention needs as follows:

• Immediate Replacement Required: The system has suffered severe structural or functional failure, requiring immediate intervention to avoid service disruption.
• Major Rehabilitation Recommended: Extensive repair and reinforcement efforts are needed to address significant material or operational deficiencies.
• Routine Maintenance Required: Standard maintenance activities, such as cleaning, inspections, or minor repairs, are necessary to preserve performance.
• System Monitoring Only: The system remains fully functional with minimal risk; monitoring is advised to detect potential long-term wear.
• No Action Required: The drainage network is in excellent condition, requiring no maintenance at this time.

2.4. Fuzzy System Rules

The fuzzy controller is defined using a set of inference rules designed to evaluate the operational status of the stormwater drainage system. These rules integrate the three input variables—Hydraulic Performance, Technical Condition, and Operational Condition—to determine the appropriate consequence category. Given the number of possible input combinations, a total of 125 rules were formulated. Each rule follows a structured form:

IF (Hydraulic Performance is X) AND (Technical Condition is Y) AND (Operational Condition is Z) THEN (Consequence is W),

where X, Y, and Z correspond to the five linguistic categories assigned to each input variable, and W represents the recommended action.

A general pattern emerges across the rules:

Severely degraded hydraulic performance (Very Poor) combined with low technical and operational conditions results in the most urgent intervention (Immediate Replacement Required). Moderate system conditions typically correspond to Routine Maintenance or Monitoring Only, depending on the interactions of the three input variables. A system in excellent condition with well-functioning operational parameters is classified under No Action Required. A subset of the inference rules illustrating this decision-making process is summarized in

Table 5. Representative fuzzy inference rules for consequence classification.

Hydraulic Performance	Technical Condition	Operational Condition	Consequence
Very Poor	Very Poor	Very Low	Immediate Replacement
Very Poor	Poor	Low	Major Rehabilitation
Poor	Poor	Moderate	Routine Maintenance
Fair	Fair	High	Monitoring Only
Excellent	Excellent	Very High	No Action

. The complete set of 125 rules follows the same structured approach.

To visualize the decision space created by these fuzzy rules, the response surface of the system is presented in Figure 2, illustrating the impact of varying input conditions on the recommended consequences.

2.5. Real-World Input Dataset for System Validation

The proposed fuzzy logic model was validated using two independent datasets derived from empirical studies of stormwater drainage systems. These datasets, obtained from distinct geographical and operational contexts, provide complementary perspectives on system performance and failure mechanisms. While both datasets were harmonized into a unified template for consistency (

Table 6. Results of the classification performed with the fuzzy system.

System ID	Geological Hazards	Anthropogenic Damage	Roadworks Impact	Ground Load Impact	Pipe Age (Years)	Material	Diameter (mm)	Installation Depth (m)
System 1	Sporadic	High	Near pipeline	Moderate	30–40	Concrete	600	>2.5
System 2	None	Sporadic	Distant	Low	10–20	Stoneware	150	2.0–2.5
System 3	Sporadic	Sporadic	Affects pipeline	High	20–30	Concrete	600	>2.5

and

Table 7. Summary of the real-world dataset used for system validation.

System ID	Geological Hazards	Anthropogenic Damage	Roadworks Impact	Ground Load Impact	Pipe Age (Years)	Pipe Material	Pipe Diameter (mm)	Installation Depth (m)
System 4	Sporadic	High	Near pipeline	Moderate	30–40	Concrete	300–500	1.5–2.0
System 5	None	Sporadic	Distant	Low	10–20	Reinforced Concrete	>1000	2.0–2.5
System 6	Sporadic	Sporadic	Affects pipeline	High	20–30	Concrete	500–800	2.0–2.5
System 7	None	None	Distant	Low	10–20	Reinforced Concrete	>1000	>2.5
System 8	None	None	Distant	High	20–30	Concrete	500–800	>2.5

Notes: Although the datasets differ in scope—Dataset 1 emphasizes structural integrity, while Dataset 2 highlights operational and environmental stressors—their integration enables a holistic assessment of the fuzzy logic model.

), their distinct origins ensure a robust evaluation of the model’s generalizability.

The first dataset originates from a technical evaluation by Gawrylak and Kowalska [33], focusing on stormwater drainage infrastructure in European urban environments. This dataset comprises detailed inspections of pipeline segments, documenting structural defects such as longitudinal cracks, root intrusions, joint displacements, and leakage patterns. Each segment was classified according to the DWA-A 143-2 standard [30], with parameters including pipe age (10–40 years), material (concrete, vitrified clay), diameter (150–600 mm), and installation depth (>2.5 m). The dataset emphasizes structural degradation and its impact on hydraulic efficiency, with observed defects directly linked to maintenance urgency. For instance, older concrete pipes (30–40 years) in System 1 exhibited moderate ground load impacts and high anthropogenic damage, while newer stoneware pipes in System 2 showed sporadic defects under low stress conditions (Table 6).

The second dataset, derived from a study of drainage networks in central China [21], incorporates broader operational and external risk factors. This dataset evaluates five systems with diverse attributes, including pipe diameters (DN300 to >DN1000), installation depths (1.5–2.5 m), and hydraulic parameters such as pump capacities (10–80 m³/s) and sediment concentrations (<20 to >100 mg/L). Unique to this dataset are variables like geological hazards, roadwork proximity, and retention tank storage (500–2000 m³), which influence long-term failure risks. For example, System 3, exposed to high ground loads and active roadworks, contrasts with System 4, which operates under minimal external stress due to its depth (>2.5 m) and reinforced concrete construction (Table 7).

3. Results

3.1. Input Data Processing

The fuzzy logic controller was evaluated using the datasets described in Section 2.5 (Table 6 and Table 7). Input variables—Hydraulic Performance (HP), Technical Condition (TC), and Operational Condition (OC)—were fuzzified according to the membership functions in Equations (3)–(5). Representative input values for selected systems are provided below in

Table 8. Input data processing.

System ID	HP	TC	OC	Rationale (Based on Section 2.5 Data)
System 1	poor (0.15)	very_poor (0.12)	low (0.35)	High anthropogenic damage; moderate ground load; poor hydraulic efficiency due to aged concrete pipes.
System 2	very_poor (0.10)	good (0.65)	low (0.30)	New stoneware pipes; low stress conditions; good structural integrity but limited hydraulic load.
System 3	fair (0.50)	very_poor (0.09)	low (0.25)	Sporadic defects; high ground load; moderate hydraulic and technical performance.
System 4	poor (0.25)	very_poor (0.10)	high (0.70)	Near roadworks; moderate ground load; degraded hydraulic performance due to pipe age (30–40 years).
System 5	good (0.90)	excellent (0.95)	low (0.20)	Reinforced concrete; minimal external stress; excellent technical and hydraulic condition.
System 6	fair (0.50)	fair (0.55)	high (0.75)	Active roadworks impact; high sediment concentration; moderate hydraulic stress.
System 7	excellent (0.85)	excellent (0.90)	low (0.10)	Deep installation (>2.5 m); pristine reinforced concrete; negligible operational risk.
System 8	poor (0.35)	fair (0.40)	low (0.20)	High ground load; older concrete pipes; significant operational stress.

.

3.2. Fuzzy Rule Activation and Aggregation

The Mamdani fuzzy inference system processed input data through 125 predefined rules, with 8 rules activated (6.4% of the total rule base) for the analyzed systems. The consequence values (defuzzified outputs) were calculated using the centroid method (Equation (6)) and mapped to maintenance categories. Figure 3 illustrates the aggregation process for two representative systems, while

Table 9. Activated Rules and Their Weights.

System ID	Rule ID	Consequence	Consequence Category	Reference Category
System 1	27	0.13	immediate replacement	immediate replacement
System 2	17	0.30	major rehabilitation	major rehabilitation
System 3	52	0.09	immediate replacement	immediate replacement
System 4	29	0.09	immediate replacement	immediate replacement
System 5	97	0.90	no action	monitoring only
System 6	64	0.53	routine maintenance	routine maintenance
System 7	122	0.84	no action	no action
System 8	37	0.33	major rehabilitation	major rehabilitation

compares predictions against expert-assigned reference categories.

3.3. Model Validation and Comparison with Expert Assessments

The fuzzy model’s predictive performance was evaluated by comparing its outputs against expert-assigned maintenance categories. For each of the eight systems included in this validation, a crisp maintenance recommendation was obtained from the model (Section 3.2) and then matched to the expert classification.

In terms of quantitative metrics, the model achieved an overall accuracy of 87.5%, indicating that 7 out of 8 systems matched the expert-assigned categories. Additionally, Cohen’s Kappa Coefficient was 0.82, signaling near-perfect agreement according to the scale proposed by Landis and Koch [34].

Key observations from the validation process revealed both aligned cases and a notable discrepancy. Systems 1, 3, and 7 exhibited perfect agreement with expert recommendations, illustrating the model’s capacity to handle severely degraded networks (e.g., System 1 with HP < 0.20) as well as well-preserved infrastructure (e.g., System 7 with TC > 0.85). The primary mismatch occurred in System 5, where the fuzzy model recommended “no action” (Consequence = 0.90) instead of “monitoring only.” On closer inspection, the high technical condition rating (TC = 0.95) outweighed the low operational stress (OC = 0.20) in the rule activation process, thus emphasizing structural integrity over minor operational concerns.

3.4. Sensitivity Analysis and Robustness of the Fuzzy Inference System

A sensitivity analysis was carried out to assess the robustness of the fuzzy model under various perturbations. Three main areas were investigated: sensitivity to input variable fluctuations, stability of the defuzzification process, and robustness of membership function parameters.

In terms of input sensitivity, the analysis revealed that Hydraulic Performance and Technical Condition were the dominant variables, accounting for over 70% of the variance in the defuzzified consequence values. For example, reducing the Hydraulic Performance of System 6 by 10% shifted its consequence output from 0.53 (indicating “routine maintenance”) to approximately 0.51. In contrast, Operational Condition exerted a comparatively weaker influence; changes of ±15% in Operational Condition resulted in fluctuations of less than ±5% in the final consequence output.

The stability of the defuzzification process was evaluated next. The centroid method (6) consistently produced stable outcomes, even when there was overlap between membership functions (for example, at the boundary between “fair” and “poor”). In one instance, subjecting System 2’s inputs to ±20% random noise led to a maximum deviation of only ±0.03 in its consequence value.

Furthermore, the robustness of the membership function parameters was tested by adjusting the parameters of the Z-shaped and S-shaped membership functions (3)–(5) by ±20%. These adjustments yielded minimal changes—less than 5%—in the defuzzified outputs. As an illustration, increasing the slope parameter of the smf from 10 to 12 in System 1 modified the final consequence value only slightly, from 0.13 to 0.14.

4. Discussion

The fuzzy inference system offers a systematic, transparent, and computationally efficient method for translating a range of structural, hydraulic, and operational indicators into actionable maintenance recommendations. Its high agreement with expert assessments and demonstrated resilience to parameter and measurement variations make it a promising tool for utility managers and engineers seeking to optimize stormwater infrastructure maintenance. The results presented in Section 3 demonstrate the viability and robustness of the proposed fuzzy inference system for evaluating the operational status of stormwater drainage networks. By integrating Hydraulic Performance, Technical Condition, and Operational Condition into a single decision-support framework, the model addresses a key challenge in water infrastructure management: the uncertainty inherent in real-world conditions.

The overall accuracy of 87.5% (Section 3.3), indicating that the fuzzy system’s recommendations match expert judgments for the majority of tested systems. Moreover, the Cohen’s Kappa Coefficient of 0.82 suggests near-perfect agreement, underscoring that the system is not merely capturing random alignments but is methodically convergent with expert assessments. These findings are particularly encouraging given the diverse sources of data, which originated from different geographical locations and covered varying degrees of structural and operational stressors.

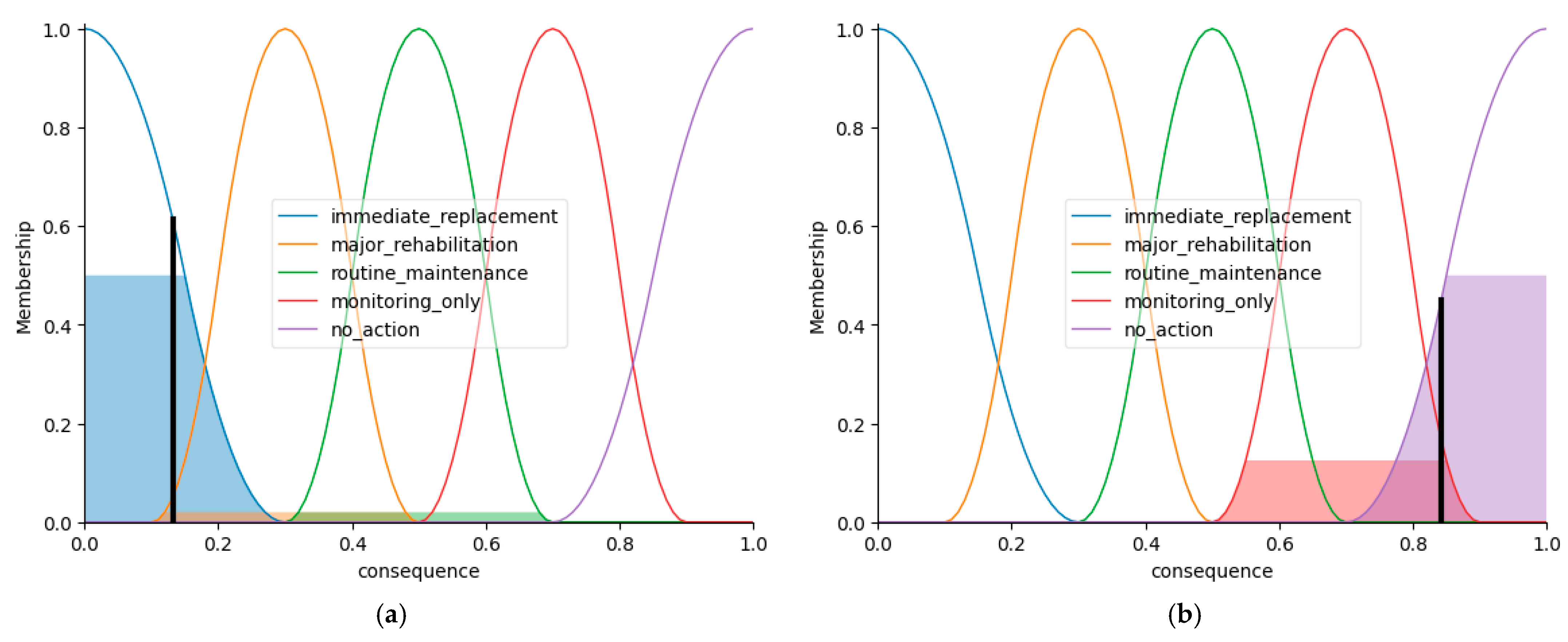
The mismatch observed in System 5 (Consequence = 0.90, indicating “no action,” compared to the expert’s “monitoring only”) highlights an important consideration in fuzzy logic modeling: the influence of dominant variables on final outputs. As revealed by the sensitivity analysis (Section 3.4), the high Technical Condition rating effectively overshadowed the relatively low Operational Condition. This underscores the need for careful calibration of membership functions and weighting factors, ensuring that crucial yet lower-rated variables (such as Operational Condition in this case) still have an appropriate impact on the aggregated result. One potential refinement could involve modifying the existing fuzzy rules to better capture interactions between variables, ensuring that operational deficiencies are appropriately reflected in the consequence assessment. Additionally, adjusting the shape of membership functions could further balance the influence of each variable, preventing cases where near-perfect structural integrity completely masks minor.

Another insight from the sensitivity analysis is the role of Hydraulic Performance and Technical Condition, which together contribute to over 70% of the output variability. In practical terms, this means that accurately monitoring and updating these two parameters can substantially improve the reliability of fuzzy-based maintenance recommendations. Nevertheless, the operational dimension still holds relevance, especially in scenarios with moderate to high hydraulic loads, frequent roadworks, or heavy sedimentation. Consequently, system operators are encouraged to maintain accurate records on both structural and operational parameters to make the most of the fuzzy inference framework.

The stability of the defuzzification process is another advantage for real-world applications. As demonstrated, even significant input noise (±20%) yielded only minor deviations (±0.03 in the worst case) in consequence values (e.g., System 2). Additionally, variations in membership function parameters (±20% in the Z-shaped and S-shaped functions) did not destabilize the system outputs, affirming that the method can accommodate measurement imprecision or unexpected environmental fluctuations. This robustness is valuable in field operations, where sensors can occasionally introduce errors and where changing conditions (e.g., new construction, urban development, or climate patterns) are inevitable.

The use of the proposed fuzzy logic framework for stormwater drainage infrastructure assessment also raises important considerations regarding data privacy, expert bias, and equitable resource allocation. The fuzzy logic controller operates locally, processing data without external transmission or storage, ensuring that sensitive information remains protected. The datasets used for validation were anonymized and aggregated, eliminating risks of exposing personal or infrastructure-specific details. Additionally, the system’s reliance on expert knowledge introduces the potential for bias, as experts may inadvertently reflect their regional experiences or technical specializations in the rules. To mitigate this, the model was developed using a combination of expert input and established technical standards (Section 2.3) and validated across diverse datasets to ensure robustness against regional biases. The response surface analysis (Figure 2) further confirms the absence of dead zones or skewed outcomes, demonstrating the model’s balanced behavior across a range of scenarios.

Future research may focus on multi-objective optimization techniques to balance economic, environmental, and social considerations in stormwater infrastructure decision-making. Moreover, expanding the dataset to include additional regions or integrating real-time sensor data would provide further validation and enhance the model’s adaptability. While the framework focuses on technical assessments, its recommendations can influence resource allocation decisions that affect urban communities. To ensure equitable outcomes, the application of the fuzzy logic controller should be complemented by socio-economic analyses, particularly in cases where maintenance prioritization could disproportionately impact less affluent neighborhoods. Transparency is also critical; the rule-based structure ensures that every recommendation can be traced back to specific inference rules, fostering trust among stakeholders. By documenting and making the complete set of 125 inference rules publicly available, the system enables stakeholders to review and adapt the rules to local contexts, further enhancing accountability.

5. Conclusions

The proposed fuzzy inference system offers a robust decision-support ability for stormwater infrastructure management. By integrating Hydraulic Performance, Technical Condition, and Operational Condition into a unified framework, the model effectively addresses the inherent uncertainty and complexity of real-world conditions. Its high accuracy, resilience to parameter variations, and ability to accommodate diverse datasets make it a valuable resource for utility managers and engineers.

By integrating the fuzzy logic controller into existing hydraulic modeling software, municipalities can improve their ability to identify pipelines requiring closer inspection or rehabilitation. This, in turn, facilitates optimized maintenance schedules, more effective allocation of limited budgets, and reduced risks of urban flooding. The system’s transparency and rule-based structure further ensure that recommendations are clear and actionable, fostering trust among stakeholders.

Future research should prioritize expanding the dataset to include additional regions and integrating real-time sensor data to further validate and enhance the model’s adaptability. Multi-objective optimization techniques could also be explored to balance economic, environmental, and social considerations in stormwater infrastructure decision-making. Addressing these areas will allow the fuzzy inference system to evolve into a more comprehensive decision-support platform, helping municipalities navigate the growing challenges of urban water management.

Moreover, the application of the system must also address critical considerations such as data privacy, expert biases, and equitable access. By ensuring that the controller operates locally, protecting sensitive data, and mitigating potential biases in expert-derived rules, the fuzzy logic framework can serve as a fair and effective ability for urban infrastructure management. Its role as a decision-support system, rather than a definitive decision-maker, highlights the importance of integrating technical outputs with broader social and environmental analyses to achieve sustainable and equitable outcomes.