Impact of the Reynolds Numbers on the Velocity of Floating Microplastics in Open Channels

Abstract

Quantitatively analyzing the factors influencing the horizontal migration of microplastics (MPs) in water bodies and understanding their movement patterns are crucial for explaining and predicting their transport principles and final destinations. This study used nearly spherical polyethylene (PE), polypropylene (PP), and polystyrene (PS) MPs as experimental subjects. By tracking their motion characteristics through video recording, we established relationships among the Reynolds number (Re), MP density, and floating velocity. The results showed that the Re and MP density jointly affect the horizontal drift of MPs. The horizontal floating velocity of MPs significantly increases with the increase in the Re and shows a power function growth trend. The difference in density of MPs mainly affects their dispersion during the floating process. Moreover, the coefficient of variation (CV) of PP’s horizontal floating velocity increased with the Re, suggesting PP’s motion is more random and discrete than that of PE and PS. Ultimately, we fitted the horizontal floating velocity of MPs to the equation to comprehensively evaluate the relationship between the floating velocity, Re, and density of MPs. This analysis underscores that the Re predominantly influences the MP velocity in water, while the MP density chiefly impacts the discrete nature of their motion.

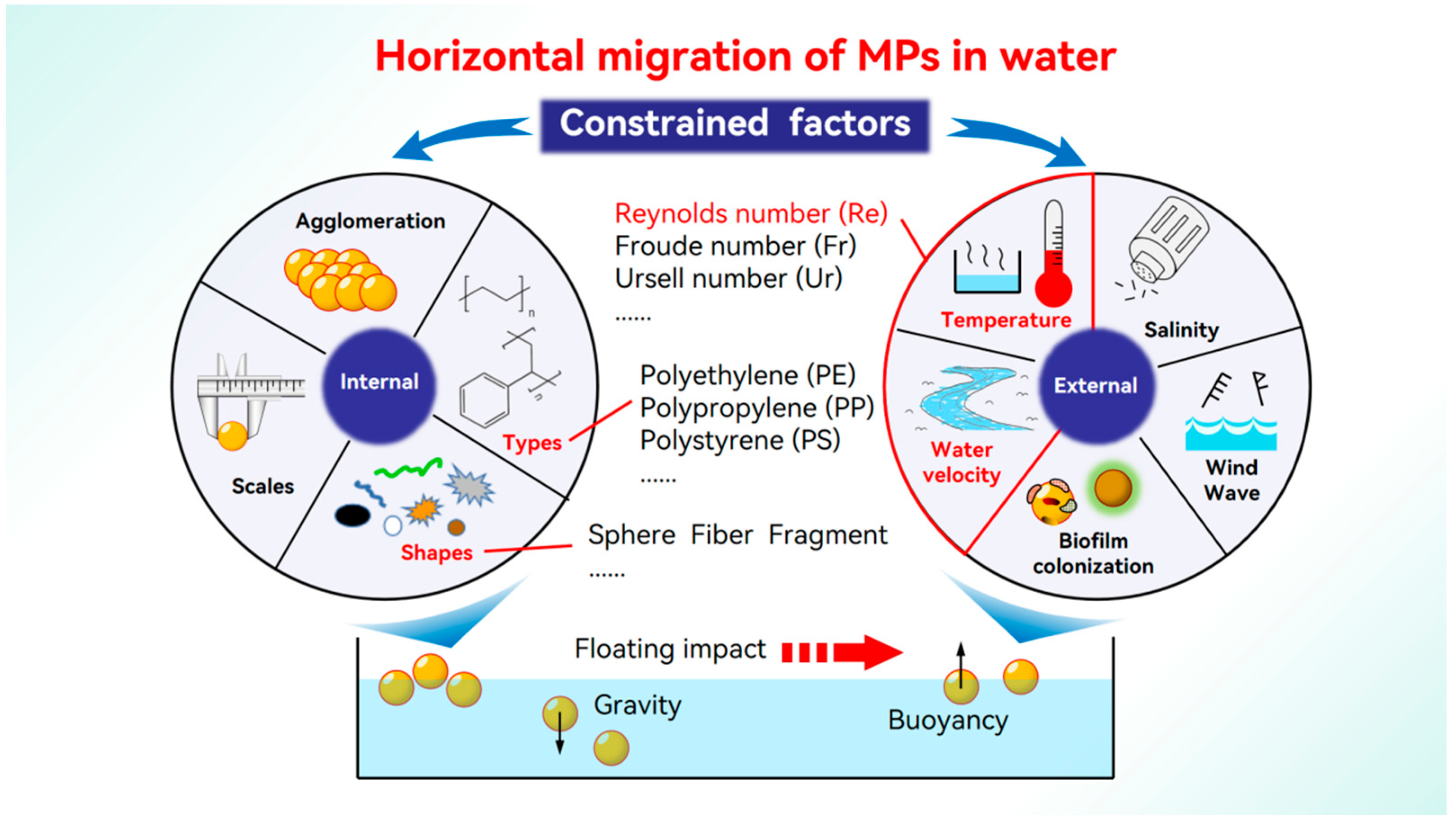
1. Introduction

As polymer organic compounds, plastics offer advantages such as their light weight, corrosion resistance, and effective insulation properties [1]. They are extensively utilized in human production and daily life. Global plastic production is projected to reach 400.3 million tons in 2023 [2] and is expected to rise to 1.2 billion tons by 2050 [3,4]. Despite the convenience they bring, the disposal of plastics has emerged as a significant issue. Nevertheless, the improper disposal of plastic waste allows some of it to enter the aquatic environment with precipitation, runoff, and sewage discharges, leading to severe water pollution [5]. Upon entering water bodies, microplastics (MPs) can adversely affect the natural environment, including aquatic plants and animals [6]. Upon ingestion by plankton, MPs can enter the human food chain, posing severe risk [7]. Furthermore, MPs are found not only in natural aquatic environments but also in everyday consumables like bottled mineral water, as well as in industrial and domestic pipelines [8]. As a result, MPs gradually enter the human body and damage human organs [9].

Due to differences in the shape and density of MPs, their retention in the water column also differs. Some MPs settle on riverbeds due to gravity, while others move along water currents, overcoming friction [10]. In estuaries that flow into lakes and oceans, MPs undergo rapid diffusion influenced by changes in the flow dynamics. Liu et al. investigated the distribution patterns of the horizontal and vertical transport of MPs in Lake Ulansuhai’s water column [11]. Variations in flow conditions at different locations led to varying MP concentrations. The movement of MPs follows a three-dimensional model characterized by vertical settling and horizontal migration [12]. Despite considering flow velocity vectors and MP characteristics (density, volume, shape), hydrodynamic conditions and MP characteristics were not quantitatively analyzed. For example, turbulence significantly impacts MPs’ migration [13]. Stride et al. analyzed the migration path of polyethylene (PE) MPs in containers, finding that under overflowing conditions from manholes, most PE followed the path of solutes, with a portion being retained on the surface or in dead zones near manhole inlets [14]. Isachenko and Chubarenko [10] conducted indoor flume experiments and demonstrated how abrupt changes in roughness affect particle movement from stagnation and MP deposition on channel bottoms, influenced by physical bottom properties. Larsen et al. estimated the Lagrangian particle transport velocity by analyzing the average stranding time of MP particles released at various coastal locations [15].

Water temperature is also a key factor influencing the migration and accumulation of MPs. Thermal stratification in lake water and changes in water temperature can affect the water’s kinematic viscosity, which in turn alters the Reynolds number (Re) and the behavior of particles [16]. Ahmadi et al. found that the settling of MPs in cold water is relatively slower [17]. When the temperature decreased from 20 °C to 10 °C and 4 °C, the TSV of MPs decreased by an average of 32% to 46%. Nakayama and Osako evaluated the spatiotemporal dynamics of MPs in a watershed by developing an ecological hydrological model [18]. Their research revealed that water temperature significantly influences the transport of MPs. Liu et al. developed a regression model using seawater temperature, salinity, and flow rate as independent variables [19]. Changes in water temperature can influence the formation of a biofilm on the surface of MP particles. Zhang et al. observed that biofilm colonization on MPs occurs more rapidly during the high temperatures of summer, which also affects their movement [20].

In recent years, research on MP pollution in water bodies has grown and advanced significantly. However, the fate of MPs remains poorly understood, and the impact of different hydrodynamic conditions on their migration process is still not fully clear [21,22,23]. Most existing studies examine the movement of MPs by treating flow velocity, water temperature, and other conditions as separate variables. However, further research is crucial to understand how hydrodynamic conditions influence the horizontal movement of MPs. Such insights are essential for accurately assessing MP pollution levels and safety risks in river ecosystems, as well as for predicting the migration, capture, and removal dynamics of MPs in natural aquatic environments. The horizontal movement of MPs is primarily driven by two factors: external influences and internal attributes. The Re, which combines dynamic viscosity (related to water temperature), flow velocity, and characteristic size (as external factors), is a key variable for quantifying changes in fluid flow patterns. Therefore, this study first uses the Re as a starting point, simplifying complex hydrodynamic conditions into a single parameter. Secondly, this study mainly considers the type (density) of MPs as a typical internal factor (Figure 1). The three types of plastics, polyethylene (PE), polypropylene (PP), and polystyrene (PS), have a wide range of applications in daily life and industrial production, these plastics are prevalent in the marine environment in the form of MPs and are the most representative in the study of MP pollution in water bodies [24,25]. Although PVC and PT are also plastic polymers with significant global production and waste volumes, these MPs have high specific gravity and quickly settle during the experimental process. The results would be hard to observe and measure in this study. The morphology and size of MPs hosted in different water body regions differ somewhat. The migration of spherical MPs is easier to study than other shapes, and most MP sizes are between 100 and 5000 μm in marine and river basins [26,27]. Therefore, PE, PP, and PS particles characterized as shown in

Table 1. MP selection.

MPs	Shapes	Density (g·cm–3)
Polyethylene (PE)	Approximate spherical shape	0.941
Polypropylene (PP)		0.908
Polystyrene (PS)		1.010

, which are white, nearly spherical, and have a particle size of approximately 950–1090 μm, were used in this study. These MPs are easier to identify during the experimental process.

Given the importance and complexity of MPs in water bodies, this study was conducted using indoor water tank experiments to simulate natural hydrodynamic conditions by varying the Re. The motion dynamics of MPs were tracked using green-light-source reflection and video recording technology. By integrating internal and external factors influencing MPs’ horizontal migration, the horizontal floating velocity of MPs was incorporated into an equation to comprehensively analyze the relationship between floating velocity, the Re, and MP density. This study investigates the combined effects of MP density (type) and channel Re changes on the horizontal floating velocity of MPs, aiming to provide a theoretical foundation and methodological framework for understanding MPs’ migration behavior in real-world water environments.

2. Materials and Methods

2.1. Experimental Setup

In this study, a rectangular cross-section flume was used for the experiments. The experimental section for MPs’ movement was approximately 3.33 m in length, 0.12 m in width, and 0.30 m in height (Figure 2a). Cleaning and a water change were required before the experiment took place and water was transferred to the tank by a submersible pump at ground level to ensure a constant head water supply, after which the flume was returned to form a closed-loop water supply and drainage system. The water on the other side passed through a double freedom diaphragm valve and an effluent master valve, which was used to control the flow rate precisely, and then entered the experimental flume. The upstream flume was equipped with a perforated pipe and deflector to stabilize the water flow, and the downstream flume was equipped with a thermometer. The bottom of the flume was lined with a layer of quartz sand with a slope of i = 0.0015 to simulate the roughness of the channel. A 200-mesh sieve was installed on the floor tank to intercept particles and MPs during the experiment (Figure 2b,c).

2.2. Hydraulic Characteristics

The flow rate of the flume was determined via the volume flow method. At the beginning of the measurement, the diaphragm valve was adjusted to the appropriate position, and the master valve was opened. At the end of a single measurement, only the master valve was closed, and the diaphragm valve was kept at a fixed value. The above measurements were repeated, and the flow rate in the flume under different working conditions, average flow rate of the cross-section Q, water depth h, average velocity of water flow V_w, and Re were calculated. Finally, the hydraulic characteristics of the flume were statistically determined (

Table 2. Working condition settings.

No.	Q (L·s−1)	H (m)	Vw (m·s−1)	Re
1	0.0498	0.0070	0.0593	360
2	0.0717	0.0088	0.0683	509
3	0.0850	0.0095	0.0746	597
4	0.1291	0.0110	0.0978	888
5	0.1604	0.0126	0.1065	1079
6	0.2134	0.0150	0.1186	1389
7	0.2556	0.0165	0.1291	1631
8	0.3063	0.0180	0.1418	1917
9	0.3420	0.0190	0.1500	2114
10	0.3788	0.0200	0.1578	2312
11	0.4404	0.0217	0.1691	2632
12	0.4744	0.0226	0.1749	2804
13	0.5245	0.0240	0.1821	3049
14	0.6141	0.0255	0.2007	3507
15	0.6812	0.0265	0.2142	3845
16	0.7740	0.0289	0.2232	4251
17	0.8604	0.0297	0.2414	4684

). The relevant calculation was carried out using the following mathematical Equations (1)–(4):

$$\mathrm{Q}={\displaystyle \frac{\mathrm{V}}{\mathrm{t}}}$$

(1)

$${\mathrm{V}}_{\mathrm{w}}={\displaystyle \frac{\mathrm{Q}}{\mathrm{A}}}$$

(2)

$$\mathsf{\mu }={\displaystyle \frac{0.001779}{1+0.03368\mathrm{T}+0.000221{·\mathrm{T}}^2}}$$

(3)

$$\mathrm{R}\mathrm{e}={\displaystyle \frac{\mathsf{\rho }{\mathrm{V}}_{\mathrm{w}}\mathrm{R}}{\mathsf{\mu }}}$$

(4)

where, Q (m³·s⁻¹) is the flow rate; V (m³) is the volume of water flow; R (m) is the hydraulic radius; A (m²) is the cross-sectional area; µ (Pa·s) is the coefficient of viscosity of the movement of water; T (°C) is the temperature of the water; ρ is the density of the water (kg·m^–3); V_w (m·s⁻¹) is the average velocity of the water flow; and the Re (dimensionless) is the Reynolds number.

According to the working condition measurements illustrated in Table 2, in the range of Re = 600–3300, the width-to-depth ratio of the channel is greater than or equal to 5 (b/h ≥ 5) in the vast majority of cases, and the wall effect is relatively low.

2.3. Video Tracking

Before starting, we made sure that the water flow had stabilized. About 10 MP particles were placed near the water’s surface. For every experimental run, the actual number of effectively recorded MP particles was within the range of three to eight. After each experiment, the flow rate was changed. Based on the hydraulic characteristics and pre-experimental results, the Re was controlled to between 600 and 3300. During the movement of the MPs, video recording was carried out with a camera with a resolution of 1920 × 1080 and a frame rate of 240 fps. With a wavelength of about 520 nm, a green light source was provided downstream to ensure that the MPs could be clearly recorded in the video (Figure 3). The entire process of MP movement was processed frame by frame by the video processing software DaVinci Resolve, from which the entry and exit moments of each MP were deduced to calculate the horizontal velocity of the MPs.

2.4. Data Processing

The movement time of the MPs was recorded through video footage, and because the default frame rate is 30 fps in DaVinci Resolve 18 by Black Magic (http://www.blackmagicdesign.com/products/davinciresolve), it was necessary to convert the frame rate to 240 fps using Equation (5) to obtain the actual movement time of the MPs (in seconds). Statistical analysis was performed using OriginPro, Version 2024b (Learning Edition) (OriginLab Corporation, Northampton, MA, USA). Combining the Re and the density of different types of MPs (ρ) with the horizontal motion of MPs during the experiment velocity (V_p), the results were curve fitted and surface fitted. The Nash–Sutcliffe efficiency coefficient (NSE), mean absolute percentage error (MAPE), and symmetric mean absolute percentage error (sMAPE) were calculated to determine the goodness of fit of the fitted equations. The magnitude of the error and the form of the equation were taken into account to determine the final MP horizontal floating velocity relation V_p (Re, ρ).

$$Actual total time (\mathrm{s})={\displaystyle \frac{\left(Entry time \right(\mathrm{s})-Terminal time (\mathrm{s}\left)\right)\times 30}{240}}$$

(5)

Since the mean floating velocities of the three MPs varied over the range of Re = 600–3300, it would be inaccurate to use the standard error to characterize the degree of dispersion of the MPs’ motion. Therefore, the coefficient of variation (CV) was used to represent the degree of dispersion of the data in Equation (6). The larger the coefficient of variation is, the greater the dispersion of the data.

$$\mathrm{C}\mathrm{V}={\displaystyle \frac{\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{d} \mathrm{D}\mathrm{e}\mathrm{v}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \left(\mathrm{S}\mathrm{D}\right)}{\mathrm{A}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{c} \mathrm{M}\mathrm{e}\mathrm{a}\mathrm{n} \left(\overline{\mathrm{A}}\right)}}={\displaystyle \frac{\sqrt{{\sum }_{\mathrm{t}=1}^{\mathrm{N}}\frac{({\mathrm{A}}_{\mathrm{t}}-\overline{\mathrm{A}}{)}^2}{\mathrm{N}}}}{\overline{\mathrm{A}}}}\times 100\mathrm{\%}$$

(6)

The Nash efficiency coefficient (NSE) is commonly used to verify the accuracy of the simulation results of hydrological models [28]. The NSE ranges from –∞ to 1 Equation (7). The closer the NSE is to 1, the more credible the model is and the better the fit is. The NSE is close to 0, which indicates that the model is generally credible when the process simulation error is large. If the NSE is much less than 0, the model is unrealistic.

$$\mathrm{N}\mathrm{S}\mathrm{E}=1-{\displaystyle \frac{{\sum }_{\mathrm{t}=1}^{\mathrm{N}}({\mathrm{A}}_{\mathrm{t}}-{\mathrm{F}}_{\mathrm{t}}{)}^2}{{\sum }_{\mathrm{t}=1}^{\mathrm{N}}({\mathrm{A}}_{\mathrm{t}} - \overline{\mathrm{A}}{)}^2}}, \mathrm{N}\mathrm{S}\mathrm{E}\in (-\mathrm{\infty }~1]$$

(7)

The mean absolute percentage error (MAPE) is capable of visually representing the magnitude of prediction error in the form of a percentage, which makes it easy to compare the prediction accuracy of different models or variables. Moreover, the MAPE is less sensitive to outliers and will not have a conspicuous impact on the overall results due to the existence of individual outliers [29]. The MAPE ranges from 0 to +∞ Equation (8). A MAPE closer to 0 indicates that the accuracy of the fit is higher.

$$\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}={\displaystyle \frac{1}{\mathrm{N}}}·{\sum }_{\mathrm{t}=1}^{\mathrm{N}}{\displaystyle \frac{\left|{\mathrm{A}}_{\mathrm{t}}-{\mathrm{F}}_{\mathrm{t}}\right|}{{\mathrm{A}}_{\mathrm{t}}}}\times 100\mathrm{\%}, \mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}\in [0~+\mathrm{\infty })$$

(8)

The MAPE has a potential drawback in that it does not limit the uncertainty of predictions higher than the actual value. Instead, the symmetric mean absolute percentage error (sMAPE) is a relevant metric that attempts to address this problem [30]. The sMAPE is in the range of 0–200% Equation (9). The closer the sMAPE is to 0, the more accurate the fit is.

$$\mathrm{s}\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}={\displaystyle \frac{1}{\mathrm{N}}}·{\sum }_{\mathrm{t}=1}^{\mathrm{N}}{\displaystyle \frac{\left|{\mathrm{A}}_{\mathrm{t}}-{\mathrm{F}}_{\mathrm{t}}\right|}{({\mathrm{A}}_{\mathrm{t}}+{\mathrm{F}}_{\mathrm{t}})/2}}\times 100\mathrm{\%}, \mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}\in [0~200\mathrm{\%}]$$

(9)

3. Results

3.1. Effect of Different Reynolds Numbers on the Horizontal Floating Velocity of MPs

The experimental results show that the variation in the Re caused by the change in the flow rate of the water tank has a significant effect on the horizontal floating velocity of the floating MPs. The variation in the horizontal floating velocity of different kinds of MPs in the range of Re = 600–3300 is shown in Figure 4. With an increasing Re, the horizontal floating velocities of PE, PP, and PS MPs showed a power-function growth trend. The horizontal floating velocity of PE changed from 0.137 m·s⁻¹ at Re = 614 to 0.333 m·s⁻¹ at Re = 3248, the velocity increased by 143% with an increase in the Re of 429%, and the velocity increased by 143%; the horizontal floating velocity of PP changed from 0.144 m·s⁻¹ at Re = 664 to 0.314 m·s⁻¹ at Re = 3173, which increased by 118% with a 378% increase in the Re; and the horizontal floating velocity of PS changed from 0.145 m·s⁻¹ at Re = 659 to Re = 3184 0.321 m·s⁻¹, a 122% increase in velocity for a 383% increase in the Re.

The difference in the density of MPs results in differences in the discreteness and stability of their movement in water. The CV values of the three MPs vary in the range of 0.3–6.9%, but the rates of change are different (Figure 5). With an increasing Re, the rates of change in the CVs of the three MPs, PE, PP, and PS, are 8.67 × 10^–7, 7.52 × 10^–6, and 2.27 × 10^–6, respectively. The regular pattern presented is k_PP > k_PS > k_PE. These results imply that the rates of change in the CVs is from PE to PS to PP.

3.2. Functional Form, Error Analysis, and Formula Fitting

The variation in the Re will cause turbulent disturbances, and the difference in the density of MPs will affect the discrete nature of their motion. For this reason, surface fitting with the Re and MP density as independent variables and the magnitude of MPs horizontal motion velocity as the dependent variable can more realistically reflect the motion of different kinds of MPs in water. In this study, four functional forms, namely, the primary polynomial, quadratic polynomial, power function, and logarithmic function, were chosen for fitting.

Quadratic polynomials, power functions, and logarithmic functions show better fitting results compared to binary primary polynomials (

Table 3. Functional form and error analysis.

Functional Form: z (x, y)	Fitting Equation: Vp (Re, ρ)	R2	MPs	NSE	MAPE	sMAPE
z =Ax + By + C	${\mathrm{V}}_{\mathrm{p}}=6.77\times {10}^{-5}·\mathrm{R}\mathrm{e}+9.66\times {10}^{-3}·\mathsf{\rho }+0.101$	0.9630	PE	0.9715	3.21%	3.21%
			PP	0.9784	3.05%	3.01%
			PS	0.9713	3.20%	3.18%
z = Ax2 + By2 + Cxy + Dx + Ey + F	${\mathrm{V}}_{\mathrm{p}}=-1.01\times {10}^{-8}·{\mathrm{R}\mathrm{e}}^2+0.13·{\mathsf{\rho }}^2-3.51\times {10}^{-5}\mathrm{R}\mathrm{e}·\mathsf{\rho }$$+1.40\times {10}^{-4}·\mathrm{R}\mathrm{e}-0.179·\mathsf{\rho }+0.135$	0.9714	PE	0.9765	2.59%	2.58%
			PP	0.9841	2.37%	2.35%
			PS	0.9792	2.80%	2.80%
z = A·xB·y+C + D	${\mathrm{V}}_{\mathrm{p}}=6.58\times {10}^{-3}·{\mathrm{R}\mathrm{e}}^{-4.62\times {10}^{-3}·\mathsf{\rho }+0.490}-0.011$	0.9714	PE	0.9771	2.53%	2.52%
			PP	0.9832	2.42%	2.40%
			PS	0.9793	2.79%	2.82%
z = A·lg(Bx + Cy + D) + E	${\mathrm{V}}_{\mathrm{p}}=0.518\mathrm{l}\mathrm{g}(0.030\times \mathrm{R}\mathrm{e}+1.33\times \mathsf{\rho }+42.87)-0.790$	0.9712	PE	0.9769	2.54%	2.53%
			PP	0.9835	2.36%	2.34%
			PS	0.9802	2.75%	2.77%

). Specifically, these three equations exhibit a superior fit for the PE, PP, and PS MPs, with PP > PS > PE in terms of fitting effectiveness. For example, in the case of the binary logarithmic function, the NSE of PE is 0.9769, which is 5.56‰ greater than that of 0.9715 for the binary polynomial fit, and the values of MAPE and sMAPE are 2.54% and 2.53%, which are 20.87% and 21.18% lower than those of 3.21% for the binary logarithmic function fit, respectively; the NSE of PP is 0.9835, which is 5.21‰ greater than that of 0.9784 for the binary logarithmic function fit, the values of MAPE and sMAPE are 2.36% and 2.34%, which are 22.62% and 22.26% lower than those of 3.05% and 3.01%, respectively, for the primary polynomial fit; PS has an NSE of 0.9802, which is an improvement of 9.16‰ compared to 0.9713 for the primary polynomial fit; and the MAPE and sMAPE are 2.75% and 2.77%, which are 14.06% and 12.89% lower than those of 3.20% and 3.18%, respectively. The fitting effects of quadratic polynomials and power functions show a similar pattern, so the fitting method of primary polynomials is rounded off. The equations are complicated due to the presence of higher-order terms (e.g., –1.01 × 10^–8, –4.62 × 10^–3, etc.) in the parameters of quadratic polynomials and power functions, which cannot be overlooked. Despite their complexity, these three types of functions exhibit comparable fitting effects. In contrast, logarithmic fitting shows fewer errors and is less intricate. Hence, the logarithmic function is chosen as the preferred fitting model, providing an approximate expression for the horizontal velocity of MPs motion within the range of Re = 600–3300, considering MP density and the Re as V_p (Re, ρ) = 0.518 lg (0.030×Re + 1.33×ρ + 42.87) − 0.790. Figure 6 depicts the fitted surface based on this function.

4. Discussion

Both the density and Re of MPs collectively impact their floating velocity in water. As the Re increases, indicating higher turbulence energy in the water body, both the transverse flow velocity and the overall velocity sum increase, intensifying fluid pulsation at the liquid surface [31]. These results are approximate to the research findings of He et al. [32]. They found that within the Re range of 2800 to 5600, the average horizontal velocity of PVC and PS particles increased with the increase in the average cross-sectional flow velocity of subcritical flow. The CV changes of PP are somewhat different from those of PE and PS. In the Re range of 600 to 3300, PP exhibits more random and discrete motion, consistent with the findings of Stride et al. [33]. They studied the settling characteristics of polymers with densities ranging from 0.9 to 1.4 g·cm⁻³ and their relationship with the critical horizontal flow velocity in channels. The results indicate that regardless of the horizontal flow velocity of the channel, PP tends to remain trapped on the water’s surface and undergoes horizontal migration without settling or suspending. PP has a lower density than PE and PS, making its motion more significantly influenced by pulsation compared to the higher-density polymers. Moreover, the activity of PP after treatment with surfactant sodium dodecylbenzenesulfonate (CTAB) is higher than that of PS, and its flowability is further increased [34]. PP in CTAB solution exhibits higher stability and a stronger migration ability than other MPs. These studies have shown that PP exhibits the highest horizontal migration rate, likely due to its unique properties, which allow it to move faster horizontally in water compared to other MPs. Notably, in this study, PE and PP, with densities lower than water, floated on the water’s surface, while PS, with a density close to that of water, also drifted on the surface until it travelled downstream. No significant settling or suspending behavior was observed during their migration. Previous studies suggest that the density of PS is nearly identical to that of water, and when combined with its low mass and hydrophobic properties, it is harder to settle. For example, Ahmadi et al. calculated the final settling velocity (TSV) of PS MPs through computational fluid dynamics (CFD) simulations, indicating that hydrophobic PS exhibited a phenomenon of harder to settle [17]. In addition, using the MPs static water settling formula fitted by Kaiser et al., in Equation (10) [35], the calculated static water settling velocity of PS is around 100 μm per second, which is relatively smaller than the channel water depth used in this study.

$$w_s=11.68+0.1991\times ESD+0.0004\times {ESD}^2-0.0993 \times \Delta \rho +0.0002\times \Delta {\rho }^2$$

(10)

where w_s (m·d⁻¹) is the sedimentation velocity; ESD (m) is used to calculate particle size expressed as the equivalent spherical diameter; and Δρ (kg·m⁻³) is the particle density minus fluid density.

Moreover, in this study, the environment where MPs are located is not static water; instead, turbulence generates pulsating velocities in the x, y, and z directions [36,37]. The low settling velocity of MPs during brief intervals is likely offset by the vertical turbulent velocity of the aquatic environments. Moreover, due to the hydrophobic properties of MPs, PS can achieve a certain migration rate in a short period. The conclusions drawn by Stride et al. [33] regarding the buoyancy characteristics of PS are not entirely consistent with the results of this study. They assume that in rivers with a flow velocity of ≥0.101 m·s⁻¹, the majority of spherical polymers with a density of 0.94–1.32 g·cm^–3 will eventually settle in the marine ecosystem. Although the density of PS falls within the aforementioned threshold range, in this study, PS did not show significant sedimentation in water. This can be attributed to two main reasons. Firstly, PS MPs do not settle significantly in a short period. In natural water bodies, the factors influencing PS deposition are more complex. Long-term external influences and the accumulation of vertical velocity ultimately result in PS deposition [33,38]; secondly, Stride et al. conducted experiments using PMMA and PEEK as polymers with a density threshold in the range of 0.94–1.32 g·cm^–3, without considering PS MPs. Therefore, the buoyancy characteristics of PS may be related to its unique molecular structure and require further research and discussion. Hence, for MPs with properties similar to PS, a comprehensive management strategy should be established. Prioritizing the proactive capture and removal of PS MPs before their complete sedimentation is crucial. This approach can prevent their accumulation in benthic sediments as well as potential resuspension. Such sedimentation and resuspension could exacerbate environmental toxicity via complex ecological interactions.

In this study, as a feature number, the Re was combined with the water flow velocity (flow velocity), channel characteristic size, and water temperature as external environmental variables, and MP density as the internal factor to fit a binary equation between these two and the horizontal movement velocity of MPs. Based on previous evidence, changes in water flow patterns caused by environmental factors such as waves and wind also affect the migration of MPs and other light polymers [39]. The quantification of these flow pattern changes will introduce dimensionless numbers other than the Re, such as the Ursell number (Ur) [40]. In addition, the salinity parameters play a crucial role in influencing the migration of MPs. Salinity affects not only the density of water but also its conductivity, which, in turn, impacts the behavior of MPs in water [41]. These environmental factors will increase the variables in the equation, especially when there are more than three independent variables. The visualization level of the equation in the traditional Cartesian coordinate system will decrease. In future studies, it is necessary to consider the internal and external factors affecting MPs’ migration separately. For instance, the wave height and wavelength, which vary uniformly under wind and wave conditions, along with the salinity of the water body, can be considered as external independent variables, while the density changes of MPs following biofilm colonization serve as internal independent variables [42,43]. This will allow for exploring their relationship with the movement speed of MPs, and fitting the actual hydrodynamic conditions of rivers and lakes from shallow to deep.

5. Conclusions

The horizontal velocity of three types of MPs—PE, PP, and PS—exhibited an increasing trend with the Re in the range of 600 to 3300, following a power function. Particularly noteworthy is the increased randomness and dispersion in the motion of PP MPs as the Re increases, whereas the dispersion in the motion of PE and PS MPs shows less dependence on the Re relatively.

Based on the horizontal floating velocity and the Re of MPs, alongside the density data for MPs, this study proposes an approximate expression, Vp (Re, ρ), to describe MPs’ floating velocity in water, which is finally expressed as V_p (Re, ρ) = 0.518 lg (0.030 × Re + 1.33 × ρ + 42.87) − 0.790.

The results showed that the Re influences the movement velocity of MPs in water. The difference in density of MPs mainly affects their dispersion during the floating process. These findings enhance our understanding of MPs’ motion behavior in aquatic environments, offering a valuable scientific foundation for assessing the environmental implications of MP pollution.