Study on Shear Creep Characteristics of Carbonaceous Mud Shale at Different Moisture Contents Under Temperature Cycling

Abstract

Mine slope landslides can lead to significant geological disasters. To investigate the impact of temperature cycling on the internal mechanisms that trigger these disasters in weak interlayers with varying moisture contents, a THMC-B multi-field coupled simulation device was employed to conduct shear creep tests on carbonaceous mud shale with varying moisture contents across 16 temperature cycles (ranging from −5 °C to 65 °C). Based on the observed creep characteristics and related patterns, a rheological constitutive model for carbonaceous mud shale was established to characterize the damage effects at different moisture contents during temperature cycling. The experimental results indicate the following: under temperature cycling conditions, an increase in moisture content rapidly reduces the mechanical properties of carbonaceous mud shale, rendering it more susceptible to shearing at the same failure stress level and consequently shortening the overall creep time; higher moisture content prolongs the duration of the deceleration creep stage in carbonaceous mud shale; and the improved constitutive model accurately represents the entire shear creep process of carbonaceous mud shale, with fitting coefficients exceeding 0.95. These research findings can provide certain references and insights for the study of shear creep characteristics of weak interlayers in mine slopes.

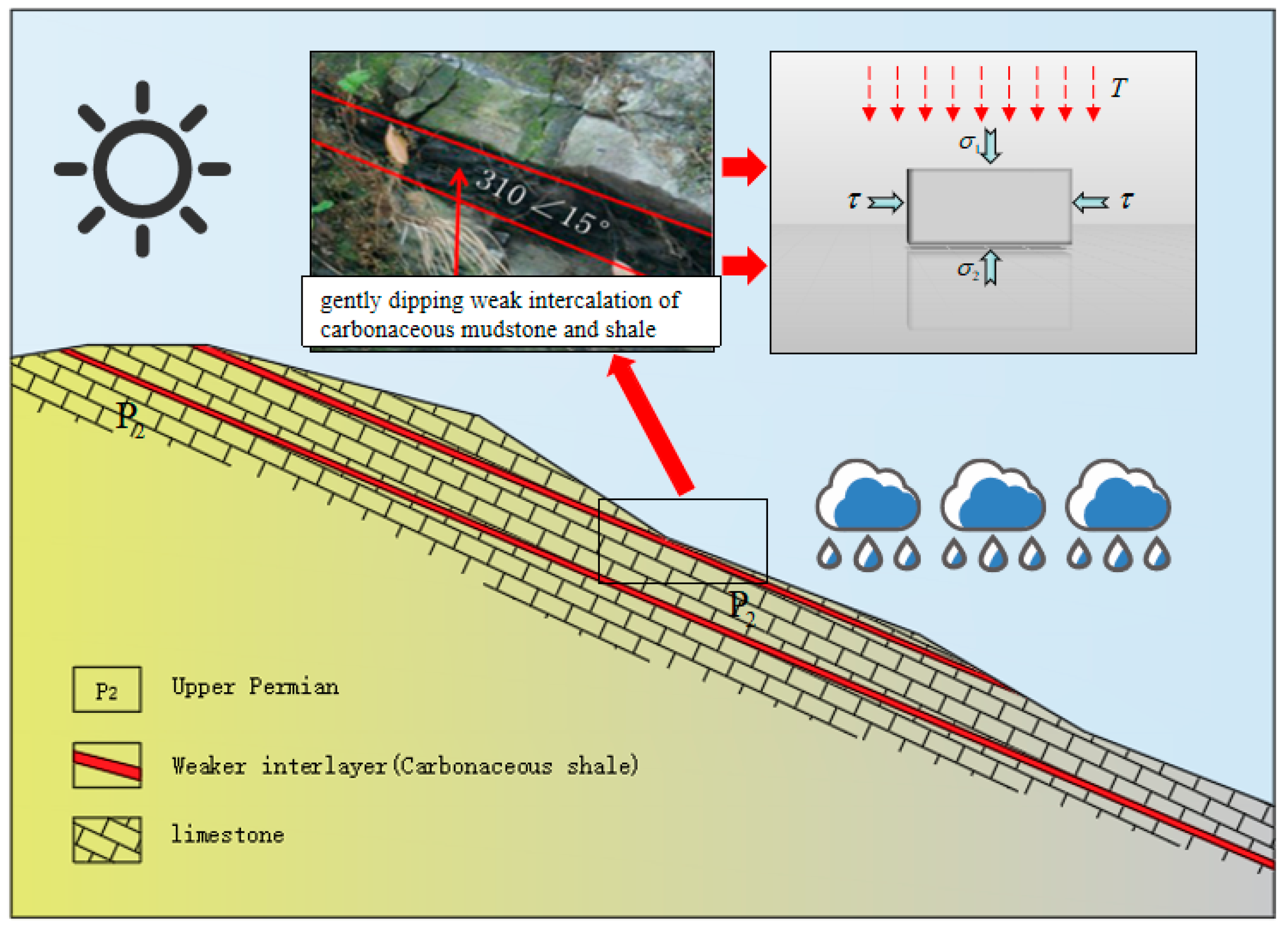
1. Introduction

China possesses abundant mineral resources, particularly high-quality limestone deposits located in the southwestern provinces of Yunnan, Guizhou, and Sichuan [1,2]. These deposits typically display a multi-layered structural grid [3,4], which contributes to the presence of numerous Permian limestone strata characterized by gently dipping weak interlayers [5,6]. This type of weak interlayer is typically composed of mudstone or shale that contains mineral components such as carbonaceous, siliceous, and sandy materials. Its mechanical properties are inadequate, and its rheological effects are quite significant [7]. Furthermore, the long-term impact of complex factors—such as repeated temperature cycles, rainfall infiltration, and chemical influences—on the weak interlayer can lead to instability and landslides in mine slopes, thereby presenting considerable safety hazards for open-pit mining [8], as illustrated in Figure 1, where $T$ represents the temperature effect on the weak interlayer, ${\sigma }_1$ and ${\sigma }_2$ denote the normal stresses, and $\tau$ indicates the shear stress on the weak interlayer. In recent years, numerous scholars have conducted extensive research on the experimental characteristics of shear creep in soft rock. Li et al. [9,10] utilized on-site monitoring, indoor rheological tests, numerical simulations, and theoretical analyses to demonstrate that the wet–dry cycle of rainfall and blasting vibrations significantly deteriorates the rheological characteristics of weak interlayers. Ma et al. [11], based on special engineering of geological conditions of a cut-slope area at the Heitanping hilly pass along the Yongzhou—Jishou highway, have studied the shear creep properties of a weak interlayer in this slope (about 30 m deep) by shear creep test to obtain shear creep curves. A shear creep constitutive model can be obtained by using a stationary parameter fractional derivative Burgers model, and long-term shear strength of the weak interlayer can be determined after the analysis of the shear creep curves. Gao et al. [12] conducted multi-stage shear creep experiments on joints subjected to various wet–dry cycling conditions and discovered the increasing wetting–drying cycles lead to a porous and disintegrated microstructure of joints, which further results in increases in shear deformation and steady-creep rate and decreases in the failure strength and long-term strength. Gutiérrez-Ch et al. [13] analyzed the application of the discrete element method (DEM) in combination with the Realistic Pore-structure Theory (RPT) for simulating rock shear creep (RSC). The findings indicated that the DEM–RPT approach can effectively reproduce all stages of RSC, including the tertiary creep phase. Additionally, the study examined the effects of applied shear stress and normal stress on RSC.

Water plays a crucial role in the physical processes of rock expansion, erosion, softening, penetration, and freeze-thaw cycles [14,15]. Its influence on the mechanical properties and rheological characteristics of weak interbedded rocks is significant [16]. Furthermore, the long-term effects of diurnal and seasonal temperature fluctuations lead to uneven heating of the structural surfaces of soft rock, resulting in repeat expansion and contraction over time, which facilitates the initiation and propagation of internal fractures [17,18,19]. Additionally, as water content increases, both the maximum creep deformation and the creep rate of soft rock significantly rise, and the time required for the rock to reach a steady-state creep also increases. Jiang et al. [20] conducted multi-loading shear creep tests on soil–rock mixture (SRM) samples with varying moisture content. The results revealed that deformation gradually increases with increasing water content, while long-term strength gradually decreases with increasing water content. Zhou et al. [21] observed from laboratory tests that reductions in the compressive and tensile strength of sandstone under static and dynamic states in different saturation processes were observed. In the drying process, all of the saturated specimens could basically regain their mechanical properties and recover their strength, as in the dry state.

The creep characteristics of soft rock serve as a key indicator for ensuring safe mining operations [22]. The detrimental effects of moisture content on the creep properties of soft rock under prolonged temperature cycling are critical factors contributing to the instability of mine slopes and the occurrence of landslides [23]. In southwestern China, notable seasonal temperature variations occur; surface temperatures can exceed 65 °C during hot summers, while severe winter conditions can lead to minimum temperatures dropping to −5 °C. Following extended and repeated cycles of these adverse conditions, the mechanical and creep properties of soft rock undergo substantial changes [24].

In summary, temperature cycling can adversely affect the fundamental mechanical properties and shear creep characteristics of soft rock due to the freeze–thaw contraction and expansion of free or bound water in weak interlayers. Further investigation into the shear creep characteristics at varying moisture contents is warranted. Building on previous studies of gently dipping weak interlayers, this paper presents a graded shear creep experiment on carbonaceous mud shale samples collected from the Huangshan limestone mine slope in Emei City, Sichuan Province, under cyclic temperature conditions. The mechanical properties and creep characteristics of carbonaceous mud shale at different moisture contents were analyzed during temperature cycling. Additionally, a theoretical model was developed to account for the damage effects of water content in rocks subjected to temperature cycling, thereby providing valuable insights into the stability analysis of similar engineering slope mechanics.

2. Experimental Scheme

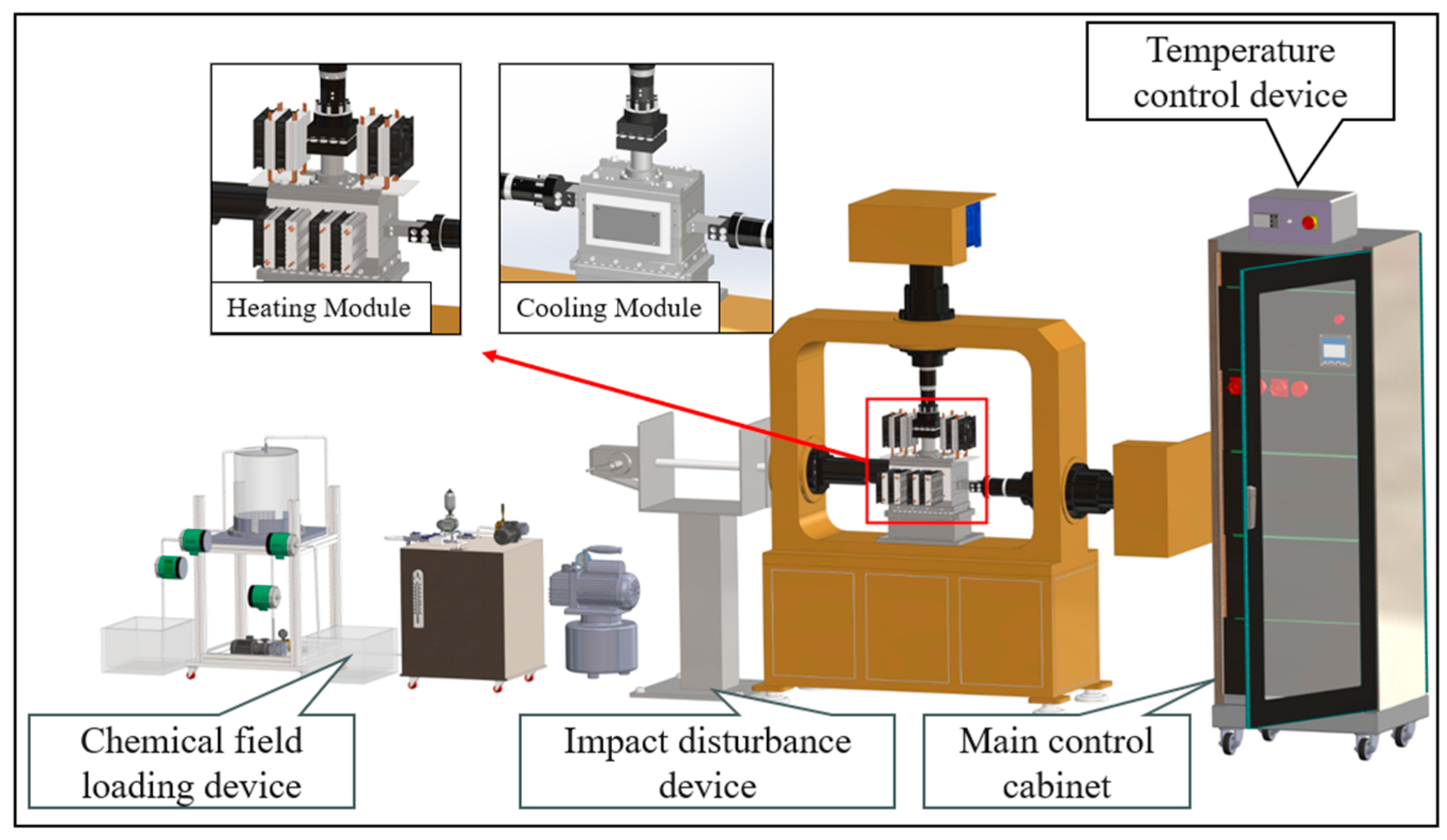
2.1. Experimental Instruments

The experiment was conducted using the THMC-B (Temperature, Hydro, Mechanics, Chemical and Blasting vibration) multi-field coupling simulation equipment designed for soft rock shear rheology, as illustrated in Figure 2. This specialized system simulates soft rock shear creep under the combined effects of stress, rainfall, blasting, seepage, and chemical interactions. In the experiment, the temperature field is primarily regulated through two components, the cooling module and the heating module, as illustrated in Figure 2. Throughout the experiment, the heating and cooling modules are periodically attached to the exterior of the shear box to facilitate temperature cycling. The temperature regulation range of this device spans from −20 °C to 75 °C, with an accuracy of 0.1 °C.

2.2. Rock Sample Preparation

The experimental rock samples were derived from the carbonaceous mud shale of the Permian system, which was collected from the exposed weak interlayers on the slope of the Huangshan limestone mine in Emei City, Sichuan Province. This type of rock primarily consists of limestone debris, sand, and a carbonaceous clay matrix. The rock surface is largely free of visible joints and appears blackish-gray in its natural state. Carbonaceous mud shale samples of suitable size were cut into large, irregularly shaped weak interlayer shear rheology specimens using a large flexible interlayer cutting device, resulting in 45 rectangular specimens measuring 150 mm × 75 mm × 75 mm, as shown in Figure 3.

Once the samples are prepared, it is important to consider that the mechanical properties of mudstone decline rapidly as water content increases after immersion [25]. Accordingly, the moisture content of the rock samples is adjusted using drying and natural soaking methods [26,27]. The procedure for adjusting the moisture content of the rock samples is outlined in accordance with the “Experimental Procedures for Physical and Mechanical Properties of Rocks (DZ/T 0276.2-2015) [28],” as presented in

Table 1. Water content of carbonaceous mud shale samples.

Rock Sample	Dry	Natural	Saturated
Sample number	S-01	S-02	S-03
moisture content/%	0	1.5	3.2

.

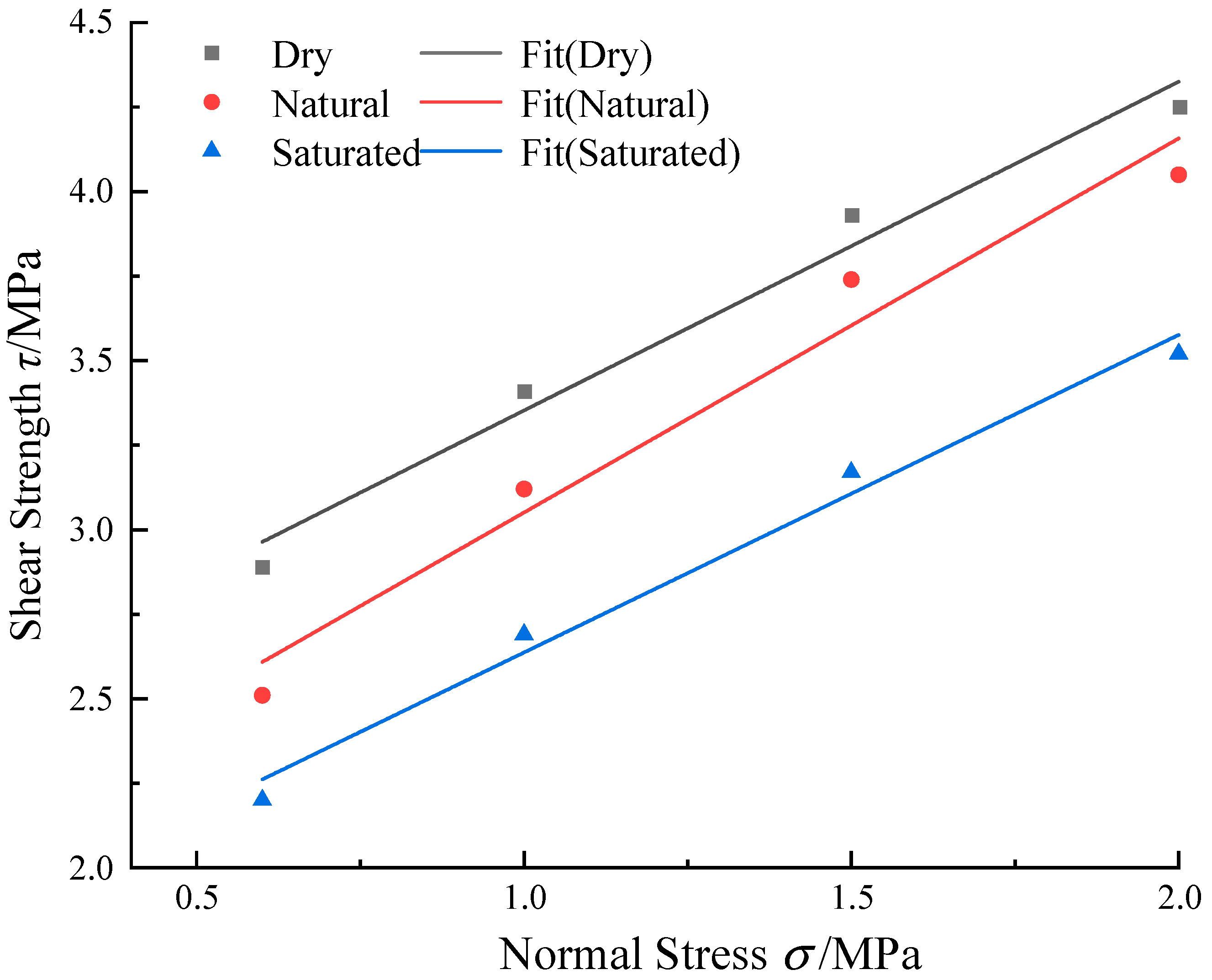
2.3. Conventional Straight Cut Test

Conventional shear tests were conducted on three distinct carbonaceous mud shale samples exhibiting varying moisture contents [29]. The normal stress values for each sample group were established at 0.6 MPa, 1.0 MPa, 1.5 MPa, and 2.0 MPa. For each normal stress value, three rock samples were tested. Samples with superior mechanical properties were selected to construct shear stress–shear displacement curves for the carbonaceous mud shale, from which the fundamental rock mechanical parameters were derived.

After the testing, data from the direct shear tests were utilized to plot curves of normal stress versus shear strength for carbonaceous mud shale under different moisture content conditions, as illustrated in Figure 4. The internal friction angle and cohesion of the corresponding carbonaceous mud shale were calculated and presented in

Table 2. Summary of basic rock mechanical parameters of direct cutting experiment.

Moisture Content	Normal Stress σ/MPa	Fitted Curve	Shear Strength τ/MPa	Cohesion C/MPa	$\mathbf{Internal} \mathbf{Friction} \mathbf{Angle} \mathit{\phi }$/°
Dry	0.6	$\tau =\sigma tan46.94°+2.25$ $R^2=0.97882$	2.96	2.25	$46.94°$
	1.0		3.35
	1.5		3.83
	2.0		4.32
Natural	0.6	$\tau =\sigma tan44.02°+1.76$ $R^2=0.96828$	2.61	1.59	44.02
	1.0		3.05
	1.5		3.60
	2.0		4.16
Saturated	0.6	$\tau =\sigma tan41.70°+1.76$ $R^2=0.97882$	2.26	$1.76$	$41.70°$
	1.0		2.63
	1.5		3.10
	2.0		3.57

. Analysis of the test data indicated that the shear strength of carbonaceous mud shale exhibited a linear growth trend with a continuous increase in normal stress. Furthermore, moisture content was found to have a negative correlation with all basic mechanical parameters of the rock.

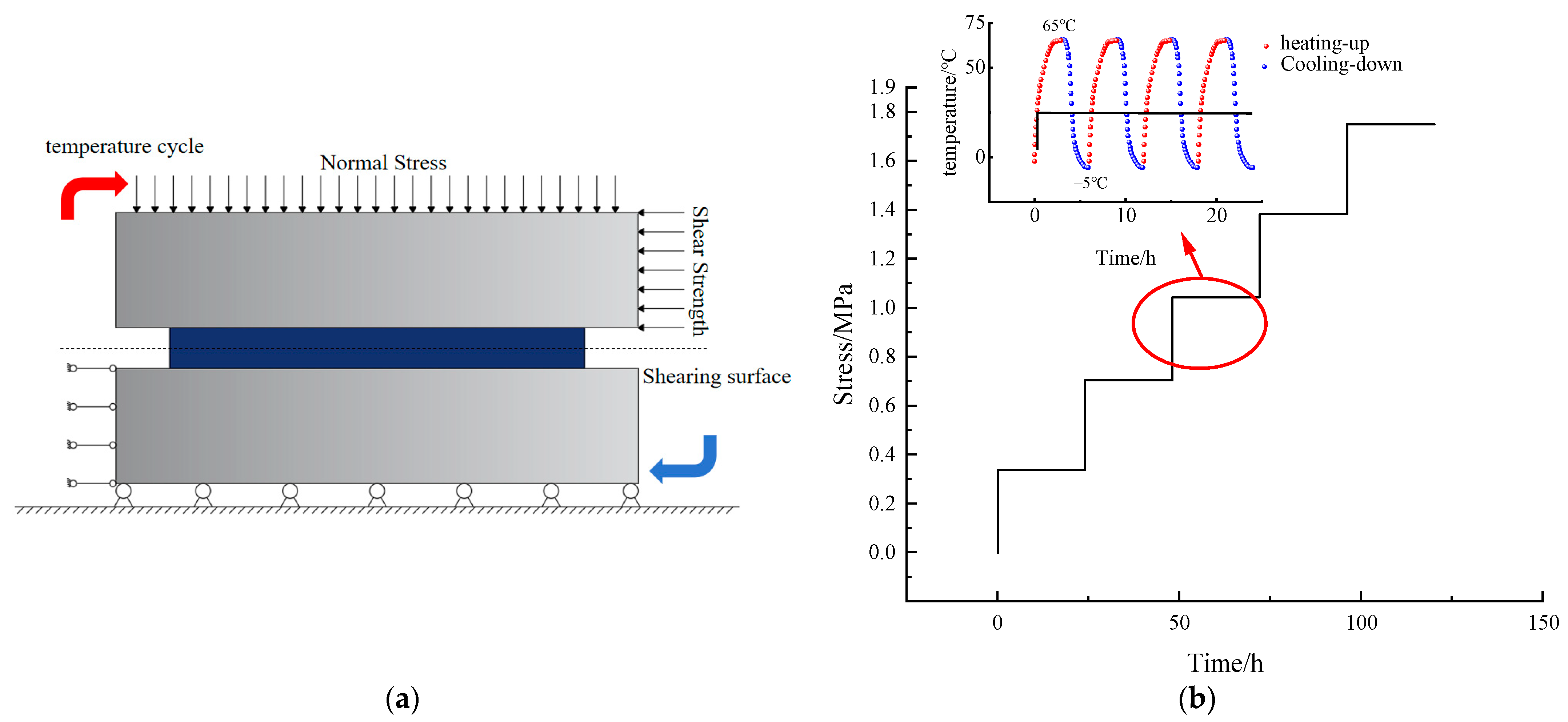
2.4. Shear Creep Test

The shear creep test was conducted on carbonaceous mud shale samples with varying water content across multiple temperature cycles within the range of −5 °C to 65 °C, aimed at determining the normal stress value of 0.6 MPa. The number of temperature cycles was set to 16, with each cycle consisting of heating and cooling periods lasting 3 h, resulting in a total duration of 6 h per cycle.

This paper employs a staged loading method to apply shear loads [30]. Based on conventional direct shear test data for carbonaceous mud shale, five distinct levels of shear force were established. The applied shear loads corresponded to 13%, 27%, 40%, 53%, and 67% of the shear strength of the rock samples [31]. Each loading level was maintained for 24 h, with the first four levels averaged across 16 temperature cycles. Specific shear creep experimental data are presented in

Table 3. Design of shear creep test scheme of carbonaceous mudstone under temperature cycle.

Rock Sample	Number of Cycles	Normal Stress σ/MPa	Shear Strength τ/MPa	Moisture Content	Level 1 Shear Stress/MPa	Level 2 Shear Stress/MPa	Level 3 Shear Stress/MPa	Level 4 Shear Stress/MPa	Level 5 Shear Stress/MPa
S-01	16	0.6	3.35	0	0.385	0.799	1.184	1.569	1.983
S-02			3.83	1.5	0.339	0.705	1.044	1.383	1.749
S-03			4.32	3.2	0.294	0.610	0.904	1.198	1.514

, while the simplified design diagram of the experimental scheme is depicted in Figure 5a, and the stress loading path, using natural shear stress as an example, is illustrated in Figure 5b.

3. Analysis of Experimental Results

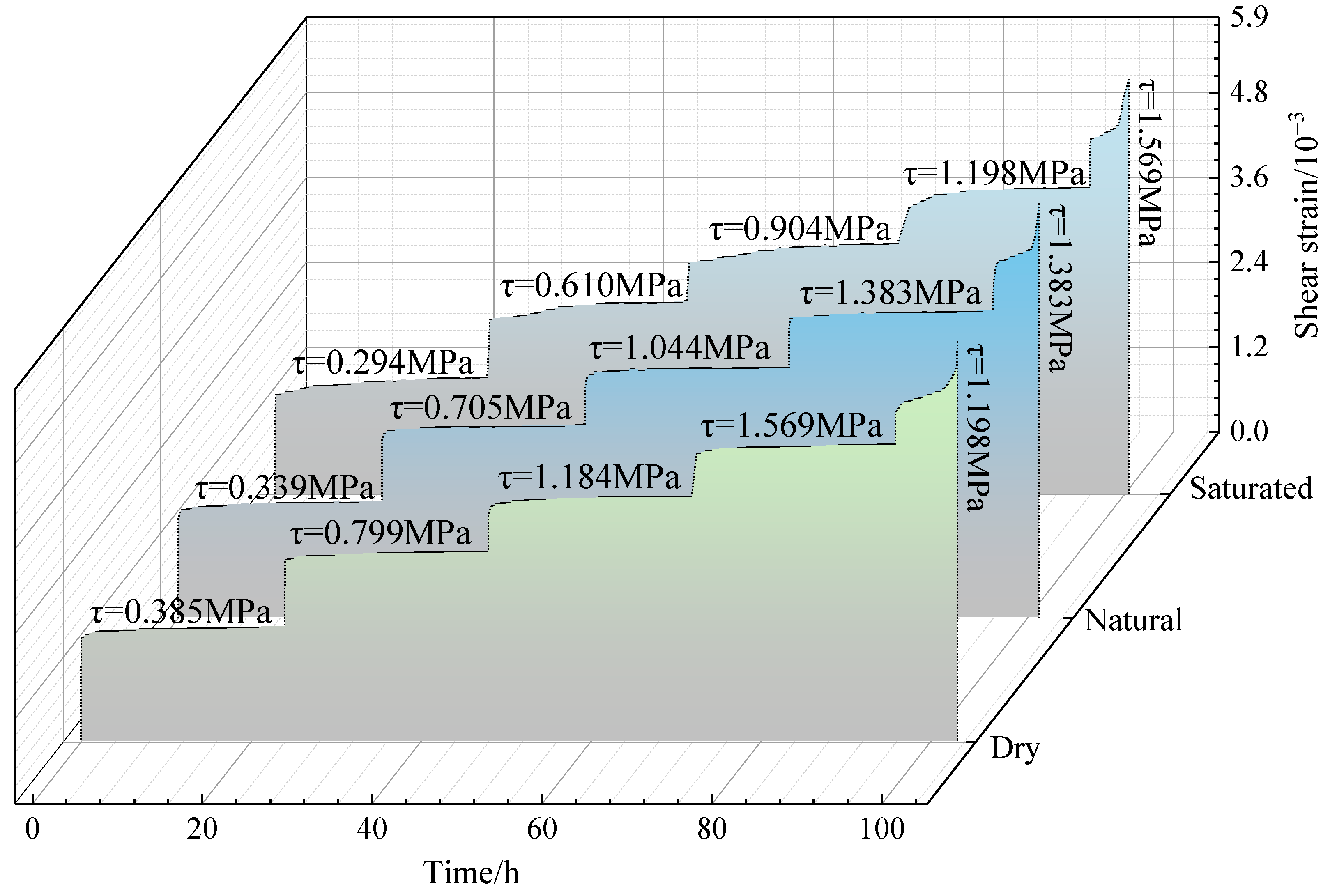
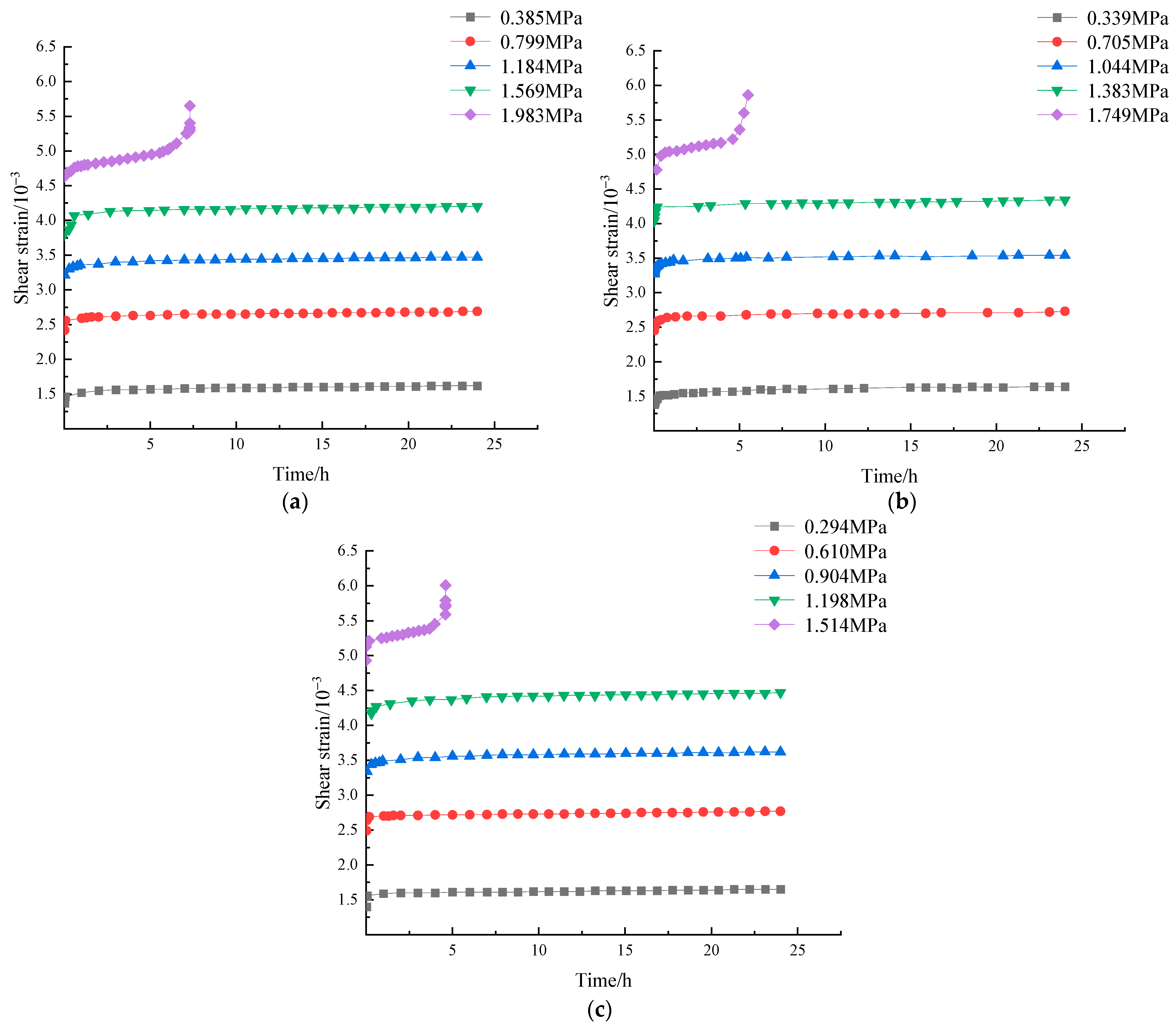
3.1. Analysis of Overall Creep Curve

Following the experiment, the strain–time curve was derived from the shear creep experimental data of carbonaceous mud shale at varying water contents, as illustrated in Figure 6.

According to Figure 6, the shear creep process of carbonaceous shale can be categorized into three stages: the accelerated creep stage, the steady-state creep stage, and the decelerated creep stage [32]. When carbonaceous shale is completely dry, its internal micro-fractures do not contain water. Under the adverse effects of temperature cycling, the material does not experience frost heave forces due to water expansion or thermal stresses resulting from the evaporation of free water within. The temperature range of −5 °C to 65 °C has minimal impact on the mineral composition of the rock sample, rendering the mechanical properties of carbonaceous shale most stable at this point, which results in the least strain generated during each level of shear creep. As the water content increases, internal micro-fractures are progressively filled with free water. Subsequently, under the adverse effects of temperature cycling, the evaporation of water leads to a rapid drop in temperature, resulting in quick condensation and frost heave forces that cause the internal micro-fractures of the rock sample to expand or even form new fractures. After each load is applied, the instantaneous strain in the rock sample significantly increases. Additionally, the water content significantly affects the rate of creep in carbonaceous mud shale; after the fifth level of loading, the deformation of the rock sample occurs more rapidly.

Figure 7 presents the uniaxial creep curves of carbonaceous mud shale under varying shear stresses. A comparison of these curves under different water contents reveals that during the initial three loading stages, the strain in the carbonaceous mud shale increases slightly with rising water content, although the change is not significant. However, during the fourth and fifth loading stages, the strain exhibits a marked increase with higher water content. This behavior can be attributed to the effects of temperature cycling during the early stages, which cause the internal moisture of the rock samples to repeatedly evaporate and condense. This process may generate and expand micro-cracks within the rock samples, but these cracks have minimal impact on the mechanical properties at this stage [33]. As the temperature cycles accumulate and loading progresses to the fourth and fifth stages, the previously formed micro-cracks expand and connect, significantly reducing the mechanical properties of the carbonaceous mud shale.

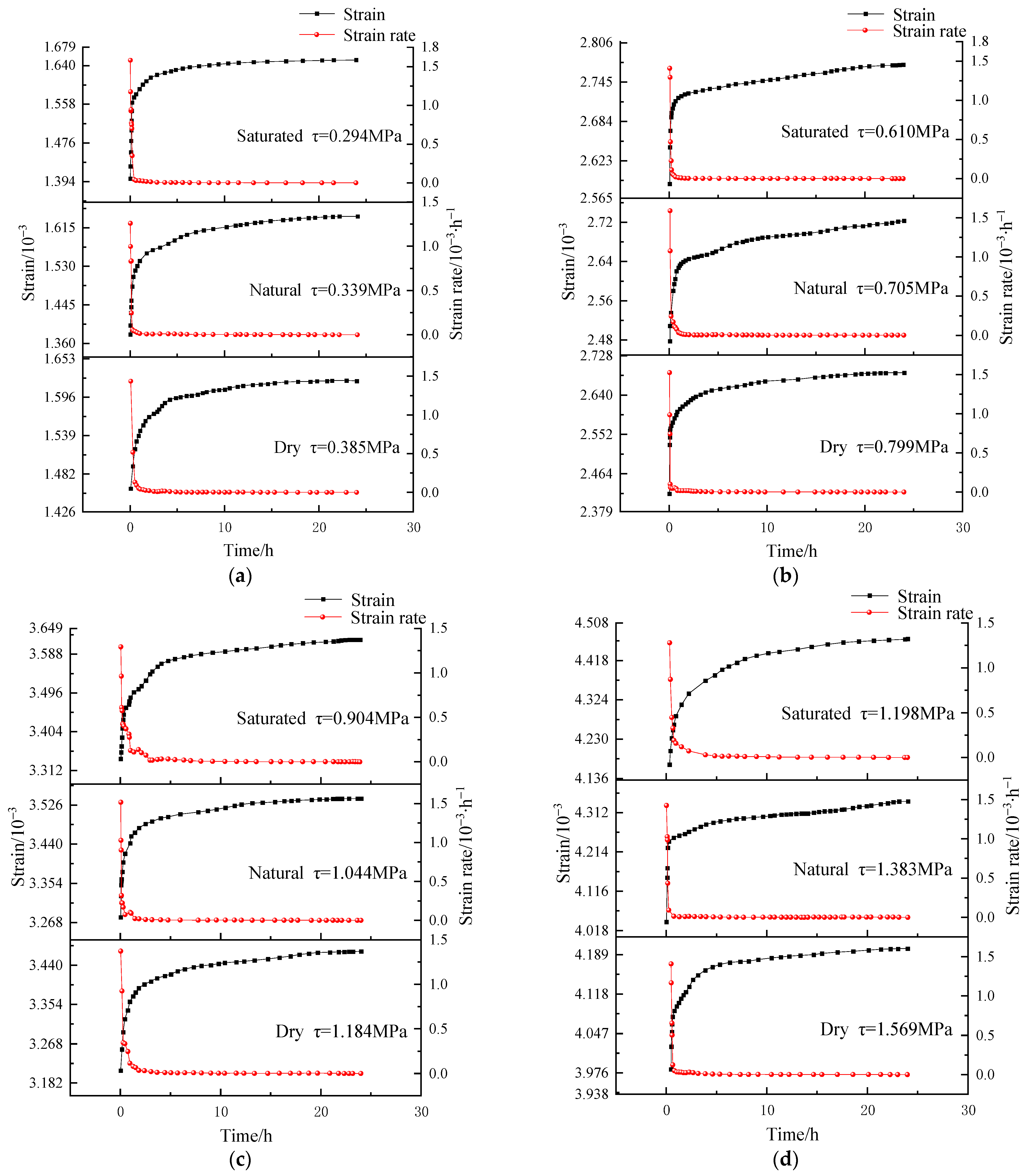
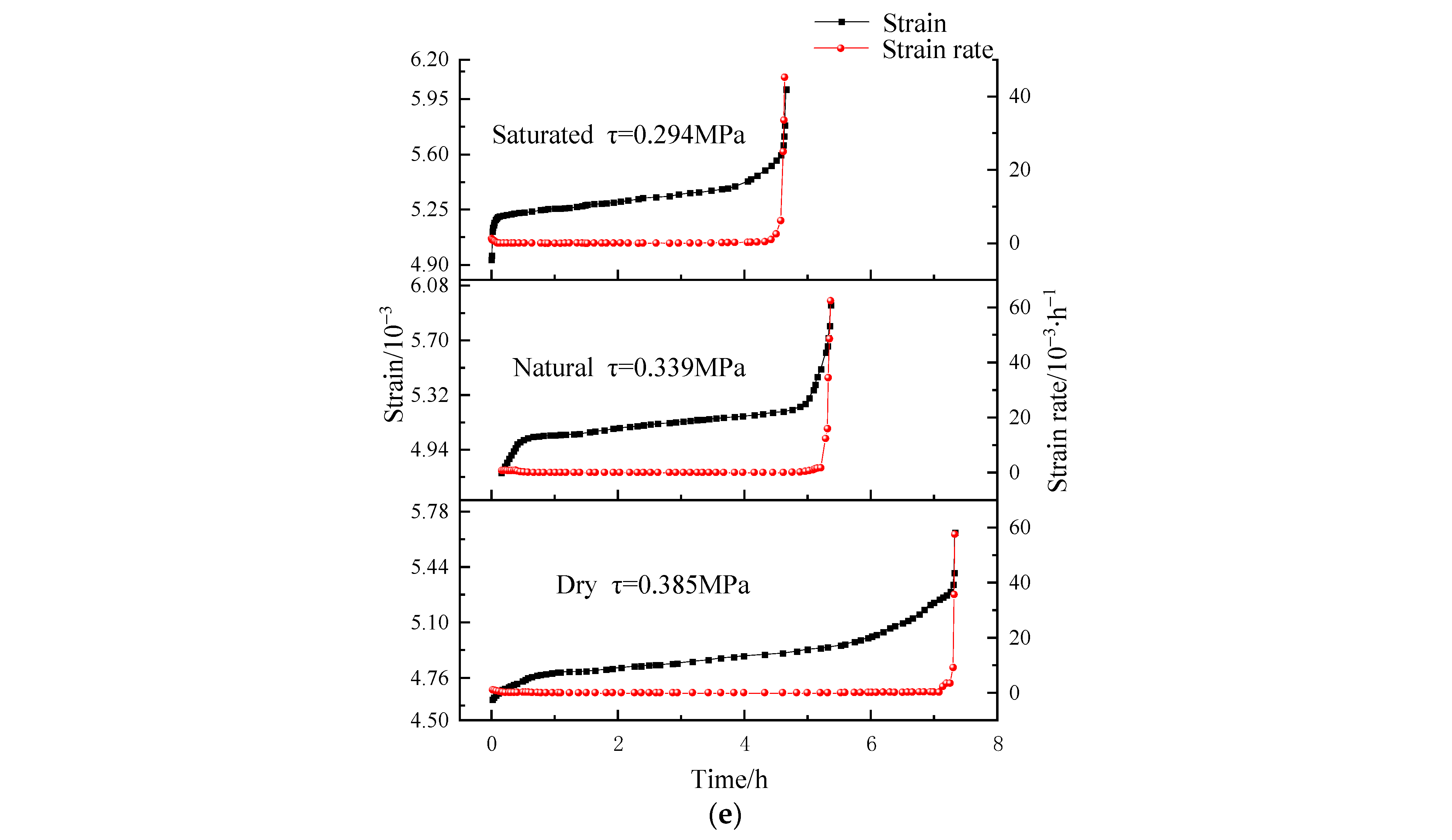
3.2. Analysis of Creep Rate

Figure 8 presents the single-stage shear creep strain and strain rate curves for carbonaceous mud shale at varying water contents. The curves illustrate that, throughout the shear creep process, carbonaceous mud shale consistently exhibits a decelerating creep stage. Following the application of each load, the strain rate initially reaches its maximum before rapidly declining and approaching zero. During the early stages of shear stress application, when the shear stress is relatively low, the duration of the decelerating creep stage is markedly brief, allowing the rock sample to swiftly transition into a steady-state creep stage. As shear stress progressively increases, energy accumulates within the rock, leading to stress fatigue, which prolongs the decelerating creep stage. Furthermore, under the influence of temperature cycling degradation, increased water content results in a shortened steady-state creep stage for carbonaceous mud shale compared to samples with lower water content when subjected to the same shear stress. This phenomenon occurs because temperature fluctuations cause internal water within the rock to evaporate and freeze, thereby accelerating stress fatigue and further diminishing mechanical properties when compared to a completely dry state. Consequently, the overall shear creep duration of carbonaceous mud shale is reduced.

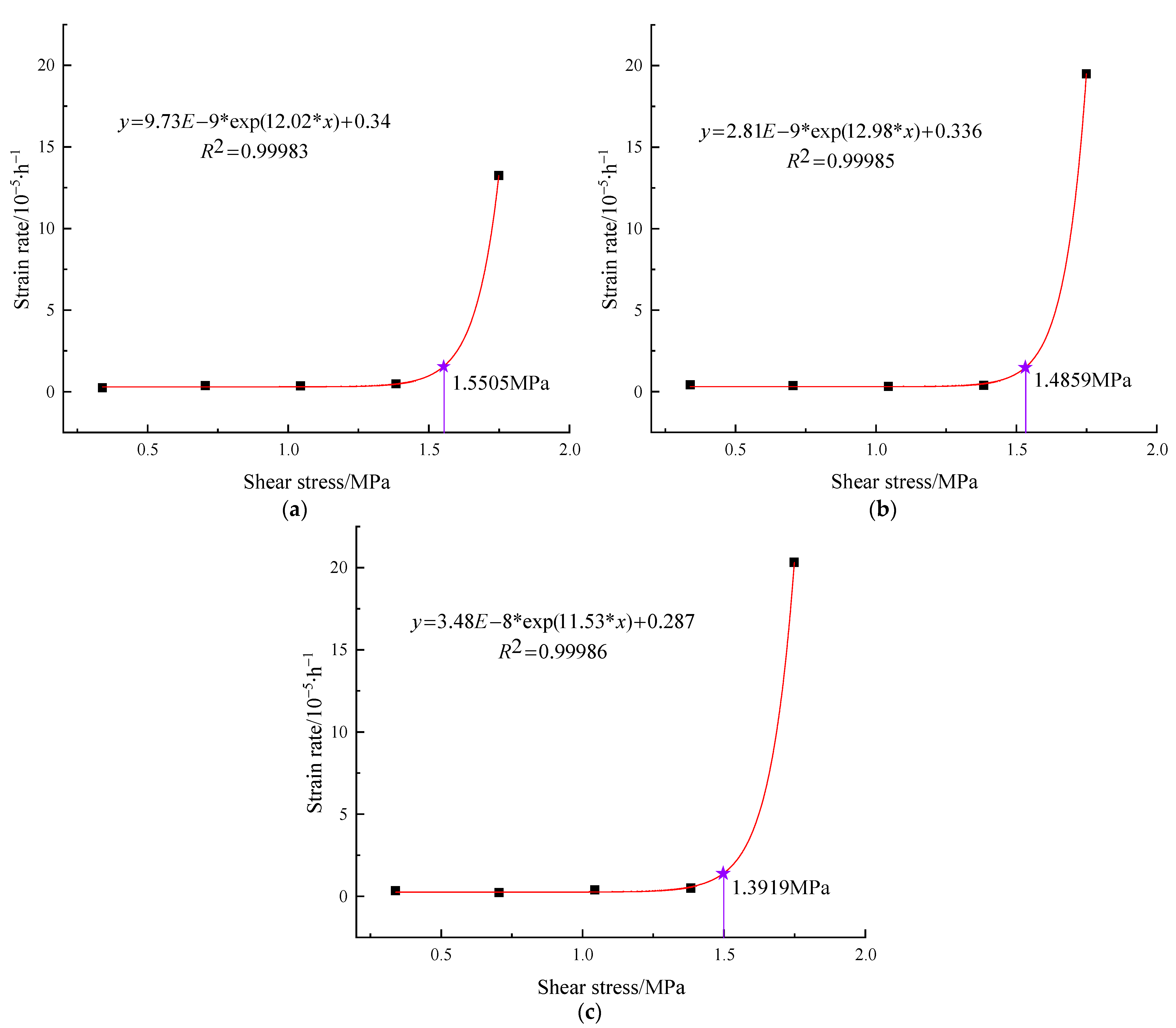
3.3. Analysis of Long-Term Strength

Engineering rock masses consist of intact rock blocks and joints, with their long-term strength generally dependent on the rheological properties of both components [34,35]. Measuring the long-term strength of rocks facilitates a more comprehensive investigation of their creep characteristics and deformation patterns, which is essential for understanding the causes of slope failures in mining operations and ultimately provides guidance for studies on slope stability over extended periods. To accurately determine the long-term strength of carbonaceous mud shale to meet practical engineering requirements, the steady-state creep rate method was employed. This method evaluated the long-term strength of carbonaceous mud shale under various conditions. The relationship between shear stress and steady-state creep rate at different moisture contents during temperature cycling was plotted, as illustrated by the fitted curve in Figure 9.

The curve reveals that the steady-state creep rate of carbonaceous mud shale approximately follows an exponential function with respect to shear stress, the fitted exponential function is shown in Figure 9. During the initial stages of loading, the creep rate increases gradually and approaches a linear trend. As the shear stress nears the critical long-term strength of carbonaceous mud shale, the creep rate escalates rapidly until the rock sample is sheared. Following the fitting process, the long-term strength of carbonaceous mudstone under varying water content conditions was evaluated based on the mutation points of the steady-state rate curve, yielding values of 1.5505 MPa, 1.4859 MPa, and 1.3919 MPa. This indicates that, under temperature cycling, the long-term strength of carbonaceous mud shale diminishes as water content increases. Consequently, under temperature cycling conditions, increased water content exerts a significantly adverse effect on the long-term strength of carbonaceous mud shale, serving as a potential factor for slope failure and impacting the long-term stability of mine slopes.

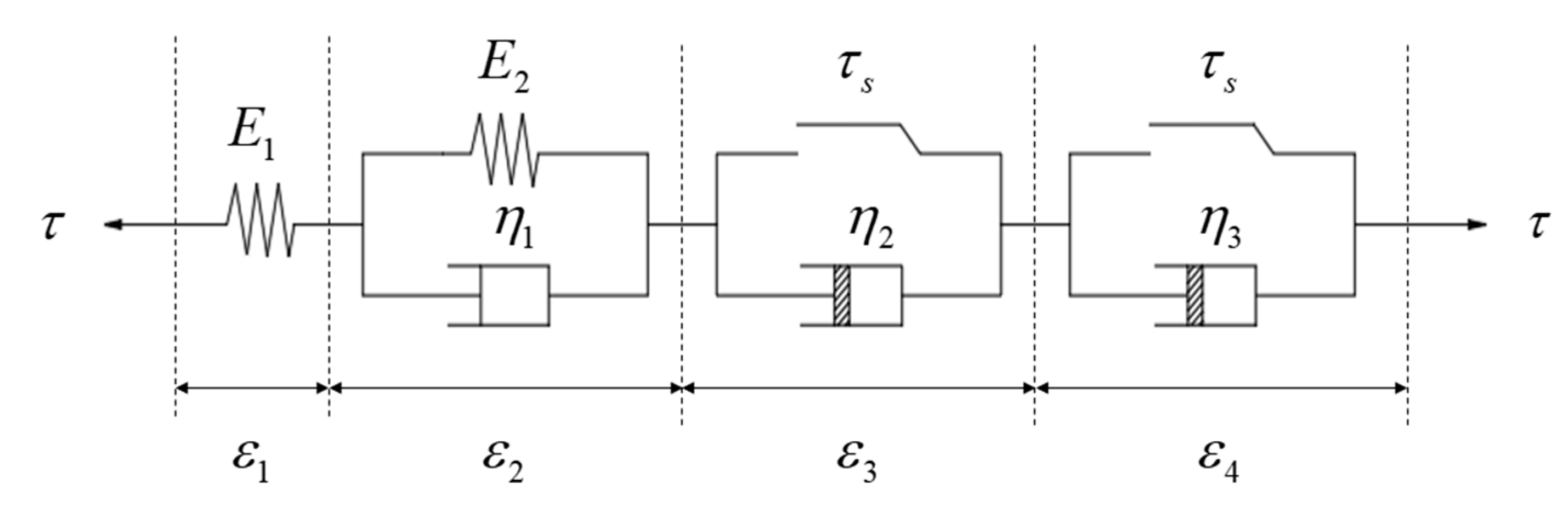
4. Creep Constitutive Model

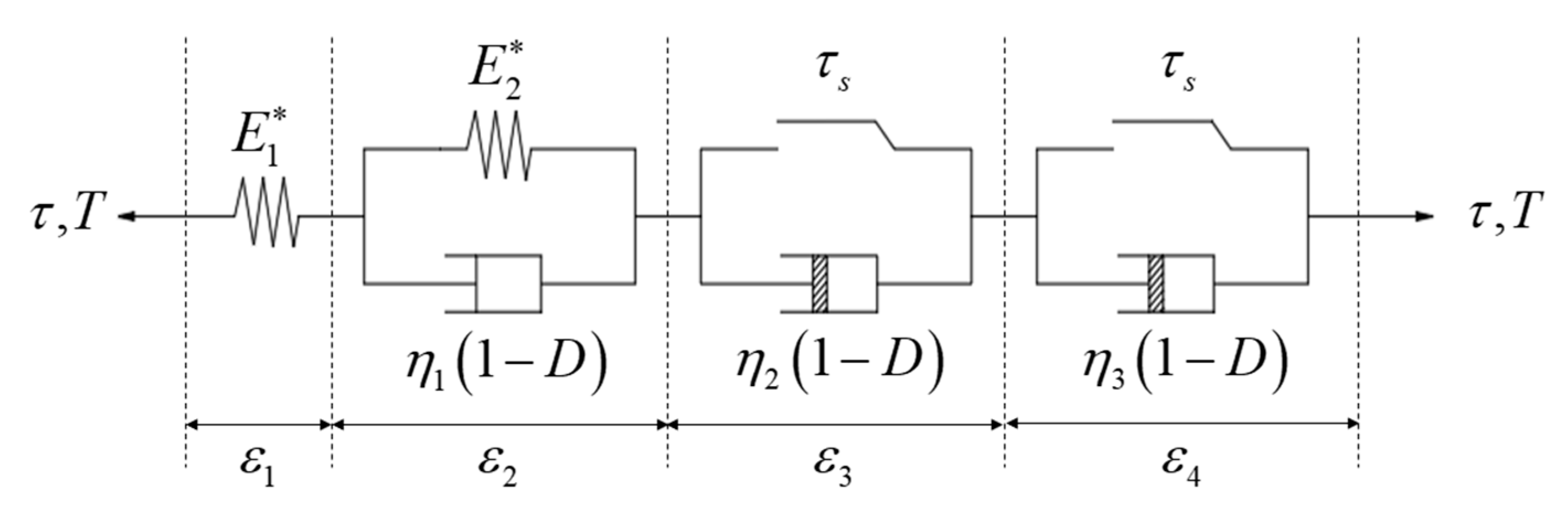
4.1. Constitutive Equation Considering Water Content Damage Under Temperature Cycling

As temperature cycles occur repeatedly over extended periods, water within the rock continuously freezes, liquefies, and evaporates, facilitating the development of micro-fractures and generating new fractures, which ultimately leads to rock damage. Currently, the statistical damage theory has advanced significantly in the study of rock damage, with common distribution patterns, including Weibull distribution, normal distribution, and power function distribution. The Weibull distribution is now more frequently employed [36,37,38,39,40]. From the perspective of macroscopic rock damage, it is assumed that rocks do not experience damage when the water content is at 0%. The degradation of macroscopic mechanical properties caused by water content is defined as follows:

$$D_w=1-{\displaystyle \frac{E_w}{E_0}}$$

(1)

where $E_w$ represents the elastic modulus of rock with water content $w\%$, $E_0$ denotes the initial elastic modulus of dry rock, and $D_w$ ranges from 0 to 1, reflecting the various stages of rock damage from non-destructive to complete failure.

The shear face of the carbonaceous mud shale rock sample can be conceptualized as a plane consisting of numerous microelements. A temperature–strain model for these microelements, considering a stable temperature field, is constructed under the assumption that this model adheres to specific statistical laws. By integrating these statistical principles with continuous damage theory, specifically the Weibull distribution and the Drucker-Prager (D-P) criterion, a simplified expression for the model’s strength is presented [41,42,43,44]:

$$D_T=1-\exp \left[-{\displaystyle \frac{F_T}{F_0}}\right]$$

(2)

$$F_T={\displaystyle \frac{1}{3}}(3\alpha +\sqrt{3})E_T{\epsilon }_T$$

(3)

$$\alpha ={\displaystyle \frac{\sin \phi }{\sqrt{3\left(3+{\sin }^2\phi \right)}}}$$

(4)

$${\epsilon }_T=nK\Delta Tt$$

(5)

where $D_T$ represents the statistical damage variable associated with temperature cycling degradation, while $F_T$ denotes the model strength of microelements considering temperature damage in this distribution variable. $F_0$ is the distribution parameter, and $E_T$ corresponds to the elastic modulus of the rock following temperature cycling. $\phi$ denotes the internal friction angle, and $\alpha$, the material constant, is related to the value of $\phi$. ${\epsilon }_T$ represents the strain induced by temperature stress, while $n$, taken as 16 in this paper, indicates the number of temperature cycles. $K$ is the thermal expansion adjustment coefficient, $\Delta T$ denotes the temperature cycle interval, and $t$ signifies the time required for the rock to experience temperature-induced damage. By simultaneously solving Equations (2)–(5), we can derive the full-process damage equation for the deformation and failure of rocks following temperature degradation.

$$D_T=1-\exp \left(-{\displaystyle \frac{CK}{F_0}}t\right)$$

(6)

where $C={\displaystyle \frac{\sqrt{3}}{3}}({\displaystyle \frac{\sin \phi }{\sqrt{3+{\sin }^2\phi }}}+1)\cdot n\Delta T{E}_T$ is a constant determined by the internal friction angle $\phi$, the number of temperature cycles $n$, the temperature cycle interval $\Delta T$, and the elastic modulus of the rock $E_T$ following temperature cycling.

To effectively couple the factors of water content and temperature deterioration, a generalized strain equivalence principle is employed [45]. In this approach, the initial state of the rock, though undamaged, is treated as a damaged state. The composite damage state arising from factors such as temperature and water content is decomposed into several independent damage states to apply the strain equivalence principle.

Utilizing the strain equivalence principle, the damage variable $D_w$, representing the impact of water content on rock properties, and the statistical damage variable $D_t$, associated with temperature cycle deterioration, are integrated to derive the constitutive relationship that accounts for the damage caused by water content under temperature cycling:

$$\sigma =E_0\left(1-D_w\right)\left(1-D_T\right)\epsilon$$

(7)

$$D=D_w+D_T-D_w{D}_T$$

(8)

By substituting Equations (1) and (6) into Equations (7) and (8), we can derive the constitutive equation for water content damage under temperature cycling:

$$D=1-{\displaystyle \frac{E_w}{E_0}}\exp \left(-{\displaystyle \frac{CK}{F_0}}t\right)$$

(9)

$$\sigma =E_w\exp \left(-{\displaystyle \frac{CK}{F_0}}t\right)\epsilon$$

(10)

4.2. Establishment of Creep Damage Constitutive Equation

The traditional Wester model, widely applied in rock rheology, effectively captures the elastic–viscoelastic–plastic behavior of rocks. However, it cannot adequately describe the nonlinear creep characteristics that occur during the accelerated creep phase. To overcome this limitation, Yan et al. [46] extended the traditional Wester model by integrating a nonlinear viscous-plastic component and introducing two improved nonlinear Newtonian components, as illustrated in Figure 10. The creep constitutive equation of the modified Wester model is:

$$\left\{\begin{array}{l}\epsilon (t)={\displaystyle \frac{{\tau }_0}{E_1}}+{\displaystyle \frac{{\tau }_0}{E_2}}\left[1-\exp (-{\displaystyle \frac{E_2}{{\eta }_1}}t)\right]\\ \tau \le {\tau }_s,t<t_s\\ \epsilon (t)={\displaystyle \frac{{\tau }_0}{E_1}}+{\displaystyle \frac{{\tau }_0}{E_2}}\left[1-\exp (-{\displaystyle \frac{E_2}{{\eta }_1}}t)\right]+{\displaystyle \frac{{\tau }_0-{\tau }_s}{{\eta }_2}}t+{\displaystyle \frac{{\tau }_0-{\tau }_s}{{\eta }_3}}\Delta t{({\displaystyle \frac{t-t_s}{\Delta t}})}^n\\ \tau >{\tau }_s,t\ge t_s\end{array}\right.$$

(11)

where $E_1$ and $E_2$ represent the elastic moduli, ${\eta }_1$, ${\eta }_2$, and ${\eta }_3$ are the viscous coefficients, ${\epsilon }_1$, ${\epsilon }_2$, ${\epsilon }_3$, and ${\epsilon }_4$ denote the strain in each component of the model, ${\tau }_0$ and ${\tau }_s$ correspond to shear stress and long-term strength, respectively, $t_s$ is the time required for soft rock to reach the long-term strength critical point, $\Delta t$ is the unit time, and $n$ is the creep index.

Although the model effectively describes the deformation characteristics of soft rock during the deceleration, steady-state, and acceleration creep stages in shear creep processes, it does not adequately capture the influence of water content on the creep behavior or the damage effects induced by complex stress conditions encountered in real-world scenarios. To address these limitations, this study (1) incorporates a damage component into the combined model to represent the evolution of rock damage due to water content under temperature degradation, thereby adjusting the viscosity coefficient, and (2) recalculates the elastic modulus of the Hooke body within the model to account for the damage effects of water content under temperature cycling [47]. These modifications yield a combined model that integrates both the damage characteristics and the viscoelastic–plastic properties of soft rock, as illustrated in Figure 11.

The viscoelastic parameters of the ideal viscous body in the original model are transformed into a form that includes the damaged body $D$ as follows:

$$E_2^{\ast }=E_2(1-D)={\displaystyle \frac{E_2{E}_w}{E_0}}\exp \left(-{\displaystyle \frac{CK}{F_0}}t\right)$$

(12)

$${\eta }_1(1-D)={\displaystyle \frac{{\eta }_1{E}_w}{E_0}}\exp \left(-{\displaystyle \frac{CK}{F_0}}t\right)$$

(13)

Thus, the constitutive equation of the viscoelastic element is expressed as:

$$\tau ={\displaystyle \frac{E_2{E}_w}{E_0}}\exp \left(-{\displaystyle \frac{CK}{F_0}}t\right)\epsilon +{\displaystyle \frac{{\eta }_1{E}_w}{E_0}}\exp \left(-{\displaystyle \frac{CK}{F_0}}t\right)\dot{\epsilon }$$

(14)

Solving Equation (14) yields:

$$\epsilon ={\displaystyle \frac{E_0\tau }{E_w}}\left[1-\exp \left\{-{\displaystyle \frac{E_2{F}_0}{K{E}_T{\eta }_1}}\exp (\left({\displaystyle \frac{CK}{F_0}}t\right)-1)\right\}\right]$$

(15)

According to the literature [48], the elastic modulus of the Hooke body in the modified model is defined as follows:

$$E_1^{\ast }=E_1\left[{\displaystyle \frac{E_w}{E_0}}\exp (-\alpha \sigma )\right]$$

(16)

where $\alpha$ represents the parameter of water content in the reactive rock during the linear elastic stage, while $\sigma$ denotes stress.

The correction of the viscosity coefficients ${\eta }_2$ and ${\eta }_3$ in a nonlinear viscoelastic body can be derived in a similar manner:

$${\eta }_2(1-D)={\displaystyle \frac{{\eta }_2{E}_w}{E_0}}\exp \left(-{\displaystyle \frac{CK}{F_0}}t\right)$$

(17)

$${\eta }_3(1-D)={\displaystyle \frac{{\eta }_3{E}_w}{E_0}}\exp \left(-{\displaystyle \frac{CK}{F_0}}t\right)$$

(18)

In summary, when $\tau \le {\tau }_s$ is present, only the elastic and viscous elements contribute to the model. At this point, the creep equation for carbonaceous mud shale is as follows:

$$\epsilon (t)={\displaystyle \frac{{\tau }_0}{E_1\left[\frac{E_w}{E_0}\exp (-\alpha {\tau }_0)\right]}}+{\displaystyle \frac{E_0{\tau }_0}{E_w}}\left[1-\exp \left\{-{\displaystyle \frac{E_2{F}_0}{K{E}_T{\eta }_1}}\exp (\left({\displaystyle \frac{CK}{F_0}}t\right)-1)\right\}\right]$$

(19)

When $\tau >{\tau }_s$ is present, all components in the constitutive model are active. According to the series rule, the state equations are as follows:

$$\left\{\begin{array}{l}{\epsilon }_1={\displaystyle \frac{{\tau }_0}{E_1\left[\frac{E_w}{E_0}\exp (-\alpha {\tau }_0)\right]}}\\ {\epsilon }_2={\displaystyle \frac{E_0{\tau }_0}{E_w}}\left[1-\exp \left\{-{\displaystyle \frac{E_2{F}_0}{K{E}_T{\eta }_1}}\exp (\left({\displaystyle \frac{CK}{F_0}}t\right)-1)\right\}\right]\\ {\epsilon }_3={\displaystyle \frac{E_0\left({\tau }_0-{\tau }_s\right)t}{{\eta }_2{E}_w\exp \left(-\frac{CK}{F_0}t\right)}}\\ {\epsilon }_4={\displaystyle \frac{E_0\left({\tau }_0-{\tau }_s\right)}{{\eta }_3{E}_w\exp \left(-\frac{CK}{F_0}t\right)}}\Delta t{({\displaystyle \frac{t-t_s}{\Delta t}})}^n\\ \epsilon ={\epsilon }_1+{\epsilon }_2+{\epsilon }_3+{\epsilon }_4\end{array}\right.$$

(20)

In summary, the constitutive equation of creep damage of carbonaceous mud shale under the coupling effect of temperature deterioration and water content is as follows:

$$\epsilon (t)=\left\{\begin{array}{l}{\displaystyle \frac{{\tau }_0}{E_1\left[\frac{E_w}{E_0}\exp (-\alpha {\tau }_0)\right]}}+{\displaystyle \frac{E_0{\tau }_0}{E_w}}\left[1-\exp \left\{-{\displaystyle \frac{E_2{F}_0}{K{E}_T{\eta }_1}}\exp (\left({\displaystyle \frac{CK}{F_0}}t\right)-1)\right\}\right]\\ (\tau \le {\tau }_s,t<t_s)\\ {\displaystyle \frac{{\tau }_0}{E_1\left[\frac{E_w}{E_0}\exp (-\alpha {\tau }_0)\right]}}+{\displaystyle \frac{E_0{\tau }_0}{E_w}}\left[1-\exp \left\{-{\displaystyle \frac{E_2{F}_0}{K{E}_T{\eta }_1}}\exp (\left({\displaystyle \frac{CK}{F_0}}t\right)-1)\right\}\right]\\ +{\displaystyle \frac{E_0\left({\tau }_0-{\tau }_s\right)t}{{\eta }_2{E}_w\exp \left(-\frac{CK}{F_0}t\right)}}+{\displaystyle \frac{E_0\left({\tau }_0-{\tau }_s\right)}{{\eta }_3{E}_w\exp \left(-\frac{CK}{F_0}t\right)}}\Delta t{({\displaystyle \frac{t-t_s}{\Delta t}})}^n\\ (\tau >{\tau }_s,t\ge t_s)\end{array}\right.$$

(21)

5. Model Validation

This paper examines the feasibility and accuracy of a modified creep constitutive model that accounts for damage related to water content under temperature cycling, based on experimental shear creep curves of carbonaceous shale with varying water contents. The experimental data are compared with improved model curves to identify relevant parameters. Due to space constraints, this study presents only the parameter identification results for the creep experiment curves of carbonaceous shale in its natural state at different water contents, as displayed in

Table 4. Fitting parameters of the creep model for carbonaceous shale, considering the effects of water content damage under temperature cycling.

Moisture Content	Shear Stress	Instantaneous Elastic Modulus ${\mathit{E}}_1$/GPa	Viscoelastic Modulus ${\mathit{E}}_2$/GPa	Viscosity Coefficient ${\mathit{\eta }}_1$/MPa∙h	Viscosity Coefficient ${\mathit{\eta }}_2$/MPa∙h	Viscosity Coefficient ${\mathit{\eta }}_3$/MPa∙h	Coefficient of Thermal Expansion $\mathit{K}$/℃−1	${\mathit{F}}_0$	${\mathit{R}}^2$
Dry	0.385	0.834	8.582	646.96	17.57	1107.60	0.39	5.56 × 10−6	0.981
	0.799	1.039	10.022	599.03			0.45	5.18 × 10−6	0.975
	1.184	0.768	17.494	437.34			0.44	6.96 × 10−6	0.979
	1.569	1.068	46.630	578.56			0.61	3.55 × 10−6	0.953
	1.983	0.689	39.198	391.80			0.50	5.57 × 10−6	0.969
Natural	0.339	0.572	6.880	587.52	15.26	998.31	0.57	5.74 × 10−6	0.985
	0.705	0.663	12.525	415.79			0.89	5.89 × 10−6	0.957
	1.044	0.483	15.291	392.17			0.62	6.22 × 10−6	0.971
	1.383	0.802	26.835	326.11			0.74	6.85 × 10−6	0.962
	1.749	0.594	32.749	500.98			1.03	7.42 × 10−6	0.980
Saturated	0.294	0.593	5.551	547.93	12.39	726.53	0.81	4.61 × 10−6	0.992
	0.610	0.780	17.546	681.93			0.66	5.71 × 10−6	0.931
	0.904	0.318	14.432	316.87			0.85	6.17 × 10−6	0.958
	1.198	0.454	20.844	259.46			1.27	6.95 × 10−6	0.981
	1.514	0.635	27.722	289.79			1.42	7.43 × 10−6	0.983

. Additionally, a comparison chart illustrating the experimental curves and model fits is provided in Figure 12.

The creep model proposed in this paper, featuring modified coefficients, effectively represents the entire shear creep process of carbonaceous shale. It demonstrates a high degree of fit for each segment of the creep curve. Although some fitting results exhibit errors due to environmental factors, experimental inaccuracies, and variations among different rock samples, the majority of experimental curves achieve a goodness of fit exceeding 0.95. This indicates that the model accurately describes changes across three stages, deceleration creep, steady-state creep, and acceleration creep, thus underscoring its validity. Additionally, under the influence of temperature cycling, an increase in water content results in a gradual rise in the thermal expansion coefficient $K$ of carbonaceous shale. In contrast, the average instantaneous elastic modulus $E_1$, average elastic modulus $E_2$, viscoelastic modulus ${\eta }_1$, and viscosity coefficients ${\eta }_2$ and ${\eta }_3$ all experience a significant decrease. This further corroborates that, under temperature cycling conditions, an increase in water content adversely affects the mechanical properties and strength of carbonaceous shale, rendering it more susceptible to shear failure and, consequently, impacting the long-term stability of mine slopes.

6. Conclusions

This study is grounded in the engineering context of mine slopes in southwestern China, characterized by gently dipping Permian soft interlayers. It focuses on carbonaceous mud shale within these interlayers and conducts shear creep experiments under varying water contents and temperature cycling effects to investigate its creep characteristics. A shear creep damage model that accounts for water content damage is established, and the validity of the model is verified. The primary conclusions are as follows:

• Under the influence of temperature cycling, the instantaneous strain generated after each load level applied during the creep process of carbonaceous mud shale significantly increased with rising water content, resulting in a marked reduction in overall creep time. This alteration has important implications for slope stability, particularly in the context of precipitation and seasonal climate changes, where the creep behavior of rock masses may accelerate the occurrence of slope failures.
• In the initial stages, when shear stress is low, the deceleration creep phase of carbonaceous mud shale lasts for a shorter duration. As shear stress progressively increases, the duration of this phase gradually lengthens. Under temperature cycling, the steady-state creep phase of carbonaceous mud shale with higher moisture content progressively shortens. Furthermore, with temperature cycling, the long-term strength of carbonaceous mud shale decreases as moisture content increases. Collectively, these changes contribute to a reduction in the long-term strength of slopes, thereby heightening the risk of landslides.
• Building upon the traditional rheological model, nonlinear Newtonian viscoelasticity is introduced, and corrections are made to the elastic modulus and viscosity coefficient, ultimately leading to the establishment of a shear creep constitutive model for carbonaceous shale that accounts for water content damage. After validation, the fitted curve of the constitutive model closely matches the experimental curve, effectively characterizing the entire shear creep process in carbonaceous shale. The R² values exceed 0.95, indicating higher fitting accuracy compared to other traditional models, thus addressing the limitation of the original model in representing complex stress damage effects. The successful application of this model can enhance the accuracy of simulating the mechanical behavior of slope rock masses under various environmental conditions, providing theoretical support for the prediction and prevention of slope landslides.