Abstract
This study presents a numerical methodology for analyzing hydroacoustic noise generation and its propagation in a homogeneous domain using Lighthill’s analogy, the finite volume method, and hybrid-Higdon boundary conditions. The approach consists of three key steps: performing an eddy-resolving Large Eddy Simulation to capture the unsteady fluid dynamics, extracting the turbulent field to compute the acoustic source term via Lighthill’s analogy, and solving a homogeneous wave equation to propagate the noise in an open domain. The methodology is applied to a turbulent plane channel flow, simulating the acoustic field for a fluid with water-like density at a Mach number of 0.1. The results reveal the spatial distribution of the acoustic pressure, highlighting the dominant noise sources and their spectral characteristics. The acoustic domain extends beyond the turbulent region, enabling the study of pressure propagation outside the flow. The findings demonstrate that noise generation is strongly linked to turbulent structures near the walls, with significant acoustic radiation occurring in the low-wavenumber range. This framework provides a powerful tool for modeling noise propagation in marine and industrial applications, offering insights into turbulence-induced sound in underwater environments. Future work could extend the approach to more complex geometries, higher Reynolds numbers, and heterogeneous domains, further advancing its applicability to real-world acoustic challenges.
1. Introduction
The propagation of noise in fluids has become a critical area of research in recent decades due to its adverse effects on both human and animal populations. Underwater radiated noise, for example, has been the subject of numerous international and interdisciplinary studies, as it negatively impacts intra-species communication, biological processes, and physiology [1]. Similarly, fluid-dynamic noise in other contexts is recognized as a significant factor affecting human mental and physical well-being. In marine engineering, for instance, noise from ship propellers and bow thrusters reduces passenger comfort during travel [2].
Industrial environments also face challenges from noise pollution. Acoustic emissions from machinery, which propagate through the air, influence workplace conditions and can serve as diagnostic tools for equipment performance. For instance, acoustic signals are often used to detect operational anomalies such as cavitation in pumps and turbines. A notable example is the work of [3], which analyzed the correlation between acoustic signals and cavitation in a Kaplan turbine. They demonstrated that the modulation and intensity of cavitation generate predictable acoustic patterns, enabling the development of a semi-empirical model linking cavitation to noise and vibration.
It is crucial to develop accurate numerical methods for modeling acoustic wave propagation, particularly in complex and dynamic environments. Recent advancements in spatial-temporal prediction and deep learning-based feature extraction have shown promise in improving computational efficiency and predictive accuracy in related fields. For instance, ref. [4] proposed a spatial-temporal attention mechanism for predicting electric bus charging station loads, demonstrating the potential of time-series modeling in dynamic systems. Similarly, ref. [5] introduced a rotation feature decoupling network for ship detection, highlighting the importance of orientation-aware feature extraction in signal processing. Inspired by these approaches, this study explores advanced modeling techniques for acoustic wave propagation, leveraging spatial-temporal frameworks and feature-aware computational methods to enhance accuracy and efficiency.
To address the challenges of noise evaluation, Lighthill’s acoustic analogy [6,7] has become a widely adopted and computationally efficient method. Lighthill’s theory models fluid flow as a distributed field of acoustic sources (quadrupoles), enabling the decoupling of the fluid-dynamic and acoustic fields. This hybrid approach allows the two problems to be solved independently, making it less computationally demanding than full Computational Aeroacoustics (CAA) simulations [8]. The equation derived by Lighthill is based on mass and momentum conservation laws, with source terms directly linked to the flow velocity field. However, the accuracy of the method depends on the underlying fluid-dynamic model. Traditional Reynolds-Averaged Navier-Stokes (RANS) simulations are often inadequate for hydroacoustic analysis, as their time-averaged formulation captures only mean flow features, neglecting the turbulent spectrum responsible for broadband noise [9].
Despite this limitation, hybrid RANS/CAA techniques, which combine RANS simulations with statistical noise models, remain widely used in industrial applications due to their low computational cost [10]. However, for more accurate noise source characterization, state-of-the-art experimental techniques [11] or eddy-resolving computational simulations [12,13] are recommended.
In recent developments, Möhring proposed an alternative acoustic analogy based on the compressible Euler equations to account for convection and refraction effects in unsteady flows [14]. While this analogy provides valuable insights into noise propagation in dynamic media, it is less suitable for incompressible flows. In the low-speed regimes considered in this study, Lighthill’s analogy remains an appropriate choice for addressing hydroacoustic and subsonic problems. A notable limitation of Lighthill’s analogy, as well as its extension by Ffowcs-Williams and Hawkings [15], is its inability to account for certain complexities in noise generation and propagation, particularly when detailed source characterization is required. To address this, the present work employs the finite volume method (FVM) combined with hybrid open boundary conditions to study the hydroacoustic noise generation in a plane channel flow at . This methodology combines the strengths of both approaches. The Lighthill analogy is correctly applied, and hydroacoustic noise is considered. Finite Volume Methods (FVM), in turn, enable the modeling of reflections and refractions in complex geometries and domains. The methodology involves performing an eddy-resolving fluid-dynamic simulation to compute the unsteady flow field. The fluid-dynamic field is then evaluated as an acoustic source using Lighthill’s analogy. Finally, the acoustic source is propagated by solving the wave equation within the computational domain. This approach effectively models the hydroacoustic problem in a homogeneous domain and demonstrates its utility in capturing the essential dynamics of noise generation and propagation in channel flows. By focusing on a well-defined and controlled setup, this study provides insights into turbulence-induced noise mechanisms without introducing complexities such as layered media or heterogeneous domains.
Underwater acoustics plays a crucial role in a variety of marine applications, ranging from stealth technology in submarines to noise reduction in underwater structures. Several recent studies have explored different aspects of underwater acoustic phenomena, including target strength, metamaterials, cavitating vortex dynamics, and acoustic radiation from stiffened structures. Understanding these concepts is essential for improving the design and efficiency of underwater vehicles, communication systems, and marine propulsion technologies. One study investigates the acoustic target strength of submarines, which is critical for stealth and detection. Through numerical simulations, factors such as submarine shape, material properties, and insonification angles are analyzed to understand their impact on acoustic reflections. These findings contribute to advancements in sonar stealth technology and the development of low-observable underwater vehicles [16]. The study of underwater acoustic metamaterials presents another area of interest. These engineered materials manipulate underwater sound waves in unique ways, exhibiting properties such as negative refraction, wave focusing, and acoustic cloaking. Their applications span sonar stealth, underwater noise control, and enhanced underwater communication. Recent developments have explored tunable and broadband designs to enhance adaptability in dynamic marine environments [17]. Cavitating tip vortex dynamics also play a significant role in underwater acoustics, particularly in marine propulsion systems. The numerical investigation of cavitation effects on tip vortices provides insights into hydroacoustic signatures and noise emissions. Understanding these interactions is crucial for designing quieter and more efficient propulsion systems, ultimately leading to reduced acoustic disturbances in marine environments [18]. Finally, another relevant study explores the vibro-acoustic behavior of a submerged stiffened cylindrical shell under multiple excitations. Using both experimental tests and numerical simulations, the research examines how structural reinforcements influence sound radiation and vibration characteristics in underwater environments. By analyzing frequency responses and pressure distributions, the study provides insights into noise control strategies for applications such as submarine stealth technology and underwater pipelines [19]. These studies collectively enhance our understanding of underwater acoustics and contribute to the advancement of marine technology. It is therefore evident that a model capable of performing open-field propagation of noise generated by various sources is of fundamental importance. In this work, a novel numerical model is proposed to address these gaps by enabling the simulation of open-field noise propagation from multiple sources. The model integrates Lighthill’s equation with the hybrid absorbing boundary conditions developed by Liu and Sen [20], ensuring an accurate and stable representation of noise radiation in an unbounded domain. Unlike previous studies that focus on localized effects, this approach explicitly considers the full-field propagation of turbulent noise, offering a more holistic and physically realistic framework for hydroacoustic analysis. Additionally, the implementation of hybrid absorbing boundary conditions mitigates artificial reflections, enhancing the fidelity of numerical simulations.
This study introduces a novel computational framework for hydroacoustic noise simulation in a turbulent plane channel flow at . The methodology integrates Large Eddy Simulation (LES) to solve the fluid dynamics, Lighthill’s analogy to characterize the acoustic source, and the finite volume method (FVM) to propagate acoustic waves in a homogeneous medium. A key innovation is the adoption of hybrid absorbing boundary conditions, based on a combination of Higdon’s approach [21] and two-way classical wave equation [20], effectively minimizing spurious reflections at domain boundaries. Compared to prior studies, traditional approaches often relied on Reynolds-Averaged Navier-Stokes (RANS) simulations, which, while computationally efficient, failed to resolve the fine scale turbulence responsible for broadband noise generation [9]. The approach also extends prior channel flow investigations by capturing acoustic wave propagation outside the fluid domain, providing deeper insights into turbulence-induced noise mechanisms. By applying this refined methodology, the study successfully characterizes the spatial distribution of acoustic pressure and validates the spectral behavior of the noise, aligning with the Kolmogorov power law in the inertial subrange. This research paves the way for further advancements in hydroacoustic modeling, particularly for higher Reynolds numbers and complex boundary conditions. This research contributes to advancing the field of underwater acoustics by providing a robust tool for analyzing the spatial and spectral characteristics of noise in open environments. Future work will further refine the model through experimental validation and the inclusion of additional physical effects to improve predictive capabilities.
This paper is structured as follows: Section 2 describes the methodology in detail, including its numerical implementation and theoretical basis. Validation of the proposed approach against analytical solutions and benchmark models from the literature is presented in Section 3. In Section 4 the application of the model to a suitable case and the results of the simulation are presented. In Section 5, the results are analyzed, and potential directions for future development are outlined.
2. Material and Methods
2.1. The Wave Equation Discretization
Lighthill wave equation is given by Equation (1):
where p is the acoustic pressure, t is the time variable, c is the speed of sound, is the fluid density, is the pressure tensor, and is the Kronecker’s delta. The right-hand term is known as the Lighthill tensor. It allows the evaluation of the acoustic source based on the fluid dynamic fields of pressure and velocity, facilitating the analysis of noise generation and propagation within the domain by applying Lighthill’s analogy. The finite volume method (FVM) has been adopted to solve the wave equation in homogeneous domains. The main advantages of FVM are related to its conservative nature. This ensures that physical quantities, such as mass, momentum, and energy, are conserved within each control volume and, consequently, throughout the entire computational domain. This conservation property is crucial for accurately simulating physical phenomena, especially those involving fluid flow and acoustics, where imbalances in conserved quantities can lead to significant errors. Furthermore, FVM’s flexibility in handling arbitrary control volumes makes it well-suited for complex geometries, allowing for accurate representation of curved boundaries and intricate domain shapes. This geometric adaptability, combined with its inherent conservation properties, makes FVM a powerful tool for solving a wide range of problems in computational fluid dynamics and acoustics. In this study, we concentrate on structured grids comprising hexahedral elements. The computational domain is discretized into elementary control volumes, and the wave equation is integrated over these volumes:
where the last term represents the source term, referred to as the Lighthill tensor in the context of the acoustic wave equation. Applying the divergence theorem to the second term transforms the equation into:
where denotes the surface bounding the control volume, and is the outward normal vector to the surface.
To approximate the value of a quantity within an elementary control volume, we assume it varies linearly inside the volume, an assumption that is second-order accurate. The surface integral of the pressure gradient can then be expressed as the sum of the surface integrals over the faces of the cell. By further assuming that the integrand’s value is approximated at the midpoint of each face, the equation becomes:
where h represents the distance from the cell center to the face centroid. Applying a second-order discretization for the temporal and spatial derivatives, the equation evolves into:
Finally, solving for , the pressure update equation is:
This equation provides a second-order approximation of the generic wave equation under the assumptions of a homogeneous medium with constant sound speed and density over time, and a fluid at rest. A similar discretization of the wave equation for FVM and finite element methods has been detailed in previous work by [22], where it was applied to problems related to room acoustics. The stability condition for Equation (6) is determined by the Courant condition, expressed as .
2.2. The Hybrid Absorbing Boundary Condition
To prevent spurious reflections at the boundaries of the domain, it is necessary to employ specific boundary conditions known as open boundary conditions or absorbing boundary conditions. Various types of such conditions exist, but in this work, we adopt the approach proposed by [23], referred to as hybrid absorbing boundary conditions (hybrid ABS).
This method introduces a transition zone between the physical domain’s boundaries, where the solution will be evaluated free of reflections, and the complete computational domain’s limits. Within this transition zone, a wave equation that results from a weighted average of the classical wave equation, as discussed in Section 2.1, and the one-way wave equation derived from second-order Higdon conditions is solved [21]. Specifically, the second-order Higdon equation is expressed as:
where and are angles defining the directionality of the absorbing conditions, c is the wave velocity, and p represents the acoustic pressure field. Physically, it mimics the behavior of a perfectly non-reflecting boundary, allowing waves to pass through the boundary as if the domain extended infinitely. The previous equation considers the space derivative in just one direction for the nature itself of one-way wave equations. Different studies have already validated the Higdon boundary condition [24]. Thanks to the adoption of varying angles in its formulation, it offers improved absorption of grazing waves. However, this type of ABC is not sufficient on its own to provide adequate absorbance for waves characterized by large wavelengths. To overcome this limitation, Liu et al. in [23] formulated a new absorbing boundary condition, the Liu hybrid condition, which effectively combines the strengths of both the Higdon condition and a perfectly matched layer (PML) approach. This hybridization allows the Liu condition to handle both grazing waves and long wavelengths efficiently, resulting in significantly reduced reflections across a wider range of frequencies and incidence angles as seen in other literature works [20,25]. The wave equation solved in the absorbing zone is given by [23]. The combined wavefield p is expressed as:
where represents the two-way wavefields, represents the one-way wavefields, and the weight is a linear function that goes from 1 to 0 expressed by . Here, i denotes the layer index, and N is the total number of layers used in the hybrid absorbing boundary conditions (hybrid ABC). This approach ensures that reflections are effectively reduced, providing more accurate solutions within the domain of interest. The discratization of the wave equation in the transition domain is given by:
In Equation (9) the two-way wave equation is solved with the classical finite volume approach. The one-way wave equation is discretized instead with the finite difference since the derivative has to be evaluated in only one direction.
3. Validation
To perform the validation of the model, a comparison between the analytical solution of a monopole field and the numerical solution of the wave equation is shown. The monopole field is given by Equation (10):
Here, k denotes the wavenumber, i is the imaginary unit, represents the medium density, c is the wave speed, signifies the monopole’s strength, r is the distance from the monopole’s center, denotes the angular frequency, and t represents time. The monopole is applied as a Dirichlet boundary condition across nine cells (a cube) located at the center of the domain. This method of applying the source is referred to as a hard source. Refer to Figure 1 for a visual representation.

Figure 1.
Schematic of the numerical domain used to validate the method. The red cells represent the position of the monopole, the white cells are the physical domain where the simulation is carried out and the cyan cells represent the absorbing domain where the Equation (9) is solved, the green cell is where the microphone is placed and the solution is sampled.
For this simulation, the cells are cubic with an edge length of , where is the wavelength of the monopole source. The monopole frequency is equal to 50 Hz and the density and speed of sound of the medium are the same of the water one, = 1000 kg/m3 and m/s. The computational domain consists of a cube of edge equal to , (50 cells). The physical domain, where only the two way wave equation is solved, is contained within a cube whose edge measures (30 cells). Absorbing boundary conditions are applied in all three directions, occupying ten cells in each direction, as illustrated in Figure 1. Here the hybrid wave Equation (9) is solved. For this simulation Higdon’s angles are taken equal to and as suggested by [24] to minimize the reflections of grizzling waves and a total of 10 layers have been used.
The results in Figure 2 demonstrate that the numerical solution is sufficiently accurate to be regarded as a reliable numerical method. While the hybrid absorbing boundary conditions are less accurate than perfectly matched layers (PML), they are faster to implement and less computationally expensive. For these reasons, the authors chose to adopt a hybrid ABC for the proposed model.
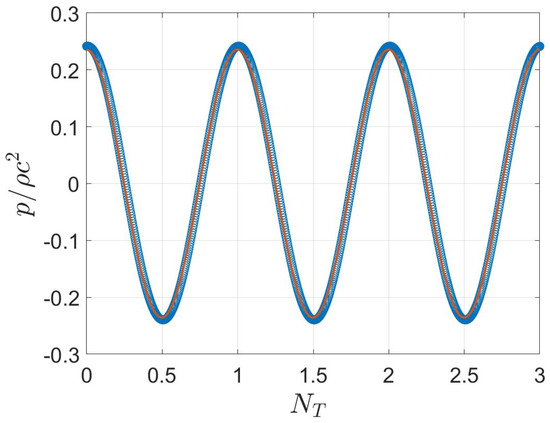
Figure 2.
Comparison between the analytical (continuous line) and numerical (circle markers) solution of the monopole. Pressure has been non-dimensionalized with density and speed of sound squared, represents the number of periods of the signal.
4. Simulation and Results
A fluid dynamic simulation has been carried out on a plane channel flow characterized by a Reynolds number equal to , being the shear velocity of the flow, h the semi-height of the channel and the kinematic viscosity. After the channel reached convergence the fluid dynamic fields were used to compute the acoustic source given in Equation (1). Only the first term of the Lighthill tensor has been considered in this study, as supported by the literature [6]. The remaining terms are negligible for small Mach number values. The channel flow simulation has been validated by comparing its statistical properties with the results of [26] (validation not shown here).
To obtain the fluid dynamic fields, a Large Eddy Simulation (LES WALE model) was performed. The dimensions of the channel are defined as in the streamwise direction, in the wall-normal direction, and in the spanwise direction, where is set to one. The channel is discretized using a grid of elements.
In non-dimensional wall units, the grid spacing is:
- ,
- ,
- at the wall, with a growth rate of 1.07 in the wall-normal direction.
The simulation was run until convergence was achieved. Once the stationary condition was reached, velocity fields were sampled every non-dimensional time unit over a total duration of 3 non-dimensional time unit. The Lighthill source was computed for each sampled timestep on the fluid dynamic grid and subsequently mapped onto the acoustic grid. The acoustic grid consists of uniform hexahedral elements without any stretching applied in any direction. This approach is justified by the distinct requirements of the two simulations: in the acoustic problem, there is no necessity for a refined grid near the walls, whereas, in the fluid dynamic simulation, grid resolution is critical for capturing the essential features of the flow. Therefore, the acoustic grid spacing is set equal to the fluid dynamic grid spacing in the streamwise and spanwise directions, while a different spacing is adopted in the wall-normal direction, where . The geometric dimensions of the acoustic problem are similar to those of the fluid dynamic domain, with the exception of the wall-normal direction, where the total height is extended. Specifically, for the acoustic simulation, . This extension allows for the sampling of the pressure propagated outside the channel.
The acoustic simulation is conducted in a fluid with a density equivalent to that of water, , and a speed of sound set to ten times the mean flow velocity of the channel, . This results in a Mach number of . The choice of this speed of sound, instead of the actual speed of sound in water, is made to enable faster simulations while maintaining the same Courant number, .
The results presented in Figure 3 are reported in terms of the non-dimensional pressure signal and its Fast Fourier Transform (FFT). The signal was sampled within the acoustic domain at various heights, providing insights into the pressure field at different locations relative to the channel.
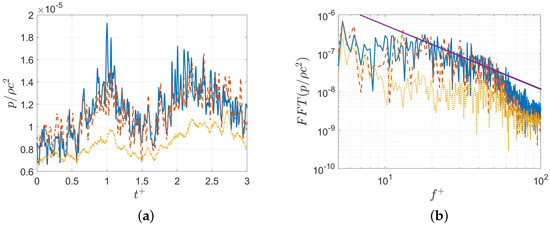
Figure 3.
Solution of the acoustic simulation in three domain points. The blue continuous lines refer to the signal of the non-dimensional pressure near the wall (). The red dashed lines refer to the pressure signal in the center of the channel () and the yellow dotted lines refer to the pressure outside the channel (). In Figure (b) the point-continuous purple line represents the power law .
The pressure signal measured near the wall exhibits the highest noise levels among the three sampling points. This can be attributed to the strong influence of the acoustic source in regions where turbulence is highly anisotropic. On the other hand, in the center of the channel, the source’s impact on the final pressure signal diminishes slightly, resulting in a moderately reduced pressure amplitude, as shown in Figure 3a. Finally, the signal sampled outside the channel is unaffected by the direct influence of the acoustic source, leaving pressure propagation as the sole mechanism contributing to the recorded signal.
Figure 3b shows the FFT of the pressure signals. Notably, the purple dashed line represents the Kolmogorov power law. For the two signals sampled within the channel, the pressure spectrum follows the Kolmogorov power law over a non-dimensional frequency range of approximately 20 to 50. This behavior indicates that, in this frequency range, the noise is generated by the inertial subrange of turbulence, which exhibits dynamics consistent with the Kolmogorov law. Conversely, the pressure signal recorded outside the fluid domain deviates significantly from this behavior. This deviation is likely due to the reduced influence of the source at this location, where propagation effects dominate.
5. Conclusions
The analysis of the results demonstrates the effectiveness of the proposed methodology in capturing the acoustic field generated and propagated by turbulent channel flow. Sampling the pressure at different heights provided key insights into the influence of the acoustic source and the propagation characteristics.
The highest noise levels observed near the wall suggest a direct link between acoustic source strength and turbulence anisotropy. The slight reduction in pressure amplitudes at the channel center indicates that the turbulence’s isotropic regions have a comparatively weaker influence on the acoustic signal. Outside the channel, the source’s direct influence vanishes, and propagation effects solely determine the pressure signal. This highlights the importance of accurately modeling both source generation and propagation mechanisms to predict the acoustic field effectively.
The FFT analysis further supports these findings by demonstrating adherence to the Kolmogorov power law within the inertial subrange for signals sampled inside the channel. The absence of this behavior in the signal sampled outside the domain underlines the reduced influence of turbulence-induced sources at greater distances.
The method has demonstrated good robustness when applied to broadband signals, such as those generated by a turbulent channel. However, the model has some limitations, primarily related to the time-step resolution required for mapping fluid dynamic fields from the fluid grid to the acoustic grid. This process involves storing the acoustic source field in memory and subsequently mapping it conservatively onto the acoustic grid. Moreover, to ensure high accuracy, multiple layers of the absorbing boundary condition are required, which significantly increases the computational cost of the simulation. Moreover, the Lighthill equation presented in this work can be applied to homogeneous materials, therefore, modifications are necessary to account for variations in density. Finally, applying Lighthill’s analogy necessitates the use of complex turbulence models such as Large Eddy Simulations (LES), which further add to the computational burden.
To overcome these limitations, future work could focus on optimizing the mapping process between the fluid and acoustic grids, potentially by implementing parallel mapping between the fluid dynamic simulation and the acoustic one. Alternative absorbing boundary conditions with improved efficiency could be explored to reduce the computational cost while maintaining accuracy. Additionally, this study could be extended by exploring how the acoustic field behaves under varying flow conditions, such as higher Reynolds numbers or non-periodic boundary conditions. Additionally, investigating the effects of different source configurations or material properties in multi-layered propagation media could provide valuable insights for practical applications in hydroacoustics and aeroacoustics.
Funding
This research has received financial support from MUR (Ministero della Università e della Ricerca) in the program PRIN 2022 with project number 20227AMAYL.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The author would like to express their sincere gratitude to Vincenzo Armenio and his research team at the University of Trieste for their invaluable guidance and support in the portion of this study undertaken by Renato Montillo during his Ph.D. We greatly appreciate their generosity in sharing their knowledge and time, which greatly contributed to the successful completion of this project.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LES | Large Eddy Simulation |
| RANS | Reynolds-Averaged Navier-Stoke |
| CAA | Computational Aeroacoustic |
| ABC | Absorbing Boundary Conditions |
| FVM | Finite Volume Method |
References
- Di Franco, E.; Pierson, P.; Di Iorio, L.; Calò, A.; Cottalorda, J.; Derijard, B.; Di Franco, A.; Galvé, A.; Guibbolini, M.; Lebrun, J.; et al. Effects of marine noise pollution on Mediterranean fishes and invertebrates: A review. Mar. Pollut. Bull. 2020, 159, 111450. [Google Scholar] [CrossRef] [PubMed]
- Borelli, D.; Gaggero, T.; Rizzuto, E.; Schenone, C. Onboard ship noise: Acoustic comfort in cabins. Appl. Acoust. 2021, 177, 107912. [Google Scholar] [CrossRef]
- Rus, T.; Dular, M.; Širok, B.; Hočevar, M.; Kern, I. An Investigation of the Relationship Between Acoustic Emission, Vibration, Noise, and Cavitation Structures on a Kaplan Turbine. J. Fluids Eng. 2007, 129, 1112–1122. [Google Scholar] [CrossRef]
- Xiao, G.; Tong, H.; Shu, Y.; Ni, A. Spatial-temporal load prediction of electric bus charging station based on S2TAT. Int. J. Electr. Power Energy Syst. 2025, 164, 110446. [Google Scholar] [CrossRef]
- Chen, X.; Wu, H.; Han, B.; Liu, W.; Montewka, J.; Liu, R.W. Orientation-aware ship detection via a rotation feature decoupling supported deep learning approach. Eng. Appl. Artif. Intell. 2023, 125, 106686. [Google Scholar] [CrossRef]
- Lighthill, M.J. On sound generated aerodynamically I. General theory. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1952, 211, 564–587. [Google Scholar]
- Lighthill, M.J. On sound generated aerodynamically II. Turbulence as a source of sound. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1954, 222, 1–32. [Google Scholar]
- Tam, C.K.W. Computational Aeroacoustics: A Wave Number Approach; Cambridge University Press: New York, NY, USA, 2012; Volume 33. [Google Scholar] [CrossRef]
- Piomelli, U.; Streett, C.L.; Sarkar, S. On the computation of sound by large-eddy simulations. J. Eng. Math. 1997, 32, 217–236. [Google Scholar] [CrossRef]
- Ewert, R.; Dierke, J.; Neifeld, A.; Appel, C.; Siefert, M.; Kornow, O. CAA broadband noise prediction for aeroacoustic design. Procedia Eng. 2010, 6, 254–263. [Google Scholar] [CrossRef]
- Felli, M.; Grizzi, S.; Falchi, M. A novel approach for the isolation of the sound and pseudo-sound contributions from near-field pressure fluctuation measurements: Analysis of the hydroacoustic and hydrodynamic perturbation in a propeller-rudder system. Exp. Fluids 2014, 55, 1651. [Google Scholar] [CrossRef]
- Posa, A.; Broglia, R.; Felli, M.; Cianferra, M.; Armenio, V. Hydroacoustic analysis of a marine propeller using large-eddy simulation and acoustic analogy. J. Fluid Mech. 2022, 947, A46. [Google Scholar] [CrossRef]
- Cianferra, M.; Armenio, V.; Ianniello, S. Hydroacoustic noise from different geometries. Int. J. Heat Fluid Flow 2018, 70, 348–362. [Google Scholar] [CrossRef]
- Mohring, W. A well posed acoustic analogy based on a moving acoustic medium. arXiv 2010, arXiv:1009.3766. [Google Scholar]
- Ffowcs Williams, J.E.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar] [CrossRef]
- Sathish, K.; Anbazhagan, R.; Venkata, R.C.; Arena, F.; Pau, G. Investigation and numerical simulation of the acoustic target strength of the underwater submarine vehicle. Inventions 2022, 7, 111. [Google Scholar] [CrossRef]
- Dong, E.; Cao, P.; Zhang, J.; Zhang, S.; Fang, N.X.; Zhang, Y. Underwater acoustic metamaterials. Natl. Sci. Rev. 2023, 10, nwac246. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Bai, X.; Cheng, H.; Ji, B.; Peng, X. Numerical investigation of cavitating tip vortex dynamics and how they influence the acoustic characteristics. Phys. Fluids 2023, 35, 062119. [Google Scholar]
- Tang, Y.; Zhao, Z.; Qin, Y.; Pang, F.; Du, Y.; Gao, C.; Li, H. Experimental and numerical investigation on vibro-acoustic performance of a submerged stiffened cylindrical shell under multiple excitations. Thin-Walled Struct. 2024, 197, 111569. [Google Scholar] [CrossRef]
- Liu, Y.; Sen, M.K. A hybrid absorbing boundary condition for elastic wave modeling with staggered-grid finite difference. In SEG Technical Program Expanded Abstracts 2010; Society of Exploration Geophysicists: Houston, TX, USA, 2010; pp. 2945–2949. [Google Scholar]
- Higdon, R.L. Numerical absorbing boundary conditions for the wave equation. Math. Comput. 1987, 49, 65–90. [Google Scholar] [CrossRef]
- Hamilton, B. Finite Difference and Finite Volume Methods for Wave-Based Modelling of Room Acoustics. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2016. [Google Scholar]
- Liu, Y.; Sen, M.K. A hybrid scheme for absorbing edge reflections in numerical modeling of wave propagation. Geophysics 2010, 75, A1–A6. [Google Scholar] [CrossRef]
- Gao, Y.; Song, H.; Zhang, J.; Yao, Z. Comparison of artificial absorbing boundaries for acoustic wave equation modelling. Explor. Geophys. 2017, 48, 76–93. [Google Scholar] [CrossRef]
- Li, B.; Liu, Y.; Zhao, Y.; Liu, X. Hybrid absorbing boundary condition for piecewise smooth curved boundary in 2D acoustic finite difference modelling. Explor. Geophys. 2018, 49, 469–483. [Google Scholar] [CrossRef]
- Moin, P.; Kim, J. Numerical investigation of turbulent channel flow. J. Fluid Mech. 1982, 118, 341–377. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).