1. Introduction
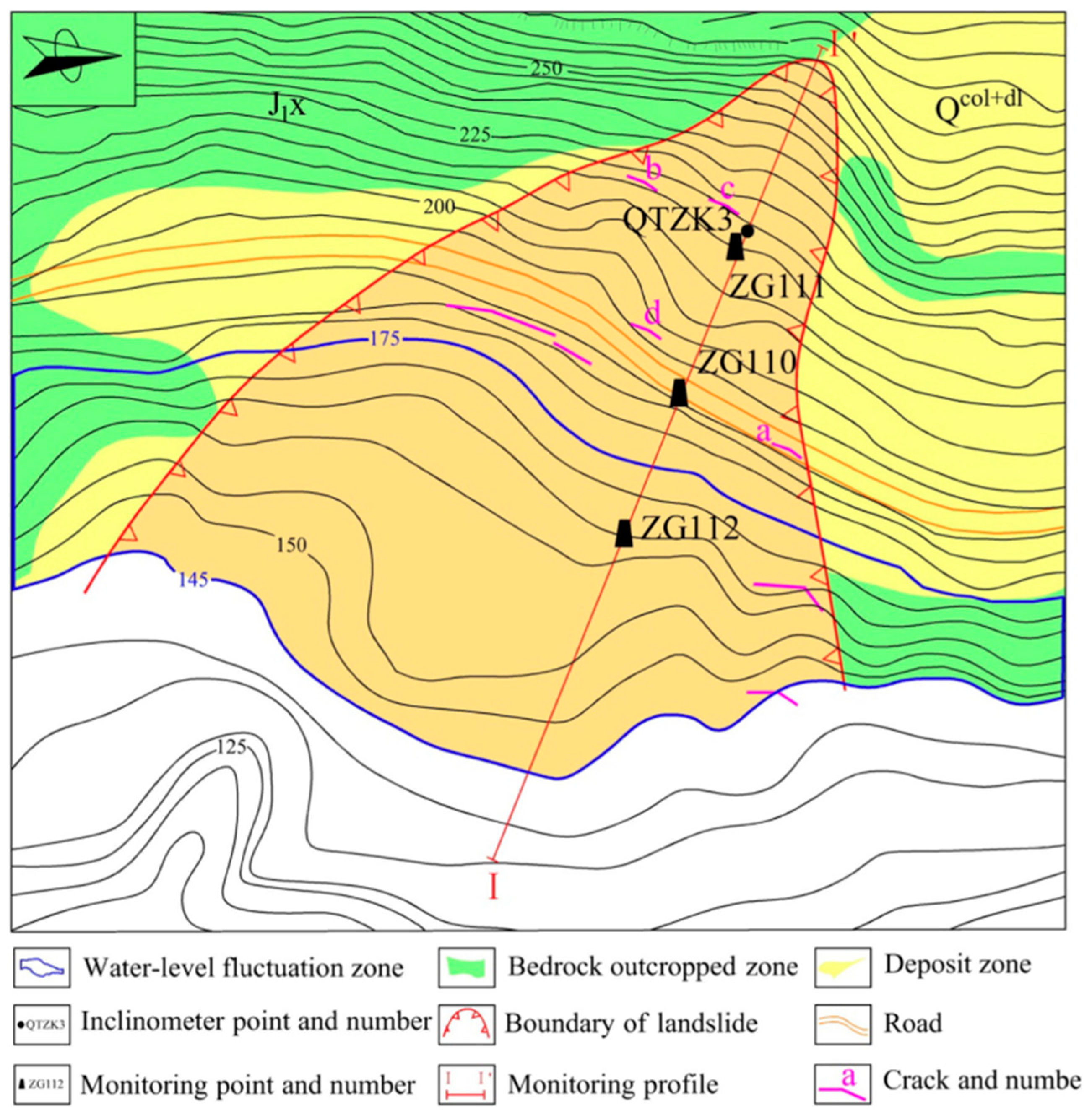
A reservoir-type accumulation layer landslide [
1,
2,
3] refers to a special type of landslide in which the accumulation layer located on the reservoir bank or in the reservoir area slides under the action of reservoir water storage, which is the result of the coupled action of a variety of factors [
4,
5,
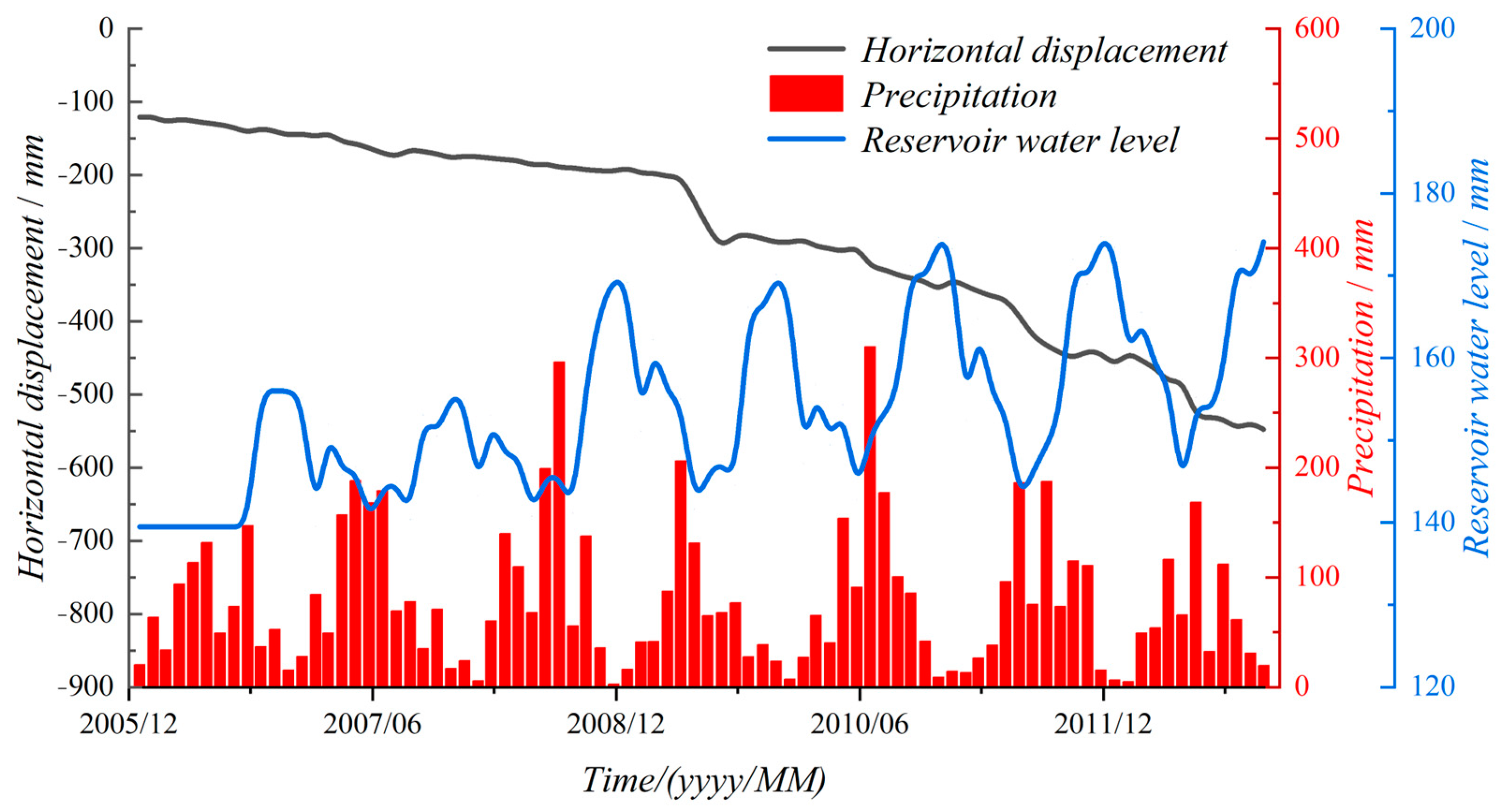
6], including the following: reservoir water storage increases the water table in the reservoir area, resulting in an increase in the internal pore water pressure of the accumulation layer, and a decrease in the effective stress, which weakens the shear strength of the accumulation layer, and is prone to sliding [
7]; when the reservoir water is impounded, the water level rises, the slope angle of the bank is subject to scouring and erosion, resulting in the expansion of the slope angle, which increases the probability of landslides [
8]; after the reservoir impoundment, the soil under the accumulation layer is subject to water pressure, and the change of the self-weight stress leads to the change in stability [
9]; the external forces such as earthquakes, rainfall and other external forces may lead to the occurrence of the issues in the accumulation layer, exacerbating the occurrence of landslides, etc. [
10]. Due to the complex and diverse formation conditions of reservoir-type stacked-layer landslides, accurate and effective landslide displacement prediction methods have been under constant exploration, and there is an urgent need for accurate, effective early warning and forecasting methods for this type of landslide hazard [
11].
Currently, there are four main types of landslide prediction models:
Physico-mechanical model [
12,
13]. This model is based on the mechanical properties and geological structure of the landslide body, and predicts the displacement of the landslide by analyzing the force on the landslide body and the deformation characteristics of the rock-soil layer, etc. Miao et al. [
14] developed a Verhulst-Grey model for landslide time prediction based on the improved Saito method, and verified its reliability by using the landslide monitoring data. To realize rainfall-type landslide prediction for landslides in the Hulu Kelang area, Kim et al. [
15] proposed the YS-Slope model by considering the groundwater level and rainfall infiltration on soil stability. Jeong et al. [
16] assessed the stability of shallow landslides in the Hulu Kelang area by combining the GIS physical model, YS-Slope, with a geohydrological model. Physico-mechanical models have numerous parameters and usually require a large number of geologic parameters and site data such as groundwater level, soil properties, rainfall characteristics, topography, and anthropogenic activities for accurate prediction [
17].
Statistical modelling [
18]. Statistical models build mathematical models to predict landslide displacements by statistically analyzing historical landslide events and related factors. Yang et al. [
19] regarded the landslide displacement prediction problem as a time series regression problem with a limited number of training samples, and proposed a probabilistic landslide displacement prediction model with quantified cognitive uncertainty, whose prediction accuracy is better than other probabilistic prediction models. Ma et al. [
20] combined the Newmark model and two statistical analysis models (logistic regression and support vector machine, LR and SVM) with critical acceleration ac data to assess earthquake landslide hazard. Statistical models often employ probabilistic statistics, regression analysis, and cluster analysis, which usually require a large amount of historical data for modelling and analysis, and the incompleteness of the data in some specific cases limits their applicability and also affects the accuracy of the model [
21].
Numerical simulation [
22]. The development trend and displacement of landslides were predicted by numerical calculations. Jiang et al. [
22] took the bridgehead landslide on the side of the Three Gorges reservoir area as an example, and through numerical simulation and experimental testing, it was found that the initial stage of the landslide deformation was mainly affected by seepage, and the later stage was mainly affected by consolidation. Dai et al. [
23] proposed a landslide early warning method based on dynamic bandwidth allocation (DBA)-long short-term memory (LSTM) algorithm by combining machine learning and numerical simulation methods. Zhao et al. [
24] conducted finite element numerical simulation of the Shuping landslide process, revealing the important role of rainfall in the occurrence of Shuping landslides. Xu et al. [
25] proposed to use the numerical simulation results to expand the dataset required for deep learning, and constructed a slope displacement prediction model combining numerical simulation and deep learning to improve the prediction accuracy. Numerical simulation is now widely used in landslide displacement prediction, but its dependence on model parameter selection significantly limits the accuracy of prediction results.
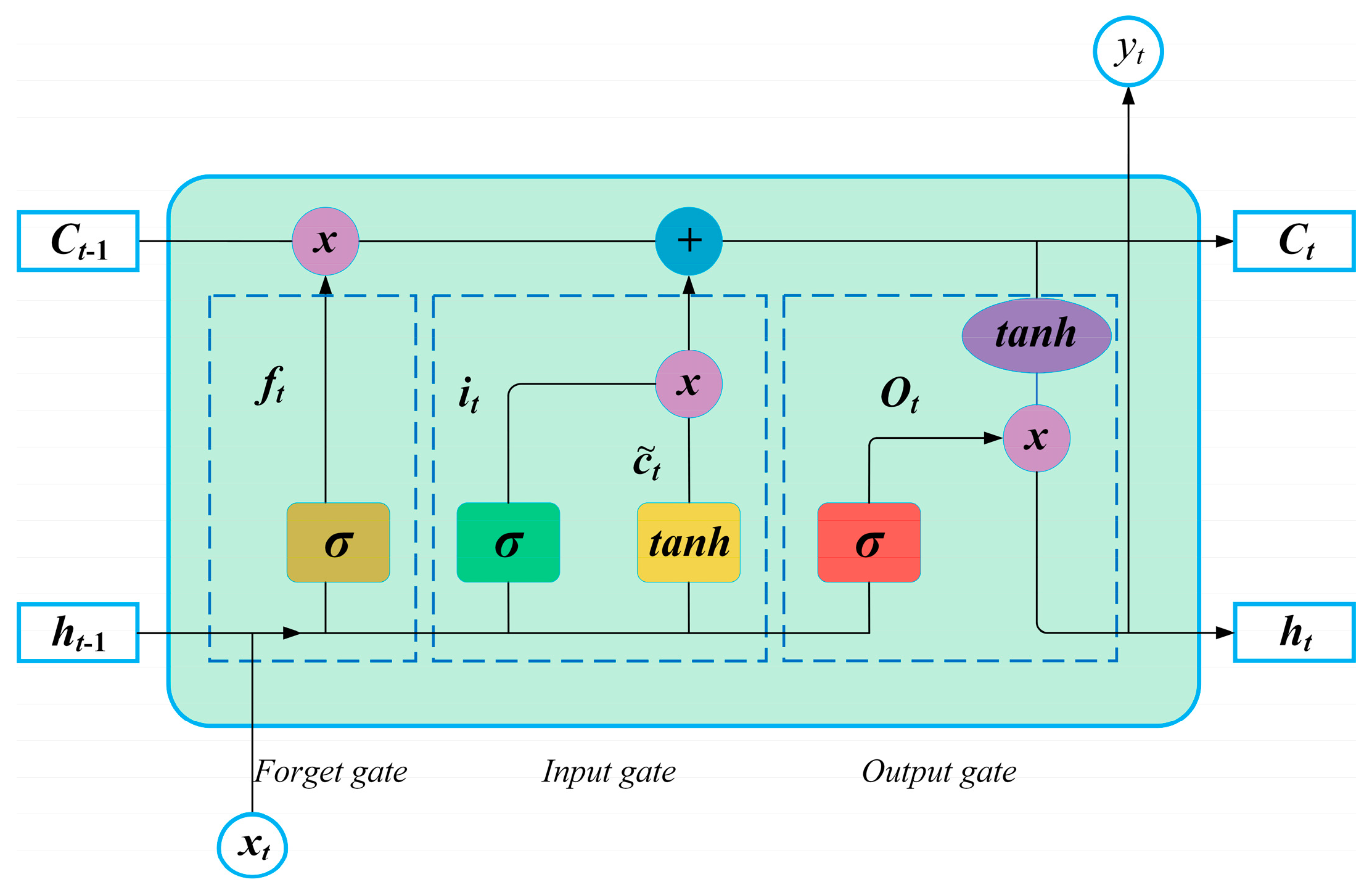
Machine learning model [
26,
27]. Machine learning algorithms are used to learn and train the landslide prediction data, and construct a model to predict landslide displacement. Miao et al. [
28] established an additive time series model for landslide displacement prediction by analyzing the deformation characteristics of the Baishui River landslide, and predicted the displacement change of the landslide. Zhang et al. [
29] proposed a landslide dynamic displacement prediction method based on the combination of gated recurrent unit (GRU) and time series analysis method: the accuracy of prediction was better than that of support vector machine (SVM). Zhou et al. [
30] examined the rainfall, reservoir level, and landslide stepwise deformation characteristics, and proposed a landslide prediction method based on the PSO-SVM coupled model. They concluded that the rainfall and the reservoir level were the dominant factors affecting most landslides in Three Gorges Reservoir area. Huang et al. [
31] proposed a multivariate chaotic extreme learning machine (ELM) model to predict the landslide displacements of reservoirs in the Three Gorges reservoir area. The model prediction accuracy is better than that of the univariate chaotic ELM model and the multivariate chaotic PSO-SVM model. Machine learning models, leveraging their robust data processing capabilities, automated modeling proficiency, and adaptability to complex nonlinear relationships, can circumvent the simplified assumptions inherent in traditional physical mechanics models, statistical models, and numerical simulation models [
32]. By reducing reliance on physical theories and assumptions, these models can fully exploit data for predictive purposes, thereby addressing some of the limitations of conventional methods in terms of accuracy, efficiency, and applicability. However, no study has yet used the displacement vector angle, a landslide stability evaluation parameter, for landslide displacement prediction, which limits the comprehensiveness and innovation of the model.
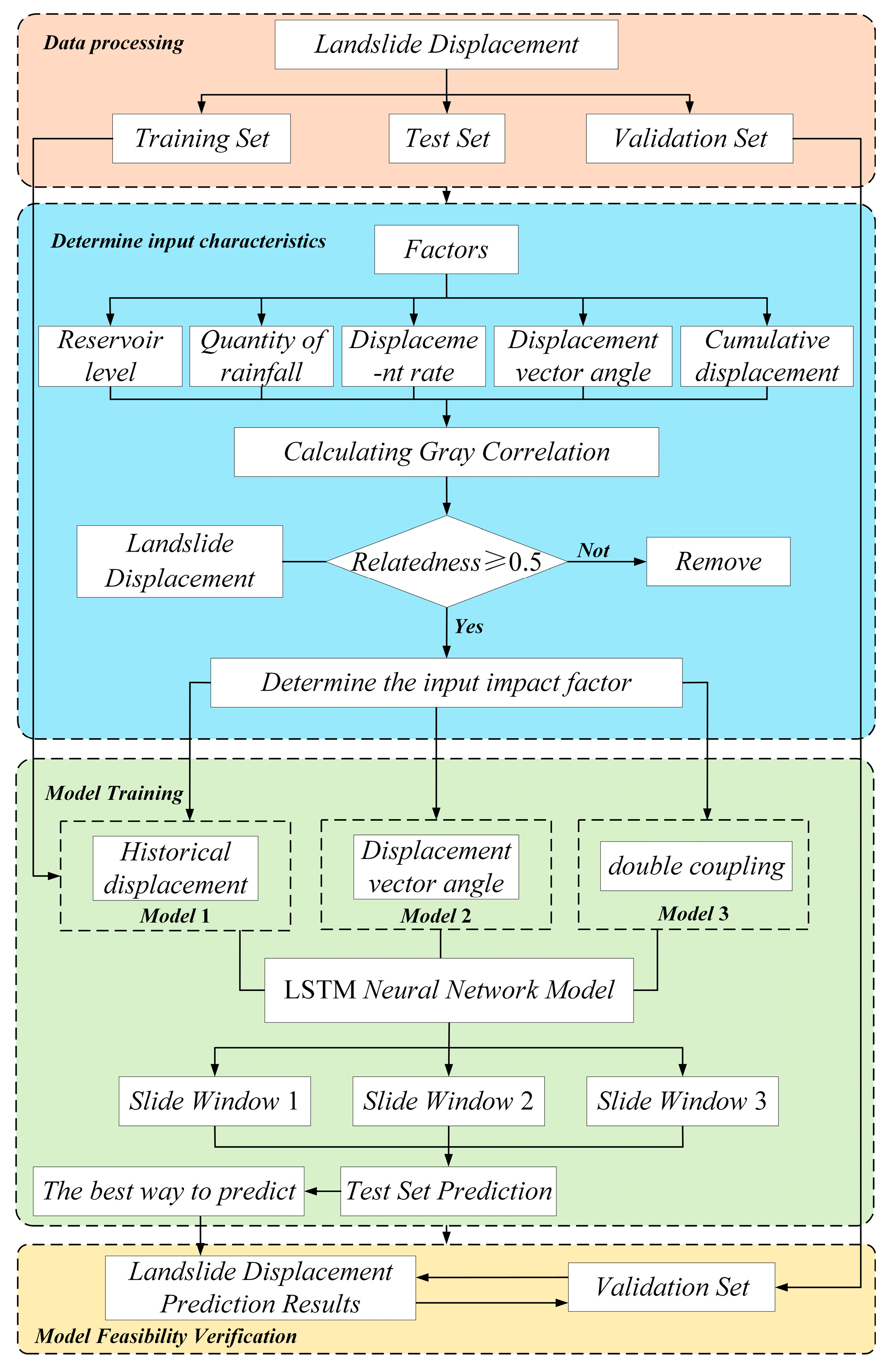
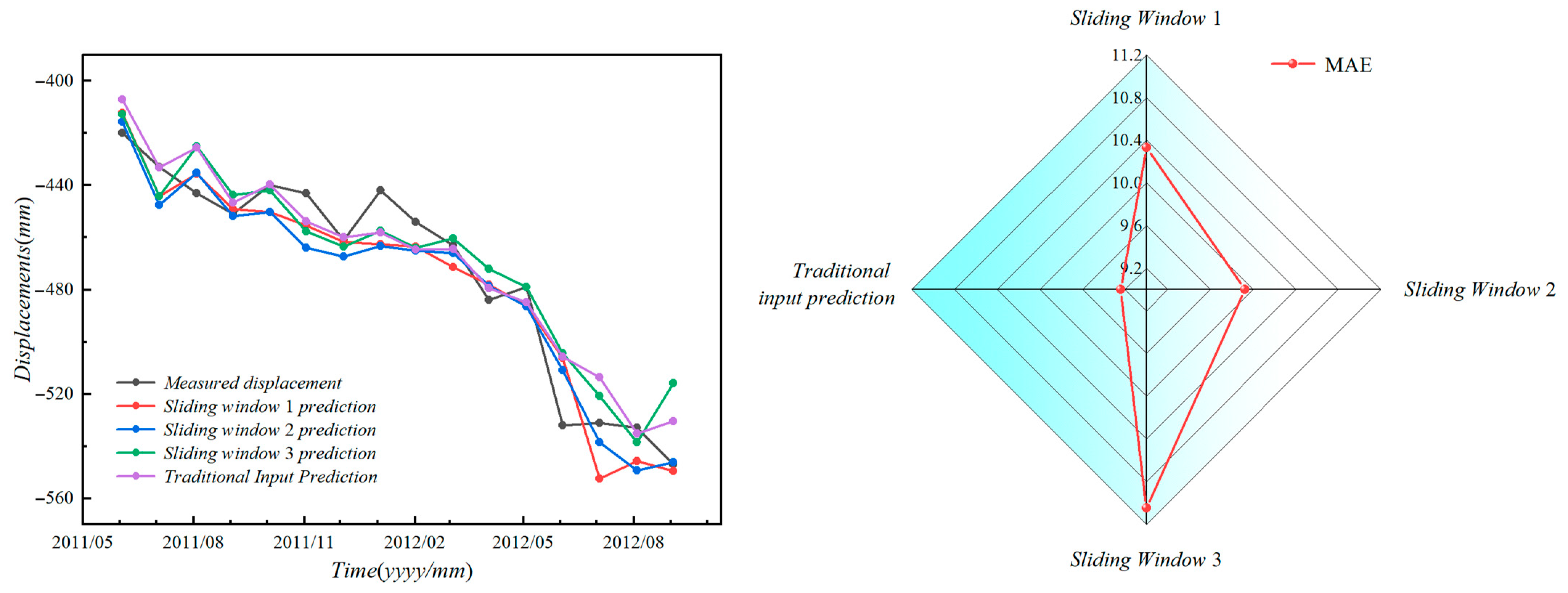
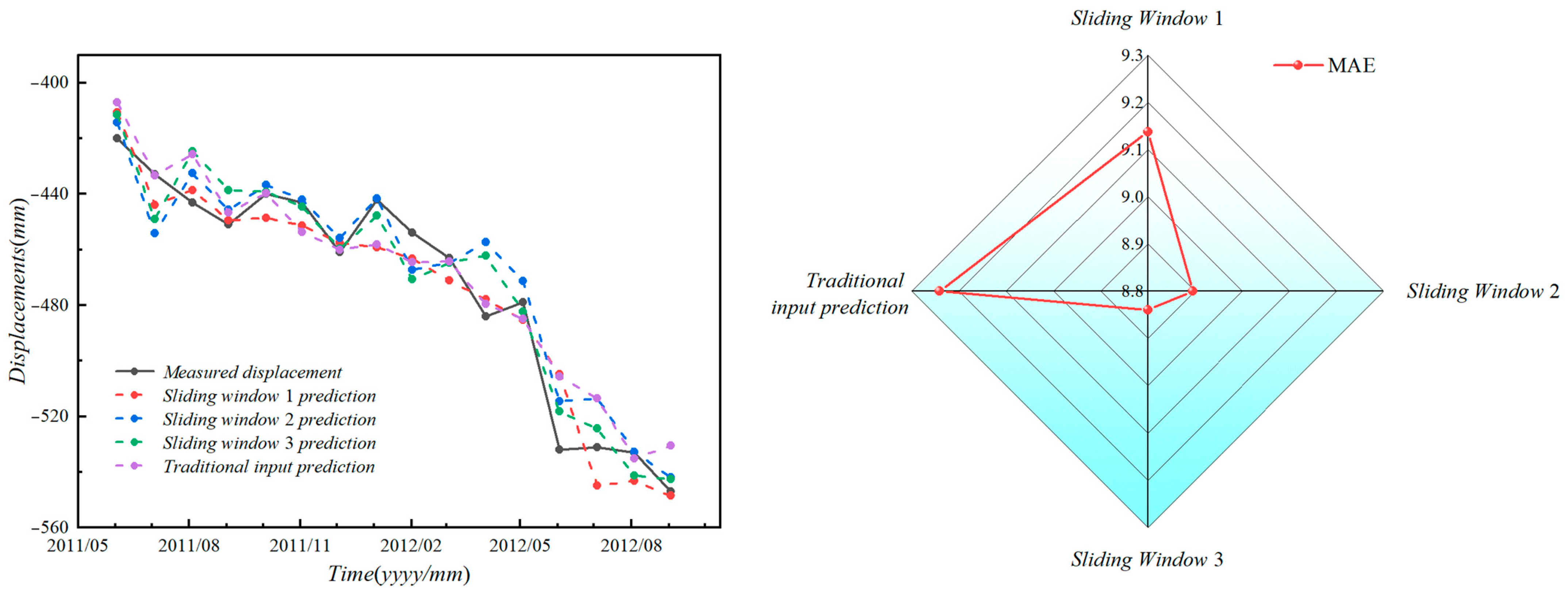
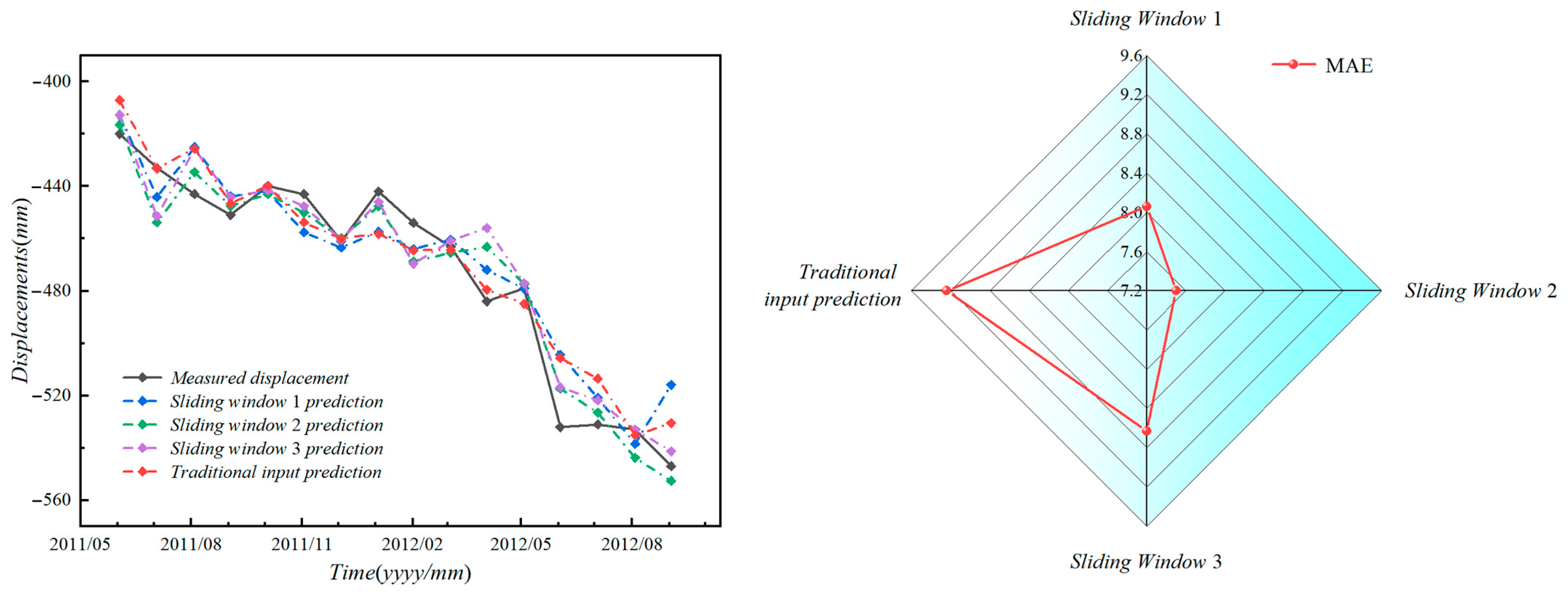
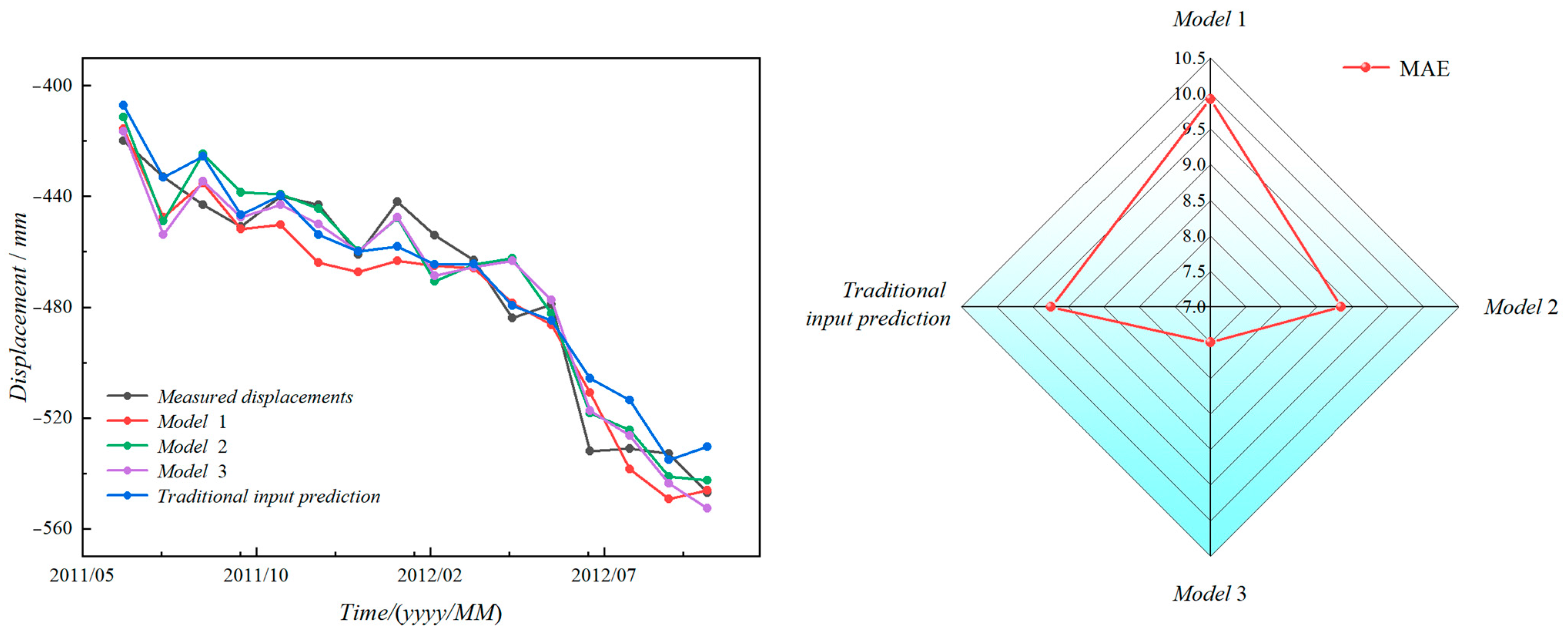
To investigate the potential of using displacement vector angles as input features for predicting landslide displacement, this study introduces historical displacement and displacement vector angles, along with reservoir water levels, rainfall, and displacement rates, as inputs to neural networks. Different feature combinations are constructed to predict landslide displacement. Gray relational analysis is employed to determine the correlation between displacement vector angles, reservoir water levels, rainfall, displacement rates, and landslide displacement, providing a preliminary assessment of the feasibility of using displacement vector angles as input features. By establishing LSTM neural network models with varying sliding window sizes, the impact of different feature combinations and sliding window sizes on landslide displacement prediction is evaluated and analyzed, thereby assessing the potential of displacement vector angles as input features for predicting landslide displacement.