An Investigation of the Thickness of Huhenuoer Lake Ice and Its Potential as a Temporary Ice Runway
Abstract
1. Introduction
2. Basic Natural Conditions at Huhenuoer Lake
3. Wind Rose Analysis and Assessment of the Ice Thickness Research Site
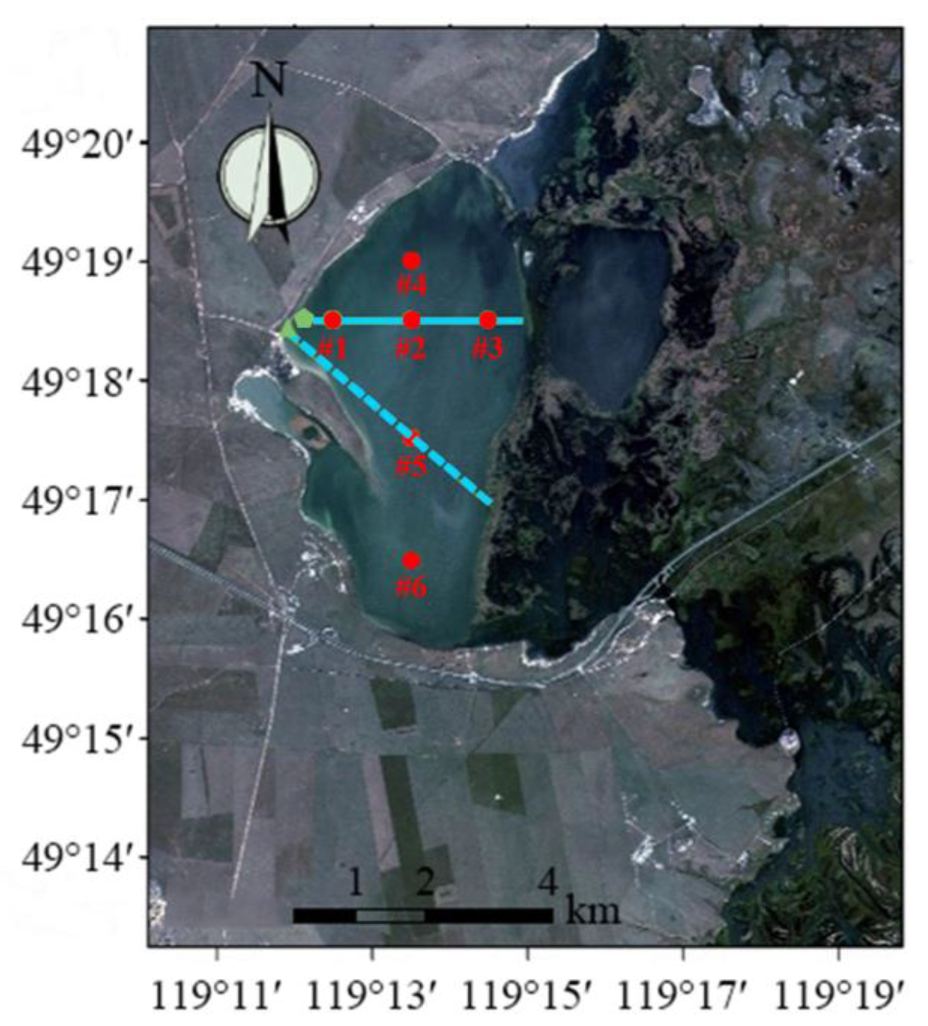
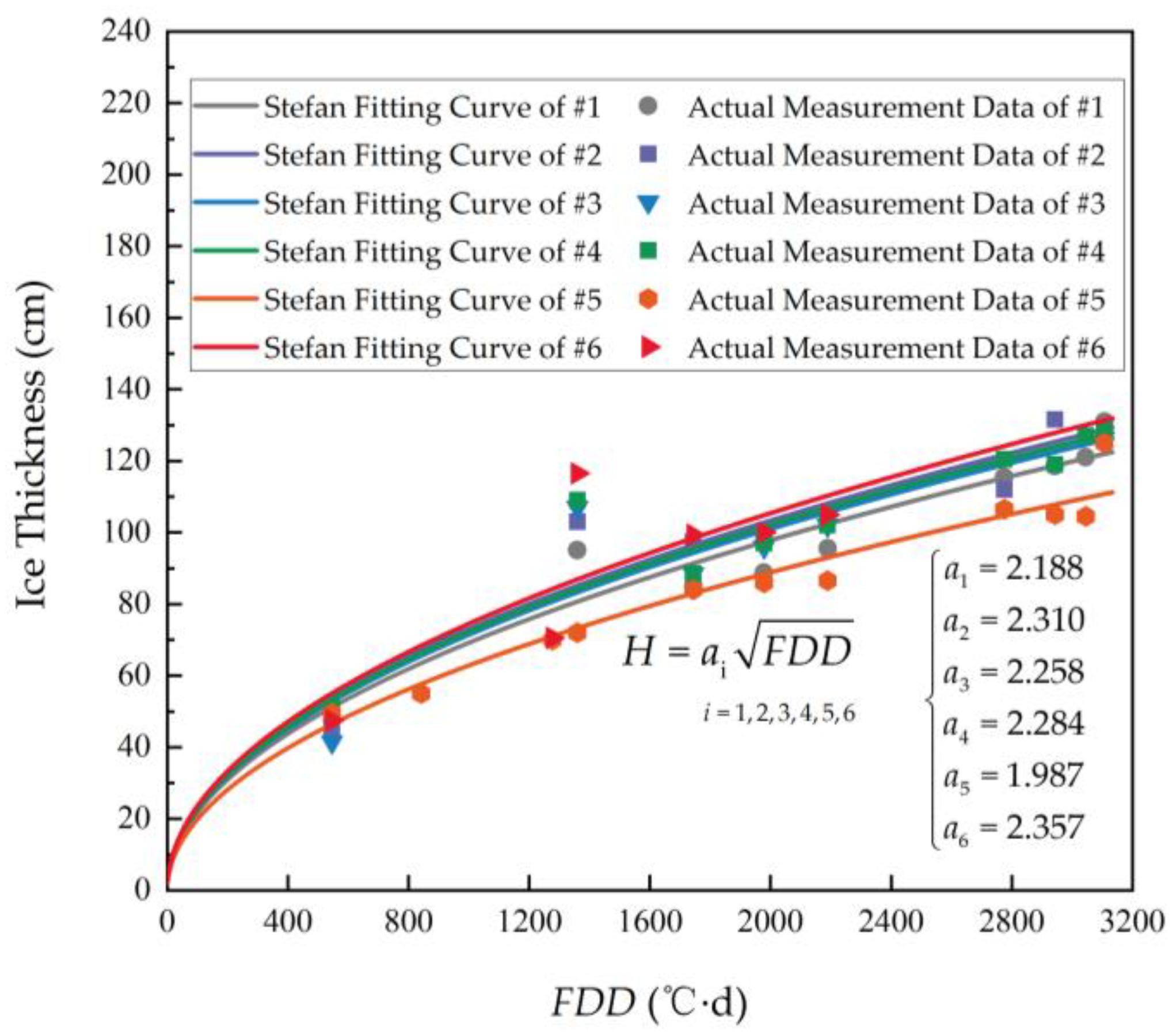
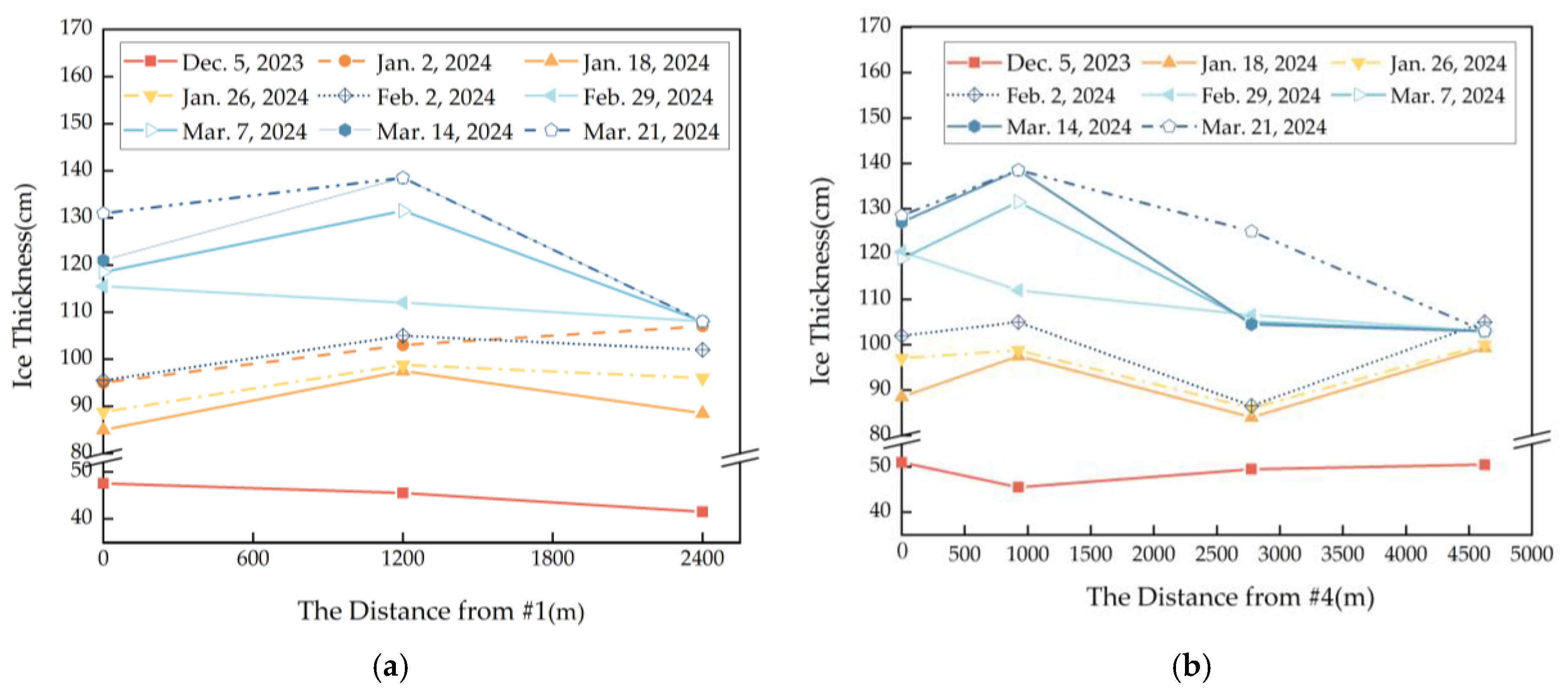
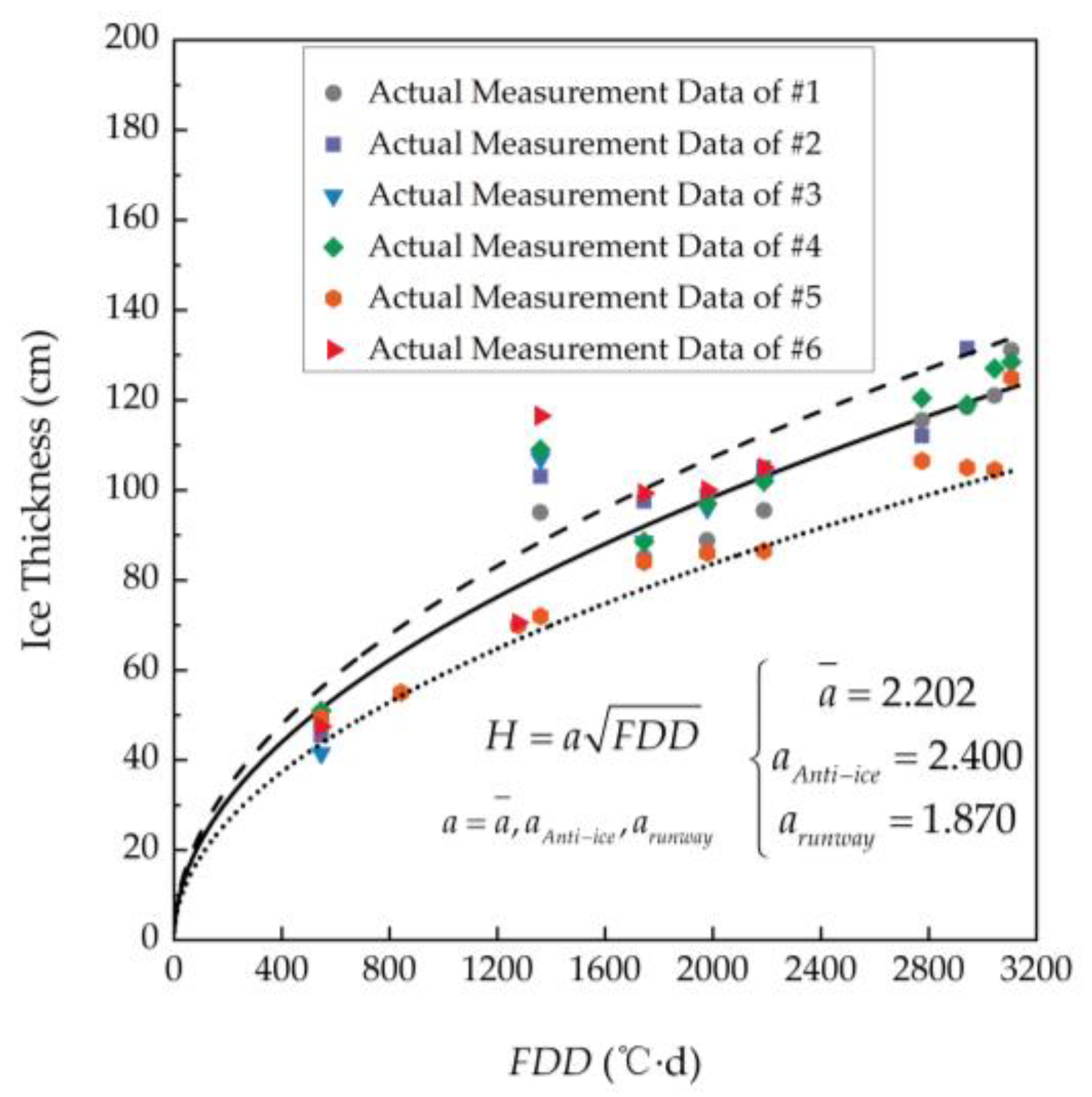
4. Measurement of Ice Thickness Distribution and Its Relationship with Negative Accumulated Temperature
5. Feasibility Analysis of Huhenuoer Lake Ice as a Temporary Runway
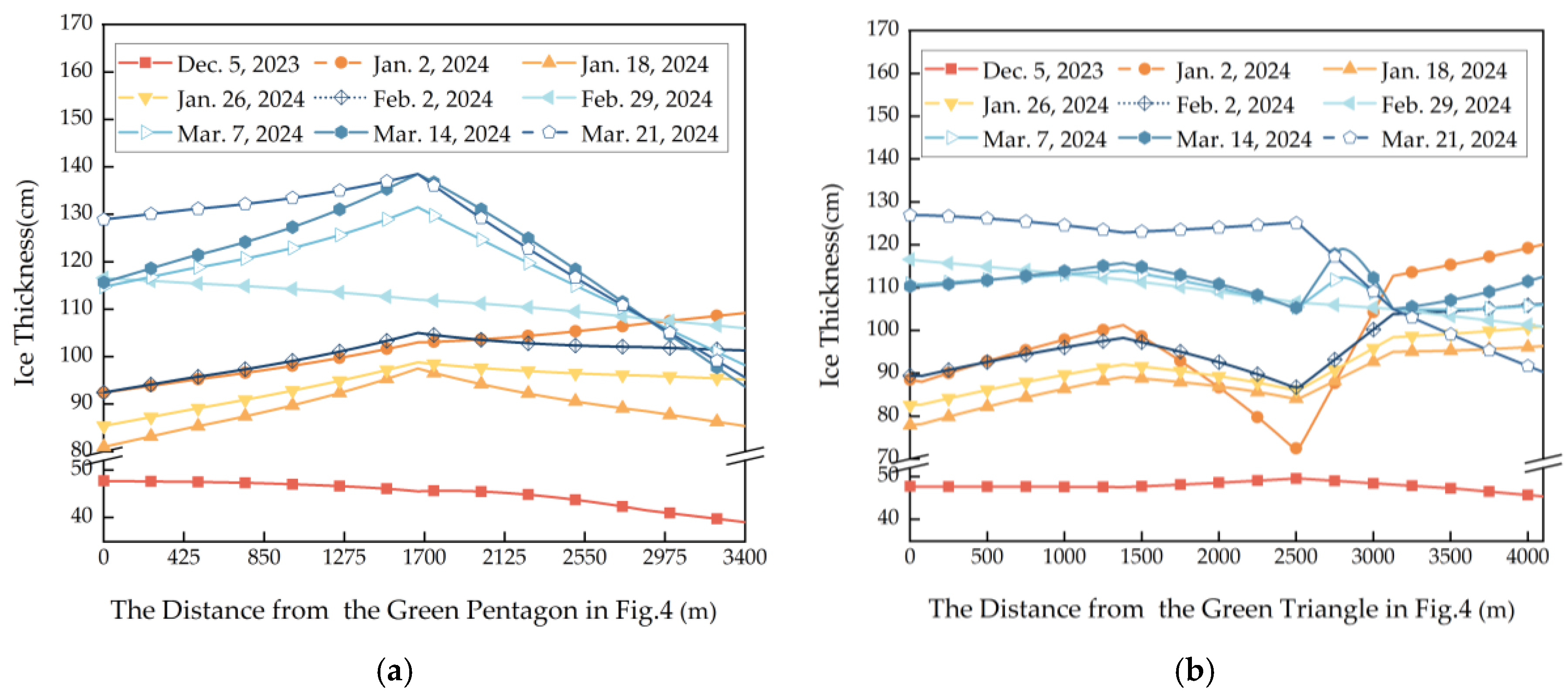
5.1. The Runway Position and Ice Thickness Distribution
- The non-uniformity should be minimized, where non-uniformity = (maximum ice thickness along the route − minimum ice thickness along the route)/maximum ice thickness along the route.
- The maximum change rate should be minimized, where the maximum change rate refers to the highest value of non-uniformity per unit length over the entire route.
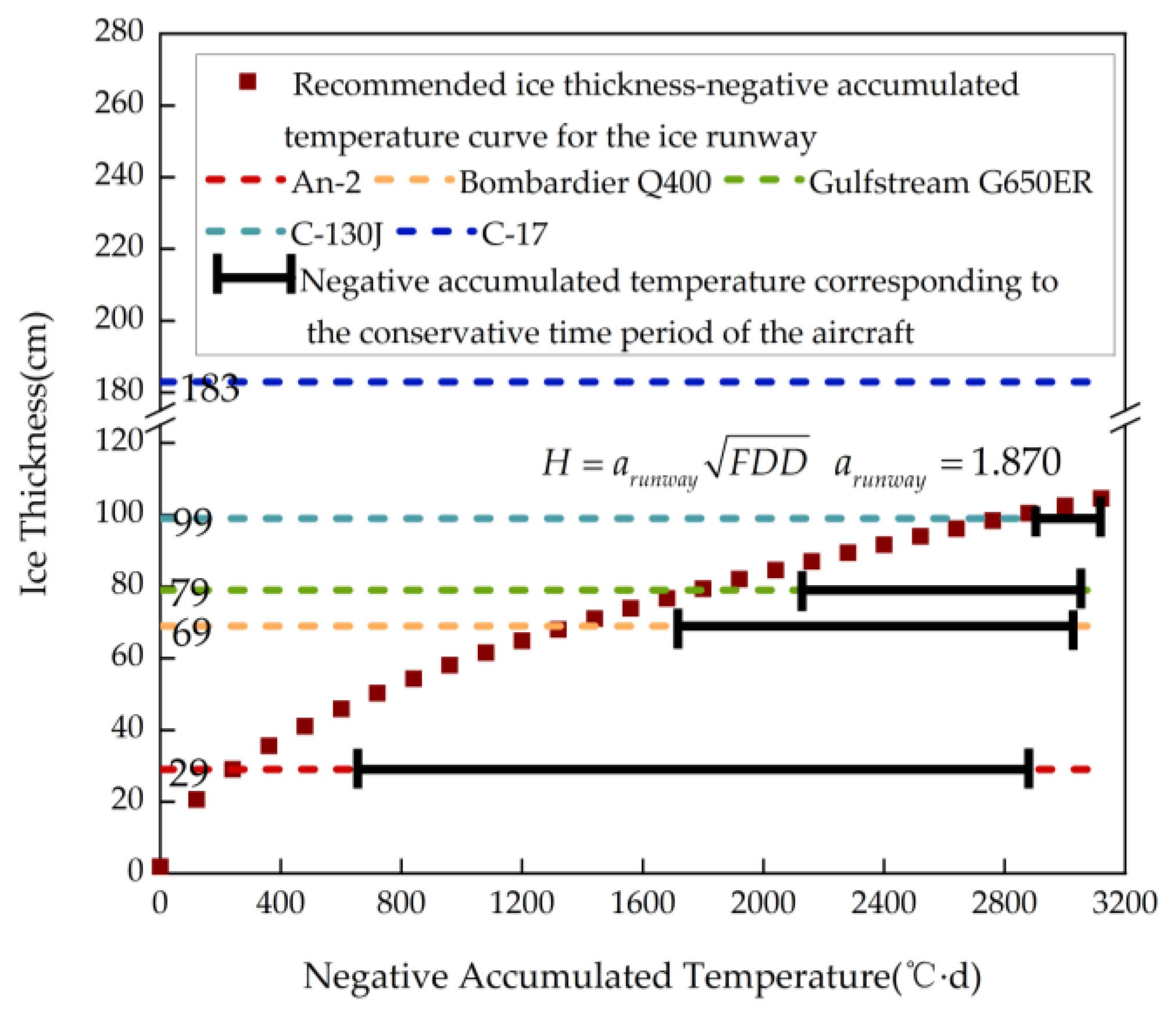
5.2. Feasibility of Using Huhenuoer Lake Ice as the Temporary Runway Every Winter in the Future
6. Conclusions and Suggestions
- Investigations have shown that the ice in the lake’s center is thin, particularly in the southwest of Huhenuoer Lake. Furthermore, the southern region of Huhenuoer Lake is shallow, and in this region, the lake ice can reach the bottom of the lake. The northern section of Huhenuoer Lake may serve as the temporary take-off and landing runway for aircraft on the lake ice during winter.
- The 30-year historical data on wind speed and direction from the Chen Barag Banner meteorological station near Huhenuoer Lake indicate the predominant wind direction and frequency throughout the winter ice season in this region. The criteria requires a 95% usability factor for aircraft takeoffs and landings in wind conditions, unaffected by crosswinds. The aircraft’s runway orientations on the Huhenuoer Lake ice are 90–270° and 130–310°.
- In the northern section of the lake, the straight-line distances of 90–270° and 130–310° indicate that the greatest lengths are 3400 m and 4100 m, respectively. Due to the low friction coefficient of an ice surface, the recommended length of an ice runway with a compacted snow layer is 1.6 times that of land. The minimum operational runway length for Huhenuoer Lake is established at 3100 m. Considering the requirements of maximum ice thickness and irregular ice distribution, it is capable of facilitating the takeoff and landing of aircraft such as the C130.
- We establish the fitting relationship between ice thickness, negative accumulated temperature, and cumulative snowfall at Huhenuoer Lake, using the safety of aircraft takeoff and landing as an engineering design requirement. We provide the designated service period for takeoff and landing for several aircraft types. An analysis of the shortest application period for the next 50 years is conducted.
- The findings of this article provide support for the design of ice aircraft takeoff and landing at Huhenuoer Lake; nonetheless, a comprehensive survey is necessary for practical implementation. This research suggests that the northern region of Huhenuoer Lake should be the primary location for a limited number of ice thickness monitoring sites, due to the thick ice, low temperatures, and challenges associated with field operations.
- For the potential runway ice and compacted snow layer, it is crucial to evaluate not only the variability in ice thickness on the proposed runway but also the undulations of the ice surface. Additionally, it is crucial to conduct research aimed at enhancing the friction coefficient and minimizing surface undulation of the compacted snow.
- The investigation assessing the bearing capability of the temporary ice runway at Huhenuoer Lake will be integrated into the field of ice engineering. The effective maintenance of the ice runway is in the construction and application stages. It requires measurement of not only ice thickness but also mechanical characteristics, including ice bending strength, elastic modulus, Poisson’s ratio, and compressive strength. Therefore, in order to implement the ice runway, it is crucial to conduct experimental research on the physical characteristics of the ice layer during future investigations of Huhenuoer Lake.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Beginning Time, Ending Time, Days, Negative Accumulated Temperature, and Cumulative Snowfall for Each Research Period from 1993 to 2023
| Number | Beginning Time | Ending Time | Days | Negative Accumulated Temperature (°C·d) | Cumulative Snowfall (mm) |
|---|---|---|---|---|---|
| 1993–1994 | 28 October 1993 | 29 March 1994 | 152 | 2749.2 | 29.5 |
| 1994–1995 | 6 November 1994 | 27 March 1995 | 141 | 2211.2 | 13.6 |
| 1995–1996 | 29 October 1995 | 5 April 1996 | 159 | 2511.2 | 19.7 |
| 1996–1997 | 23 October 1996 | 25 March 1997 | 153 | 3009.9 | 30.6 |
| 1997–1998 | 20 October 1997 | 25 March 1998 | 156 | 2509.2 | 17.7 |
| 1998–1999 | 30 October 1998 | 5 April 1999 | 157 | 2746.4 | 21.6 |
| 1999–2000 | 20 October 1999 | 6 April 2000 | 169 | 3228.8 | 47.9 |
| 2000–2001 | 2 November 2000 | 3 April 2001 | 152 | 3150.8 | 15.7 |
| 2001–2002 | 30 October 2001 | 10 March 2002 | 131 | 2367.5 | 22.6 |
| 2002–2003 | 17 October 2002 | 29 March 2003 | 163 | 3076.2 | 24.2 |
| 2003–2004 | 1 November 2003 | 25 March 2004 | 145 | 2811.3 | 28.2 |
| 2004–2005 | 4 November 2004 | 1 April 2005 | 148 | 2869.3 | 22.1 |
| 2005–2006 | 6 November 2005 | 31 March 2006 | 145 | 2811.2 | 28.9 |
| 2006–2007 | 4 November 2006 | 6 April 2007 | 153 | 2770.8 | 33.1 |
| 2007–2008 | 25 October 2007 | 7 March 2008 | 134 | 2524.6 | 13.1 |
| 2008–2009 | 23 October 2008 | 1 April 2009 | 160 | 2858.5 | 41.1 |
| 2009–2010 | 6 November 2009 | 17 April 2010 | 162 | 3249.3 | 35.2 |
| 2010–2011 | 6 November 2010 | 2 April 2011 | 147 | 3016.1 | 40.2 |
| 2011–2012 | 2 November 2011 | 27 March 2012 | 146 | 3433.6 | 46.9 |
| 2012–2013 | 27 October 2012 | 19 April 2013 | 174 | 3490.7 | 59.1 |
| 2013–2014 | 5 November 2013 | 22 March 2014 | 137 | 2519.5 | 33.4 |
| 2014–2015 | 30 October 2014 | 24 March 2015 | 145 | 2474.3 | 25.7 |
| 2015–2016 | 14 November 2015 | 19 March 2016 | 126 | 2636.3 | 18.6 |
| 2016–2017 | 17 October 2016 | 27 March 2017 | 161 | 2837.5 | 21.5 |
| 2017–2018 | 28 October 2017 | 23 March 2018 | 146 | 3072.4 | 18.4 |
| 2018–2019 | 3 November 2018 | 16 March 2019 | 133 | 2135.0 | 4.4 |
| 2019–2020 | 1 November 2019 | 23 March 2020 | 143 | 2739.9 | 19.7 |
| 2020–2021 | 12 November 2020 | 12 March 2021 | 120 | 2263.0 | 4.6 |
| 2021–2022 | 4 November 2021 | 8 March 2022 | 124 | 2344.9 | 9.8 |
| 2022–2023 | 31 October 2022 | 27 March 2023 | 147 | 2766.3 | 22.9 |
| 2023–2024 | 30 October 2023 | 26 March 2024 | 148 | 3135.0 | 34.9 |
Appendix B. The Maximum Landing Weight (MLW) for Some Aircraft Types, the Needed Ice Thickness, and the Needed Length on an Ice Runway (Covered with Compacted Snow)
| Aircraft Types | The MLW (t) | Needed Ice Thickness (cm) | Needed Length on Ice Runway Covered with Compacted Snow (m) |
|---|---|---|---|
| CZAW SportCruiser LSA | 0.6 | 10 | 200 |
| Cessna 172N | 1 | 13 | 470 |
| Cessna Caravan | 4 | 24 | 1000 |
| Cessna Citation CJ4 Gen2 | 7 | 34 | 1660 |
| Saab 340 | 13 | 46 | 2060 |
| Bombardier CRJ700 | 30 | 71 | 2500 |
| Embraer 170 | 33 | 74 | 2630 |
| Bombardier Global Express | 36 | 77 | 2700 |
| ARJ21-700 | 38 | 79 | 2720 |
| ERJ 190 | 43 | 84 | 3290 |
| Airbus A220-100 | 51 | 92 | 2340 |
| Boeing 737-700 | 58 | 98 | 2930 |
| Airbus A319neo | 63 | 102 | 2960 |
Appendix C. The Details of P-III Analysis
References
- Abele, G.; Frankenstein, G.E. Snow and Ice Properties as Related to Roads and Runways in Antarctica; US Army Cold Regions Research & Engineering Laboratory: Hanover, NH, USA, 1967; Volume 176. [Google Scholar]
- White, G.; McCallum, A. Review of ice and snow runway pavements. Int. J. Pavement Res. Technol. 2018, 11, 311–320. [Google Scholar] [CrossRef]
- Masterson, D.M. State of the art of ice bearing capacity and ice construction. Cold Reg. Sci. Technol. 2009, 58, 99–112. [Google Scholar] [CrossRef]
- Blaisdell, G.L.; Lang, R.M.; Crist, G.; Kurtti, K.; Harbin, R.J.; Flora, D. Construction, Maintenance, and Operation of a Glacial Runway, McMurdo Station, Antarctica; ERDC/CRREL M-98-1; US Army Corps of Engineers, Engineer Research and Development Center: Washington, DC, USA, 1998. [Google Scholar]
- Sharp, R.P. Suitability of ice for aircraft landings. Trans. Am. Geophys. Union 1947, 28, 111–119. [Google Scholar] [CrossRef]
- Flight Safety Foundation. Landing Distances. In FSF ALAR Briefing Note; Flight Safety Foundation: Alexandria, VA, USA, 2000. [Google Scholar]
- Swithinbank, C. Ice Runways Near the South Pole; ERDC/CRREL R-89-19; US Army Corps of Engineers, Engineer Research and Development Center: Washington, DC, USA, 1989. [Google Scholar]
- Squire, V.A.; Robinson, W.H.; Langhorne, P.J.; Haskell, T.G. Vehicles and aircraft on floating ice. Nature 1988, 333, 159–161. [Google Scholar] [CrossRef]
- McCallum, A.B. Movement and expected lifetime of the Casey ice runway. In Proceedings of the 13th International Conference on Cold Regions Engineering, Orono, ME, USA, 23–26 July 2006; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2006; pp. 1–19. [Google Scholar]
- Editorial Committee of Encyclopedia of Rivers and Lakes in China. Encyclopedia of Rivers and Lakes in China: Section of Heilong River and Liaohe River Basins; China Water & Power Press: Beijing, China, 2014; p. 17. (In Chinese) [Google Scholar]
- Lu, J.; Xia, C. Investigation for emphasis cold water domain of inland in China Investigation for the cold water domain and its resources in Neimonggu autonomous region. Chin. J. Fish. 2005, 18, 47–52. (In Chinese) [Google Scholar]
- Graf, R. Estimation of the Dependence of Ice Phenomena Trends on Air and Water Temperature in River. Water 2020, 12, 3494. [Google Scholar] [CrossRef]
- Mousa, R.M.; Mumayiz, S.A. Optimization of runway orientation. J. Transp. Eng. 2000, 126, 228–236. [Google Scholar] [CrossRef]
- Ashford, N.; Wright, P.H. Airport Engineering, 3rd ed.; John Wiley & Sons, Inc: New York, USA, 1992. [Google Scholar]
- Sarsam, S.I. Runway orientation problems–A case study of Middle Euphrates International Airport MEIA. In Proceedings of the 2nd International Conference of Buildings, Construction and Environmental Engineering (BCEE2-2015), Beirut, Lebanon, 17–18 October 2015. [Google Scholar]
- Haehnel, R.B.; Blaisdell, G.L.; Melendy, T.D.; Shoop, S.; Courville, Z. A Snow Runway for Supporting Wheeled Aircraft: Phoenix Airfield, McMurdo, Antarctica; ERDC/CRREL TR-19-4; US Army Corps of Engineers, Engineer Research and Development Center: Washington, DC, USA, 2019. [Google Scholar]
- Lotsari, E.; Lind, L.; Kämäri, M. Impacts of Hydro-Climatically Varying Years on Ice Growth and Decay in a Subarctic River. Water 2019, 11, 2058. [Google Scholar] [CrossRef]
- Brooks, R.N. Quantifying Peak Freshwater Ice Across the Northern Hemisphere Using a Regionally Defined Degree-Day Ice-Growth Model. Master’s Thesis, University of Victoria, Victoria, BC, Canada, 2012. [Google Scholar]
- Korhonen, J. Long-term changes in lake ice cover in Finland. Hydrol. Res. 2006, 37, 347–363. [Google Scholar] [CrossRef]
- Solarski, M.; Rzetala, M. A Comparison of Model Calculations of Ice Thickness with the Observations on Small Water Bodies in Katowice Upland (Southern Poland). Water 2022, 14, 3886. [Google Scholar] [CrossRef]
- Stefan, J. Ueber die Theorie der Eisbildung, insbesondere über die Eisbildung im Polarmeere. Ann. Phys. 1891, 278, 269–286, In German. [Google Scholar] [CrossRef]
- Leppäranta, M. A review of analytical models of sea-ice growth. Atmos. Ocean 1993, 31, 123–138. [Google Scholar] [CrossRef]
- Husselmann, M.L.; Van Zyl, J.E. Effect of stand size and income on residential water demand. J. S. Afr. Inst. Civ. Eng. 2006, 48, 12–16. Available online: https://hdl.handle.net/10520/EJC26987 (accessed on 9 December 2024).
- Lin, L. Study on Effect of Ice Deformation on Reservoir Piers. Master’s Thesis, Dalian University of Technology, Dalian, China, 2023. (In Chinese). [Google Scholar]
- Schiff, B. Antonov AN-2 The Flying Bear. Available online: https://www.aopa.org/news-and-media/all-news/2001/october/pilot/antonov-an-2 (accessed on 9 December 2024).
- Aero Corner. Bombardier Q400. Available online: https://aerocorner.com/aircraft/bombardier-q400/ (accessed on 9 December 2024).
- Austrian Airlines. Bombardier Q400. Available online: https://www.austrian.com/nl/en/bombardier-q400 (accessed on 9 December 2024).
- GlobalAir.com. Gulfstream G650ER. Available online: https://www.globalair.com/aircraft-for-sale/specifications?specid=1520 (accessed on 9 December 2024).
- Rocco. Lockheed C-5 Galaxy vs. Lockheed C-130 Hercules. Available online: https://aerocorner.com/comparison/lockheed-c-5-galaxy-vs-lockheed-c-130-hercules/ (accessed on 9 December 2024).
- Ultimate Specs. C-17 Globemaster III Technical Data. 1991. Available online: https://www.ultimatespecs.com/aircraft-specs/boeing/boeing-c-17-globemaster-iii-1991 (accessed on 9 December 2024).
- GlobalAir.com. CZAW SportCruiser LSA. Available online: https://www.globalair.com/aircraft-for-sale/specifications?specid=1378 (accessed on 9 December 2024).
- GlobalAir.com. Cessna 172N. Available online: https://www.globalair.com/aircraft-for-sale/specifications?specid=1237 (accessed on 9 December 2024).
- Textron Aviation Inc. Citation CJ4 Gen2. Available online: https://cessna.txtav.com/citation/cj4-gen2#_model-specs (accessed on 9 December 2024).
- English Wikipedia. List of Airliners by Maximum Takeoff Weight. Available online: https://en.wikipedia.org/wiki/List_of_airliners_by_maximum_takeoff_weight#cite_note-27 (accessed on 9 December 2024).
- Li, Z.; Fu, X.; Shi, L.; Huang, W.; Li, C. Recent Advances and Challenges in the Inverse Identification of Thermal Diffusivity of Natural Ice in China. Water 2023, 15, 1041. [Google Scholar] [CrossRef]
- Shi, L.; Li, Z.; Lu, P.; Feng, E. Influence of ice temperature on thermal diffusivity of natural freshwater ice. J. Hydraul. Eng. 2013, 44, 1112–1117. (In Chinese) [Google Scholar] [CrossRef]
- Wang, T. Exploring of the Relationship between Cold Ice Thickness Reservoir of Growth and Negative Accumulated Temperature. Bohai University: Jinzhou, China, 2011. (In Chinese) [Google Scholar]
- Shen, H.T.; Yapa, P.D. A unified degree-day method for river ice cover thickness simulation. Can. J. Civ. Eng. 1985, 12, 54–62. [Google Scholar] [CrossRef]
- Gu, H.; Yu, Z.; Li, G.; Ju, Q. Nonstationary Multivariate Hydrological Frequency Analysis in the Upper Zhanghe River Basin, China. Water 2018, 10, 772. [Google Scholar] [CrossRef]
- Lu, Y. Impacts of Climate Change on Hydrological Hazards: Mechanisms, Predictions and Coping Strategies. Appl. Math. Nonlinear Sci. 2024, 9, 1–17. [Google Scholar] [CrossRef]
- Mo, C.; Jiang, C.; Lei, X.; Cen, W.; Yan, Z.; Tang, G.; Li, L.; Sun, G.; Xing, Z. Optimal Scheduling of Reservoir Flood Control under Non-Stationary Conditions. Sustainability 2023, 15, 11530. [Google Scholar] [CrossRef]
- Xu, K.; Ma, C.; Lian, J.; Bin, L. Joint Probability Analysis of Extreme Precipitation and Storm Tide in a Coastal City under Changing Environment. PLoS ONE 2014, 9, e109341. [Google Scholar] [CrossRef]
- Cui, Y.; Tang, H.; Jin, J.; Zhou, Y.; Jiang, S.; Chen, M. System Structure–Based Drought Disaster Risk Assessment Using Remote Sensing and Field Experiment Data. Remote Sens. 2022, 14, 5700. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, H.; Wang, T.; Yang, D. Estimating the annual runoff frequency distribution based on climatic conditions and catchment characteristics: A case study across China. Int. Soil Water Conserv. Res. 2023, 11, 470–481. [Google Scholar] [CrossRef]
- Ke, Q.; Jonkman, S.N.; Van Gelder, P.H.A.J.M.; Bricker, J.D. Frequency Analysis of Storm-Surge-Induced Flooding for the Huangpu River in Shanghai, China. J. Mar. Sci. Eng. 2018, 6, 70. [Google Scholar] [CrossRef]
- Minh, H.V.T.; Lavane, K.; Lanh, L.T.; Thinh, L.V.; Cong, N.P.; Ty, T.V.; Downes, N.K.; Kumar, P. Developing Intensity-Duration-Frequency (IDF) Curves Based on Rainfall Cumulative Distribution Frequency (CDF) for Can Tho City, Vietnam. Earth 2022, 3, 866–880. [Google Scholar] [CrossRef]
- Ashton, G.D. Thin ice growth. Water Resour. Res. 1989, 25, 564–566. [Google Scholar] [CrossRef]
- Ashton, G.D. River and lake ice thickening, thinning, and snow ice formation. Cold Reg. Sci. Technol. 2011, 68, 3–19. [Google Scholar] [CrossRef]

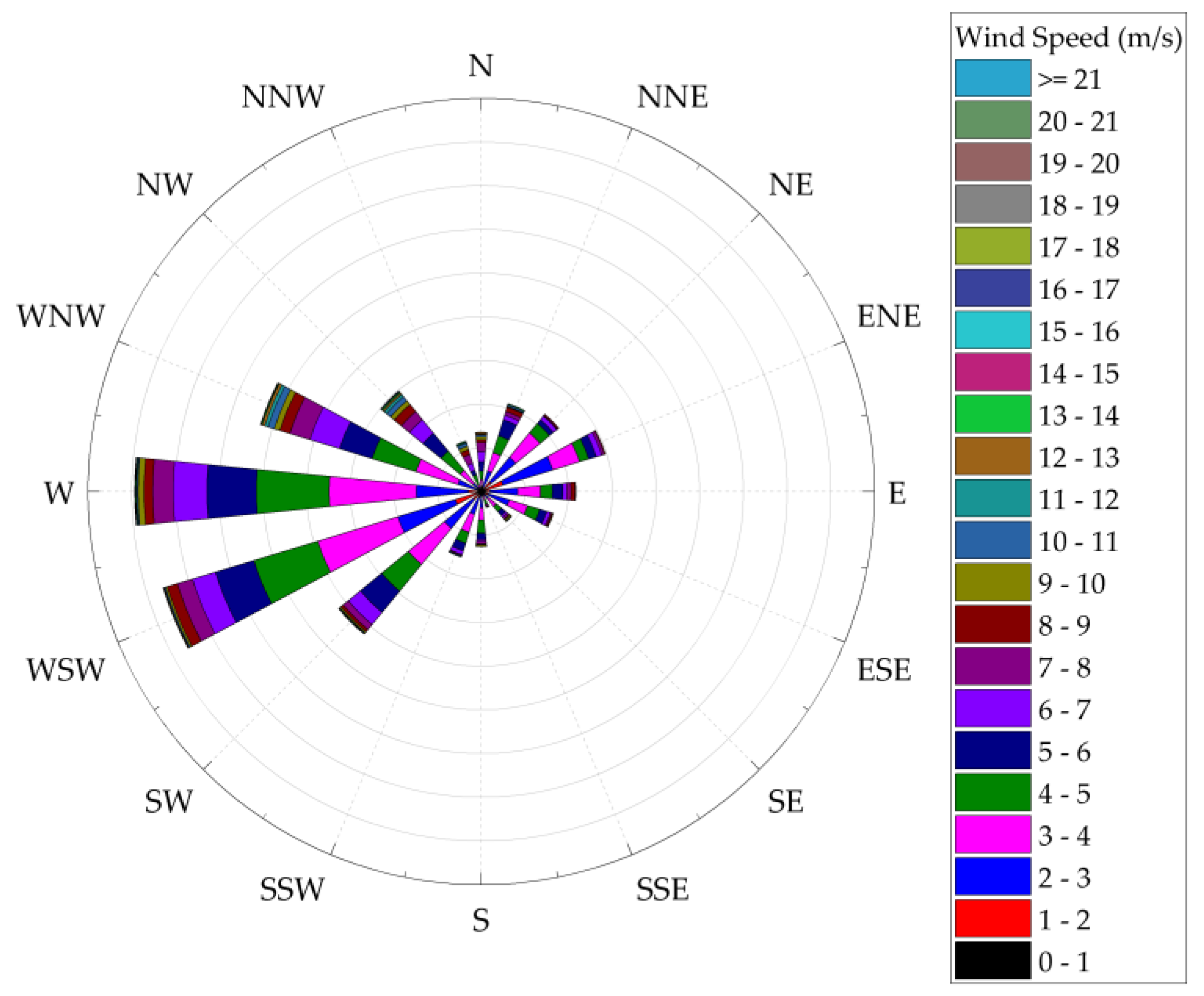
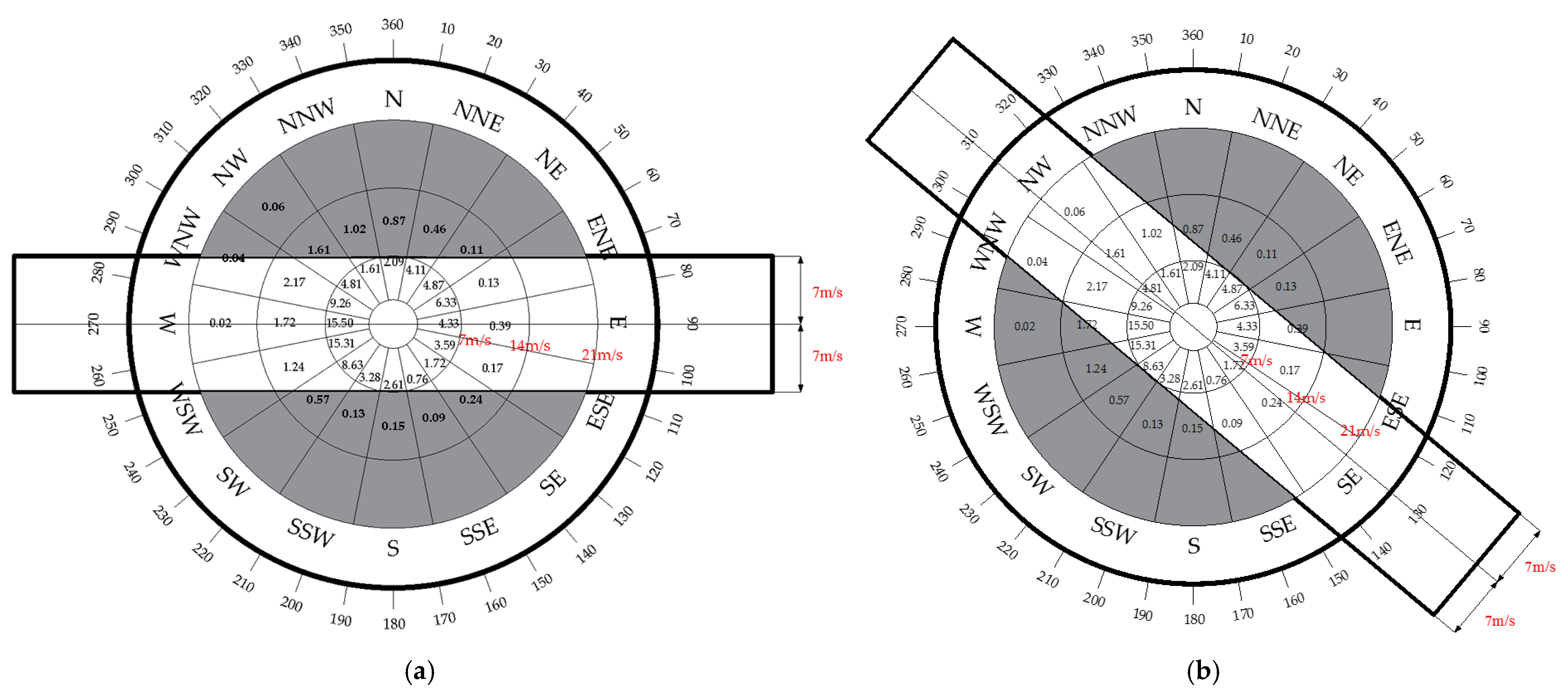
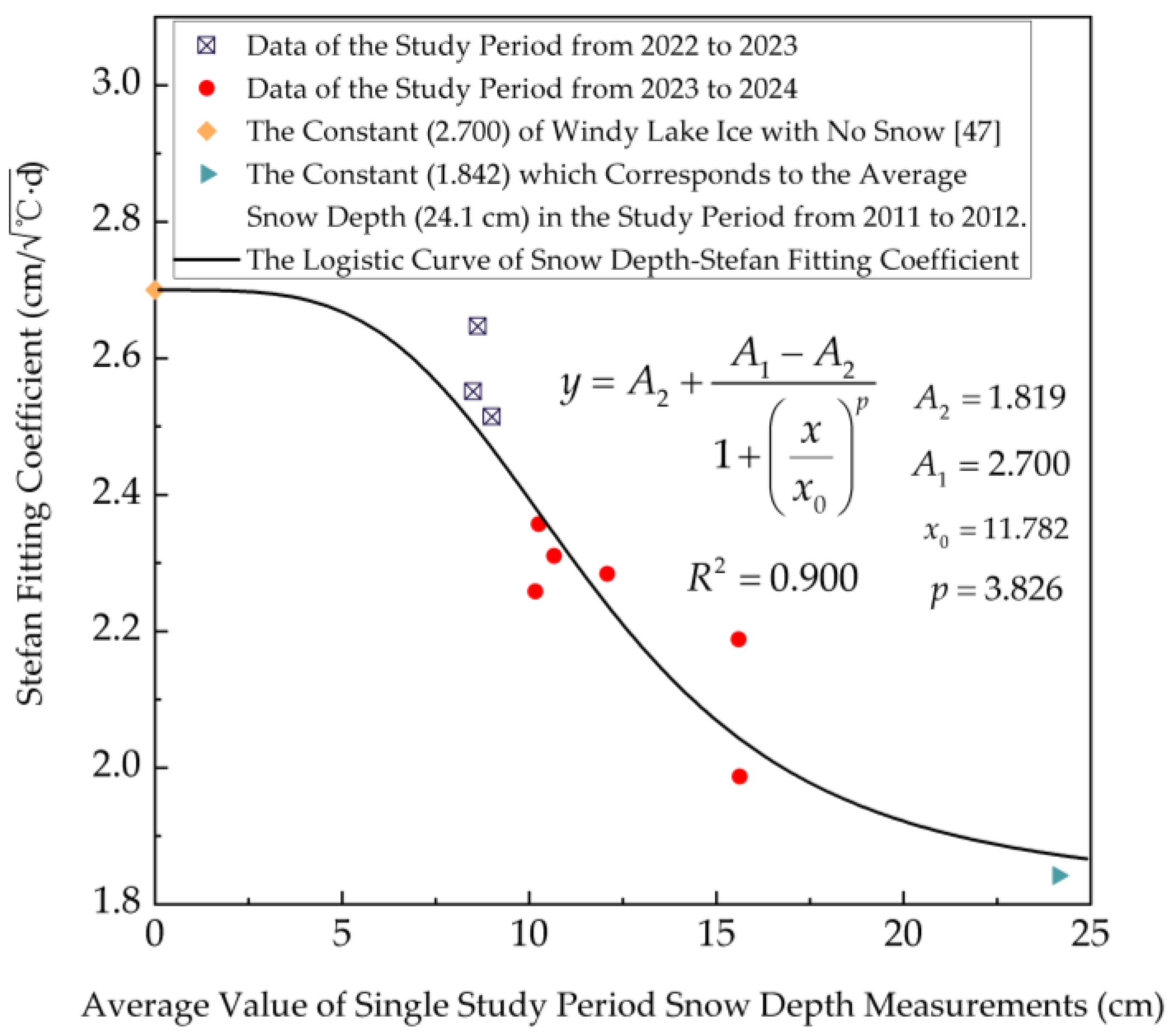
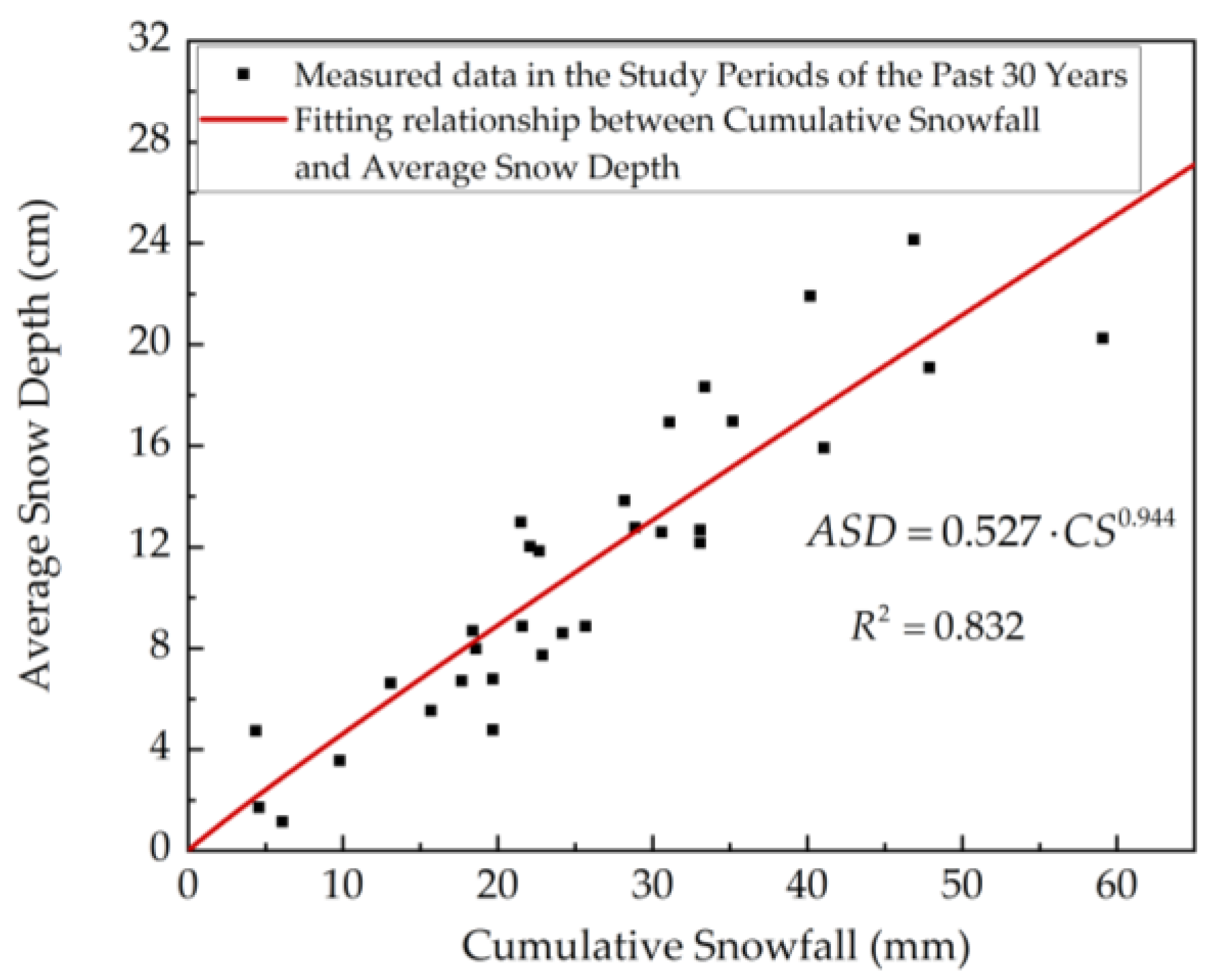
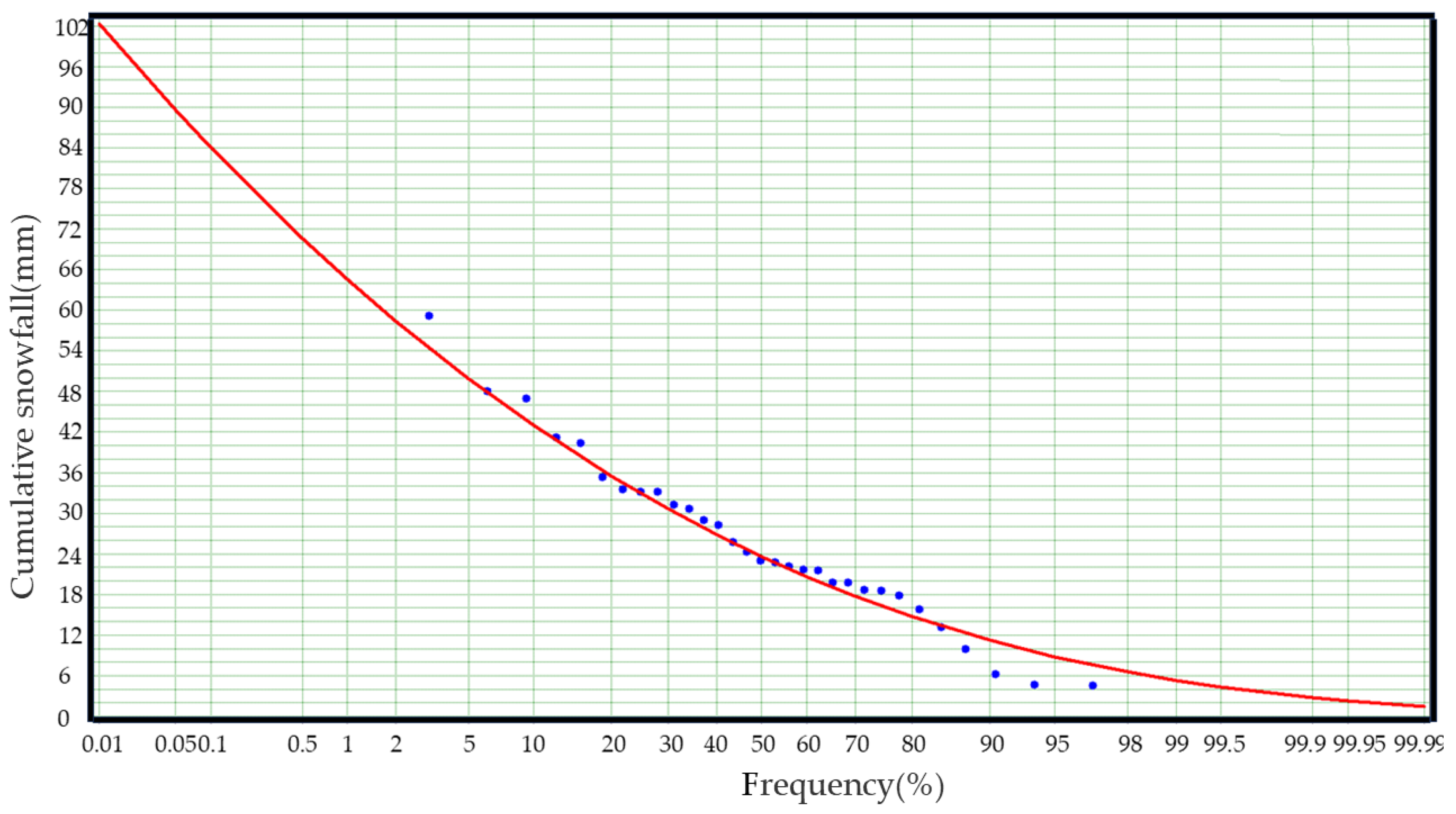

| Orientation | 0~7 m/s | 7~14 m/s | 14~21 m/s | Orientation | 0~7 m/s | 7~14 m/s | 14~21 m/s |
|---|---|---|---|---|---|---|---|
| N | 2.09 | 0.87 | S | 2.61 | 0.15 | ||
| NNE | 4.11 | 0.46 | SSW | 3.28 | 0.13 | ||
| NE | 4.87 | 0.11 | SW | 8.63 | 0.57 | ||
| ENE | 6.33 | 0.13 | WSW | 15.31 | 1.24 | ||
| E | 4.33 | 0.39 | W | 15.50 | 1.72 | 0.02 | |
| ESE | 3.59 | 0.17 | WNW | 9.26 | 2.17 | 0.04 | |
| SE | 1.72 | 0.24 | NW | 4.81 | 1.61 | 0.06 | |
| SSE | 0.76 | 0.09 | NNW | 1.61 | 1.02 |
| Site Number | Longitude | Latitude |
|---|---|---|
| #1 | 119°12′30″ E | 49°18′30″ N |
| #2 | 119°13′30″ E | 49°18′30″ N |
| #3 | 119°14′30″ E | 49°18′30″ N |
| #4 | 119°13′30″ E | 49°19′00″ N |
| #5 | 119°13′30″ E | 49°17′30″ N |
| #6 | 119°13′30″ E | 49°16′30″ N |
| Date of Measurement | Snow Depth (cm) | Ice Thickness (cm) | ||||||
|---|---|---|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | #6 | Average Value | ||
| 5 December 2023 | 13 | 48 | 46 | 42 | 51 | 50 | 48 | 48 |
| 15 December 2023 | 15 | 55 | 55 | |||||
| 29 December 2023 | 19 | 70 | 71 | 71 | ||||
| 2 January 2024 | 18 | 95 | 103 | 107 | 109 | 72 | 117 | 101 |
| 18 January 2024 | 20 | 85 | 98 | 89 | 89 | 84 | 99 | 91 |
| 26 January 2024 | 19 | 89 | 99 | 96 | 97 | 86 | 100 | 95 |
| 2 February 2024 | 20 | 96 | 105 | 102 | 102 | 87 | 105 | 100 |
| 29 February 2024 | 22 | 116 | 112 | 108 | 121 | 107 | 103 | 111 |
| 7 March 2024 | 21 | 119 | 132 | 108 | 119 | 105 | 103 | 114 |
| 14 March 2024 | 19 | 121 | 139 | 108 | 127 | 105 | 103 | 117 |
| 21 March 2024 | 16 | 131 | 139 | 108 | 129 | 125 | 103 | 123 |
| Date of Measurement | Runway Orientation | Ice Thickness on The Route (cm) | Non-Uniformity (%) | Maximum Change Rate (‰) | |
|---|---|---|---|---|---|
| Min Value | Max Value | ||||
| 5 December 2023 | 90–270° | 39 | 48 | 18.2 | −0.1 |
| 130–310° | 45 | 50 | 8.5 | −0.0 | |
| 2 January 2024 | 90–270° | 92 | 109 | 15.4 | 0.1 |
| 130–310° | 72 | 120 | 39.7 | 0.7 | |
| 18 January 2024 | 90–270° | 81 | 98 | 16.9 | 0.1 |
| 130–310° | 78 | 96 | 19.1 | 0.2 | |
| 26 January 2024 | 90–270° | 85 | 99 | 13.6 | 0.1 |
| 130–310° | 83 | 101 | 18.2 | 0.2 | |
| 2 February 2024 | 90–270° | 92 | 105 | 12.0 | 0.1 |
| 130–310° | 87 | 106 | 18.4 | 0.3 | |
| 29 February 2024 | 90–270° | 106 | 117 | 9.1 | −0.0 |
| 130–310° | 101 | 117 | 13.4 | −0.1 | |
| 7 March 2024 | 90–270° | 98 | 132 | 25.4 | −0.2 |
| 130–310° | 105 | 114 | 8.0 | −0.3 | |
| 14 March 2024 | 90–270° | 94 | 139 | 32.4 | −0.3 |
| 130–310° | 105 | 119 | 11.8 | −0.6 | |
| 21 March 2024 | 90–270° | 96 | 139 | 31.0 | −0.3 |
| 130–310° | 90 | 127 | 28.9 | −0.3 | |
| Aircraft Type | Maximum Landing Weight (t) | Start of the Conservative Period | End of the Conservative Period | Conservative Period (d) | Needed Length (m) |
|---|---|---|---|---|---|
| An-2 | 7 | 10 December 2023 | 4 March 2024 | 85 | 400 |
| Bombardier Q400 | 29 | 17 January 2024 | 12 March 2024 | 55 | 2240 |
| Gulfstream G650ER | 38 | 31 January 2024 | 15 March 2024 | 44 | 3070 |
| C-130J | 59 | 5 March 2024 | 23 March 2024 | 18 | 2520 |
| C-17 | 203 | — | — | — | 3780 |
| Return Periods (Years) | Value of the Corresponding Return Period by Cumulative Snowfall P-III Curve (mm) | Value of the Corresponding Return Period by Negative Accumulated Temperature P-III Curve (°C·d) |
|---|---|---|
| 50 | 58.4 | 2092.5 |
| 45 | 57.5 | 2105.5 |
| 30 | 53.7 | 2158.7 |
| 25 | 52.0 | 2184.3 |
| 20 | 49.9 | 2217.0 |
| 15 | 47.0 | 2262.1 |
| 10 | 43.0 | 3577.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhao, Q.; Zhang, B.; Wang, Q.; Lu, P.; Wang, Q.; Bao, X.; He, J. An Investigation of the Thickness of Huhenuoer Lake Ice and Its Potential as a Temporary Ice Runway. Water 2025, 17, 400. https://doi.org/10.3390/w17030400
Wang Y, Zhao Q, Zhang B, Wang Q, Lu P, Wang Q, Bao X, He J. An Investigation of the Thickness of Huhenuoer Lake Ice and Its Potential as a Temporary Ice Runway. Water. 2025; 17(3):400. https://doi.org/10.3390/w17030400
Chicago/Turabian StyleWang, Ying, Qiuming Zhao, Bo Zhang, Qingjiang Wang, Peng Lu, Qingkai Wang, Xinghua Bao, and Jiahuan He. 2025. "An Investigation of the Thickness of Huhenuoer Lake Ice and Its Potential as a Temporary Ice Runway" Water 17, no. 3: 400. https://doi.org/10.3390/w17030400
APA StyleWang, Y., Zhao, Q., Zhang, B., Wang, Q., Lu, P., Wang, Q., Bao, X., & He, J. (2025). An Investigation of the Thickness of Huhenuoer Lake Ice and Its Potential as a Temporary Ice Runway. Water, 17(3), 400. https://doi.org/10.3390/w17030400




