Co-Optimization of Valve Placement and Chlorine Dosing in Water Distribution Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Modeling the Chlorine Propagation
- water sources (e.g. reservoirs or tanks);
- nodes (e.g. consumer household or industry);
- pipes connecting the water sources and nodes;
- pipe loops in the WDS.
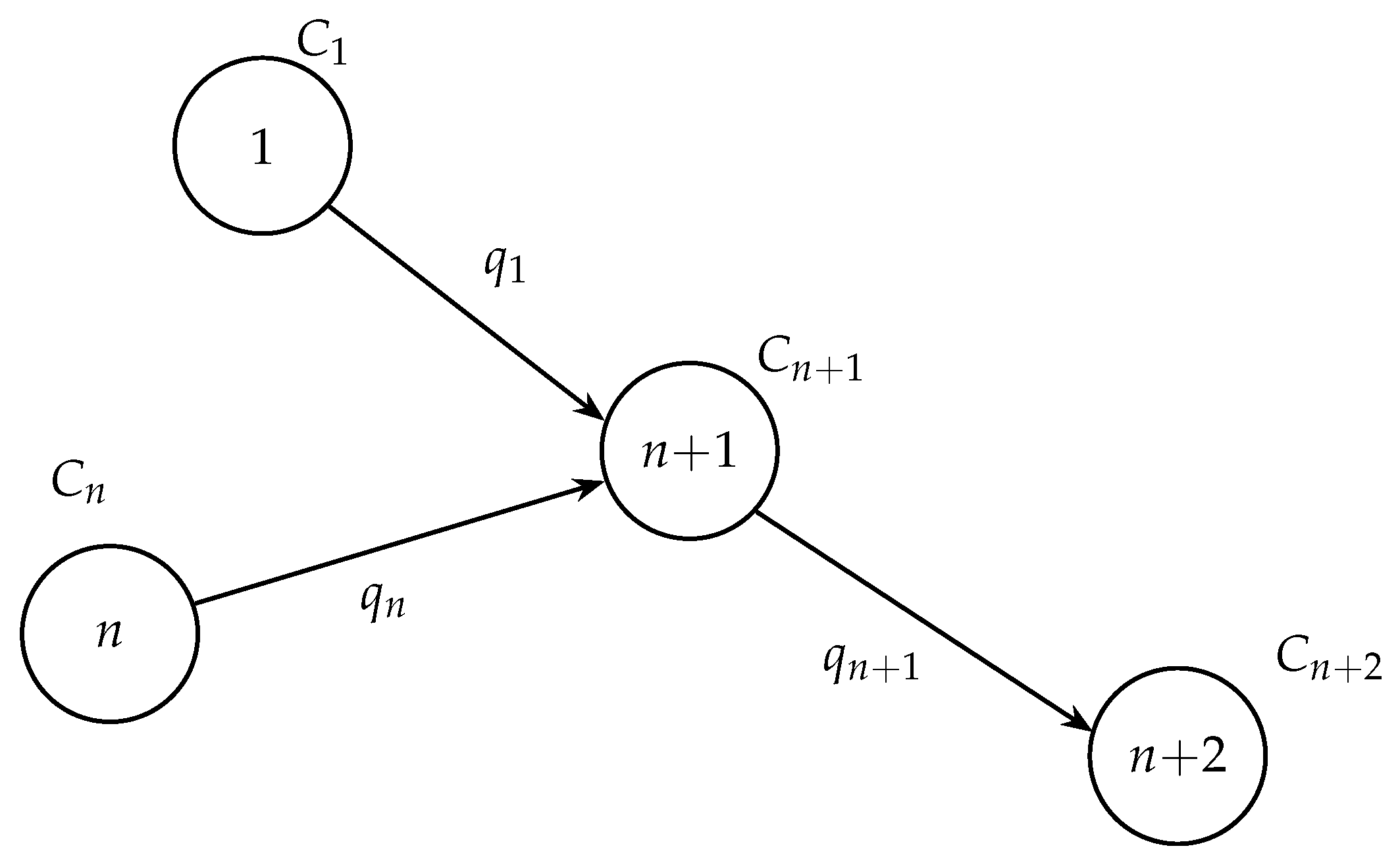
2.1.1. Chlorine Propagation Model
2.1.2. Hydraulic Model
2.2. Optimization Problem Formulations
2.2.1. The NLP Problem
2.2.2. The MINLP Problem
2.2.3. The Extended MINLP Problem
3. Results and Discussion
3.1. Solution of the NLP Problem
3.2. Solution of the MINLP Problem
3.3. Solution of the Extended MINLP Problem
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rosario-Ortiz, F.; Rose, J.; Speight, V.; Gunten, U.; Schnoor, J. How do you like your tap water? Science 2016, 351, 912–914. [Google Scholar] [CrossRef]
- Avvedimento, S.; Todeschini, S.; Manenti, S.; Creaco, E. Comparison of Techniques for Maintaining Adequate Disinfectant Residuals in a Full-Scale Water Distribution Network. Water 2022, 14, 1029. [Google Scholar] [CrossRef]
- US Environmental Protection Agency (USEPA). National Primary Drinking Water Regulations: Disinfectants and Disinfection Byproducts; Final Rule; U.S. Environmental Protection Agency (EPA): Washington, DC, USA, 1998. [Google Scholar]
- World Health Organization. Guidelines for Drinking-Water Quality: Fourth Edition Incorporating the First Addendum; WHO Press: Geneva, Switzerland, 2017. [Google Scholar]
- Lansey, K.; Pasha, F.; Pool, S.; Elshorbagy, W.; Uber, J.G. Locating Satellite Booster Disinfectant Stations. J. Water Resour. Plan. Manag. 2007, 133, 372–376. [Google Scholar] [CrossRef]
- Islam, N.; Rodriguez, M.; Farahat, A.; Sadiq, R. Minimizing the impacts of contaminant intrusion in small water distribution networks through booster chlorination optimization. Stoch. Environ. Res. Risk Assess. 2017, 31, 1759–1775. [Google Scholar] [CrossRef]
- Pecci, F.; Stoianov, I.; Ostfeld, A. Relax-tighten-round algorithm for optimal placement and control of valves and chlorine boosters in water networks. Eur. J. Oper. Res. 2021, 295, 690–698. [Google Scholar] [CrossRef]
- Kumari, M.; Gupta, S. Occurrence and Exposure to Trihalomethanes in Drinking Water: A Systematic Review and Meta-analysis. Expo. Health 2022, 14, 915–939. [Google Scholar] [CrossRef]
- Sadiq, R.; Rodriguez, M.J. Disinfection by-products (DBPs) in drinking water and predictive models for their occurrence: A review. Sci. Total Environ. 2004, 321, 21–46. [Google Scholar] [CrossRef] [PubMed]
- Stoianov, I.; Aisopou, A. Chlorine Decay under Steady and Unsteady-state Hydraulic Conditions. Procedia Eng. 2014, 70, 1592–1601. [Google Scholar] [CrossRef]
- Eliades, D.G.; Vrachimis, S.G.; Moghaddam, A.; Tzortzis, I.; Polycarpou, M.M. Contamination event diagnosis in drinking water networks: A review. Annu. Rev. Control 2023, 55, 420–441. [Google Scholar] [CrossRef]
- Mazhar, M.A.; Khan, N.A.; Ahmed, S.; Khan, A.H.; Hussain, A.; Rahisuddin; Changani, F.; Yousefi, M.; Ahmadi, S.; Vambol, V. Chlorination disinfection by-products in municipal drinking water—A review. J. Clean. Prod. 2020, 273, 123159. [Google Scholar] [CrossRef]
- Rossman, L.; Clark, R.; Grayman, W. Modeling Chlorine Residuals in Drinking-Water Distribution Systems. J. Environ. Eng. 1994, 120, 803–820. [Google Scholar] [CrossRef]
- Onyutha, C.; Kwio-Tamale, J.C. Modelling chlorine residuals in drinking water: A review. Int. J. Environ. Sci. Technol. 2022, 19, 11613–11630. [Google Scholar] [CrossRef]
- Rossman, L.; Woo, H.; Tryby, M.; Shang, F.; Janke, R.; Haxton, T. EPANET Users Manual; EPA-Environmental Protection Agency: Washington, DC, USA, 1994. [Google Scholar]
- Clark, R.M. Chlorine Demand and TTHM Formation Kinetics: A Second-Order Model. J. Environ. Eng. 1998, 124, 16–24. [Google Scholar] [CrossRef]
- Clark, R.; Sivaganesan, M. Predicting Chlorine Residuals in Drinking Water: Second Order Model. J. Water Resour. Plan. Manag. 2002, 128, 152–161. [Google Scholar] [CrossRef]
- Huang, J.; McBean, E. Using Bayesian statistics to estimate the coefficients of a two-component second-order chlorine bulk decay model for a water distribution system. Water Res. 2007, 41, 287–294. [Google Scholar] [CrossRef]
- Jonkergouw, P.; Khu, S.T.; Savic, D.; Zhong, D.; Hou, X.; Zhao, H.B. A Variable Rate Coefficient Chlorine Decay Model. Environ. Sci. Technol. 2009, 43, 408–414. [Google Scholar] [CrossRef]
- Fisher, I.; Kastl, G.; Sathasivan, A. Evaluation of Suitable Chlorine Bulk-Decay Models for Water Distribution Systems. Water Res. 2011, 45, 4896–4908. [Google Scholar] [CrossRef]
- Powell, J.; West, J.; Hallam, N.; Forster, C.; Simms, J. Performance of Various Kinetic Models for Chlorine Decay. ASCE J. Water Resour. Plan. Manag. 2001, 126, 13–20. [Google Scholar] [CrossRef]
- Wu, H.; C. Dorea, C. Towards a Predictive Model for Initial Chlorine Dose in Humanitarian Emergencies. Water 2020, 12, 1506. [Google Scholar] [CrossRef]
- Riyadh, A.; Zayat, A.; Chaaban, A.; Peleato, N.M. Improving chlorine residual predictions in water distribution systems using recurrent neural networks. Environ. Sci. Water Res. Technol. 2024, 10, 2533–2545. [Google Scholar] [CrossRef]
- Pankaj, S.; Jaykrishnan, G.; Ostfeld, A. Robust Optimal Booster Disinfectant Injection in Water Systems under Uncertainty. Water 2023, 15, 1777. [Google Scholar] [CrossRef]
- Ohar, Z.; Ostfeld, A. Optimal design and operation of booster chlorination stations layout in water distribution systems. Water Res. 2014, 58C, 209–220. [Google Scholar] [CrossRef] [PubMed]
- Ostfeld, A.; Salomons, E. Conjunctive optimal scheduling of pumping and booster chlorine injections in water distribution systems. Eng. Optim. 2006, 38, 337–352. [Google Scholar] [CrossRef]
- Altan-Sakarya, A.; Mays, L. Optimal Operation of Water Distribution Pumps Considering Water Quality. ASCE J. Water Resour. Plan. Manag. 2000, 126, 210–220. [Google Scholar] [CrossRef]
- Prasad, T.; Walters, G. Minimizing residence times by rerouting flows to improve water quality in distribution networks. Eng. Optim. 2006, 38, 923–939. [Google Scholar] [CrossRef]
- Alfonso, L.; Jonoski, A.; Solomatine, D. Multiobjective Optimization of Operational Responses for Contaminant Flushing in Water Distribution Networks. J. Water Resour. Plan. Manag. ASCE 2010, 136, 48–58. [Google Scholar] [CrossRef]
- Hu, C.; Cai, J.; Zeng, D.; Yan, X.; Gong, W.; Wang, L. Deep reinforcement learning based valve scheduling for pollution isolation in water distribution network. Math. Biosci. Eng. 2019, 17, 105–121. [Google Scholar] [CrossRef] [PubMed]
- Abraham, E.; Blokker, E.; Stoianov, I. Network Analysis, Control Valve Placement and Optimal Control of Flow Velocity for Self-Cleaning Water Distribution Systems. Procedia Eng. 2017, 186, 576–583. [Google Scholar] [CrossRef]
- Abraham, E.; Blokker, E.; Stoianov, I. Decreasing the Discoloration Risk of Drinking Water Distribution Systems through Optimized Topological Changes and Optimal Flow Velocity Control. J. Water Resour. Plan. Manag. 2018, 144, 04017093. [Google Scholar] [CrossRef]
- Moeini, M.; Sela, L.; Taha, A.F.; Abokifa, A.A. Optimization Techniques for Chlorine Dosage Scheduling in Water Distribution Networks: A Comparative Analysis. In World Environmental and Water Resources Congress 2023; ASCE Press: Reston, VA, USA, 2023; pp. 987–998. [Google Scholar] [CrossRef]
- Haider, H.; Haydar, S.; Sajid, M.; Tesfamariam, S.; Sadiq, R. Framework for optimizing chlorine dose in small- to medium-sized water distribution systems: A case of a residential neighbourhood in Lahore, Pakistan. Water SA 2015, 41, 614–623. [Google Scholar] [CrossRef]
- Wang, D.; Xiang, H. Composite Control of Post-Chlorine Dosage During Drinking Water Treatment. IEEE Access 2019, 7, 27893–27898. [Google Scholar] [CrossRef]
- Kourbasis, N.; Patelis, M.; Tsitsifli, S.; Kanakoudis, V. Optimizing Water Age and Pressure in Drinking Water Distribution Networks. Environ. Sci. Proc. 2020, 2, 51. [Google Scholar] [CrossRef]
- Dai, P. A new mathematical program with complementarity constraints for optimal localization of pressure reducing valves in water distribution systems. Appl. Water Sci. 2021, 11, 152. [Google Scholar] [CrossRef]
- Dai, P.; Li, P. Optimal Localization of Pressure Reducing Valves in Water Distribution Systems by a Reformulation Approach. Water Resour. Manag. 2014, 28, 3057–3074. [Google Scholar] [CrossRef]
- Cao, H.; Hopfgarten, S.; Ostfeld, A.; Salomons, E.; Li, P. Simultaneous Sensor Placement and Pressure Reducing Valve Localization for Pressure Control of Water Distribution Systems. Water 2019, 11, 1352. [Google Scholar] [CrossRef]
- Korder, K.; Cao, H.; Salomons, E.; Ostfeld, A.; Li, P. Simultaneous Minimization of Water Age and Pressure in Water Distribution Systems by Pressure Reducing Valves. Water Resour. Manag. 2024, 38, 3561–3579. [Google Scholar] [CrossRef]
- Pecci, F.; Abraham, E.; Stoianov, I. Penalty and relaxation methods for the optimal placement and operation of control valves in water supply networks. Comput. Optim. Appl. 2017, 67, 201–223. [Google Scholar] [CrossRef]
- Bagirov, A.; Birkett, H.; Al Nuaimat, A.; Ahmed, S.; Sultanova, N.; Barton, A. Minimization of Pumping Costs in Water Distribution Systems Using Explicit and Implicit Pump Scheduling. In Proceedings of the 34th Hydrology and Water Resources Symposium, HWRS 2012, Sydney, NSW, Australia, 19–22 November 2012. [Google Scholar]
- Pecci, F.; Abraham, E.; Stoianov, I. Global optimality bounds for the placement of control valves in water supply networks. Optim. Eng. 2019, 20, 457–495. [Google Scholar] [CrossRef]
- Constans, S.; Bremond, B.; Morel, P. Simulation and Control of Chlorine Levels in Water Distribution Networks. ASCE J. Water Resour. Plan. Manag. 2003, 129, 135–145. [Google Scholar] [CrossRef]
- Rossman, L.; Boulos, P.; Altman, T. Discrete Volume-Element Method for Network Water-Quality Models. ASCE J. Water Resour. Plan. Manag. 1993, 119, 505–517. [Google Scholar] [CrossRef]
- Rossman, L. Epanet 2 Users Manual; EPA-Environmental Protection Agency: Washington, DC, USA, 2000; Volume 38. [Google Scholar]
- Pecci, F.; Abraham, E.; Stoianov, I. Mathematical Programming Methods for Pressure Management in Water Distribution Systems. Procedia Eng. 2015, 119, 937–946. [Google Scholar] [CrossRef]
- Ghaddar, B.; Claeys, M.; Mevissen, M.; Eck, B.J. Polynomial optimization for water networks: Global solutions for the valve setting problem. Eur. J. Oper. Res. 2017, 261, 450–459. [Google Scholar] [CrossRef]
- Mottahedin, A.; Giudicianni, C.; Di Nunno, F.; Granata, F.; Cunha, M.; Walski, T.; Creaco, E. Analysis, design, and maintenance of isolation valves in water distribution networks: State of the art review, insights from field experiences and future directions. Water Res. 2024, 262, 122088. [Google Scholar] [CrossRef]
- GAMS Development Corporation. GAMS-Documentation; GAMS Development Corporation: Fairfax, VA, USA, 2023. [Google Scholar]
- Wächter, A.; Biegler, L. On the Implementation of an Interior-Point Filter Line-Search Algorithm for Large-Scale Nonlinear Programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Bonami, P.; Lee, J. BONMIN Users’ Manual. 2011. Available online: https://www.researchgate.net/publication/265311363_BONMIN_Users%27_Manual (accessed on 8 November 2025).
- Eliades, D.G.; Kyriakou, M.; Vrachimis, S.; Polycarpou, M.M. EPANET-MATLAB Toolkit: An Open-Source Software for Interfacing EPANET with MATLAB. In Proceedings of the 14th International Conference on Computing and Control for the Water Industry (CCWI), Amsterdam, The Netherlands, 7–9 November 2016; p. 8. [Google Scholar] [CrossRef]
- Sterling, M.; Bargiela, A. Leakage reduction by optimised control of valves in water networks. Trans. Inst. Meas. Control 1984, 6, 293–298. [Google Scholar] [CrossRef]

| Chlorine Concentration (mg/L) | Initial | GAMS (Optimization) | EPANET (Simulation) |
|---|---|---|---|
| Reservoirs (IDs: 23, 24, 25) | 0.6 | 0.2847 | 0.2847 |
| Minimum | 0.2020 | 0.2 | 0.1923 |
| Maximum | 0.5807 | 0.2818 | 0.2818 |
| Avg Residual Chlorine | 0.4550 | 0.2296 | 0.2305 |
| Residual Chlorine Reduction (%) | 0% | 49.55% | 49.35% |
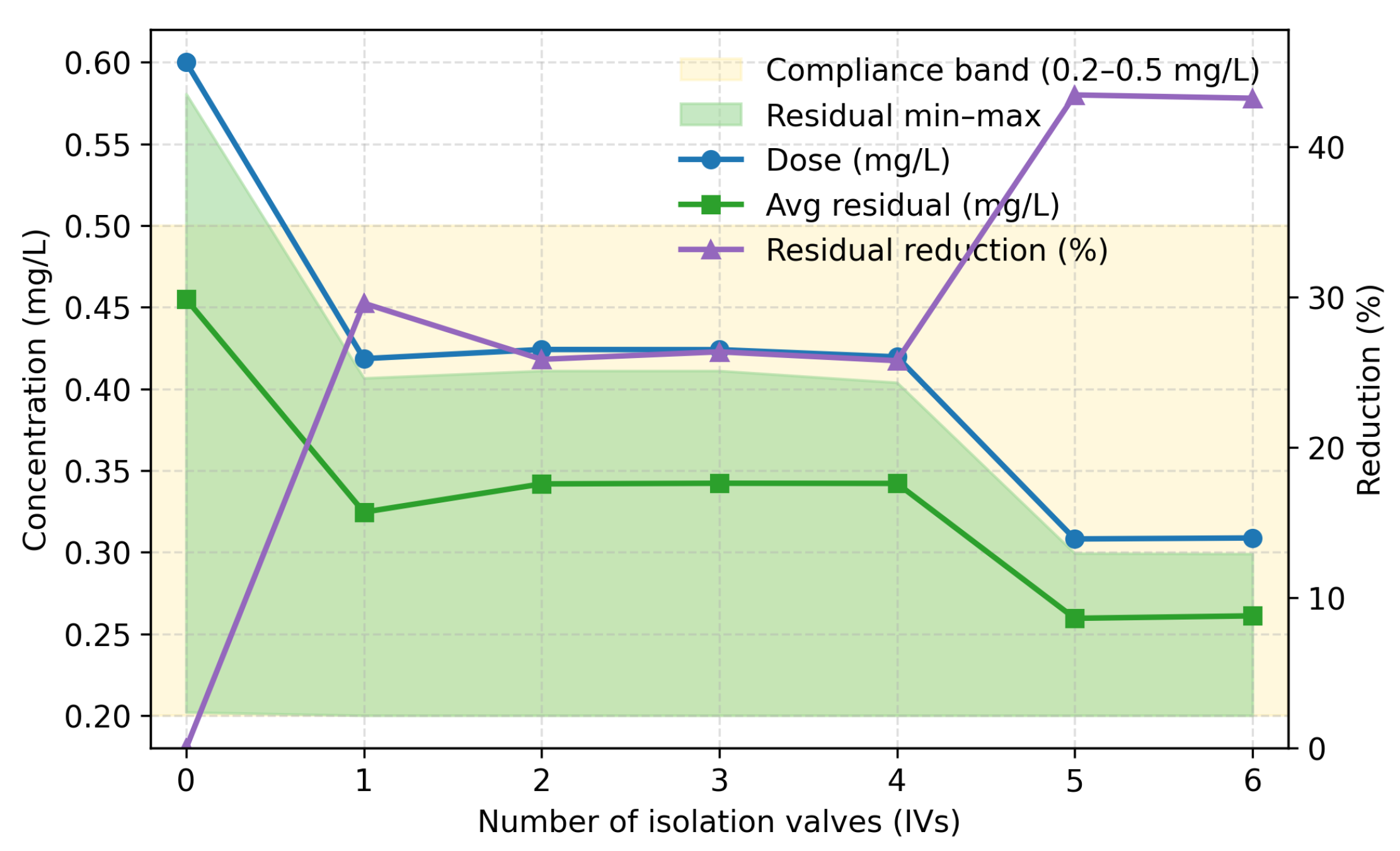
| Number of IVs | Locations of IVs (Pipe IDs) |
|---|---|
| 1 | 31 |
| 2 | 31, 21 |
| 3 | 33, 31, 21 |
| 4 | 17, 31, 21, 20 |
| 5 | 16, 29, 10, 31, 20 |
| 6 | 16, 22, 27, 28, 29, 30 |
| Objective | PRVs (No.) | IVs (No.) | Reservoirs Dosing (mg/L) | Min Chlorine (mg/L) | Max Chlorine (mg/L) | Avg Residual Chlorine (mg/L) | Min Pressure (m) | Max Pressure (m) | Total Pressure (m) |
|---|---|---|---|---|---|---|---|---|---|
| Minimize Chlorine dosing () | 1 | 0 | 0.4296 | 0.2000 | 0.4198 | 0.3486 | 34.5219 | 43.3157 | 849.0499 |
| 1 | 1 | 0.4122 | 0.2000 | 0.4099 | 0.3357 | 34.5151 | 43.2296 | 848.0437 | |
| 1 | 2 | 0.3596 | 0.2000 | 0.3497 | 0.2871 | 31.0949 | 42.2399 | 827.8520 | |
| 1 | 3 | 0.3001 | 0.2000 | 0.2940 | 0.2516 | 31.1153 | 42.4825 | 841.9206 | |
| Minimize Chlorine dosing and Pressure () | 1 | 0 | 0.4936 | 0.2000 | 0.4818 | 0.4022 | 29.4085 | 40.7529 | 806.8855 |
| 1 | 1 | 0.3675 | 0.2000 | 0.3542 | 0.3027 | 31.0753 | 43.1549 | 846.6835 | |
| 1 | 2 | 0.4680 | 0.2000 | 0.4511 | 0.3715 | 24.9102 | 40.5722 | 741.4982 | |
| 1 | 3 | 0.3194 | 0.2000 | 0.3175 | 0.2934 | 31.0878 | 42.4924 | 823.5606 | |
| Minimize Chlorine dosing () | 2 | 0 | 0.3338 | 0.2000 | 0.3239 | 0.2690 | 31.1524 | 40.3501 | 810.9467 |
| 2 | 1 | 0.4357 | 0.2000 | 0.4122 | 0.3568 | 31.1136 | 43.2178 | 847.8847 | |
| 2 | 2 | 0.2981 | 0.2000 | 0.2904 | 0.2641 | 32.2709 | 40.3661 | 786.5580 | |
| 2 | 3 | 0.2996 | 0.2000 | 0.2938 | 0.2641 | 31.1251 | 40.3228 | 816.4152 | |
| Minimize Chlorine dosing and Pressure () | 2 | 0 | 0.4838 | 0.2000 | 0.4779 | 0.4078 | 28.7497 | 40.7384 | 781.7898 |
| 2 | 1 | 0.4655 | 0.2000 | 0.4550 | 0.3921 | 21.6023 | 33.3100 | 630.6005 | |
| 2 | 2 | 0.4134 | 0.2000 | 0.4107 | 0.3345 | 31.2451 | 41.9138 | 805.2318 | |
| 2 | 3 | 0.3023 | 0.2000 | 0.3003 | 0.2603 | 22.8751 | 40.9555 | 729.7666 |
| Objective | PRVs (No.) | IVs (No.) | Locations of PRVs (Pipe IDs) | Locations of IVs (Pipe IDs) |
|---|---|---|---|---|
| Minimize Chlorine dosing () | 1 | 0 | 31 | |
| 1 | 1 | 36 | 19 | |
| 1 | 2 | 1 | 31, 20 | |
| 1 | 3 | 10 | 12, 19, 31 | |
| Minimize Chlorine dosing and Pressure () | 1 | 0 | 28 | |
| 1 | 1 | 10 | 3 | |
| 1 | 2 | 20 | 31, 21 | |
| 1 | 3 | 18 | 12, 35, 31 | |
| Minimize Chlorine dosing () | 2 | 0 | 9, 21 | |
| 2 | 1 | 10, 31 | 17 | |
| 2 | 2 | 24, 18 | 10, 31 | |
| 2 | 3 | 8, 21 | 17, 10, 31 | |
| Minimize Chlorine dosing and Pressure () | 2 | 0 | 13, 28 | |
| 2 | 1 | 1, 11 | 31 | |
| 2 | 2 | 36, 5 | 17, 27 | |
| 2 | 3 | 28, 36 | 12, 27, 35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, H.; Li, P. Co-Optimization of Valve Placement and Chlorine Dosing in Water Distribution Systems. Water 2025, 17, 3360. https://doi.org/10.3390/w17233360
Cao H, Li P. Co-Optimization of Valve Placement and Chlorine Dosing in Water Distribution Systems. Water. 2025; 17(23):3360. https://doi.org/10.3390/w17233360
Chicago/Turabian StyleCao, Hao, and Pu Li. 2025. "Co-Optimization of Valve Placement and Chlorine Dosing in Water Distribution Systems" Water 17, no. 23: 3360. https://doi.org/10.3390/w17233360
APA StyleCao, H., & Li, P. (2025). Co-Optimization of Valve Placement and Chlorine Dosing in Water Distribution Systems. Water, 17(23), 3360. https://doi.org/10.3390/w17233360






