Evaluation of the Abiotic Components of the Nutrient Balance in the Barents Sea and Its Influence on Primary Production

Abstract

This study builds on our prior research to refine the methodology for estimating marine primary production (PP) in the Barents Sea. It examines how abiotic factors—vertical mixing and horizontal advection—affect nutrient concentrations in the euphotic zone and subsequently influence PP. The analysis utilized salinity and nutrient data from the World Ocean Atlas (NCEI WOA). The δ¹⁸O parameter, used in conjunction with salinity, helped quantify the proportion of water from different origins. The results revealed a spatial heterogeneity in nutrient transport, identifying zones of both synchronous and asynchronous nutrient flows. Asynchronous flow was characterized by the removal of phosphorus and silicon alongside the influx of nitrogen. A significant correlation between these physical fluxes and PP was observed in the eastern part of the sea, where asynchronous flow prevails. Our calculations indicate that nitrogen influx increases PP by an average of 38% as high as 68%. The simultaneous fluxes of silicon and phosphorus showed no statistically significant effect. The study concludes that nitrogen is the primary limiting factor for PP in this region.

1. Introduction

The synthesis of organic matter by primary producer communities forms the basis of the marine ecosystem’s biological productivity. The Barents Sea is recognized as one of the most productive subarctic shelf seas [1,2,3], a status attributed to its high illumination and sufficient nutrient concentrations [4]. Its primary production (PP) constitutes approximately 40% of the total PP of all Arctic seas [1]. The average value is 44.5 gC m⁻² year⁻¹ [5]. Several factors account for the high primary productivity observed in the Barents Sea. These include a large shelf region occupying nearly 90% of its total area; the absence of ice cover over half its area throughout the year; the mixing of warm Atlantic and cold Arctic water masses, which stabilizes the Polar Front and drives the upwelling of deep, nutrient-rich waters; and glacial melt [3].

The Barents Sea ecosystem is predominantly shaped by Atlantic waters (AW), with primary production being significantly influenced by the inflow of warm, saline water from the northern North Atlantic [6,7]. The pelagic ecosystem is characterized by a series of water masses, each supporting a distinct biological community. The water masses differ in characteristics such as temperature and salinity, and other abiotic and biotic parameters.

Situated at the confluence of the Arctic and Atlantic Oceans, the Barents Sea is primarily composed of Arctic and Atlantic Waters (AW), which are distinguished by their unique production processes [8]. The hydrographic composition of these waters originates from Atlantic, river, and melting sources, and is also transformed by ice-formed water [9,10,11,12,13].

The highest PP values in the Barents Sea are observed in shallow water areas (such as the Murmansk, Finnmarken, and Nordka Banks), in the coastal zone, and in areas where Atlantic and local Barents Sea waters mix [8]. These areas of high productivity are confined to the euphotic layer and are primarily driven by intensive vertical circulation on shallow-water slopes. This circulation results from the confluence of warm, mobile AW and colder, local waters, which enriches the photic zone with nutrients and sustains high summer production [13]. Southwestern maritime zones exhibit substantially greater productivity than their northeastern counterparts. Arctic water masses demonstrate a mean annual primary production of 50–100 g C m⁻² year⁻¹, compared to 100–200 g C m⁻² year⁻¹ observed in AW. The average annual gross PP in the Atlantic, coastal, and Barents Seas is calculated to be between 82 and 174 g C m⁻² year⁻¹ [13].

Phytoplankton growth cycles in the Barents Sea are primarily influenced by solar irradiance and sea ice, which dictate the onset and duration of blooms across different latitudes. The active growing season decreases from eight to nine months in the south to just two to three months in the north. The simultaneous presence of phytoplankton communities at various developmental stages within the pelagic zone governs the seasonal heterogeneity in PP patterns. Frontal zones with enhanced productivity show little variation and are correlated with the vertical ascent of water at the frontal interface [4,14].

It should be noted that phytoplankton biomass is subject to significant interannual variability. For instance, within the Atlantic-influenced region, phytoplankton biomass exhibited a fourfold increase during the warm period of the 1930s compared to the colder period of the late 1960s and early 1970s, when mean annual water temperatures decreased from 4.2 °C to 3.7 °C [15].

While environmental factors are well-known drivers of PP, accurately quantifying their direct contribution remains challenging. In our previous work [16,17], we proposed a scheme for estimating PP based on nutrient consumption. However, estimates derived from this method can deviate significantly from empirical measurements, such as those derived from Earth remote sensing. This discrepancy arises because the ratio of nutrient consumption over the annual cycle serves as an integrated indicator reflecting the entire period of intra-annual succession. In contrast, measured chlorophyll or particulate organic carbon (POC) data are temporally specific, representing a single point within the annual sequence.

To address this, our proposed PP calculation scheme accounts for the abiotic component (Q_ab) affecting nutrient dynamics within the euphotic zone. This component Q_ab represents the abiotic flux of nutrients from deeper layers, where organic matter decomposition occurs, to the surface waters, as well as horizontal advection. An example of such an abiotic component is found in the Sea of Okhotsk. According to Arzhanova and Zubarevich (1995) [18], the cyclonic vortex over Kashevarov Bank, approximately 80 km in diameter, drives a daily upwelling of roughly 430 km³ of water. This upwelled water contains concentrations of about 22, 2, and 40 milligram-atoms per cubic meter of nitrogen, phosphorus, and silicon, respectively. The abiotic component can be either positive (indicating nutrient inflow into the euphotic layer) or negative (indicating nutrient outflow). Our earlier articles [16,17] reported Q_ab values as intermediate results without a detailed description.

This article aims to address this gap through the following objectives:

• Presenting a procedure for assessing variations in the total nutrient content of the euphotic zone.
• Quantifying the alteration in primary production resulting from variations in the abiotic nutrient flux Q_ab within the euphotic zone.

Although the Barents Sea has been studied more extensively than other Arctic seas, significant knowledge gaps persist. These pertain to seasonal productivity variations, the roles of individual producer groups and biotopes, the contributions of specific primary production components, and the spatial distribution of primary production in relation to the diverse hydrological structure of the water body. Our investigation focuses on clarifying the pathways of primary organic matter in the Barents Sea, leading to a more complete understanding of this critical process.

2. Materials and Methods

Researchers typically distinguish a limited number of primary production types. According to their definitions [19]:

Gross Primary Production (GPP) is defined as the total rate of photosynthetic carbon fixation, excluding contemporaneous algal respiration and heterotrophic metabolism.

Net Primary Production (NPP) is calculated as GPP minus algal respiration.

Net Community Production (NCP) is defined as GPP minus both autotrophic and heterotrophic respiration.

In this study, we applied the methodology of Arzhanova et al. [18,20,21], where silicon production (NCP_Si) is used as a proxy for overall production, while nitrogen production (NCP_N) yields the “new” production. The explanation and assumptions are detailed in the works of Arzhanova et al. The regeneration of silicon proceeds significantly more slowly than that of nitrogen and phosphorus. Consequently, the lowest production values typically correspond to the losses of nitrogen and phosphorus in the euphotic layer, while the highest correspond to the losses of silicon. Moreover, when assessing phytoplankton production based on changes in silicon concentration, the portion of production formed through the recycling of nitrogen and phosphorus is also taken into account. Nitrates sustain primary production (new production) and are considered to facilitate the uptake of nutrients that were present at the start of the growing season or were introduced into the euphotic zone from external sources.

Summarizing the presented analysis according to the approach of N.V. Arzhanova et al. [18,21] it can be concluded that production calculated from silicon (NCPSi) reflects total production, whereas calculation based on nitrogen (NCPN) provides an estimate of “new” production.

“New” production for these authors implies GPP minus both autotrophic and heterotrophic respiration, i.e., NCP. This model allows gross and net production to be estimated through silicon and nitrogen balances, where GPP is equated to NCP_Si and NCP to NCP_N, respectively. Although this model requires further validation, we employ it here as a working hypothesis. This paper adheres to the same definitions and notation.

The computation of net community production (NCP) using a nutrient consumption-based methodology is thoroughly described in the works by Namyatov et al. [16,17]. These articles demonstrate that the shift in nutrient concentration between winter and summer is attributable to two main factors: the “productive” component ($C_{phyto}$), which includes photosynthetic activity and mineralization of organic matter, and the “non-productive” component ($C_{ab}$), resulting from vertical and advective exchange.

The main purpose of this study was to evaluate the contribution of $C_{ab}$ to primary production (PP) in different areas of the Barents Sea. The methodological basis for estimating the ($C_{ab}$) contribution cannot be described without first outlining the general methodology for PP calculation. Therefore, it is essential to reiterate the methodological part of the PP calculation described in the works by Namyatov et al. [16,17], with some modifications and additions (Supplementary Materials).

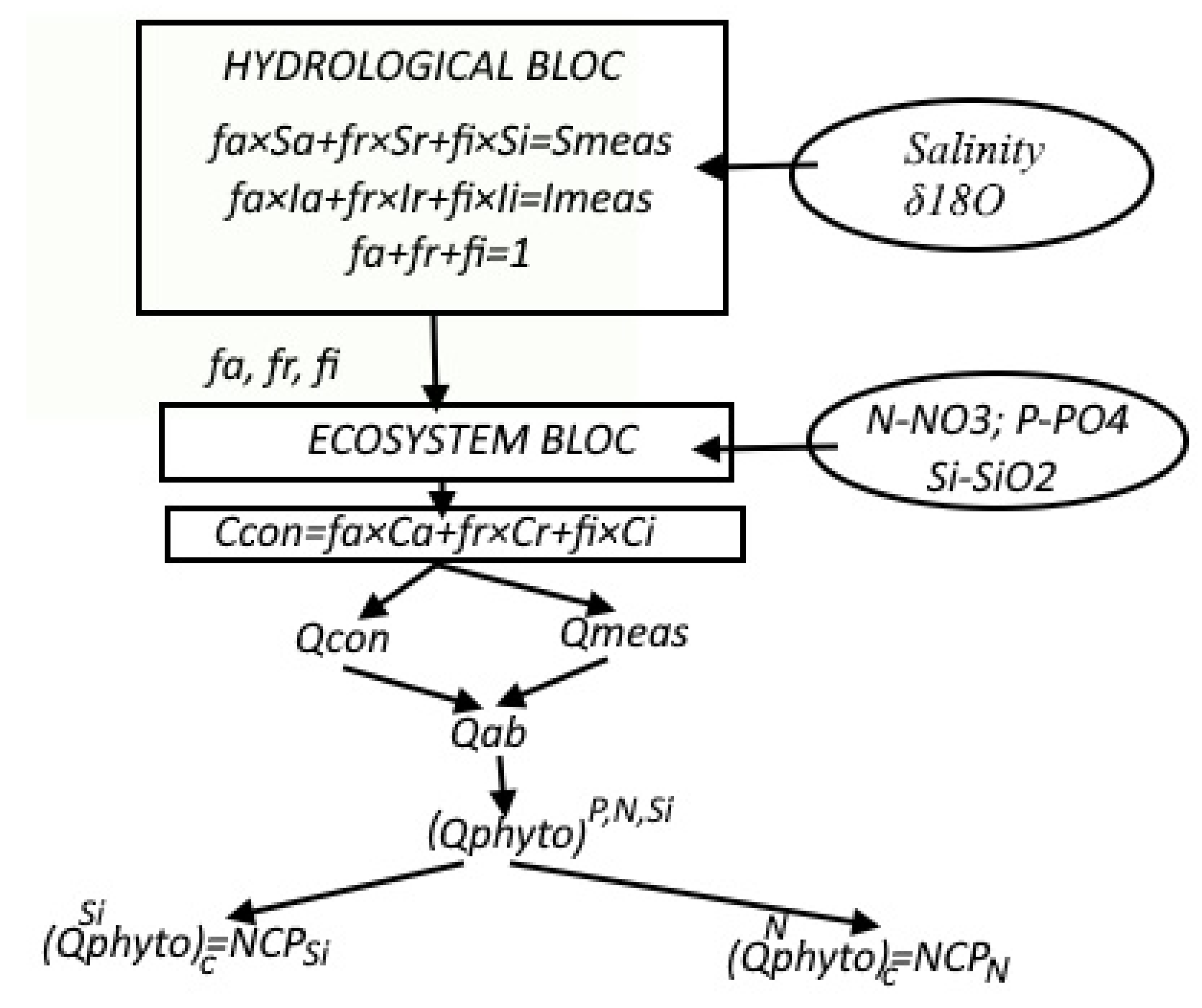
The proposed methodology consists of two main blocks (Figure 1). In the hydrological block, the relative contributions of different types of waters to the resulting seawater are estimated using the parameters δ¹⁸O and salinity. Within the ecosystem block, primary production is calculated based on baseline water properties and nutrient concentrations.

Accepted assumptions of the presented methodology

When developing this method, three assumptions were made:

(1)

The contribution of the non-productive component ($\Delta Q_{ab}$) varies from region to region but is constant throughout the year in the region.

(2)

The entire phytoplankton of the Barents Sea consists of only two systematic groups of phytoplankton: diatoms and dinoflagellates (peridinium). According to the Biological Atlas of the Barents Sea, which analyzed 1000 samples, these two systematic groups constitute, on average, 94% of the total phytoplankton biomass in the sea.

(3)

The regeneration coefficient (Equation (S15)) varies from region to region but is constant throughout the year within a given region. The absolute value of the regeneration value will vary from month to month.

2.1. Methodology for Calculating the Fractions f_a, f_r, and f_i (Hydrological Block)

The calculation of the fractions of different water types—Atlantic water (f_a), river runoff (f_r), and sea ice meltwater (f_i)—is based on solving a simple system of water mixing equations (Supplementary Materials Equation (S1)). The input parameters for this model are salinity and the stable oxygen isotope ratio (δ¹⁸O).

This methodological approach is well-established in oceanographic literature and has been extensively applied in numerous studies, including [9,10,11,12,13,22,23,24,25,26,27,28,29,30,31], among others.

2.2. Principle Scheme of Primary Production Calculation (Ecosystem Block)

In these works, the measured concentration (C_meas—resulting concentration) of elements is presented as comprising four main components:

$C_{phyto}$ is the productive component of the nutrient balance.

$C_{rem}$ is the component resulting from the nutrient supply due to remineralization of organic matter during the photosynthesis process.

C_ab (abiotic component) is the concentration change conditioned by the inflow or outflow of nutrients from/to the euphotic layer as a result of horizontal advection or vertical mixing during the photosynthesis period.

C_con is the conservative concentration of the nutrient *j*. $C_{conj}$ is the concentration that depends only on the mixing of different types of waters (1) and (2) and is independent of photosynthetic activity or short-term abiotic exchange (e.g., from sedimentation, deposition, or advection).

C_non-con—non-conservative part. This component consists of the “productive” component C_phyto and the “non-productive” component C_ab (3) and (4).

$$C_{con}=f_a\times C_a+f_r\times C_r+f_i\times C_i$$

(1)

$$f_a+f_r+f_i=1$$

(2)

where

C_a—the average concentration of the studied element in “purely” Atlantic waters;

f_a—the relative volume of “purely” Atlantic waters in the resulting water mass (%);

C_r—the average concentration of the studied element in “pure” river waters;

f_r—the relative volume of “pure” river water in (%);

C_i—the average concentration of the studied element in “ice” waters;

f_i—the volume of sea ice formed or melted, reduced to the density of water or the volume of meltwater in %, for simplicity, we will call this value “ice” waters. The following equations define the key components of the nutrient balance (3) and (4):

$$C_{non-con}=C_{con}-C_{meas}$$

(3)

$$C_{non-con}=C_{phyto}+C_{ab}$$

(4)

The conservative and resulting reserves can be determined using the following Equation (5):

$$Q_{meas}^n={\int }_0^h{C}_{meas}^{n}dh\hspace{1em}\mathrm{and}\hspace{1em}{ Q}_{con}^n={\int }_0^h{C}_{con}^{n}dh$$

(5)

Index n indicates the month (1, 2, … 12).

dh is the distance between water horizons.

$Q_{con}^{P,N,Si}$ is a conservative reserve of phosphorus, silicon, or nitrogen in the euphotic layer; h is the maximum horizon at which, during the year, the saturation of water with dissolved oxygen shifts from values > 100% to values < 100%; and dh represents the measurement horizons of $C_{meas}$.

For each month, the non-conservative component $\Delta Q^n$ was calculated as the difference between the values of the integrals $Q_m^n$ and $Q_c^n \left(6\right)$.

$$\Delta Q^n=Q_{con}^n-Q_{meas}^n$$

(6)

The minimum value of the $\Delta Q^n$ over the year, which occurs before the start of photosynthesis (typically February–March in different sea areas), is taken as the value of the non-productive component (7).

$$Q_{ab}=\mathrm{m}in(\Delta Q^n)$$

(7)

Similarly, $Q_{meas}^{P,N,Si}$ is the measured amount of nutrients; $Q_{rem}^{P,N,Si}$ is the amount supplied by remineralization; $Q_{ab}^{P,N,Si}$ is the change in amount due to abiotic processes; and $Q_{phyto}^{P,N,Si}$ is the change in the amount of nutrients due to the photosynthesis process.

In this context, the final value of nutrient (j) consumption in month n, in the process of photosynthesis, will be determined by Equation (8):

$$\left(Q_{phyto}^n\right)j=\left(Q_{con}^n\right)j-\left(Q_{meas}^n\right)j+\left(Q_{rem}^n\right)j\pm {(Q}_{ab})j+(Q_{phyto}^{n-1}) j \ast Kj$$

(8)

$Kj$—remineralization coefficient of accumulated nutrient j in organic matter.

As a result, primary production is calculated (9) using the values of d and p.

$$(Q_{phyto}^n{)}_C=(Q_{phyto}^n{)}_j\ast (d{S}_d+p{S}_p)$$

(9)

d—the relative contribution of carbon from diatom plankton biomass to total primary production;

p—the relative contribution of carbon in peridinium plankton biomass to total primary production;

S_d and S_p—stoichiometric ratios of carbon to the j-th biogenic element for the systematic groups of diatoms and peridinium phytoplankton.

Here, ($Q_{phyto}^{Si}$)_c = NCPSi represents the calculation of the amount of carbon involved in photosynthesis (calculated by silicon), corresponding to total production.

Here ($Q_{phyto}^N$)_c = NCP_N, the calculation of the amount of carbon involved in photosynthesis (calculated by nitrogen), corresponds to new production.

The relative magnitude of the nutrient uptake will be used as a criterion for assessing the influence of an abiotic factor on the PP value in this study:

Relative to the conservative stock, including the value of remineralization (10),

$${PC}_{P,N, Si}={\displaystyle \frac{Q_{phyto}^{P,N,Si}}{\left(Q_{con}^{P,N,Si}\right)+Q_{rem}^{P,N,Si}}}\ast 100(\%)$$

(10)

Relative to the conservative stock, including the value of remineralization and the value of the abiotic component (11),

$${PT}_{P,N, Si}={\displaystyle \frac{Q_{phyto}^{P,N,Si}}{\left(Q_{con}^{P,N,Si}\right)+Q_{rem}^{P,N,Si}+Q_{ab}^{P,N,Si}}}\ast 100(\%)$$

(11)

The methodology for calculating the magnitude of primary production from nutrient values has already been described in two papers and is provided in the Supplementary Materials (Equations (S1)–(S23)).

2.3. Data

This study utilized hydrological and biogeochemical data, including salinity, phosphate–phosphorus, nitrate–nitrogen, and silicate–silicon, obtained from the World Ocean Atlas 2023 [32,33]. The data are presented as monthly averages on a 1° × 1° grid across standard depth horizons from 0 to 300 m (0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 125, 150, 175, 200, 225, 250, 275, and 300).

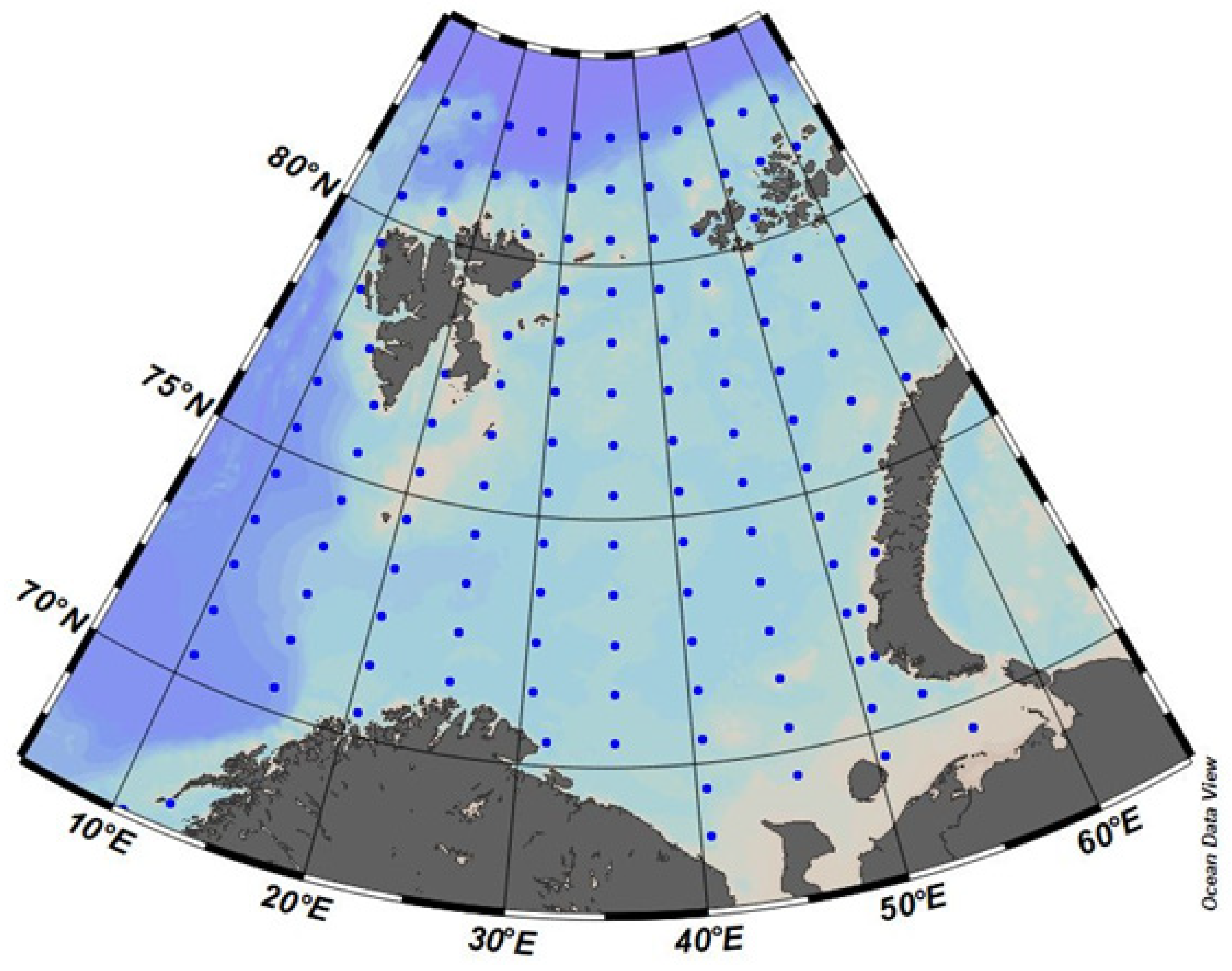
The spatial resolution of the analysis was enhanced compared to previous studies [16,17], which employed a coarse grid of 35 squares (10° longitude × 2° latitude). In this work, calculations were performed at 137 discrete points spaced at 1° latitude and 5° longitude intervals across the study area (Figure 2).

Stable oxygen isotope data (δ¹⁸O) and complementary salinity measurements were sourced from public archives NASA [33,34], covering the period from 1972 to 2008. A comprehensive list of these datasets is provided in Namyatov [12]. Furthermore, this study incorporated the following:

• In addition, the results of the 2014 study [35];
• New data from the 2021 expedition aboard the R/V Dalnie Zelentsy, including concurrent measurements of δ¹⁸O in seawater, sea ice, and under-ice water in the Barents Sea [12].

Compiled data on δ¹⁸O values in rivers discharging into the Barents and White Seas (error: ±0.025‰) are provided in Table S1.

The measurement precision for δ¹⁸O was 0.03–0.07‰ for samples from 1993 to 1995 and 0.1–0.2‰ for samples collected prior to 1989 [12,27].

A key methodological step involved estimating δ¹⁸O values at the WOA23 grid points, where direct measurements were unavailable. This was achieved by leveraging the well-established, strong correlation between salinity and δ¹⁸O documented in numerous studies.

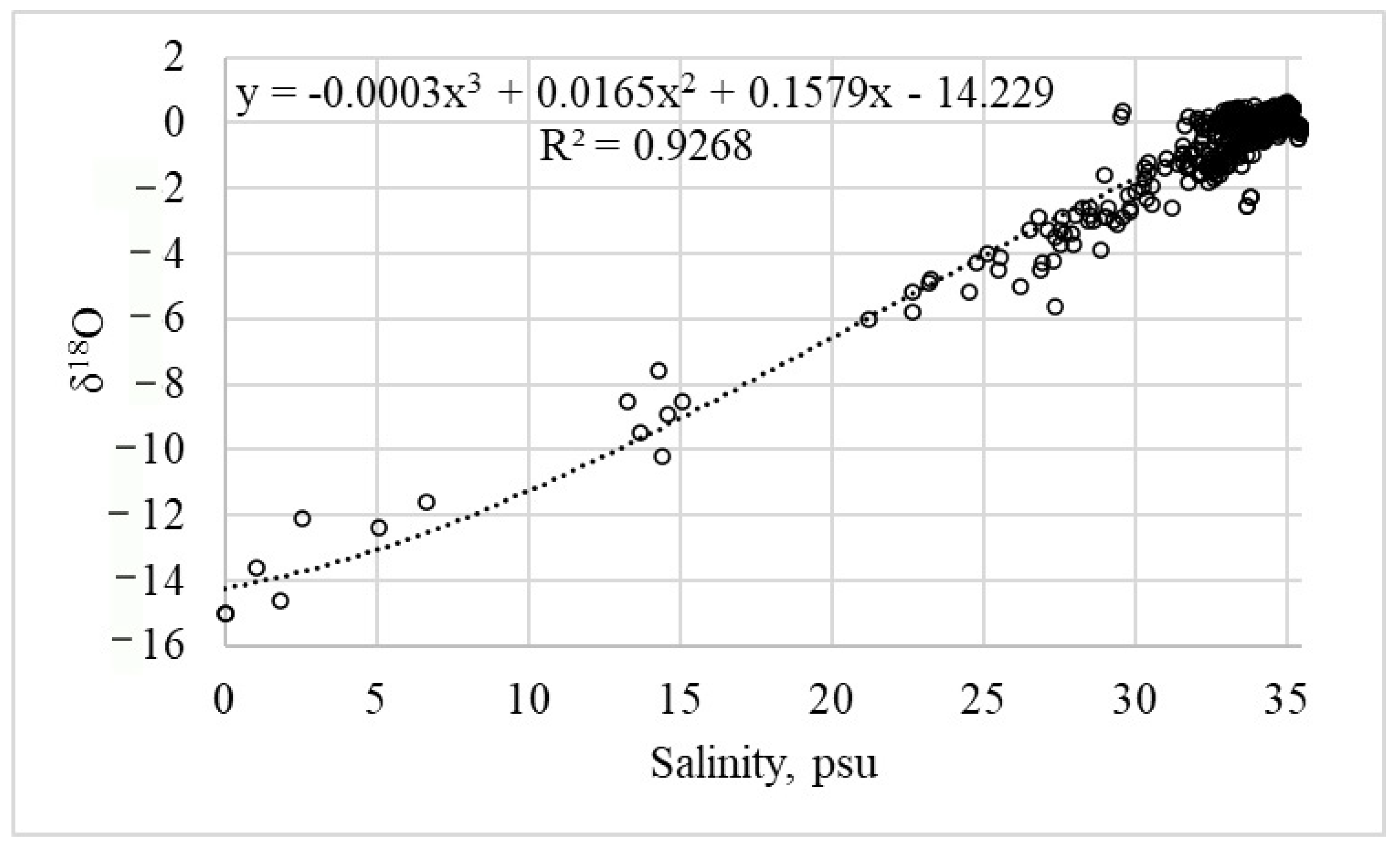
The generalized relationship between salinity and δ¹⁸O was established using a compilation of 2342 measurements from 344 stations in the Barents Sea, as reported in previous studies [11]. This dataset is presented in Figure 2. The relationship is strong, with a linear regression yielding a high coefficient of determination (R² = 0.91, p < 0.001).

Since the dataset integrates data from various seasons and years, the resulting regression equation is considered universally applicable for estimating δ¹⁸O from salinity across the study region, even in the absence of direct isotopic measurements.

To validate this approach, we tested the robustness of the relationship. The full dataset was randomly split into two equal subsets (n = 1100 each). The regression equation derived from the first subset was used to predict δ¹⁸O values from salinity data in the second subset. The predicted values were then compared against the actual measured δ¹⁸O values.

The agreement between the measured and predicted δ¹⁸O values was statistically validated using Fisher’s F-test. Furthermore, Student’s t-test confirmed that the means of the two datasets were not significantly different. Both tests showed a high level of statistical significance (p < 0.01), thus confirming our hypothesis.

Consequently, the validated regression equation (shown in Figure 3) was applied to calculate δ¹⁸O values for all salinity measurements within our study, enabling a comprehensive analysis.

2.4. Verification of the Results Obtained

2.4.1. Verification with Direct Measurements of Phytoplankton Biomass

Before analyzing the obtained data, it is necessary to verify it against the results obtained by other methods. The method and results of verification have already been published and are presented in detail in Section S3 of the Supplementary Materials. It makes no sense to compare the absolute values of primary production and measured phytoplankton biomass. However, it is possible to compare the relative contribution of diatoms and dinoflagellates to the total production (calculated values) with their relative contribution to the total phytoplankton biomass (direct measurements) (Figure S5) presented in the study by Namyatov et al. [16,17]. The biomass values are from the archive of the Murmansk Marine Biological Institute, Russian Academy of Sciences, from 1979 to 2013, for the July–September season, the period with the most data available. This comparison may not seem entirely correct, as the calculated values are integrated over the euphotic layer, while the direct biomass measurements are from the surface layer only. Nevertheless, the distribution patterns and the relative contributions of these two systematic groups are quite similar. Furthermore, by the beginning of summer, the intensity of photosynthesis reaches its maximum and stabilizes, leading to peak primary production and the maximum decrease in nutrient reserves. Under these conditions, the relative calculation error is minimal.

Verification showed that the calculated relative contributions of diatoms and dinoflagellates to the total primary production are similar to their directly measured contributions to the total phytoplankton biomass, not only in their distribution pattern but also in magnitude.

2.4.2. Verification with Other Methods for Calculating Primary Production

For comparison with other results from the Barents Sea, we used the data presented by Reigstad et al. [36] for the waters surrounding the Svalbard archipelago. A detailed comparison is presented in Namyatov et al. [16,17]. In their study [36], primary production was calculated using hydrodynamic and ecosystem models. The hydrodynamic model is large-scale with a horizontal grid spacing of 20 km and a nested model resolution of 4 km. The ecosystem module includes nitrates, ammonium, silicates, diatoms, flagellates, microzooplankton, bacteria, heterotrophic nanoflagellates, fast-sinking detritus, slow-sinking detritus, and two groups of mesozooplankton (Calanus finmarchicus and Calanus glacialis).

Based on the modeling results, six regions with different PP values were identified in this area (Table S4). Because their model had a much higher resolution than ours, it identified six regions. Based on our results, we identified three regions. We believe that the boundaries of our three regions encompass the six regions from the aforementioned study [36] (Table S3), and the results show good agreement. A particularly high degree of similarity was obtained for the PP estimate in region III, adjacent to the archipelago in the northeastern part and extending further to the northeast. Both studies indicate a two-fold decrease in PP values in this region compared to others. However, according to our data, the relative standard deviation of the mean PP in this area is several times larger than that reported in the compared study.

Although the calculations were carried out with different resolutions, comparable results were obtained (Supplementary Materials).

2.5. Software

The monthly averaged nutrient concentration data from the WOD were processed and visualized using the ODV software Version 5.8.2 [37]. This software was used to interpolate the data onto a regular grid with a resolution of 10° longitude × 2° latitude. The calculation of integral (1) was also performed within ODV.

All subsequent computations, including the determination of the fa, fr, and fi ratios, nutrient uptake, and primary production rates, were carried out in Microsoft Excel.

The statistical analysis comprised the following steps:

Cluster Analysis: This was performed using the STATISTICA 7 software package [38]. The analysis incorporated 12 calculated parameters: h, $Q_{sed}^P$, $Q_{sed}^N$, $Q_{sed}^{Si}$, $Q_{phyto}^P$, $Q_{phyto}^N$, $Q_{phyto}^{Si}$, ${PT}_P$, ${PT}_N$, ${PT}_{Si}$, d, and ${(Q}_{phyto}^{Si}{)}_c$. Ward’s hierarchical clustering method with Euclidean distances was applied to normalized data [39]. The optimal number of clusters for the k-means algorithm was determined using the Elbow method (Figure A3).

Descriptive Statistics: The mean values and standard deviations for the parameters were calculated in Microsoft Excel.

3. Results

This article presents the findings for the period of minimum nutrient content (August–September), which corresponds to the highest accumulated primary production (PP) values. The PP value represents production accumulated from the beginning of the photosynthesis process (March–April) until its termination in September. The calculated value characterizes total PP for the entire photosynthesis period and is comparable to annual PP values expressed in g (mg) C year⁻¹.

Previous studies by Namyatov et al. [16,17] detailed the primary spatial distributions of PP values in the Barents Sea using the aforementioned methodology. However, several differences in input data should be noted. First, the present study utilizes the newer WOA 2023 database [33], while previous research was based on WOA 2018 [40]. Second, previous calculations were performed for average values in 35 grid squares of 10° longitude × 2° latitude, whereas the current study analyzed 137 individual points with 5° longitude × 1° latitude spacing.

Despite these methodological differences, the main patterns of PP distribution in the Barents Sea remain consistent with previous findings:

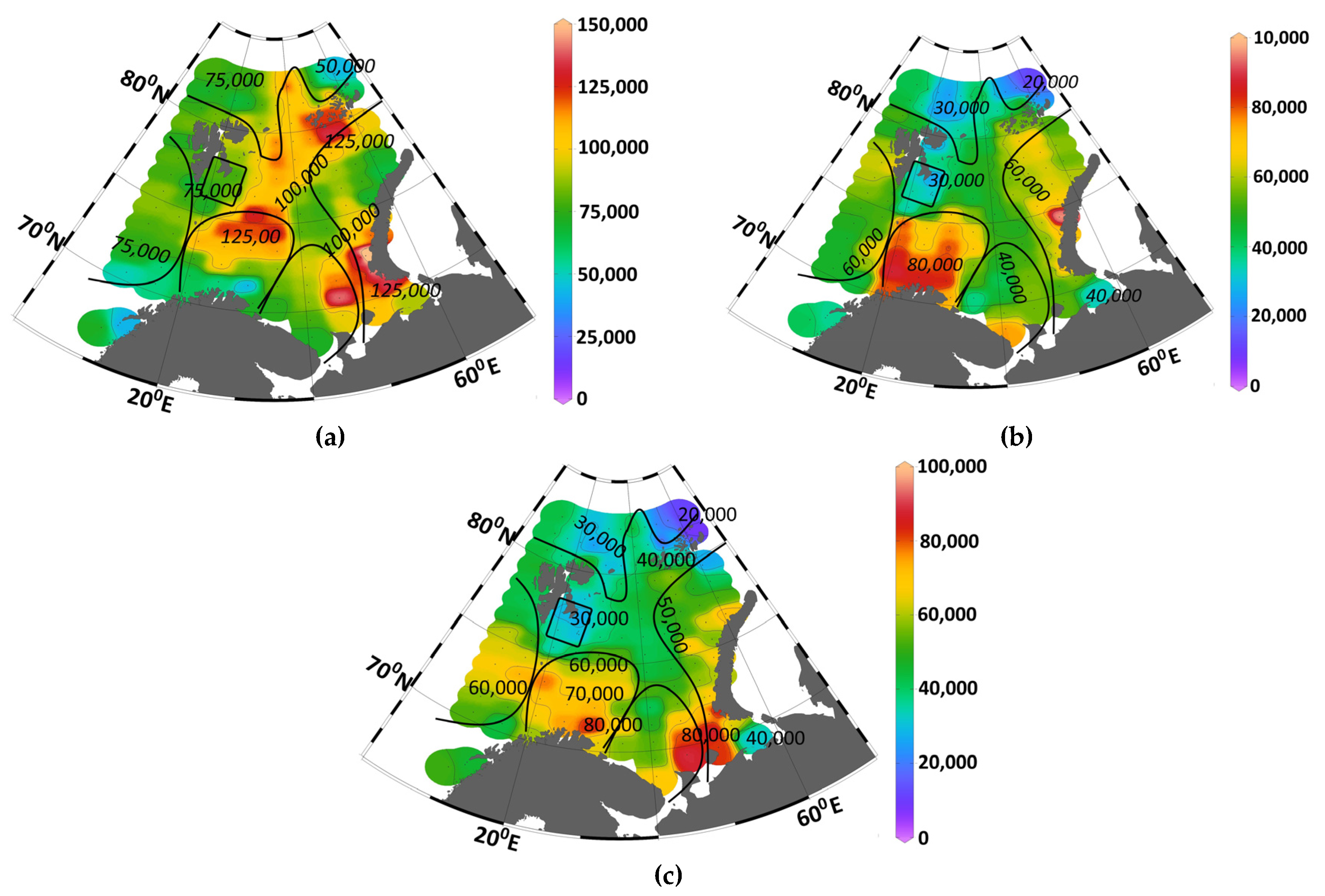
Four areas with elevated PP values (NCP_Si) were identified: the Medvezhinsky shallow water area, the southwestern part of the sea, the southeastern Barents Sea, and the area adjacent to the southeastern part of Franz Josef Land.

Two areas with reduced PP values (NCP) were observed: the northern border between Svalbard and Franz Josef Land, and the coastal area extending from Varanger Fjord to the White Sea mouth along the Kola Peninsula.

Phosphorus does not limit photosynthetic processes in the Barents Sea. Nitrogen serves as the limiting element from 40° E eastward to Novaya Zemlya up to 80° N. Silicon potentially limits production in the area between Svalbard and Franz Josef Land (75° N–80° N).

When the change in the non-productive component ($Q_{ab}$) of nutrient concentrations is significant, it must be accounted for in estimating photosynthetic uptake. Although this parameter was utilized in previous studies [16,17], it was not thoroughly described. The estimation method is presented in Supplementary Materials (Equation (S8)).

This study aims to quantify the input/output of mineral forms of silicon, phosphorus, and nitrogen and their influence on PP. The analysis is based on the contribution of the non-productive component ($Q_{ab}$) varies regionally but remains constant throughout the year within each specific location. Calculated nutrient balance and PP values are presented in

Table 1. Assessment results of nutrient balance and PP values in September (average values for the euphotic layer of the Barents Sea).

1 Parameter	Units	Magnitude	sd	2 Equation
h	(m)	60.6	21.3	(5)
$Q_{con}^P$	mg m−2	1425.7	499.8	(1)
$Q_{ab}^P$	mg m−2	–95.9	163.6	(7)
$Q_{rem}^P$	mg m−2	216.9	407.5	(S15)
$Q_{phyto}^P$	mg m−2	876.4	317.2	(8)
${\left(Q_{phyto}^P\right)}_C$	mg m−2	49,284	18,917	(9)
${\displaystyle \frac{{\left(Q_{phyto}^P\right)}_C}{h}}$	mg m−3	812.8	285.8
PTP	%	56.7		(10)
PCP	%	53.4		(11)
$Q_{con}^N$	mg m−2	6898	2450	(1)
$Q_{ab}^N$	mg m−2	1706	1571	(7)
$Q_{rem}^N$	mg m−2	1238.2	1593.9	(S15)
$Q_{phyto}^N$	mg m−2	7524	2194	(8)
($Q_{phyto}^N$)c (NCPN)	mg m−2	52,615	16,158	(9)
${\displaystyle \frac{{\left(Q_{phyto}^N\right)}_C}{h}}$	mg m−3	867.7	305.1
PTN	%	76.4		(10)
PCN	%	92.5		(11)
$Q_{con}^{Si}$	mg m−2	11,785	2756	(1)
$Q_{ab}^{Si}$	mg m−2	−1296	1980	(7)
$Q_{rem}^{Si}$	mg m−2	1025	1806	(S15)
$Q_{phyto}^{Si}$	mg m−2	7614	2684	(8)
($Q_{phyto}^{Si}$)c (NCPSi)	mg m−2	93,501	26,321	(9)
${\displaystyle \frac{{\left(Q_{phyto}^{Si}\right)}_C}{h}}$	mg m−3	1542	695
PTSi	%	66.1		(10)
PCSi	%	59.4		(11)
d	%	18.6		(S21)

Notes: ¹—parameter descriptions are provided in Section 2; ²—equation numbers are provided in Section 2 and Supplementary Materials; sd–standard deviations.

.

On average, for the entire sea, we observed an outflow of mineral phosphorus and silicon from the euphotic layer alongside nitrogen an inflow. The mean outflow of phosphorus and silicon during photosynthesis ($Q_{ab}^{P,Si}$) was estimated at 7% and 11% ${\left(\right|Q}_{ab}^{P,Si}|/Q_{con}^{P,Si}\ast 100\%$), of their conservative reserve ($Q_{con}^{P,Si}$), respectively. The mean nitrogen inflow $(Q_{ab}^N$ ) relative to its conservative concentration ($Q_{con}^N$) was estimated at 24% (${|Q}_{ab}^N|/Q_{con}^N\ast 100\%)$.

Figure A1 illustrates distributions of total PP (NCP_SI) and new PP (NCP_N) values, while Figure A2 presents relative nutrient intake values. The mean total accumulated PP (NCP_SI) by September reached 94 ± 26 gC m⁻² or 1.5 ± 0.7 gC m⁻³ for the entire sea. Corresponding new PP (NCP_N) values were 53 ± 16 gC m⁻² or 0.9 ± 0.3 gC m⁻³ (Table 1).

The Redfield–Richards ratios (C:Si:N:P = 106:23:16:1 molar or 41:21:7:1 mass) represent commonly applied stoichiometric ratios [41]. Our study identified different stoichiometric ratios for new primary production (NCP_N) in the Barents Sea: C:Si:N:P = 155:10:19:1 (molar) or 60:9:9:1 (mass) (

Table 2. Nutrient ratios in the euphotic layer of the Barents Sea in September (mass).

Ratio	$Q_{con}$		$Q_{phyto}$		$Q_{rem}$		$Q_{ab}$		3 Diatom	3 Peridinium
		sd		sd		sd		sd
1 Ctot:P			106.7	48.9
2 Cnew:P			60.0	28.5					37.0	58.8
Ctot:Si			12.3	5.6
Cnew:Si			6.9	3.3					1.08	15.15
Ctot:N			12.4	5.0
Cnew:N			7.0	3.0					5.49	7.25
4 Si:P	8.3	3.5	8.7	3.1	4.7	8.9	13.5	23.0	34.44	3.88
4 Si:N	1.7	0.7	1.0	0.3	0.8	1.1	5 -		5.11	0.48
4 N:P	4.8	2.4	8.6	3.1	5.7	10.7	5 -		6.74	8.12

Notes: ¹—Ctot = (NCP_Si); ²—Cnew = (NCP_N); P = $Q_{phyto}^P$; Si = $Q_{phyto}^{Si}$; N = $Q_{phyto}^N$; ³—nutrient ratios in diatoms and peridinium algae (Table S3); ⁴—nutrient element ratios in balance elements; ⁵—multidirectional flows; sd–standard deviations

). Specifically, silicon-to-carbon mass ratios were considerably more than those predicted by the Redfield–Richards model [41]. Such an increase in the C:Si ratio from 1.95 (according to the Redfield–Richards model) to 6.67 (based on our calculations) is likely associated with the different diatom biomasses considered in these two models. The C:Si ratio in diatoms is approximately 1 (100:93 by mass), while in dinoflagellates it is significantly higher, around 15 (100:6.6) [41]. Therefore, an increase in dinoflagellate biomass naturally leads to a higher overall C:Si ratio in the community.

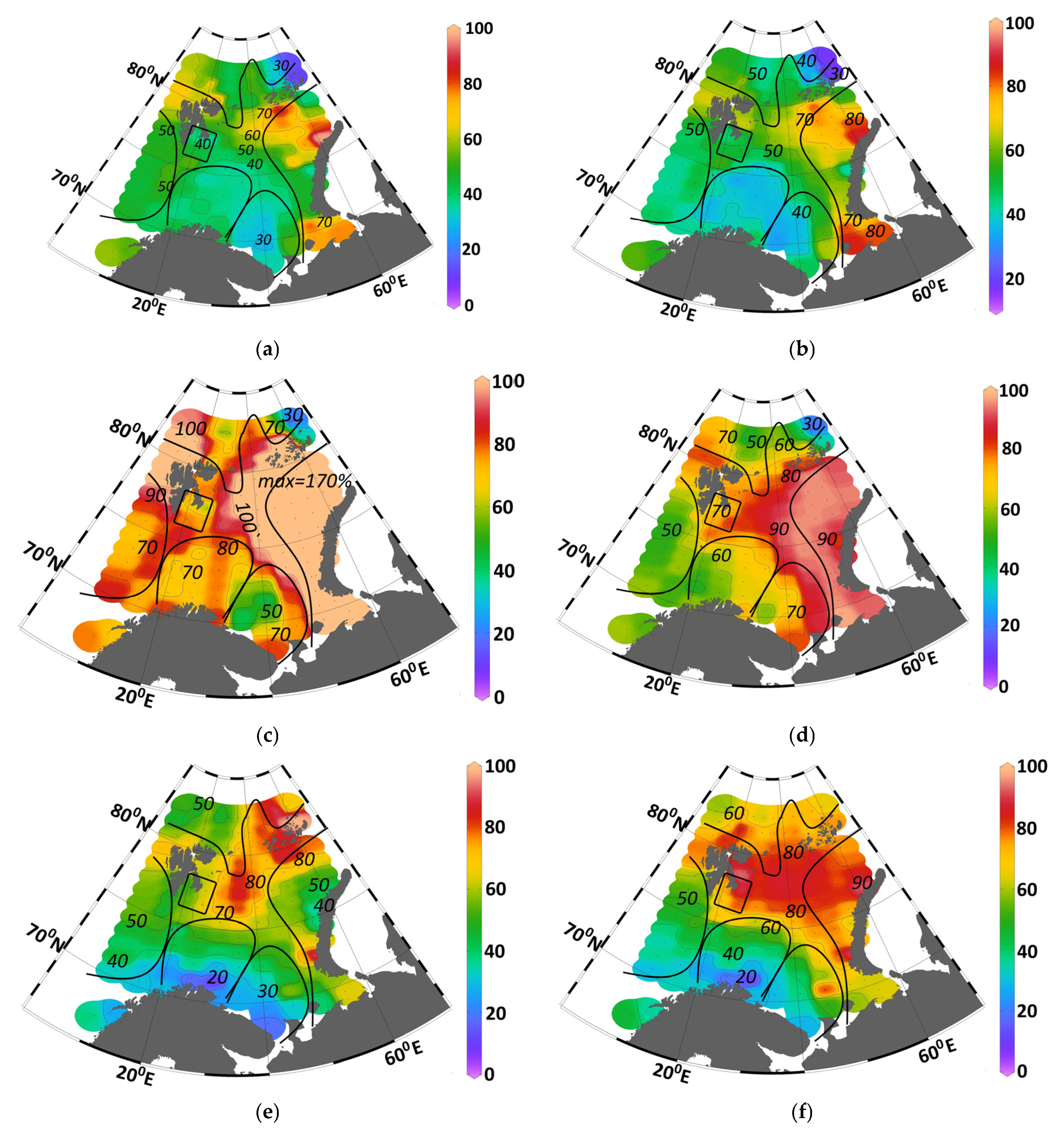
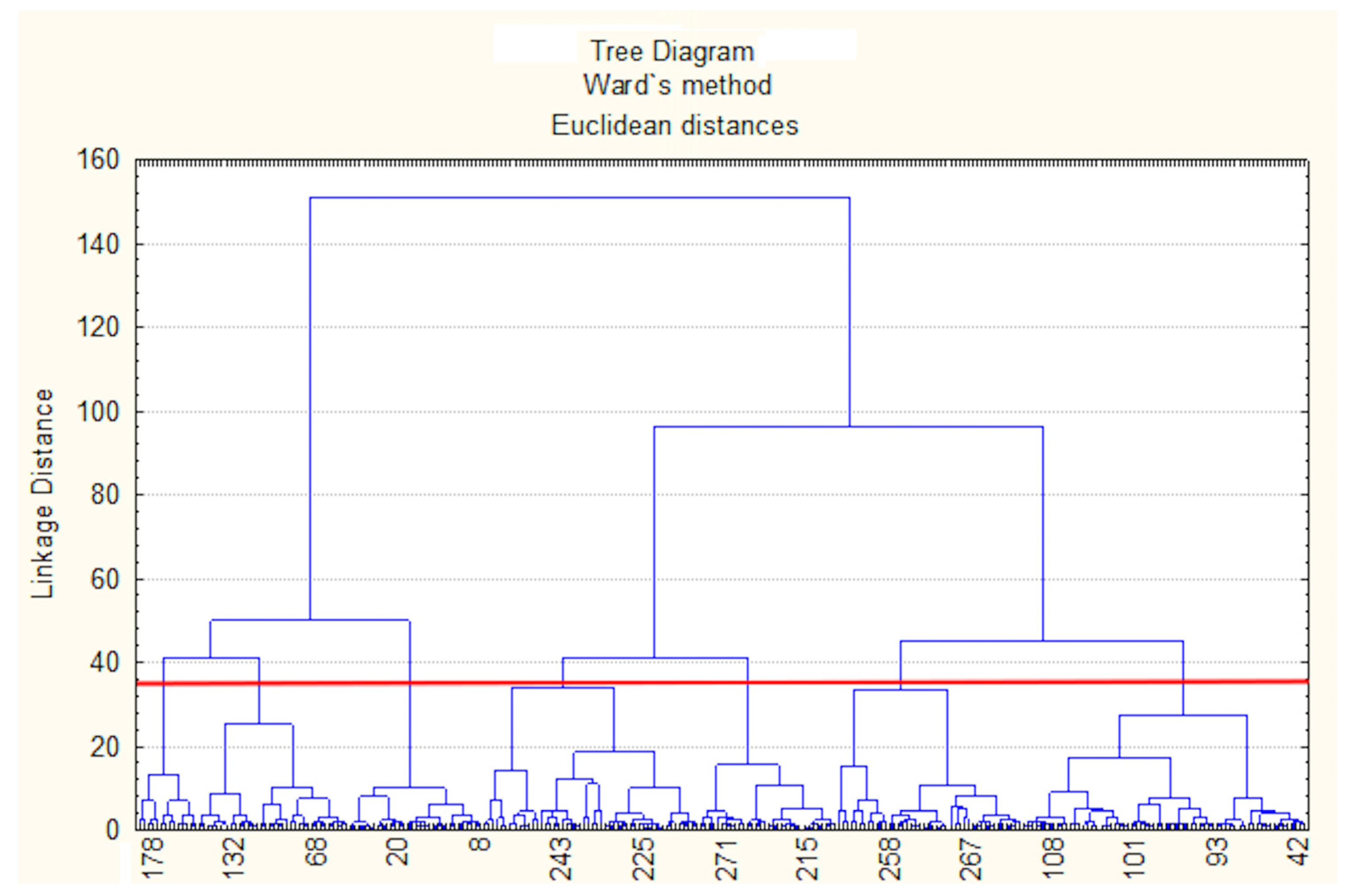
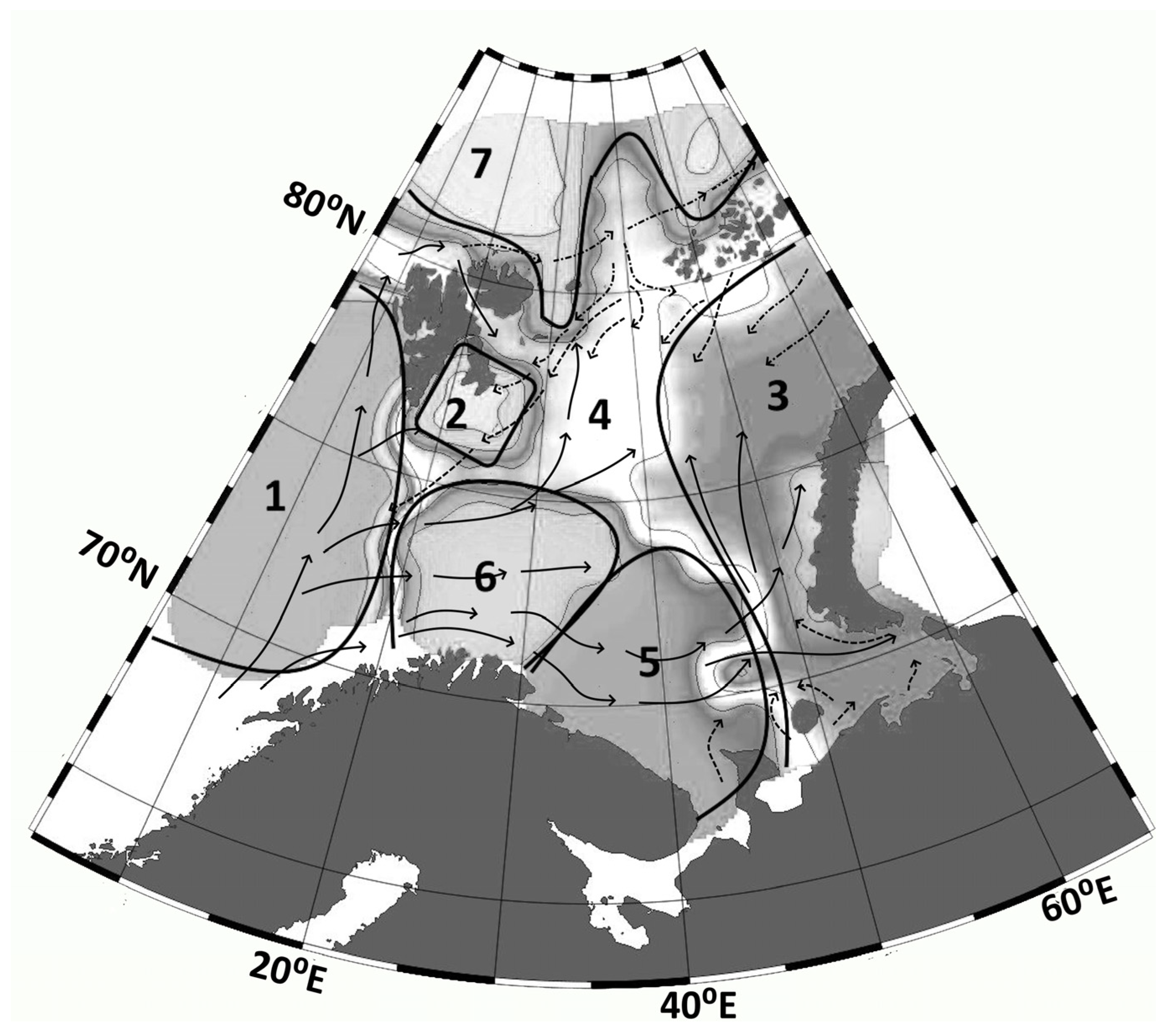
Cluster analysis of results from 137 stations in September identified boundaries between areas with different Q_ab values. The analysis incorporated 12 calculated parameters (Equations (S6)–(S18)): h, $Q_{sed}^P$, $Q_{sed}^N$, $Q_{sed}^{Si}$, $Q_{phyto}^P$, $Q_{phyto}^N$, $Q_{phyto}^{Si}$, ${PT}_P$, ${PT}_N$, ${PT}_{Si}$, d, and ${(Q}_{phyto}^{Si}{)}_c$. Ward’s hierarchical clustering method with Euclidean distances was applied to normalized data [39]. The optimal number of clusters for the k-means algorithm was determined using the Elbow method (Figure A3). Seven clusters were identified (Figure 4), with four exhibiting synchronous nutrient flows and three showing asynchronous patterns characterized by phosphorus and silicon outflow coupled with nitrogen inflow.

The following sections discuss how $Q_{ab}^{P,N,Si}$ values affect primary production levels across different locations, along with taxonomic characteristics, abundance, and biomass of phytoplankton communities.

Complete alignment between the relative content of diatom algae and dinoflagellates and calculated values is unlikely. This uncertainty arises because the resulting nutrient consumption ratio by September represents an integral indicator reflecting not only photosynthetic activity throughout the annual succession but also other factors, including differential nutrient remineralization rates and external inputs to the euphotic layer. In contrast, calculated phytoplankton parameters characterize specific sampling times during intra-annual succession. Taxonomic characteristics, abundance, and biomass indices of phytoplankton communities were obtained from previous studies and literature sources [7,14,44,45,46,47].

3.1. Areas of Synchronous Inflow and Outflow of Nutrients in the Euphotic Layer (Clusters 1, 6, 5, and 2)

Results of the nutrient balance and primary production assessment are presented in

Table 3. Nutrient balance and primary production assessment results for Clusters 1, 6, 5, and 2.

1 Parameter	Units	clu_1		clu_6		clu_5		clu_2		2 Equation
		Value	sd	Value	sd	Value	sd	Value	sd
h	(m)	67.2	3.6	104.5	9.9	87.5	11.8	46.3	1.2
$Q_{meas}^P$	mg m−2	841.9	79.9	1550.8	173.0	1099.8	377.7	516.7	35.9	(5)
$Q_{con}^P$	mg m−2	1572.2	85.0	2468.5	219.6	2048.8	276.9	1125.3	40.4	(1)
$Q_{ab}^P$	mg m−2	67.0	28.4	25.4	73.3	−324.3	156.6	−204.0	84.7	(7)
$Q_{rem}^P$	mg m−2	330.8	155.9	259.0	750.8	279.9	186.5	86.6	38.5	(S15)
$Q_{phyto}^P$	mg m−2	1128.1	197.7	1202.0	180.0	904.7	247.1	491.3	66.8	(8)
${\left(Q_{phyto}^P\right)}_C$ = (NCPP)	mg m−2	65,014	11,316	67,974	11,203	52,623	14,605	25,500	4555	(9)
${\displaystyle \frac{{\left(Q_{phyto}^P\right)}_C}{h}}$	mg m−3	967.1	52.3	650.2	61.5	601.7	81.3	550.4	13.8
PTP	%	56.7		43.7		45.1		48.7		(10)
PCP	%	53.4		44.1		38.8		40.5		(11)
$Q_{meas}^N$	mg m−2	4483	743	5457	1518	2184	1114	1624	281	(5)
$Q_{con}^N$	mg m−2	7663	415	12,013	1070	9937	1337	5420	204	(1)
$Q_{ab}^N$	mg m−2	3307	284	2039	1401	−1262	1365	−403	606	(7)
$Q_{rem}^N$	mg m−2	1277.9	258.3	1905.8	1437.8	1122.9	1363.8	636.3	970.2	(S15)
$Q_{phyto}^N$	mg m−2	7765	432	10,501	1149	7614	1272	4030	707	(8)
($Q_{phyto}^N$)c = (NCPN)	mg m−2	55,521	2788	73,991	8969	54,775	9499	26,895	5429	(9)
${\displaystyle \frac{{\left(Q_{phyto}^N\right)}_c}{h}}$	mg m−3	825.9	44.6	707.7	67.0	626.3	84.7	580.5	14.6
PTN	%	63.4		65.8		77.7		71.3		(10)
PCN	%	86.8		75.4		68.8		66.5		(11)
$Q_{meas}^{Si}$	mg m−2	5825	1167	8378	1813	9015	2804	1417	664	(5)
$Q_{con}^{Si}$	mg m−2	9783	594	16,361	1313	15,511	3077	10,650	666	(1)
$Q_{ab}^{Si}$	mg m−2	1105	659	267	671	−3104	2464	−2506	708	(7)
$Q_{rem}^{Si}$	mg m−2	758	504	1199	3034	997	972	608	342	(S15)
$Q_{phyto}^{Si}$	mg m−2	5821	1221	9449	1475	4389	1887	7335	817	(8)
($Q_{phyto}^{Si}$)c = (NCPSi)	mg m−2	83,389	15,895	126,354	13,692	63,064	26,084	75,368	5851	(9)
${\displaystyle \frac{{\left(Q_{phyto}^{Si}\right)}_C}{h}}$	mg m−3	1240	246	1209	174	721	314	1627	133
PTSi	%	50.0		53.0		32.7		83.8		(10)
PCSi	%	55.2		53.8		26.6		65.2		(11)
d	%	4.4		13.8		7.1		37.2		(S21)

Note: ¹—see Table 1 in Section 2 for parameter descriptions; ²—see Section 2 for equation references.

. The surface euphotic layer exhibited pronounced synchronous fluxes of mineral phosphorus, nitrogen, and silicon associated with photosynthesis. Clusters 1 and 6 are characterized by synchronous nutrient inflow, while Clusters 5 and 2 demonstrate synchronous outflow.

3.1.1. Cluster 1

This area is located on the western slope of the Barents Sea shelf. Depths range from 1500 m in the Norwegian Sea to 500 m in the Barents Sea. Upwelling of deep Atlantic waters along the continental slope creates a stable reservoir of these nutrients.

However, the conservative stock ($Q_{con}$) here is not the highest in the Barents Sea. This is likely because maximum depths are ~500 m, and the conservative stock in the euphotic layer is formed by only a small fraction of nutrients upwelling along the slope and reaching the euphotic layer.

Simultaneously, nutrient inflow during photosynthesis ${(Q}_{ab}$) constantly replenishes the euphotic layer stock (Figure 5). Relative to the conservative stock ($Q_{con}^{P,N,Si}$), the photosynthetic inflow ($Q_{ab}^{P,N,Si}$) accounts for 4%, 43%, and 11% for phosphorus, nitrogen, and silicon, respectively. The most probable pathway for entry of mineral phosphorus, nitrogen, and silicon into the surface euphotic layer is upwelling of nutrient-rich deep waters via the Nordkapp Current (Figure 4). Similar euphotic layer enrichment has been reported on the continental slope off Sakhalin Island and the Kamchatka Peninsula [20,21] and on the Chukchi Sea slope [47]. The lower boundary of the euphotic layer in the area of cluster 1 during the period of minimum nutrient content averaged 67 ± 4 m.

Three algal groups dominate the integral water column biomass: cryptophytes, dinoflagellates, and small flagellates. Dinoflagellates are capable of mixotrophy, which is a combination of autotrophic (photosynthesis) and heterotrophic (consumption of organic substances) nutrition. They can switch between these modes depending on environmental conditions. Under sufficient light, they act as photosynthetic organisms, while in the case of light deficiency, they readily switch to phagocytosis or osmotrophy (absorption of dissolved organic matter). Diatoms make a negligible contribution to the total biomass of the autumnal phytoplankton assemblage. Dominant and abundant species include representatives of the genera Amphidinium, Gymnodinium, Gyrodinium, and Protoperidinium pellucidum (Dinophyceae); Chaetoceros, Nitzschia, Thalassiosira (Bacillariophyceae); Plagioselmis (Cryptophyceae), and small unidentified flagellates. Ice-associated diatoms Nitzschia frigida and N. promare were also recorded. Their presence in the autumnal phytoplankton is due to persistent ice cover melting in the western Fram Strait.

The autumnal phytoplankton community here is characterized by increasing absolute and relative biomass of small flagellates and dinoflagellates, concurrent with a general decline in quantitative indicators. Heterotrophic dinoflagellates comprise >60% of community biomass. Direct measurements showed dinoflagellates constituted 95% of the dinoflagellate–diatom ratio. This value aligns with the calculated relative dinoflagellate abundance, which averages 95.5% for this cluster (Table 3). Dinoflagellate cysts also contributed significantly to total phytoplankton biomass at numerous stations.

3.1.2. Cluster 6

Cluster 6 is also characterized by synchronous nutrient inflow into the euphotic layer during photosynthesis. Nutrient inflow ($Q_{ab}^{P,N,Si}$) relative to the conservative stock ($Q_{con}^{P,N,Si}$) was estimated at 1%, 17%, and 2% for phosphorus, nitrogen, and silicon, respectively. The nutrient stock in the euphotic layer here was maximal, likely due to further vertical displacement of waters advancing into the Barents Sea. This is particularly pronounced on the Medvezhinsko–Spitsbergen shallow waters, where at minimum depths (≤50 m), rising waters entered the euphotic layer directly. The euphotic layer’s lower boundary in this area is significantly deeper, averaging 104 ± 10 m.

Dinoflagellates and diatoms dominate taxonomically and productively. Total biomass is primarily formed by species from Protoperidinium and Dinophysis (Dinophyceae), and Chaetoceros and Rhizosolenia (Bacillariophyceae). However, in some years, autumn phytoplankton biomass peaks were formed by large dinoflagellates (mainly Ceratium spp.) or the diatom Skeletonema costatum. Phytocenosis biomass during this period rarely exceeds 100 µg L⁻¹, consisting primarily of diatoms and dinoflagellates. Their biomass ratio was nearly equal (52% dinoflagellates vs. 48% diatoms). Nutrient uptake ratios also indicate a corresponding increase in diatom relative abundance, though less pronounced than direct measurements suggest (87% vs. 17% for dinoflagellates and diatoms, respectively).

Total PP in the Cluster 1 area during August-September was 83 ± 16 gC m⁻², slightly below the Barents Sea average. In Cluster 6, PP was 50% higher (126 ± 14 gC m⁻²). This difference is likely due to the greater euphotic layer thickness, as primary production per unit volume was nearly identical in both clusters (1.2 ± 0.2 gC m⁻³).

3.1.3. Cluster 5

A synchronous outflow of nutrients from the euphotic layer during photosynthesis is observed in both Clusters 5 and 2. Cluster 5 is located east of Cluster 6. Its defining feature is the continued eastward movement of Atlantic waters. The outflow of nutrients from the euphotic layer ${(Q}_{ab}^{P,N,Si}$) relative to the conservative stock ($Q_{con}^{P,N,Si}$) was estimated at 16%, 13%, and 20% for phosphorus, nitrogen, and silicon, respectively.

The average total primary production (PP) in this area was 63 ± 26 gC m⁻², which is half that of the adjacent western region (Cluster 6), despite considerable spatial variability. With an average euphotic layer depth of 87 ± 12 m, the volumetric PP was significantly lower, at 0.7 ± 0.3 gC m⁻³.

Planktonic algal quantitative indicators in Cluster 5 show relatively uniform spatial distribution, reflecting considerable taxonomic homogeneity of the pelagic phytocenosis throughout the water body. The Atlantic and Barents Sea neritic zones are characterized by a predominance of mixotrophic and heterotrophic cold-water dinoflagellates. The dominant microalgal community consists of dinoflagellates from the genera Ceratium, Dinophysis, and Protoperidinium. Subdominants include the diatoms Proboscia alata and Rhizosolenia hebetata f. semispina, along with rare representatives of the genus Chaetoceros. Some years feature blooms of the coccolithophore Emiliania huxleyi. Total community biomass in this area can reach 250 µg L⁻¹.

The measured biomass ratio of dinoflagellates to diatoms was 65:35%, which does not match the calculated ratio from nutrient uptake data. This discrepancy may be explained by the significant presence of mixotrophic and heterotrophic dinoflagellates, as their nutrient uptake patterns may differ from those of purely autotrophic algae. Unfortunately, we lack data on the elemental composition of these mixotrophic and heterotrophic dinoflagellates, as well as other phytoplankton groups, which is crucial for fully understanding and modeling this inconsistency.

3.1.4. Cluster 2

Cluster 2 also exhibits a synchronous release of nutrients from the euphotic layer during photosynthesis. The nutrient outflow ($Q_{ab}^{P,N,Si}$) relative to the conservative stock ($Q_{con}^{P,N,Si}$) was estimated at 18%, 7%, and 23% for phosphorus, nitrogen, and silicon, respectively.

The hydrological regime in Cluster 2 contrasts sharply with that of Cluster 5. This area is influenced by the West Spitsbergen Current, deep Atlantic waters, and cold Arctic waters from the central ocean. The average total PP was 75 ± 6 gC m⁻². Despite this moderate value, the shallower euphotic layer (46.3 ± 1.2 m) resulted in a higher volumetric PP of 1.6 ± 0.1 gC m⁻³.

Available phytoplankton data for this region are limited. Analysis of the existing dataset indicates that the North Atlantic Current shapes the phytocenosis, which is characterized by low abundance, a near absence of diatoms (observed only infrequently), and a predominance of coccolithophorids and small mixotrophic dinoflagellates. The measured dinoflagellate-to-diatom biomass ratio is approximately 80:20%, which aligns reasonably well with the 63:37% ratio derived from nutrient uptake data (Table 3).

3.2. Areas of Asynchronous Nutrient Inflow and Outflow in the Euphotic Layer (Clusters 3, 4, and 7)

Cluster analysis identified three regions with asynchronous nutrient exchange between the euphotic zone and surrounding waters. All regions showed net outflow of mineral phosphorus and silicon with concurrent net inflow of nitrogen (

Table 4. The results of the assessment of the nutrient balance and primary production values for Clusters 3, 4, and 7.

1 Parameter	Units	clu_3		clu_4		clu_7		2 Equation
		Value	sd	Value	sd	Value	sd
h	m	47.0	6.8	48.7	8.7	46.3	6.9	(5)
$Q_{meas}^P$	mg m−2	274.1	85.88	532.4	191.1	585.8	127.1	(5)
$Q_{con}^P$	mg m−2	1108.4	161.0	1146.9	203.2	1085.9	161.8	(1)
$Q_{ab}^P$	mg m−2	−156.9	137.0	−59.3	118.0	−66.2	82.9	(7)
$Q_{rem}^P$	mg m−2	258.6	556.8	133.0	271.7	67.0	86.4	(S15)
$Q_{phyto}^P$	mg m−2	974.8	260.2	688.3	144.5	501.0	74.0	(8)
${\left(Q_{phyto}^P\right)}_{\mathrm{C}}$ = (NCPP)	mg m−2	55,597	15,534	37,066	8061	26,593	3741	(9)
${\displaystyle \frac{{\left(Q_{phyto}^P\right)}_C}{h}}$	mg m−3	1032.4	204.4	760.6	135.3	574.3	85.5
PTP	%	80.6		56.4		46.1		(10)
PCP	%	71.3		53.8		43.5		(11)
$Q_{meas}^N$	mg m−2	375	190	1615	746	2795	645	(5)
$Q_{con}^N$	mg m−2	5347	795	5518	998	5218	776	(1)
$Q_{ab}^N$	mg m−2	2255	824	1466	1126	1523	906	(7)
$Q_{rem}^N$	mg m−2	1153.4	1210.6	1301.5	1233.2	644.9	454.5	(S15)
$Q_{phyto}^N$	mg m−2	8085	1014	6670	1663	4591	1191	(8)
($Q_{phyto}^N$)c = (NCPN)	mg m−2	57,164	7214	45,129	11,387	30,371	7357	(9)
${\displaystyle \frac{{\left(Q_{phyto}^N\right)}_C}{h}}$	mg m−3	1052.2	208.3	926.0	164.8	655.9	97.7
PTN	%	92.3		80.5		62.2		(10)
PCN	%	124.4		97.8		78.3		(11)
$Q_{meas}^{Si}$	mg m−2	2230.0	1817.8	1971	911	2428	901	(5)
$Q_{con}^{Si}$	mg m−2	10,087.8	1196.1	11,250	1242	11,051	1801	(1)
$Q_{ab}^{Si}$	mg m−2	−2325.0	1406.6	−425	1587	−1594	2241	(7)
$Q_{rem}^{Si}$	mg m−2	954	1320	1006	3795	1104	1657	(S15)
$Q_{phyto}^{Si}$	mg m−2	6703	1454	9860	1955	8133	2698	(8)
$(Q_{phyto}^{Si}$)c = (NCPSi)	mg m−2	90,929.9	15,041.0	107,516	18,534	79,102	10,515	(9)
${\displaystyle \frac{{\left(Q_{phyto}^{Si}\right)}_C}{h}}$	mg m−3	1593	446	2206	546	1708	341
PTSi	%	76.9		83.3		77.0		(10)
PCSi	%	60.7		80.5		66.9		(11)
d	%	13.2		32.7		40.3		(S21)

Note: ¹—see Table 1 in Section 2 for parameter descriptions; ²—see Section 2 for equation references.

).

3.2.1. Cluster 3

This south–north-oriented region extends from the Barents Sea coast to Franz Josef Land, bounded at ~45° E. Hydrologically diverse, it contains mixtures of Atlantic, riverine, meltwater, and ice-transformed waters. Southern and central areas receive modified Atlantic waters (Kolguyev–Pechora and Novozemel currents), while the north receives cold deep Atlantic waters from the Arctic.

Primary production ($Q_{phyto}^{Si}$)_c averaged 90 ± 15 gC m⁻². With euphotic depth of 47.0 ± 6.8 m, volumetric PP reached 1.6 ± 0.4 gC m⁻³. Diatom abundance calculated from nutrient uptake was low (13.2%).

Phytoplankton distribution was heterogeneous. Southern areas showed near-equal diatom–dinoflagellate biomass, dominated by Arctic–boreal neritic species. Diatoms (Skeletonema, Leptocylindrus, Chaetoceros) dominated numerically, but dinoflagellates (Ceratium, Goniaulax, Dinophysis) contributed most biomass (90%, matching the calculated 87:13 ratio).

Northern areas had higher diversity but lower productivity. Diatom contribution increased to 40%, altering community structure.

Nutrient fluxes showed 19% phosphorus and 23% silicon outflow versus 38% nitrogen inflow. By September, only 20% of the initial phosphorus and silicon remained. Mineral nitrogen was depleted completely (PC_N 124–167%), potentially limiting photosynthesis. Silicon consumption in selected areas reached 92% of the initial stock.

3.2.2. Cluster 4

This north-central region receives central Nordkapp Current waters (south) and cold Perseus Current waters (north). Nutrient fluxes showed minimal phosphorus (5%) and silicon (4%) outflow but significant nitrogen inflow (26%).

Primary production ($Q_{phyto}^{Si}$)_c averaged 108 ± 19 gC m⁻². With euphotic depth of 48.7 ± 8.7 m, volumetric PP peaked at 2.2 ± 0.5 gC m⁻³. The calculated diatom abundance (33%) was underestimated compared to the measured values (~58%).

Phytoplankton dominated by cold-water Arctic species: ice-associated diatoms (Thalassiosira) and bloom-forming centric diatoms. Dinoflagellates (Dinophysis, Gyrodinium, Gymnodinium) were scarce (~40% biomass).

Conservative phosphorus and silicon stocks exceeded consumption. By September, 56% of phosphorus and 83% of silicon were consumed. Nitrogen was fully utilized (PC_N 98%). External nitrogen enhanced PP only where PC_N > 100%.

3.2.3. Cluster 7

This northern cluster spans Spitsbergen–Franz Josef Land waters with Arctic extensions. The euphotic layer contains cold surface waters overlying Atlantic inflow. Euphotic depth averaged 46.3 ± 6.9 m.

Nutrient fluxes showed moderate phosphorus (6%) and silicon (14%) outflow with significant nitrogen inflow (29%). Primary production ($Q_{phyto}^{Si}$)_c reached 79 ± 11 gC m⁻² (1.7 ± 0.3 gC m⁻³). Diatoms contributed 40% to biomass.

Limited September data suggest West Spitsbergen Current influence. Dinoflagellates dominated (80–90% biomass). Diatom occurrence correlated with ice margin proximity.

The primary factor limiting the level of primary production (PP) in this region is not the availability of nitrogen, but probably rather the year-round ice cover. A key feature of this water area is that the core of the warm Atlantic Water lies at depths of 100–200 m [34]. As a result, the surface euphotic zone is largely isolated from the mixing zone between Atlantic and Arctic Ocean waters. As noted previously, it is precisely in these mixing zones that the highest PP values are observed.

Consequently, this cluster’s waters are characterized by relatively low net community production (NCP) values, which measured 30 g m⁻² by the end of September. A lower value was recorded only in Cluster 2 (26 g m⁻²). Although this assumption still needs to be studied.

4. Discussion

The nutrient balance in the euphotic zone comprises four principal components: the conservative stock, photosynthetic consumption, remineralization, and the abiotic flux. The relative nutrient consumption during photosynthesis, quantified by parameters ${PC}_{P,N, Si}$ and ${PT}_{P,N, Si}$, serves as a key indicator for assessing nutrient dynamics:

• When abiotic nutrient inflow occurs (positive ${Q }_{ab}^{P,N,Si}$), the ${PC}_{P,N, Si}$ parameter (Equation (2)) represents consumption relative to the conservative stock plus remineralization.
• When abiotic outflow occurs (negative ${Q }_{ab}^{P,N,Si}$), the ${PT}_{P,N, Si}$ parameter (Equation (3)) represents consumption relative to the total available stock, which includes the conservative stock, remineralization, and the abiotic outflow.

These parameters are analogous to oxygen saturation levels, indicating how closely nutrient concentrations approach their theoretical availability.

The relationship between PC and PT depends on the direction of the abiotic flux. Two distinct cases can be identified (12) and (13):

Case 1:

$$\begin{gathered} Q_{ab}^{P,N,Si}<0 \\ {PC}_{P,N,Si}<{PT}_{P,N,Si} \end{gathered}$$

(12)

Case 2:

$$\begin{gathered} Q_{ab}^{P,N,Si}>0 \\ {PC}_{P,N,Si}>{PT}_{P,N,Si} \end{gathered}$$

(13)

In both cases, the ${PT}_{P,N,Si}$ value indicates the residual amount of the nutrient. If this value reaches 100%, the entire nutrient supply will be exhausted.

4.1. Regional Patterns and Asynchrony

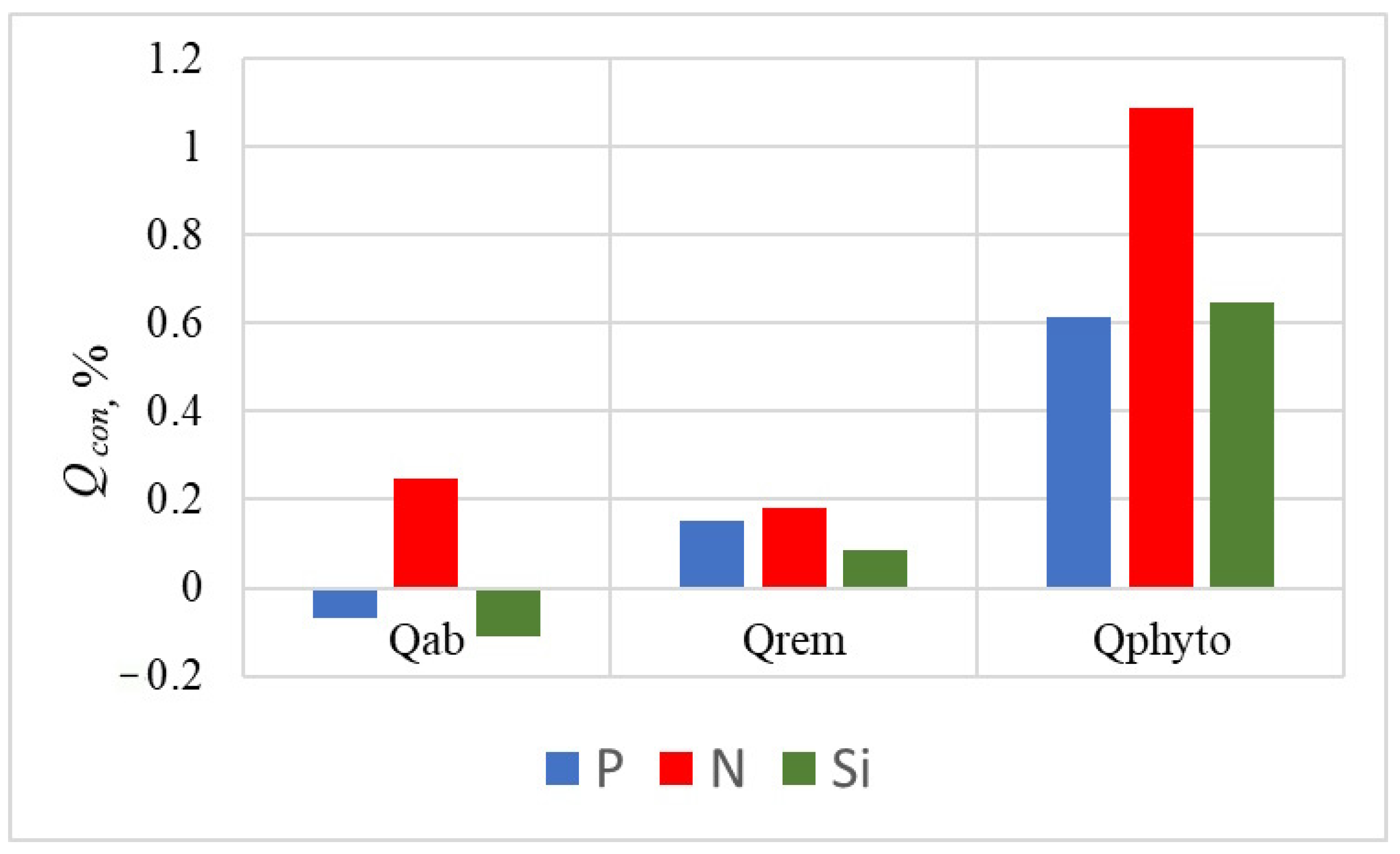
Averaged across the entire sea, phosphorus (−0.1 ± 0.2 gP m⁻²) and silicon (−1.3 ± 2.0 gSi m⁻²) exhibit a net outflow from the euphotic layer, while nitrogen shows a net inflow (1.5 ± 1.6 gN m⁻²; Table 1). The components of the nutrient balance, as well as the asynchrony of abiotic component flows for the entire Barents Sea area, are presented in Figure 6.

This asynchrony in nutrient fluxes can be explained by differential remineralization rates and the elemental composition of the phytoplankton community. Nitrogen recycles rapidly from organic to mineral form, while the silicon frustules of diatoms dissolve slowly. Furthermore, the stoichiometric composition of the dominant algal groups plays a crucial role. Diatoms have a higher relative phosphorus content, indicated by their lower C:P ratio (37.0) compared to peridinium algae (C:P of 58.8). Consequently, the gravitational settling of partially mineralized diatom remains creates a downward flux of silicon and phosphorus that can dominate over the upward abiotic fluxes.

The mean relative abundance of diatoms, estimated from nutrient consumption ratios, was 18.6% in the Barents Sea euphotic layer during August–September. For phosphorus and silicon, the average consumption during photosynthesis is less than their total available stock (14):

$$Q_{phyto}^N<{(Q}_{con}^N+Q_{rem}^N)$$

(14)

Therefore, their outflow does not limit primary production (PP), as a significant residual stock remains (the average for ($100-{PT}_P$) is 43% and for ($100-{PT}_{ Si}$) is 33%, respectively (Table 1).

Although the sea-averaged nitrogen consumption ($Q_{phyto}^N$) is less than its total initial stock ($Q_{con}^N+Q_{rem}^N$), it nearly depletes it. The average PC_N value is 92%, and in some areas, it reaches 167%. The supply of mineral nitrogen accumulated during the winter is effectively depleted, and photosynthesis is sustained primarily by abiotic inflow. This indicates that PP in these regions depends on external nitrogen sources. At the location of the maximum value, 67% of the nitrogen consumed was supplied from external sources.

4.2. Spatial Clustering of Nutrient Fluxes

Cluster analysis revealed three distinct regimes in the Barents Sea:

Synchronous Inflow: Clusters 1 and 6—western areas;

Synchronous Outflow: Clusters 5 and 2—central areas;

Asynchronous Regime: Clusters 3, 4, and 7, characterized by outflow of phosphorus and silicon coupled with inflow of nitrogen—parts of the central, eastern, and northern areas.

4.2.1. Western Areas with Synchronous Inflow (Clusters 1 and 6)

In these areas, the total nutrient stock (conservative + remineralization) exceeds photosynthetic consumption (Equation (15):

$$Q_{phyto}^{P, Si,N}<Q_{con}^{P, Si, N}+Q_{rem}^{P, Si, N}$$

(15)

By September, consumption (${PC}_{P,N,Si}$) accounted for 53% (Cluster 1) and 44% (Cluster 6) of phosphorus, 55% and 54% of silicon, and 87% and 75% of nitrogen, respectively. Since consumption is substantially below 100% of the conservative stock, the additional abiotic inflow does not significantly enhance PP.

4.2.2. Parts of Central Areas with Synchronous Outflow (Clusters 5 and 2)

Despite the outflow, the total available stock (conservative + remineralization − outflow) still exceeds consumption (Equation (16)):

$$Q_{phyto}^{P, Si,N}<Q_{con}^{P, Si, N}+Q_{rem}^{P, S, N}-\left|Q_{ab}^{P, S,N}\right|$$

(16)

By September, nutrient consumption (PT/PC%) in Clusters 5 and 2 was as follows:

• Phosphorus: 45/39% and 49%/40%;
• Nitrogen: 78/69% and 71%/66%;
• Silicon: 33/27% and 84%/65%.

Even accounting for the abiotic outflow of nutrients from the euphotic zone, the remaining pool of nutrients—factoring in remineralization—was not fully depleted. Thus, the outflow did not limit primary production, as resources were never exhausted.

4.2.3. Parts of Central, Eastern, and Northern Areas with an Asynchronous Regime (Clusters 3, 4, and 7)

In these clusters, the behavior of phosphorus and silicon differs from that of nitrogen.

Phosphorus and Silicon: Their outflow does not limit PP, as consumption is less than the total available stock (Equation (16)). The consumption (${PT}_{P,Si}$) by September ranged from 46% to 81% for phosphorus and 77% to 83% for silicon.

Nitrogen: The abiotic nitrogen inflow is a key factor.

In Cluster 3, the average PC_N is 124%, indicating complete depletion of the initial stock and remineralization flux. Photosynthesis here depends on external nitrogen inflow, with total consumption (PTN) reaching 92%. This confirms nitrogen as the limiting factor. An estimate of the contribution of this external inflow to the so-called “new” production (NCP_N) shows an increase of 19.7 gC m⁻², with a maximum of 26 gC m⁻². On average, the contribution of additional nitrogen input to the NCP_N is 33% across the area of this cluster.

In Cluster 4, the situation is heterogeneous. The average PC_N is 98%, but it exceeds 100% in some areas (max. 162%), where inflow stimulates PP, and falls below 100% in others (min. 61%), where it has no effect.

In Cluster 7, despite the nitrogen inflow, consumption is low (PC_N = 78%, PT_N = 62%), and thus it does not influence PP.

4.3. Current Limitations and Future Directions

The methodological framework presented in this study, which employs the δ¹⁸O isotope parameter, offers distinct advantages but also has inherent limitations that point toward necessary future refinements.

4.3.1. Key Advantages and Methodological Rationale

The primary strength of this approach is its reliance on chemical nutrient analysis—a set of relatively simple, internationally standardized, and well-established field techniques. The availability of extensive and growing nutrient databases for the World Ocean further enhances its utility. Furthermore, as validated in the “Materials and Methods” section and previous studies, a robust correlation (R ≈ 0.95) exists between salinity and δ¹⁸O in the Barents Sea. This strong relationship enables the accurate reconstruction of isotopic values across a wide salinity range, creating a powerful synergy between isotopic and nutrient data. This integration facilitates a holistic study of the marine ecosystem by linking hydrological (water masses via salinity and δ¹⁸O), hydrochemical (nutrients), and hydrobiological (phytoplankton) components into a single, unified framework.

4.3.2. Current Limitations and Pathways for Refinement

Despite its promise, the current implementation of the method faces several challenges:

Challenges in Defining End-Members. The method requires well-constrained average values for the isotope parameters and nutrient concentrations in the source water masses (e.g., river discharge and incoming oceanic waters). For shelf seas, these parameters can be established from long-term observational data. However, for larger-scale applications, such as across the Arctic Ocean, defining these initial values is a significant challenge. While the signatures of incoming Atlantic and Pacific waters can be reasonably derived from existing databases, characterizing riverine input in the open ocean beyond the shelf is far more complex due to the high variability caused by vast catchment areas and longitudinal dispersion. The question arises as to what value of δ¹⁸O should be taken as end-members for river flow, given that this value varies from 11‰ in the western Barents Sea to 20‰ in the Laptev Sea (Lena River) and 23–24‰ in the Bering Strait area.

Spatial Bias in the δ¹⁸O-Salinity Relationship. This study is based on a robust salinity-δ¹⁸O correlation; however, the underlying data for the Barents Sea come predominantly from the waters around the Svalbard archipelago and the southeastern part of the sea. To improve the model’s accuracy and spatial resolution, this existing dataset must be expanded with new measurements. For high-precision assessments in localized areas, we recommend using direct measurements of δ¹⁸O alongside concurrent salinity and nutrient data, rather than relying on reconstructed values.

Outdated and Incomplete Stoichiometric Ratios. A critical assumption of our model is the nutrient content of plankton, for which we used values published in 1942. Revising these stoichiometric ratios is now essential. The primary focus should be to refine the stoichiometric ratios for diatoms and dinoflagellates, as these groups constitute approximately 94% of the total biomass. Furthermore, it is essential to establish the stoichiometric ratios for the class Prymnesiophyceae.

While Prymnesiophyceae play a sub-dominant role in forming phytoplankton biomass peaks in the Barents Sea—being locally distributed and episodic on a seasonal scale—their impact on nutrient ratios in seawater can be traced in the aftermath of their blooms. Therefore, when considering primary production on an annual scale, the alteration of nutrient ratios induced by this class of algae remains detectable even after their peak abundance has passed.

Methodological Inconsistencies at Low Biomass. In some areas, during the early photosynthetic season, when nutrient consumption ($Q_{phyto}^N$) is low, the calculated relative abundances of diatoms (d) and peridinium (p) sometimes summed to more than 1—a methodological impossibility. This anomaly stems from two factors: high relative error at low $Q_{phyto}^N$ values and, more importantly, an incomplete representation of the phytoplankton community. The model assumes that diatoms and peridinium algae constitute the entire biomass, an assumption that is often incorrect. For instance, blooms of Phaeocystis pouchetii (Prymnesiophyceae) can dominate the phytoplankton, accounting for up to 95% of the total biomass in some areas during spring. Excluding such significant contributors skews the expected nutrient uptake ratios and introduces errors into the calculations. The calculation of primary production for the consumption of nutrients at low biomass at the beginning of the photosynthesis season should be singled out as a separate task.

4.3.3. Future Directions and Broader Implications

Addressing these limitations—by expanding the isotopic database, refining end-members, and updating the stoichiometric model—will significantly improve the method’s robustness. Furthermore, the availability of long-term time series for salinity and nutrient data opens up opportunities for investigating climatic ecosystem variability. This integrated approach enables the analysis of long-term trends, tracing the pathway from changes in nutrient consumption dynamics to subsequent shifts in regional productivity, thus providing a powerful tool for understanding and predicting marine ecosystem responses to environmental change. For instance, several authors have noted an intensification of Atlantification since 2007, characterized by an increased inflow of Atlantic waters. This process leads to a weakening or even a disappearance of the seasonal halocline, which enhances the upward flux of heat and nutrients from the ocean’s interior. This, in turn, triggers rapid sea-ice melt and increases primary productivity [48]. Processes like this underscore the need for precise analytical tools. Addressing the mentioned limitations—by expanding the isotopic database, refining end-members, and updating the stoichiometric model—will significantly improve the method’s robustness for investigating such complex ecosystem changes. Furthermore, the availability of long-term time series for salinity and nutrient data opens up opportunities to directly investigate climatic ecosystem variability, as demonstrated by the Atlantification trend. This integrated approach enables the analysis of long-term trends, tracing the pathway from changes in nutrient consumption dynamics to subsequent shifts in regional productivity, thus providing a powerful tool for understanding and predicting marine ecosystem responses to environmental change.

5. Conclusions

This study used the WOA digital atlas to improve the assessment of primary production by analyzing nutrient consumption. It focused on the detailed quantification of abiotic inflows and outflows of mineral phosphorus, nitrogen, and silicon in the euphotic zone.

Throughout the Barents Sea, the average outflow of mineral phosphorus and silicon from the euphotic zone by September reached 7% and 11%, respectively. In contrast, the nitrogen inflow constituted 24% of the conservative stock. The impact of abiotic change on primary production was generally negligible. This is because the average consumption of phosphorus and silicon during photosynthesis was lower than the conservative stock. The conservative stock is defined to account for processes such as remineralization and outflow from the euphotic zone. Similarly, mean nitrogen inputs did not enhance primary production in most areas, as nitrogen uptake during photosynthesis was less than the conservative stock of nitrogen.

Cluster analysis identified seven distinct zones within the sea. The two western zones exhibited synchronous nutrient inflow, while the two central zones were characterized by outflow. Three other zones showed a pattern of phosphorus and silicon outflow coupled with nitrogen inflow.

A significant impact of increased nitrogen input on primary production was confined to the eastern part of the sea (predominantly east of 40° E). Here, the average nitrogen utilization exceeded the conservative stock by 24%, reaching 124% and peaking at 167%. This high level of utilization, which includes nitrogen from organic matter remineralization, indicates that, on average, abiotic enrichment of the euphotic zone with nitrogen resulted in a 24% increase in primary production in this region.

The presented methodology does not allow for the direct estimation of primary production from individual observations. This limitation arises from the inability to assess the contributions of the abiotic factor, organic matter remineralization, and, in some cases, the precise location of the euphotic zone’s lower boundary from a single data point. However, these missing parameters can be derived via interpolation of the WOA atlas data and used as constant monthly values for each location. This approach enables the estimation of primary production from measured nutrient concentrations during the study period.

The future development of this work is associated with three main directions:

Methodology refinement:

• Refining stoichiometric ratios in key systematic groups (diatoms and dinoflagellates).
• Incorporating additional phytoplankton taxonomic groups into the model.
• Investigating the seasonal dynamics of abiotic factors.
• Analyzing the intra-annual variability of the nutrient regeneration coefficient.

Analysis of climatic variability: Using the available long-term time series of temperature, salinity, and nutrient concentrations, we plan to investigate the climatic variability of the components of the nutrient balance and primary production.

Expansion to other basins: A key objective is to apply this approach to other Arctic seas, primarily the Kara and Laptev Seas.