A Novel Biomorphodynamic Model to Enhance Bedload Transport Modelling in Emergent and Submerged Rigid Vegetation
Abstract
1. Introduction
2. Materials and Methods
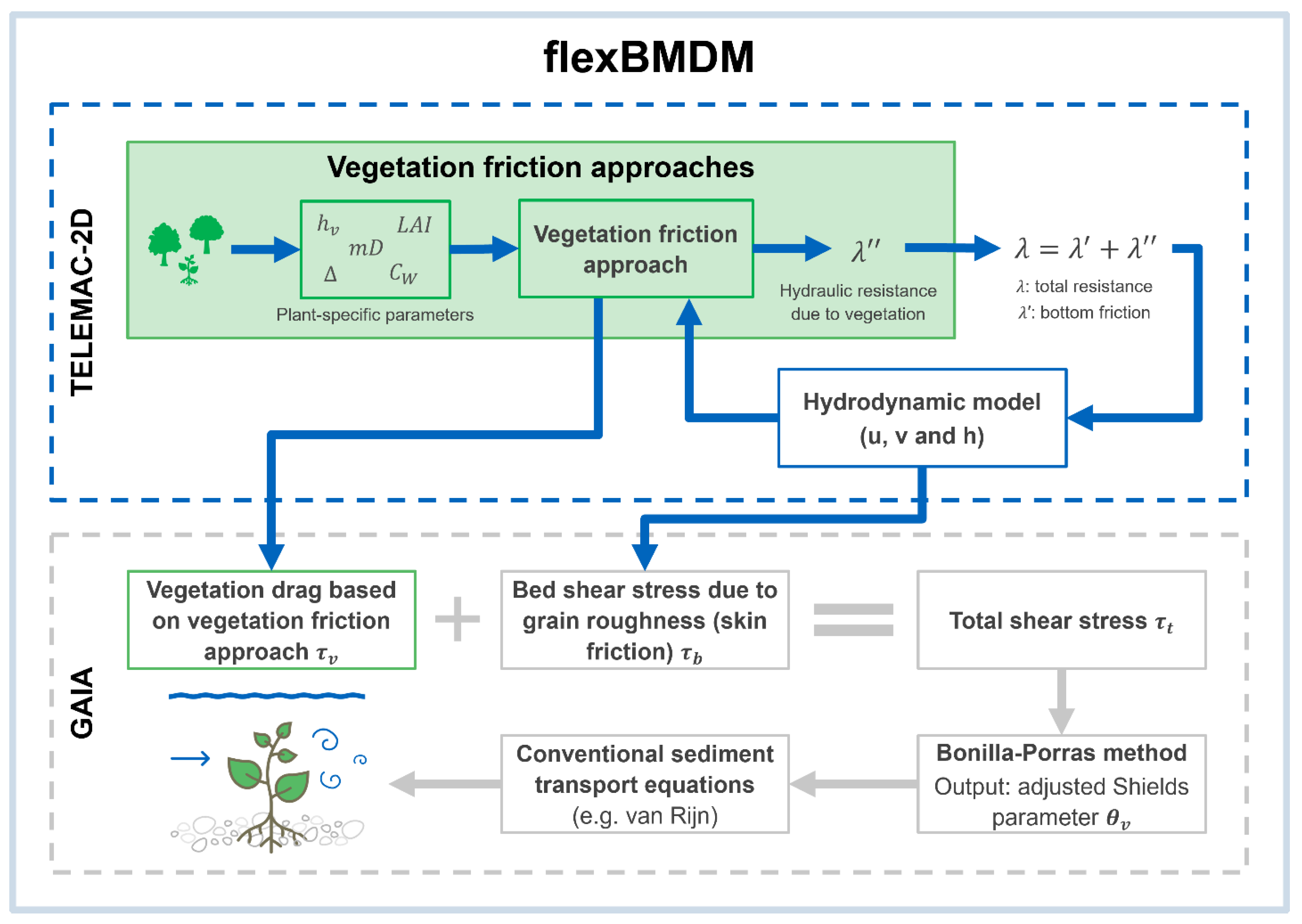
2.1. Development of the Novel Biomorphodynamic Model
- vegetation-induced hydraulic resistance, represented using vegetation friction approaches, and
- adjustment of sediment transport using suitable methods.
2.2. Validation of the flexBMDM
2.2.1. Overview
2.2.2. Emergent Rigid Vegetation
2.2.3. Submerged Rigid Vegetation
3. Results
3.1. Emergent Rigid Vegetation
3.2. Submerged Rigid Vegetation
4. Discussion
4.1. Advantages of the flexBMDM
4.2. Sensitivity of Bonilla-Porras Method
- Implementing a correction factor for morphodynamic drag:
- 2.
- Incorporate alternative sediment transport adjustment methods:
4.3. Limitations and Prospects of the flexBMDM
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Fundamentals of Li-BMDM
Appendix A.2. Derivation of the Vegetation Friction Approach WULI
Appendix B
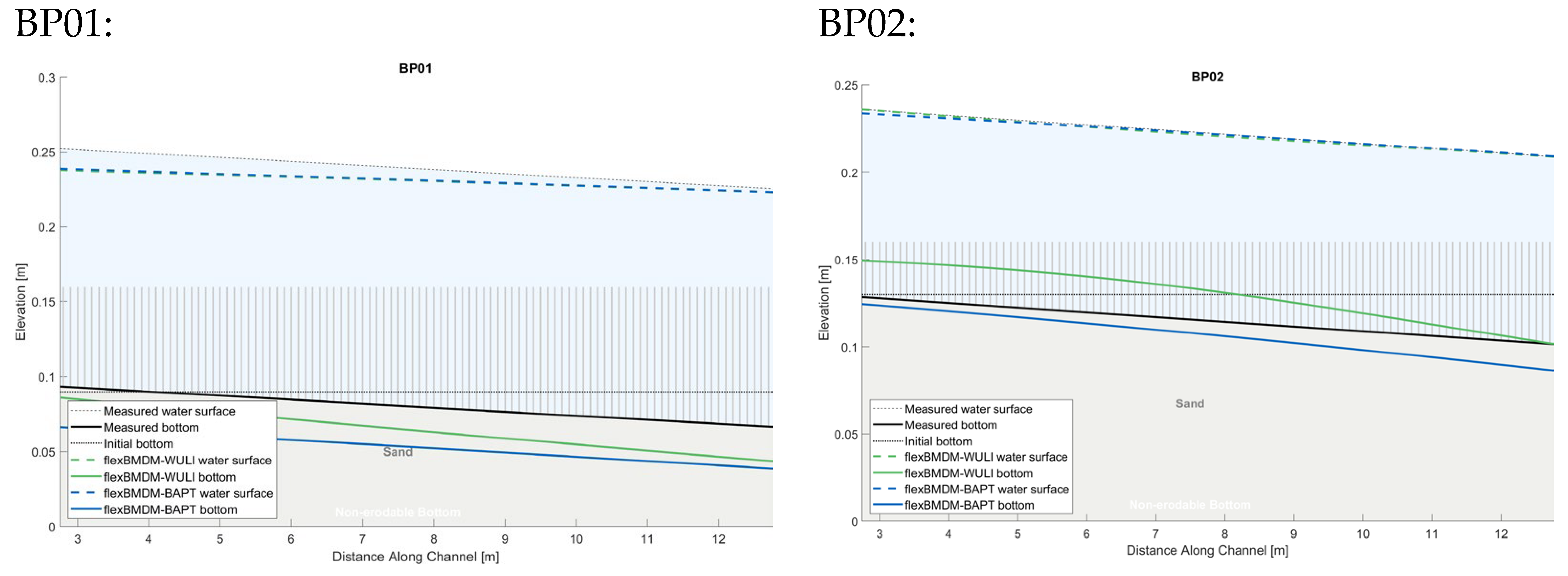
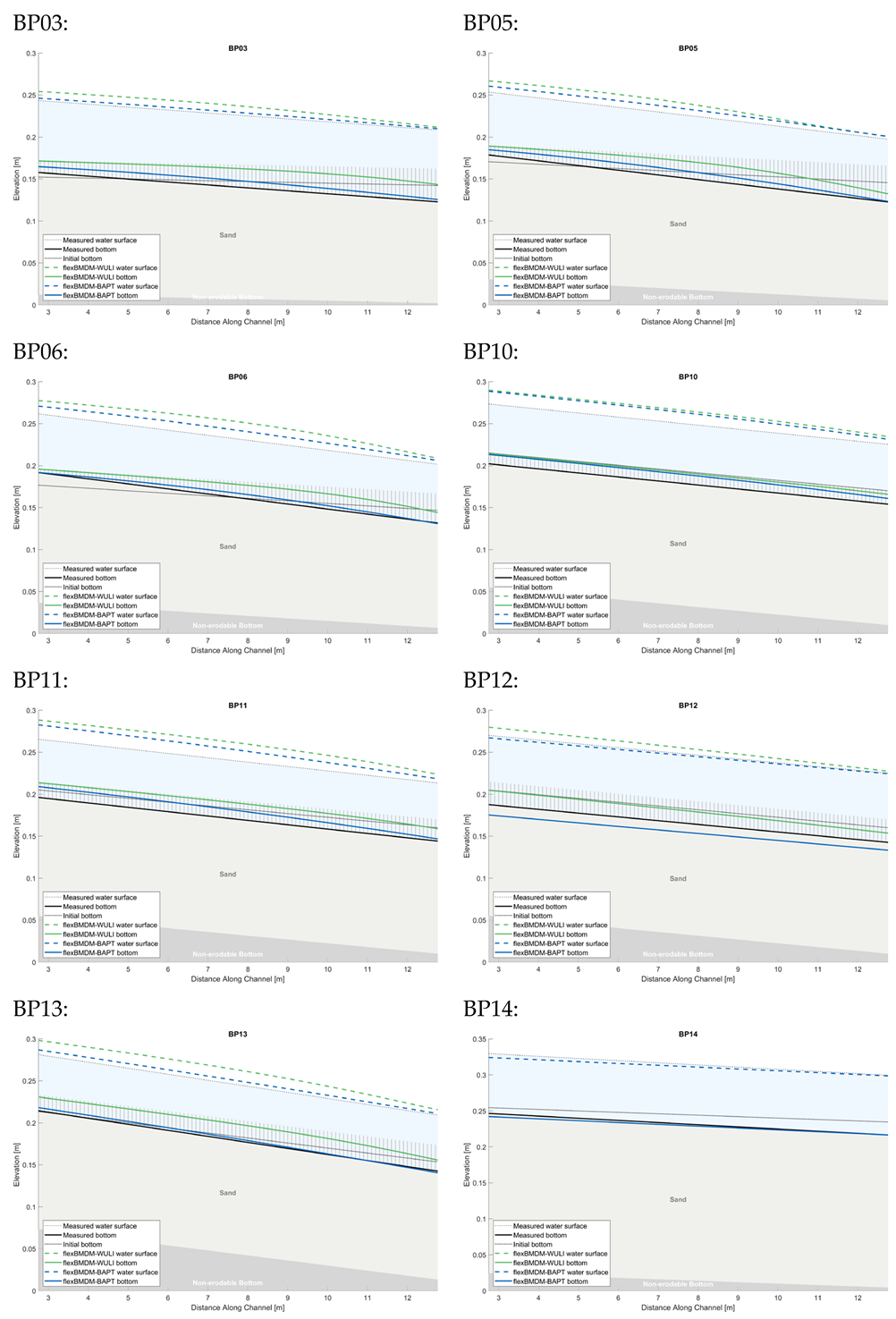
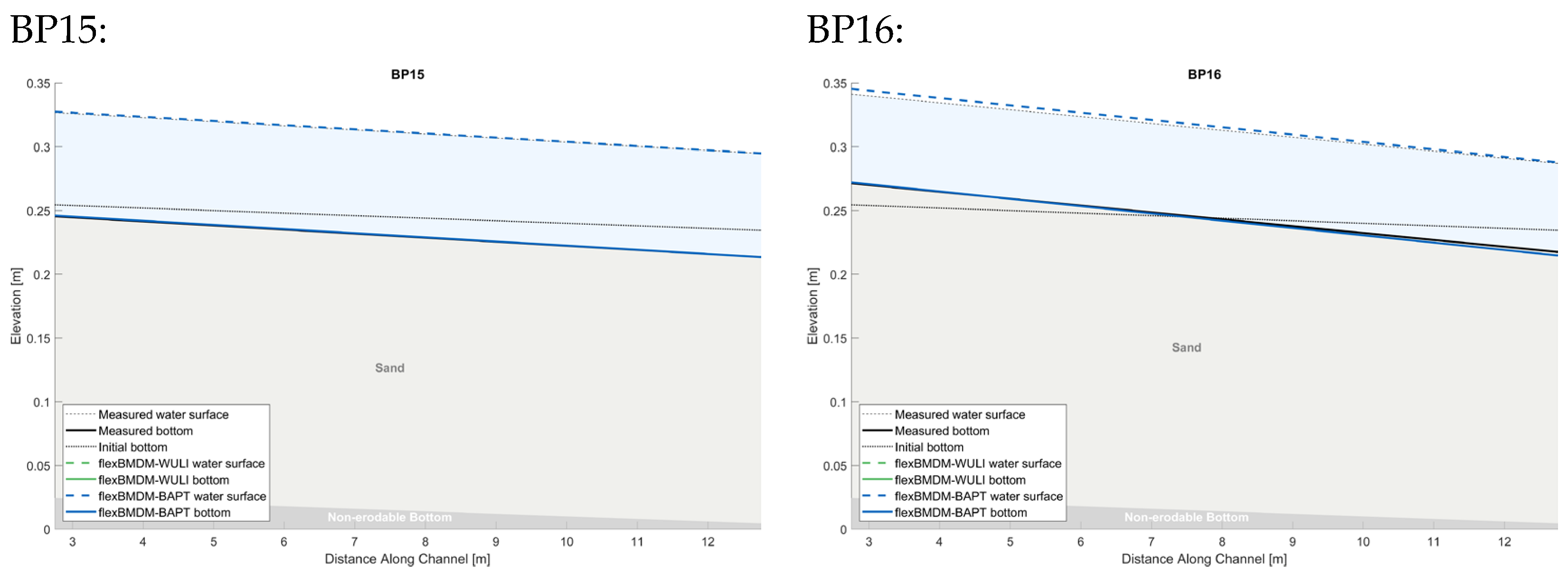
Appendix B.1. Supplementary Results of the Emergent Rigid Vegetation Test Case

Appendix B.2. Supplementary Results of Submerged Rigid Vegetation Test Case
References
- Gurnell, A. Plants as river system engineers. Earth Surf. Process. Landf. 2014, 39, 4–25. [Google Scholar] [CrossRef]
- Bertoldi, W.; Gurnell, A.M.; Drake, N.A. The topographic signature of vegetation development along a braided river: Results of a combined analysis of airborne lidar, color air photographs, and ground measurements. Water Resour. Res. 2011, 47, 1–13. [Google Scholar] [CrossRef]
- Reinhardt, L.; Jerolmack, D.; Cardinale, B.J.; Vanacker, V.; Wright, J. Dynamic interactions of life and its landscape: Feedbacks at the interface of geomorphology and ecology. Earth Surf. Process. Landf. 2010, 35, 78–101. [Google Scholar] [CrossRef]
- Fathi-Maghadam, M.; Kouwen, N. Nonrigid, Nonsubmerged, Vegetative Roughness on Floodplains. J. Hydraul. Eng. 1997, 123, 51–57. [Google Scholar] [CrossRef]
- Baptist, M.J. Modelling Floodplain Biogeomorphology. Ph.D. Thesis, Technical University Delft, Delft, The Netherlands, 2005. [Google Scholar]
- Bennett, S.J.; Wu, W.; Alonso, C.V.; Wang, S.S.Y. Modeling fluvial response to in-stream woody vegetation: Implications for stream corridor restoration. Earth Surf. Process. Landf. 2008, 33, 890–909. [Google Scholar] [CrossRef]
- Le Bouteiller, C.; Venditti, J.G. Vegetation-driven morphodynamic adjustments of a sand bed. Geophys. Res. Lett. 2014, 41, 3876–3883. [Google Scholar] [CrossRef]
- Vargas-Luna, A.; Crosato, A.; Uijttewaal, W.S. Effects of vegetation on flow and sediment transport: Comparative analyses and validation of predicting models. Earth Surf. Process. Landf. 2015, 40, 157–176. [Google Scholar] [CrossRef]
- Anderson, B.G.; Rutherfurd, I.D.; Western, A.W. An analysis of the influence of riparian vegetation on the propagation of flood waves. Environ. Model. Softw. 2006, 21, 1290–1296. [Google Scholar] [CrossRef]
- Ghavasieh, A.-R.; Poulard, C.; Paquier, A. Effect of roughened strips on flood propagation: Assessment on representative virtual cases and validation. J. Hydrol. 2006, 318, 121–137. [Google Scholar] [CrossRef]
- Rak, G.; Kozelj, D.; Steinman, F. The impact of floodplain land use on flood wave propagation. Nat. Hazards 2016, 83, 425–443. [Google Scholar] [CrossRef]
- Tranmer, A.W.; Ji, U.; Ahn, M.; Jung, S.H.; Yager, E.M. Characterizing Erosion and Deposition in and Around Ri-parian Vegetation Patches: Complex Flow Hydraulics, Sediment Supply, and Morphodynamic Feedbacks. Water Resour. Res. 2024, 60, e2023WR034859. [Google Scholar] [CrossRef]
- Nepf, H.M. Hydrodynamics of vegetated channels. J. Hydraul. Res. 2012, 50, 262–279. [Google Scholar] [CrossRef]
- Yager, E.M.; Schmeeckle, M.W. The influence of vegetation on turbulence and bed load transport. JGR Earth Surf. 2013, 118, 1585–1601. [Google Scholar] [CrossRef]
- López, F.; García, M. open-channel flow through simulated vegetation: Suspended sediment transport modelling. Water Resour. Res. 1998, 34, 2341–2352. [Google Scholar] [CrossRef]
- Sand-Jensen, K.; Pedersen, O. Velocity gradients and turbulence around macrophyte stands in streams. Freshw. Biol. 1999, 42, 315–328. [Google Scholar] [CrossRef]
- Tsujimoto, T. Fluvial processes in streams with vegetation. J. Hydraul. Res. 1999, 37, 789–803. [Google Scholar] [CrossRef]
- Tal, M.; Paola, C. Effects of vegetation on channel morphodynamics: Results and insights from laboratory experiments. Earth Surf. Process. Landf. 2010, 35, 1014–1028. [Google Scholar] [CrossRef]
- Bertoldi, W.; Welber, M.; Gurnell, A.M.; Mao, L.; Comiti, F.; Tal, M. Physical modelling of the combined effect of vegetation and wood on river morphology. Geomorphology 2015, 246, 178–187. [Google Scholar] [CrossRef]
- Caponi, F.; Siviglia, A. Numerical Modelling of Plant Root Controls on Gravel Bed River Morphodynamics. Geophys. Res. Lett. 2018, 45, 9013–9023. [Google Scholar] [CrossRef]
- Vargas-Luna, A.; Duró, G.; Crosato, A.; Uijttewaal, W. Morphological Adaptation of River Channels to Vegetation Establishment: A Laboratory Study. JGR Earth Surf. 2019, 124, 1981–1995. [Google Scholar] [CrossRef]
- D’Ippolito, A.; Calomino, F.; Dey, S.; Gaudio, R.; Penna, N. Bedload transport through emergent vegetation: Current status and its future prospect. Env. Fluid Mech. 2023, 23, 711–733. [Google Scholar] [CrossRef]
- Wu, W. Computational River Dynamics; CRC Press: Boca Raton, FL, USA, 2007; ISBN 9780203938485. [Google Scholar]
- Abad, J.D.; Buscaglia, G.C.; Garcia, M.H. 2D stream hydrodynamic, sediment transport and bed morphology model for engineering applications. Hydrol. Process. 2008, 22, 1443–1459. [Google Scholar] [CrossRef]
- Tassi, P.; Benson, T.; Delinares, M.; Fontaine, J.; Huybrechts, N.; Kopmann, R.; Pavan, S.; Pham, C.-T.; Taccone, F.; Walther, R. GAIA—A unified framework for sediment transport and bed evolution in rivers, coastal seas and transitional waters in the TELEMAC-MASCARET modelling system. Environ. Model. Softw. 2023, 159, 105544. [Google Scholar] [CrossRef]
- Jordanova, A.A.; James, C.S. Experimental Study of Bed Load Transport through Emergent Vegetation. J. Hydraul. Eng. 2003, 129, 474–478. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hashimoto, H.; Hayashi, K. Effect of tall vegetation on sediment transport by channel flows. J. Hydraul. Res. 2009, 47, 700–710. [Google Scholar] [CrossRef]
- Stone, B.M.; Shen, H.T. Hydraulic Resistance of Flow in Channels with Cylindrical Roughness. J. Hydraul. Eng. 2002, 128, 500–506. [Google Scholar] [CrossRef]
- Le Bouteiller, C.; Venditti, J.G. Sediment transport and shear stress partitioning in a vegetated flow. Water Resour. Res. 2015, 51, 2901–2922. [Google Scholar] [CrossRef]
- Baptist, M.J. A flume experiment on sediment transport with flexible, submerged vegetation. In Proceedings of the International Workshop on Riparian Forest Vegetated Channels: Hydraulic, Morphological and Ecological Aspects, Trento, Italy, 20–22 February 2003. [Google Scholar]
- Armanini, A.; Cavedon, V.; Righetti, M. Evaluation of the flow resistance in mobile bed vegetated rivers. In River Flow 2010: Proceedings of the [5th] International Conference on Fluvial Hydraulics, Braunschweig, Germany, 8–10 June 2010; Dittrich, A., Koll, K., Aberle, J., Geisenhainer, P., Eds.; Bundesanstalt für Wasserbau: Karlsruhe, Germany, 2010; pp. 277–284. ISBN 9783939230007. [Google Scholar]
- Coscarella, F.; Penna, N.; Ferrante, A.P.; Gualtieri, P.; Gaudio, R. Turbulent Flow through Random Vegetation on a Rough Bed. Water 2021, 13, 2564. [Google Scholar] [CrossRef]
- Rezaie, B.; Hosseini, S.A.; Allah Yonesi, H.; Hosein Mohajeri, S. Hydraulic investigation of flow and bed load transport in diverging compound channels with rigid and flexible vegetation. Flow Meas. Instrum. 2024, 97, 102604. [Google Scholar] [CrossRef]
- van Rijn, L.C. Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas: Part I.; Aqua Publications: Amsterdam, The Netherlands, 1993; ISBN 9080035629. [Google Scholar]
- Hervouet, J.-M. Hydrodynamics of Free Surface Flows; Wiley: Hoboken, New Jersey, 2007; ISBN 9780470035580. [Google Scholar]
- García, M.H. Sedimentation Engineering: Processes, Measurements, Modelling, and Practice; American Society of Civil Engineers: Reston, VA, USA, 2008; ISBN 0784471282. [Google Scholar]
- Guan, M.; Liang, Q. A two-dimensional hydro-morphological model for river hydraulics and morphology with vegetation. Environ. Model. Softw. 2017, 88, 10–21. [Google Scholar] [CrossRef]
- Bertoldi, W.; Siviglia, A.; Tettamanti, S.; Toffolon, M.; Vetsch, D.; Francalanci, S. Modeling vegetation controls on fluvial morphological trajectories. Geophys. Res. Lett. 2014, 41, 7167–7175. [Google Scholar] [CrossRef]
- Caponi, F.; Vetsch, D.F.; Siviglia, A. A model study of the combined effect of above and below ground plant traits on the ecomorphodynamics of gravel bars. Sci. Rep. 2020, 10, 17062. [Google Scholar] [CrossRef]
- Li, J.; Claude, N.; Tassi, P.; Cordier, F.; Crosato, A.; Rodrigues, S. Implementation of a novel approach accounting for the influence of vegetation on sediment transport in GAIA. In Online proceedings of the 2020 TELEMAC-MASCARET User Conference, October 2020, Antwerp, Belgium; Breugem, W.A., Frederickx, L., Koutrouveli, T., Chu, K., Kul-Karni, R., Decrop, B., Eds.; International Marine & Dredging Consultants (IMDC): Antwerp, Belgium, 2020; p. 2. [Google Scholar]
- Li, J.; Claude, N.; Tassi, P.; Cordier, F.; Vargas-Luna, A.; Crosato, A.; Rodrigues, S. Effects of Vegetation Patch Pat-terns on Channel Morphology: A Numerical Study. JGR Earth Surf. 2022, 127, e2021JF006529. [Google Scholar] [CrossRef]
- Armanini, A.; Cavedon, V. Bed-load through emergent vegetation. Adv. Water Resour. 2019, 129, 250–259. [Google Scholar] [CrossRef]
- Bonilla-Porras, J.A.; Armanini, A.; Crosato, A. Extended Einstein’s parameters to include vegetation in existing bedload predictors. Adv. Water Resour. 2021, 152, 103928. [Google Scholar] [CrossRef]
- Bonilla-Porras, J.A. Bedload Transport in Water Courses with Submerged Vegetation. University of Trento: Trento, Italy, 2022. [Google Scholar]
- Västilä, K.; Järvelä, J.; Koivusalo, H. Flow–Vegetation–Sediment Interaction in a Cohesive Compound Channel. J. Hydraul. Eng. 2016, 142, 04015034. [Google Scholar] [CrossRef]
- Folke, F.; Attieh, M.; Kopmann, R. In search of friction laws for vegetated flow within 2D largscale applications. In Proceedings of the 38th IAHR World Congress—Water: Connecting the World. 38th IAHR World Congress, Panama City, PA, USA, 1–6 September 2019; (E-Proceedings). The International Association for Hydro-Environment Engineering and Research (IAHR): Madrid, Spain, 2019; pp. 5527–5536. [Google Scholar]
- Folke, F. Abbildung der Rauheitswirkung von Vorlandvegetation in der Ingenieurtechnischen Anwendung. Ph.D. Thesis, TU Braunschweig, Braunschweig, Germany, 2023. [Google Scholar]
- Dallmeier, A.; Folke, F.; Rüther, N. Advanced representation of near-natural vegetation in hydrodynamic modelling. In Proceedings of the XXIXth TELEMAC Users Conference, Karlsruhe, Germany, 12–13 October 2023; Kopmann, R., Folke, F., Eds.; Bundesanstalt für Wasserbau: Karlsruhe, Germany, 2023; pp. 205–210. [Google Scholar]
- Farina, G.; Bacchi, V.; Pilotti, M. Implementation and validation of a new friction vegetation law in TELEMAC-2D. In Proceedings of the XXXth TELEMAC User Conference Chambéry, Chambéry, France, 8–9 October 2024. [Google Scholar]
- Järvelä, J. Determination of flow resistance caused by non-submerged woody vegetation. Int. J. River Basin Manag. 2004, 2, 61–70. [Google Scholar] [CrossRef]
- Baptist, M.J.; Babovic, V.; Rodríguez Uthurburu, J.; Keijzer, M.; Uittenbogaard, R.E.; Mynett, A.; Verwey, A. On inducing equations for vegetation resistance. J. Hydraul. Res. 2007, 45, 435–450. [Google Scholar] [CrossRef]
- Luhar, M.; Nepf, H.M. From the blade scale to the reach scale: A characterization of aquatic vegetative drag. Adv. Water Resour. 2013, 51, 305–316. [Google Scholar] [CrossRef]
- Lindner, K. Der Strömungswiderstand von Pflanzenbeständen. Ph.D. Thesis, TU Braunschweig, Braunschweig, Germany, 1982. [Google Scholar]
- Petryk, S.; Bosmajian, G. Analysis of Flow through Vegetation. J. Hydraul. Eng. 1975, 101, 871–884. [Google Scholar] [CrossRef]
- Einstein, H.A.; Banks, R.B. Fluid resistance of composite roughness. Eos Trans. AGU 1950, 31, 603–610. [Google Scholar] [CrossRef]
- Huthoff, F.; Augustijn, D.C.M.; Hulscher, S.J.M.H. Analytical solution of the depth-averaged flow velocity in case of submerged rigid cylindrical vegetation. Water Resour. Res. 2007, 43, 1–10. [Google Scholar] [CrossRef]
- Västilä, K.; Järvelä, J. Modeling the flow resistance of woody vegetation using physically based properties of the foliage and stem. Water Resour. Res. 2014, 50, 229–245. [Google Scholar] [CrossRef]
- Box, W.; Järvelä, J.; Västilä, K. New formulas addressing flow resistance of floodplain vegetation from emergent to submerged conditions. Int. J. River Basin Manag. 2022, 22, 333–349. [Google Scholar] [CrossRef]
- Folke, F.; Niewerth, S.; Aberle, J. Modelling of just-submerged and submerged flexible vegetation. In Abstract Book of the 6th IAHR Europe Congress, Warsaw, Poland, 15-18 February 2021; International Association for Hydro-Environment Engineering and Research (IAHR): Madrid, Spain, 2021; pp. 263–264. [Google Scholar]
- Dallmeier, A.; Kopmann, R.; Folke, F.; Ruether, N. Assessment of Different Vegetation Friction Approaches in Numerical Hydrodynamic Modelling. In Proceedings of the EGU General Assembly 2024, Vienna, Austria, 14–19 April 2024. EGU24-10751. [Google Scholar] [CrossRef]
- DWA. DWA-Merkblatt M 524: Hydraulische Brechnung Von Fließgewässern Mit Vegetation; Deutsche Vereinigung für Wasserwirtschaft, Abwasser und Abfall e.V.: Hennef, Germany, 2020. [Google Scholar]
- Wu, W.; Shields, F.D.; Bennett, S.J.; Wang, S.S.Y. A depth-averaged two-dimensional model for flow, sediment transport, and bed topography in curved channels with riparian vegetation. Water Resour. Res. 2005, 41, 1–15. [Google Scholar] [CrossRef]
- van Velzen, E.H.; Jesse, P.; Cornelissen, P. Stromingsweerstand Vegetatie in Uiterwaarden: Deel 1 Handboek; Versie 1-2003; Ministerie van Verkeer en Waterstaat Directoraat-Generaal Rijkswaterstaat RIZA Rijksinstituut voor Integraal Zo-etwaterbeheer en Afvalwaterbehandeling: Arnhem, The Netherlands, 2003; ISBN 9789036956420. [Google Scholar]
- Li, J. Numerical Study of the Biomorphodynamics of Alternate Bars in Gravel-Bed Rivers. Ph. D. Thesis, Université de Tours, Tours, France, 2022. [Google Scholar]
- Folke, F.; Kopmann, R.; Dalledonne, G.; Attieh, M. Comparison of different vegetation models using TELEMAC-2D. In Proceedings of the XXVIth TELEMAC-MASCARET User Conference, Toulouse, France, 15–17 October 2019. [Google Scholar] [CrossRef]
- van Rijn, L.C. Sediment Transport, Part I: Bed Load Transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
- National Research Council Canada (NRC). Blue Kenue™ (Version 3.3.4): Software tool for hydraulic modellers. Ottawa, Ontario, Canada. Available online: https://nrc.canada.ca/en/research-development/products-services/software-applications/blue-kenuetm-software-tool-hydraulic-modellers (accessed on 19 November 2025).
- Koch, F.G.; Flokstra, C. Bed level computations for curved alluvial channels. In Proceedings of the XIXth Congress of the International Association for Hydraulic Research, New Delhi, India, 2–7 February 1981. [Google Scholar]
- Nikuradse, J. Laws of Flow in Rough Pipes. In NACA Technical Memorandum 1292; National Advisory Committee for Aeronautics: Washington, DC, USA, 1950; (Translation of Strömungsgesetze in rauhen Rohren, VDI-Forschungsheft 361, 1933.). [Google Scholar]
- Einstein, H.A.; Barbarossa, N.L. River Channel Roughness. Trans. Am. Soc. Civ. Eng. 1952, 117, 1121–1132. [Google Scholar] [CrossRef]
- Brownlie, W.R. Prediction of Flow Depth and Sediment Discharge in Open Channels; Report No. KH-R-43A.; W.M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology: Pasadena, CA, USA, 1982. [Google Scholar]
- Li, J.; Claude, N.; Tassi, P.; Cordier, F.; Crosato, A.; Rodrigues, S. River restoration works design based on the study of early-stage vegetation development and alternate bar dynamics. River Res. Applic. 2023, 39, 1682–1695. [Google Scholar] [CrossRef]
- Yang, J.Q.; Kerger, F.; Nepf, H.M. Estimation of the bed shear stress in vegetated and bare channels with smooth beds. Water Resour. Res. 2015, 51, 3647–3663. [Google Scholar] [CrossRef]
- Wang, X.; Gualtieri, C.; Huai, W.; Liu, H.; Yu, S. An improved formula for bed-load rate in open channel flows with emergent vegetation. Phys. Fluids 2024, 36, 013309. [Google Scholar] [CrossRef]
- Lu, Y.; Cheng, N.-S.; Wei, M. Formulation of bed shear stress for computing bed-load transport rate in vegetated flows. Phys. Fluids 2021, 33, 115105. [Google Scholar] [CrossRef]
- Yang, J.Q.; Nepf, H.M. A Turbulence-Based Bed-Load Transport Model for Bare and Vegetated Channels. Geophys. Res. Lett. 2018, 45, 10–428. [Google Scholar] [CrossRef]
- Folke, F.; Kopmann, R.; Hohnschop, A. Influence of uncertainties of vegetation parameters in a 2D model. In Proceedings of the 2020 TELEMAC-MASCARET User Conference, Karlsruhe, Germany, 14–15 October 2021; pp. 2–9. [Google Scholar]
- Vargas-Luna, A.; Crosato, A.; Calvani, G.; Uijttewaal, W.S. Representing plants as rigid cylinders in experiments and models. Adv. Water Resour. 2016, 93, 205–222. [Google Scholar] [CrossRef]

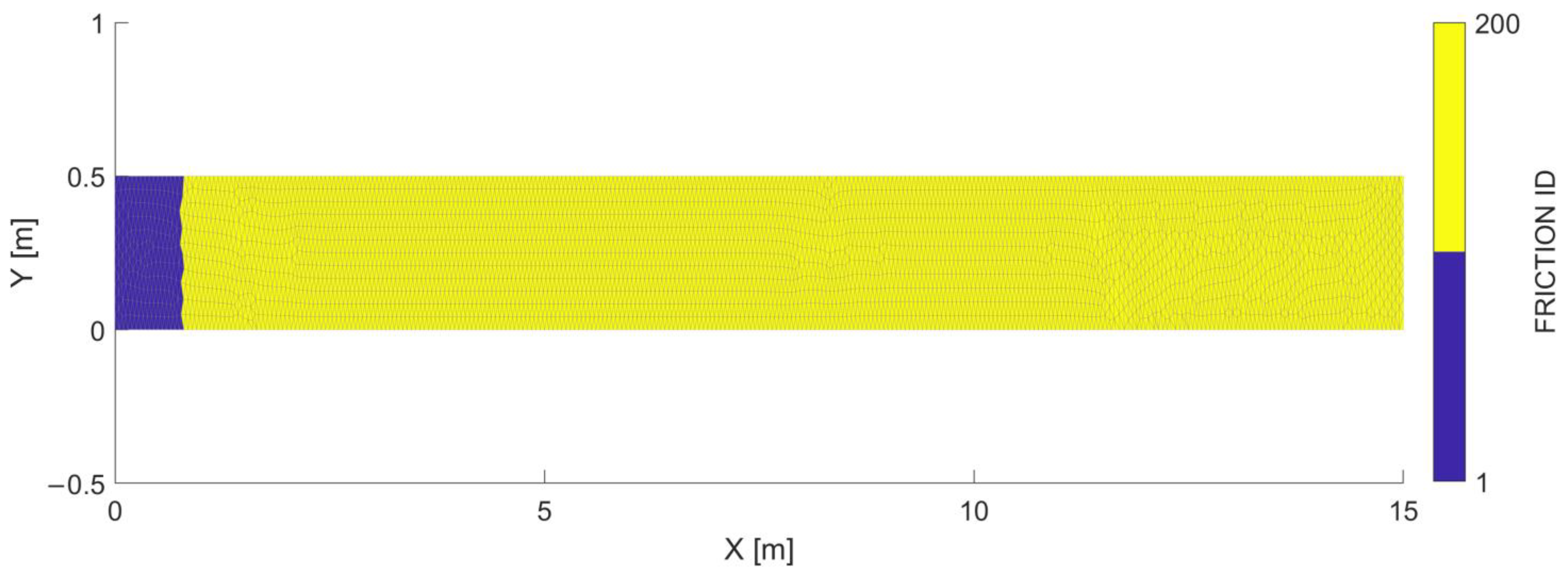
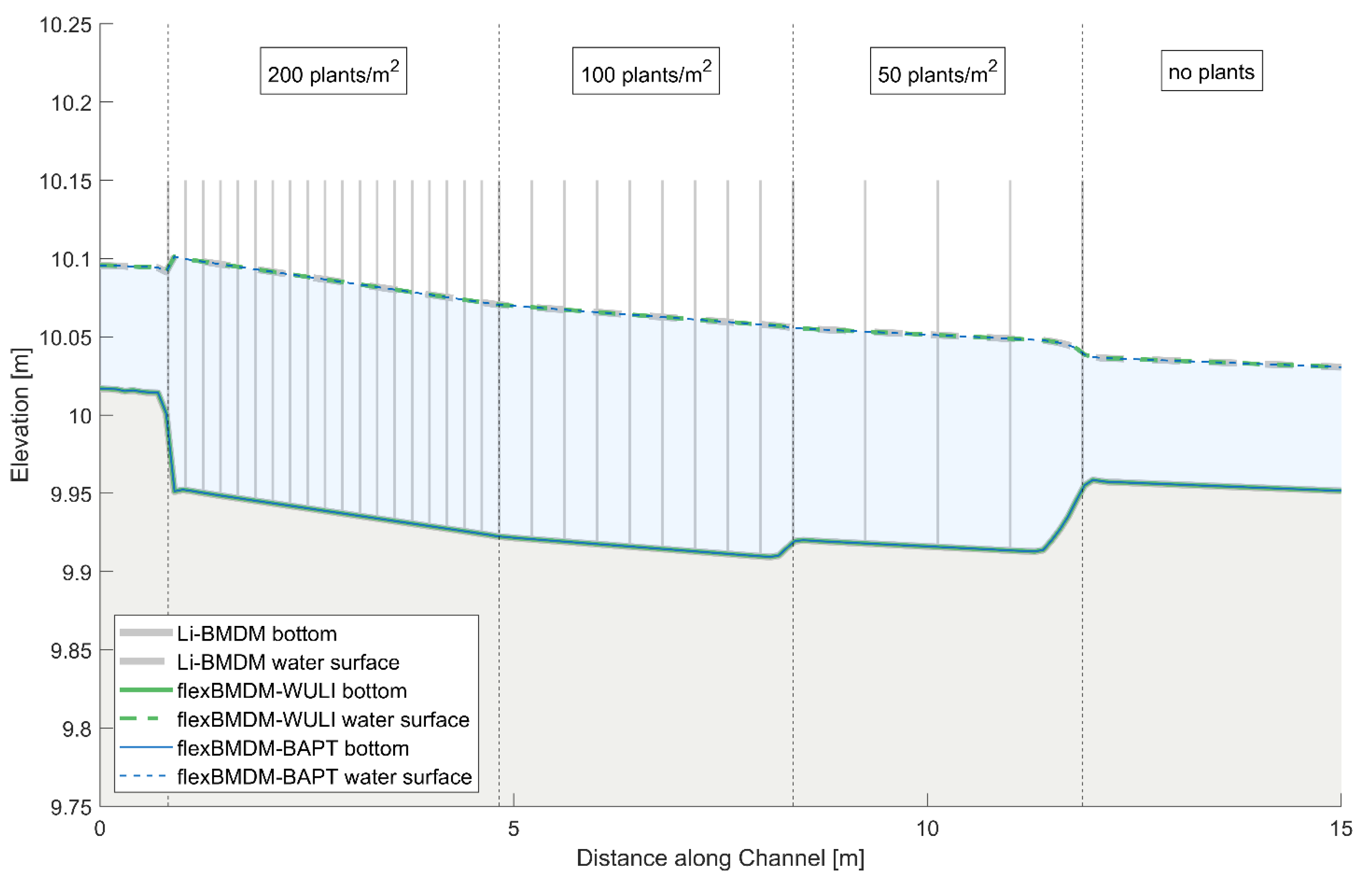


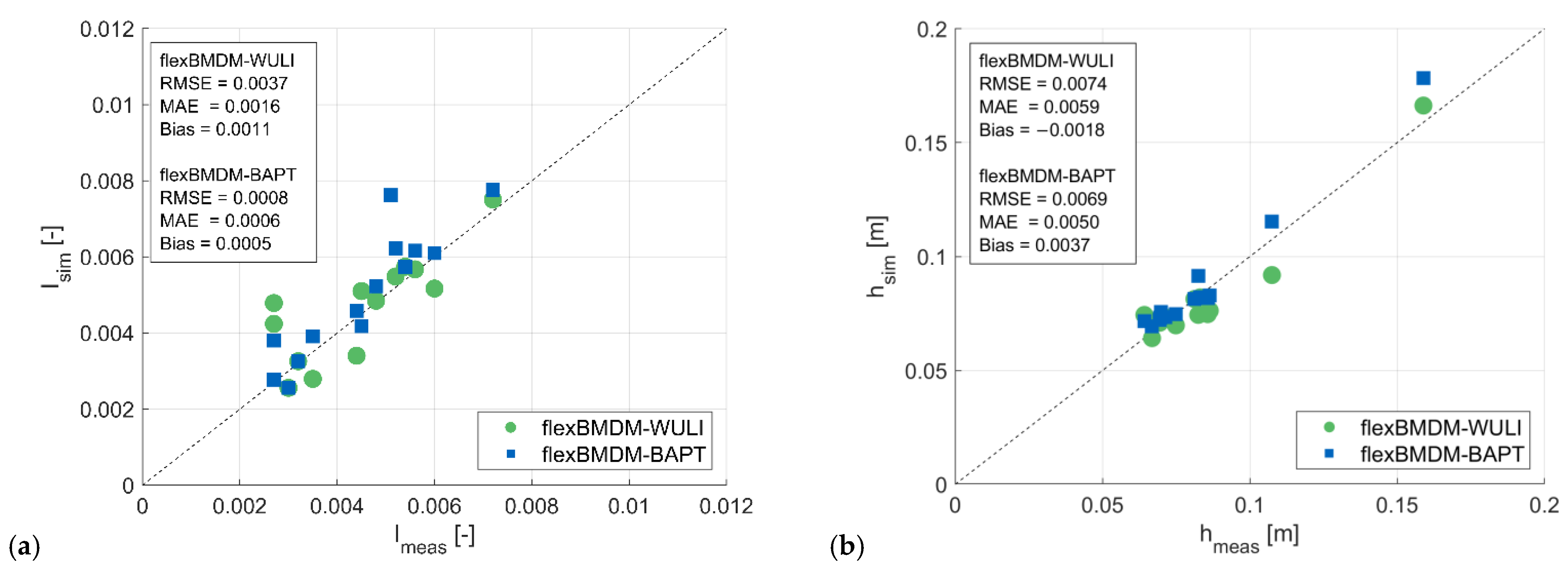
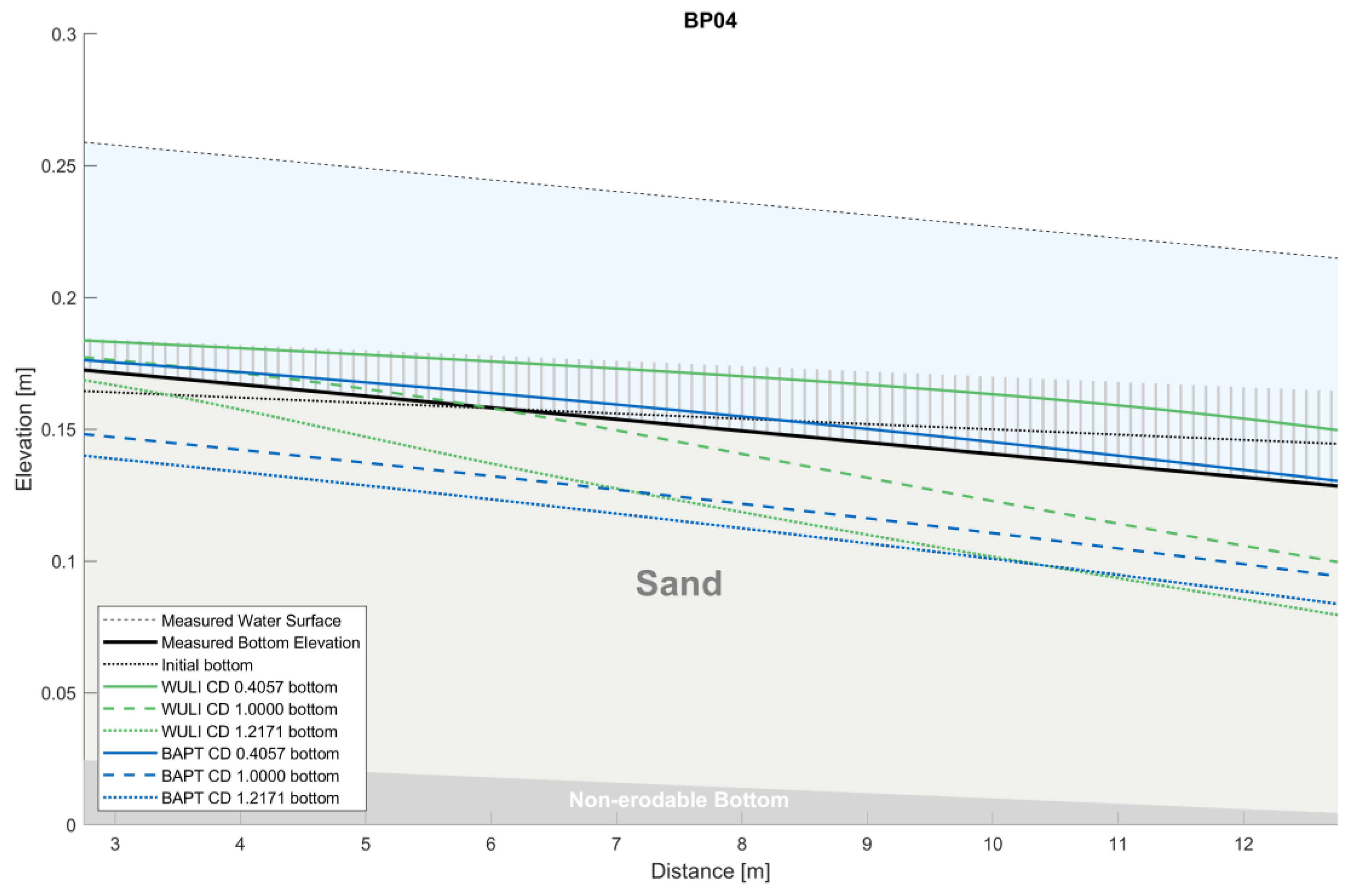
| Laboratory Experiment | Flow Conditions | Applied Frameworks | Aim |
|---|---|---|---|
| Armanini and Cavedon [42] | emergent | Li-BMDM flexBMDM-WULI flexBMDM-BAPT | Validation of the flexBMDM against the Li-BMDM |
| Bonilla-Porras et al. [43] | submerged | flexBMDM-WULI flexBMDM-BAPT | Demonstrating the influence of different vegetation friction approaches |
| Reference | Label | Emergent | Submerged |
|---|---|---|---|
| Baptist et al. [51] | BAPT | ||
| Wu et al. [62], Li et al. [40] | WULI | With |
| Scenario | Zone | [1/m2] | [-] | [m3/s] | [kg/s] | [m] | [-] |
|---|---|---|---|---|---|---|---|
| 1.R20 | A | 200 | 0.0157 | 0.020 | 3.757 × 10−3 | 0.155 | 0.0080 |
| B | 100 | 0.0073 | 0.136 | 0.0044 | |||
| C | 50 | 0.0039 | 0.127 | 0.0037 | |||
| D | 0 | 0 | 0.102 | 0.0014 | |||
| 2.R9 | A | 200 | 0.0157 | 0.009 | 1.213 × 10−4 | 0.115 | 0.0049 |
| B | 100 | 0.0073 | 0.097 | 0.0026 | |||
| C | 50 | 0.0039 | 0.093 | 0.0018 | |||
| D | 0 | 0 | 0.080 | 0.0008 | |||
| 3.R10 | A | 200 | 0.0157 | 0.010 | 5.078 × 10−4 | 0.111 | 0.0056 |
| B | 100 | 0.0073 | 0.099 | 0.0028 | |||
| C | 50 | 0.0039 | 0.098 | 0.0023 | |||
| D | 0 | 0 | 0.076 | 0.0010 | |||
| NP1-NV | A | 200 | 0.0157 | 0.010 | 9.457 × 10−5 | 0.112 | 0.0050 |
| B | 100 | 0.0073 | 0.096 | 0.0026 | |||
| C | 50 | 0.0039 | 0.088 | 0.0020 | |||
| D | 0 | 0 | 0.078 | 0.0011 | |||
| NP2-NV | A | 200 | 0.0157 | 0.020 | 3.368 × 10−3 | 0.132 | 0.0101 |
| B | 100 | 0.0073 | 0.110 | 0.0056 | |||
| C | 50 | 0.0039 | 0.100 | 0.0037 | |||
| D | 0 | 0 | 0.092 | 0.0019 |
| Test | [m3/s] | [kg/s] | [-] | [-] | [m] | [m] | [-] | [m] |
|---|---|---|---|---|---|---|---|---|
| BP01 | 0.0230 | 7.13 × 10−5 | 0.0157 | 0.0000 | 0.09 | 0.17 | 0.5610 | 0.07 |
| BP02 | 0.0200 | 1.07 × 10−3 | 0.0157 | 0.0000 | 0.13 | 0.165 | 0.4964 | 0.03 |
| BP03 | 0.0180 | 3.17 × 10−3 | 0.0157 | 0.0010 | 0.14 | 0.16 | 0.3764 | 0.02 |
| BP04 | 0.0200 | 6.02 × 10−3 | 0.0157 | 0.0020 | 0.14 | 0.15 | 0.4057 | 0.02 |
| BP05 | 0.0200 | 9.67 × 10−3 | 0.0157 | 0.0025 | 0.14 | 0.135 | 0.3145 | 0.02 |
| BP06 | 0.0220 | 1.34 × 10−2 | 0.0157 | 0.0030 | 0.14 | 0.135 | 0.2324 | 0.02 |
| BP07 | 0.0220 | 1.33 × 10−2 | 0.0157 | 0.0030 | 0.15 | 0.155 | 0.1404 | 0.01 |
| BP08 | 0.0220 | 1.33 × 10−2 | 0.0157 | 0.0030 | 0.16 | 0.175 | 0.1584 | 0.001 |
| BP09 | 0.0220 | 2.95 × 10−2 | 0.0157 | 0.0030 | 0.14 | 0.115 | -0.0540 | 0.02 |
| BP10 | 0.0210 | 1.45 × 10−2 | 0.0157 | 0.0045 | 0.16 | 0.16 | 0.2199 | 0.001 |
| BP11 | 0.0210 | 1.58 × 10−2 | 0.0118 | 0.0045 | 0.15 | 0.16 | 0.2715 | 0.01 |
| BP12 | 0.0210 | 6.55 × 10−3 | 0.0118 | 0.0045 | 0.15 | 0.17 | 0.4245 | 0.01 |
| BP13 | 0.0200 | 1.87 × 10−2 | 0.0118 | 0.0060 | 0.14 | 0.15 | 0.3348 | 0.02 |
| BP14 | 0.0180 | 4.81 × 10−3 | 0.0000 | 0.0020 | 0.23 | 0.25 | 0.0000 | 0.00 |
| BP15 | 0.0200 | 9.57 × 10−3 | 0.0000 | 0.0020 | 0.23 | 0.25 | 0.0000 | 0.00 |
| BP16 | 0.0220 | 3.07 × 10−2 | 0.0000 | 0.0020 | 0.23 | 0.23 | 0.0000 | 0.00 |
| WULI | BAPT | ||||||
|---|---|---|---|---|---|---|---|
| Test | [-] | [m] | [1/m2] | [m] | [-] | [1/m] | [m] |
| BP01 | 0.5610 | 0.01 | 200 | 0.07 | 0.5610 | 2.0 | 0.07 |
| BP02 | 0.4964 | 0.01 | 200 | 0.03 | 0.4964 | 2.0 | 0.03 |
| BP03 | 0.3764 | 0.01 | 200 | 0.02 | 0.3764 | 2.0 | 0.02 |
| BP04 | 0.4057 | 0.01 | 200 | 0.02 | 0.4057 | 2.0 | 0.02 |
| BP05 | 0.3145 | 0.01 | 200 | 0.02 | 0.3145 | 2.0 | 0.02 |
| BP06 | 0.2324 | 0.01 | 200 | 0.02 | 0.2324 | 2.0 | 0.02 |
| BP10 | 0.2199 | 0.01 | 200 | 0.001 | 0.2199 | 2.0 | 0.001 |
| BP11 | 0.2715 | 0.01 | 150 | 0.01 | 0.2715 | 1.5 | 0.01 |
| BP12 | 0.4245 | 0.01 | 150 | 0.01 | 0.4245 | 1.5 | 0.01 |
| BP13 | 0.3348 | 0.01 | 150 | 0.02 | 0.3348 | 1.5 | 0.02 |
| BP01 | 0.5610 | 0.01 | 200 | 0.07 | 0.5610 | 2.0 | 0.07 |
| BP02 | 0.4964 | 0.01 | 200 | 0.03 | 0.4964 | 2.0 | 0.03 |
| BP03 | 0.3764 | 0.01 | 200 | 0.02 | 0.3764 | 2.0 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dallmeier, A.; Kopmann, R.; Casas Mulet, R.; Schwedhelm, H.; Folke, F.; Rüther, N. A Novel Biomorphodynamic Model to Enhance Bedload Transport Modelling in Emergent and Submerged Rigid Vegetation. Water 2025, 17, 3336. https://doi.org/10.3390/w17233336
Dallmeier A, Kopmann R, Casas Mulet R, Schwedhelm H, Folke F, Rüther N. A Novel Biomorphodynamic Model to Enhance Bedload Transport Modelling in Emergent and Submerged Rigid Vegetation. Water. 2025; 17(23):3336. https://doi.org/10.3390/w17233336
Chicago/Turabian StyleDallmeier, Antonia, Rebekka Kopmann, Roser Casas Mulet, Hannah Schwedhelm, Frederik Folke, and Nils Rüther. 2025. "A Novel Biomorphodynamic Model to Enhance Bedload Transport Modelling in Emergent and Submerged Rigid Vegetation" Water 17, no. 23: 3336. https://doi.org/10.3390/w17233336
APA StyleDallmeier, A., Kopmann, R., Casas Mulet, R., Schwedhelm, H., Folke, F., & Rüther, N. (2025). A Novel Biomorphodynamic Model to Enhance Bedload Transport Modelling in Emergent and Submerged Rigid Vegetation. Water, 17(23), 3336. https://doi.org/10.3390/w17233336






