1. Introduction
To reduce the waste of natural resources and protect the environment, nations worldwide have implemented various energy and water conservation strategies. In addition to improving resource-use efficiency and developing alternative resources, minimizing the unnecessary exploitation of natural resources is a key principle for sustainable development. Groundwater serves as an essential resource for domestic, industrial, and agricultural uses. However, during the construction of high-rise buildings, deep excavation is often required to establish stable foundations within the soil layer. In areas with abundant groundwater, such excavation commonly leads to construction difficulties, particularly where the groundwater table is high. In such cases, groundwater must be extracted to lower the water table to maintain a dry environment suitable for foundation work. This process, which uses pumping systems to lower groundwater levels, is known as dewatering engineering.
However, dewatering systems are temporary facilities rather than part of the building’s structural framework. Their environmental impact is often overlooked by contractors or developers, resulting in excessive groundwater discharge directly into surface drainage systems or even the sea. Over-pumping may also cause soil void formation or subsidence at the construction site and in nearby residential areas. Thus, reducing groundwater extraction during construction is essential for groundwater conservation. Therefore, understanding the behavior of groundwater and developing methods for the intelligent control of pumping rates in high-rise construction dewatering systems are of critical importance.
In current engineering practice, dewatering operations are typically implemented in compliance with regulatory provisions that require maintaining groundwater levels approximately 1–2 m below the excavation surface during construction, while simultaneously preventing soil instability and ground subsidence in surrounding areas. However, this long-term and imprecise pumping strategy often leads to excessive groundwater discharge and wastage. This study further investigates the incremental loading behavior associated with the completion of each building floor and applies the expert judgment method to establish fuzzy membership functions representing construction progress. Based on this, a smart, energy- and water-saving dewatering model is developed to reduce unnecessary groundwater extraction. By applying the concept of balancing buoyant forces from higher groundwater levels against the increasing structural loads of the building during construction, the proposed method enables the early reduction in pumping volumes, thereby mitigating excessive dewatering before project completion.
Regarding previous studies, the theory of artificial neural networks (ANNs) was first proposed in a pioneering paper by the American mathematicians and logicians Walter Pitts and Warren Sturgis McCulloch, titled “A Logical Calculus of Ideas Immanent in Nervous Activity” (1943), which introduced the first mathematical model of a neural network [
1]. In more recent studies, ANNs have been widely applied in groundwater-related fields to predict groundwater levels [
2,
3,
4,
5,
6,
7,
8,
9,
10], and the resulting models have been further utilized for water resource management. Notably, Xian Li et al. (2012) [
9] conducted a sensitivity analysis, whereas Emery Coppola Jr et al. (2003) [
2] investigated groundwater level simulations across different geological layers. However, previous studies on artificial neural networks (ANNs) have primarily focused on groundwater at large-scale aquifers, catchments, or basins, while groundwater in small, local aquifers has been rarely investigated.
Regarding studies that integrate fuzzy theory with expert judgment, Mehrbakhsh Nilashi et al. (2015) [
11] and Manuel Carpio et al. (2021) [
12] adopted a similar approach by expressing the relative importance of evaluation criteria as fuzzy numbers derived from expert assessments, which were subsequently processed through fuzzy inference systems to obtain reasoned outcomes. Aleksandras Krylovas et al. (2015) [
13] and Yih-Tzoo Chen et al. (2024) [
14] primarily concentrated on theoretical analyses, whereas Aminah Robinson Fayek (2019) [
15] and Konstantinos A. Chrysafis et al. (2012) [
16] integrated expert judgment, fuzzy theory, and other related methodologies to address practical applications. Similarly, Debashree Guha et al. (2010) [
17] and Shahab Hosseini et al. (2024) [
18] focused on enhancing conventional methodological frameworks. Furthermore, Mehrdad Sadeghi et al. (2022) [
19] and Pemika Hirankittiwong et al. (2025) [
20] applied the Fuzzy Analytic Hierarchy Process (FAHP) to effectively handle the inherent uncertainty embedded in expert evaluations. Overall, these studies indicate that fuzzy theory combined with expert judgment has been commonly used in the past to address practical uncertainty issues; however, most existing models remain limited to specific applications and lack applicability to dynamic construction systems, thereby highlighting the need for more adaptable frameworks, particularly since the behavioral process during the construction of building floors has rarely been addressed.
In this study, academic search engines were used to retrieve journal articles published between 2019 and 2024 on the topics of MODFLOW and ANN. After screening, four recent related papers that integrated MODFLOW with ANN modeling were identified and used for comparison with the proposed model of this study. A detailed comparative analysis between this study and other related studies is presented in
Table 1.
In previous studies [
2,
3,
4,
5,
6,
7,
8,
9,
10,
21,
22,
23] on water resource management using artificial neural networks (ANNs), most research has focused on large-scale aquifers within watershed areas, whereas studies targeting small-scale or localized aquifers have been relatively rare. The most significant distinction lies in the fact that this research is the first to use a building foundation site as its case study target, investigating the impact of dewatering activities during the construction process on the underlying groundwater. The study area covers a relatively small scale, with the model domain extending about 3 km in all directions around the building site.
Based on the literature review [
2,
3,
4,
5,
6,
7,
8,
9,
10] and recent studies (2014–2024) [
21,
22,
23], it can be observed that previous applications of artificial neural networks (ANNs) have primarily focused on large-scale groundwater prediction, such as at the catchment or entire aquifer level. Few studies have targeted groundwater prediction in localized areas. This study is the first to consider building sites as the research object and demonstrates that, once appropriately trained, ANNs can accurately simulate groundwater conditions even within small, localized areas, highlighting their superiority. Furthermore, previous research has rarely addressed the variations in building floor weights during construction. In this study, an expert-based approach is employed to develop, for the first time, a “fuzzy logic floor completion membership function.” By establishing this membership function, a novel water-saving dewatering model is implemented, ultimately achieving the goal of water conservation.
This study focuses on the impacts of dewatering works for high-rise building foundations in metropolitan areas of Taiwan on the complex subsurface environment. Under conditions of limited data and resources, an intelligent management model for groundwater dewatering in high-rise building sites is developed to achieve the goal of water conservation. The main highlights of this study are summarized as follows:
Previous applications of artificial neural networks (ANNs) in water resources management have primarily focused on large-scale areas, such as aquifers, catchments, watersheds, or basins. Groundwater conditions in localized aquifers, particularly the impacts of dewatering activities at building sites, have rarely been investigated. This study is the first to simulate dewatering behavior at small-scale aquifer building sites using ANNs. The results demonstrate that ANNs can achieve a high level of accuracy in simulating groundwater conditions even within such localized areas.
Previous studies have rarely employed the expert judgment method to evaluate building behaviors during high-rise construction under uncertain conditions. In this study, an expert-opinion-based approach is proposed to construct fuzzy membership functions representing floor completion status. By leveraging the concept of balancing buoyant forces from preemptively elevated groundwater levels against the gravitational load of completed floors, unnecessary pumping during construction is significantly reduced. This approach constitutes a new intelligent water-saving dewatering model for high-rise building foundations.
2. Materials and Methods
2.1. Theoretical Framework and Methodological Basis
As described in the Introduction, dewatering operations at high-rise building construction sites produce complex physical effects on groundwater. The construction period of high-rise buildings generally lasts 2–3 years; during this period, the rise and fall of groundwater levels after dewatering involve complex hydrogeological conditions, which change over time. Geological factors include soil surface infiltration, soil porosity, hydraulic conductivity, and aquifer storage capacity, while hydrological factors include solar radiation, precipitation, evapotranspiration, and the influence of nearby rivers. Given the limitations of these traditional numerical methods, artificial neural networks (ANNs) offer an alternative for predicting dynamic and highly nonlinear systems. The ANN provides a robust tool for modeling complex and uncertain groundwater environments, offering a new and effective approach for simulating nonlinear groundwater dynamics.
The limited measured datasets at the study site include head test data, pumping rate data from dewatering wells, and groundwater level measurements. One monitoring well experienced data loss, and the remaining wells had insufficient data to train, test, and validate an ANN model independently. Therefore, secondary datasets from governmental agencies, universities, and research institutions were collected, while constant-head test data at the study site were used to calibrate the MODFLOW model, enabling the generation of sufficient simulated data to train and validate the ANN model. Finally, the ANN predictions were compared with available field measurements in order to assess the accuracy and reliability of the ANN-based groundwater simulation.
In addition, fuzzy theory often plays a key role in handling uncertain factors; its main advantage is that it does not require detailed data to construct models for uncertainty. In particular, for uncertainty analysis in situations lacking historical data or when analyzing knowledge accumulated from human experience, fuzzy theory provides a robust tool for quantifying uncertainty.
In this study, experts were directly consulted to determine the typical patterns of weight addition during construction. The resulting membership function quantifies the relationship between the weight added by completed floors and the net buoyant effect on groundwater levels caused by reduced dewatering, thereby achieving net force equilibrium. This approach allows for reduced groundwater extraction during construction, thereby achieving the water-saving objective.
2.2. Methodology Description
This study involves several theoretical frameworks and techniques, including artificial neural networks (ANNs), fuzzy theory, expert opinion methods, and finite difference methods. A brief description of each is provided below.
2.2.1. Artificial Neural Networks (ANNs)
Since machine learning (including deep learning) is currently the dominant approach in AI development, one key method to endow machines with learning capabilities is to imitate the computational patterns of biological neural networks, particularly those in the human brain. This approach constructs models that simulate the operation of biological neural networks and is referred to as artificial neural networks (ANNs). ANNs are a nonlinear statistical modeling tool, typically optimized through a mathematically based learning method.
- (a)
Artificial Neural Networks
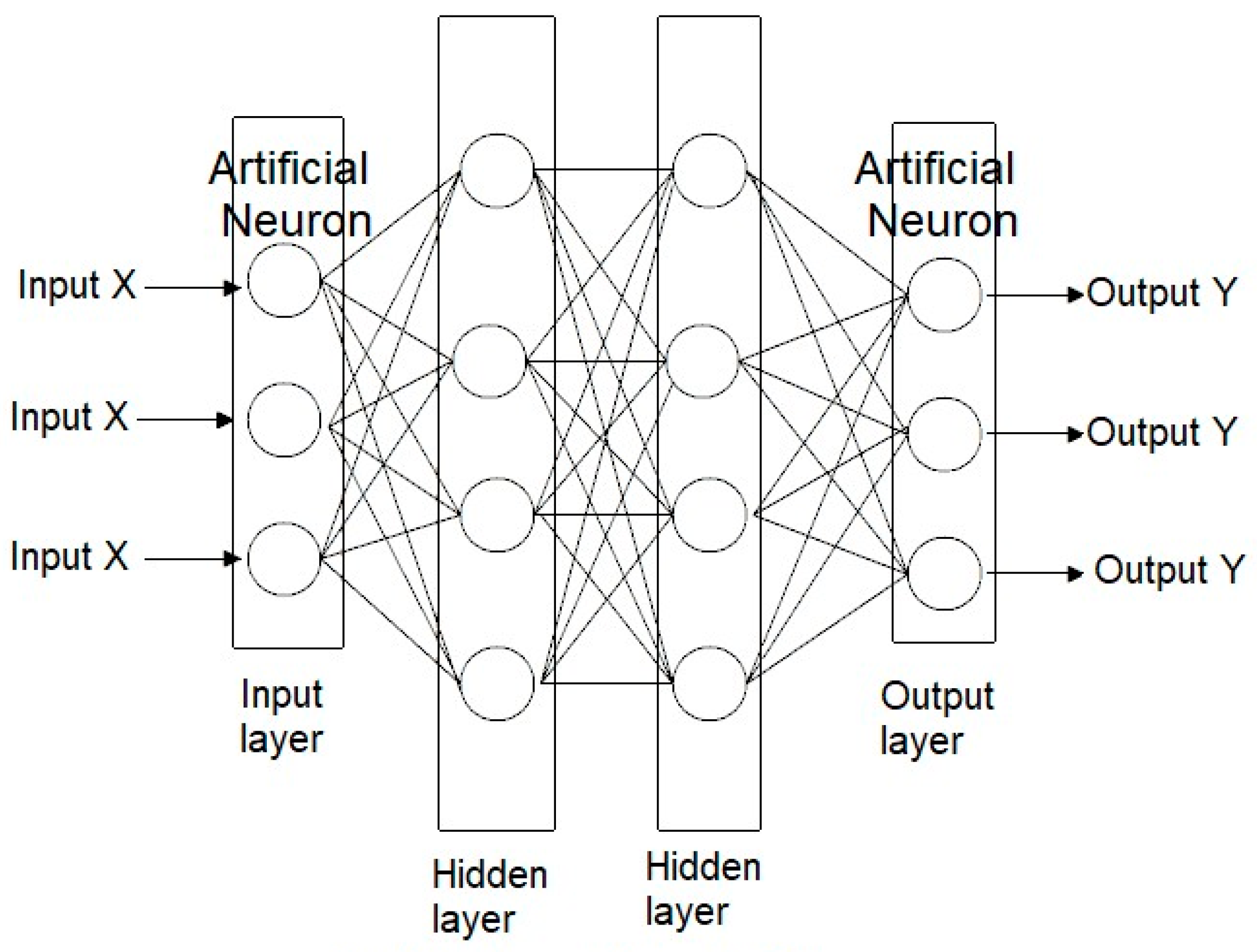
An artificial neuron (also called a perceptron) is designed to mimic the function of biological neurons as a unit for information processing. The basic relationships and components of an artificial neuron are inputs (X), weights, an activation function (f (·)), and an output (Y). These components together form the essential computational structure of an artificial neuron. However, to enable an artificial neural system to achieve better judgment and more complex predictive capabilities, it is necessary to increase the number of neurons. Multiple neurons can form a neural layer, and multiple layers together constitute an artificial neural network (ANN).
Figure 1 illustrates the typical architecture of such a neural network.
2.2.2. Fuzzy Theory and Expert Opinion Methods
- (a)
Fuzzy Theory and Fuzzy Membership Function
Fuzzy theory is specifically designed to handle situations where the human brain processes imprecise or incomplete information. It allows for correct judgment without requiring complex or precise calculations, which is the key feature of the theory. The distinction between a fuzzy set and a classical binary set (crisp set, with elements 0 or 1, where 1 represents “belongs” and 0 represents “does not belong”) lies in how membership is defined. In a fuzzy set, the degree to which an element belongs to a set X is expressed by a membership function , which takes values in the interval [0, 1], rather than being limited to only 0 or 1.
Formally, let X denote the universe of discourse, i.e., the complete set of all objects under consideration, and let A be a fuzzy subset of X, representing a finite set within the domain. The fuzzy set A can be expressed as
where
is the membership degree of element x in A.
- (b)
Expert Opinion Methods
The expert opinion method is a knowledge-based approach that collects and synthesizes information derived from the expertise and experience of professionals. It has been widely applied across various disciplines. Accordingly, this study employed the expert opinion method to establish the floor completion membership function.
In this study, the floor completion fuzzy membership function is used to calculate the static equilibrium between the weight added by completed floors and the buoyancy generated by the rise in groundwater level. The increase in groundwater level is achieved by reducing the pumping volume.
For each floor, the floor weight is derived from the high-rise building project budget and acts as a downward gravitational force. When the groundwater level rises by , the resulting buoyant force can be expressed as the product of the foundation area , the height increase , and the soil water content m; the reason for multiplying by the water content m is that only the water in the soil can provide buoyancy, whereas the other substances in the soil cannot.
The static force equilibrium can therefore be expressed as
where
is the floor completion fuzzy membership function, with t representing construction time. A value of
indicates that the floor has not been constructed, while
indicates that the floor is completed.
is a function of the pumping volume Q and pumping duration t, obtained from ANN-based simulation data.
Since the rise in groundwater level is achieved by reducing the dewatering volume in advance, this approach effectively prevents unnecessary groundwater extraction, contributing to water-saving measures at the construction site.
2.3. Theoretical Basis and Calibration of the MODFLOW Model
The MODFLOW groundwater flow model, officially named the Modular Groundwater Flow Model, was developed by the U.S. Geological Survey (USGS). MODFLOW is an essential numerical simulation program in the GMS (Groundwater Modeling System) version 10.6. The model is fundamentally based on the principle of mass conservation, which is applied to develop the continuity equation and subsequently the finite-difference form (FDM) of the groundwater flow equation to obtain approximate numerical solutions.
In MODFLOW, PEST (Parameter Estimation) is a model-independent, nonlinear parameter estimation tool used for model calibration (inverse modeling) and data interpretation. PEST repeatedly runs the model while adjusting parameters to match simulated outputs with observed data.
2.4. Research Workflow and Implementation Steps
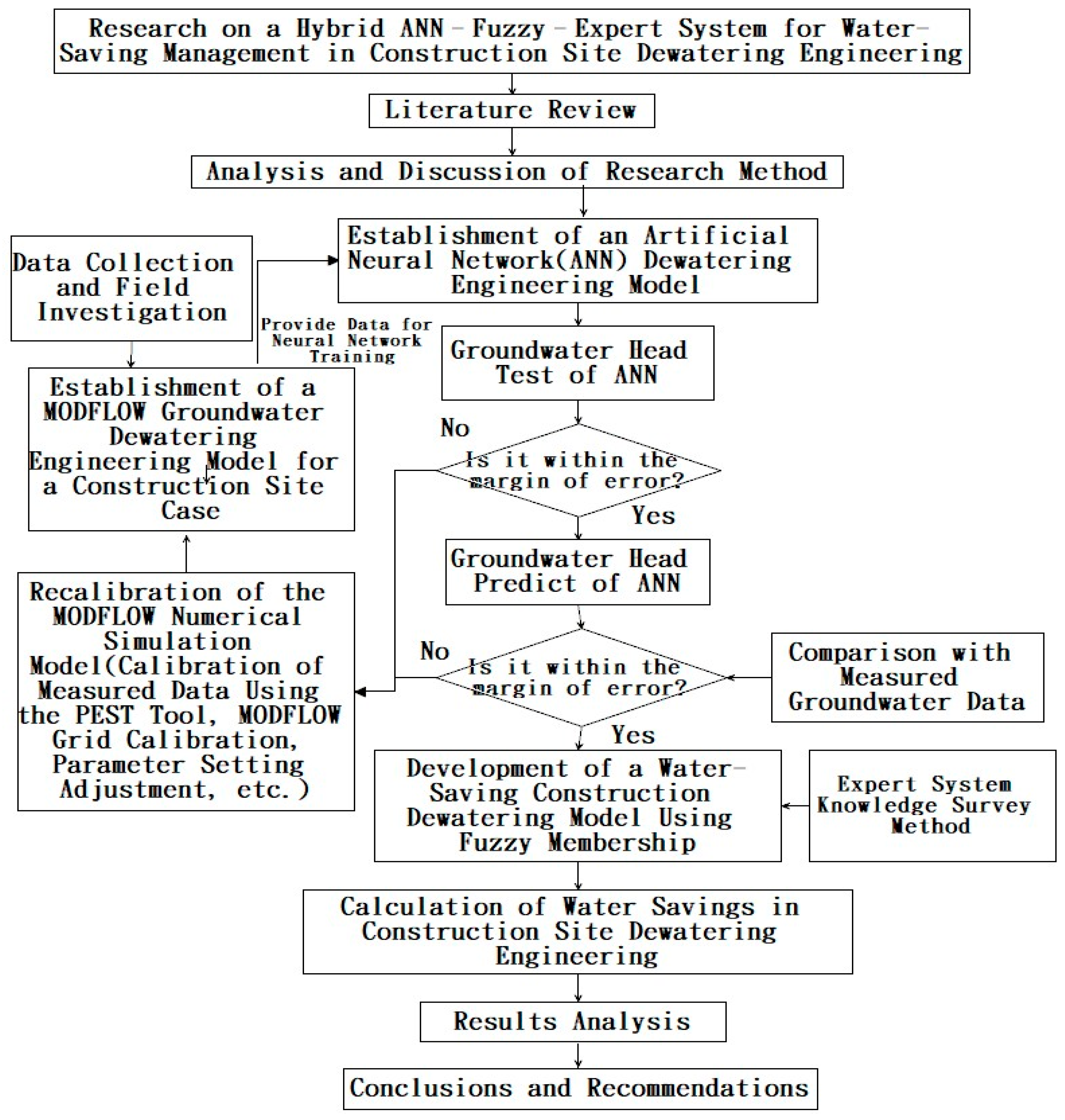
The workflow and implementation steps of this study are summarized as follows:
Literature Review;
Exploration of Research Methods;
Establishment of a Water-Saving Dewatering Model for Construction Sites;
Case Study;
Conclusions and Recommendations.
The detailed flowchart of this study is shown in
Figure 2.
2.5. Case Study
To evaluate the effectiveness of an intelligent water-saving dewatering model for high-rise building construction sites in urban areas, this study conducted modeling and assessment at an actual construction site in Taichung City, Taiwan (
Figure 3). The site is a steel-framed high-rise building covering a total area of approximately 10,500 m
2. Based on pre-construction groundwater monitoring data collected in June 2019, the surrounding groundwater level was approximately 6 m below ground level (GL ≈ −6 m). The building design includes 5 basement levels and 21 above-ground floors, with dewatering operations initiated concurrently with foundation excavation in 2019.
The site is equipped with 13 perimeter pumping wells, which also function as monitoring wells, and 1 central monitoring well to track groundwater levels. During the construction period, the 13 perimeter wells were scheduled to operate for 500 days. However, continuous monitoring data from some wells were missing or incomplete, and the limited number of measurements was insufficient for effective training and validation of the ANN model.
To address these limitations, a MODFLOW-based groundwater simulation model for the construction site was developed using the Groundwater Modeling System (GMS 10.6). The model integrated observed hydrogeological and geotechnical monitoring data, along with secondary data, to establish a representative groundwater dewatering system for the Taichung steel high-rise construction project. The MODFLOW model was calibrated against actual constant-head test data collected on site to ensure the accuracy of the simulations.
Once the MODFLOW model was established, it was used to generate large datasets for the training and testing of the ANN model representing the site’s groundwater dewatering system. The ANN predictions were subsequently compared with the limited actual measurements to validate their accuracy. Based on these results, a smart, water-saving dewatering model for the high-rise construction site was developed to optimize groundwater extraction, allowing for the quantification of potential reductions in water resource usage achievable through intelligent dewatering management during the construction process.
2.6. Model Application and Parameter Setting
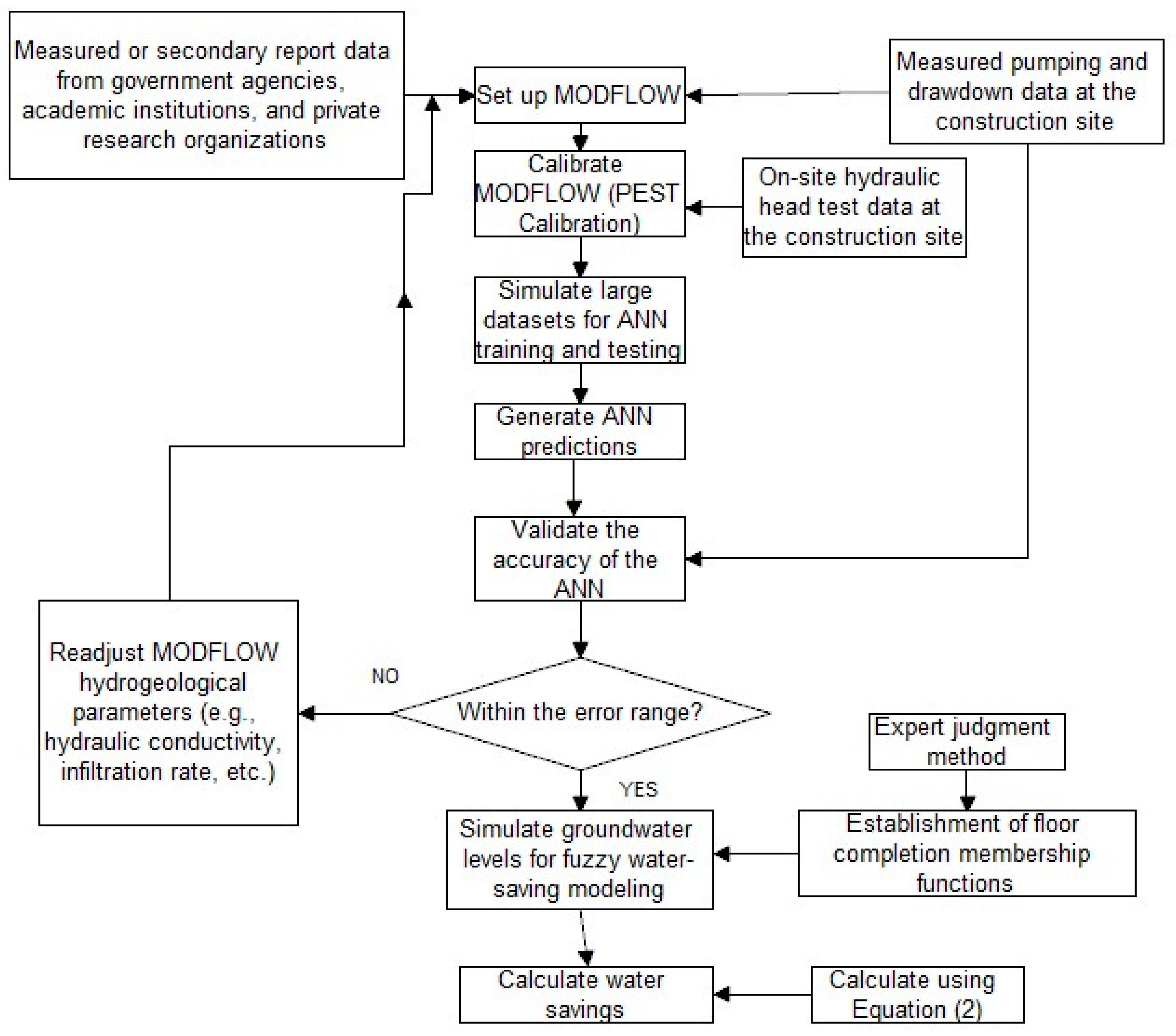
The computational steps of the intelligent water-saving model in this study are as follows:
Step 1: Collect the required hydrogeological parameters (e.g., hydraulic conductivity, evapotranspiration, and infiltration rate) from government agencies, academic institutions, and private research organizations. Obtain pumping rates, drawdown measurements, and hydraulic head test data from on-site measurements at the construction site. Using these parameters, establish a MODFLOW numerical model, employing the hydraulic head test data for PEST calibration of MODFLOW.
Step 2: Use the calibrated MODFLOW model from Step 1 to simulate a large dataset for ANN training and testing.
Step 3: Validate the accuracy of the ANN using the on-site pumping and drawdown data collected in Step 1.
Step 4: If the ANN accuracy validation in Step 3 falls within the acceptable error range, proceed to Step 5. If it does not meet the error criteria, return to Step 1 to readjust the hydrogeological parameters and repeat the sequence of steps.
Step 5: Use the ANN, which meets the error criteria, to simulate groundwater predictions for application in the water-saving model. This water-saving model is established based on expert judgment, using floor completion fuzzy membership functions. It achieves water savings by counterbalancing the buoyant effect generated from reduced groundwater pumping with the weight of completed floors.
Step 6: Finally, calculate the water-saving volume using the net force equilibrium equation between the weight of the completed floors and the buoyant force caused by the rise in the groundwater level.
A computational flowchart of the intelligent water-saving model is shown in
Figure 4.
2.6.1. Construction of the Artificial Neural Network (Programming Language: MATLAB)
The artificial neural network (ANN) in this study was implemented using the MATLAB programming language. MATLAB R2024b, an abbreviation of Matrix Laboratory, is a high-level programming language specifically designed for numerical computation, matrix operations, engineering, and scientific applications.
A key feature of MATLAB is its matrix-centric computational framework, which allows all data types—including scalars, vectors, images, and other datasets—to be naturally represented and processed as matrices. MATLAB is equipped with an extensive mathematical function library capable of addressing problems in linear algebra, statistics, signal processing, control systems, and optimization.
Furthermore, MATLAB provides specialized toolboxes that extend its capabilities to various professional domains, such as machine learning, image processing, and financial engineering (
Figure 5). The MATLAB programming environment is not only graphical and user-friendly but also highly versatile, making it suitable for the development and implementation of complex ANN models.
2.6.2. Implementation and Calibration of MODFLOW in Groundwater Modeling Systems and Big Data Modeling
As the training data required for constructing the neural network, the data generated by MODFLOW are used in this study, as illustrated in
Figure 6.
2.6.3. Questionnaire Design for Expert Opinion Survey and Guidance on Expert Knowledge and Experience
In this study, the questionnaire was structured into two sections. The first section provided an overview of the survey objectives and the relevant theoretical background, while the second section focused on eliciting expert opinions, including detailed explanations of the fuzzy membership functions representing the completion status of high-rise steel building floors.
A total of 65 questionnaires were distributed to professionals in civil and construction engineering, comprising 50 university professors, 9 government officials, and 6 industry practitioners. A total of 38 responses were received; however, 10 questionnaires were either blank or contained responses beyond the respondents’ professional expertise, leaving 28 valid expert responses for analysis. The full questionnaire is provided in
Appendix A.
3. Results and Discussion
This study developed a localized aquifer artificial neural network (ANN) and, based on its groundwater prediction results, established a water-saving dewatering model for building construction. The computational results of the artificial neural network indicated that the optimal network architecture comprises a single hidden layer with 25 neurons. The final ANN model was trained for 1000 epochs (trainParam.epochs = 1000). A total of 2447 data samples were used for training, testing, and validation, with 70% of the data allocated for training and the remaining 30% equally split between testing and validation. The normalization process was performed during network training. Notably, when a large dataset simulated by MODFLOW is used for training and testing the ANN, the measured data constitute only about 19.86% of the simulated dataset (486 out of 2447 points). Nevertheless, if accuracy verification against measured values falls within the acceptable error range, the ANN can still be regarded as sufficiently accurate, despite the limited amount of measured data. Therefore, the 486 measured values in this study are considered sufficient to validate the ANN’s accuracy.
The neural network was trained using five methods, including the Levenberg–Marquardt (L-M) algorithm, Bayesian Regularization (BR), Conjugate Gradient with Fletcher–Reeves updates (CGF), Scaled Conjugate Gradient (SCG), and the Broyden–Fletcher–Goldfarb–Shanno quasi-Newton method (BFG), all implemented in MATLAB. Evaluation metrics included error analysis between the training, testing, and validation data, as well as the coefficient of determination (), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), and Correlation Coefficient (R), to assess the fitting performance of the neural network.
Furthermore, sensitivity analysis was conducted to evaluate the contributions of all input parameters, identifying the key influential factors in the groundwater dewatering process at the construction site. The final sections present an analysis of the expert survey results on the fuzzy floor completion membership function and the model’s calculated water-saving effect.
3.1. Neural Network Training, Testing, Prediction, and Validation Results
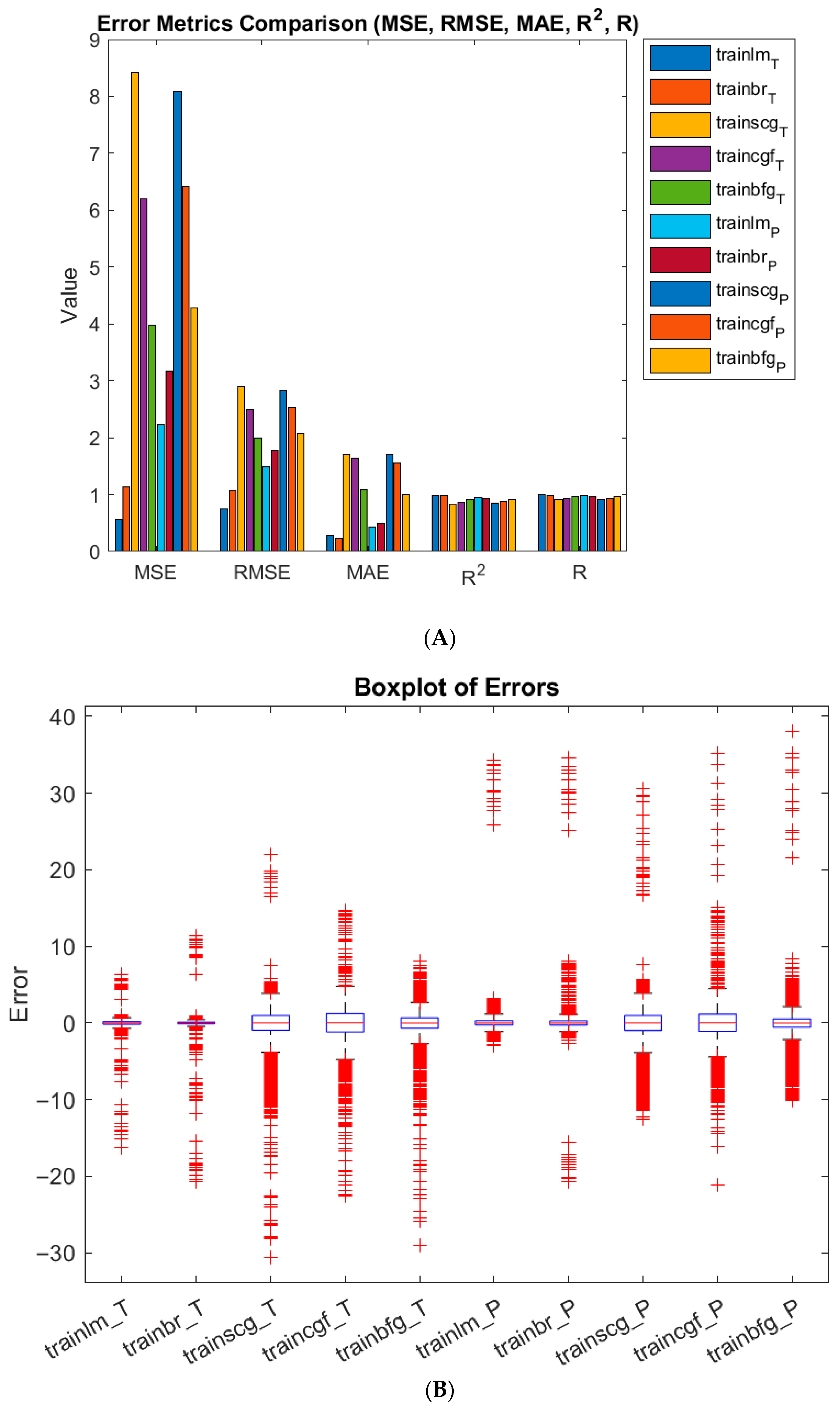
Figure 7 presents the results of training, testing, prediction, and validation for various neural networks (including box plots, histograms, and CDF plots). The figure also includes five performance metrics used to evaluate the accuracy of each method. As shown in the figure, both L-M and BR exhibit smaller errors than the other three methods (CGF, SCG, and BFG) for both training and prediction values, indicating that these two training methods are more accurate.
Table 2 presents the calculated values of the performance metrics for various neural network methods. The error values in the table directly indicate that the L-M and BR training methods are relatively more accurate. The correlation coefficient (R) obtained using the L m training algorithm exceeds 0.99, demonstrating a high level of accuracy and precision.
Among the five ANN models evaluated (LM, BR, SCG, CGF, and BFG), the training, testing, and validation results—assessed using five performance metrics (MSE, RMSE, MAE, R
2, and R)—indicate that the LM and BR algorithms outperformed the others. This observation is generally consistent with previous studies [
3,
5,
6,
7].
Regarding the optimization of activation functions, both the present study and prior research [
6,
7] show no consistent trend in the selection of the most suitable activation function.
For the optimization of hidden layers and neuron numbers, the optimal network configuration in this study consists of a single hidden layer, which aligns with previous findings [
4,
9], where one to two layers were typically found to be optimal. However, greater variability was observed in the determination of the optimal number of neurons compared with prior studies [
4,
9], likely due to differences in the number of input variables, which inherently affect the selection of the optimal neuron count.
3.2. Parameter Sensitivity Analysis Results
Based on the results of the neural networks trained with five different training algorithms shown in
Figure 8, it can be observed that an increase in the dispersion of the simulated data leads to insufficient data representativeness. This condition may cause stronger interdependence among parameters, resulting in the overlapping of the effects of each parameter on the output values. Such interactions are likely responsible for the poor training performance observed with the SCG, CGF, and BFG algorithms, and consequently for the partial distortion that appeared in the sensitivity analysis. Therefore, according to the sensitivity analysis results (
Figure 8), the LM training algorithm provides more reliable and interpretable outcomes. The sensitivity results obtained using the LM method indicate that the key parameter influencing groundwater level output is the hydraulic conductivity of the soil layer, followed by surface soil evaporation. The sensitivities of the remaining input parameters to the output are relatively similar, with only minor differences.
The sensitivity analysis conducted in this study reveals a distinct contrast with previous findings. In large-scale aquifer or watershed investigations [
9], groundwater behavior was primarily governed by anthropogenic factors, such as pumping activities. In contrast, for the localized, small-scale aquifer examined in this study, although human activities still exert a noticeable influence on ANN outputs, the effects of natural hydrogeological factors are more pronounced. This distinction highlights the differing sensitivity characteristics between confined local areas and extensive aquifer systems. Furthermore, the results indicate that input variables of the same type contribute to ANN outputs at comparable levels, which is consistent with trends reported in previous studies [
8].
3.3. Training Time and Error Analysis of Different ANN Training Methods
Based on the two calculation results of training time and MSE in
Table 3, it can be concluded that among the five ANN training methods, the L-M (Levenberg–Marquardt) method remains the most advantageous. When combined with the
tansig activation function, it achieves sufficiently fast training speed and the smallest MSE, with a minimum value as low as MSE = 1.5646535.
Overall, the findings confirm that artificial neural networks (ANNs) are highly effective in simulating dewatering activities at high-rise building construction sites. The proposed ANN framework accurately predicts variations in groundwater levels, demonstrating strong predictive capability even under complex hydrogeological conditions. Moreover, the analysis identified the Levenberg–Marquardt (LM) training algorithm combined with the tansig activation function as the most suitable network configuration. This optimized ANN model was subsequently employed to generate groundwater level predictions that serve as the foundation for developing the proposed water-saving dewatering model.
3.4. Survey Results of Floor Completion Membership Functions
Due to the “gradual” characteristic of fuzzy theory, which allows for consideration of the differences in actual completion levels, the gradual membership functions can be represented as continuous functions. Based on the expert survey questionnaire results, two main types of floor completion membership functions were selected: Type A and Type E.
Further consultation with the surveyed experts revealed that the reason for choosing Type A (linear increase throughout the construction process) is that human resources and material transportation remain consistent during construction and do not fluctuate with the process. Hence, the linear membership function can reflect the completion process.
The difference between Type E (S-curve increase throughout the construction process) and Type A is that near the completion of each floor, interface integration issues may occur in Type E, affecting the construction speed at the beginning and near the end of each floor completion.
Therefore, these two membership functions were used as the basis for calculating the reduction in groundwater extraction. The Type A membership function can be represented by a linear equation, while the Type E membership function can be expressed by an S-curve equation (as in Equations (3) and (4)). Since the number of experts selecting each type was similar, equal weighting was roughly applied to calculate the potential groundwater savings.
Linear membership function:
S-curve membership function:
where
t = floor construction time,
a = each floor construction start time,
b = each floor completion time, and
k = shape adjustment parameter for the S-curve (here
k = 2 was used).
Here,
a and
b are two time points that define the span of the S-curve.
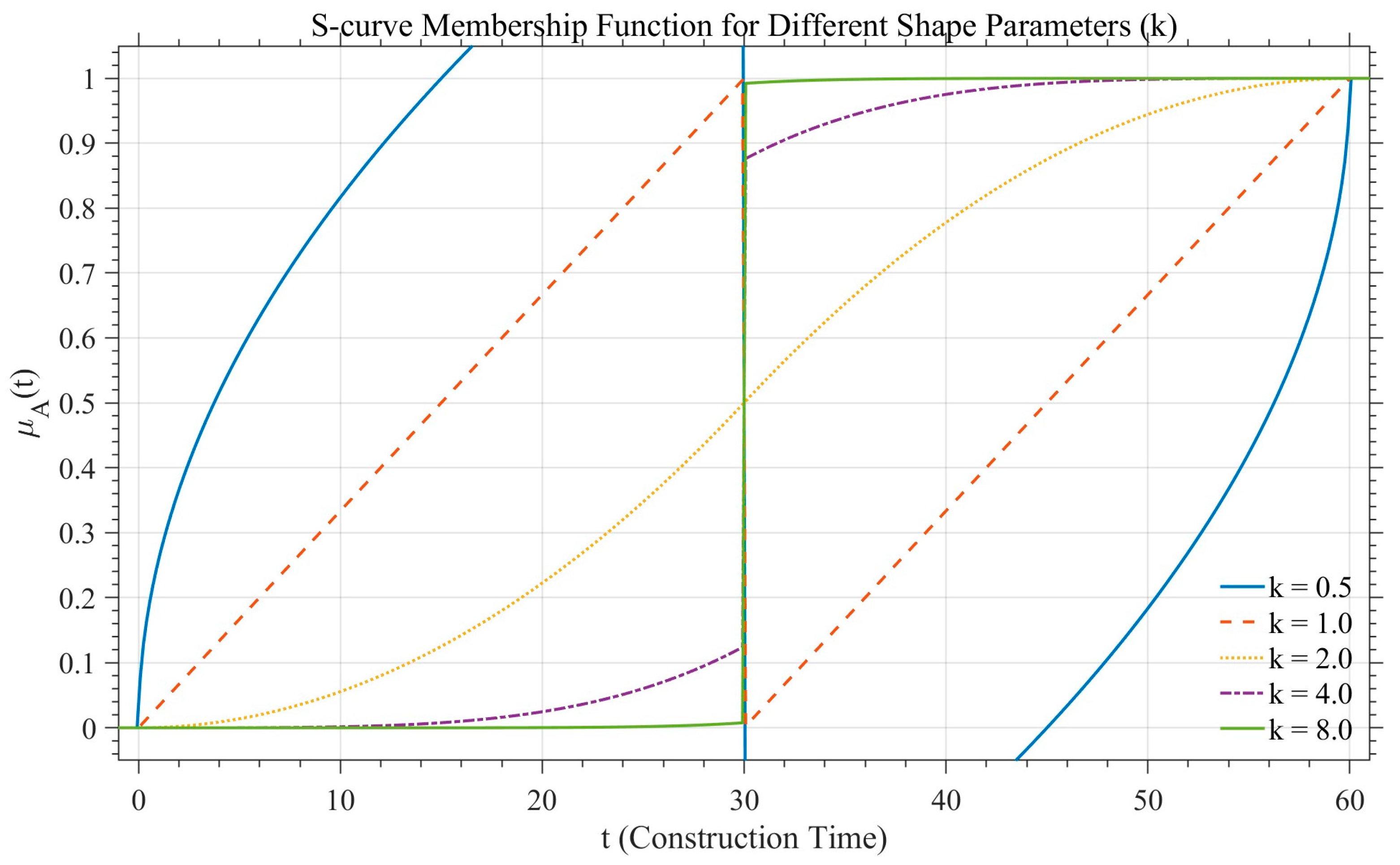
k is the shape parameter of the S-curve, determining its steepness or flatness. The S-curves corresponding to different membership functions with their respective
k values are shown in
Figure 9. Among them,
k = 2 matches best the E-type floor completion membership function derived from this study’s survey.
3.5. Water Savings Calculation Results Using the Fuzzy Floor Completion Membership Function Mode
Conventional dewatering practices typically remove groundwater in a coarse and uniform manner, with pumping conducted at a fixed rate and only halted upon completion of each floor (as shown in
Figure 10). However, the actual load on the soil gradually increases as construction progresses. Ideally, pumping should be reduced in proportion to the building’s cumulative weight, allowing the rising groundwater to generate a buoyant force that counteracts the structural load, thereby promoting water savings.
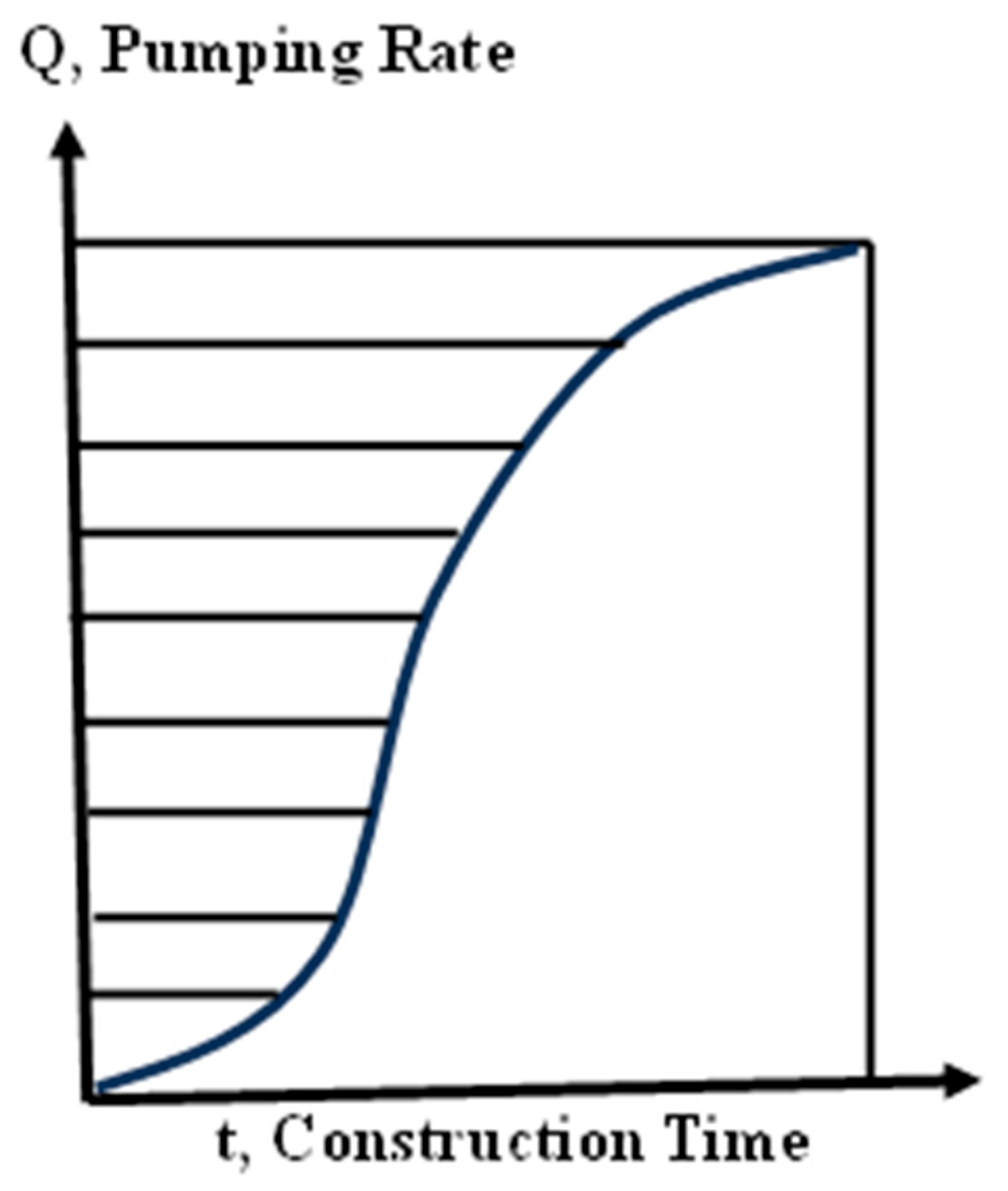
Due to the lack of detailed probabilistic or statistical data to mathematically represent the incremental floor weight, this study employs a non-probabilistic fuzzy membership function approach. Expert knowledge and experience were elicited through structured surveys to directly establish floor completion membership functions ranging from 0 to 1. Multiplying these functions by the design weight of each floor provides an estimate of the weight increment during construction.
Water savings were subsequently calculated using Equation (2), with the resulting volume corresponding to the blank area shown in
Figure 11. The curve in
Figure 11 reflects the floor completion membership functions derived from expert judgment.
In the case study presented here, the original groundwater level was approximately −6 m. The building consisted of 5 basement levels and 21 above-ground floors, with a foundation excavation depth of approximately 21 m. Prior to the commencement of floor construction, the groundwater level was maintained at roughly 1.5 m below the foundation slab. Using 13 dewatering wells operating at a uniform fixed rate, the expected drawdown at the site center was approximately 22.5 m from the start of foundation excavation. The construction of each main structural floor required approximately 60 days.
After the initiation of underground floor construction, the proposed fuzzy water-saving dewatering model—where the increase in groundwater level (buoyancy) offsets the weight of completed floors—was applied. The model calculations indicate that the total dewatering volume for the construction site was reduced by approximately 2927,400 metric tons compared with conventional regulatory-compliant dewatering practices. The conserved groundwater can be used for multiple purposes, such as domestic drinking water, agricultural irrigation and aquaculture, or industrial water supply, providing a significant contribution to the protection of groundwater resources.
4. Conclusions and Recommendations
Previous applications of artificial neural networks (ANNs) in water resources management have predominantly focused on large-scale systems such as aquifers and catchments. In contrast, the primary objective of this study was to investigate groundwater behavior in localized, small-scale aquifers and to develop a predictive ANN-based model for dewatering operations at building sites. The results demonstrate that ANNs can accurately predict groundwater levels even within such confined areas. Based on these ANN-derived groundwater predictions, a water-saving dewatering model for building sites was successfully developed.
A comparison between this study and previous ANN studies on large-scale regions shows generally consistent trends in optimal network architecture—specifically in the number of hidden layers, neurons, and training algorithms. However, the sensitivity analysis reveals a notable difference: while anthropogenic factors dominate in large-scale studies, natural hydrogeological factors are found to be the primary influences in localized, small-scale aquifer systems.
To promote sustainable groundwater management, this study applied ANNs to simulate groundwater behavior at high-rise construction sites, integrating the principle of balancing building weight with groundwater buoyancy to proactively minimize dewatering volumes. This approach directly addresses the practical challenge of excessive groundwater extraction commonly encountered during construction.
In this case study, limited and incomplete field measurements of groundwater and geological data posed challenges to fully exploiting the ANN’s predictive potential. By combining large synthetic datasets generated by MODFLOW with available field measurements for training and validation, the ANN achieved high prediction accuracy. This confirms its superior capability to model nonlinear and complex hydrogeological systems and suggests that with sufficient and comprehensive field data, highly accurate predictions of groundwater dynamics are achievable in the future.
Because ANNs do not require explicit formulations of intermediate physical processes or governing equations, accurate predictions can be obtained through iterative training and the adjustment of neuron weights and biases. Future studies could enhance the developed ANN by incorporating additional input variables (e.g., aquifer leakage, thickness, solar radiation, air temperature, and other hydrogeological parameters) and output variables (e.g., groundwater levels at multiple monitoring points) to better capture their interrelationships.
It is worth noting that the water-saving performance of the intelligent dewatering model was evaluated under the hydrogeological conditions of Taichung City; therefore, its applicability to other regions may vary. Modeling studies in areas with different geological and climatic characteristics are expected to yield distinct results.
Future intelligent dewatering management can focus on integrating regional geological variability, climatic conditions, real-time site monitoring, and the use of emerging technologies such as the Internet of Things (IoT) and digital twins. These advancements are expected to enhance adaptive decision-making and support the sustainable management of urban groundwater resources.
 Type A
Type A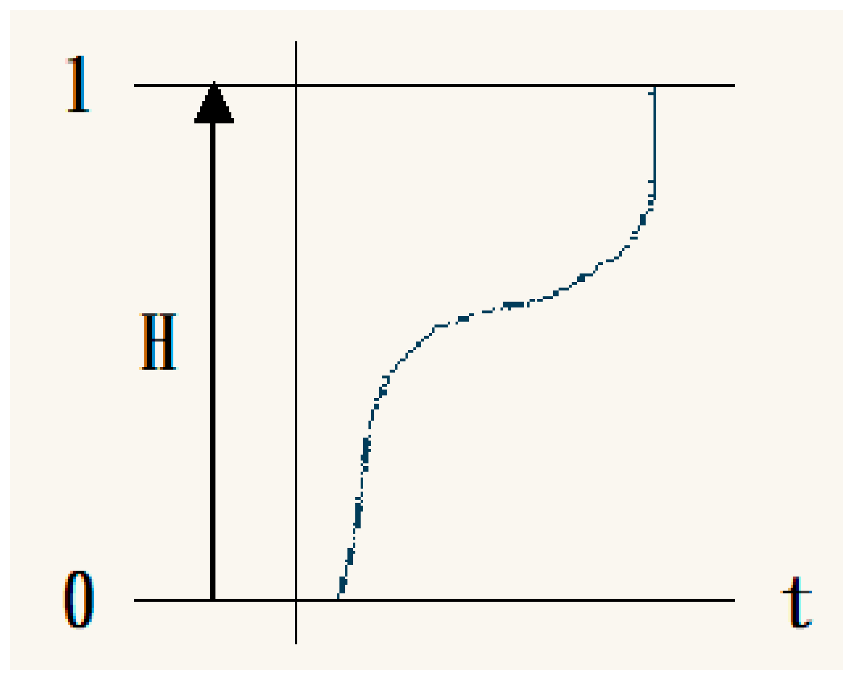 Type B
Type B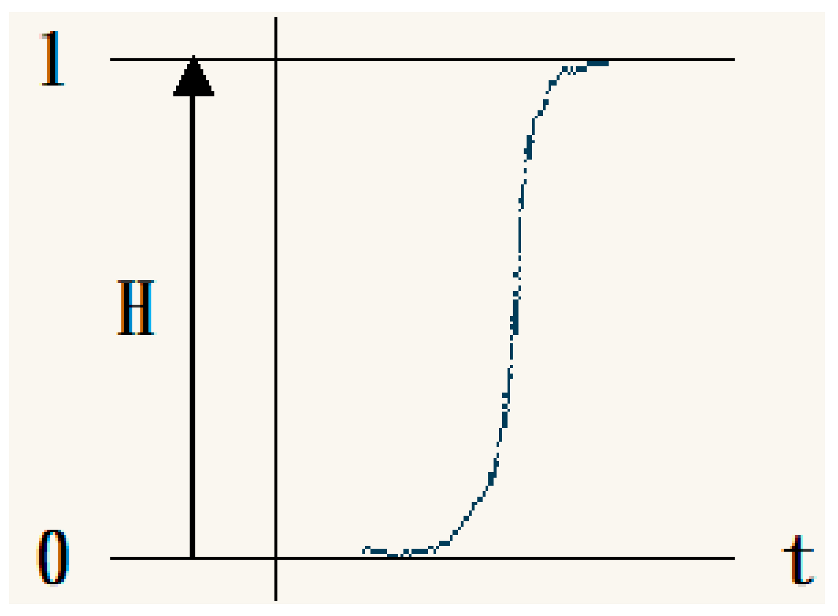 Type C
Type C 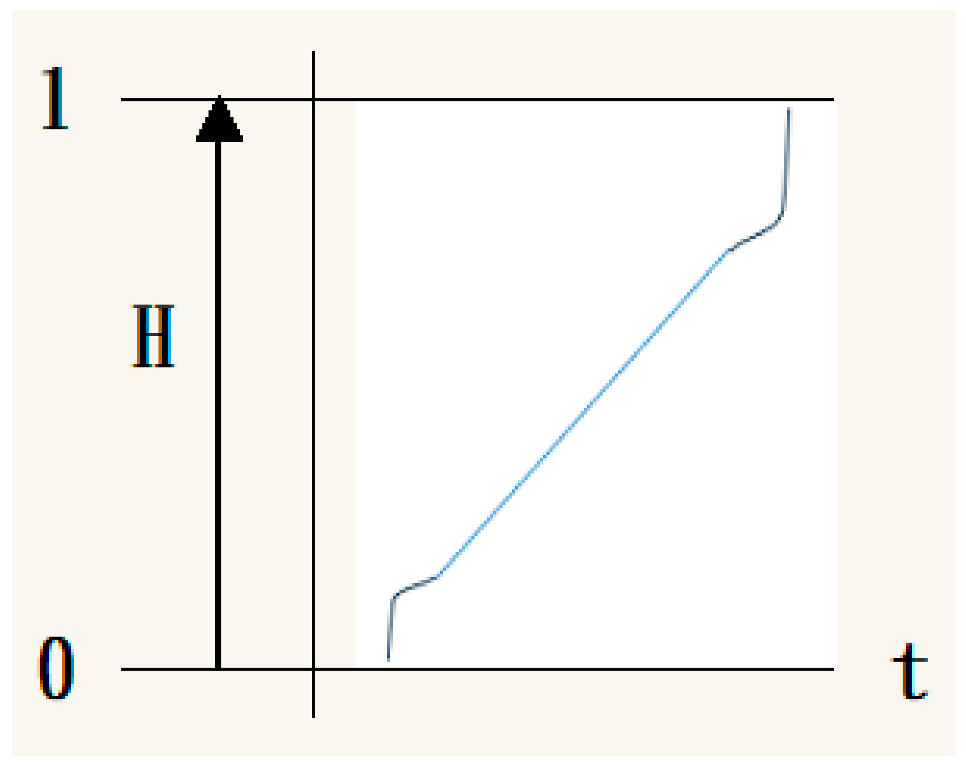 Type D
Type D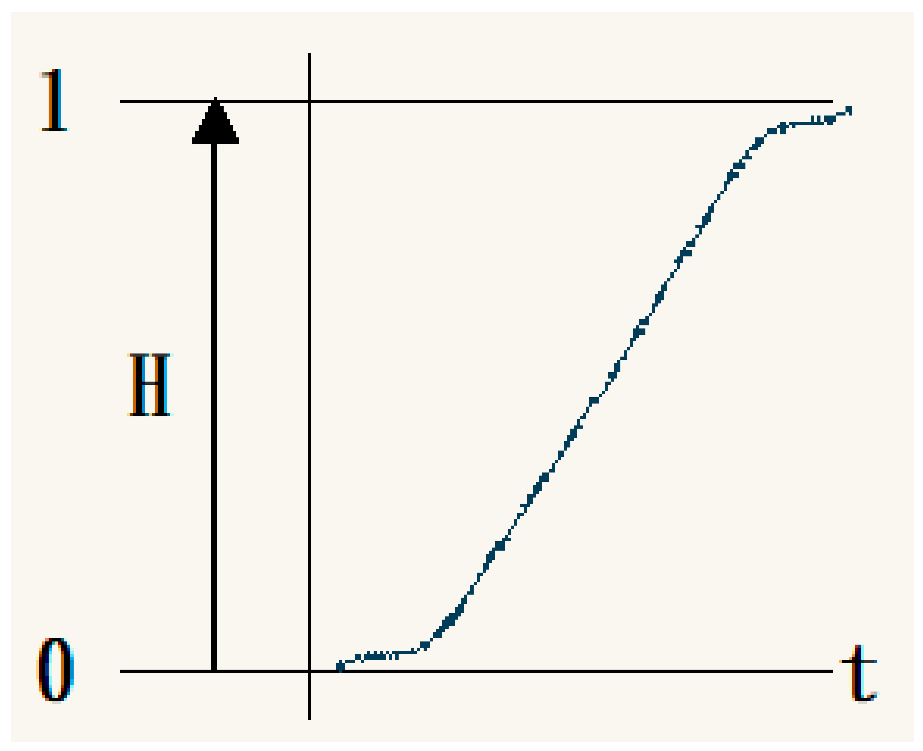 Type E
Type E