Numerical Analysis of 3D Slope Stability in a Rainfall-Induced Landslide: Insights from Different Hydrological Conditions and Soil Layering
Abstract
1. Introduction
2. Model Theory
2.1. Soil Water Flow
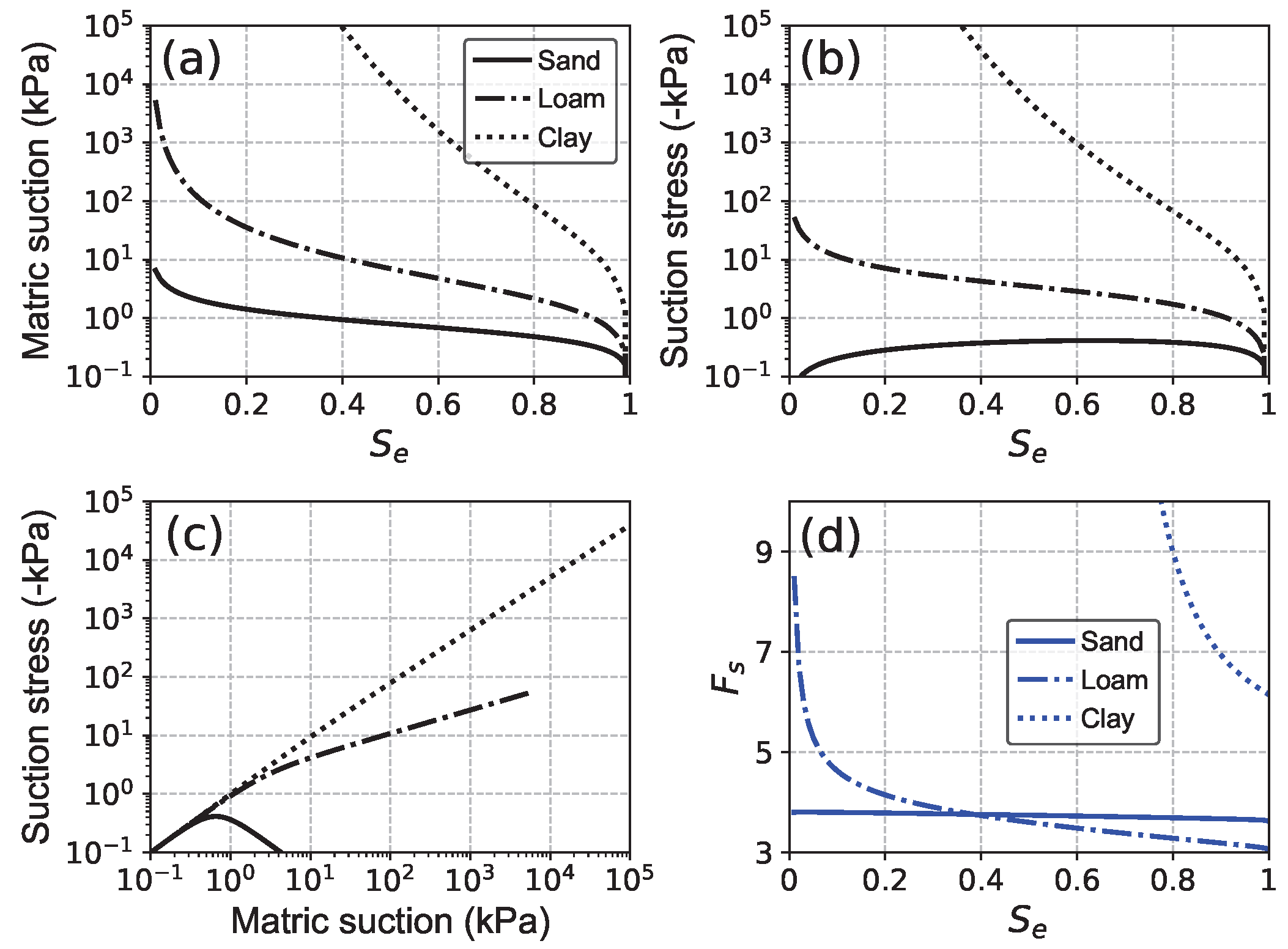
2.2. Soil Effective Stress
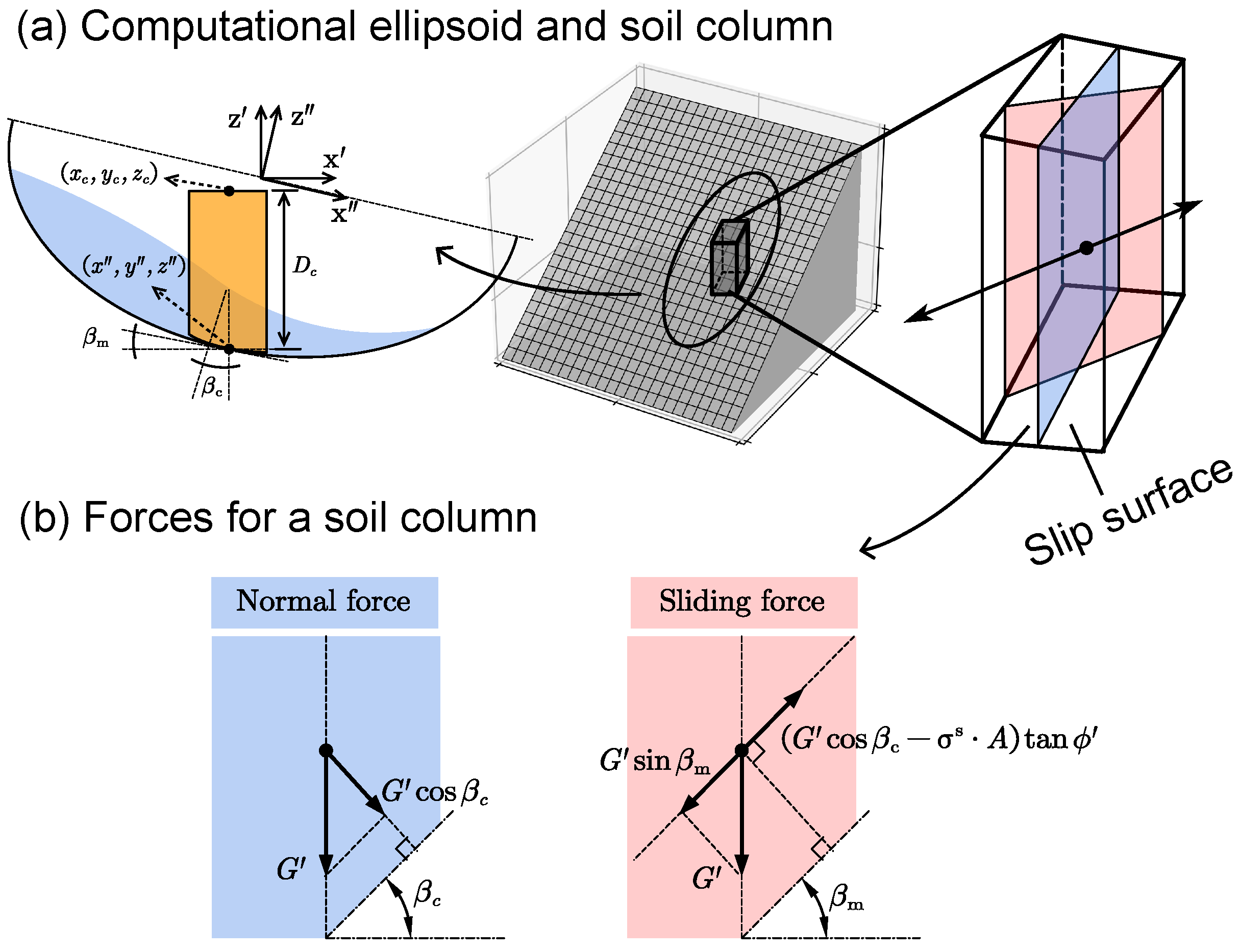
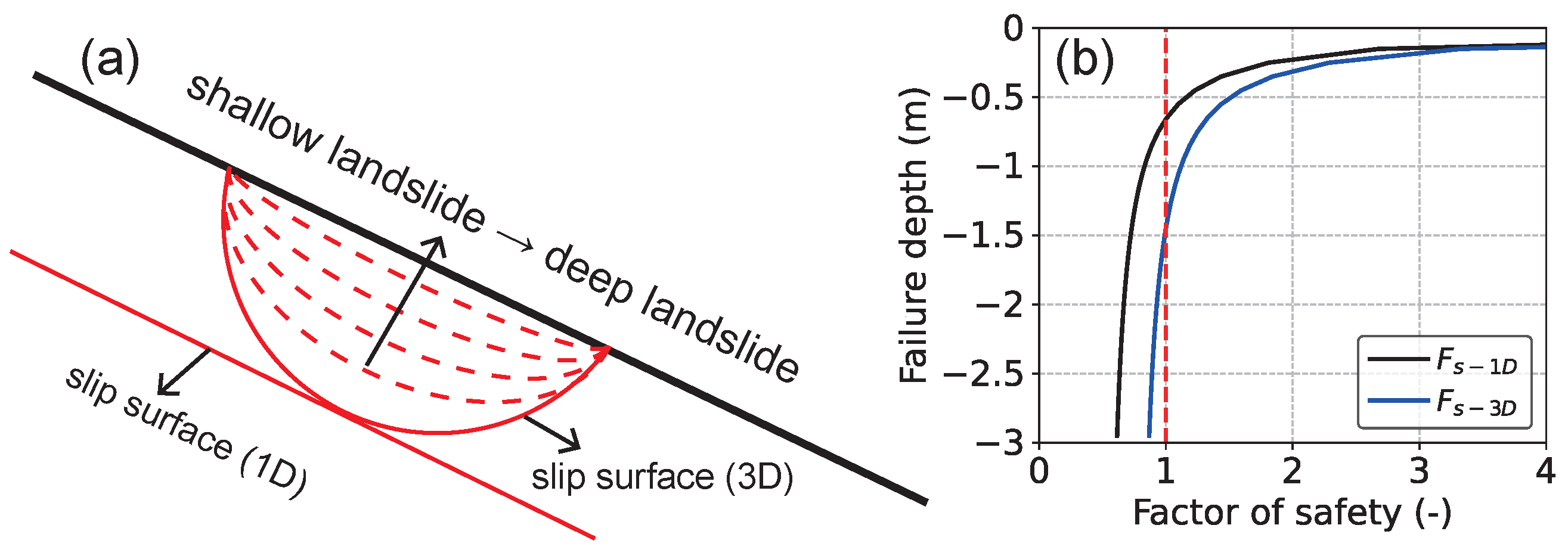
2.3. 3D Slope Stability
3. Validation and Analysis
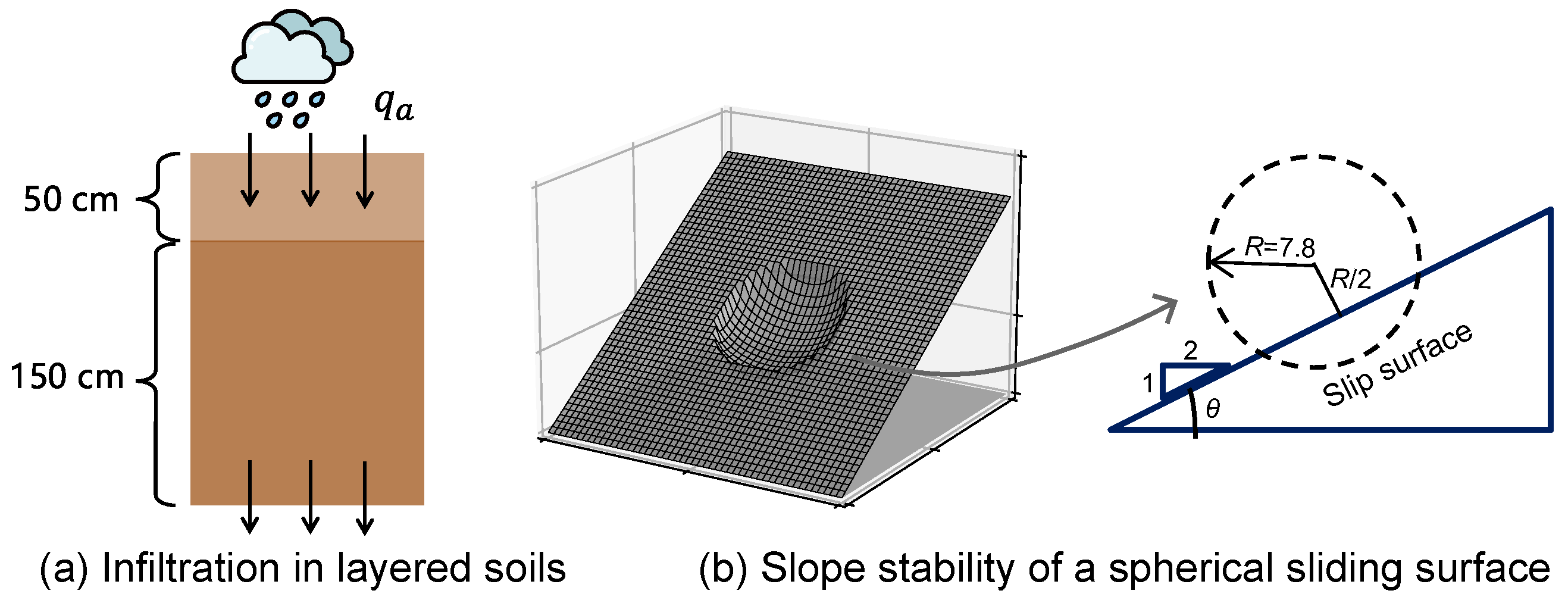
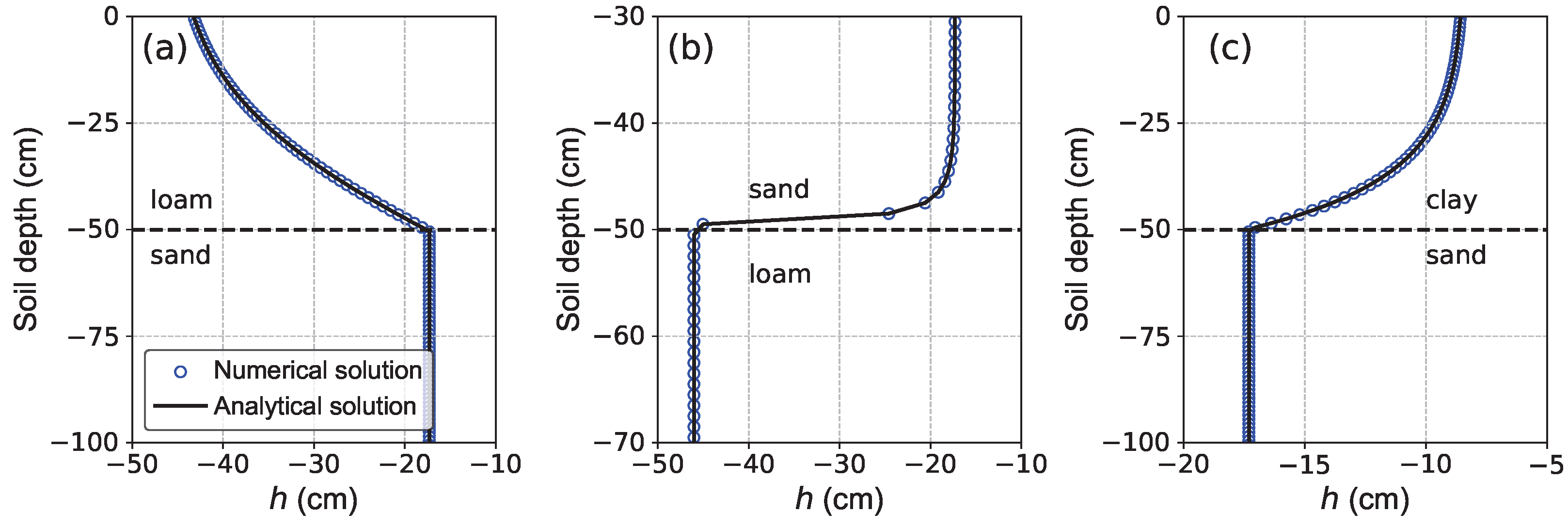
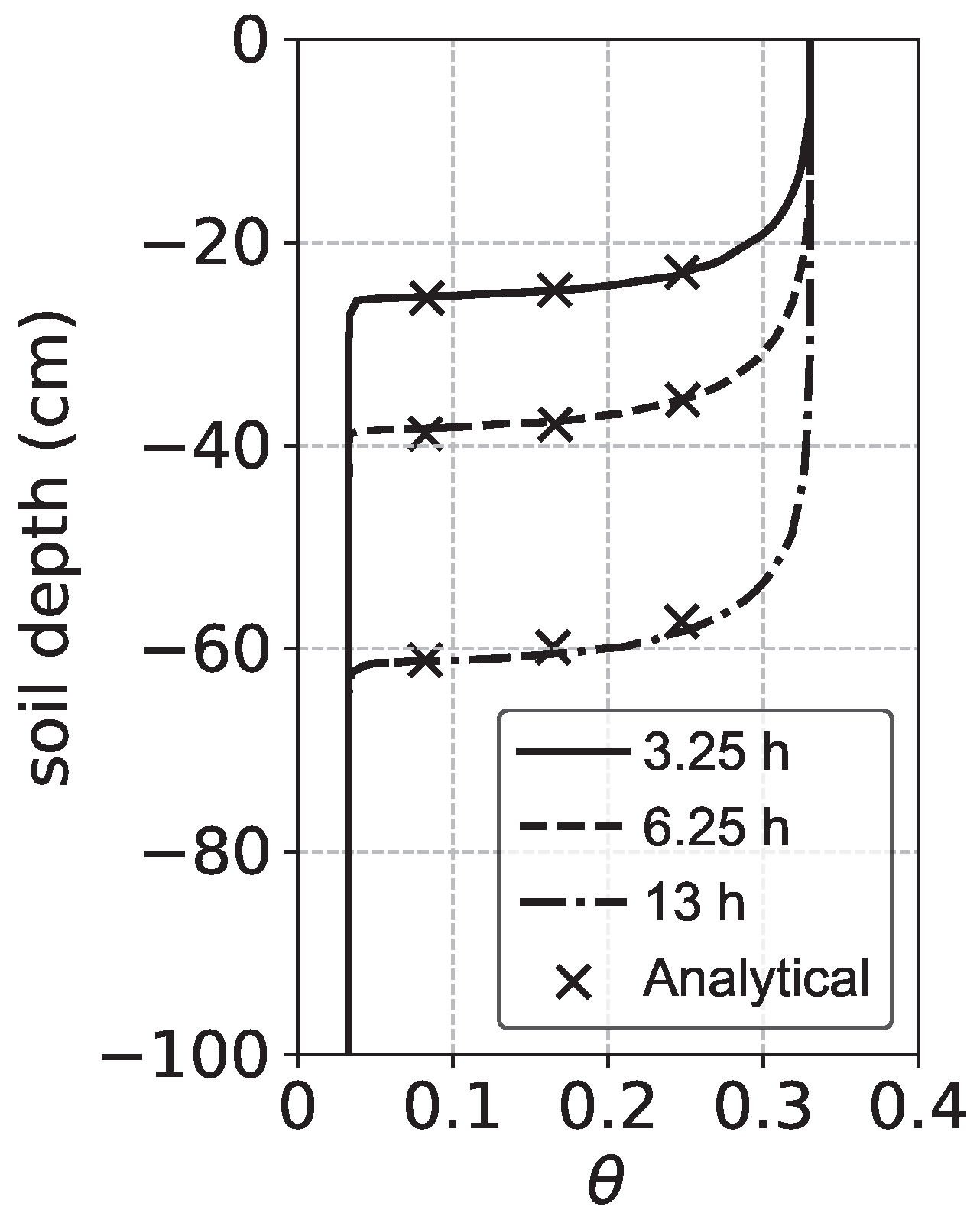
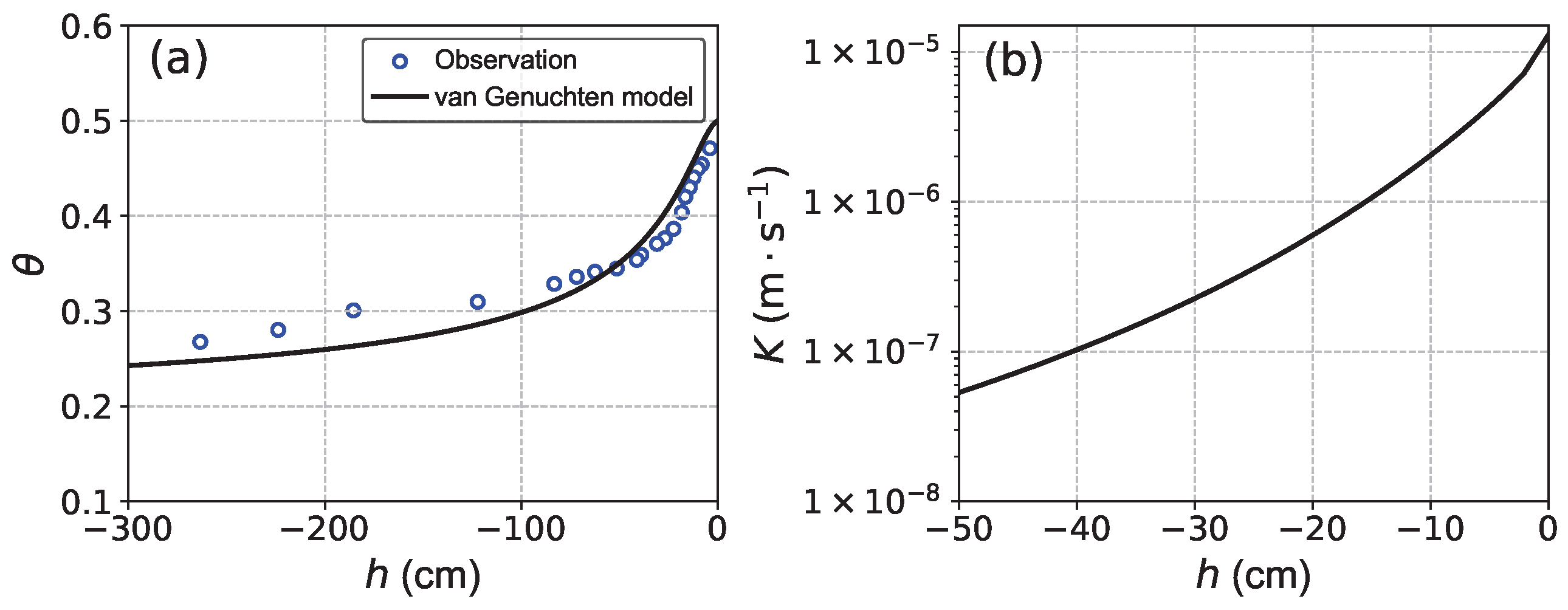
3.1. Validation of Variably Saturated Subsurface Flow
3.2. Validation of the Slope Stability
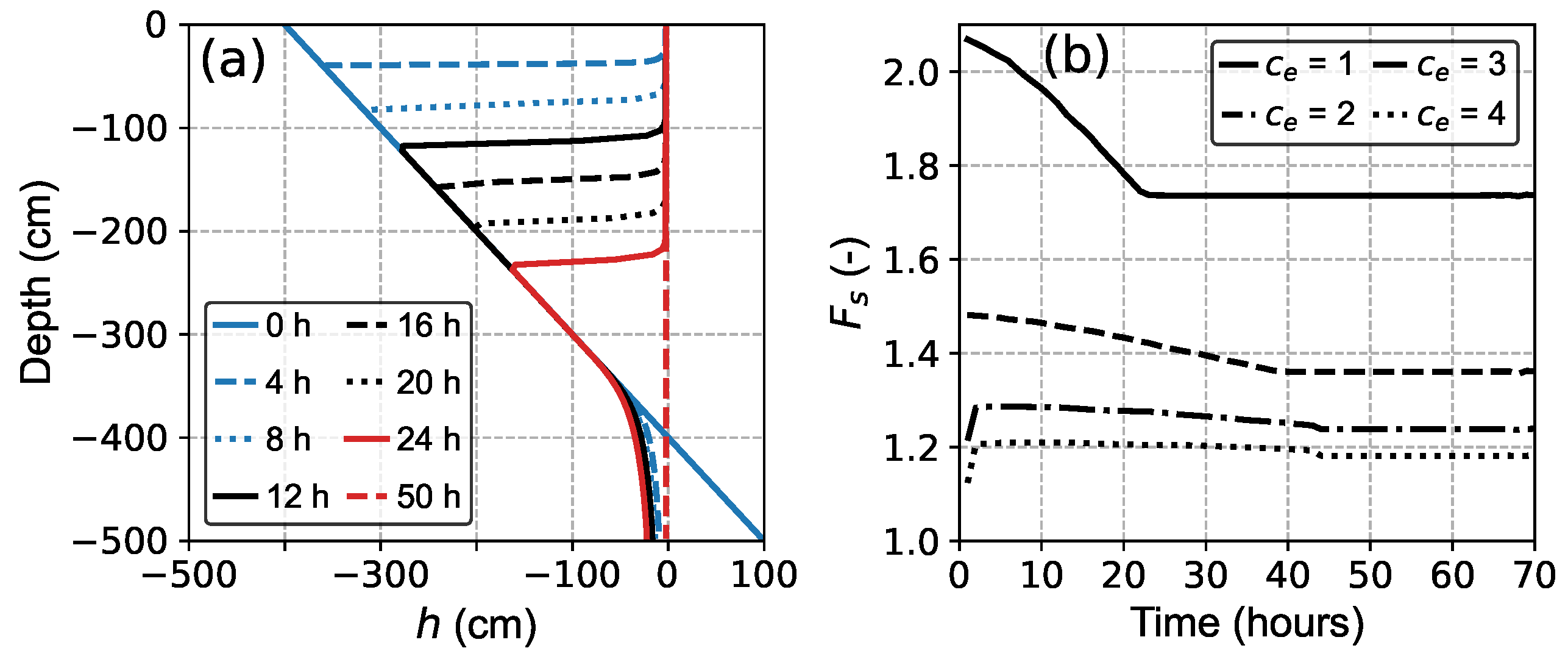
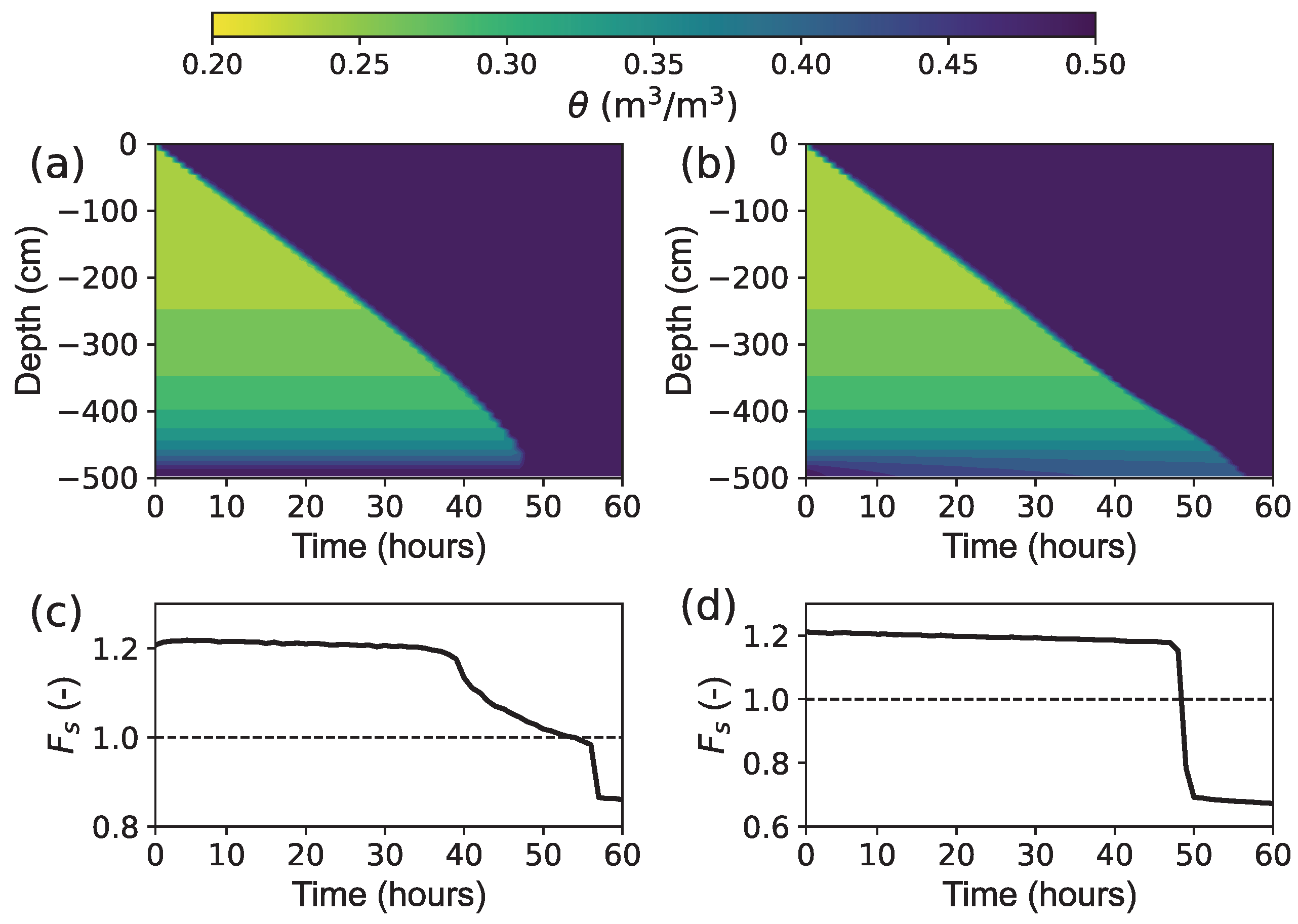
3.3. Coupled Response of Soil Water and
4. Numerical Experiments Setup
5. Results
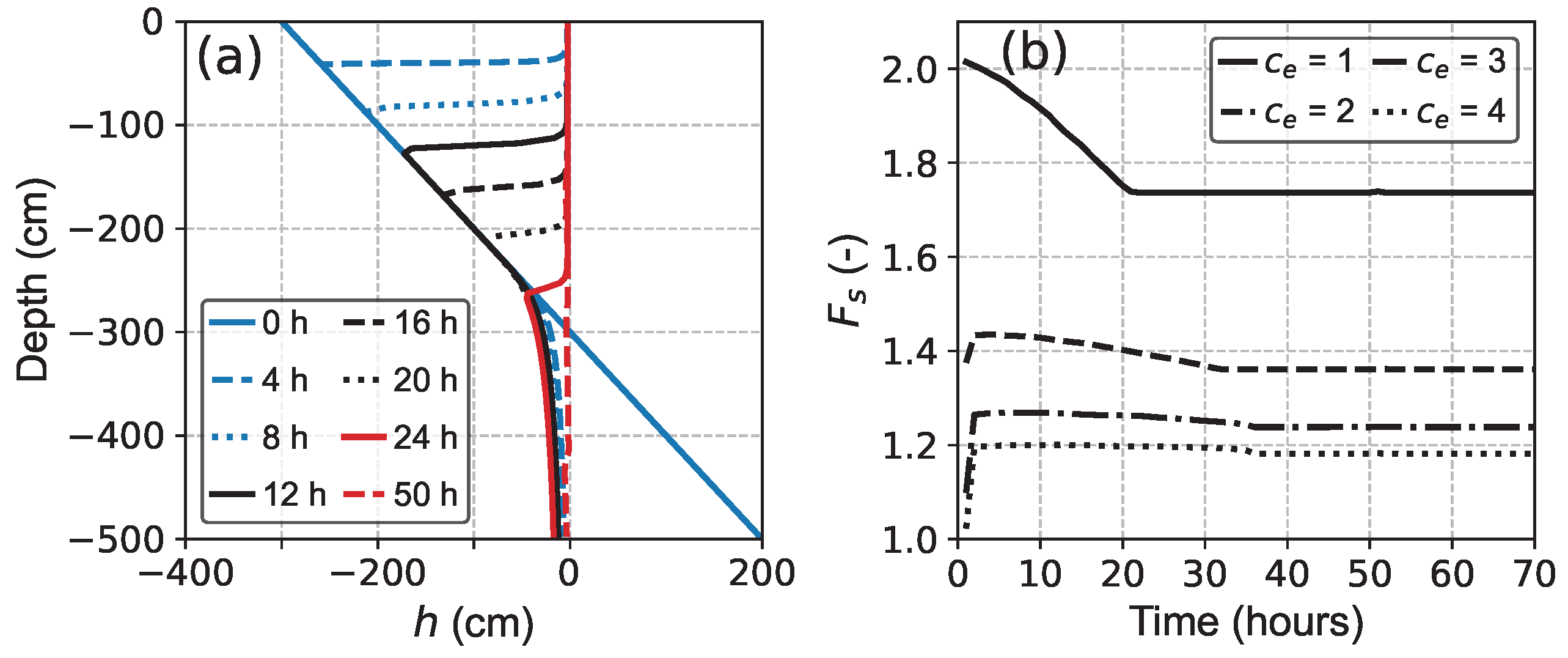
5.1. Effect of Rainfall Intensity on Slope Stability
5.2. Effect of Initial Conditions on Slope Stability
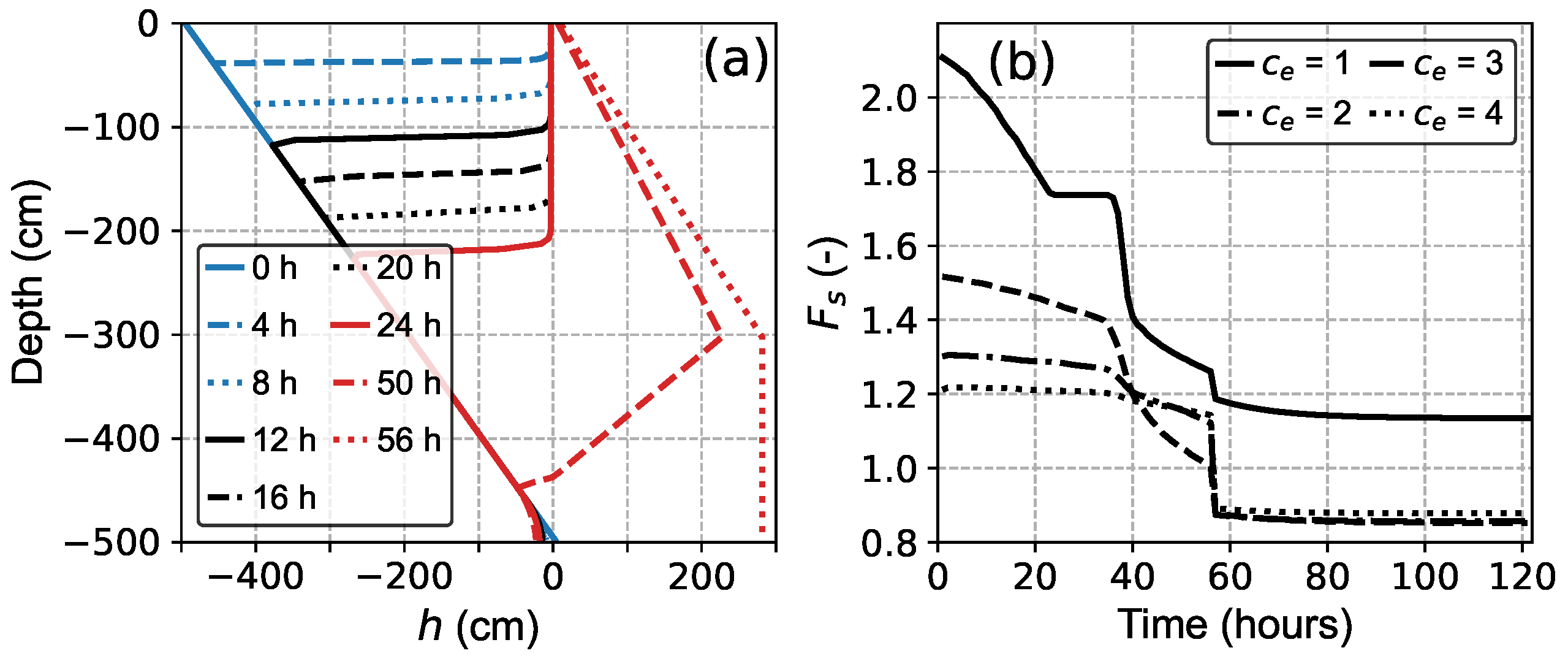
5.3. Effect of Soil Layers on Slope Stability
5.4. Effect of Boundary Conditions on Slope Stability
6. Discussion
6.1. Coupled Infiltration–Stability Model
6.2. Slope Stability Under Various Hydrological and Soil Layer Conditions
6.3. Limitations and Future Work
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alcántara-Ayala, I. Landslides in a changing world. Landslides 2025, 22, 2851–2865. [Google Scholar] [CrossRef]
- Zhang, K.; Xue, X.; Hong, Y.; Gourley, J.J.; Lu, N.; Wan, Z.; Hong, Z.; Wooten, R. iCRESTRIGRS: A coupled modeling system for cascading flood–landslide disaster forecasting. Hydrol. Earth Syst. Sci. 2016, 20, 5035–5048. [Google Scholar] [CrossRef]
- Marín-Rodríguez, N.J.; Vega, J.; Zanabria, O.B.; González-Ruiz, J.D.; Botero, S. Towards an understanding of landslide risk assessment and its economic losses: A scientometric analysis. Landslides 2024, 21, 1865–1881. [Google Scholar] [CrossRef]
- Sato, T.; Shuin, Y. Rainfall characteristics and magnitude control the volume of shallow and deep-seated landslides: Inferences from analyses using a simple runoff model. Geomorphology 2024, 466, 109453. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J.W. Hillslope Hydrology and Stability; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Bogaard, T.A.; Greco, R. Landslide hydrology: From hydrology to pore pressure. Wiley Interdiscip. Rev. Water 2016, 3, 439–459. [Google Scholar] [CrossRef]
- Greco, R.; Marino, P.; Bogaard, T.A. Recent advancements of landslide hydrology. Wiley Interdiscip. Rev. Water 2023, 10, e1675. [Google Scholar] [CrossRef]
- Rosso, R.; Rulli, M.C.; Vannucchi, G. A physically based model for the hydrologic control on shallow landsliding. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Godt, J.W.; Baum, R.L.; Lu, N. Landsliding in partially saturated materials. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Baum, R.L.; Godt, J.W.; Savage, W.Z. Estimating the timing and location of shallow rainfall-induced landslides using a model for transient, unsaturated infiltration. J. Geophys. Res. Earth Surf. 2010, 115. [Google Scholar] [CrossRef]
- Montrasio, L.; Valentino, R. A model for triggering mechanisms of shallow landslides. Nat. Hazards Earth Syst. Sci. 2008, 8, 1149–1159. [Google Scholar] [CrossRef]
- Lu, N.; Şener-Kaya, B.; Wayllace, A.; Godt, J.W. Analysis of rainfall-induced slope instability using a field of local factor of safety. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, K.; Wang, S.; Xia, Y.; Chao, L. iHydroSlide3D v1.0: An advanced hydrological–geotechnical model for hydrological simulation and three-dimensional landslide prediction. Geosci. Model Dev. 2023, 16, 2915–2937. [Google Scholar] [CrossRef]
- Liao, Z.; Hong, Y.; Wang, J.; Fukuoka, H.; Sassa, K.; Karnawati, D.; Fathani, F. Prototyping an experimental early warning system for rainfall-induced landslides in Indonesia using satellite remote sensing and geospatial datasets. Landslides 2010, 7, 317–324. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, K.; Wang, S.; Chao, L. A prototype adaptive mesh generator for enhancing computational efficiency and accuracy in physically-based modeling of flood-landslide hazards. Environ. Model. Softw. 2025, 189, 106458. [Google Scholar] [CrossRef]
- Celia, M.A.; Bouloutas, E.T.; Zarba, R.L. A general mass-conservative numerical solution for the unsaturated flow equation. Water Resour. Res. 1990, 26, 1483–1496. [Google Scholar] [CrossRef]
- Srivastava, R.; Yeh, T.C.J. Analytical solutions for one-dimensional, transient infiltration toward the water table in homogeneous and layered soils. Water Resour. Res. 1991, 27, 753–762. [Google Scholar] [CrossRef]
- Yu, H.; Salgado, R.; Sloan, S.; Kim, J. Limit analysis versus limit equilibrium for slope stability. J. Geotech. Geoenviron. Eng. 1998, 124, 1–11. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef]
- Simoni, S.; Zanotti, F.; Bertoldi, G.; Rigon, R. Modelling the probability of occurrence of shallow landslides and channelized debris flows using GEOtop-FS. Hydrol. Processes Int. J. 2008, 22, 532–545. [Google Scholar] [CrossRef]
- Reid, M.E.; Christian, S.B.; Brien, D.L.; Henderson, S.T. Scoops3D: Software to Analyze 3D Slope Stability Throughout a Digital Landscape; Technical Report; US Geological Survey: Reston, VA, USA, 2015.
- Mergili, M.; Marchesini, I.; Rossi, M.; Guzzetti, F.; Fellin, W. Spatially distributed three-dimensional slope stability modelling in a raster GIS. Geomorphology 2014, 206, 178–195. [Google Scholar] [CrossRef]
- Aristizábal, E.; Vélez, J.I.; Martínez, H.E.; Jaboyedoff, M. SHIA_Landslide: A distributed conceptual and physically based model to forecast the temporal and spatial occurrence of shallow landslides triggered by rainfall in tropical and mountainous basins. Landslides 2016, 13, 497–517. [Google Scholar] [CrossRef]
- Brinkgreve, R.; Kumarswamy, S.; Swolfs, W.; Waterman, D.; Chesaru, A.; Bonnier, P.G.; Haxaire, A. PLAXIS 2016; PLAXIS bv: Delft, The Netherlands, 2016; pp. 1–16. [Google Scholar]
- Zhan, T.L.; Jia, G.; Chen, Y.M.; Fredlund, D.; Li, H. An analytical solution for rainfall infiltration into an unsaturated infinite slope and its application to slope stability analysis. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 1737–1760. [Google Scholar] [CrossRef]
- Fan, L.; Lehmann, P.; Zheng, C.; Or, D. Rainfall intensity temporal patterns affect shallow landslide triggering and hazard evolution. Geophys. Res. Lett. 2020, 47, e2019GL085994. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Leung, A.K. Numerical investigation of rainfall intensity and duration control of rainfall-induced landslide at a specific slope using slope case histories and actual rainfall records. Bull. Eng. Geol. Environ. 2023, 82, 333. [Google Scholar] [CrossRef]
- Oguz, E.A.; Depina, I.; Thakur, V. Effects of soil heterogeneity on susceptibility of shallow landslides. Landslides 2022, 19, 67–83. [Google Scholar] [CrossRef]
- Schilirò, L.; Poueme Djueyep, G.; Esposito, C.; Scarascia Mugnozza, G. The role of initial soil conditions in shallow landslide triggering: Insights from physically based approaches. Geofluids 2019, 2019, 2453786. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Vereecken, H.; Weynants, M.; Javaux, M.; Pachepsky, Y.; Schaap, M.; Genuchten, M.T.v. Using pedotransfer functions to estimate the van Genuchten–Mualem soil hydraulic properties: A review. Vadose Zone J. 2010, 9, 795–820. [Google Scholar] [CrossRef]
- Schaap, M.G.; Van Genuchten, M.T. A modified Mualem–van Genuchten formulation for improved description of the hydraulic conductivity near saturation. Vadose Zone J. 2006, 5, 27–34. [Google Scholar] [CrossRef]
- Vogel, T.; Van Genuchten, M.T.; Cislerova, M. Effect of the shape of the soil hydraulic functions near saturation on variably-saturated flow predictions. Adv. Water Resour. 2000, 24, 133–144. [Google Scholar] [CrossRef]
- Ippisch, O.; Vogel, H.J.; Bastian, P. Validity limits for the van Genuchten–Mualem model and implications for parameter estimation and numerical simulation. Adv. Water Resour. 2006, 29, 1780–1789. [Google Scholar] [CrossRef]
- van Dam, J.C.; Groenendijk, P.; Hendriks, R.F.; Kroes, J.G. Advances of modeling water flow in variably saturated soils with SWAP. Vadose Zone J. 2008, 7, 640–653. [Google Scholar] [CrossRef]
- Lu, N.; Likos, W.J. Suction stress characteristic curve for unsaturated soil. J. Geotech. Geoenviron. Eng. 2006, 132, 131–142. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J.W.; Wu, D.T. A closed-form equation for effective stress in unsaturated soil. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Hovland, H.J. Three-dimensional slope stability analysis method. J. Geotech. Geoenviron. Eng. 1979, 105. [Google Scholar] [CrossRef]
- Xie, M.; Esaki, T.; Qiu, C.; Wang, C. Geographical Information System-Based Computational Implementation and Application of Spatial Three-Dimensional Slope Stability Analysis. Comput. Geotech. 2006, 33, 260–274. [Google Scholar] [CrossRef]
- Mergili, M.; Marchesini, I.; Alvioli, M.; Metz, M.; Schneider-Muntau, B.; Rossi, M.; Guzzetti, F. A Strategy for GIS-Based 3-D Slope Stability Modelling over Large Areas. Geosci. Model Dev. 2014, 7, 2969–2982. [Google Scholar] [CrossRef]
- Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. The HYDRUS Software Package for Simulating Two- and Three-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media; Technical Manual, Version 1.0; PC Progress: Prague, Czech Republic, 2006; 241p. [Google Scholar]
- Wieder, W.; Boehnert, J.; Bonan, G.; Langseth, M. Regridded Harmonized World Soil Database v1.2. ORNL DAAC. 2014. Available online: https://ui.adsabs.harvard.edu/abs/2014ornl.data.1247W/abstract (accessed on 1 November 2025).
- Vanderborght, J.; Kasteel, R.; Herbst, M.; Javaux, M.; Thiéry, D.; Vanclooster, M.; Mouvet, C.; Vereecken, H. A set of analytical benchmarks to test numerical models of flow and transport in soils. Vadose Zone J. 2005, 4, 206–221. [Google Scholar] [CrossRef]
- Warrick, A.; Lomen, D.; Yates, S. A generalized solution to infiltration. Soil Sci. Soc. Am. J. 1985, 49, 34–38. [Google Scholar] [CrossRef]
- Li, Z.; Özgen-Xian, I.; Maina, F.Z. A mass-conservative predictor-corrector solution to the 1D Richards equation with adaptive time control. J. Hydrol. 2021, 592, 125809. [Google Scholar] [CrossRef]
- Phoon, K.K.; Tan, T.S.; Chong, P.C. Numerical simulation of Richards equation in partially saturated porous media: Under-relaxation and mass balance. Geotech. Geol. Eng. 2007, 25, 525–541. [Google Scholar] [CrossRef]
- Hungr, O.; Salgado, F.M.; Byrne, P. Evaluation of a three-dimensional method of slope stability analysis. Can. Geotech. J. 1989, 26, 679–686. [Google Scholar] [CrossRef]
- Gens, A.; Hutchinson, J.; Cavounidis, S. Three-dimensional analysis of slides in cohesive soils. Geotechnique 1988, 38, 1–23. [Google Scholar] [CrossRef]
- Lam, L.; Fredlund, D. A general limit equilibrium model for three-dimensional slope stability analysis. Can. Geotech. J. 1993, 30, 905–919. [Google Scholar] [CrossRef]
- Tozato, K.; Dolojan, N.L.J.; Touge, Y.; Kure, S.; Moriguchi, S.; Kawagoe, S.; Kazama, S.; Terada, K. Limit equilibrium method-based 3D slope stability analysis for wide area considering influence of rainfall. Eng. Geol. 2022, 308, 106808. [Google Scholar] [CrossRef]
- An, H.; Viet, T.T.; Lee, G.; Kim, Y.; Kim, M.; Noh, S.; Noh, J. Development of time-variant landslide-prediction software considering three-dimensional subsurface unsaturated flow. Environ. Model. Softw. 2016, 85, 172–183. [Google Scholar] [CrossRef]
- Park, D.W.; Nikhil, N.V.; Lee, S.R. Landslide and Debris Flow Susceptibility Zonation Using TRIGRS for the 2011 Seoul Landslide Event. Nat. Hazards Earth Syst. Sci. 2013, 13, 2833–2849. [Google Scholar] [CrossRef]
- Tran, T.V.; Alvioli, M.; Lee, G.; An, H.U. Three-dimensional, time-dependent modeling of rainfall-induced landslides over a digital landscape: A case study. Landslides 2018, 15, 1071–1084. [Google Scholar] [CrossRef]
- He, J.; Qiu, H.; Qu, F.; Hu, S.; Yang, D.; Shen, Y.; Zhang, Y.; Sun, H.; Cao, M. Prediction of spatiotemporal stability and rainfall threshold of shallow landslides using the TRIGRS and Scoops3D models. Catena 2021, 197, 104999. [Google Scholar] [CrossRef]
- Rangarajan, S.; Rahardjo, H.; Satyanaga, A.; Li, Y. Influence of 3D subsurface flow on slope stability for unsaturated soils. Eng. Geol. 2024, 339, 107665. [Google Scholar] [CrossRef]
- He, X.; Hong, Y.; Vergara, H.; Zhang, K.; Kirstetter, P.E.; Gourley, J.J.; Zhang, Y.; Qiao, G.; Liu, C. Development of a coupled hydrological-geotechnical framework for rainfall-induced landslides prediction. J. Hydrol. 2016, 543, 395–405. [Google Scholar] [CrossRef]
- Cui, H.; Ji, J.; Hürlimann, M.; Medina, V. Probabilistic and physically-based modelling of rainfall-induced landslide susceptibility using integrated GIS-FORM algorithm. Landslides 2024, 21, 1461–1481. [Google Scholar] [CrossRef]
- Kim, J.; Mohanty, B.P. Influence of lateral subsurface flow and connectivity on soil water storage in land surface modeling. J. Geophys. Res. Atmos. 2016, 121, 704–721. [Google Scholar] [CrossRef]
- Pham, K.; Kim, D.; Choi, H.J.; Lee, I.M.; Choi, H. A numerical framework for infinite slope stability analysis under transient unsaturated seepage conditions. Eng. Geol. 2018, 243, 36–49. [Google Scholar] [CrossRef]
- Milledge, D.; Griffiths, D.; Lane, S.; Warburton, J. Limits on the validity of infinite length assumptions for modelling shallow landslides. Earth Surf. Process. Landf. 2012, 37, 1158–1166. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Sun, G. Phreatic surface calculation and stability analysis of three-dimensional slopes under rainfall infiltration. Bull. Eng. Geol. Environ. 2024, 83, 51. [Google Scholar] [CrossRef]
- Wasowski, J.; Lamanna, C.; Gigante, G.; Casarano, D. High resolution satellite imagery analysis for inferring surface–subsurface water relationships in unstable slopes. Remote Sens. Environ. 2012, 124, 135–148. [Google Scholar] [CrossRef]
- Ye, X.; Zhu, H.H.; Wang, J.; Zhang, Q.; Shi, B.; Schenato, L.; Pasuto, A. Subsurface multi-physical monitoring of a reservoir landslide with the fiber-optic nerve system. Geophys. Res. Lett. 2022, 49, e2022GL098211. [Google Scholar] [CrossRef]
- Xia, M.; Ren, G.M.; Zhu, S.S.; Ma, X.L. Relationship between landslide stability and reservoir water level variation. Bull. Eng. Geol. Environ. 2015, 74, 909–917. [Google Scholar] [CrossRef]
- Kafle, L.; Xu, W.J.; Zeng, S.Y.; Nagel, T. A numerical investigation of slope stability influenced by the combined effects of reservoir water level fluctuations and precipitation: A case study of the Bianjiazhai landslide in China. Eng. Geol. 2022, 297, 106508. [Google Scholar] [CrossRef]
- Wicki, A.; Lehmann, P.; Hauck, C.; Seneviratne, S.I.; Waldner, P.; Stähli, M. Assessing the potential of soil moisture measurements for regional landslide early warning. Landslides 2020, 17, 1881–1896. [Google Scholar] [CrossRef]
- Marino, P.; Peres, D.J.; Cancelliere, A.; Greco, R.; Bogaard, T.A. Soil moisture information can improve shallow landslide forecasting using the hydrometeorological threshold approach. Landslides 2020, 17, 2041–2054. [Google Scholar] [CrossRef]
- Abraham, M.T.; Satyam, N.; Rosi, A.; Pradhan, B.; Segoni, S. Usage of antecedent soil moisture for improving the performance of rainfall thresholds for landslide early warning. CATENA 2021, 200, 105147. [Google Scholar] [CrossRef]
- Rahardjo, H.; Hritzuk, K.; Leong, E.; Rezaur, R. Effectiveness of horizontal drains for slope stability. Eng. Geol. 2003, 69, 295–308. [Google Scholar] [CrossRef]
- Sun, H.y.; Ge, Q.; Yu, Y.; Shuai, F.x.; Lü, C.c. A new self-starting drainage method for slope stabilization and its application. Bull. Eng. Geol. Environ. 2021, 80, 251–265. [Google Scholar] [CrossRef]
- Alvioli, M.; Baum, R.L. Parallelization of the TRIGRS model for rainfall-induced landslides using the message passing interface. Environ. Model. Softw. 2016, 81, 122–135. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, K.; Wang, S.; Jia, T. PHyL v1.0: A parallel, flexible, and advanced software for hydrological and slope stability modeling at a regional scale. Environ. Model. Softw. 2024, 172, 105882. [Google Scholar] [CrossRef]
- Luo, Y.; Hou, X.; Zhang, J.; Wang, Y.; Hu, M.; Jiang, G.; Tang, C.S. Exploring the effects of weather-driven dynamics of desiccation cracks on hydrological process of expansive clay slope: Insights from physical model test. J. Hydrol. 2025, 656, 133011. [Google Scholar] [CrossRef]
- Zhang, B.; Tian, L.; He, C.; He, X. Response of erosive precipitation to vegetation restoration and its effect on soil and water conservation over China’s Loess Plateau. Water Resour. Res. 2023, 59, e2022WR033382. [Google Scholar] [CrossRef]


| Soil | () | n | () | (kPa) | () | ||||
|---|---|---|---|---|---|---|---|---|---|
| Sand | 0.045 | 0.43 | 0.15 | 3.0 | 1000 | 5 | 40 | 0.43 | 21 |
| Loam | 0.080 | 0.43 | 0.04 | 1.6 | 50 | 10 | 22.5 | 0.43 | 13 |
| Clay | 0.100 | 0.40 | 0.01 | 1.1 | 10 | 40 | 19.5 | 0.47 | 19.5 |
| Reference | |
|---|---|
| Hungr et al. [49] | 1.422 |
| Gens et al. [50] | 1.41 |
| Lam and Fredlund [51] | 1.386∼1.472 |
| Xie et al. [41] | 1.443 |
| Mergili et al. [42] | 1.38 |
| Tozato et al. [52] | 1.392 |
| Reid et al. [21] (Scoops3D) | 1.400 |
| This work | 1.408 |
| () | n | () | (kPa) | (°) | () | |||
|---|---|---|---|---|---|---|---|---|
| 0.18 | 0.50 | 0.05 | 1.6 | 112.32 | 0.5 | 10.17 | 29.63 | 18.38 |
| Case | Vertical Depth (cm) | Soil Type | Initial Condition | Bottom Boundary | Rainfall |
|---|---|---|---|---|---|
| 1 | 500 | S1 | cm | Free drainage | 0.5 |
| 2 | 500 | S1 | cm | Free drainage | 1.0 |
| 3 | 500 | S1 | cm | Free drainage | 1.5 |
| 4 | 500 | S1 | cm | Free drainage | 0.5 |
| 5 | 500 | S1 | cm | Free drainage | 0.5 |
| 6 | 300 + 200 | S1 + S2 | cm | Free drainage | 0.5 |
| 7 | 500 | S1 | cm | Zero flux | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Wu, X.; Hu, L.; Chi, Y.; Jia, T.; Luo, Y. Numerical Analysis of 3D Slope Stability in a Rainfall-Induced Landslide: Insights from Different Hydrological Conditions and Soil Layering. Water 2025, 17, 3316. https://doi.org/10.3390/w17223316
Chen G, Wu X, Hu L, Chi Y, Jia T, Luo Y. Numerical Analysis of 3D Slope Stability in a Rainfall-Induced Landslide: Insights from Different Hydrological Conditions and Soil Layering. Water. 2025; 17(22):3316. https://doi.org/10.3390/w17223316
Chicago/Turabian StyleChen, Guoding, Xiuguang Wu, Linlin Hu, Yunfei Chi, Tianlong Jia, and Yi Luo. 2025. "Numerical Analysis of 3D Slope Stability in a Rainfall-Induced Landslide: Insights from Different Hydrological Conditions and Soil Layering" Water 17, no. 22: 3316. https://doi.org/10.3390/w17223316
APA StyleChen, G., Wu, X., Hu, L., Chi, Y., Jia, T., & Luo, Y. (2025). Numerical Analysis of 3D Slope Stability in a Rainfall-Induced Landslide: Insights from Different Hydrological Conditions and Soil Layering. Water, 17(22), 3316. https://doi.org/10.3390/w17223316







