Modeling Solar Radiation Data for Reference Evapotranspiration Estimation at a Daily Time Step for Poland

Abstract

The Penman–Monteith formula (P-M) is a well-established indirect method for estimating reference evapotranspiration (ET₀). The key input for this equation is global solar radiation (H). When real data are unavailable, other weather parameters are used to estimate H. In this study, sixteen years’ worth daily registers of H, sunshine duration (S), and air temperature (t) from 10 sites across Poland were used to determine coefficients for the Angström–Prescott (A-P) and Hargreaves–Sammani (H-S) equations. The H values obtained with locally calibrated, general Polish and global A-P and H-S equations were applied to the P-M formula. The ET₀ results thus obtained were compared to those derived with the P-M method and measured solar radiation data. The method of determination of the radiation component had a significant but sometimes unexpected impact on the ET₀ values. The better predictive power of the solar radiation model usually resulted in better accuracy of the evapotranspiration estimation; however, there were exceptions to this rule.

1. Introduction

The climate change-induced extreme phenomena of heat waves and droughts make the question of how much water we lose from the soil through evapotranspiration relevant. Due to the costly and complex procedure, actual evapotranspiration (ETa) measurements are not standard. In hydrological practice, ETa is often assessed using reference evapotranspiration (ET₀) calculated with the Penman–Monteith (P-M) equation [1].

According to Howell and Evet [2], the P-M equation was proposed and developed by John Monteith in his seminal paper [3], in which he illustrated its thermodynamic basis with a psychometric chart (a graph of vapor pressure at various relative saturations versus air temperature at a known air pressure). Monteith’s derivation was built upon that of Howard Penman [4] in the now well-known combination equation (so named based on its “combination” of an energy balance and an aerodynamic formula).

The equation was adopted by [5] to determine reference evapotranspiration and became widespread in agricultural and hydrological practice as the FAO-56 method.

The main driving force for water vapor and heat flux exchange between the ground and the atmosphere is energy reaching the Earth’s surface; thus, solar radiation (H) is a weather parameter determining the evapotranspiration process. Due to the sparse actinometric network (only 27 actinometric versus over 2000 meteorological and hydrological stations in Poland), real solar radiation data are commonly replaced with simulated ones.

To estimate solar radiation, its relationship with other widely available meteorological parameters is used [6], i.e., sunshine duration (S) [7,8,9], air temperature (t) [10,11,12], cloudiness (C) [13,14], relative air humidity (RH) [15], or precipitation (p) [16]. The accuracy of radiation models can be increased by transforming the basic formulas or using more complex equations based on several variables [17]. However, the simplest method of improving their accuracy is local calibration. Numerous research papers compare solar radiation models’ accuracy [18,19,20], but studies on their performance with the P-M formula are rare, and it is not evident how the modeling of solar radiation influences the ET₀ estimates under different time scales and climate conditions.

It is important to explore solar and net radiation models, since the guidelines provided by the FAO are not suitable for all climatic conditions [21].

In this context, this study aimed to calibrate and evaluate the accuracy of solar radiation (H) models based on two types of standard meteorological variables, i.e., sunshine duration and air temperature across Poland, and assess how they affect ET₀ estimation results.

2. Materials and Methods

2.1. Study Region and Data Collection

The study area (Poland, Central Europe) lies between a warm summer, humid, continental (Dfb) and temperate, no dry season, warm summer (Cfb) climate zone according to the Köppen classification [22]. For this type of climate, the characteristic seasonal variability of meteorological elements is observed yearly, with four seasons and a growing season lasting from April to September. Additionally, seasonal and vegetation period duration and their meteorological characteristics are regionally varied. The Polish climate depends on atmospheric circulation [23] and is influenced by oceanic air masses from the west and continental ones from the east. Some authors, however, underline a strong correlation between air temperature and sunshine duration and the influence of radiation components on Polish climate. In the summer, it is even considered to be dominant [24].

Sites across Poland with at least 16 years of solar radiation records were selected for this study. The exception was Kołobrzeg, where 14 years of string data were available.

Table 1. The details of the stations and data records used in this study.

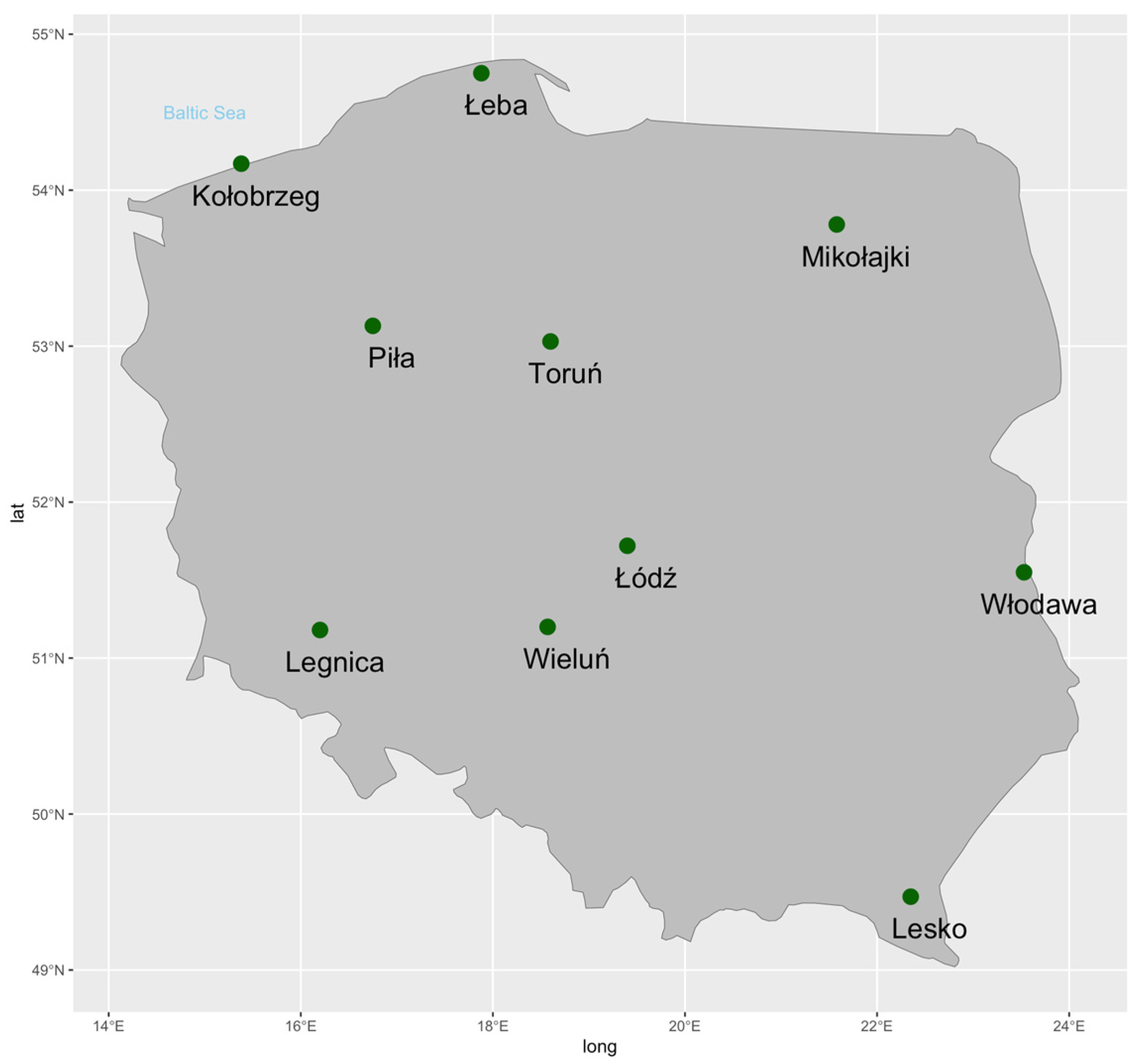
No.	Site Name	Latitude	Longitude	Altitude [m.a.s.l.]	tmax [°C]	tmin [°C]	Sunshine Hours	Years of Record
1.	Kołobrzeg	54°10′57″ N	15°34′47″ E	3	12.3	5.7	1727	2000–2013
2.	Legnica	51°11′33″ N	16°12′28″ E	122	14.4	5.2	1774	2000–2015
3.	Lesko	49°27′59″ N	22°20′30″ E	420	12.9	4.2	1738	2000–2015
4.	Łeba	54°45′13″ N	17°32′05″ E	2	11.9	5.2	1901	2000–2015
5.	Łódź	51°43′06″ N	19°23′14″ E	175	13.3	4.7	1782	2000–2015
6.	Mikołajki	53°47′21″ N	21°35′23″ E	127	12.0	4.6	1799	2000–2015
7.	Piła	53°07′50″ N	16°44′50″ E	72	13.3	4.4	1790	2000–2015
8.	Toruń	53°02′31″ N	18°35′44″ E	69	13.5	4.5	1742	2000–2015
9.	Wieluń	51°12′37″ N	18°33′24″ E	199	13.6	5.2	1777	2000–2015
10.	Włodawa	51°33′12″ N	23°31′46″ E	177	13.0	4.2	1840	2000–2015

contains the details of the stations used in this study. The spatial distribution of the sites is presented in Figure 1.

The mean yearly air temperature in the period 2000–2015 for the study area varied from 8.1 °C in the northeast (Mikołajki) to 9.7 °C in the southwest (Legnica). The mean daily air temperature amplitudes for the study period in the north, at the seaside, were significantly lower (6.6 °C) than those inland (9.2 °C). In the same period, sunshine duration varied from 1727 h in Kołobrzeg to 1901 h in Łeba.

This study uses data from 2 coastal stations, Łeba and Kołobrzeg (north), and 8 inland stations, Mikołajki (northeast, great lakes region), Piła, Toruń, Wieluń (central Poland), Legnica (southwest) and Włodawa (eastern edge of the country with the most continental climate characteristics). All stations chosen for this study are operated by the Institute of Meteorology and Water Management—Polish Research Institute, and source data are available at https://danepubliczne.imgw.pl/data/dane_pomiarowo_obserwacyjne/ (accessed on 30 July 2025).

The dataset was checked for quality by looking for significant errors and incidental values. In any case, the gaps in the data records (each station and each parameter) did not exceed 3.1% of the total. For each site, the daily minimum (t_dmin) and maximum (t_dmax) air temperature was determined for 24 h (from 00 to 24 UTC), as recommended by Mahmood and Hubbard [25]. Daily sums of solar radiation (H) were calculated as a sum of hourly data from sunrise to sunset.

Data for each site were divided at random into two sets. The first one, 11 years long, was used to determine regression coefficients, and the second one, 5 years long, was used to validate the models at the same site. The validation set contained data from the years 2002, 2010, 2011, 2013, and 2015. The thermal conditions of these years varied. 2002 was classified as mildly warm, while 2011 and 2013 were classified as normal. The year 2015 was very warm and 2010 extremely cold according to (CLIMATE MONITORING BULLETIN OF POLAND YEAR 2024 IMGW [26] and Miętus et al., 2002 [27] classification of thermal conditions). Regarding the precipitation characteristics, it was based on the twelve-month Relative Precipitation Index (RPI12) and Kaczorowska’s classification (1962) [28]. 2002 varied significantly depending on the station, with the RPI12 from 82.1% (dry year, Mikołajki station) to 129.9% (very wet year, Piła station). 2010 was a very wet year (RPI12 between 126.1% and 139.5% in Lesko, Legnica, Wieluń, Łódź, Piła, Łeba). In Toruń, 2010 was classified as extremely wet with RPI12 exceeding 151%. The year 2011 was dry (RPI12 = 76–87%) or normal (RPI12 = 92.9–116.3%), while 2015 was dry or very dry (RPI12 = 74.5–83.9%).

Daily total extraterrestrial solar radiation (H₀) and daily maximum sunshine duration (S₀) were calculated with R software (R 4.2.2) [29] and solaR package [30] using Michalsky’s method [31]. The regression coefficients for each site were determined using the least squares method. The coefficients generalized for Poland were obtained by averaging the local values, while the global ones were taken from the literature [5]. The accuracy of the regression models was assessed through the determination coefficient (R²), Root Mean Square Error (RMSE) and Mean Bias Error (MBE). Mean Bias Error was calculated as the mean difference between the modeled and observed daily values. RMSE and MBE are also presented as percentages of the daily mean values of the analyzed meteorological elements (RMSPE-Root Mean Square Percentage Error and MPE-Mean Percentage Error, respectively).

The H values obtained with site calibrated, general Polish and global coefficients for both A-P and H-S radiation models were applied to the P-M formula for daily ET₀ estimation. The results were compared against reference evapotranspiration calculated with P-M formula and real solar radiation data.

ET₀ calculations were made for the warm half of the year (from the 1 April to 30 September).

2.2. Equations

2.2.1. Estimation of Global Solar Radiation with Sunshine Duration-Based Model

Angström [7] developed a model of solar radiation based on the relationship of solar radiation (H) on clear sky days with relative sunshine duration (S/S₀). Since Prescott [8] modified the formula by replacing the radiation on days with a clear sky with extraterrestrial radiation (H₀), it is known as the Angström–Prescott equation,

$$\mathrm{H}={\mathrm{H}}_0·\left(\mathrm{a}+\mathrm{b}{\displaystyle \frac{\mathrm{S}}{{\mathrm{S}}_0}}\right)$$

(1)

Here, the following pertains:

a, b are regression coefficients;

H is the daily sum of solar radiation [MJ·m⁻²];

H₀ is the daily sum of extraterrestrial solar radiation [MJ·m⁻²];

S is the daily sum of sunshine duration [h];

S₀ is the daily maximum sunshine duration [h].

Empirical coefficient a has the physical meaning of the fraction of diffuse radiation to extraterrestrial radiation, and b has the meaning of the fraction of direct radiation to H₀ [32]. In Poland, the Angström–Prescott model is also recognized as Black’s model [33] with coefficients calibrated by Podogrocki [34,35].

2.2.2. Estimation of Global Solar Radiation with a Temperature-Based Model

Hargreaves and Sammani [10] used daily temperature extremes to estimate solar radiation as

$$\mathrm{H}=\mathrm{A}{\mathrm{H}}_0\sqrt{{\mathrm{t}}_{\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{t}}_{\mathrm{d}\mathrm{m}\mathrm{i}\mathrm{n}}}$$

(2)

where

A is an empirical coefficient;

H is the daily sum of solar radiation [MJ·m⁻²];

H₀ is the daily sum of extraterrestrial solar radiation [MJ·m⁻²];

t_dmax is the maximum daily air temperature [°C];

t_dmin is the minimum daily air temperature [°C].

2.2.3. Estimation of Reference Evapotranspiration

The radiation values obtained with both solar radiation models using coefficients calibrated at the local and general Polish levels were applied to the Penman–Monteith formula to calculate the reference evapotranspiration (ET₀) using FAO-56 procedure [5].

The FAO-56 method for reference evapotranspiration (ET₀) estimation is

$${\mathrm{E}\mathrm{T}}_0={\displaystyle \frac{0.408·\mathsf{\Delta }·\left({\mathrm{R}}_{\mathrm{n}}-\mathrm{G}\right)+\mathsf{\gamma }·\left(\frac{900}{\mathrm{t} + 273}\right)·{\mathrm{u}}_2·\left({\mathrm{e}}_{\mathrm{s}}-{\mathrm{e}}_{\mathrm{a}}\right)}{\mathsf{\Delta }+\mathsf{\gamma }·\left(1+0.34·{\mathrm{u}}_2\right)}}$$

(3)

where

ET₀ is the daily sum of reference evapotranspiration [mm·day⁻¹];

R_n is the daily sum of net radiation at the crop surface [MJ·day⁻¹];

G is the daily sum of soil heat flux density [MJ·day⁻¹], calculated as 0.1·R_n;

t is the mean daily air temperature at 2 m height [°C];

u₂ is the mean daily wind speed at 2 m height [m·s·⁻¹];

e_s is the mean daily saturation vapor pressure [kPa];

e_a is the mean daily actual vapor pressure [kPa];

Δ is the slope of the vapor pressure–temperature curve [kPa·°C⁻¹];

$\mathsf{\gamma }$ is the psychrometric constant [$\mathsf{\gamma }$ = 0.0666 kPa·°C⁻¹].

The slope of the saturation vapor pressure–temperature curve was calculated as:

$$\mathsf{\Delta }={\displaystyle \frac{2503·\exp \left(\frac{17.27·\mathrm{t}}{\mathrm{t} + 237.3}\right)}{{\left(\mathrm{t}+237.3\right)}^2}}$$

(4)

The mean saturation vapor pressure was computed as the mean between the saturation vapor pressure at the daily maximum (t_dmax [°C]) and minimum (t_dmin [°C]) air temperature (due to the non-linearity of air temperature and the saturation vapor pressure relation),

$${\mathrm{e}}_{\mathrm{s}}={\displaystyle \frac{{\mathrm{e}}^{\mathrm{o}}\left({\mathrm{t}}_{\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}}\right)+{\mathrm{e}}^{\mathrm{o}}\left({\mathrm{t}}_{\mathrm{d}\mathrm{m}\mathrm{i}\mathrm{n}}\right)}{2}}$$

(5)

Here, e^o is saturation vapor pressure at the temperature t [°C], calculated by

$${\mathrm{e}}^{\mathrm{o}}\left(\mathrm{t}\right)=0.6108·\exp \left({\displaystyle \frac{17.27·\mathrm{t}}{\mathrm{t}+237.3}}\right)$$

(6)

The actual vapor pressure was derived from mean daily value of relative humidity (RH [%]) and mean saturation vapor pressure,

$${\mathrm{e}}_{\mathrm{a}}={\displaystyle \frac{\mathrm{R}\mathrm{H}}{100}}·{\mathrm{e}}_{\mathrm{s}}$$

(7)

Wind speed u₂ was calculated as:

$${\mathrm{u}}_2={\mathrm{u}}_{\mathrm{z}}·\left({\displaystyle \frac{4.87}{\ln \left(67.8·{\mathrm{z}}_{\mathrm{w}}-5.42\right)}}\right)$$

(8)

where

z_w is the height of wind speed measurements above the ground surface [m] and,

u_z is the measured daily mean of wind speed at z_w above the ground surface [m·s⁻¹].

The net radiation (R_n) is the difference between the incoming net shortwave radiation (R_ns) and the outgoing net longwave radiation (R_nl),

$${\mathrm{R}}_{\mathrm{n}}={\mathrm{R}}_{\mathrm{n}\mathrm{s}}-{\mathrm{R}}_{\mathrm{n}\mathrm{l}}$$

(9)

The net longwave radiation was calculated using the expression:

$${\mathrm{R}}_{\mathrm{n}\mathrm{l}}=\mathsf{\sigma }·\left[{\displaystyle \frac{{\mathrm{T}}_{\mathrm{m}\mathrm{a}\mathrm{x}}^4+{\mathrm{T}}_{\mathrm{m}\mathrm{i}\mathrm{n}}^4}{2}}\right]·(0.34-0.14\sqrt{{\mathrm{e}}_{\mathrm{a}}})·(1.35·{\displaystyle \frac{\mathrm{H}}{{\mathrm{R}}_{\mathrm{s}\mathrm{o}}}}-0.35)$$

(10)

where

T_max and T_min are the daily maximum and minimum air temperature, respectively [K], and R_so is the daily sum of clear-sky solar radiation [MJ·m⁻²], which was calculated from the expression

$${\mathrm{R}}_{\mathrm{s}0}=(0.75+2·\mathrm{l}0-5·\mathrm{z})·{\mathrm{H}}_0$$

(11)

Here,

z is the station’s elevation above sea level [m] and

H₀ is the daily sum of extraterrestrial radiation [MJ·m⁻²].

The net shortwave radiation is given by

$${\mathrm{R}}_{\mathrm{n}\mathrm{s}}=(1-\mathsf{\alpha })·\mathrm{H}$$

(12)

where

α is albedo (equals 0.23 for the hypothetical grass reference crop [-]) and

H is the daily sum of global solar radiation [MJ·m⁻²], obtained from (i) measurements (dataset used in this article) and (ii) the new sunshine duration and temperature models calibrated for stations in Poland.

3. Results and Discussion

3.1. Solar Radiation Modeling Results

The values of site-calibrated, general Polish, and original global coefficients for the A-P equation, as well as statistical parameters, are shown in

Table 2. The mean daily sum of solar radiation (H) for the validation set and statistical parameters R², RMSE, RMSPE, MBE and MPEfor the Angström-Prescott equation.

Site Name H [MJ·m−2]	Site Coefficients						Poland Coefficients a = 0.21, b = 0.54				Global Coefficients a = 0.25, b = 0.50
	R2	a b	RMSE [MJ·m−2]	RMSPE [%]	MBE [MJ·m−2]	MPE [%]	RMSE [MJ·m−2]	RMSPE [%]	MBE [MJ·m−2]	MPE [%]	RMSE [MJ m−2]	RMSPE [%]	MBE [MJ m−2]	MPE [%]
Legnica 11.3	0.97	0.22 0.56	1.48	13.1	−0.05	−0.5	1.60	14.2	−0.51	−4.5	1.57	13.9	0.03	0.3
Lesko 11.4	0.93	0.19 0.59	1.75	15.3	−0.49	−4.3	1.92	16.8	−0.52	−4.5	2.00	17.5	0.06	0.5
Łódź 10.1	0.95	0.22 0.51	1.71	16.9	0.53	5.2	1.78	17.6	0.61	6.0	2.05	20.3	1.14	11.2
Mikołajki 10.9	0.97	0.22 0.53	1.49	13.6	−0.01	−0.1	1.52	13.9	−0.35	−3.2	1.58	14.5	0.15	1.4
Piła 10.4	0.97	0.20 0.54	1.30	12.5	0.05	0.5	1.34	12.9	0.29	2.8	1.61	15.5	0.81	7.8
Toruń 10.4	0.96	0.21 0.50	1.69	16.3	−0.36	−3.5	1.61	15.5	0.05	0.47	1.73	16.7	0.60	5.6
Wieluń 11.1	0.97	0.23 0.55	1.63	14.6	0.21	1.9	1.68	15.1	−0.38	−3.4	1.67	15.1	0.17	1.5
Włodawa 10.9	0.89	0.23 0.49	2.67	24.5	0.02	0.2	2.71	24.9	0.09	0.8	2.76	25.3	0.61	5.6
Kołobrzeg 10.2	0.97	0.22 0.55	1.49	14.6	0.22	2.2	1.49	14.6	−0.11	−1.0	1.57	15.3	0.42	4.1
Łeba 10.8	0.96	0.19 0.53	1.88	17.5	−0.67	−6.2	1.67	15.6	−0.11	−1.0	1.76	16.4	0.36	3.4

.

The values of a for the A-P equation ranged from 0.19 in Łeba and Lesko (coastal and submontane sites, respectively) to 0.23 in Wieluń and Włodawa in the central and central-east, while b values were between 0.49 and 0.59 (in Włodawa and Lesko, respectively). Both coefficients were close to those reported in the literature for sites in Austria and the Czech Republic [19] and similar to those estimated by Podogrodzki for the period 1958–1967 [34] for other sites in Poland (Gdynia, Kołobrzeg, Suwałki, Warszawa, Brwinów, Zakopane). Similarly to his results, our values for the coefficient b showed greater variation between stations than in the case of coefficient a, which was more stable.

The generalized values for a and b we obtained for Poland were 0.21 and 0.54, respectively, and these comply with the results for other European countries, i.e., Spain [36], as well as previous estimates for Poland (0.21, 0.57, respectively [35]). We had determined the coefficients for Poland from datasets other than those of previous studies, which may explain the differences in b values, as the b coefficient is more site-dependent than a.

Table 3. Regression coefficient A and statistical parameters R², RMSE, RMSPE, MBE and MPE for the Hargreaves–Sammani equation.

Site Name	Site Coefficients						Poland Coefficients “A” for Inland Stations = 0.15 “A” for Coastal Stations = 0.18				Global Coefficients “A” for Inland Stations = 0.16 “A” for Coastal Stations = 0.19
	R2	A	RMSE [MJ·m−2]	RMSPE [%]	MBE [MJ·m−2]	MPE [%]	RMSE [MJ·m−2]	RMSPE [%]	MBE [MJ·m−2]	MPE [%]	RMSE [MJ·m−2]	RMSPE [%]	MBE [MJ·m−2]	MPE [%]
Legnica	0.84	0.15	3.46	30.6	0.14	1.2	3.46	30.6	0.14	1.2	3.56	31.5	0.80	7.1
Lesko	0.81	0.15	3.89	34.0	−0.20	−1.7	3.89	34.0	−0.20	−1.7	3.86	33.7	0.55	4.8
Łódź	0.85	0.15	3.23	31.6	0.74	7.3	3.23	31.6	0.74	7.3	3.50	34.2	1.48	14.4
Mikołajki	0.85	0.17	3.47	31.8	0.40	3.6	3.69	33.8	−0.93	−8.5	3.49	31.9	−0.27	−2.5
Piła	0.85	0.14	3.20	31.2	0.08	0.8	3.28	32.0	0.82	8.0	3.59	35.0	1.56	15.2
Toruń	0.85	0.14	3.27	31.6	−0.05	−0.5	3.31	32.0	0.69	6.6	3.58	34.6	1.42	13.8
Wieluń	0.84	0.16	3.33	30.0	0.60	5.3	3.32	29.9	−0.14	−1.2	3.33	30.0	0.60	5.3
Włodawa	0.81	0.15	3.69	33.9	0.26	2.4	3.69	33.9	0.26	2.4	3.82	35.0	0.96	8.8
Kołobrzeg	0.75	0.18	4.33	41.7	0.38	3.7	4.33	41.7	0.38	3.7	4.45	42.8	0.98	9.4
Łeba	0.74	0.17	4.65	43.2	−0.50	−4.7	4.61	42.9	0.10	1.0	4.69	43.6	0.71	6.6

contains statistical parameters and the values of site-calibrated, general Polish, and original global coefficients for the H-S equation.

The local values of A for the H-S equation ranged from 0.14 in central Poland (Piła, Toruń) to 0.18 in the seaside (Kołobrzeg). The mean annual coefficients for Poland for the H-S equation were 0.15 and 0.18 for inland and coastal sites, respectively. According to the authors’ best knowledge, generalized H-S coefficients for Poland have not been published before. However, those estimated in this study were close to the global ones proposed by Hargreaves [5].

Although these sites were located in a transitional temperate zone between the two climate types and the regression coefficients showed some variation for both models, we did not see any particular pattern in the spatial distribution of the coefficients. It is only noticeable that the Hargreaves coefficients estimated for stations located near the water bodies (Baltic Sea and Mazuria Great Lakes region) were similar to and higher than those inland.

A perfect fit for the locally calibrated A-P equation, expressed by R² above 0.9, was obtained for 9 out of 10 measurement stations taken into the analysis; the highest value for R², of 0.97, was obtained for the Legnica, Mikołajki, Piła, Wieluń, and Kołobrzeg stations, whilst the lowest one, of 0.89, was in Włodawa.

A good model fit (R² above 0.8) was obtained for the H-S equation for 8 out of 10 stations. The lowest values of 0.74 and 0.75 were recorded for the coastal stations in Łeba and Kołobrzeg, whilst the highest one was 0.85, for the Łódź, Mikołajki, Piła, and Toruń sites.

The best results for the A-P equation were obtained with locally calibrated coefficients; the RMSE values ranged between 1.30 [MJ·m⁻²] in Piła and 2.67 [MJ·m⁻²] in Włodawa, i.e., from 12.5% to 24.5% of the average H for these stations. Trnka et al. [19] obtained similar error values using local coefficients for stations located in the Czech and Austrian lowlands. The RMSE there ranges from 1.41 [MJ m⁻²] to 1.80 [MJ m⁻²], i.e., from 13 to 17.3% of the annual mean.

Applying generalized coefficients for Poland in this formula, at the same stations, resulted in RMSE values that were only slightly higher (1.34 [MJ·m⁻²] and 2.71 [MJ·m⁻²], respectively), but which were lower than those derived with global ones (1.61 [MJ·m⁻²] and 2.76 [MJ·m⁻²]). The RMSE obtained with coefficients determined for Poland was lower than that derived with the global ones at 8 out of 10 sites. There were only two exceptions, to this rule (Legnica and Wieluń), but the results are still very close.

Applying the A-P model with global coefficients resulted in an overestimation at all stations, as reflected by a positive MBE ranging between 0.03 and 1.14 MJ·m⁻². For the locally calibrated and general model for Poland, the MBE ranged from −0.67 to 0.53 [MJ·m⁻²], and from −0.52 to 0.61 [MJ·m⁻²], respectively (at some sites they underestimated, and at other overestimated H values, Table 2).

In the case of the locally calibrated H-S model, we recorded the highest RMSE for the coastal stations in Łeba and Kołobrzeg (4.65; 4.33 [MJ·m⁻²], respectively); the lowest, in the range of 3.2–3.27 [MJ·m⁻²], was observed at the stations located in the center of the country (Pila, Łódź, Toruń). These values are comparable to the results obtained in other European countries, where local H-S model gave RMSE values between 3.50 [MJ·m⁻²] and 3.77 [MJ·m⁻²], i.e., from 28.7% to 37.35% of annual mean [19].

Applying the mean coefficients for Poland had a similar impact on the results to the sunshine duration-based model. The errors obtained with generalized coefficients determined separately for coastal and inland areas in Poland were lower than those derived with the global ones, estimated by Hargeraves, at 9 out of 10 sites. The H-S model tended the overestimation of H (Table 3), reaching 15.2% with global coefficients, 8.0% with generalized for Poland and 7.3% locally in the center of Poland (Łódź).

Local calibration allowed us to reduce the RMSE value by 0.04 [MJ·m⁻²] to 0.34 [MJ·m⁻²] for the A-P equation and by 0.02 [MJ·m⁻²] to 0.39 [MJ·m⁻²] for the H-S equation compared to results achieved with global coefficients. The application of coefficients for Poland allowed us to reduce the RMSE value by 0.05 [MJ·m⁻²] to 0.37 [MJ·m⁻²] for the A-P and by 0.01 [MJ·m⁻²] to 0.31 [MJ·m⁻²] for the H-S equation compared to results achieved with global coefficients.

Comparing the site-calibrated A-P and H-S models (generalized for Poland and global, respectively), site to site, the estimation of global solar radiation as a function of air temperature was burdened with errors approximately twice as large as when using sunshine duration as a variable.

3.2. Evapotranspiration Results

The mean ET₀ sums for the warm half years of 2000–2015 (

Table 4. The mean ET₀ sums for the warm half years of 2000–2015 obtained with measured and calculated solar radiation data.

No.	Site Name	ET0(H) [mm]	ET0(A-P_S) [mm]	ET0(A-P_PL) [mm]	ET0(A-P_G) [mm]	ET0(H-S_S) [mm]	ET0(H-S_PL) [mm]	ET0(H-S_G) [mm]
		Model 1.	Model 2.	Model 3.	Model 4.	Model 5.	Model 6.	Model 7.
1.	Legnica	582	581	568	580	583	583	604
2.	Lesko	519	512	509	523	521	521	542
3.	Łódź	565	573	576	588	578	578	598
4.	Mikołajki	529	533	523	535	541	503	522
5.	Piła	537	540	546	558	536	557	578
6.	Toruń	540	538	550	563	547	568	589
7.	Wieluń	585	588	573	585	598	578	598
8.	Włodawa	569	567	571	583	574	574	594
9.	Kołobrzeg	484	484	475	487	490	490	507
10.	Łeba	485	478	492	502	481	496	511

Notes: ET₀—reference evapotranspiration calculated using: measured solar radiation data (ET_0(H)), A-P model with site calibrated coefficients (ET_{0(A-P_S)}), A-P model with generalized coefficient for Poland (ET_{0(A-P_PL)}), A-P model with global coefficient (ET_{0(A-P_G)}), H-S model with site calibrated coefficients (ET_{0(H-S_S)}), H-S model with generalized coefficients for Poland (ET_{0(H-S_PL)}) and H-S model with global coefficients (ET_{0(H-S_G)}).

, Figure 2), calculated using measured solar radiation data, show considerable spatial variation (100 mm on average). The lowest mean ET₀ values of 484 mm and 485 mm were observed along the Baltic Sea coast, in Kołobrzeg and Łeba, respectively. The highest mean values were in Wieluń and Legnica (585 mm and 582 mm, respectively). A relatively low mean ET₀ also occurred in the foothill area (Lesko 519 mm) and the Masurian Lake District (Mikołajki 529 mm).

Year-by-year analysis revealed that the lowest ET₀ sum of 416 mm (Figure 2) occurred in Łeba in 2001, while the highest one of 673 mm was observed in Łódź in 2015. The last site also features the highest year-over-year ET₀ variability (sd = 51.8 mm), while the lowest ET₀ variability was noted for Kołobrzeg (sd = 17.1 mm).

The accuracy of models 2–4 (P-M model with A-P equations), assessed using RMSE and MBE and compared to the results obtained with measured H values, is shown in

Table 5. RMSE, RMSPE, MBE and MPE for ET₀ calculation with models 2–4.

Site Name	ET0(A-P_S)				ET0(A-P_PL)				ET0(A-P_G)
	Model 2				Model 3				Model 4
	RMSE [mm]	RMSPE [%]	MBE [mm]	MPE [%]	RMSE [mm]	RMSPE [%]	MBE [mm]	MPE [%]	RMSE [mm]	RMSPE [%]	MBE [mm]	MPE [%]
Legnica	0.1760	5.5	−0.0550	−1.7	0.1917	6.2	−0.0735	−2.4	0.1838	5.8	−0.0100	−0.3
Lesko	0.2682	9.6	0.0431	1.5	0.2772	10.0	−0.0573	−2.1	0.2814	9.8	0.0181	0.6
Łódź	0.2119	6.8	−0.0409	−1.3	0.2224	7.1	0.0590	1.9	0.2462	7.7	0.1237	3.8
Mikołajki	0.1800	6.2	−0.0220	−0.8	0.1798	6.3	−0.0294	−1.0	0.1895	6.5	0.0353	1.2
Piła	0.1578	5.3	−0.0123	−0.4	0.1667	5.6	0.0462	1.5	0.2025	6.6	0.1124	3.7
Toruń	0.2035	6.9	0.0101	0.3	0.2187	7.3	0.0565	1.9	0.2448	8.0	0.1255	4.1
Wieluń	0.1923	6.0	−0.0214	−0.7	0.2027	6.5	−0.0647	−2.1	0.1946	6.1	0.0043	0.1
Włodawa	0.3431	11.1	0.0070	0.2	0.3495	11.2	0.0150	0.5	0.3574	11.2	0.0770	2.4
Kołobrzeg	0.1860	7.0	0.0004	0.0	0.1925	7.4	−0.0488	−1.9	0.1891	7.1	0.0183	0.7
Łeba	0.1995	7.6	−0.0346	−1.3	0.2018	7.5	0.0399	1.5	0.2244	8.2	0.0938	3.4

.

The best results for the site calibrated (model 2) and general Polish model (model 3) were obtained in Piła (RMSE = 0.1578 mm and 0.1667 mm, respectively). The global Angströem coefficients (model 4) performed the best in the P-M formula, in the context of Legnica (RMSE = 0.1838 mm). The highest RMSE values for all (2–4) models were observed at the Włodawa site (0.3431 mm, 0.3495 mm and 0.3574 mm, respectively).

Applying the A-P model with locally calibrated coefficients in the P-M formula (model 2) improved the accuracy of ET₀ estimations for 7 out of 10 of the analyzed stations comparedto the results obtained with global ones. The maximum RMSE drop of 0.0447 mm was observed at the Piła station. The exceptions were Mikołajki, Wieluń, and Kołobrzeg, where the locally calibrated A-P model did not improve ET₀ estimates compared to the results obtained for radiation only data simulation.

The A-P coefficients for Poland (model 3) performed worse than global ones (model 4) at three sites, i.e., Legnica, Wieluń, and Kołobrzeg. This is worth emphasizing, because the coefficients for Poland improved the radiation model accuracy for Kołobrzeg, and were expected to improve the ET₀ calculations as well.

Applying the A-P model with global coefficients (model 4) resulted in overestimating the ET₀ sums, reflected in the positive MBE values for 9 out of 10 of the stations (Table 5). Models 2–3 did not tend to overestimate or underestimate ET₀ calculations (positive MBE for ~50% locations).

The accuracy of models 5–7, assessed using RMSE and MBE, comparedto the results obtained with measured H values, is shown in

Table 6. RMSE, RMSPE, MBE and MPE for ET₀ calculation with models 5–7.

Site Name	ET0(H-S_S)				ET0(H-S_PL)				ET0(H-S_G)
	Model 5				Model 6				Model 7
	RMSE [mm]	RMSPE [%]	MBE [mm]	MPE [%]	RMSE [mm]	RMSPE [%]	MBE [mm]	MPE [%]	RMSE [mm]	RMSPE [%]	MBE [mm]	MPE [%]
Legnica	0.4328	13.6	0.0085	0.3	0.4328	13.6	0.0085	0.3	0.4505	13.6	0.1235	3.7
Lesko	0.4595	16.1	0.0157	0.6	0.4595	16.1	0.0157	0.6	0.4674	15.8	0.1189	4.0
Łódź	0.3939	12.5	0.0698	2.2	0.3939	12.5	0.0698	2.2	0.4281	13.1	0.1783	5.5
Mikołajki	0.4277	14.5	0.0663	2.2	0.4590	16.7	−0.1400	−5.1	0.4289	15.0	−0.0368	−1.3
Piła	0.4037	13.8	−0.0050	−0.2	0.4163	13.7	0.1088	3.6	0.4631	14.7	0.2226	7.0
Toruń	0.4016	13.4	0.0420	1.4	0.4302	13.9	0.1560	5.0	0.4899	15.2	0.2700	8.4
Wieluń	0.4168	12.8	0.0740	2.3	0.4175	13.2	−0.0380	−1.2	0.4168	12.8	0.0740	2.3
Włodawa	0.4613	14.7	0.0269	0.9	0.4613	14.7	0.0269	0.9	0.4809	14.8	0.1376	4.2
Kołobrzeg	0.5603	20.9	0.0093	0.3	0.5603	20.9	0.0093	0.3	0.5776	20.8	0.1004	3.6
Łeba	0.3529	13.4	0.0246	0.9	0.3771	13.9	0.0638	2.4	0.4111	14.7	0.1029	3.7

.

The best results were obtained for the Łeba station where the site calibrated, general Polish and global models gave RMSE values of 0.3529 mm, 0.3771 mm and 0.4111 mm, respectively. The highest RMSE values for all (5–7) models were observed at the other sea-side station, Kołobrzeg (0.5603 mm and 0.5776 mm).

The local calibration of the H-S model in the P-M formula improved the accuracy of the ET₀ estimations at all 10 of the analyzed stations. The highest RMSE drops of 0.0883 mm, 0.0594 mm and 0.0582 mm were obtained for Toruń, Piła and Łeba, respectively. The H-S coefficients for Poland (inland and coastal) performed better than the global ones in the P-M formula at eight stations. The RMSE values for model 6 were higher than those for model 5 at only four stations (Mikołajki, Piła, Toruń and Łeba). Applying 5–7 temperature-based models caused the overestimation of ET₀, as reflected in positive MBE values (Table 6), except for at Mikołajki and Wieluń.

4. Conclusions

In this study, the coefficients for 10 stations and the average coefficients for Poland using the A-P and H-S equations were determined.

The radiation data estimated with obtained and global (original A-P and H-S) coefficients were applied to the Penman–Monteith equation for reference evapotranspiration estimation using the FAO method, and were compared to the reference evapotranspiration obtained with the same formula and real radiation values.

The best accuracy of both solar radiation models was obtained with site calibrated coefficients. These can be used to fill data gaps and can be applied to neighboring areas where solar data are not available, although within a limited range.

When real radiation data are unavailable, the generalized coefficients for Poland (temperature and sunshine duration-based) published in this paper may be a solution. They allow for solar radiation estimations with a degree of accuracy worse than that achieved when using local coefficients, but better than that achieved when using global ones.

Our study has confirmed that in the Polish climate, the A-P model performed much better than the H-S. However, if sunshine duration is not available, solar radiation can still be predicted with satisfactory accuracy using the H-S equation with coefficients generalized for coastal and inland areas.

A worse predictive power of the Hargreaves model was observed, especially in the context of nearby large water bodies (the lowest R² and the highest RMSE were observed for the coastal stations). In those regions, daily temperature amplitudes were lower and less correlated with the amount of incoming solar energy. The reduced daily air temperature amplitudes caused the temperature-based model to underestimate actual incoming energy.

The method of determination of the radiation component had a significant but sometimes unexpected impact on the results of ET₀ estimation with the P-M formula. The better predictive power of the solar radiation model, in terms of R² and RMSE, usually resulted in a better accuracy of evapotranspiration estimation using the P-M equation; however, there were exceptions to this rule, as evapotranspiration depends on many variables.

In general, our results are in line with the FAO’s recommendations, but in some locations (within the same moderate climate zone), the better predictive power of the radiation model did not result in better ET₀ accuracy, so indirect methods should always be applied with caution.

We observed that the application of both sunshine- and temperature-based models, with global coefficients tended to yield overestimated ET₀. We did not notice such a rule for the other (locally calibrated and general Polish) models for some locations. In some instances, they overestimated and, in some others, they underestimated the ET₀ results.

The local calibration of the H-S radiation model included in the ET₀ formula resulted in similar RMSEs to those derived using the generalized coefficients for Poland. However, the latter yielded significantly better results than global ones.

We did not rank any model as the best. Our goal was to present the possible errors and limitations of each method depending on location, data availability, and the purpose of use.