High-Resolution Spatiotemporal Mapping of Surface Soil Moisture Using ConvLSTM Model and Sentinel-1 Data
Abstract
1. Introduction
2. Materials and Methods
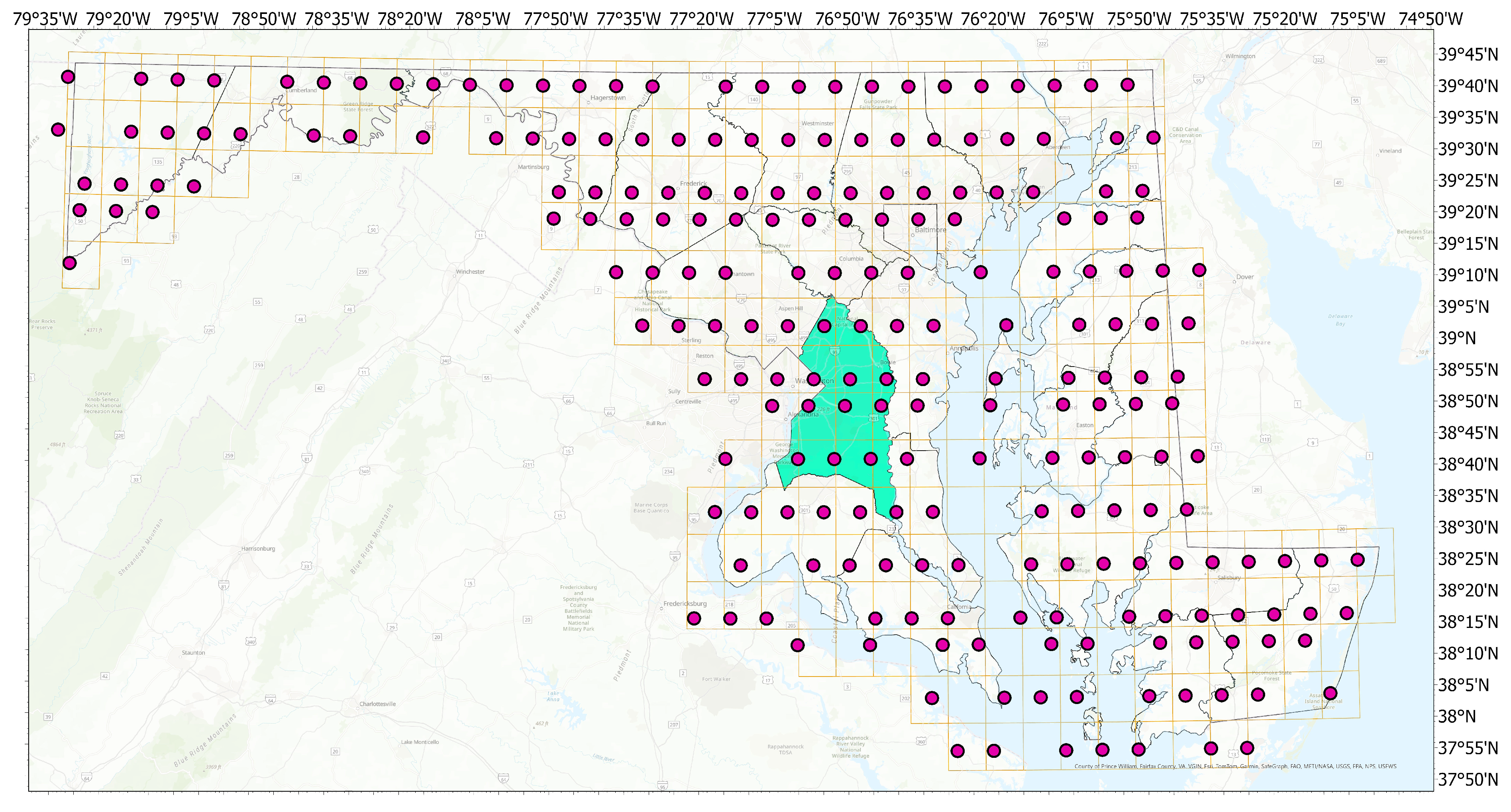
2.1. Study Area
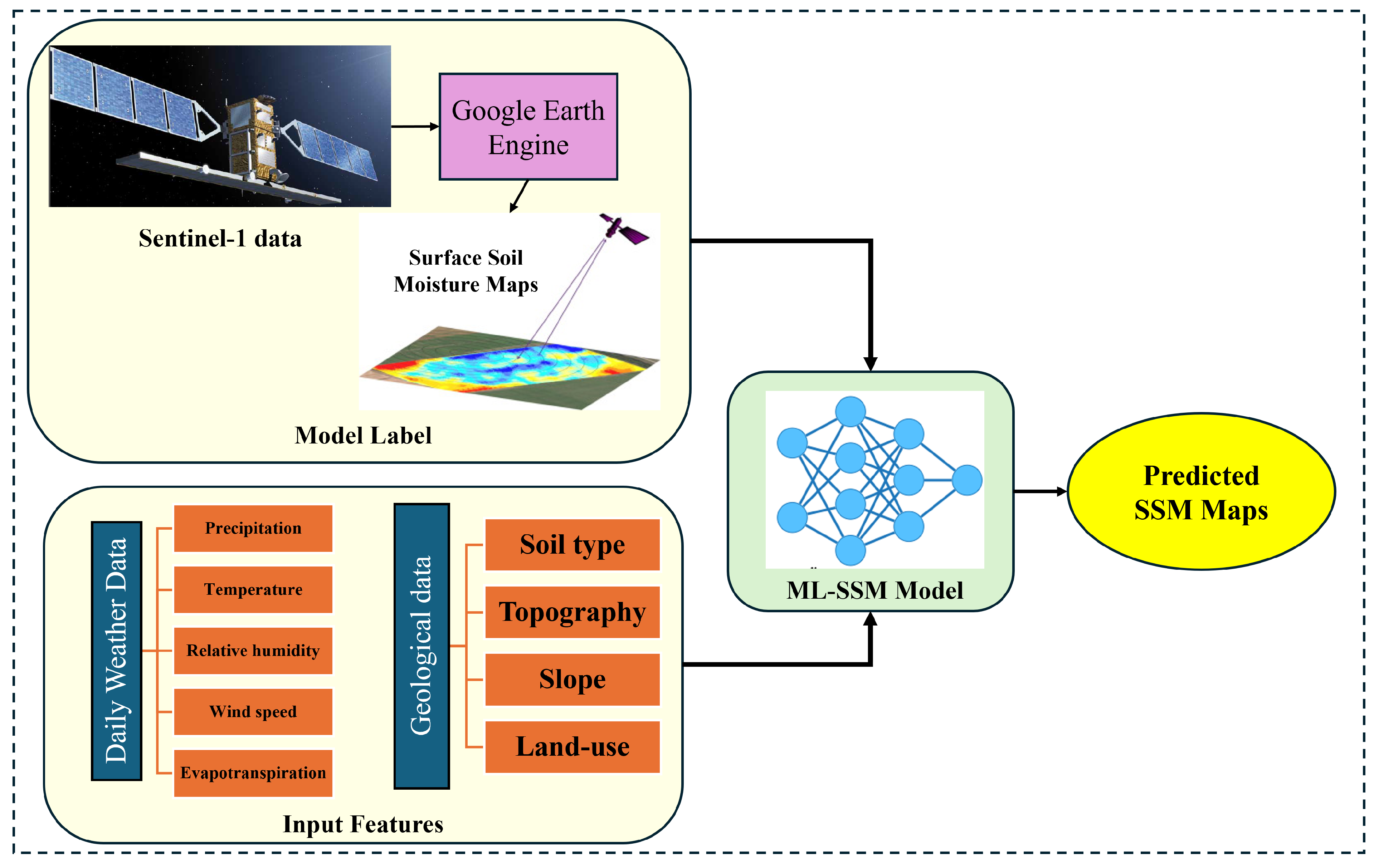
2.2. Data Preparation
2.2.1. Sentinel-1 Data to Generate SSM Maps
2.2.2. Weather Data
- 1-day model: exact date values.
- 2-day model: observation date + 1 day before.
- 3-day model: observation date + 2 days before.
2.2.3. Geological Data
2.3. Methodology
2.3.1. Producing SSM Maps Using Sentinel-1
2.3.2. Develop the ML-SSM Model
- Step 1: Data Preparation and Patch Extraction
- Step 2: Patch Dataset Management
- Step 3: Patch Data Generators
- Step 4: Model Architecture and Training
- Step 5: Model Evaluation
3. Results
3.1. ML-SSM Model Performance
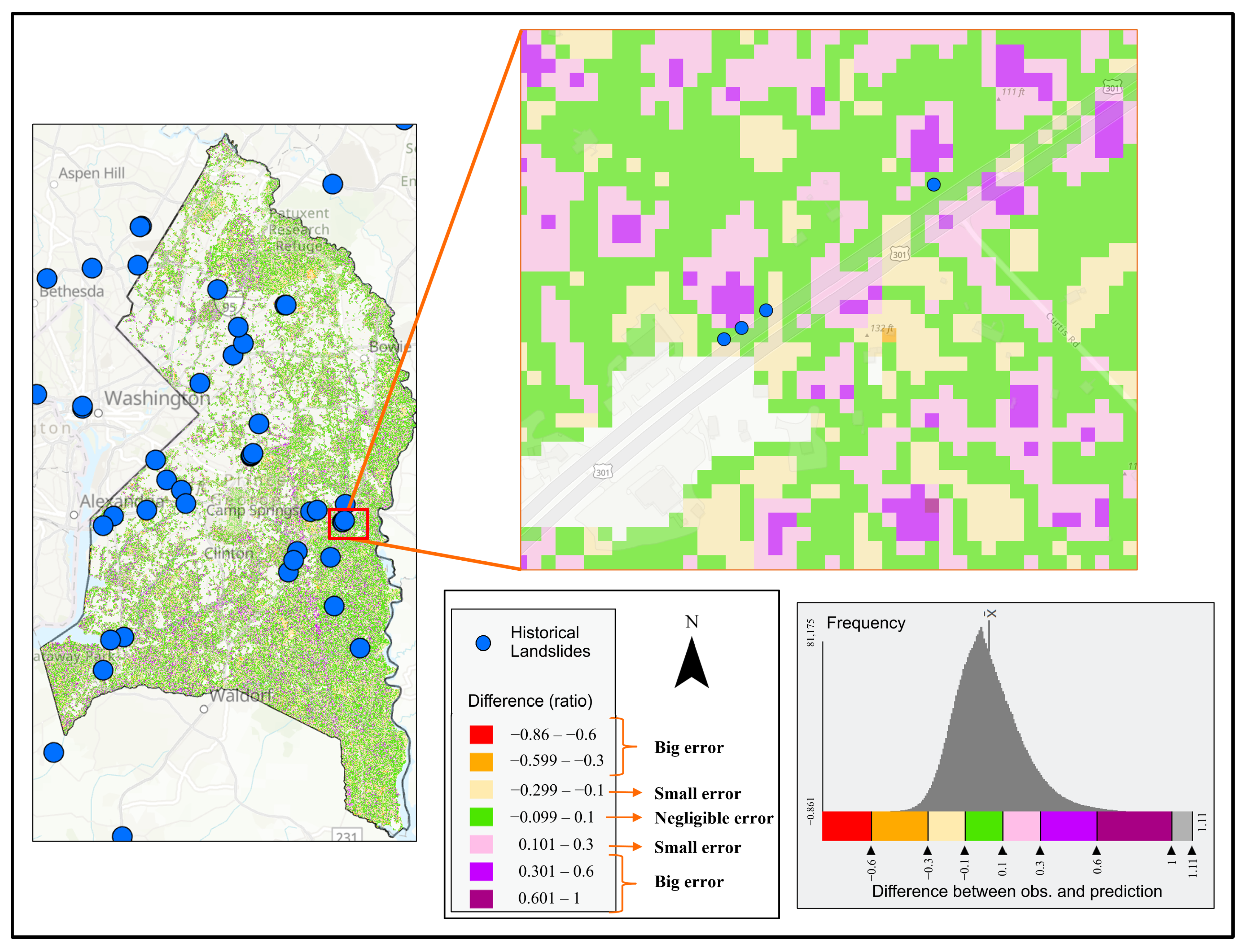
3.2. Mapping of Predicted SSM Using ML-SSM Model
4. Conclusions
- 1-day model: Uses meteorological variables from the exact observation date of the SSM map.
- 2-day model: Uses cumulative rainfall and evapotranspiration and averages other variables over the observation date and the preceding day.
- 3-day model: Extends this to the observation date plus the two preceding days.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SSM | Surface Soil Moisture |
| ML | Machine Learning |
| ML-SSM | Machine Learning-based Surface Soil Moisture model |
| MDOT | Maryland Department of Transportation |
| SHA | State Highway Administration |
| USGS | United States Geological Survey |
| NASA | National Aeronautics and Space Administration |
| SAR | Synthetic Aperture Radar |
| IW | Interferometric Wide |
| VV | Vertical-Vertical |
| VH | Vertical-Horizontal |
| IDW | Inverse Distance Weighting method |
| DEM | Digital Elevation Model |
| SSURGO | Soil Survey Geographic Database |
| GEE | Google Earth Engine |
| NDVI | Normalized Difference Vegetation Index |
| ESA | European Space Agency |
| ET | Evapotranspiration |
| ConvLSTM | Convolutional Long Short-Term Memory |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Squared Error |
References
- Bordoni, M.; Meisina, C.; Valentino, R.; Lu, N.; Bittelli, M.; Chersich, S. Hydrological factors affecting rainfall-induced shallow landslides: From the field monitoring to a simplified slope stability analysis. Eng. Geol. 2015, 193, 19–37. [Google Scholar] [CrossRef]
- Galanti, Y.; Barsanti, M.; Cevasco, A.; D’Amato Avanzi, G.; Giannecchini, R. Comparison of statistical methods and multi-time validation for the determination of the shallow landslide rainfall thresholds. Landslides 2018, 15, 937–952. [Google Scholar] [CrossRef]
- Zhang, Z.; Zeng, R.; Meng, X.; Zhao, S.; Wang, S.; Ma, J.; Wang, H. Effects of changes in soil properties caused by progressive infiltration of rainwater on rainfall-induced landslides. Catena 2023, 233, 107475. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, F.; Zhang, H.; Zhang, L.; Zhang, J. Influences of internal erosion on infiltration and slope stability. Bull. Eng. Geol. Environ. 2019, 78, 1815–1827. [Google Scholar] [CrossRef]
- Liu, Q.; Su, L.; Zhang, C.; Hu, B.; Xiao, S. Dynamic variations of interception loss-infiltration-runoff in three land-use types and their influence on slope stability: An example from the eastern margin of the Tibetan Plateau. J. Hydrol. 2022, 612, 128218. [Google Scholar] [CrossRef]
- Emberson, R.; Kirschbaum, D.; Stanley, T. New global characterisation of landslide exposure. Nat. Hazards Earth Syst. Sci. 2020, 20, 3413–3424. [Google Scholar] [CrossRef]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Nelson, S. Slope stability, triggering events, mass movement hazards. Nat. Disasters 2013. Available online: https://amser.org/r7499/slope_stability_triggering_events_mass_wasting_events (accessed on 11 November 2025).
- Kirschbaum, D.B.; Stanley, T.; Simmons, J. A dynamic landslide hazard assessment system for Central America and Hispaniola. Nat. Hazards Earth Syst. Sci. 2015, 15, 2257–2272. [Google Scholar] [CrossRef]
- Rahardjo, H.; Nistor, M.M.; Gofar, N.; Satyanaga, A.; Xiaosheng, Q.; Chui Yee, S.I. Spatial distribution, variation and trend of five-day antecedent rainfall in Singapore. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2020, 14, 177–191. [Google Scholar] [CrossRef]
- Cevasco, A.; Pepe, G.; Brandolini, P. The influences of geological and land use settings on shallow landslides triggered by an intense rainfall event in a coastal terraced environment. Bull. Eng. Geol. Environ. 2014, 73, 859–875. [Google Scholar] [CrossRef]
- Glade, T.; Anderson, M.G.; Crozier, M.J. Landslide Hazard and Risk; Wiley Online Library: Hoboken, NJ, USA, 2005; Volume 807. [Google Scholar]
- Zêzere, J.L.; Trigo, R.M.; Trigo, I.F. Shallow and deep landslides induced by rainfall in the Lisbon region (Portugal): Assessment of relationships with the North Atlantic Oscillation. Nat. Hazards Earth Syst. Sci. 2005, 5, 331–344. [Google Scholar] [CrossRef]
- Bogaard, T.; Greco, R. Invited perspectives: Hydrological perspectives on precipitation intensity-duration thresholds for landslide initiation: Proposing hydro-meteorological thresholds. Nat. Hazards Earth Syst. Sci. 2018, 18, 31–39. [Google Scholar] [CrossRef]
- Kim, J.H.; Fourcaud, T.; Jourdan, C.; Maeght, J.L.; Mao, Z.; Metayer, J.; Meylan, L.; Pierret, A.; Rapidel, B.; Roupsard, O.; et al. Vegetation as a driver of temporal variations in slope stability: The impact of hydrological processes. Geophys. Res. Lett. 2017, 44, 4897–4907. [Google Scholar] [CrossRef]
- Özçelik, F.V.; Selçuk, M.E. Parametric Analysis of Factors that Affects the Rainfall Induced Slope Stability. Turk. J. Geosci. 2022, 3, 49–57. [Google Scholar] [CrossRef]
- Wu, L.; Zhou, J. Rainfall Infiltration in Unsaturated Soil Slope Failure; Springer Nature: Berlin/Heidelberg, Germany, 2023. [Google Scholar] [CrossRef]
- Chen, R.; Chen, H.; Chen, K.; Zhung, H. Simulation of a slope failure induced by rainfall infiltration. Environ. Geol. 2009, 58, 943–952. [Google Scholar] [CrossRef]
- Mukhlisin, M.; Taha, M.R. Numerical model of antecedent rainfall effect on slope stability at a hillslope of weathered granitic soil formation. J. Geol. Soc. India 2012, 79, 525–531. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, H.W.; Zhang, L.M.; Zhu, H.H.; Shi, B. Probabilistic prediction of rainfall-induced slope failure using a mechanics-based model. Eng. Geol. 2014, 168, 129–140. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Ardizzone, F.; Cardinali, M.; Galli, M. Estimating the quality of landslide susceptibility models. Geomorphology 2006, 81, 166–184. [Google Scholar] [CrossRef]
- Tung, Y.K.; Zhang, H.; Ng, C.W.W.; Kwok, Y. Transient seepage analysis of rainfall infiltration using a new conjunctive surface-subsurface flow model. In Proceedings of the 57th Canadian Geotechnical Conference and the 5th Joint CGS-IAH Conference, Quebec, QC, Canada, 24–27 October 2004; Volume 7, pp. 17–22. [Google Scholar]
- He, W.; Ishikawa, T.; Zhu, Y. Wide/narrow-area slope stability analysis considering infiltration and runoff during heavy precipitation. Soils Found. 2023, 63, 101248. [Google Scholar] [CrossRef]
- Chiu, Y.Y.; Chen, H.E.; Yeh, K.C. Investigation of the influence of rainfall runoff on shallow landslides in unsaturated soil using a mathematical model. Water 2019, 11, 1178. [Google Scholar] [CrossRef]
- Dolojan, N.L.J.; Moriguchi, S.; Hashimoto, M.; Terada, K. Mapping method of rainfall-induced landslide hazards by infiltration and slope stability analysis: A case study in Marumori, Miyagi, Japan, during the October 2019 Typhoon Hagibis. Landslides 2021, 18, 2039–2057. [Google Scholar] [CrossRef]
- Cui, H.; Ji, J.; Hürlimann, M.; Medina, V. Probabilistic and physically-based modelling of rainfall-induced landslide susceptibility using integrated GIS-FORM algorithm. Landslides 2024, 21, 1461–1481. [Google Scholar] [CrossRef]
- Chansorn, R.; Chotpantarat, S.; Klongvessa, P. Hydrological model of landslide risk in Huai Nam Phung subbasin, Thailand. Bull. Eng. Geol. Environ. 2023, 82, 140. [Google Scholar] [CrossRef]
- Hosseinizadeh, A.; Sheng, Z.; Qian, S.; Liu, Y. Separating Infiltration and Runoff from Precipitation over the Anacostia River Watershed, Maryland. In Proceedings of the World Environmental and Water Resources Congress 2024, Milwaukee, WI, USA, 19–22 May 2024; pp. 1595–1607. [Google Scholar] [CrossRef]
- Chaudhary, S.K.; Srivastava, P.K.; Gupta, D.K.; Kumar, P.; Prasad, R.; Pandey, D.K.; Das, A.K.; Gupta, M. Machine learning algorithms for soil moisture estimation using Sentinel-1: Model development and implementation. Adv. Space Res. 2022, 69, 1799–1812. [Google Scholar] [CrossRef]
- Chrysanthopoulos, E.; Kallioras, A. Temporal and geographic extrapolation of soil moisture using machine learning algorithms. Catena 2025, 257, 109156. [Google Scholar] [CrossRef]
- Acharya, U.; Daigh, A.L.; Oduor, P.G. Machine learning for predicting field soil moisture using soil, crop, and nearby weather station data in the Red River Valley of the North. Soil Syst. 2021, 5, 57. [Google Scholar] [CrossRef]
- Gill, M.K.; Asefa, T.; Kemblowski, M.W.; McKee, M. Soil moisture prediction using support vector machines 1. JAWRA J. Am. Water Resour. Assoc. 2006, 42, 1033–1046. [Google Scholar] [CrossRef]
- Mittelbach, H.; Seneviratne, S.I. A new perspective on the spatio-temporal variability of soil moisture: Temporal dynamics versus time-invariant contributions. Hydrol. Earth Syst. Sci. 2012, 16, 2169–2179. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Morbidelli, R. Spatial-temporal variability of soil moisture and its estimation across scales. Water Resour. Res. 2010, 46, W02516. [Google Scholar] [CrossRef]
- Houben, T.; Ebeling, P.; Khurana, S.; Schmid, J.S.; Boog, J. Machine-learning based spatiotemporal prediction of soil moisture in a grassland hillslope. Vadose Zone J. 2025, 24, e70011. [Google Scholar] [CrossRef]
- Jiang, P.; Niu, G.; Li, G. Soil Moisture Prediction Based on Long Short-Term Memory Networks and Meteorological Data. Res. Sq. 2024. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, L.; Hu, Y.; Hu, X.; Song, W.; Wang, L. A comprehensive study of deep learning for soil moisture prediction. Hydrol. Earth Syst. Sci. Discuss. 2023, 28, 917–943. [Google Scholar] [CrossRef]
- Ahmad, S.; Kalra, A.; Stephen, H. Estimating soil moisture using remote sensing data: A machine learning approach. Adv. Water Resour. 2010, 33, 69–80. [Google Scholar] [CrossRef]
- Senyurek, V.; Lei, F.; Boyd, D.; Kurum, M.; Gurbuz, A.C.; Moorhead, R. Machine learning-based CYGNSS soil moisture estimates over ISMN sites in CONUS. Remote Sens. 2020, 12, 1168. [Google Scholar] [CrossRef]
- Vereecken, H.; Huisman, J.; Pachepsky, Y.; Montzka, C.; Van Der Kruk, J.; Bogena, H.; Weihermüller, L.; Herbst, M.; Martinez, G.; Vanderborght, J. On the spatio-temporal dynamics of soil moisture at the field scale. J. Hydrol. 2014, 516, 76–96. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Batchu, V.; Nearing, G.; Gulshan, V. A machine learning data fusion model for soil moisture retrieval. arXiv 2022, arXiv:2206.09649. [Google Scholar] [CrossRef]
- Liu, Y.; Jing, W.; Wang, Q.; Xia, X. Generating high-resolution daily soil moisture by using spatial downscaling techniques: A comparison of six machine learning algorithms. Adv. Water Resour. 2020, 141, 103601. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Miranda, N.; Torres, R.; Geudtner, D.; Pinheiro, M.; Potin, P.; Gratadour, J.B.; O’Connell, A.; Bibby, D.; Navas-Traver, I.; Cossu, M. Sentinel-1 First Generation Status, Past and Future. In Proceedings of the IGARSS 2023—2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; IEEE: New York, NY, USA, 2023; pp. 4560–4563. [Google Scholar] [CrossRef]
- Massart, S.; Vreugdenhil, M.; Bauer-Marschallinger, B.; Navacchi, C.; Raml, B.; Wagner, W. Mitigating the impact of dense vegetation on the Sentinel-1 surface soil moisture retrievals over Europe. Eur. J. Remote Sens. 2024, 57, 2300985. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. A Review of Spatial Interpolation Methods for Environmental Scientists; Geoscience Australia: Canberra, Australia, 2008. [Google Scholar]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A method for estimating soil moisture from ERS scatterometer and soil data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Bauer-Marschallinger, B.; Freeman, V.; Cao, S.; Paulik, C.; Schaufler, S.; Stachl, T.; Modanesi, S.; Massari, C.; Ciabatta, L.; Brocca, L.; et al. Toward global soil moisture monitoring with Sentinel-1: Harnessing assets and overcoming obstacles. IEEE Trans. Geosci. Remote Sens. 2018, 57, 520–539. [Google Scholar] [CrossRef]
- van Hateren, T.C.; Chini, M.; Matgen, P.; Pulvirenti, L.; Pierdicca, N.; Teuling, A.J. On the potential of Sentinel-1 for sub-field scale soil moisture monitoring. Int. J. Appl. Earth Obs. Geoinf. 2023, 120, 103342. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.k.; Woo, W.c. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; Curran Associates, Inc.: Vancouver, BC, Canada, 2015; Volume 28, pp. 802–810. [Google Scholar]
- Ulloa, N.I.; Yun, S.H.; Chiang, S.H.; Furuta, R. Sentinel-1 spatiotemporal simulation using convolutional LSTM for flood mapping. Remote Sens. 2022, 14, 246. [Google Scholar] [CrossRef]
- ElSaadani, M.; Habib, E.; Abdelhameed, A.; Bayoumi, M. Assessment of a Spatiotemporal Deep Learning Approach for Soil Moisture Prediction. Front. Artif. Intell. 2021, 4, 636234. [Google Scholar] [CrossRef] [PubMed]


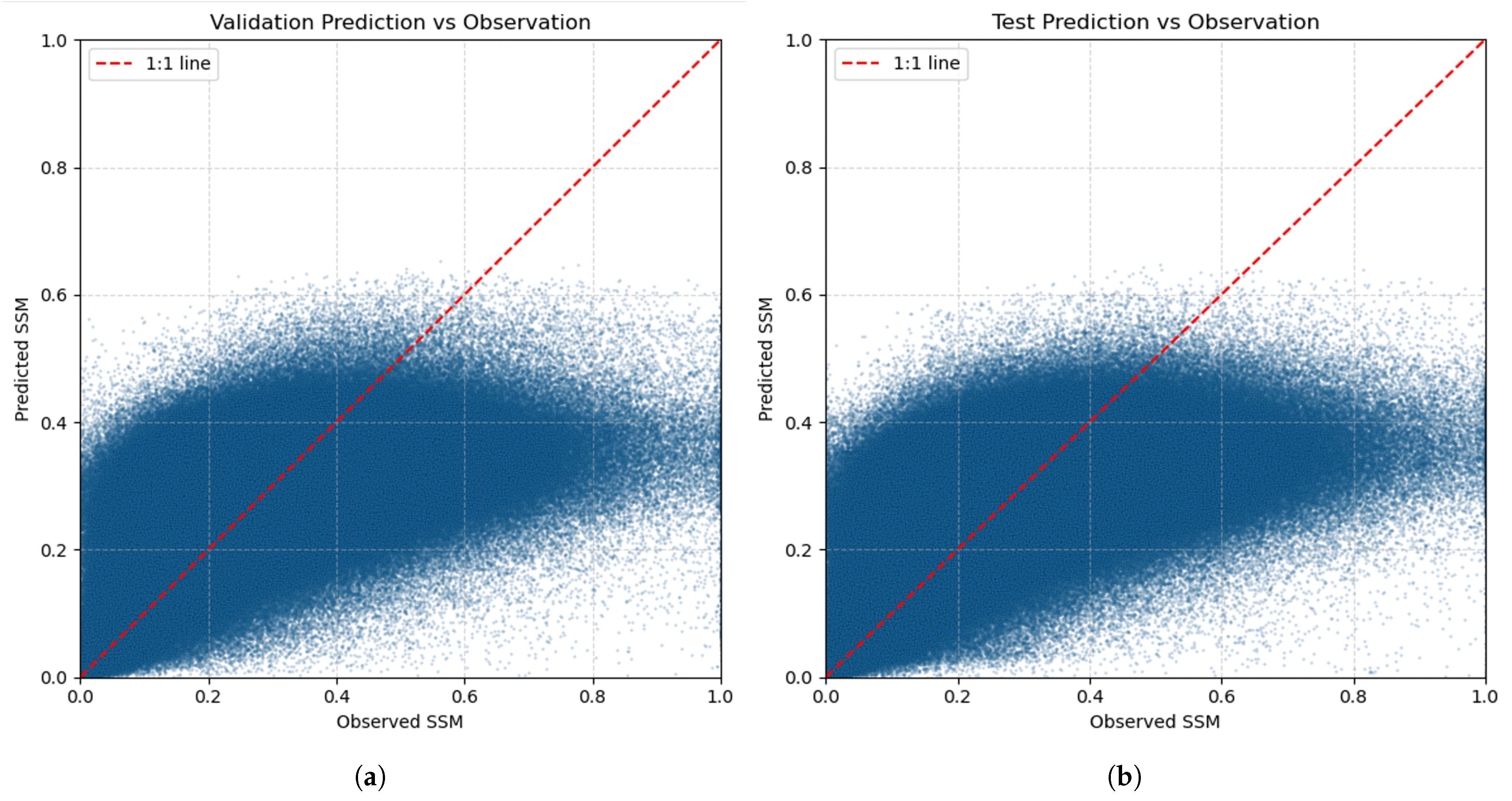
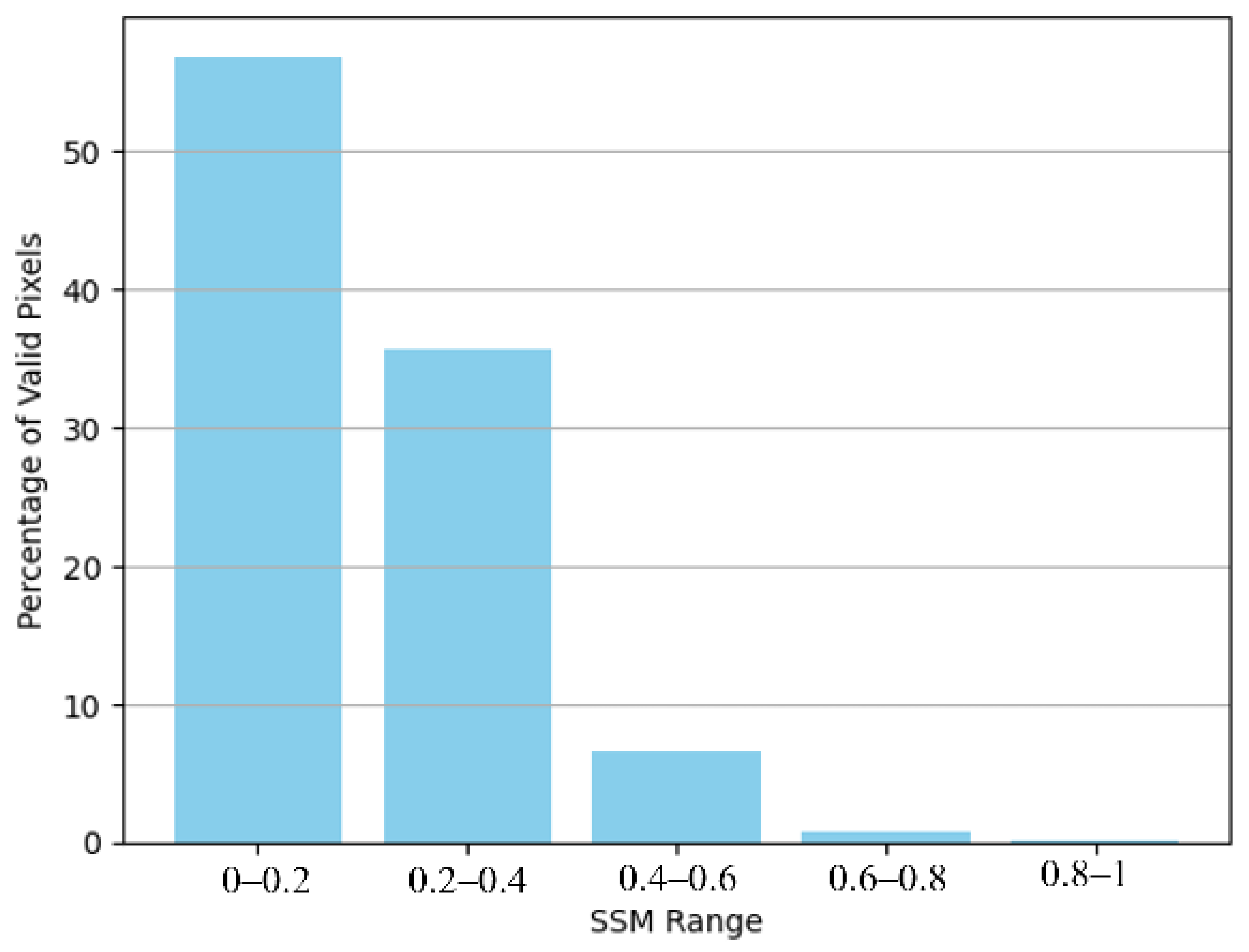
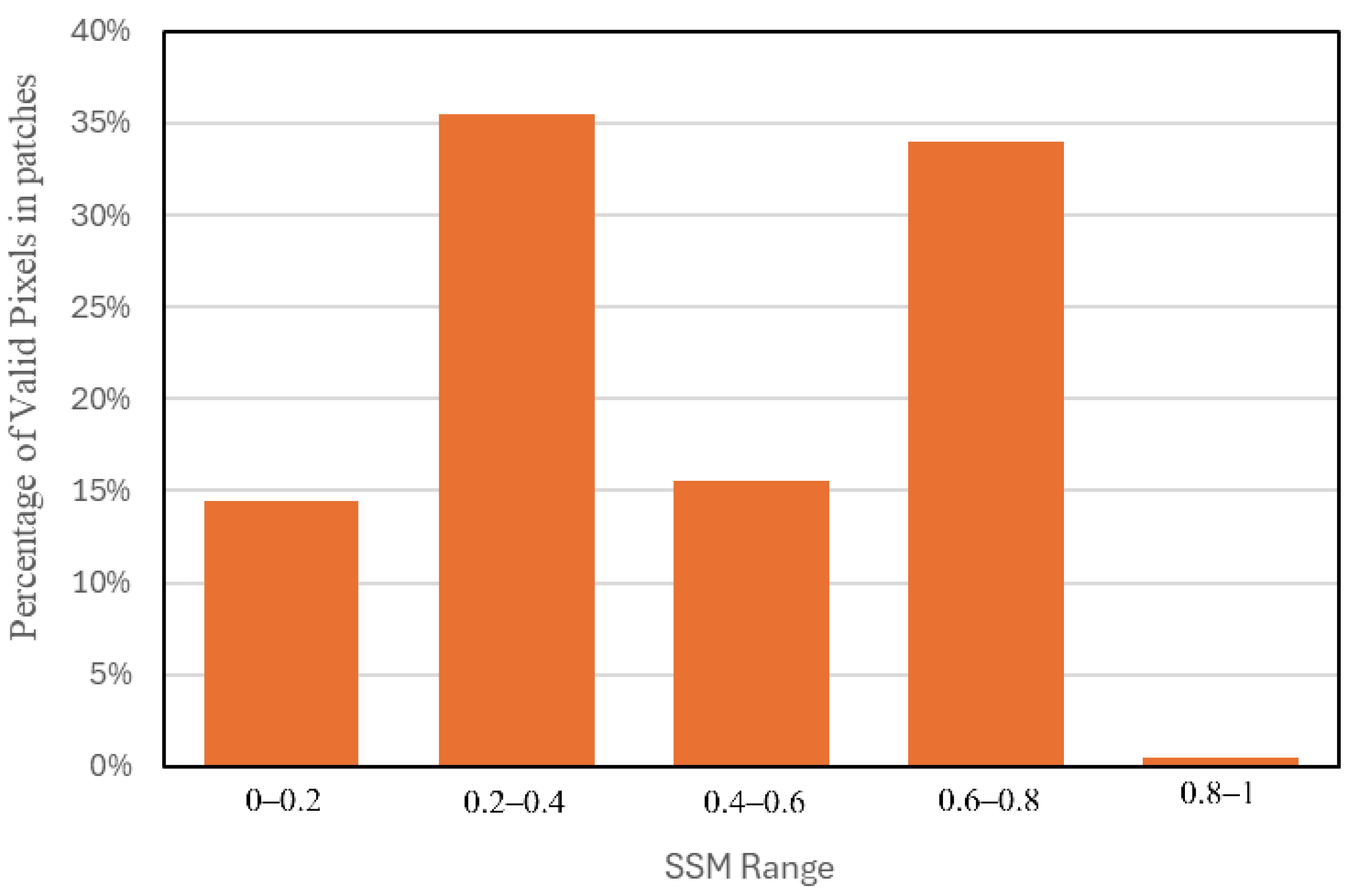
| Metric | Rebalance | 1-Day Model | 2-Day Model | 3-Day Model | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Training | Validation | Test | Training | Validation | Test | Training | Validation | Test | ||
| R2 | Before | 0.2135 | 0.2035 | 0.2076 | 0.1936 | 0.1834 | 0.1917 | 0.1992 | 0.1896 | 0.1970 |
| After | 0.7170 | 0.7137 | 0.7166 | 0.7224 | 0.7173 | 0.7171 | 0.7204 | 0.7122 | 0.7151 | |
| RMSE | Before | 0.1492 | 0.1504 | 0.1498 | 0.1511 | 0.1523 | 0.1513 | 0.1506 | 0.1518 | 0.1508 |
| After | 0.1520 | 0.1530 | 0.1519 | 0.1523 | 0.1537 | 0.1541 | 0.1528 | 0.1550 | 0.1547 | |
| MAE | Before | 0.1139 | 0.1148 | 0.1146 | 0.1148 | 0.1157 | 0.1151 | 0.1148 | 0.1156 | 0.1152 |
| After | 0.1016 | 0.1021 | 0.1014 | 0.1021 | 0.1029 | 0.1033 | 0.1029 | 0.1045 | 0.1040 | |
| Correlation | Before | 0.4664 | 0.4572 | 0.4596 | 0.4510 | 0.4415 | 0.4485 | 0.4522 | 0.4433 | 0.4492 |
| After | 0.8471 | 0.8452 | 0.8469 | 0.8508 | 0.8477 | 0.8489 | 0.8489 | 0.8442 | 0.8459 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseinizadeh, A.; Sheng, Z.; Liu, Y. High-Resolution Spatiotemporal Mapping of Surface Soil Moisture Using ConvLSTM Model and Sentinel-1 Data. Water 2025, 17, 3300. https://doi.org/10.3390/w17223300
Hosseinizadeh A, Sheng Z, Liu Y. High-Resolution Spatiotemporal Mapping of Surface Soil Moisture Using ConvLSTM Model and Sentinel-1 Data. Water. 2025; 17(22):3300. https://doi.org/10.3390/w17223300
Chicago/Turabian StyleHosseinizadeh, Atieh, Zhuping Sheng, and Yi Liu. 2025. "High-Resolution Spatiotemporal Mapping of Surface Soil Moisture Using ConvLSTM Model and Sentinel-1 Data" Water 17, no. 22: 3300. https://doi.org/10.3390/w17223300
APA StyleHosseinizadeh, A., Sheng, Z., & Liu, Y. (2025). High-Resolution Spatiotemporal Mapping of Surface Soil Moisture Using ConvLSTM Model and Sentinel-1 Data. Water, 17(22), 3300. https://doi.org/10.3390/w17223300






