Dual-Objective Pareto Optimization Method of Flapping Hydrofoil Propulsion Performance Based on MLP and Double DQN
Abstract
1. Introduction
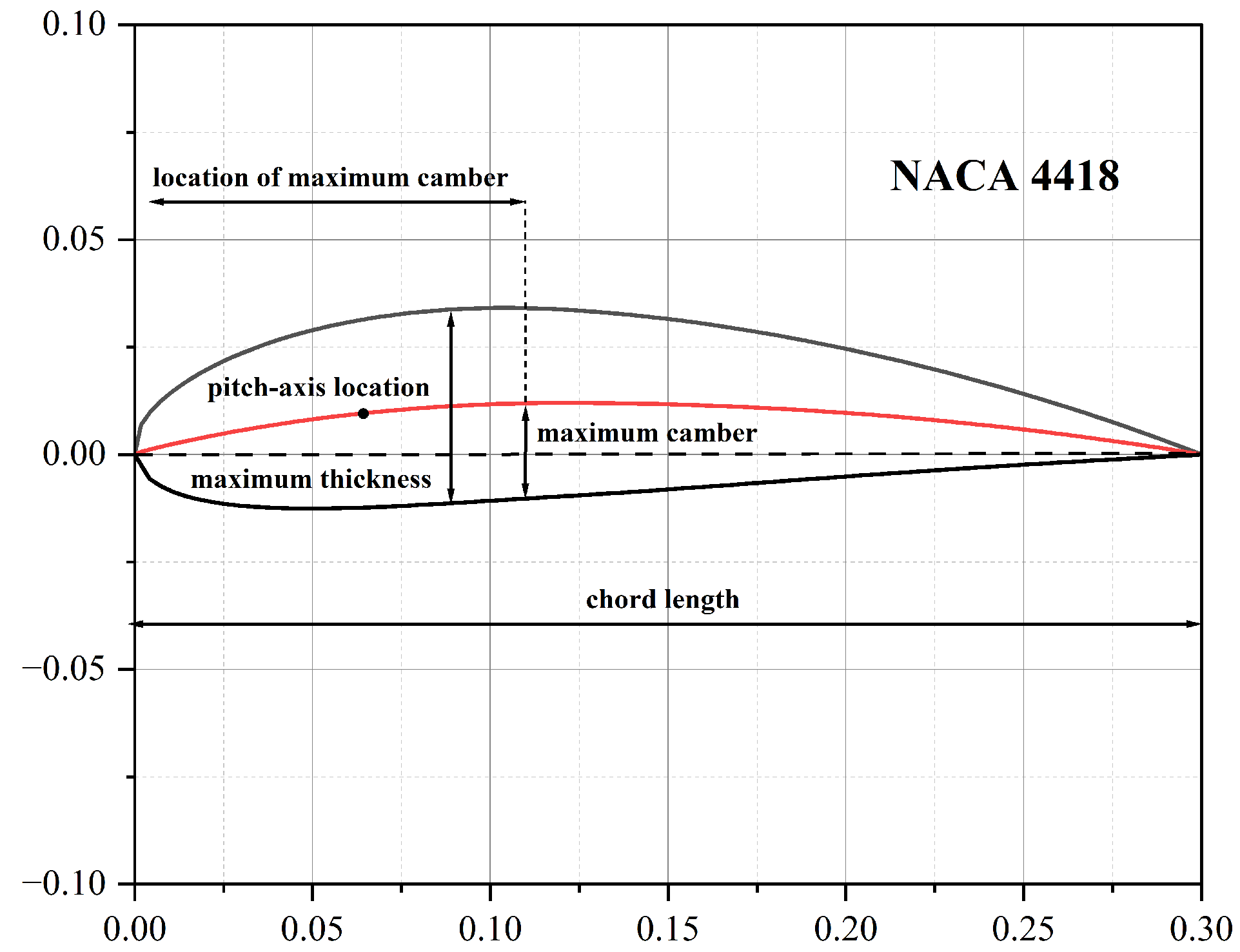
2. Flapping Hydrofoil Propulsion Problem
3. Numerical Method
3.1. Control Equations and Turbulence Modeling
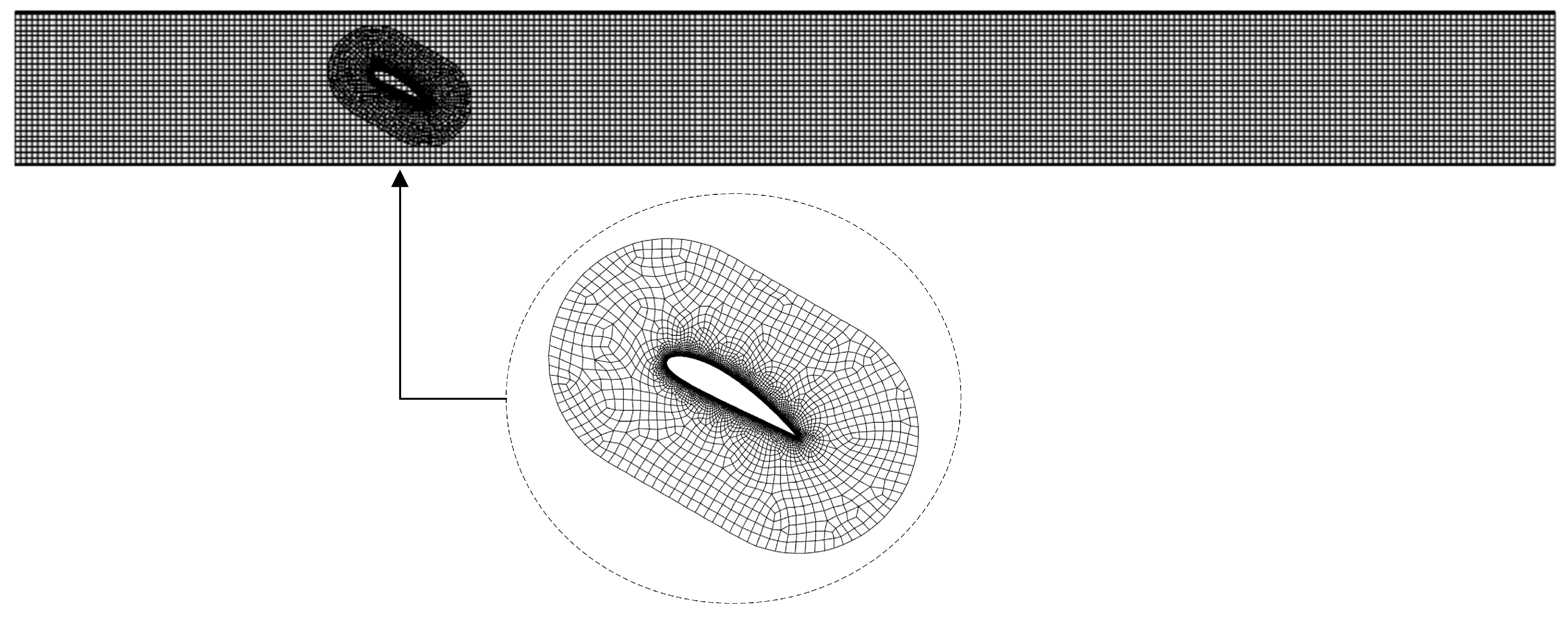
3.2. Computational Domain and Meshing
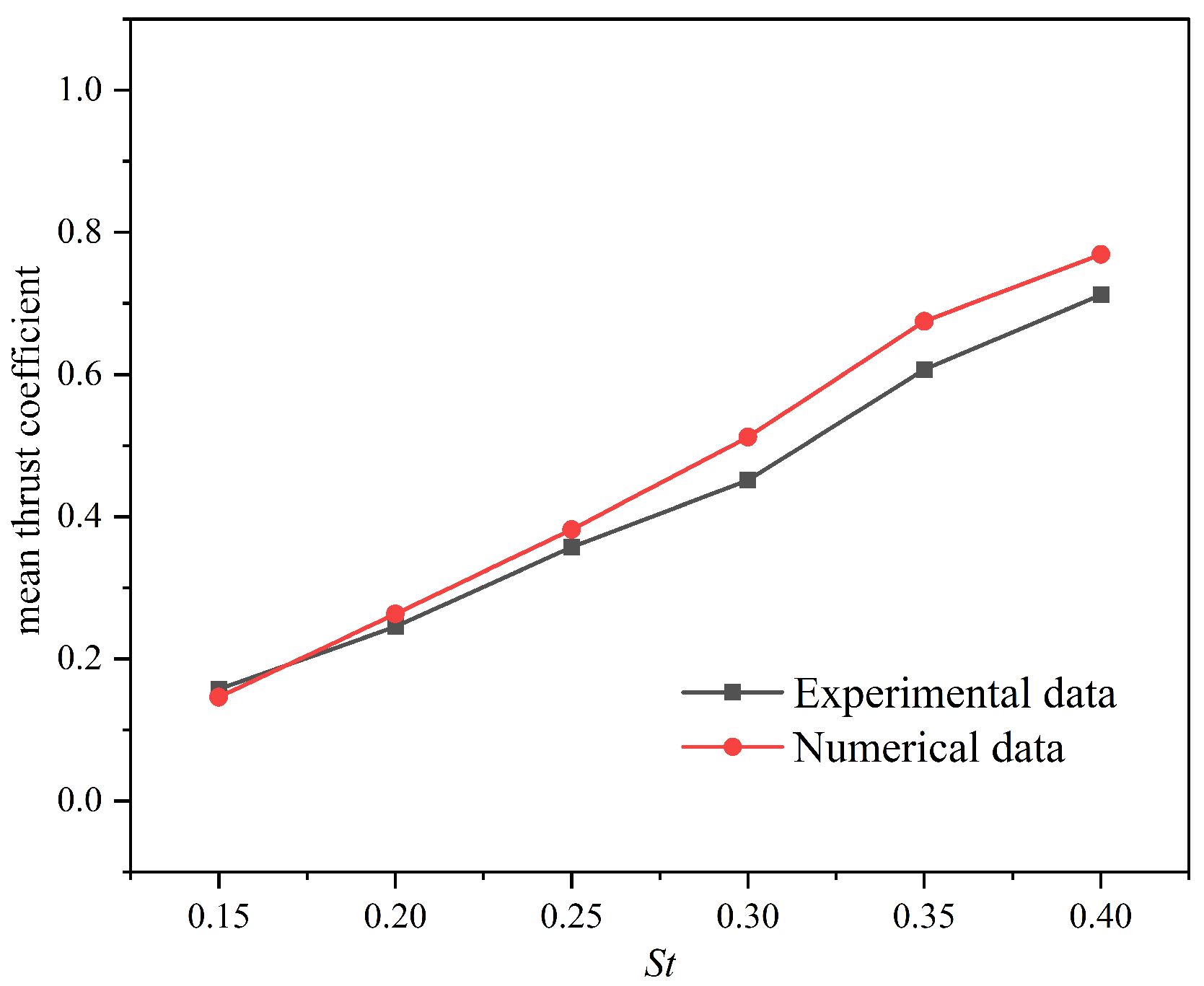
3.3. Numerical Method Validation
4. Methodology
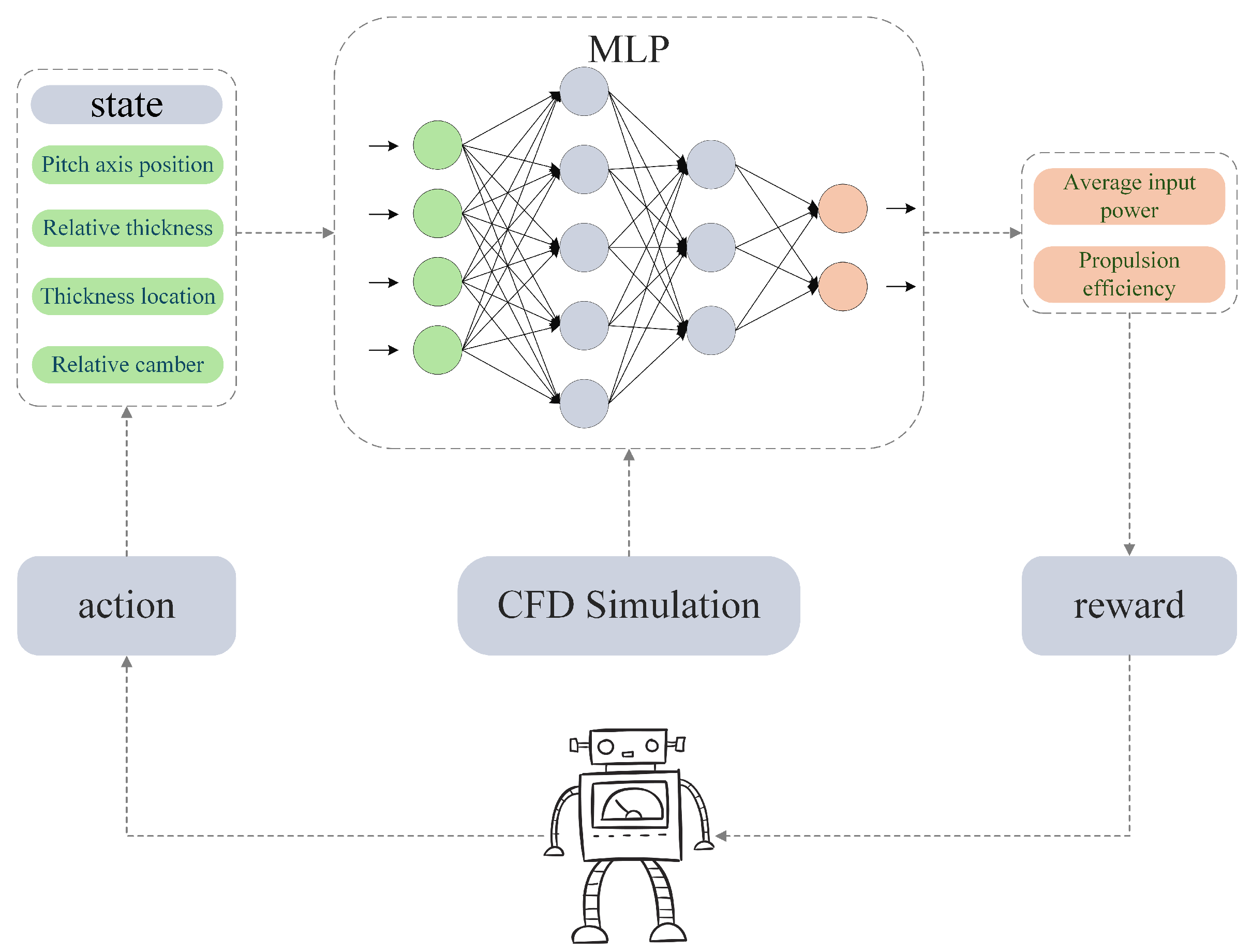
4.1. Overview of MLP-DDQN Framework
4.2. MLP for Hydrofoil Parameter-Performance Mapping
4.2.1. Introduction to MLP Model
4.2.2. MLP Architecture and Training
4.3. DDQN Incorporating Pareto Frontier Information
4.3.1. Introduction to Deep Reinforcement Learning
4.3.2. DDQN for Hydrofoil Optimization
| Algorithm 1 DDQN with Pareto Optimization |
|
4.3.3. MLP-DDQN for the Fluid Solver
5. Results and Discussion
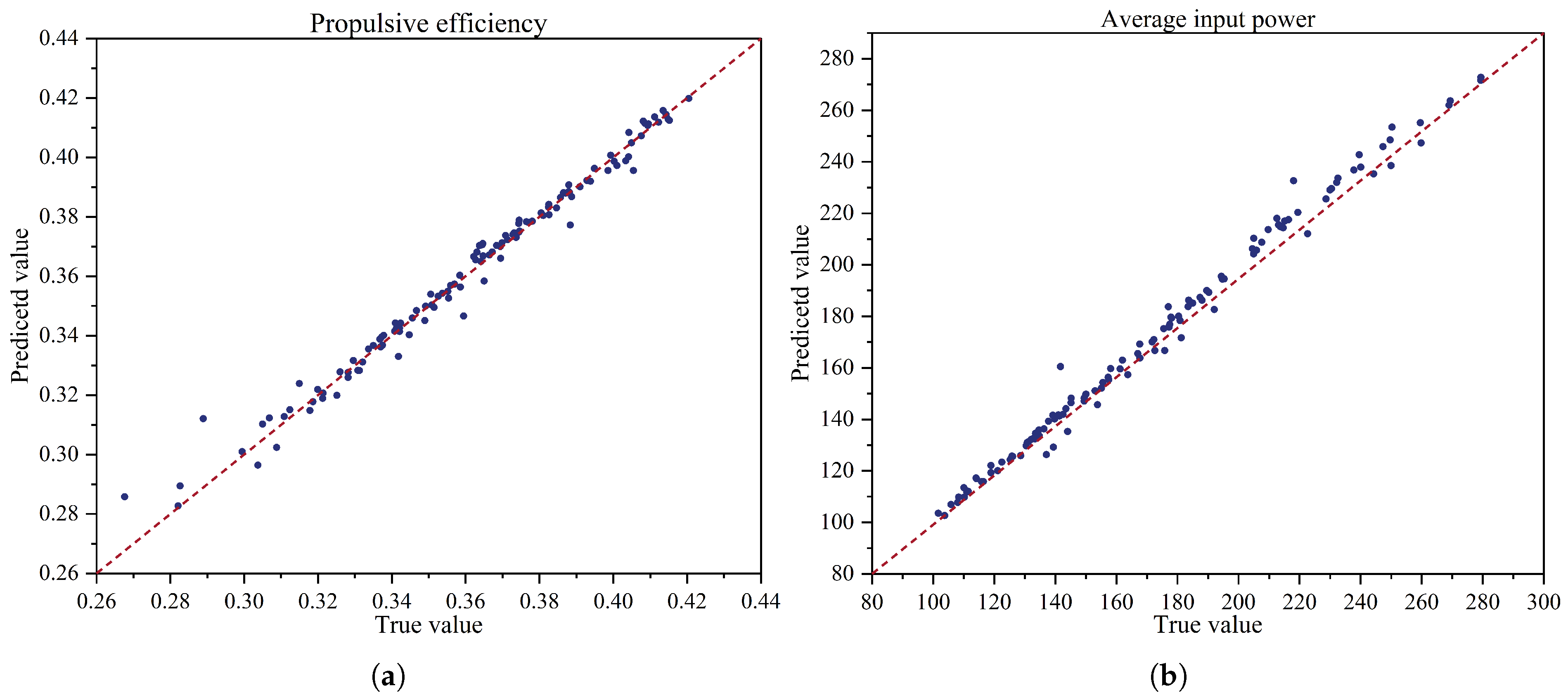
5.1. MLP Surrogate Model
5.2. DDQN Agent
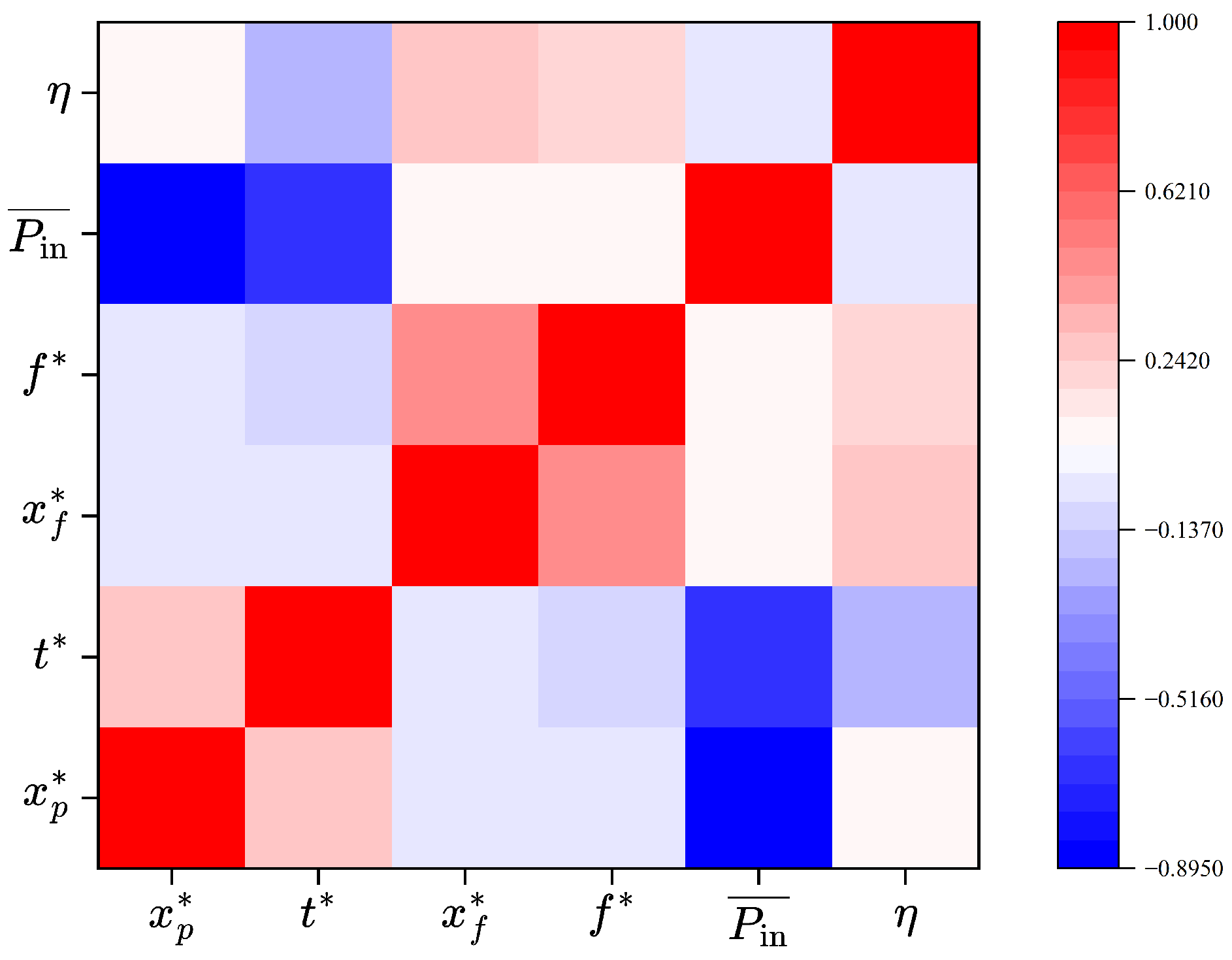
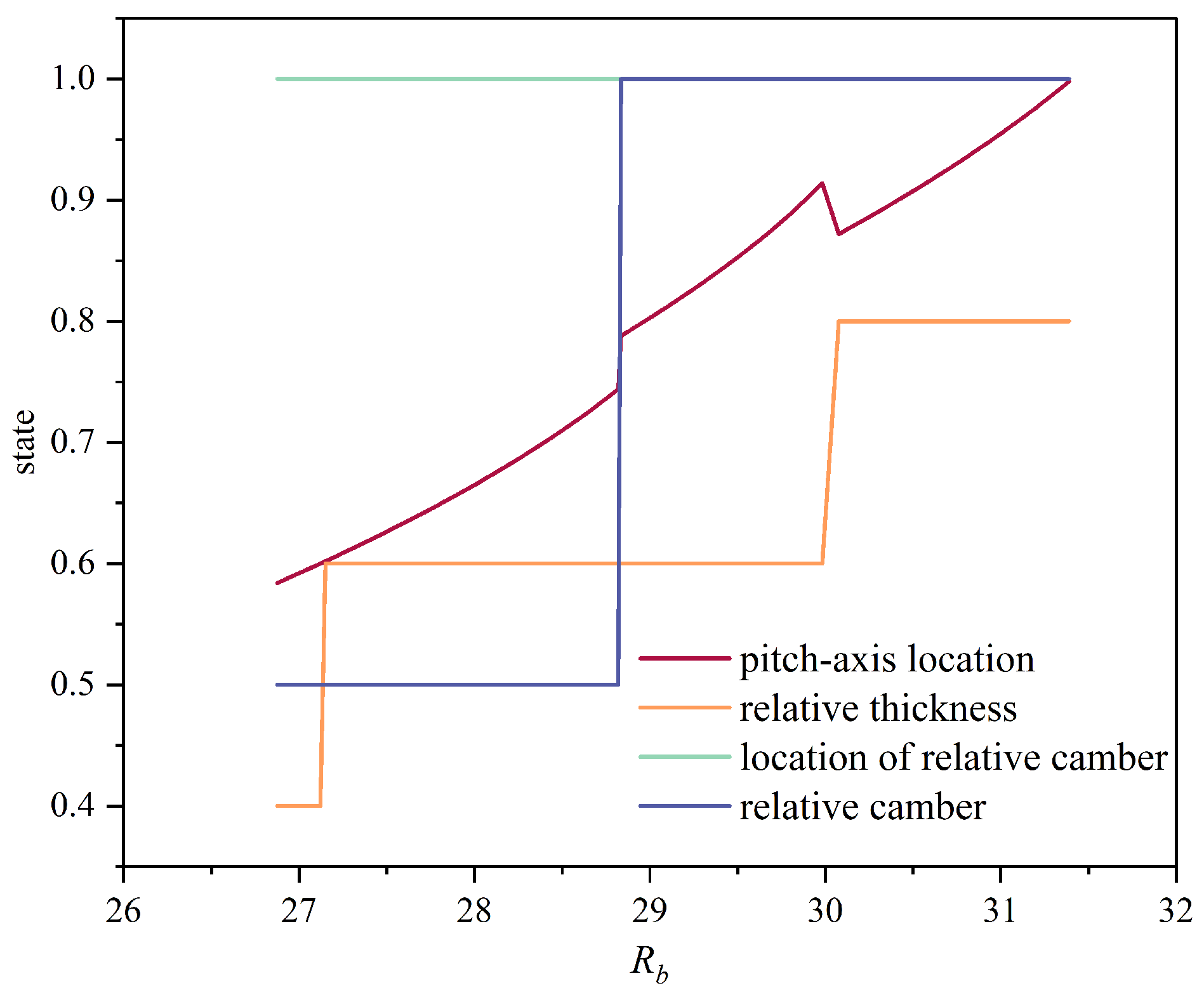
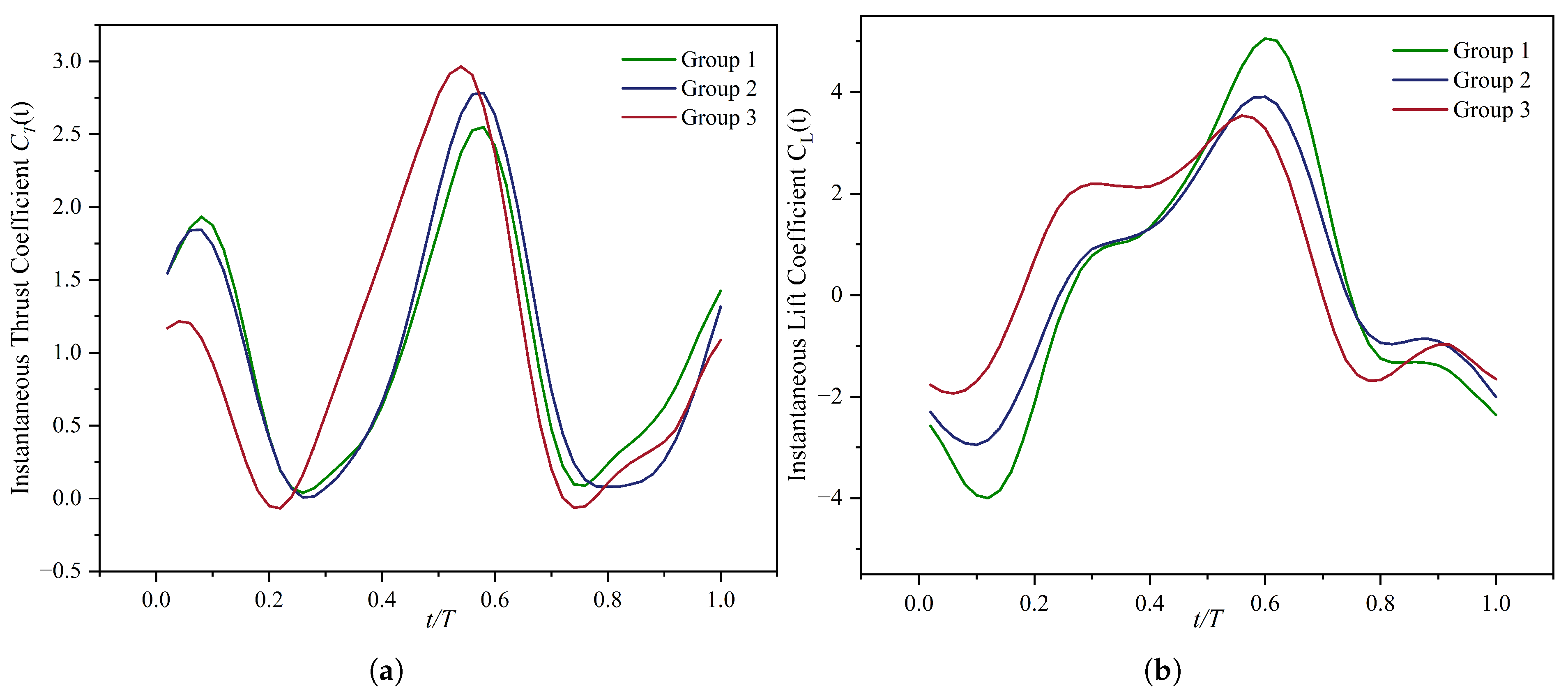
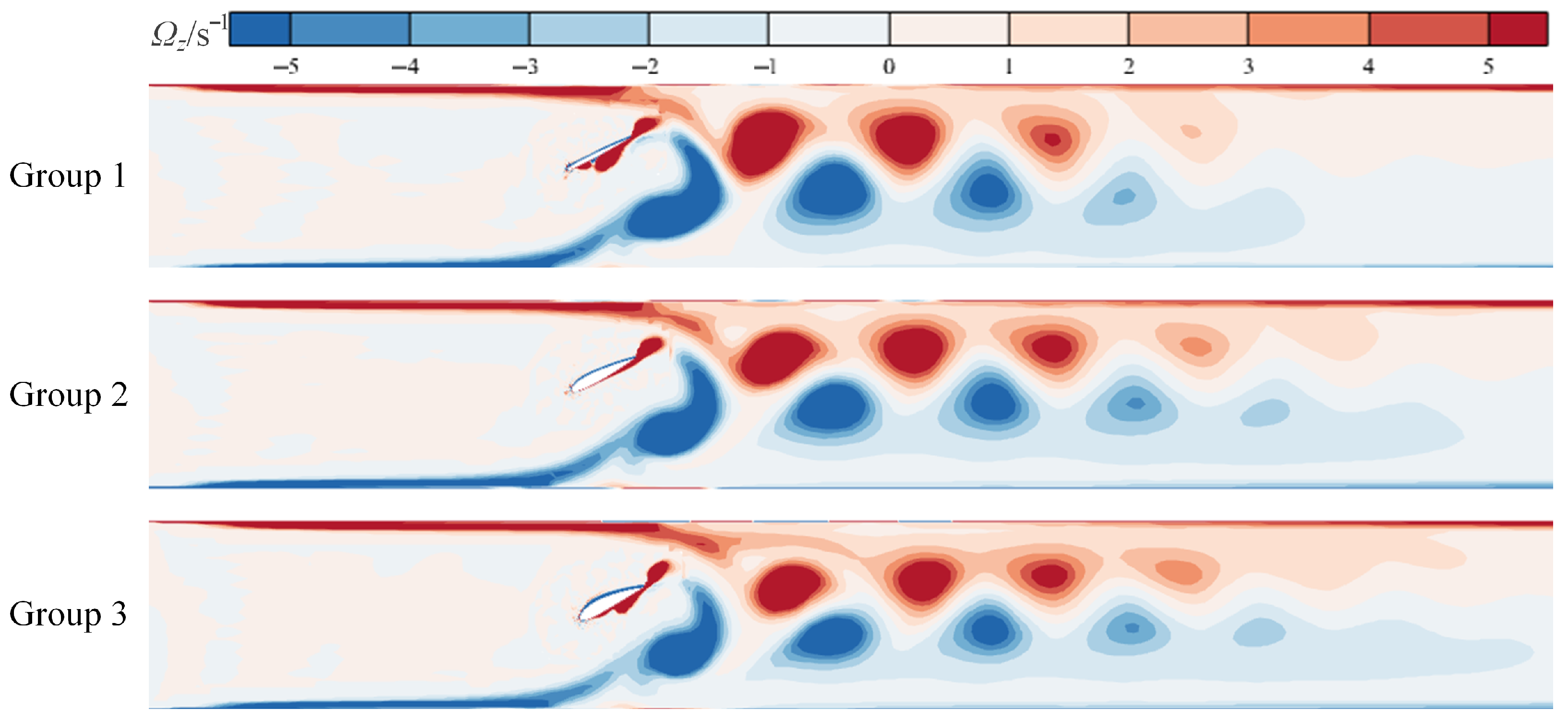
5.3. Influence of the Parameter Combinations on the Propulsive Performance
6. Conclusions
- After training, the MLP-DDQN method rapidly locates multiple optima within the design domain using few samples and also returns competitive solutions near local optima. Relative to direct optimization in the original CFD environment, it achieves wall-time speedups of several orders of magnitude and requires only about of the samples used by conventional deep reinforcement learning, thereby improving training efficiency.
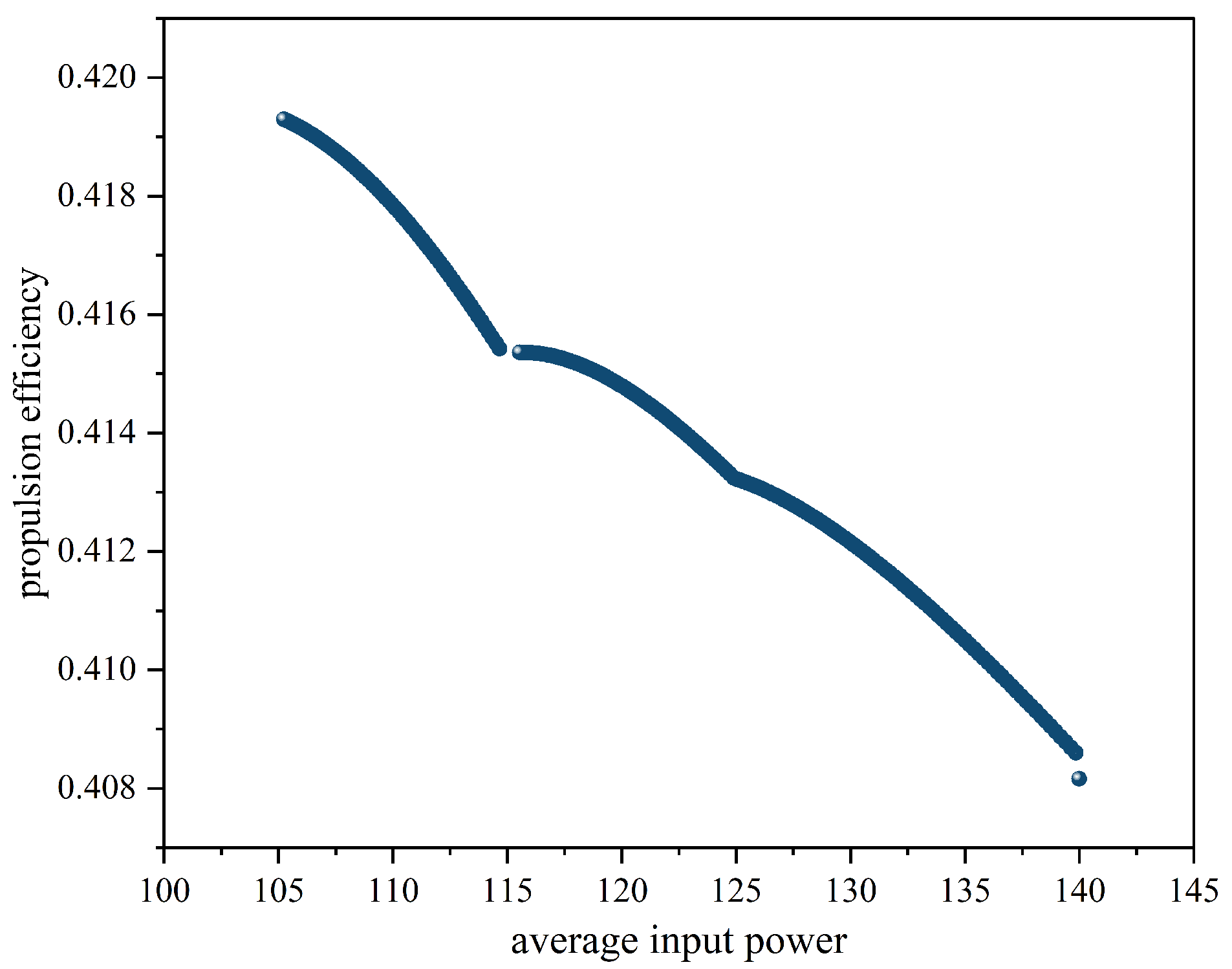
- The Pareto set produced by the MLP-DDQN method exhibits a mean averaged input power of and a mean propulsive efficiency of . Moreover, with reward shaping, the optimal solutions obtained under different power constraints differ from the corresponding simulation targets by only –.
- Flow-field analyses across geometric parameter combinations indicate that a moderate rearward shift of the pitch-axis location, together with an appropriately shaped leading edge, promotes an orderly reverse von Kármán vortex street over the flapping hydrofoil, enhancing jet momentum transfer while reducing dissipation of shed vortices. This reduces energy loss and yields higher propulsive efficiency.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Segura, E.; Morales, R.; Somolinos, J.A.; Lopez, A. Techno-Economic Challenges of Tidal Energy Conversion Systems: Current Status and Trends. Renew. Sustain. Energy Rev. 2017, 77, 536–550. [Google Scholar] [CrossRef]
- Picardi, G.; Astolfi, A.; Chatzievangelou, D.; Aguzzi, J.; Calisti, M. Underwater Legged Robotics: Review and Perspectives. Bioinspiration Biomim. 2023, 18, 031001. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Chen, Y.; Zuo, X.; Jiang, Q.; Ye, X.; Xue, G. Hydrodynamic Performance Analysis and Diving Trajectory Prediction of a Novel Deep-Sea Lander with Flapping Hydrofoils. Ocean. Eng. 2024, 310, 118664. [Google Scholar] [CrossRef]
- Liu, Z.; Qu, H.; Song, X.; Chen, Z. A State-of-the-Art Review on Energy-Harvesting Performance of the Flapping Hydrofoil with Influential Parameters. Renew. Energy 2025, 245, 122849. [Google Scholar] [CrossRef]
- Xing, J.; Yang, L. Wave Devouring Propulsion: An Overview of Flapping Foil Propulsion Technology. Renew. Sustain. Energy Rev. 2023, 184, 113589. [Google Scholar] [CrossRef]
- Mohammed Arab, F.; Augier, B.; Deniset, F.; Casari, P.; Astolfi, J.A. Effects on Cavitation Inception of Leading and Trailing Edge Flaps on a High-Performance Hydrofoil. Appl. Ocean. Res. 2022, 126, 103285. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, J.; Zhang, J.; Qin, J. Numerical Analysis of Effect of Bionic Hydrofoil Structure on Cavitation Suspension. J. Drain. Irrig. Mach. Eng. 2024, 42, 685–692, 700. [Google Scholar]
- Zhang, S.; Mei, L.; Zhou, J. Numerical Prediction of Hydrodynamic Performance of Differently Shaped Flapping Foil Propulsors. Chin. J. Ship Res. 2021, 16, 1. [Google Scholar] [CrossRef]
- Gupta, S.; Sharma, A.; Agrawal, A.; Thompson, M.C.; Hourigan, K. Role of Shape and Kinematics in the Hydrodynamics of a Fish-Like Oscillating Hydrofoil. J. Mar. Sci. Eng. 2023, 11, 1923. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, Z.; Xu, P. Hydrodynamic Experiment and Mechanism of Improved Oscillating Hydrofoil. J. Huazhong Univ. Sci. Technol. (Natural Sci. Ed.) 2019, 47, 87–93. (In Chinese) [Google Scholar]
- Zhe, H.; Liu, Y.; Tan, J.; Si, X.; Yuan, P.; Wang, S. Influence of Different Vortex Generator Parameters on Hydrodynamic Characteristics of Tidal Current Turbine Hydrofoil. Acta Energiae Solaris Sin. 2022, 43, 350–356, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Wang, L.; Xu, J.; Luo, W.; Luo, Z.; Xie, J.; Yuan, J.; Tan, A.C.C. A Deep Learning-Based Optimization Framework of Two-Dimensional Hydrofoils for Tidal Turbine Rotor Design. Energy 2022, 253, 124130. [Google Scholar] [CrossRef]
- Song, Z.; Zhu, J.; Lu, D. Optimization of Flapping Hydrofoil Propulsion Performance Based on Combined Neural Network and CFD. Acta Aerodyn. Sin. 2024, 42, 53–63. (In Chinese) [Google Scholar]
- Najafi, A.; Nowruzi, H.; Ghassemi, H. Performance Prediction of Hydrofoil-Supported Catamarans Using Experiment and ANNs. Appl. Ocean. Res. 2018, 75, 66–84. [Google Scholar] [CrossRef]
- Wang, L.; Xu, J.; Wang, Z.; Zhang, B.; Luo, Z.; Yuan, J.; Tan, A.C.C. A Novel Cost-Efficient Deep Learning Framework for Static Fluid–Structure Interaction Analysis of Hydrofoil in Tidal Turbine Morphing Blade. Renew. Energy 2023, 208, 367–384. [Google Scholar] [CrossRef]
- Yang, Y.; Wei, H.; Fan, D.; Li, A. Optimization Method of Underwater Flapping Foil Propulsion Performance Based on Gaussian Process Regression and Deep Reinforcement Learning. J. Shanghai Jiaotong Univ. 2025, 59, 70. [Google Scholar] [CrossRef]
- Kostas, K.V.; Ginnis, A.I.; Politis, C.G.; Kaklis, P.D. Shape-Optimization of 2D Hydrofoils Using an Isogeometric BEM Solver. Comput.-Aided Des. 2017, 82, 79–87. [Google Scholar] [CrossRef]
- Zhu, G.; Feng, J.; Li, P.; Wang, Z.; Wu, G.; Luo, X. Multi-Condition Optimisation Design of a Hydrofoil Based on Deep Belief Network. Ocean. Eng. 2023, 272, 113846. [Google Scholar] [CrossRef]
- Sun, Q.; Hua, E.; Sun, L.; Qiu, L.; Song, Y.; Xiang, M. Study on the Hydrodynamic Performance of Swing-Type Flapping Hydrofoil Bionic Pumps Affected by Foil Camber. Water 2024, 16, 595. [Google Scholar] [CrossRef]
- Hua, E.; Lu, C.; Xiang, M.; Song, Y.; Wang, T.; Sun, Q. Study on the Influence of Relative Chord Length and Frequency of Flapping Hydrofoil Device on Hydrodynamic Performance and Bank Slope Scour. Water 2025, 17, 1026. [Google Scholar] [CrossRef]
- Zhang, X.; Su, Y.; Yang, L.; Wang, Z. Hydrodynamic Performance of Flapping-Foil Propulsion in the Influence of Vortices. J. Mar. Sci. Appl. 2010, 9, 213–219. [Google Scholar] [CrossRef]
- Ji, B.; Luo, X.; Arndt, R.E.A.; Wu, Y. Numerical simulation of three-dimensional cavitation shedding dynamics with special emphasis on cavitation–vortex interaction. Ocean. Eng. 2014, 87, 64–77. [Google Scholar] [CrossRef]
- Shaheed, R.; Mohammadian, A.; Kheirkhah Gildeh, H. A comparison of standard k–ε and realizable k–ε turbulence models in curved and confluent channels. Environ. Fluid Mech. 2019, 19, 543–568. [Google Scholar] [CrossRef]
- Schouveiler, L.; Hover, F.S.; Triantafyllou, M.S. Performance of flapping foil propulsion. J. Fluids Struct. 2005, 20, 949–959. [Google Scholar] [CrossRef]
- West, D. Neural Network Credit Scoring Models. Comput. Oper. Res. 2000, 27, 1131–1152. [Google Scholar] [CrossRef]
- Mirjalili, S. How Effective Is the Grey Wolf Optimizer in Training Multi-Layer Perceptrons. Appl. Intell. 2015, 43, 150–161. [Google Scholar] [CrossRef]
- Tang, J.; Deng, C.; Huang, G.B. Extreme Learning Machine for Multilayer Perceptron. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 809–821. [Google Scholar] [CrossRef] [PubMed]
- Talaei Khoei, T.; Ould Slimane, H.; Kaabouch, N. Deep Learning: Systematic Review, Models, Challenges, and Research Directions. Neural Comput. Appl. 2023, 35, 23103–23124. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-Level Control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep Reinforcement Learning: A Brief Survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Hessel, M.; Modayil, J.; Van Hasselt, H.; Schaul, T.; Ostrovski, G.; Dabney, W.; Horgan, D.; Piot, B.; Azar, M.; Silver, D. Rainbow: Combining Improvements in Deep Reinforcement Learning. Proc. AAAI Conf. Artif. Intell. 2018, 32, 3215–3222. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, H.; Zheng, W.; Xia, Y.; Li, Y.; Chen, P.; Guo, K.; Xie, H. Multi-Objective Workflow Scheduling with Deep-Q-Network-Based Multi-Agent Reinforcement Learning. IEEE Access 2019, 7, 39974–39982. [Google Scholar] [CrossRef]



| Parameter | Value Range |
|---|---|
| relative thickness | {6, 9, 12, 15, 18, 24} |
| relative camber | {0, 1, 2, 4} |
| location of relative camber | {0, 4} |
| pitch-axis location | [0, 50] |
| Target | Set | MAE | MSE | Training Time (s) | Inference Time (ms) | |
|---|---|---|---|---|---|---|
| averaged input power | Training | 1.7485 | 8.0898 | 0.9961 | 5.90 | – |
| – | Validation | 1.8794 | 10.8440 | 0.9944 | – | 0.27 |
| propulsive efficiency | Training | 0.0026 | 0.9867 | 7.73 | – | |
| – | Validation | 0.0028 | 0.9819 | – | 0.25 |
| Category | State Vector | CFD | Prediction | MLP–DDQN Samples | Traditional CFD Samples |
|---|---|---|---|---|---|
| Algorithmic optimum | [49.8, 18, 4, 4] | [104.52, 42.05] | [105.85, 41.67] | 624 | 4300 |
| averaged input power | [42.5, 15, 4, 4] | [120.04, 41.47] | [118.77, 41.37] | 624 | 4300 |
| averaged input power | [34.2, 15, 4, 2] | [129.94, 41.22] | [130.44, 41.64] | 624 | 4300 |
| averaged input power | [29.2, 15, 4, 2] | [139.98, 40.86] | [139.13, 40.43] | 624 | 4300 |
| ID | Average Input Power (W) | Propulsive Efficiency (%) | ||||
|---|---|---|---|---|---|---|
| Group 1 | 20.0 | 6 | 0 | 0 | 189.62 | 32.18 |
| Group 2 | 30.0 | 15 | 4 | 1 | 140.37 | 40.32 |
| Group 3 | 49.8 | 18 | 4 | 4 | 104.52 | 42.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Qiu, X.; Chen, W.; Hua, E.; Shen, Y. Dual-Objective Pareto Optimization Method of Flapping Hydrofoil Propulsion Performance Based on MLP and Double DQN. Water 2025, 17, 3290. https://doi.org/10.3390/w17223290
Zhang J, Qiu X, Chen W, Hua E, Shen Y. Dual-Objective Pareto Optimization Method of Flapping Hydrofoil Propulsion Performance Based on MLP and Double DQN. Water. 2025; 17(22):3290. https://doi.org/10.3390/w17223290
Chicago/Turabian StyleZhang, Jingling, Xuchen Qiu, Wenyu Chen, Ertian Hua, and Yajie Shen. 2025. "Dual-Objective Pareto Optimization Method of Flapping Hydrofoil Propulsion Performance Based on MLP and Double DQN" Water 17, no. 22: 3290. https://doi.org/10.3390/w17223290
APA StyleZhang, J., Qiu, X., Chen, W., Hua, E., & Shen, Y. (2025). Dual-Objective Pareto Optimization Method of Flapping Hydrofoil Propulsion Performance Based on MLP and Double DQN. Water, 17(22), 3290. https://doi.org/10.3390/w17223290





