Empirical Recalibration of Hunter’s Method for Peak Flow Estimation in Institutional Buildings: A Pilot Study in Data-Scarce Contexts

Abstract

Accurate estimation of peak water demand remains a challenge in institutional settings with floating populations, particularly in regions where design standards may require revision and validation to accommodate evolving consumption patterns. This pilot study assesses the potential of a probabilistic adaptation of Hunter’s method, calibrated through high-resolution flow and pressure monitoring, for peak flow estimation in five academic buildings in Loja, Ecuador. Over 62 days, usage parameters, duration (t), frequency (i), and peak period (h), were disaggregated from 1 min interval data to derive building-specific binomial probability distributions. The adapted model was compared against three benchmarks: the Neyman–Scott Rectangular Pulse Model (NSRPM), the Water Demand Calculator (WDC), and Ecuador’s Hydro-Sanitary Standard (NHE 2011). Results indicate the proposed approach estimates peak flows within −11.6% to +20.0% of observed values, outperforming WDC (systematic underestimation up to −81.5%) and NHE 2011 (average underestimation of −31.3%), though NSRPM achieved high accuracy for one site (−1.1%) with high inter-building variability (average −38.4%). While limited to a small sample in a single climatic context, this pilot demonstrates that temporal disaggregation of stochastic demand enables a context-sensitive recalibration of Hunter’s method, offering a methodologically sound basis for future validation across diverse institutional settings in the Global South.

1. Introduction

A properly sized internal water distribution network, designed to meet pressure and flow demands, ensures rational and sustainable water use, which is essential under global water stress conditions [1,2]. Water demand trends can be categorized as deterministic or stochastic. Deterministic demands, such as those from industrial activities, can be reliably estimated from operating conditions. In contrast, stochastic demands, like residential consumption, reflect variable and continuously changing usage patterns [3,4].

Some residential networks are designed using deterministic flow rate assumptions, which can negatively affect their performance [5,6]. The Simultaneity Factor (SF) is an empirical deterministic method based on experimentation, considered optimal for small networks and widely applied in design handbooks. It was first adopted in the French Standard, Norme Française de Plomberie (NFP) 41-201, with subsequent adaptations such as the Spanish Standards Ecuadorian Technical Standard of Construction (NTEC) and Ecuadorian Technical Standard (NTE) [7]. In Ecuador, the Ecuadorian Hydro-Sanitary Standard (NHE) 2011 proposes a determination of the maximum probable flow (Q_mp) through a modification to the French Standard NFP 41-204 [8].

On the other hand, Hunter’s method (HM) is supported by a probabilistic analysis of maximum consumption periods [9]. The Colombian standard NTC 1500 is based on an adaptation of HM, which considers variations around the factors of consumer units, generating lower demand than the original Hunter [10].

According to [11], who developed a probabilistic model for Q_mp determination, the probability of simultaneous consumption of several sanitary appliances (SA) is low, so the Q_mp should not be a simple sum of SA consumption. To determine the Q_mp, HM assigns dimensionless capacity factors to different sanitary devices with a maximum frequency of use and assumed duration, generating a corresponding maximum probable demand.

Ref. [11] indicated that a system works satisfactorily whenever a certain number of m devices out of a total n operate simultaneously 99% of the time. In other words, Hunter used the 99th percentile as the standard design margin to estimate maximum demand [12]. Hunter introduced the concept of supply units, or capacity factors, for the various SAs to measure the incidence in a hydraulic system, with the supply units, Hunter generated consumption curves in a single design curve. This curve is known as the Hunter curve [9].

Both HM and SF consider demands according to the SAs available at the time they were developed. SAs are currently manufactured with a trend of low consumption, more efficiency, and with lower flow rates [13]. In addition, SF and HM were developed considering consumption habits from different eras and regions [12]. The daily cycle in water consumption has a close relationship with the weather factors that occur in a geographic location [14], so the demand that can be generated at the domestic level can vary between latitudes. Those factors must be considered for the updating of methods of sanitary hydraulic design [15].

In practice, the variation of drinking water demand is often estimated in an approximate way from measurements taken in one supply pipe, assuming that this variation curve can be applied to any other section of the network, no matter the number of users connected. However, studies like [16] demonstrate that this approach is limited, because the real consumption at household level has a very stochastic character, with short duration pulses and long periods with no demand. For this reason, they propose a methodology based on the Neyman–Scott Rectangular Pulse Mode (NSRPM), which can reproduce the instantaneous variation of demand at different aggregation levels and under continuous or intermittent supply conditions.

On the other hand, ref. [17] was compiled by the International Association of Plumbing and Mechanical Officers (IAPMO) and the American Society of Plumbing Engineers (ASPE) to review the methodology and adequately estimate local demands. The research consisted of developing a probability model capable of predicting the maximum demand for domestic water, resulting in the Water Demand Calculator (WDC) model. For that, they used a database of measurements taken between 1996 and 2011 in more than 1000 single-family homes in the United States. An average of 11 days of monitoring per household, 2.72 residents per household, and 831.4 events per household were achieved.

Another proposal was set up in [18] on the basis that residential consumption is random in nature. Authors presented a stochastic model for their daily characterization. They generated a mixed probabilistic distribution, combining a random discrete variable distribution fusion and a continuous random variable. Their model was generated based on records from three real networks. The synthetic series generated demonstrated the efficiency of the stochastic model for residential water demand.

In Bogotá, Colombia, more recent research [19] evaluated peak water usage in residential buildings under different estimation methods. The study contrasted observed consumption patterns with theoretical approaches, including Hunter-based adaptations and local standards, and found that conventional methods tend to misrepresent actual peak demands. Results indicated that traditional procedures may lead either to underestimation or overestimation depending on fixture efficiency and household characteristics.

In Mexico City, Mexico [20], an update of Hunter’s method for hydraulic installations in buildings was presented, performing a wide field data collection such as the duration, frequency, and volumetric expenditure of each SA, aiming to determine different design curves for buildings of different uses. Ref. [9] in India made a modification to the Hunter curve incorporating the low flow rates of modern accessories and decreasing the level of confidence in the binomial probability function as raised by Hunter (1940).

Despite these advances, a critical gap persists for institutional settings in the Global South, which are often characterized by data scarcity and non-standardized infrastructure. Recent studies confirm that occupancy dynamics, not fixture efficiency, are the primary drivers of peak demand in such contexts [21,22]. For instance, research has demonstrated that institutional buildings exhibit non-deterministic, time-variable peak events, rendering residential models like the WDC inadequate [4]. Similarly, studies in Latin America have reported systematic misestimation (15–35% error) when applying legacy methods in institutional facilities [19]. These findings collectively underscore the critical need for building type-specific calibration, particularly for academic and public buildings [5,22].

Currently, in Ecuador, no research validates the NHE 2011 methodology against measured maximum instantaneous flows, nor are there proposals linked to the probabilistic basis of Hunter’s method for non-residential settings. This study addresses this gap by developing and validating a context-specific adaptation of Hunter’s method for academic facilities in Loja, Ecuador. The novelty lies in the empirical disaggregation of high-resolution (1 min) flow and pressure time series to derive building-specific usage parameters—duration (t), frequency (i), and peak period (h)—which recalibrate the binomial probability function. Unlike prior adaptations focused on residential or fixed-occupancy contexts [9,20], this work explicitly accounts for the stochastic timing of demand in floating-population environments, where peak events occur unpredictably throughout the day. For the comparative analysis, synthetic series were simulated using the NSRPM model [16,23]. The maximum probable flow was also estimated with the WDC model [17] and the NHE 2011 handbook.

While geographically focused, this study provides a methodologically rigorous and transferable framework for recalibrating probabilistic models in data-scarce institutional contexts of the Global South. The approach requires only 10–15 days of flow monitoring and a basic fixture inventory, resources accessible to municipal utilities, making it practically usable for updating hydro-sanitary design standards in similar highland urban areas.

2. Materials and Methods

2.1. Sites Selected for Study

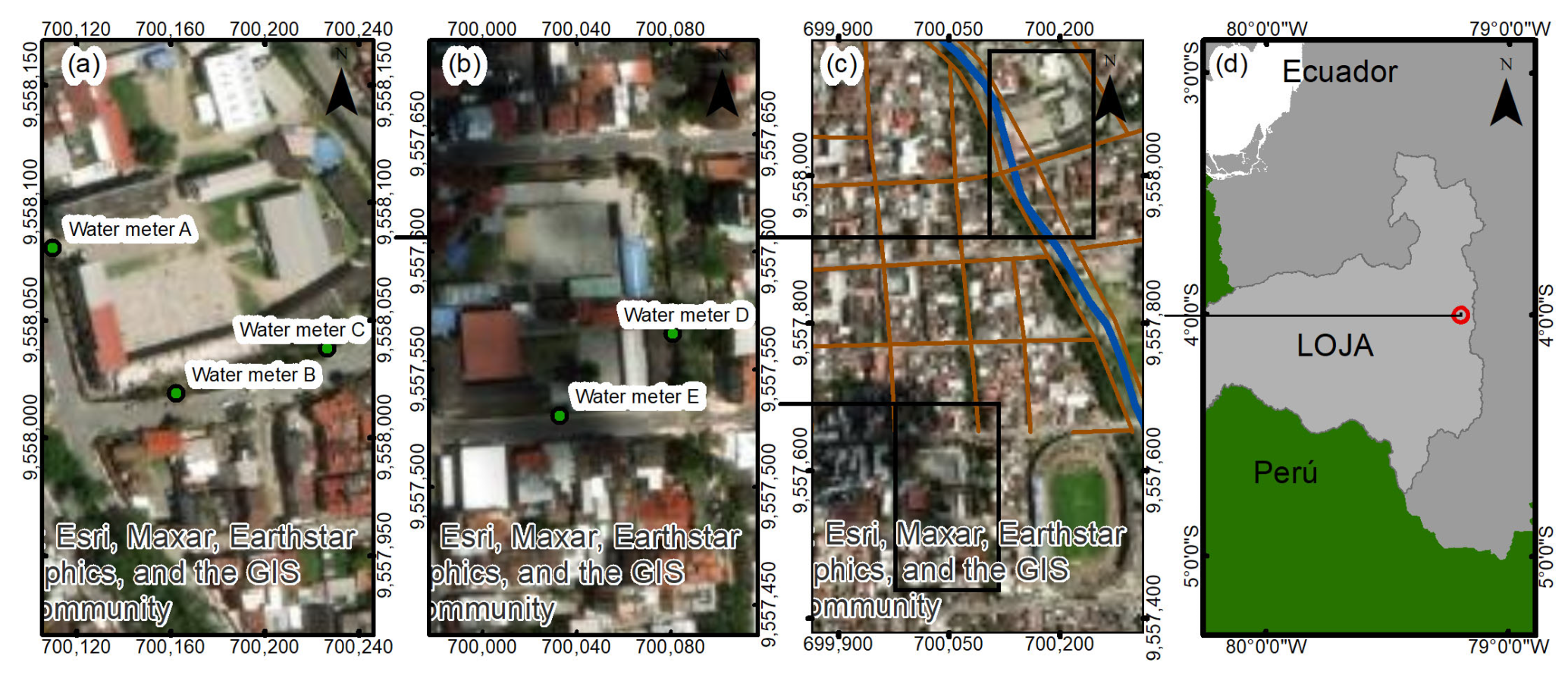
The study was carried out in the city of Loja, Ecuador, in five educational buildings, locating the equipment immediately after each water meter. A water meter with a source pipe of 0.0254 m (1″) diameter recording the consumption of 1514 people was designated the A water meter. Another water meter with a 0.0254 m (1″) source pipe detecting the consumption of 817 people was named the B water meter. The water meter with a source pipe of 0.0200 m (3/4″) diameter measuring the water consumption of 312 people was named the C water meter. Another water meter with a source pipe of 0.0125 m (1/2″) diameter recording the consumption of 360 people was named the D water meter. Finally, a water meter with a source pipe of 0.0200 m (3/4″) detecting the consumption of 220 people was named the E water meter. The academy facilities were chosen due to its population, which resembles the student occupancy rate typical of the location [24].

Demographic data were obtained from institutional enrollment records for the 2023–2024 academic year. Across the five educational facilities—comprising three secondary schools and two combined primary–secondary institutions—the student population totaled 3223 individuals, with a gender distribution of 52% female and 48% male. This proportion aligns closely with national enrollment statistics reported by Ecuador’s Ministry of Education [25], which indicate a nationwide average of 51.8% female students in basic education (grades 1–10). The age range spanned 6 to 17 years. Teaching and administrative staff accounted for an additional 11% of total occupants. Given the standardized sanitary infrastructure across public schools in Loja (typically water closets, urinals, and washbasins per Ministry of Education facility guidelines) and the homogeneous age–gender structure of the student body, demographic variability was not expected to significantly influence peak water demand patterns in these settings.

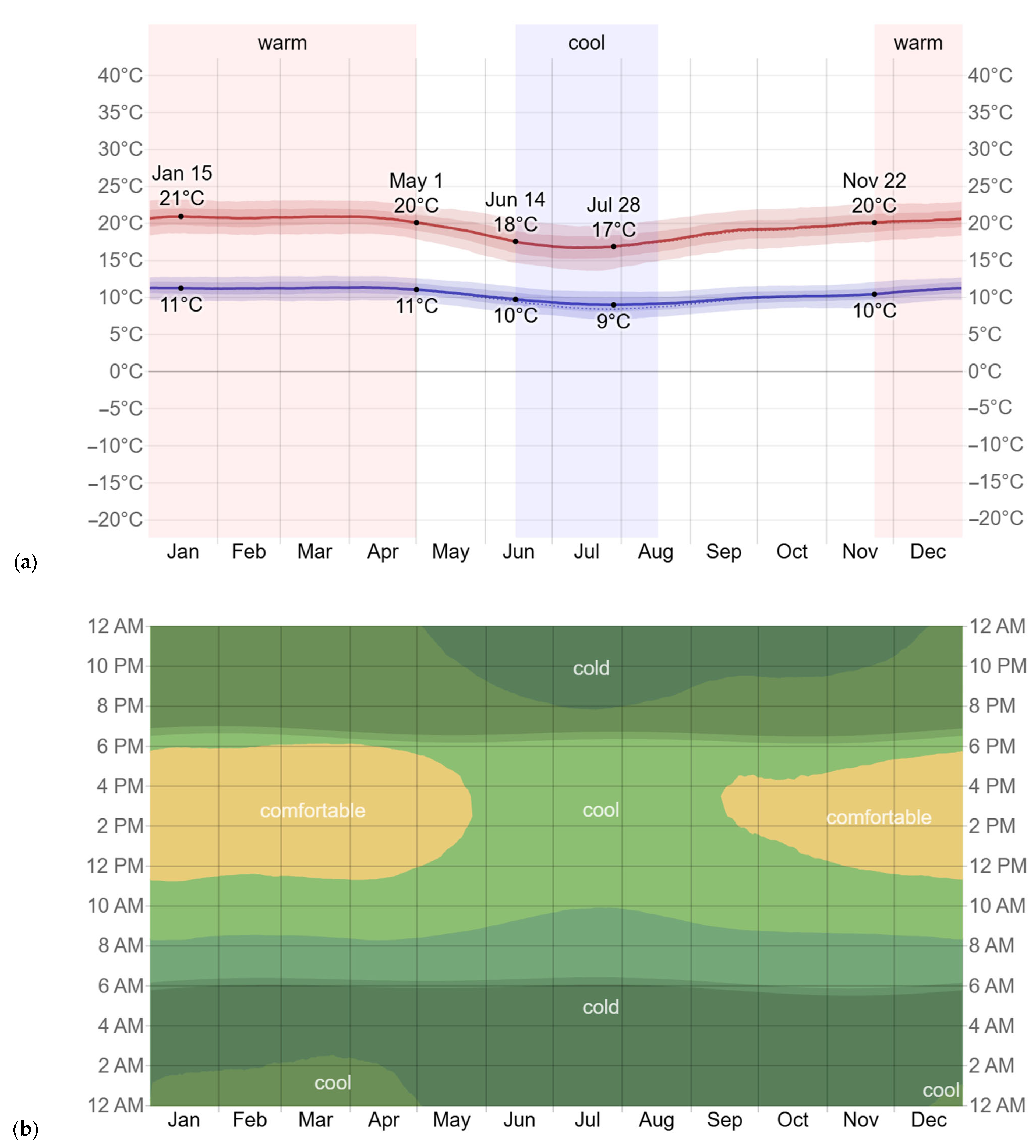
The monitoring campaign was conducted from August to November, encompassing the transition from the cool to the mild-warm season in Loja. Unlike temperate regions characterized by four distinct seasons (spring, summer, autumn, and winter), Loja—situated in the southern Ecuadorian Andes—exhibits a subtropical highland climate with only two dominant thermal periods. According to long-term climatological data [26], the mild-warm season lasts 5.3 months (22 November–1 May), with average daily high temperatures exceeding 20 °C; March is the warmest month, with average highs of 21 °C and lows of 11 °C. Conversely, the cool season spans 2.1 months (14 June–17 August), with average daily highs below 18 °C; July is the coldest month, featuring average highs of 17 °C and lows of 9 °C. Precipitation follows a bimodal pattern, with moderate rainfall and no pronounced dry or wet extremes, resulting in relatively stable indoor water demand throughout the year. Utility records [27] indicate that non-residential water consumption in Loja varies by less than 10% across months, supporting the representativeness of the monitoring period for typical annual conditions. This climatic stability enhances the generalizability of the findings to similar highland urban contexts in the tropical Andes. See Figure 1.

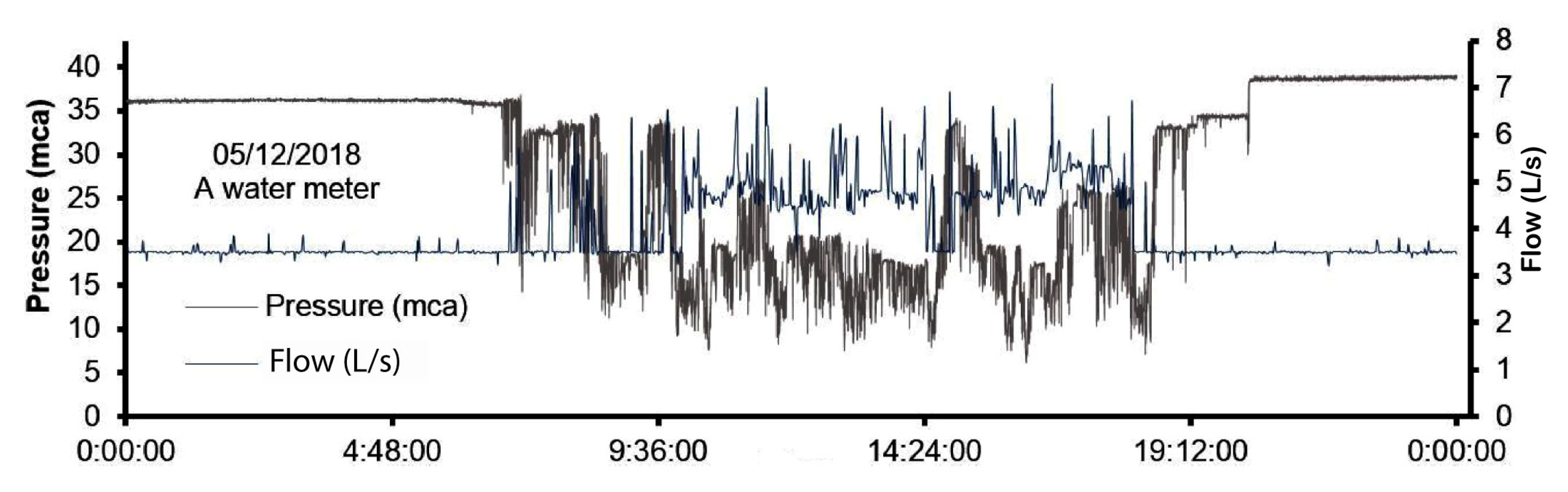
A survey was carried out of the existing sanitary hydraulic infrastructure in each studied educational establishment. The number and type of appliances were determined in relation to the water meter from which they are supplied. With data from pressure records and flow records, double-axis daily graphs were generated, representing pressure variation and expenditure per unit of time.

To provide a comprehensive understanding of the study’s spatial scope, Figure 2 illustrates the geographical location of Loja, a prominent town in Ecuador, alongside the specific facilities encompassed within this investigation. This map serves as a reference point, enabling readers to contextualize the study’s regional focus and the distribution of the examined facilities. See Figure 2.

2.2. Monitoring Node

The monitoring node installed after each water meter consisted of a Temperature Pressure Transduce Model PX1004L1-500AV [28], Pressure Data Logger, and an Invasive Compact Inductive Magnetic Flow Meter of type MIK-5NA50 A F300 [29]. The temporal flow and pressure variation were recorded.

Equipment type PX1004L1 has a margin of error of 0.25% in the pressure register, with a working range of 0.0 KPa to 3447.4 KPa (0 psi to 500 psi) [28]. The MIK-5NA50 Flow Meter records flow rates from 0.053 L/s, with an accuracy of 2.00% [29]. Pressure data were processed using the OM-PL Series Interface Software Version 2.31x program (Omega Engineering, Michigan City, IN, USA).

Recorded information and monitoring time.

The flow rate record was performed at one-minute intervals, for an average of 12 days for each water meter. Network pressures were recorded in shorter periods, varying from 4 s to 1 min, depending on the memory availability on the computer, in an average of 12 days per pressure data logger.

2.3. Hunter’s Method

Based on the methodology set out in [20] and developed in [9], data collection was performed for the variables involved in the probabilistic support of Hunter’s method. The duration of use (t) in seconds, the frequency of use (i) in seconds, and the maximum consumption period (h) in seconds also known as the top period were obtained through the pressure and flow graphs over time.

Both the intervals between discharges (i) and the duration (t) during the peak period (h) were set as averages in the entire observation period [11]. The adaptation of Hunter’s method is based on a stochastic simulation with evenly distributed random numbers. As explained in [20], if n SAs exist, used every i seconds, for t-seconds, the probability that r number of SAs operate simultaneously can be determined by Equations (1)–(6).

The n probability of finding the discharge of a sanitary appliance at any time is determined by Equation (1) [20]:

$$p=t/i$$

(1)

For the r selection, a total of n as combinations of n appliances taken from r at a given moment was estimated by Expression (2) [20]:

$$C_r^n={\displaystyle \frac{n!}{r!\left(n-r\right)!}}$$

(2)

Finally, the probability of r devices working at the same time was determined by Equation (3) [20]:

$$P_r^n=C_r^n{p}^r{(1-p)}^{n-r}$$

(3)

The maximum instantaneous flow Qm was determined through Equation (4) [20]:

$$Qm=mq$$

(4)

where q is the volumetric flow per unit of time of a sanitary appliance, m is the design factor, understood as the r value taken from the n SA in simultaneous use, i.e., the amount m of SA that they are discharging during the interval of t seconds immediately preceding the observation time.

Equation (5) is the mathematical condition used to evaluate the percentage of time in which the appliances are operating simultaneously (known as confidence level), proposed in [20]:

$${p_0}^n+{p_1}^n\dots +{p_{m-1}}^n+{p_m}^n\ge 0.99$$

(5)

From Equation (5), it can be interpreted that when the sum of probabilities, determined with several r values $P_r^n$ applied in Equation (3) for a random number n, is greater than 0.99, the last value of r for which this condition was given becomes m and to be applied in Equation (4). To find the capacity factors of the appliances, Equation (6) was used [20]:

$${\displaystyle \frac{f}{f_i}}={\displaystyle \frac{n_i}{n}}$$

(6)

where f is the arbitrary capacity factor assumed for the most energy-intensive furniture; f_i is the capacity factor to find, n is the SA number corresponding to f, and n_i corresponds to the number of SAs different from n for which the same probable flow is generated. Capacity factors are arbitrary values that weigh and measure the effect of demand.

Two types of consumption curves have been developed: (i) Probable flow based on n and (ii) Probable flow depending on appliance or consumption units. For the elaboration of these graphs, determination of n through Equation (1) is carried out. With random values of n, different values of r are evaluated with Equations (2) and (3) until Condition (5) is met. Once m values are determined for corresponding random values of n, Equation (4) is applied, with a given flow q for each water meter. Subsequently, consumption factors are assigned to each piece of appliance, giving a factor of 10 to the most flow generator that is the sink, generalizing a value per weight for each building, assuming a proportional consumption of each SA.

2.4. Neyman Scott Rectangular Pulse (NSRPM)

NSRPM is a stochastic approach for representing domestic consumption which can work with different logging intervals when considering a temporary demand disaggregation. It has been used mainly in the field of hydrology to generate synthetic series of precipitation using statistical parameters similar to the observed records, such as the average, variance, and covariance [23].

For this study, a process of disaggregation was followed, which consisted of data analysis, model formulation, estimation of statistical parameters, and validation of the synthetic series [30].

The theoretical and observed moments were determined in the data analysis. The observed moments were used in the minimization of an objective function considering a nonlinear mathematical programming (NLP), obtaining the theoretical moments [16,21,22].

The analysis interval was set to one minute, as the flow records have that measurement interval. Following the methodology set out in [16], the flow records were assembled into a data series, from which the average time between two events ${\lambda }^{-1}$ was determined, as well as the average time between each individual pulse and the event source ${\beta }^{-1}$, the average pulse duration $n^{-1}$, the average intensity (flow) of the pulses $u_x$, and the aggregation/disaggregation interval analyzed $h$ (1 min).

The average of the observed moments is given in Equation (7) and variance for the observed moments is determined by Expression (8) [16]:

$$E\left[{Y_i}^{\left(h\right)}\right]={\displaystyle \frac{\lambda }{\eta }}{\mu }_c{\mu }_x\mathrm{h}$$

(7)

In Equation (7), ${\mu }_c$ represents the average value of cells or pulses per event.

$$\begin{gathered} \mathrm{V}\mathrm{a}\mathrm{r}\left[{Y_i}^{\left(h\right)}\right]=\left[{\displaystyle \frac{\lambda }{{\eta }^3}}\left(\eta h-1+e^{-nh}\right)\right]\left[2{\mu }_{c}E{\left[x\right]}^2+E\left[C^2+C\right]{{\mu }^2}_X{\displaystyle \frac{{\beta }^2}{{\beta }^2-{\eta }^2}} \right] \\ -\mathsf{\lambda }\left(\beta h-1+e^{-\beta h}\right)E\left[C^2-C\right]{{\mu }^2}_X\left[{\displaystyle \frac{{\beta }^2}{\beta ({\beta }^2+{\eta }^2)}}\right] \end{gathered}$$

(8)

Equation (8) corresponds to an exponential distribution, so E[x²] responds to Equation (9) [16]:

$$E{[x]}^2=2{\mu }_x$$

(9)

As $E\left[C\right]={\mu }_c$, we have Equation (10) for a case of type Poisson [16]:

$$E\left[C^2+C\right]={\mu }_c^2-1$$

(10)

The covariance calculated from the observed moments is determined by Equation (11) [16]:

$$\mathrm{C}\mathrm{o}\mathrm{v}\left[{Y_i}^{\left(h\right)},{Y_{i+k}}^{\left(h\right)}\right]=\left[{\displaystyle \frac{\lambda }{{\eta }^3}}{(1-e^{-\eta h})}^2{e}^{-\eta \left(k-1\right)h}\right]\left[{\mu }_{c}E{[X]}^2+{\displaystyle \frac{1}{2}}E\left[C^2-C\right]{{\mu }_X}^2{\displaystyle \frac{1}{\beta ({\beta }^2+{\eta }^2)}}\right]\mathsf{\lambda }\left(1-e^{-\beta h}\right)\left[{\displaystyle \frac{1}{2}}E\left[C^2-C\right]{{\mu }^2}_X{\displaystyle \frac{1}{\beta ({\beta }^2+{\eta }^2)}}\right]e^{-\beta \left(k-1\right)h}$$

(11)

The target function of minimization is given by Equation (12) [16]:

$$\mathrm{Z}=\left[{\left({\displaystyle \frac{F_1\left(\xi \right)}{{F^{\prime }}_1}}-1\right)}^2+\left({\displaystyle \frac{F_2\left(\xi \right)}{F^{\prime }2}}-1\right)+...+{\left({\displaystyle \frac{F_n\left(\xi \right)}{{F^{\prime }}_n}}-1 \right)}^2\right]$$

(12)

where ${F^{\prime }}_1$, ${F^{\prime }}_2$… ${F^{\prime }}_n$ are the observed moments, i.e., average, variance, and covariance. On the other hand, $F_1, F_2$… $F_n$ are the theoretical moments that are sought to find the necessary theoretical statistical parameters $\{\lambda , x$, ${\mu }_c$, ${\mu }_{x, } \eta$, $\beta$} for their introduction in a computational model of synthetic series. In this study, NSRPM was set up using the code data developed in [23].

2.5. Water Demand Calculator (WDC)

The WDC was developed in [17] to determine the probable demand for indoor water. WDC chooses between 4 methodologies and 2 topological aspects of consumption (individual and multifamily house). To choose the method, in addition to the topological aspects, Hunter’s number is determined using Equation (13):

$$\mathrm{H}\left(n,p\right)=\sum _{k=1}^k{n}_k{p}_k$$

(13)

where $n_k$ is the total of sanitary appliances belonging to the same class $k$ and $p_k$ is the probability that a single type $k$ appliance is operating. Equation (7) represents the estimated number of sanitary appliances occupied simultaneously over a peak period.

2.6. Simultaneity Factor Method NHE 2011

The Q_mp according to the methodology set out by Miduvi [8] was determined from Equations (14) and (15):

$$Q_{mp}=K_s\sum qi$$

(14)

$$K_s={\displaystyle \frac{1}{\sqrt{n-1}}}+\mathrm{F}(0.04+0.04\mathit{log}\left(\mathit{log}\left(n\right)\right)$$

(15)

where n is the total number of SA, K_s is the simultaneity coefficient, qi is the unit flow of each SA, F is a factor that takes the value of 4 for academic buildings.

The overall workflow of this study is summarized in the flowchart shown in Figure 3. This visual protocol clarifies the logical progression from data acquisition to model evaluation.

The diagram outlines the seven sequential phases of the research:

(1) Site selection and sanitary infrastructure inventory in five academic facilities in Loja, Ecuador; (2) High-resolution field monitoring of flow (1 min intervals, ≥0.053 L s⁻¹, ±2% accuracy) and pressure (4 s to 1 min intervals, ±0.25% accuracy) over 12 days per meter; (3) Data pre-processing, including time-series synchronization and outlier removal (values <0.05 L s⁻¹ or above the 99.5th percentile); (4) Probabilistic adaptation of Hunter’s method through temporal disaggregation of usage parameters (i, t, h), binomial probability calibration (ΣP ≥ 0.99), and assignment of capacity factors (sink = 10); (5) Calibration of the NSRPM stochastic model via moment-matching (mean, variance, covariance) and minimization of the objective function Z; (6) Implementation of reference models, including the Water Demand Calculator (WDC) and Ecuador’s NHE 2011 standard (simultaneity factor K_s); and (7) Comparative validation and synthesis of peak flow estimates, culminating in a 99% confidence design envelope that integrates results from all approaches.

3. Results

3.1. Hunter’s Probabilistic Adaptation

In order to determine a design flow rate under Hunter’s methodology, it is necessary to determine the duration of consumption (t) and frequency of use (i). To obtain these values, the vertical double axis plots are used, generated with daily information on each water meter.

As consumption is realized, the pressure in the system decreases; having a consumption variation in the pressure and flow in time, the values of i and t could be analyzed as a hydrograph for each peak period h. This was carefully performed with analysis of the database generated from the logs.

With the values of i and t, the probability p, described in Equation (4), was determined. Authors of [20,31] mention that in order to determine the daily p-value, only the values of i and t in morning and night peak flows should be determined. Since the variation in consumption in the academic facility studied has shown that peak flow rates can occur at different points of the day, several values of i and t were determined, for each day in analysis.

Periods of maximum consumption h, identified daily, do not show patterns of influence in common peak hours (morning and night), and their appearance does not appear to have a pattern of deterministic behavior, as they appear at any time of the day when the population of the academic facilities resides in it. Therefore, more than only two daily values of p should be determined; there should be as many values of i, t, and therefore p as possible.

Having in mind the unforeseeable nature of the method, having multiple data describing the phenomenon helps the discrete random variable n applied in Equations (2) and (3) as a distribution function. A probability value should be generated that ensures the occurrence of a given concurrency event [9].

For the case in Figure 4, 22 t-values and 22 i-values were determined. The average of the values was applied in Equation (1), i.e., a daily p-value was obtained.

The daily n-values obtained were averaged, generalizing a single probability of discharge value per water meter. The n-value of each water meter was applied in Equations (2) and (3) using different m-values until the condition described by Expression (5) was reached, that is, until m of n appliances operated 99% of the time, as suggested by [20]. Ordered pairs of n and m were generated for each building.

For the graph describing the Q_mp according to the number of sanitary appliances, a weighted flow for each building studied was determined, as detailed in

Table 1. SAs and weighted flow per water meter.

Sanitary Appliances	A	Q Weighted A	B	Q Weighted B	C	Q Weighted C	D	Q Weighted D	E	Q Weighted E	Q Unit (L/s)
Water closet	22	0.042	30	0.047	6	0.031	16	0.042	12	0.035	0.1
Wash basin	16	0.030	18	0.028	4	0.021	8	0.021	8	0.023	0.1
Urinal	12	0.034	12	0.028	3	0.023	4	0.015	6	0.026	0.15
Sink	2	0.007	3	0.009	6	0.063	10	0.052	8	0.047	0.2
Total	52	0.115	63	0.114	19	0.139	16	0.042	34	0.035	-

. The unit flow for each SA was obtained from NHE 2011 [8].

Equation (4) was applied, multiplying the weighted flow of each building by the m-value of n appliances operating simultaneously (ordered pairs), which is shown in Figure 5a.

To plot consumption based on source units, the highest consumption for individual flow appliance was assigned a factor of 10, as suggested in [11,20]. Considering the flow of each existing appliance, Equation (6) was used to obtain the different source units per sanitary appliance.

Since water consumption is based on several types of appliances, a total value f was determined based on the total n of each building, as shown in

Table 2. Weighted supply units per water meters.

Water Meter		A		B		C		D		E
Sanitary Appliances	Supply Units f Calculated	SA	f Total	SA	f Total	SA	f Total	SA	f Total	SA	f Total
Water closet	5	22	110	30	150	6	30	16	80	12	60
Wash basin	5	16	80	18	90	4	20	8	40	8	40
Urinal	7.5	12	90	12	90	3	22.5	4	30	6	45
Sink	10	2	20	3	30	6	60	10	100	8	80
Total		52	300	63	360	63	132.5	38	250	34	225

. Considering the correspondence between n and f for each building, the values of f were determined for each Q_mp value, generating Figure 5b. It is suggested in [20] to average the values of the expense plots according to the discharge units considering the similarity of use in buildings. See result in Figure 6.

3.2. NSRPM Synthetic Series

From the flow records, a database was generated from which, independently on each water meter, a curve was assembled for analysis, and following what is set in [16], the average time between two events ${\lambda }^{-1}$, the average time between each individual pulse and the event source ${\beta }^{-1}$, the average pulse duration $n^{-1}$, the average intensity (flow) of the pulses $u_x$, and the aggregation/disaggregation interval analyzed (1 min) $h$ were determined.

From these, the variables of average, variance, and covariance of each of the assembled series were determined. In order to determine the theoretical moments by minimizing the target function the model in [23] can be used for the generation of the synthetic series. Due to the stochastic nature of the model, several simulations with different random seeds were developed in order to reduce uncertainty within the NSRPM. A random seed that generates a flow equal to or greater than that observed in the assembled series was considered optimal. The five assembled series, one for each gauge, represent an average value of the recorded flow rate. Of these, of synthetic series were developed that can be observed in Figure 7.

3.3. Reference Models: WDC and NHE

The peak flows estimated with the NHE 2011 method were consistently lower than the observed maximums, with an average underestimation of 31.3%. However, for Meters D and E, the results were closer to the measured values, with differences near 10%. In contrast, the WDC model produced the widest deviations, underestimating the observed maximums by up to 81.5%, reflecting its limited applicability in academic facilities with floating populations. These differences are summarized in Figure 8, which compares observed peak flows against the values estimated by each model through a 1:1 validation plot.

4. Discussion

This study demonstrates that a probabilistic adaptation of Hunter’s method, calibrated through temporal disaggregation of high-resolution flow and pressure data, provides more accurate peak flow estimates than existing normative and stochastic approaches in academic facilities characterized by floating populations. The adapted model yielded deviations ranging from −11.6% (Meter C) to +20.0% (Meter D), with an interbuilding spread of 31.6%. While a 20% overestimation is non-negligible, this level of uncertainty falls within the range commonly reported in the literature for probabilistic peak demand estimation in non-residential settings. In [19], deviations of 15–35% were documented when comparing theoretical and observed peak flows across Latin American institutional buildings, attributing such dispersion to behavioral heterogeneity and occupancy dynamics. Similarly, in [32], it was acknowledged that preliminary hydraulic sizing based on probabilistic models may exhibit errors up to ±25% without compromising system functionality, provided the model captures the correct order of magnitude and directional trend of demand.

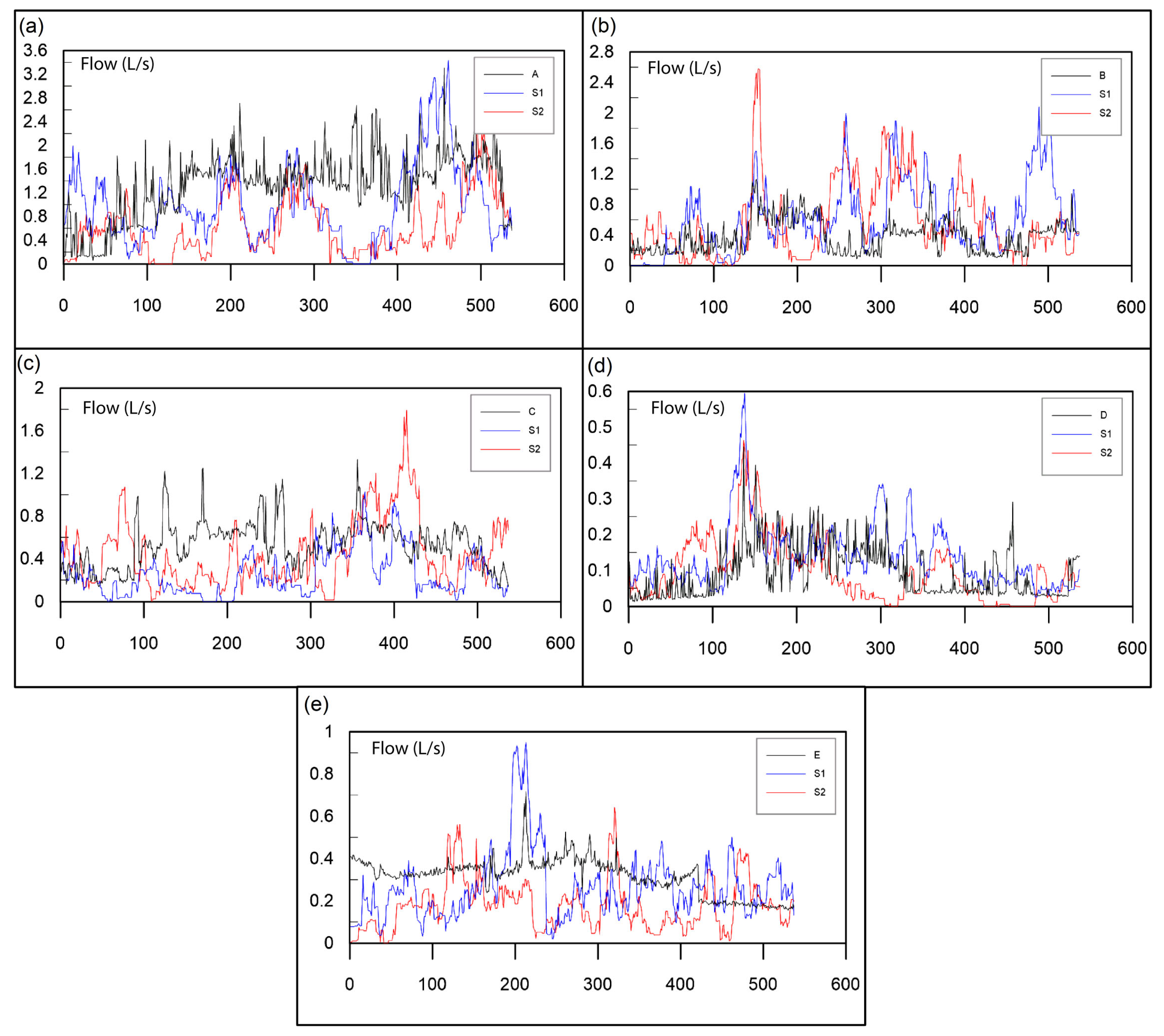
The greater relative error observed in Meters D (360 users) and E (220 users) compared to larger facilities (Meters A–C, ≥312 users) reflects the well-documented sensitivity of stochastic models to sample size. As demonstrated in [15], relative variability in peak flow estimates is inversely proportional to the number of users due to the law of large numbers in binomial processes. In smaller populations, random fluctuations in fixture use exert a proportionally greater influence on aggregate demand, leading to higher relative errors—even when absolute deviations remain small. This explains why Meter C (312 users) showed the lowest error (−11.6%), while Meter D exhibited the highest (+20.0%), likely due to its lower absolute flow and specific fixture inventory.

In contrast, the Water Demand Calculator (WDC) systematically underestimated observed peak flows by up to 81.5%. This significant deviation stems from its calibration to single-family residential data in the United States [15], where occupancy is fixed and fixture use follows predictable diurnal patterns. Academic facilities with floating populations exhibit fundamentally different demand dynamics—characterized by sporadic, high-concurrency events—rendering WDC unsuitable for this context.

The Neyman–Scott Rectangular Pulse Model (NSRPM) showed high accuracy for Meter C (−1.1%) but an average underestimation of 38.4% across all sites. This variability arises from the model’s reliance on statistical moments derived from aggregated time series, which may smooth out short-duration, high-intensity pulses typical of institutional settings. As noted in Section 3.2, multiple stochastic realizations are required to capture extreme events, and selecting the seed that yields the highest peak flow improves alignment with observations—a practice consistent with [16].

Unlike residential studies that prioritize morning and evening peaks [5,33], this research confirms that in academic buildings, maximum demand can occur at any time during occupancy hours, necessitating full-time monitoring. This finding challenges assumptions embedded in standards like NHE 2011, which apply fixed simultaneity factors without accounting for population type (fixed vs. floating). Hunter’s probabilistic framework, when locally recalibrated using disaggregated usage parameters (i, t, h), implicitly incorporates occupancy behavior, offering a more adaptive alternative.

In [16,18,34], a short registration frequency (1 Hz) was established over several days of monitoring for the characterization of residential consumption in the studies. This study had a recording frequency of (1/60 Hz) for flow rates; bearing in mind that consumption occurred in educational facilities, the duration of hydrograph or pulses and the time between events had long intervals, so no lower frequency of registration was necessary. The results generated in [20] largely resemble the getable curve depending on the appliance units or consumption generated in this study. Also, NHE 2011 does not consider the resident population of a building, as well as its characteristics (fixed or floating); the likelihood of simultaneous use increases if resident population is higher. Hunter implicitly considers it as its consumption curve is given to reason for duration and frequencies of consumption, as well as the time between events.

The proposed approach also advances upon prior adaptations of Hunter’s method. Cortés (2008) [9,20] focused on residential or fixed-occupancy contexts and modern low-flow fixtures but did not address the stochastic timing of demand in floating-population settings. More recent work [4] confirmed that occupancy dynamics—not fixture efficiency—dominate peak demand generation in institutional buildings, validating the core rationale of our disaggregation strategy.

As a pilot study, this work is inherently limited in statistical generalizability. The sample of five academic buildings in a single highland city represents a narrow class of institutional contexts. While the methodological framework is rigorously applied, the findings should not be extrapolated as universally representative. Instead, they serve as a proof of concept for context-specific recalibration of probabilistic models under data-scarce conditions. Nevertheless, this study has several limitations that should be acknowledged. First, the analysis is restricted to five academic buildings in Loja, Ecuador, limiting statistical generalizability. Second, although climatic seasonality is minimal in this highland region (Section 2.1) [26], the monitoring period (August–November) did not cover the full annual cycle. While municipal records indicate less than 10% monthly variation in non-residential demand [27], unobserved behavioral shifts during holidays or extreme events could affect peak patterns. Third, NSRPM outcomes remain sensitive to random seed selection, necessitating multiple stochastic realizations to ensure robustness, a known constraint in synthetic demand modeling [16]. Finally, the approach assumes homogeneous user behavior and standardized fixture inventories; its transferability to mixed-use, residential, or industrial settings remains untested.

Despite these constraints, the adaptation offers practical usability: it requires only 10–15 days of flow monitoring and a basic fixture inventory—resources accessible to municipal utilities in resource-limited settings. The resulting consumption curves enable context-specific hydraulic design that avoids the systematic underestimation of standards like NHE 2011 (−31.3% avg.) or the misalignment of residential models like WDC (−81.5%). Future work should validate the approach across diverse building typologies (e.g., hospitals, offices) and climatic zones to assess transferability and refine probabilistic parameters.

5. Conclusions

This pilot study demonstrates that an empirical recalibration of Hunter’s method—calibrated through temporal disaggregation of high-resolution flow and pressure data—provides more accurate peak flow estimates than conventional normative and residential models in academic buildings with floating populations. The approach consistently outperforms the Water Demand Calculator (WDC), which exhibits systematic underestimation up to −81.5%, and Ecuador’s Hydro-Sanitary Standard (NHE 2011), which underestimates peak flows by −31.3% on average. Although the Neyman–Scott Rectangular Pulse Model (NSRPM) achieves high site-specific accuracy (−1.1% for Meter C), it shos significant inter-building variability (average −38.4%), reflecting its sensitivity to random seed selection and aggregation assumptions.

Fundamentally, the study confirms that peak demand in institutional settings occurs unpredictably throughout the day, challenging the deterministic assumptions embedded in standards like NHE 2011. The adapted Hunter framework implicitly accounts for occupancy dynamics through empirically derived usage parameters (i, t, h), offering a more responsive and context-sensitive alternative for hydraulic design.

However, as a pilot study limited to five educational facilities in Loja, Ecuador, the results are not statistically generalizable. Key limitations include: (1) restricted validation to a narrow class of institutional buildings; (2) monitoring confined to the August–November period, despite minimal seasonality in the region (Section 2.1); (3) assumptions of homogeneous user behavior and standardized fixtures; and (4) higher relative errors in smaller facilities (e.g., +20.0% for Meter D), consistent with the known sensitivity of probabilistic models to low user counts.

Nevertheless, the methodological protocol, requiring only 10–15 days of flow monitoring and a basic fixture inventory, provides a replicable, low-barrier foundation for future validation across diverse building typologies, occupancy profiles, and climatic zones in the Global South. This work thus serves as a necessary first step toward context-sensitive hydraulic design standards in underrepresented regions, particularly where data scarcity limits the application of more complex stochastic models.