Sustainable Dye Removal Using Date Stones and Adsorption Process Optimization: Factorial Design, Kinetics, and Isotherm Analysis

Abstract

This study aims to present the preparation of date stone activated carbon (DSAC) through physical activation with carbon dioxide. The Brunauer–Emmett–Teller (BET) technique, Boehm titrations, elemental analysis, Raman and Fourier-transform infrared (FTIR) spectroscopy have been used to characterize the raw material (date stone), date stone activated carbon (DSAC) produced, Congo Red (CR) and to investigate the adsorption phenomena. The study of the DSAC porous material revealed the dominance of micropores with a specific surface area greater than 535.9 m² g⁻¹ and an approximate volume value equal to 0.208 cm³ g⁻¹. The Langmuir model predicted an adsorption capacity of approximately 27.77 mg g⁻¹, while a 90% removal efficiency for CR dye was achieved under neutral pH conditions. Thermodynamic analysis confirmed that the adsorption of CR on DSAC has a spontaneous (ΔG° < 0) and exothermic (ΔH° < 0) character. The adsorption mechanism of CR on DSAC was proposed and discussed, based on the determination of electrostatic interactions being identified as a critical factor that controls the adsorption phenomenon of CR on DSAC. A 2³ full factorial design was implemented to systematically investigate the effects of three critical parameters (temperature, adsorbent dosage, and pH) on the adsorption performance. Statistical analysis indicated that all three primary factors significantly influenced the results. The square correlation coefficient of the model (R²-sq of 97.26%) was in good agreement with the statistical model. The variable is considered statistically significant when the p-value is lower than 0.05. These findings, supported by experimental data, strongly indicate that DSAC possesses remarkable potential as a sustainable and effective bio-adsorbent for wastewater remediation applications capable of removing diverse contaminants with high efficiency.

1. Introduction

In general, it has long been known that much research has focused on protecting our environment from dangers that directly affect our ecosystem, such as polluted waters. It is worth highlighting that various pollutants such as pesticides, organic substances, heavy metals, dyes, etc., have been discharged without any treatment in rivers, sea, groundwater, and lakes [1]. Therefore, these pollutants indisputably cause serious environmental pollution and harmful effects on vegetal, animal and human health [2]. Among these pollutants, dyes used in many fields such as the formulation of histological stains, textiles, cosmetic products, the plastic industry, coloring pigments, leather dyes, the paper industry, and wood coating have been considered a major risk to the environment and human health [3,4,5]. In fact, dyes released from the pharmaceutical [6], food [7], and textile [8] industries have a serious dangerous effect on our environment because they are highly visible even at very low concentrations. These organic pollutants can inhibit light penetration in aquatic environments with a stable chemical structure [9]. In addition, dye products have undoubtedly toxic [10], genotoxic, and mutagenic effects on living organisms [11]. It is very important to note that dyes, with their complex and stable aromatic structures, confer in particular resistance to biodegradation, which makes them persistent in aquatic environments [12].

Indeed, according to their ionic character, dyes can be classified into three main groups: cationic dyes (such as malachite green, toluidine blue, and methylene blue), which contain quaternary ammonium (−N⁺) groups [13]; anionic dyes (such as Congo Red and methyl orange), which usually contain carboxylate (−COO⁻) or sulfonate (−SO₃⁻) groups [14]; and non-ionic dyes. In addition, physicochemical parameters such as pH, concentration, temperature, contact time and conductivity play a significant role in the adsorption behavior of dyes. For example, the pH value has a significant influence on the surface charge of the adsorbent as well as the ionization state of the dye molecule, which subsequently affects the electrostatic interactions and the adsorption efficiency [15]. Meanwhile, temperature may alter the adsorption and diffusion capacity.

Therefore, in their studies, researchers have focused on solutions that are both efficient and low-cost to remove dyes from wastewater using efficient treatment technologies in order to return water to the environment that is healthy and clean.

As mentioned above, cationic and anionic dyes are complex and resistant to degradation, even at low concentrations [16]. Congo Red is an anionic diazo dye that contains two azo groups [17]. Another study showed that Congo Red dye is resistant to biodegradation due to its xenobiotic nature, the higher stability of its organic dye molecules, and its carcinogenic nature [18].

It is therefore crucial to treat these compounds before releasing them into the wastewater system. Consequently, extensive research has been conducted to eliminate the threat posed by dyes in industrial effluents. [19,20,21]. To address this challenge, diverse treatment strategies have been explored, including precipitation [22], biodegradation [23], coagulation [24], adsorption [25,26,27,28,29], electrochemical treatment [30,31,32], membrane processes [33,34,35,36,37], and advanced oxidation processes [38,39,40]. Each method offers distinct advantages in targeting the complex chemical structures and persistence of synthetic dyes in aqueous environments. However, the majority of these techniques are costly in terms of operation and maintenance. In fact, among the methods mentioned, adsorption is one of the most simple, economical, and effective ways to remove colors from wastewater [41]. Furthermore, this method’s primary benefits are its low energy consumption and conceptual simplicity [42,43,44]. Numerous adsorbents are used to remove dye from wastewater such as clays [44], nanoparticles [45], zeolites [46], composite materials, Ce-MOFs [47], graphene oxide composites [48], Spirogyra sp. Algae Biomass [49], and activated carbon [50]. In fact, activated carbon, a critical adsorbent in various applications, is predominantly derived from renewable, locally abundant, and low-cost biomass. Examples of feedstock include almond shells and orange peel [51], corn husk sucrose [52], palm leaves [53], the rumexabyssinicus plant [54], sugarcane bagasse [55], pecan shells, and coconut shells [56]. All these biomaterial are utilized to prepare activated carbon for adsorption processes.

Date stones, one of the most abundant and readily accessible forms of biomass waste in Tunisia, are byproducts of date cultivation—a practice deeply rooted in the region’s history, having served as a cornerstone of its economy and society for over 7000 years [57].

Activated carbon is predominantly produced through two established methods: chemical activation and physical activation. Chemical activation utilizes chemical agents such as ZnCl₂, KOH, and H₃PO₄, which pose environmental risks due to their toxicity and generate harmful byproducts. Although effective, this method is both time-intensive and ecologically unsustainable. Conversely, physical activation is a two-step process involving biomass carbonization (e.g., date stones) followed by activation with steam or CO₂ as a greener alternative [57,58]. This approach enhances pore structure development during carbonization, eliminates reliance on hazardous chemicals, and reduces production costs, positioning it as a more sustainable and efficient choice for industrial applications.

This study investigates the synthesis of activated carbon from date stones (DSAC) using CO₂-assisted physical activation as a novel approach that, to our knowledge, has not been previously reported for adsorption applications. The results of the characterization of the prepared activated carbon by BET, elemental analysis, FT-IR, and Boehm titrations have been presented and discussed in this paper. The adsorption capacity was investigated under different physical and chemical parameters such as pH, temperature, contact time and initial dye concentration. Moreover, the influence of these parameters and the interaction between the different factors on CR removal efficiency were investigated by a 2³ full factorial design.

2. Materials and Methods

2.1. Chemicals

All the used reagents (Na₂CO₃, NaHCO₃, NaOH and HCl) were analytical-grade. Congo red (CR), as an anionic diazo dye with chemical formula of C₃₂H₂₂N₆Na₂O₆S₂ and molecular weight 696.65 g mol⁻¹, was used as an adsorbent model. The molecular structure of CR is illustrated in Scheme 1. CR stock solution of (500 mg L⁻¹) was prepared by dissolving an appropriate quantity in distilled water.

2.2. Preparation of Date Stone Activated Carbon (DSAC)

-

Sample preparation

To prepare the activated carbon, date stones were used as precursor. They were first washed with water to get rid of impurities, dried at 60 °C for 48 h, crushed using a disk mill, sieved and the portion with a size of 250 µm was used for activated carbon production.

-

Physical activation

The drying of the powder of date stone was performed at atmospheric pressure at 110 °C, and then at 150 °C under vacuum for 2 h to eliminate the humidity. The ground raw material was then placed in metal crucibles and then introduced into a horizontal tubular furnace. The pyrolysis is carried out at a temperature of 900 °C with a rate of 1 °C min⁻¹ and under a nitrogen flow of 100 mL min⁻¹. The obtained char was activated at 900 °C for 30 min using a CO₂ flow of 100 mL min⁻¹ (heating rate 5 °C min⁻¹). The final activated carbon date stone (DSAC) is preserved in hermetically closed bottles.

2.3. Characterization Techniques

The elemental analysis of date stone activated carbon (DSAC) was carried out using micro analytic devices at the central laboratory analysis of CNRS France. FTIR analysis of DSAC before and after dye adsorption was carried out in wave number range 400–4000 cm⁻¹ (resolution of 4 cm⁻¹) by Spectrophotometer model IRAffinity-1 SHIMADZU (CERTE, Soliman, Tunisia). In order to determine the specific surface area of the studied compound, nitrogen sorption was measured on a Micromeritics ASAP 2010 analyzer (Micromeritics, Bourdeau, French). The collected data was subjected to (BET) treatment. The volume of mesopores as well as micropores has been obtained through the application of the t-Plot methods to the nitrogen adsorption data. The structural characteristics of prepared DSAC were obtained with Raman spectroscopy. Raman spectrum was recorded in the wavenumber domain of 1000–2000 cm⁻¹ using a Horiba scientific LabRAM HR Evolution device (Horiba, Bourdeau, French). The Raman wave number has been obtained using a laser excitation wavelength at 633 nm with laser acquisition time = 30 s. The surface behavior of the prepared DSAC has been investigated by point of zero charge (pH_PZC). In fact, at this pH, activated carbon date stones have a neutral surface charge. According to the pH of the reaction contents, activated carbon surface charges can be positive or negative. It is important to mention that pH_z was realized by the salt addition method [59]. The amount of 0.15 g of DSAC was mixed with 50 mL of NaCl (0.01 M) solutions at a different initial pH value ranging from 2 to 12. Then, all obtained solutions were stirred at 220 rpm for 48 h. After that, the final pH was measured. The obtained values were plotted versus the initial pH. Thus, the pH_z correspond to the value for which pH_final = pH_initial.

In order to determine lactonic, phenolic and carboxylic groups on the surface of DSAC, Boehm titration was used [60,61]. Indeed, 0.15 g of DSAC was added to 50 mL (0.01 M) of the following solutions (NaOH, Na₂CO₃, NaHCO₃, and HCl). The obtained mixture was stirred for 48 h at constant speed of 220 rpm under room temperature. Back-titration of the filtrate (10 mL) was achieved with standard solution of HCl (0.01 M) in order to determine the amount of the acidic group. Basic group’s contents were achieved by titration of the filtrate with NaOH (0.01 M) solution.

2.4. Experimental Set-Up

To better understand the adsorption model of the studied compound, equilibrium studies were carried out by contacting a fixed amount of DSAC (0.10 g) with 50 mL of dye solution of different initial concentrations in 100 mL stopper conical flasks at room temperature (25 ± 1 °C) and pH of 6.8. At equilibrium the concentration of dye in aqueous solution was measured by using thermospectronic UV Spectrophotometer (CERTE, Tunisia) at λ_max = 497 nm wavelength. The amount of adsorption at equilibrium (mg g⁻¹) was calculated according to Equation (1):

$$q_e=\left(C_i-C_e\right){\displaystyle \frac{\mathrm{V}}{\mathrm{W}}}$$

(1)

where C_i and C_e are the initial and equilibrium concentrations of dye (mg L⁻¹), respectively. V is the volume of dye solution (L), and W is the weight of the adsorbent used (g). The performance of dye adsorption by activated carbon was calculated by the percentage of dye removal according to Equation (2):

$$\% Dye removal= {\displaystyle \frac{C_i-C_e}{C_i}}\times 100$$

(2)

The adsorption experiments investigated the effects of contact time, pH, and initial dye concentration on Congo Red (CR) removal. For these trials, predetermined adsorbent doses were added to 50 mL of dye solutions with varying initial concentrations in 100 mL conical glass flasks. The mixtures were agitated at a constant speed of 220 rpm. Samples were collected at predetermined time intervals, filtered, and the supernatant’s absorbance was measured using a spectrophotometer at a wavelength of 497 nm.

Table 1. The values of parameters in each experimental analysis.

Experimental	pH	t (min)	T (°C)	C0 (mg/L)
Effect of contact time on adsorption	6.8	0–180	25	20, 50
Effect of pH on adsorption	2.8–10.5	180	25	30
Effect of temperature on adsorption	6.8	180	25–55	30
Effect of concentration on adsorption	6.8	180	25	2–110

t, contact time; T, temperature; C₀, initial concentration.

summarizes the parameters investigated in each experimental study. The kinetics of the adsorption process were evaluated by measuring the removal efficiency of Congo Red (CR) from aqueous solutions at varying time intervals. For adsorption isotherm analysis, dye solutions with different initial concentrations were mixed with a predetermined mass of adsorbent and agitated continuously until equilibrium was attained under controlled conditions (25 °C).

2.5. The Factorial DESIGN

A 2³ full factorial design was employed to systematically investigate the individual and interactive effects of three independent variables, adsorbent dosage (A), pH (B), and temperature (C), on the removal efficiency of Congo Red (CR). Each factor was evaluated at two levels, coded as −1 (low) and +1 (high), as detailed in

Table 2. Experimental range and levels of independent variables.

Factor	Code	Low Level (−1)	Center level (0)	High Level (+1)
DSAC dose (g L−1)	A	0.2	1.1	2.0
pH	B	6.8	8.8	10.8
Temperature (°C)	C	25	40	55

.

This design comprises 8 unique experimental conditions. Each condition was replicated twice, leading to a total of 16 trials. To mitigate systematic errors, the experimental sequence was randomized, and all data were analyzed using Minitab17^® statistical software [62]. Within the studied parameter ranges, the relationship between responses and influencing factors was modeled mathematically through a response function. The adsorption capacity was represented by a polynomial regression model developed through analysis of variance (ANOVA) and a factorial experimental design framework. The relationship between the response (CR removal efficiency, Y) and the coded factors was modeled using a first-order polynomial model with interaction terms, as represented by Equation (3):

Y = α₀+ α₁ A + α₂ B + α₃ C + α₁₂ AB + α₁₃ AC + α₂₃ BC + α₁₂₃ ABC + ε

(3)

where Y, α₀, and α_i represent the model predicted response, the global mean, and the regression coefficient corresponding to the main factor effects and interactions, respectively.

The term ε is the random error component. A, B and C are the independent coded variables corresponding to adsorbent dosage, pH and temperature, respectively.

3. Results and Discussion

3.1. Characterization of DSAC

Table 3. Elemental analysis of the DS and DSAC.

Sample Reference	Elemental Content (wt. %)
		H	N	O	S
DS	50.65	6.23	0.64	42.33	0.15
DSAC	84.25	1.12	2.13	7.21	<0.2

displays the elemental analysis findings of DS and DSAC. It can be seen from this table that the percentages of carbon and nitrogen have been increased, while those of hydrogen and oxygen have been decreased.

Actually, the pyrolysis step leads to the formation of carboneous material by oxygen, hydrogen, nitrogen and sulphur dioxide trace valorization.

During the pyrolysis operation, many steps have been observed:

-

Hydrogen and oxygen are eliminated as CO, CO₂, and H₂O.

-

In addition, the liberation of carbon monoxide and dioxide is usually observed in the range of 200–300 °C. However, between 240 °C and 360 °C, cellulose degradation occurs [59].

-

Furthermore, the discharge of hydrocarbons takes place between 300 °C and 400 °C, while between 400 °C and 500 °C, a significant quantity of gaseous hydrocarbons as well as heavy tars are generated. It is important to note that gas generation mainly involves hydrogen, carbon monoxide and hydrocarbons and takes place at temperatures ranging from 500 to 700 °C.

-

Therefore, between 700 and 1000 °C, the carbon residue is the main substance remaining. In DSAC, carbon levels increased while hydrogen and oxygen levels decline.

This result is mainly due to the discharge of volatiles throughout the pyrolysis process that leads to the removal of non-carbon species but increasing the carbon. It is evident that the carbon amount of activated carbon has been increased notably following its activation, while the oxygen and hydrogen portions have been diminished. Furthermore, when the temperature exceeds 700 °C, the creation of micropores during the activation process has been caused through other elements.

The study based on physical adsorption isotherms is a commonly used method to establish the porous texture of a specific solid [63]. In this investigation, CO₂ was used as the activation gas. In fact, the major reason for this choice is due to the ability to control the activation process. Date stone exhibits a highly microporous structure, evidenced by an S_micro/S_BET ratio of 93% (

Table 4. Reports the textural properties of the DSAC obtained from N₂ adsorption isotherms at 77 K.

Characteristic	Value	Unit
Langmuir (SLangmuir)	531.62	m2 g−1
BET (SBET)	535.91	m2 g−1
External Surface (Sext)	33.06	m2 g−1
Micropore Surface (Smicro)	502.84	m2 g−1
Micropore Volume (Vmicro)	0.208	cm3 g−1
Mesopore Volume (Vmeso)	0.058	cm3 g−1
Total Pore Volume (VT)	0.266	cm3 g−1
Smicro/SBET	93	%
Vmicro/VT	78	%
Average Pore Width (Dp)	1.99	nm

), while the ratio of the microporous volume to the total pore volume (V_micro/V_T) is near 78%.

Thus, the pores that appear when the pore size reaches 7 nm present mainly the micropore dimensions and also exceed half of the total pore volume (Vmicro/VT). The Vmicro/VT confirms the predominance of micropore volumes.

It is well known that activation aims to increase porosity and establish a specific structure to produce a highly porous solid as the final product [64]. During the activation process, pore formation usually occurs in three distinct phases: (i) the opening of previously inaccessible pores; (ii) the establishment of new pores; and (iii) the extension of existing pores [65].

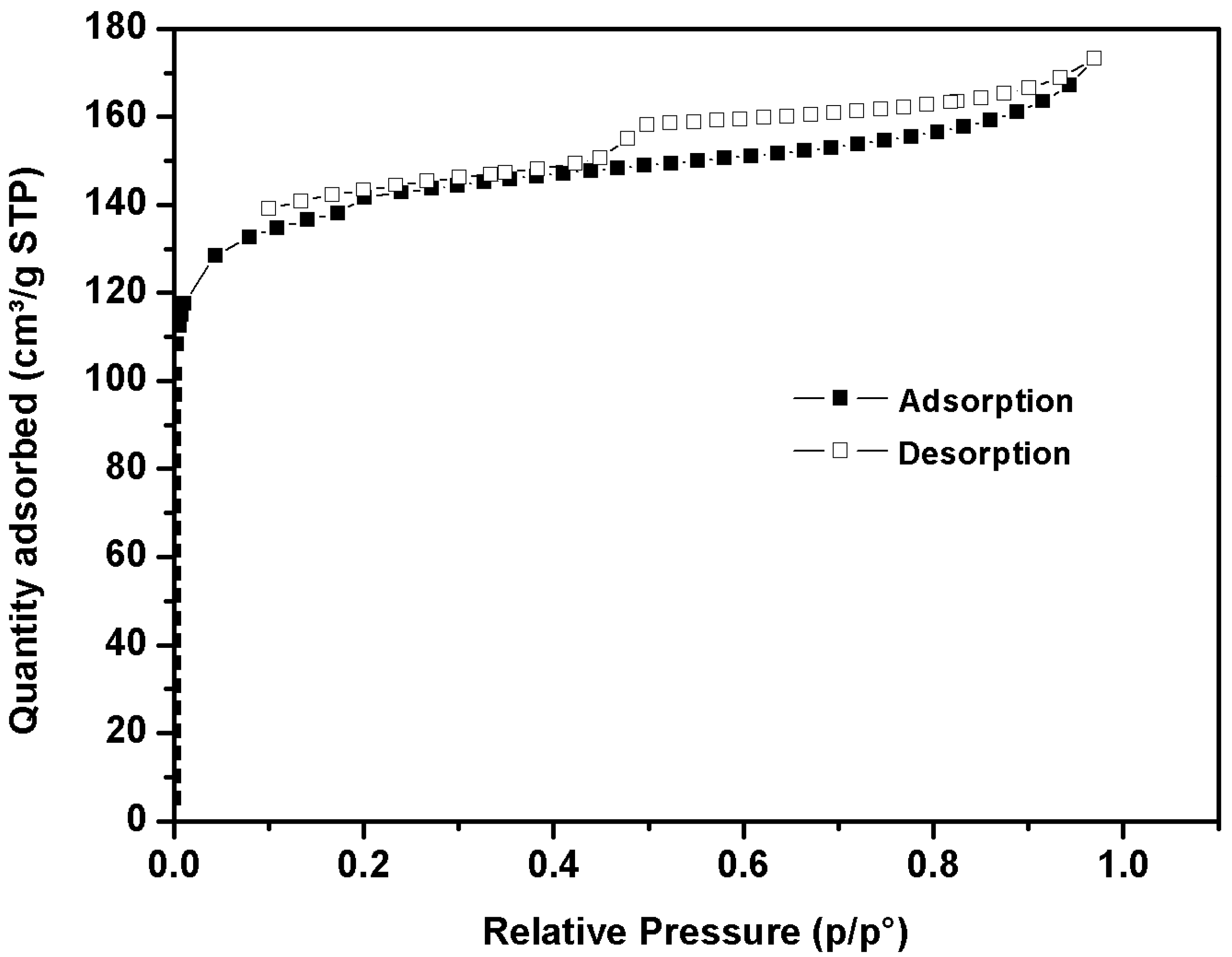
The N₂ adsorption/desorption isotherms at 77 K for activated carbon derived from date stone char are shown in Figure 1.

The isotherm, at low relative pressure, indicates significant adsorption related to the microporous materials [66]. Furthermore, the isotherm displays a weak hysteresis loop, indicating the presence of very small mesopore volume. The pH_pzc plays a crucial role in describing the surface behavior. The pH_pzc of activated carbon derived from date stone was 8.2 (

Table 5. Chemical properties of DSAC.

Precursor	Yield (%)	Total Acidity (mmol g−1)	Total Basicity (mmol g−1)	pHPZC
DSAC	24.42	0.075	0.435	8.2

).

The surface chemistry of carbon adsorbents is characterized by two key criteria: surface acidity and surface basicity. Like that, the type and quantity of the surface functional groups have a significant impact on the surface characteristics of activated carbon.

Table 5 illustrates the acidic and the basic site concentration of DSAC; it seems that the total basic sites were dominant. Indeed, after carbonization between 400 and 500 °C, phenolic and carboxylic groups were excessively formed but decreased when the carbonization exceeded 600 °C and disappeared completely above 800 °C.

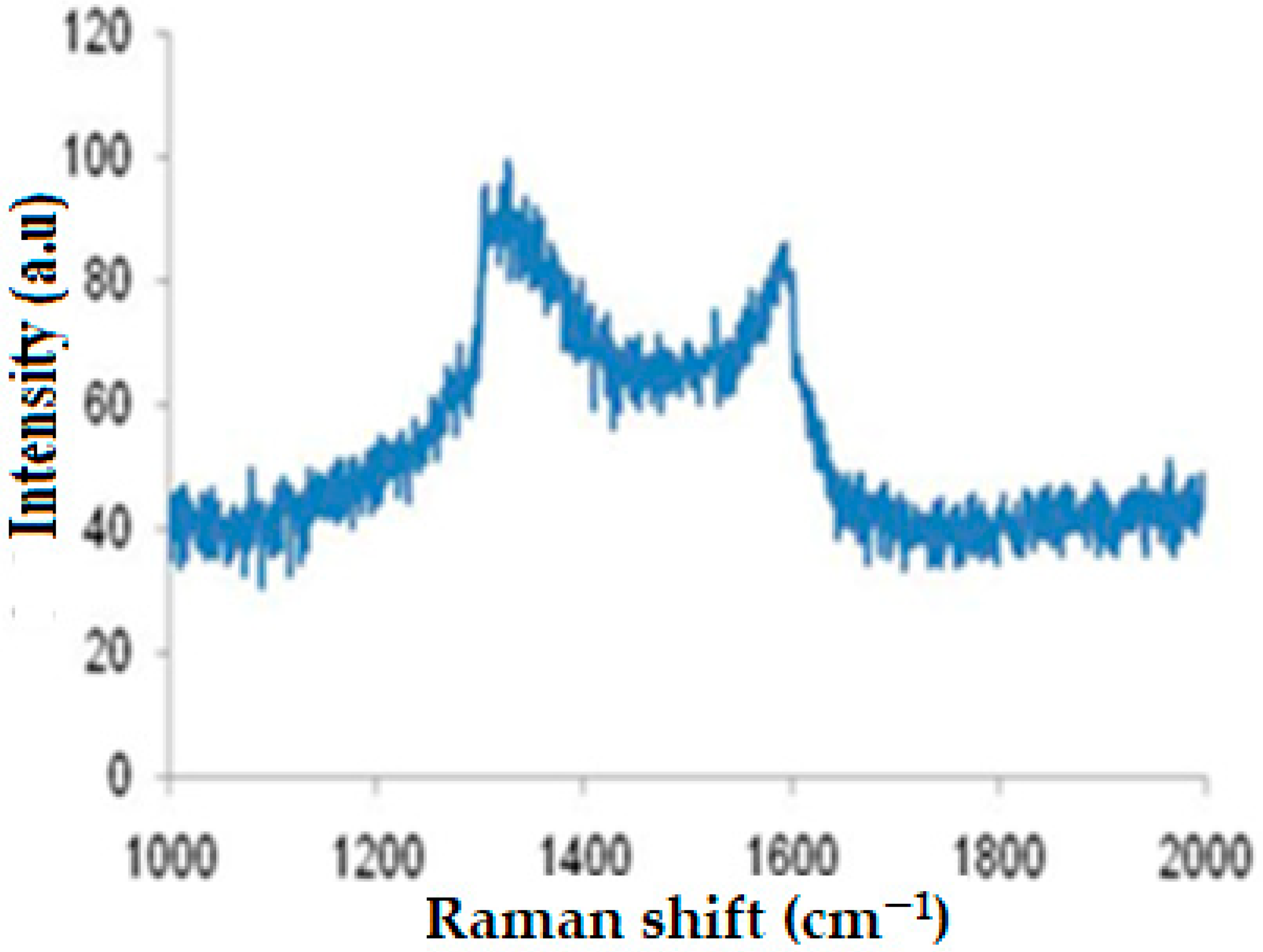
Raman spectroscopy is a useful tool to describe the molecular structure of carbon-based materials [67]. Thus, it was used to characterize and identify the graphitic nature of DSAC. Figure 2 illustrates the Raman spectrum of DSAC sample.

This figure clearly shows the presence of two distinct peaks attributed to the activated carbons. The peak located at 1327 cm⁻¹ is responsible for D-band linked to the disordered carbon. Moreover, the peak at 1589 cm⁻¹ is characteristic of G-band, related to the graphitized carbon. In addition, the intensity ratio (R = I_D/I_G) of the D and G bands provides an overview of the carbon material structure [68]. For DSAC composite, I_D/I_G = 1.14, indicating that the pores are too small (microporous), which confirms the BET observations.

3.2. Adsorption Test

Results related to the adsorption test are depected in the following Figure 3 and Figure 4.

-

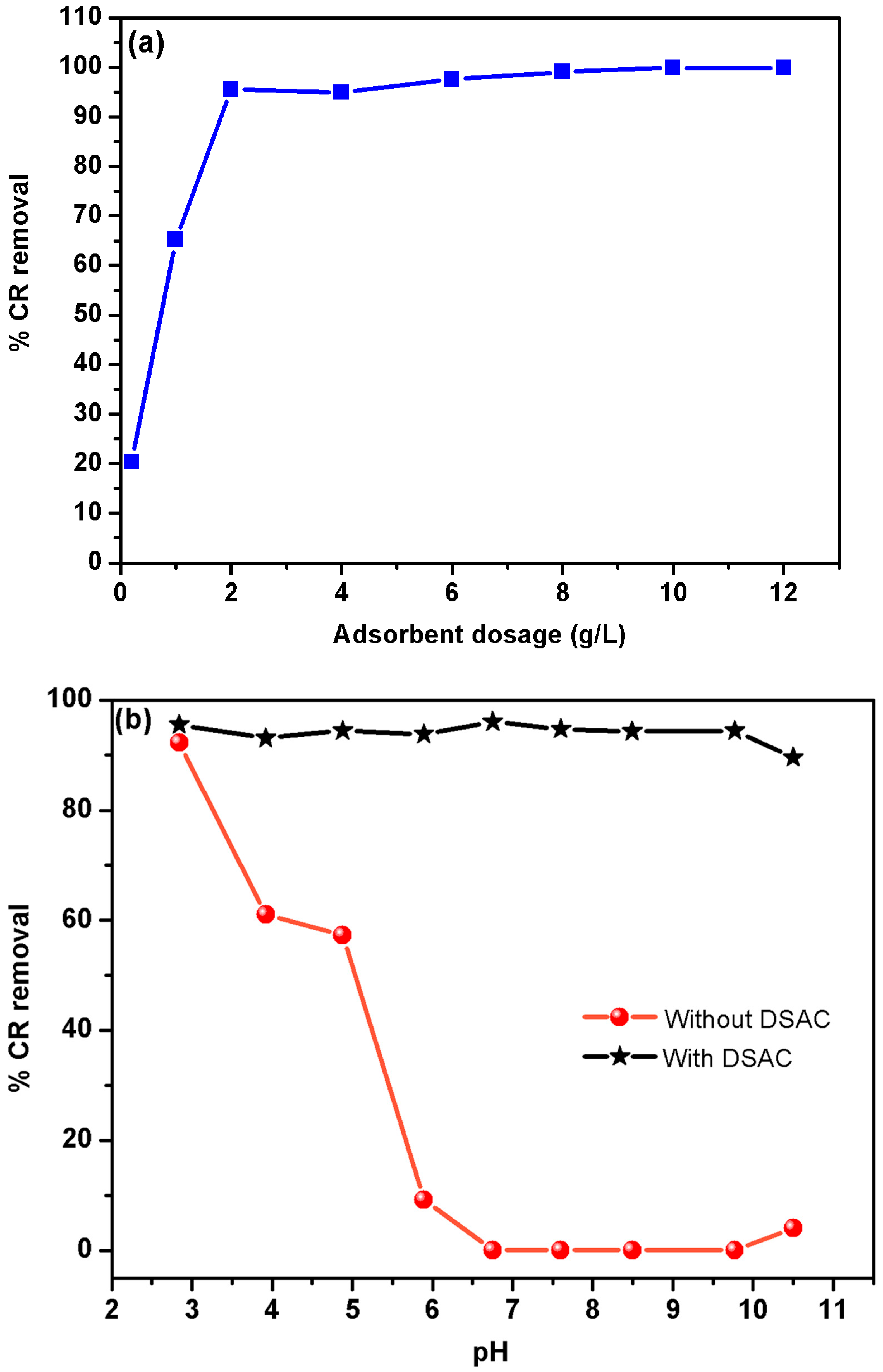
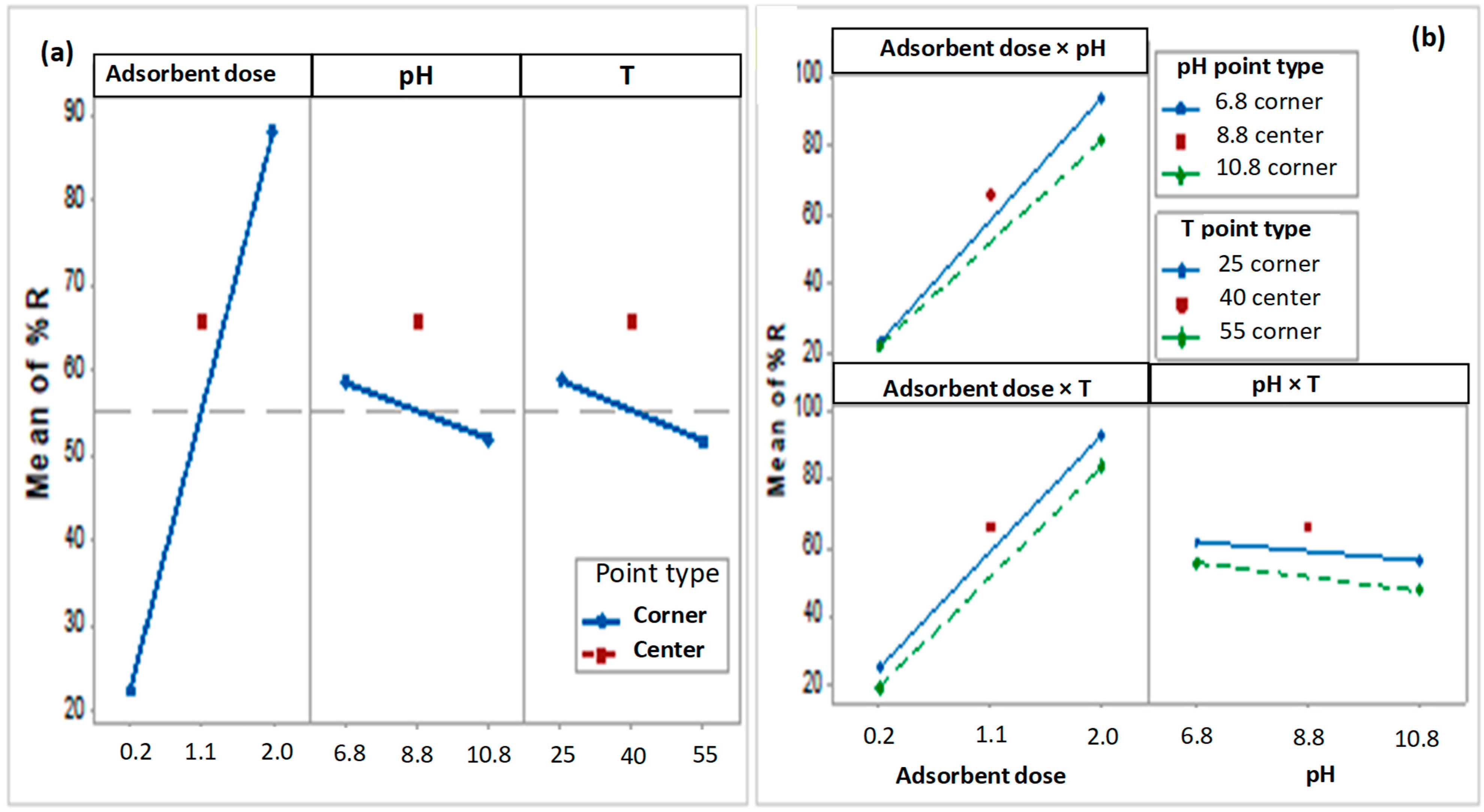
Effect of adsorbent dose

The study of the effect of the adsorbent concentration on CR dye removal was investigated over a range from 0.2 g L⁻¹ to 12 g L⁻¹, as shown in Figure 3a. The result of this study demonstrates that the increase in the DSAC dosage led to a significant improvement in CR removal efficiency, from 20.3% at 0.2 g L⁻¹ to 99.8% at 12 g L⁻¹. Therefore, the increase in DSAC amount enhances the active sorption sites on the adsorbent surface [69]. After the significant improvement in CR retention, the curve reaches a stable phase. This behavior can be attributed to the aggregation phenomenon of the adsorbent particles caused by the excess dose. Consequently, the effective surface area of the adsorbent was notably improved [70]. Since the maximum practical efficiency was achieved at 2.0 g L⁻¹, this dosage was selected as the optimal and economically favorable condition for all subsequent experiments, including the factorial design analysis.

-

Effect of pH solution

The pH value of the solution plays a crucial role in the adsorption of anionic dyes. In fact, the pH value influences the surface bonds of the activated carbon as well as the CR molecule. In addition, the color intensity as well as the structural stability of the CR dye is influenced by the pH value [69]. It was observed that the CR dye solution exhibits color changes depending on the pH, both for acidic and basic solution. Depending on the pH, its structure can undergo protonation or deprotonation, which modifies its adsorption characteristics, and consequently, its color [71,72]. Therefore, the impact of initial pH value on blank CR dye solution was investigated at a concentration equal to 30 mg L⁻¹. Firstly, the adjusted pH solution was kept for 1 h to evaluate the stability of CR dye. The results show that the optimum pH is pH₀ = 6.8. Figure 3b illustrates the effect of pH in the range [2.8–10.5] on CR removal in the presence and absence of DSAC adsorbent. This behavior indicates that the structure of CR was affected by the pH value of the solution [73]. As a consequence, the % of dye degradation was very low. In addition, Figure 3b shows that the adsorption of dye onto the new composite DSAC is independent of the pH value. More than 90% of CR dye was removed [74]. This study involves a newcomer in the adsorbent family that particularly presents a very stable structure, which significantly removes the dye molecules for all ranges of pH.

-

Effect of contact time

The effect of contact time on the CR removal using DSAC at C₀ = 20 mg L⁻¹ and 50 mg L⁻¹ was studied. The contact time curve shows a rapid adsorption of CR in the first 15 min followed by a gradually decrease and the adsorption reaches equilibrium (optimum contact time) (Figure 3c). Adsorption equilibrium for CR was attained within 180 min, beyond which adsorption rates decreased significantly. The process exhibited two distinct kinetic phases. (i) An initial rapid phase, characterized by a sharp increase in adsorption capacity. This is attributed to the immediate occupancy of readily available sites on the adsorbent’s external surface. (ii) A subsequent slower phase, contributing minimally to the overall dye uptake. This stage reflects diffusion-controlled adsorption into the material’s internal pore structure [75].

-

Adsorption isotherm

To better understand the type of interaction between the adsorbent and adsorbate, the adsorption isotherm investigation has been carried out. Isotherm models were used to characterize the relationship between equilibrium adsorption capacity (q_e) and equilibrium dye concentration (C_e) under the experimental conditions (concentration range 2–110 mg L⁻¹, adsorbent dose 2 g L⁻¹, temperature 25 ± 1 °C, contact time 3 h and stirring speed 220 rpm). 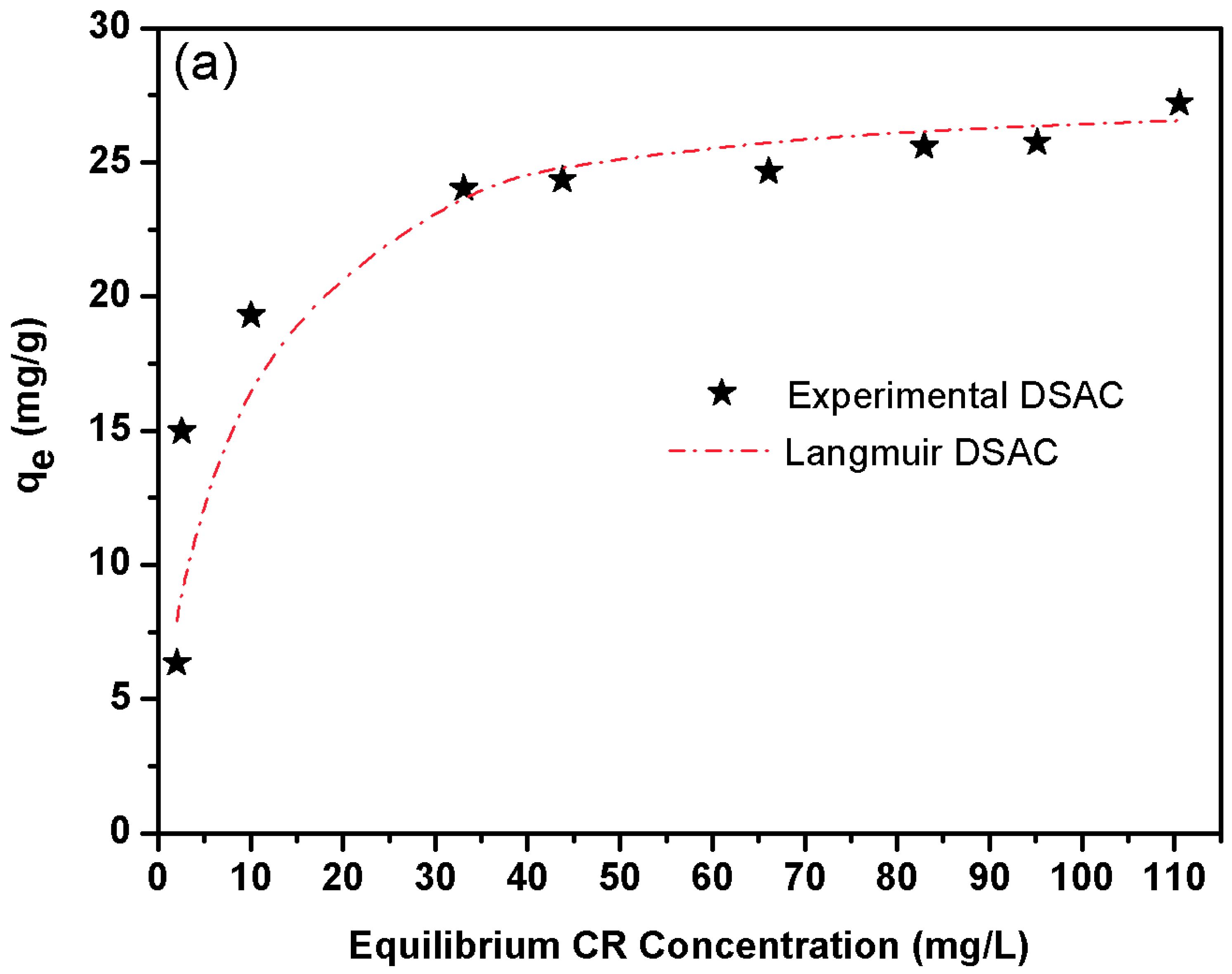Figure 4a displays the DSAC isotherm profiles for CR. The experimental data demonstrate a strong correlation with the Langmuir isotherm model, suggesting monolayer adsorption onto a homogeneous surface. Notably, this behavior contrasts with literature reports emphasizing mesopore-dominated adsorption mechanisms [76]. This study explicitly confirms that the adsorbent’s active sites are primarily microporous rather than mesoporous. The microporous structure effectively restricts the leaching of chemical residues, thereby mitigating potential environmental contamination risks. Furthermore, the retention percentage, found to be equal to 94%, can be attributed to the optimized microporous architecture, which enhances dye capture and stability within the adsorbent matrix.

The Langmuir model assumes monolayer adsorption occurs on a homogeneous surface where all sites are energetically equivalent and exhibit no intermolecular interactions. This applies to systems with saturable, single-layer coverage. The Langmuir isotherm model for non-linear form [77] is determined as follows:

$$q_e={\displaystyle \frac{q_{m}b{C}_e}{(1+b{C}_e)}}$$

(4)

where C_e: the equilibrium concentration of dye molecules adsorbed (mg L⁻¹); q_e: the concentration of dye molecules adsorbed (mg g⁻¹); q_m and b: the monolayer adsorption capacity and the affinity of the adsorbent towards the adsorbate, respectively, exhibiting the Langmuir constants. The curve of q_e vs. C_e illustrates a fitted curve, and from

Table 6. Parameters of adsorption models for CR adsorption onto DSAC.

Isotherm Model	Parameter	DSAC
Langmuir	qm (mg/g)	27.77
	b (mg/L)	0.197
	R2	0.997
Freundlich	N	3.80
	KL (mg/g)	8.48
	R2	0.762
Temkin	A	6.73
	B	4.15
	R2	0.894
D-R	qmD-R (mg/g)	24.92
	βD-R (mol2/j2)	10−6
	E (j/mol)	1000
	R2	0.902

, the Langmuir constants were produced from the plot of sorption data. Furthermore, a R_L value between 0 and 1 (0 < R_L < 1) confirms a favorable adsorption process for CR dye molecules.

The R_L factor is given by the following equation [78]:

$$R_L={\displaystyle \frac{1}{(1+b{C}_0)}}$$

(5)

where b presents the Langmuir constant, and C₀ is the initial dye concentration (mg L⁻¹).

The Freundlich equation is an empirically derived mathematical model used to characterize adsorption phenomena, particularly for heterogeneous surfaces. The non-linear form is designated [79] by:

$$q_e=K_F{C}_e^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}}$$

(6)

where q_e: the adsorbed amounts at equilibrium (mg g⁻¹); C_e: the equilibrium concentration of the adsorbate (mg L⁻¹); K_F and n present the Freundlich equilibrium coefficients, n provides information about the adsorption process efficiency, and K_F displays the adsorption ability of the adsorbate. The poor curves plotted by q_e against C_e confirms that the adsorption process does not support the model. The K_F and n values, as Freundlich equilibrium coefficients, were engendered from the plot of sorption data illustrated in Table 6. Moreover, the parameter 1/n with a value ranging between 0 and 1 specified the adsorption intensity or surface heterogeneity.

Temkin’s model allows for the determination of thermodynamic conditions related to the adsorption process. It assumes a linear decrease in the heat of adsorption as a function of the adsorption capacity. The following equation illustrates the Temkin model [80]:

$$q_e=Bln\left(A C_e\right)$$

(7)

where B: the head of adsorption; q_e: the experimental adsorption capacity (mg g⁻¹); and C_e: the adsorbed dye concentration at equilibrium (mg L⁻¹).

$$B={\displaystyle \frac{RT}{b_T}}$$

(8)

where 1/b_T: the adsorption potential of the adsorbent, R: the universal gas constant (8.314 kJ mol⁻¹) and T: the temperature degree in Kelvin (K).

The decrease in the adsorption energy is confirmed by the plot of q_e against C_e, which indicates a linearity when the adsorption sites are filled. Due to the interaction between adsorbent and adsorbate, the surface coverage increases, leading to the linear decreases in heat adsorption of all molecules in the layer. In addition, it can be assumed that the adsorption process is described by uniform distribution of binding energies up to a maximum value. The parameter data of the Temkin model are illustrated in Table 6.

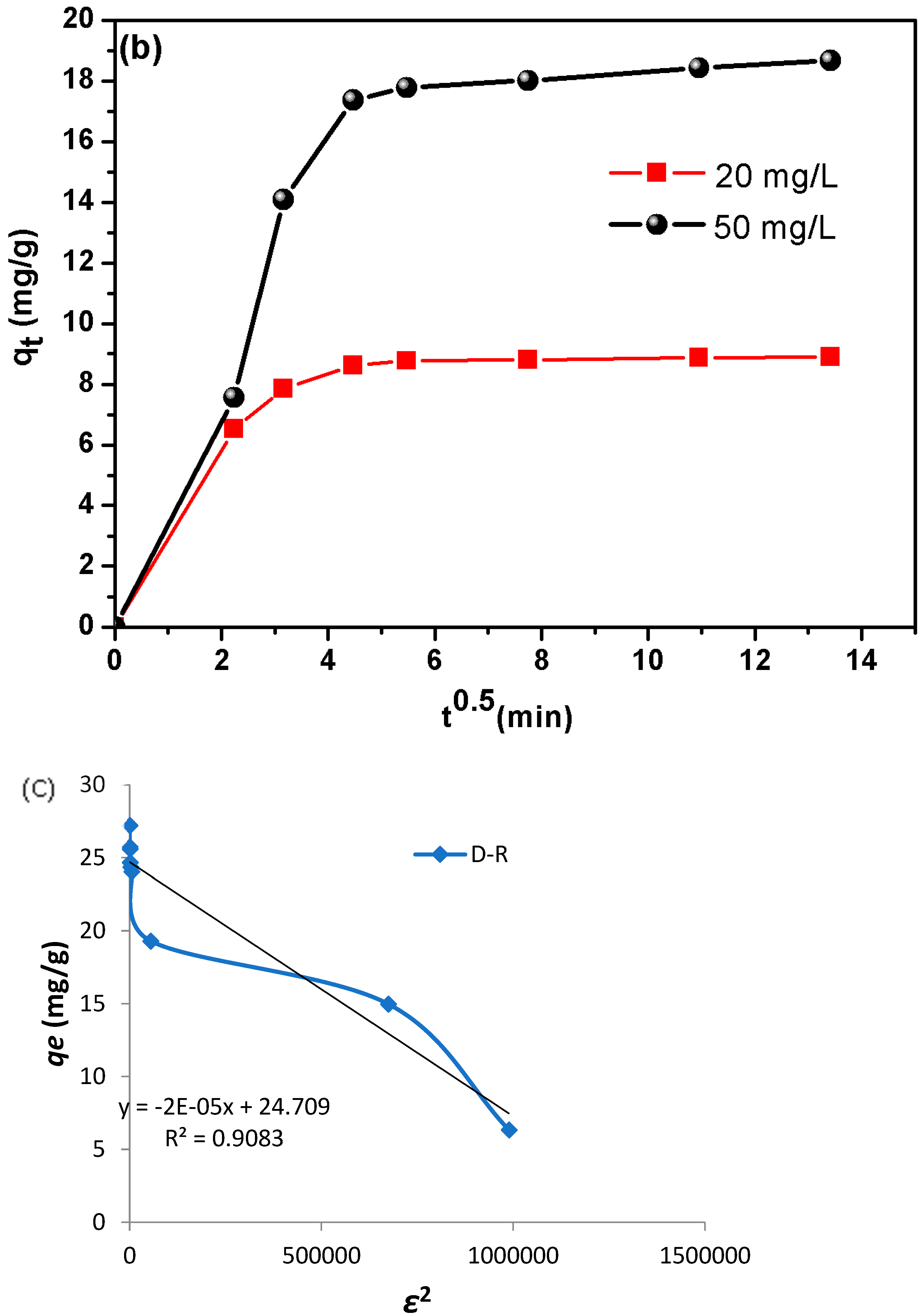
The Dubinin–Radushkevich (D-R) model [81] is applied to estimate the porosity nature and the free energy appearance of the adsorption.

In addition, the D-R model serves to investigate the adsorption process types (physical or chemical). Furthermore, D-R sorption is more general than the Langmuir isotherm since it does not assume a homogenous surface or constant sorption potential. The non-linear isotherm equation of the D-R is as follows:

$$q_e=q_m\mathit{exp}\left(-\beta {\epsilon }^2\right)$$

(9)

where q_e: the dye molecule concentration (mg L⁻¹), q_m: the maximum adsorption capacity (mg g⁻¹), β: the activity coefficient related to adsorption mean free energy mol² j⁻² and ε is the Polanyi potential stated by:

$$\epsilon =TLn(1+{\displaystyle \frac{1}{C_e}})$$

(10)

As the plot of q_e vs. ε² presents nonlinear graphs (Figure 4c), the adsorption mean free energy E (kJ mol⁻¹) is given as:

$$E={\displaystyle \frac{1}{{\left(2\beta \right)}^{0.5}}}$$

(11)

A literature review highlights that the mean free energy (E) derived from the D-R model serves as a critical indicator of the adsorption mechanism’s nature. Specifically, an E value between 8 and 16 kJ mol⁻¹ suggests a chemically driven process, such as ion-exchange interactions, whereas values below 8 kJ mol⁻¹ signify physical adsorption (e.g., van der Waals forces or hydrogen bonding) [82]. This distinction underscores the utility of E in elucidating whether adsorbent–adsorbate interactions are governed by chemical bonding or weaker physical forces.

Indeed, the four model parameters are illustrated in Table 6. So, it seems that Langmuir isotherm provides a good model for the sorption system deduced by comparing the correlation coefficient. In fact, we know that the Langmuir model is based on monolayer sorption on a surface made up of a finite number of identical sorption sites. It is worth mentioning that the maximum value capacity adsorption of DSAC for CR is 27.77 mg g⁻¹ at 25 °C.

Table 7. Comparison of adsorption capacities of various adsorbents for Congo red.

Adsorbent	Adsorbent Capacity (mg/g)	References
Activated Eucalyptus wood saw dust carbon	5.10–66.66	[5]
Citric acid-treated water chestnut (CPWC)	7.95	[83]
Apricot Stone Activated Carbon (ASAC)	32.85	[84]
Neem bark (NBC)	25.84	[85]
Tea waste	23.26	[86]
Date stone Activated carbon (DSAC)	27.77	This study

presents a comparative study of DSAC versus other biosorbents used to remove CR [5,83,84,85,86]. Under optimal conditions (maximum adsorption), the DSAC product showed superior adsorption performance compared to all other materials evaluated in Table 7. This high efficiency, combined with the abundance of raw material in the form of residual biomass and a simple preparation protocol, gives our product an importance and efficiency in industrial applications. Collectively, these findings position DSAC as a highly promising adsorbent for scalable CR remediation.

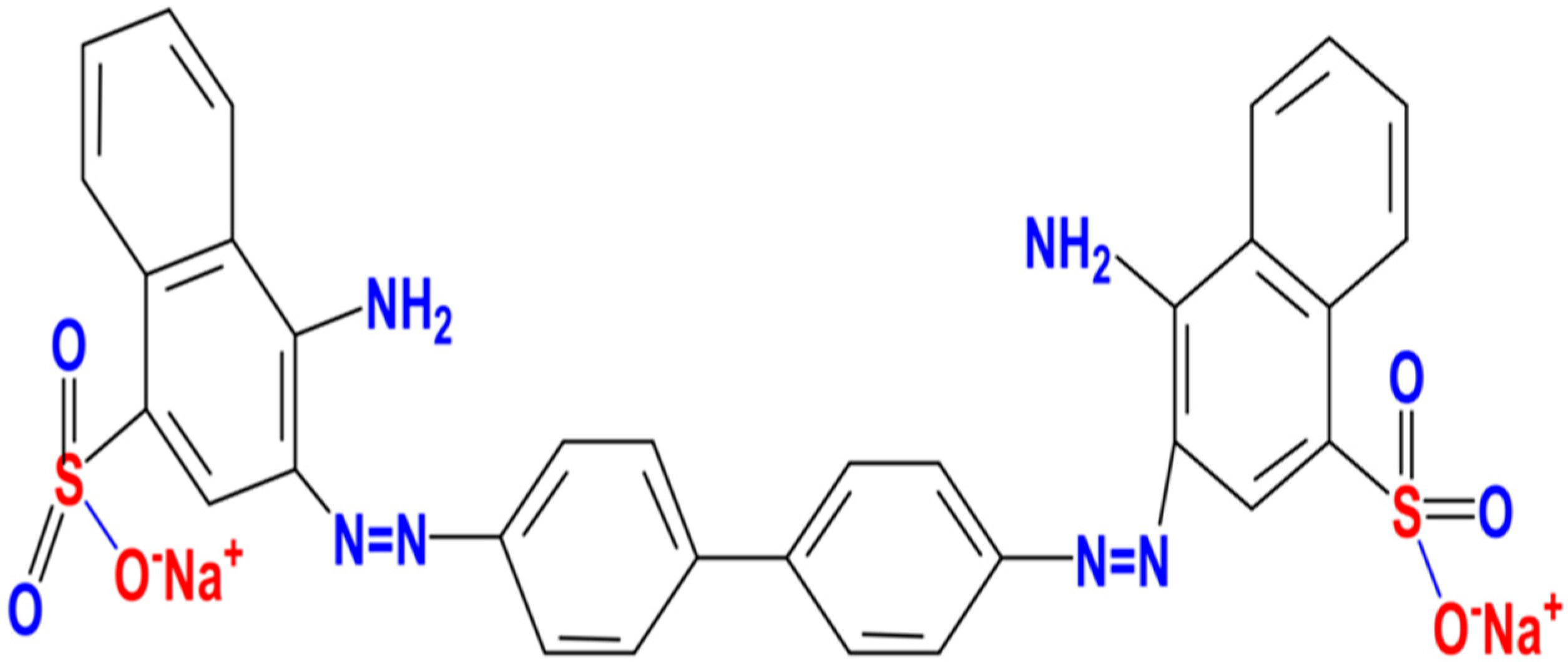
According to the literature survey, it is commonly recognized that AC can adsorb dyes within electrostatic, van der Waals as well as H-bonding interactions. The adsorption capacity of different adsorbents for Congo red (CR) dye depends on several interrelated factors. These include (1) the surface area and total pore volume of the adsorbent, which vary depending on the material composition; (2) the prevalence of mesopores over micropores, as mesoporous structures are more accessible to larger dye molecules; (3) experimental parameters such as pH, initial dye concentration, and contact time, which influence adsorption kinetics and equilibrium; and (4) the molecular size of Congo red relative to the adsorbent’s pore structure, which determines physical compatibility and diffusion efficiency. Collectively, these factors govern the adsorption performance, with mesopore availability and molecular size matching playing particularly critical roles in CR removal.

According to the experimental results, we conclude that date stone activated carbon could be a potential material to remove CR dye from polluted solution.

Furthermore, the R_L values indicate that the adsorption is suitable (0 < R_L < 1). In the case of synthesized DSAC composite, the R_L values are between 0.256 and 0.029 for all concentrations studied. Furthermore, the mean free energy of adsorption (E) derived from the Dubinin–Radushkevich (D-R) isotherm was less than 8 kJ mol⁻¹, confirming a physically driven adsorption process (physisorption).

These results align with the work of Alharbi et al. (2022), who systematically evaluated activation methods for producing activated carbon from date palm residues (DPRs) [87]. Their study shows that DPR-derived activated carbon achieves comparable efficiency to commercial activated carbon in adsorbing textile dyes, validating its role as a good ecological and economical alternative for industrial wastewater treatment. All this evidence proved the high potential of DSAC-based materials in sustainable dye removal applications.

-

Adsorption kinetics study

The study of adsorption kinetics is essential for characterizing the time dependence of the process, using models (such as pseudo-first-order, pseudo-second-order, and intraparticle diffusion) to elucidate the underlying mechanisms, rate-limiting steps, and surface interactions. These models allow for tracking the evolution of adsorption over time.

Table 8. Kinetic parameters for adsorption of CR onto DSAC.

	Parameter	DSAC
	C0 (mg/L)	20	50
Pseudo-first-order	qe (mg/g)	1.73	6.39
	k1 (min−1)	0.003	0.029
	R2	0.735	0.734
Pseudo-second-order	qe (mg/g)	9.00	19.23
	k2(g mg min−1)	0.091	0.013
	R2	1	0.999

compares the rate constants derived from the pseudo-first-order, pseudo-second-order, and intra-particle diffusion models under varying initial dye concentrations. Kinetic analysis of CR adsorption onto DSAC is essential for optimizing operating parameters in scaled-up batch processes.

Adsorption process scalability and rate behavior are modeled using experimental kinetic parameters for optimized system design. Thus, three kinetic models, intraparticle diffusion, pseudo-first-order (PFO) and pseudo-second-order (PSO), were used to examine the CR adsorption onto DSAC.

The pseudo-first-order kinetic model from Lagergren related to the adsorption of solid/liquid systems is illustrated in the following formula [88]:

$$\log \left(q_e-q_t\right)=\log \left(q_e\right)-\left({\displaystyle \frac{k_1}{2.303}}\right)t$$

(12)

where q_t (mg g⁻¹) and q_e (mg g⁻¹) represent the adsorbed dye concentration at the time t (min) and at the equilibrium time, respectively.

k₁ (1/min) represents the constant rate of the pseudo-first-order adsorption, which is obtained from the log (q_e − q_t) against t plot. Despite that, Table 8 reveals significant deviations of q_e values, demonstrating that the pseudo-first-order kinetic model is inappropriate for DSAC-CR adsorption systems.

The pseudo-second-order kinetic model with linear form is represented as [89]:

$${\displaystyle \frac{t}{q_t}}= {\displaystyle \frac{1}{k_2{q}_e^2}} + {\displaystyle \frac{t}{q_e}}$$

(13)

where k₂ (mg min)⁻¹ is the rate constant of the pseudo-second-order adsorption, obtained from linear plots of t/q_t against t. The experimental and calculated q_e values exhibit close agreement. Table 8 shows consistently higher R² values for pseudo-second-order kinetics, indicating its stronger correlation with experimental adsorption data.

To assess pore diffusion’s role in Congo red (CR) adsorption on DSAC, kinetic data was modeled using the intra-particle diffusion equation [90]:

$$q_t= k_{id}{t}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}+C$$

(14)

where q_t is adsorption capacity (mg g⁻¹) at time t, k_id is the diffusion rate constant (mg g⁻¹·min^−1/2), and C (mg g⁻¹) represents boundary layer thickness (Figure 4b).

If C = 0, intra-particle diffusion acts as the sole rate-controlling step in the adsorption process. The increase in the value of C confirms that there is a greater contribution from the phenomenon of surface adsorption. Although the curves representing the kinetic studies deviate from linearity during the experiment, they can be divided into two or three distinct linear phases, suggesting multiple stages in the adsorption mechanism. The high regression coefficients (R² = 0.9) across these phases further confirm that intra-particle diffusion plays a dominant role during the Congo red (CR) adsorption phenomenon on the DSAC composite, whereas the plot line does not pass through the origin, which confirms the presence of other steps controlling the adsorption process alongside the intra-particle diffusion.

-

Thermodynamic parameters

In order to further investigate the adsorption phenomena in our study, the variation of thermodynamic parameters, such as the change in Gibbs free energy (∆G⁰), entropy (∆S⁰) and enthalpy (∆H⁰), was studied. Therefore, an investigation of temperature dependence for the adsorption process gives, undoubtedly, knowledge on whether the reaction is spontaneous or not. The thermodynamics of the adsorption reaction towards spontaneity can be evaluated. We point out that, using the following equations, parameters were calculated.

$$∆G^0=-RT\mathit{ln}\left(K_0\right)$$

(15)

$$\mathit{Ln}{K}_{0 }=-{\displaystyle \frac{{∆G}^0}{RT}}=-{\displaystyle \frac{∆H^0}{RT}}+{\displaystyle \frac{∆S^0}{R}}$$

(16)

where R constitutes the universal gas constant (8.314 kJ. mol⁻¹), T represents the absolute temperature (K) and K₀ is the distribution coefficient equal to q_e/C_e. The plot of LnK₀ against 1/T illustrates straight-line form, in which ∆H⁰ and ∆S⁰ were obtained from the slope and intercept, respectively.

Table 9. Thermodynamic parameters for adsorption of CR onto DSAC.

∆H0 (kJ/mol)	∆S0 (kJ/mol)	∆G0 (kJ/mol)				R2
		298 K	308 K	318 K	328 K
–8.230	–0.008	−5.642	−5.555	−5.468	−5.382	0.992

recapitulates the thermodynamic parameters obtained from different temperatures.

The negative values of ΔG⁰ prove that the adsorption process was established spontaneously. It is worth noting that ΔG⁰ values for physisorption ranged from −20 to 0 kJ mol⁻¹, while that of chemisorption are between −80 and −400 kJ mol⁻¹ [91]. For the DSAC composite, the ΔG⁰ values ranging from −5.64 to −5.38 kJ·mol⁻¹ indicate adsorption stronger than typical physisorption. The negative ΔH⁰ value of −8.23 kJ mol⁻¹ confirms the exothermic nature of this process. Comparing the magnitude of this ΔH⁰ to characteristic adsorption energies—van der Waals forces (4–10 kJ mol⁻¹), hydrophobic interactions (~5 kJ·mol⁻¹), coordination exchange (~40 kJ mol⁻¹), and chemical bonds (>60 kJ mol⁻¹)—suggests that van der Waals forces and hydrophobic interactions likely contribute alongside electrostatic attraction. Furthermore, the negative value of ΔS⁰ indicates a decrease in randomness at the solid/solution interface [92].

-

Proposed adsorption mechanism

The adsorption mechanism of CR on DSAC composite is influenced by pH-dependent electrostatic interactions and interstitial diffusion. In aqueous solution, CR shows pH-sensitive behavior; at neutral pH (~7), it appears as a solid red, turning dark blue in acidic medium (cationic form), and retaining an anionic sulfonate structure (D–SO₃⁻) at alkaline pH (10–12). At pH > 5, CR exists as a large, negatively charged molecule due to sulfonate group dissociation (D–SO₃Na → D–SO₃⁻ + Na⁺); an aggregation phenomenon may occur in solution [84]. The DSAC surface charge, governed by its zero-point charge (pH_pzc = 8.2), shifts from positive (pH < 8.2) to negative (pH > 8.2). Below pH 8.2, electrostatic attraction occurs between the positively charged surface of DSAC and the CR sulfonate group, resulting in adsorption. At higher pH, competition with OH⁻ ions and surface repulsion reduce adsorption efficiency. Despite this, significant adsorption persists in the alkaline range (pH 7–10), supported by pore diffusion after initial rapid surface-site occupancy [93,94].

FTIR analysis (Figure 5) corroborates this mechanism; the appearance of a new S=O stretching peak (1265 cm⁻¹) in CR-loaded DSAC confirms sulfonate group interaction, while shifts in hydroxyl (3300–3700 cm⁻¹), alkyl (2927, 2853 cm⁻¹), and carbonyl (1741 cm⁻¹) bands suggest additional interactions involving polar and aromatic moieties.

Thus, CR adsorption on DSAC is firstly controlled by electrostatic forces at almost neutral pH (6.8), followed by slower intra-particle diffusion into pores, with a secondary contribution from hydrogen bonding or π-π interactions inferred from spectral changes. The adsorption mechanism can be explained by the electrostatic interaction between the negatively charged SO³⁻ groups and the positive charge of the activated carbon surface.

3.3. Fractional Factorial Design

-

Statistical study

Factorial design is a statistical methodology used to optimize experimental efficiency by systematically reducing the number of trials required to evaluate multiple variables. This approach minimizes time, cost, and resource expenditure while maximizing the accuracy of identifying critical factors and their interactions [95]. A 2³ full factorial design was used to evaluate the statistical significance of three factors, their interactions, and their effects on activated carbon’s (AC) performance in removing Congo red (CR).

In order to verify whether there is any curvature in the model to be fitted and estimate the experimental error, three center points were added. The software MINITAB 17.1.0 [96] was used for planning the Factorial Design and analyzing experimental data. The experimental matrix designs presented in

Table 10. Design matrix and the results of the 2³ full factorial design.

Run Order	Coded Factors			A (g L−1)	B	C (°C)	%Removal Rate
1	0	0	0	1.1	8.8	40	65.31
2	−1	+1	−1	0.2	10.8	25	24.54
3	−1	+1	+1	0.2	10.8	55	19.28
4	+1	−1	−1	2.0	6.8	25	97.13
5	−1	−1	−1	0.2	6.8	25	26.11
6	+1	−1	+1	2.0	6.8	55	91.20
7	0	0	0	1.1	8.8	40	67.41
8	+1	+1	−1	2.0	10.8	25	87.67
9	+1	+1	+1	2.0	10.8	55	75.98
10	0	0	0	1.1	8.8	40	64.85
11	−1	−1	+1	0.2	6.8	55	20.09

were executed in a random order to avoid systematic errors [96].

A first-degree polynomial model, representing CR removal efficiency (%R), was established. The relationship between Congo red (CR) removal efficiency and the three process parameters (A, B, C), including their interaction effects, is described by the following regression model:

%R = 55.250 + 32.745 A − 3.382 B − 3.612 C − 2.788 AB − 0.793 AC − 0.625 BC − 0.815 ABC

Table 11. Estimated effects and coefficients for CR removal (coded units).

Term	Effect	Coefficient	SE Coef	T-Value	p-Value
Constant		55.250	0.483	114.51	0.000
A	65.490	32.745	0.483	67.86	0.000
B	−6.765	−3.382	0.483	−7.01	0.020
C	−7.225	−3.612	0.483	−7.49	0.017
AB	−5.575	−2.788	0.483	−5.78	0.029
AC	−1.585	−0.793	0.483	−1.64	0.242
BC	−1.250	−0.625	0.483	−1.30	0.325
ABC	−1.630	−0.815	0.483	−1.69	0.233

SE Coef: Standard Error Coefficient; T-value: Student’s test value; p-value: probability.

presents the interaction effects, coefficients of the model, standard error coefficient, T-values and p-values and regression coefficients. In addition, the square correlation coefficient of the model (R²-sq of 97.26%) was in good agreement with the statistical model.

R²-sq: 97.26% and R²-sq(adj): 90.87%

To determine whether the calculated main and interaction effects were statistically significant, p-values and Pareto chart are used. The factor is considered as statistically significant when p-value is lower than 0.05 [97,98,99]. Figure 6 displays these effects as vertical bars, illustrating their relative importance.

All the values presenting an absolute value higher than the t-value (t = 4.30, for α risk of 5%, and 10 degrees of freedom), which indicates minimum statistically significant effect magnitude, are significant [100,101].

The final empirical model for CR removal efficiency was refined from the initial full factorial model (Equation (3)) by retaining only the statistically significant terms (p-value < 0.05), as determined by the ANOVA results in Table 11. This stepwise exclusion of non-significant factors (AC, BC, ABC) is a standard practice to develop a more parsimonious and robust model without compromising predictive accuracy. Consequently, the relationship between the significant parameters and the response is best described by the following reduced model in terms of coded factors:

%R = 55.250 + 32.745 A − 3.382 B − 3.612 C − 2.788 AB

-

Main and interaction effects of the factors

Figure 7a presents the main effects of process parameters (A, B, and C) on Congo red (CR) removal.Main effect plots visualize the relative influence of each factor on the response. As established [101,102], the magnitude of a factor’s effect corresponds to the vertical distance of its line; a larger distance indicates a greater change in removal efficiency when the factor shifts from a low to high level. Analysis revealed that adsorbent dosage exhibits the steepest slope, indicating substantial variation in CR removal across its levels. This pronounced effect signifies that adsorbent dosage is a highly significant factor. However, pH and temperature have less negative influence upon removal efficiency. Thus, an increase of one of these two factors decreases the CR removal efficiency.

The significant factor interactions indicated that main effects were non-additive and level-dependent; it is necessary to take into account the interaction between the different parameters on the adsorption of CR. Figure 7b shows the interaction effects of each parameter on the dye removal, which would favor a better statement of the process. Non-parallel lines indicate that the interaction among control factors is strong. Since the lines of adsorbent dosage and pH are far from being parallel, the important interaction is AB and less important interactions are between absorbent dosage and temperature (AC) then between pH and temperature (BC). The same observations were also shown on the Pareto chart.

3.4. Reusability Study

Reusability studies evaluated DSAC over four consecutive cycles. After each run, the DSAC was recovered by centrifugation at 4000 rpm, washed twice with methanol to remove any residual dye and dried in an oven at 60˚C for 2 h. The dried powder was then reused in the next adsorption cycle. Figure 8 reveals that the CR dye removal efficiency exhibited excellent stability across cycles. Even after the fourth regeneration, DSAC maintained a high removal rate of 87%, compared to the initial 90%. This consistent performance confirms the structural robustness of DSAC through repeated regeneration.

4. Conclusions

In this study we have investigated the valorization of date stones, an abundant form of agricultural waste in Tunisia, as a sustainable adsorbent for removing Congo Red (CR) dye from wastewater. It was observed that the adsorption capacity increased proportionally with the dose of the date stone-activated carbon (DSAC). Optimal dye removal (90%) occurred under acidic conditions and, notably, even at a neutral pH value. Kinetic studies and equilibrium both aligned with the Langmuir isotherm, monolayer adsorption and pseudo-second-order models (chemisorption), respectively. This result confirms the dominance of surface-driven chemical interactions. These findings highlight DSAC’s potential as a sustainable, low-cost adsorbent for textile wastewater treatment. The Langmuir isotherm yielded a maximum monolayer adsorption capacity of 27.77 mg g⁻¹ for CR on DSAC at pH = 7 and at T = 25 °C. Spontaneous and exothermic adsorption behavior, indicated by thermodynamic parameters (ΔG° < 0, ΔH° < 0), arose predominantly from electrostatic interactions. Full factorial design confirmed that all tested parameters (adsorbent dosage, pH, and temperature) have significantly influenced the CR removal from wastewater. Beyond its high adsorption capacity, the practical potential of DSAC is underscored by its excellent reusability. The adsorbent retained over 87% of its original efficiency after four regeneration cycles using a simple methanol wash. This robust performance suggests that the initial cost of producing DSAC can be amortized over multiple treatment cycles, significantly enhancing its economic feasibility for scalable industrial wastewater remediation. Future work will focus on optimizing the regeneration process and conducting a detailed techno-economic analysis.