In Situ Tests on the Flexural Strength and Effective Elastic Modulus of Brackish Ice During Different Ice Periods
Abstract
1. Introduction
2. Materials and Methods
2.1. Research Area
2.2. Cantilever Beam Test
2.3. Ice Physical Properties
3. Results
3.1. Physical Properties of Ice Layers
3.1.1. Crystal Structure
3.1.2. Physical Parameters
3.2. Flexural Strength and Effective Modulus Derived from Cantilever Beam Tests
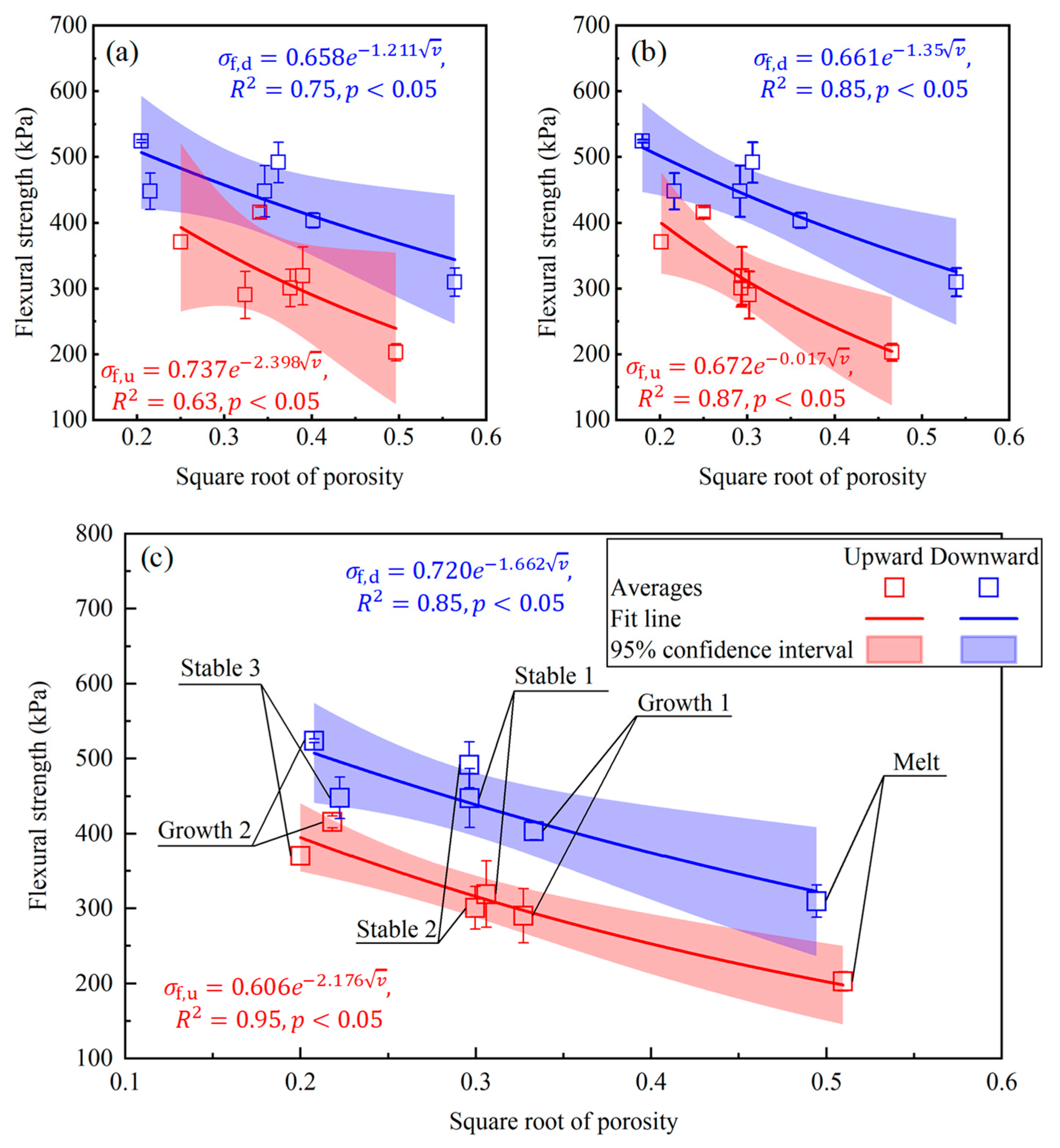
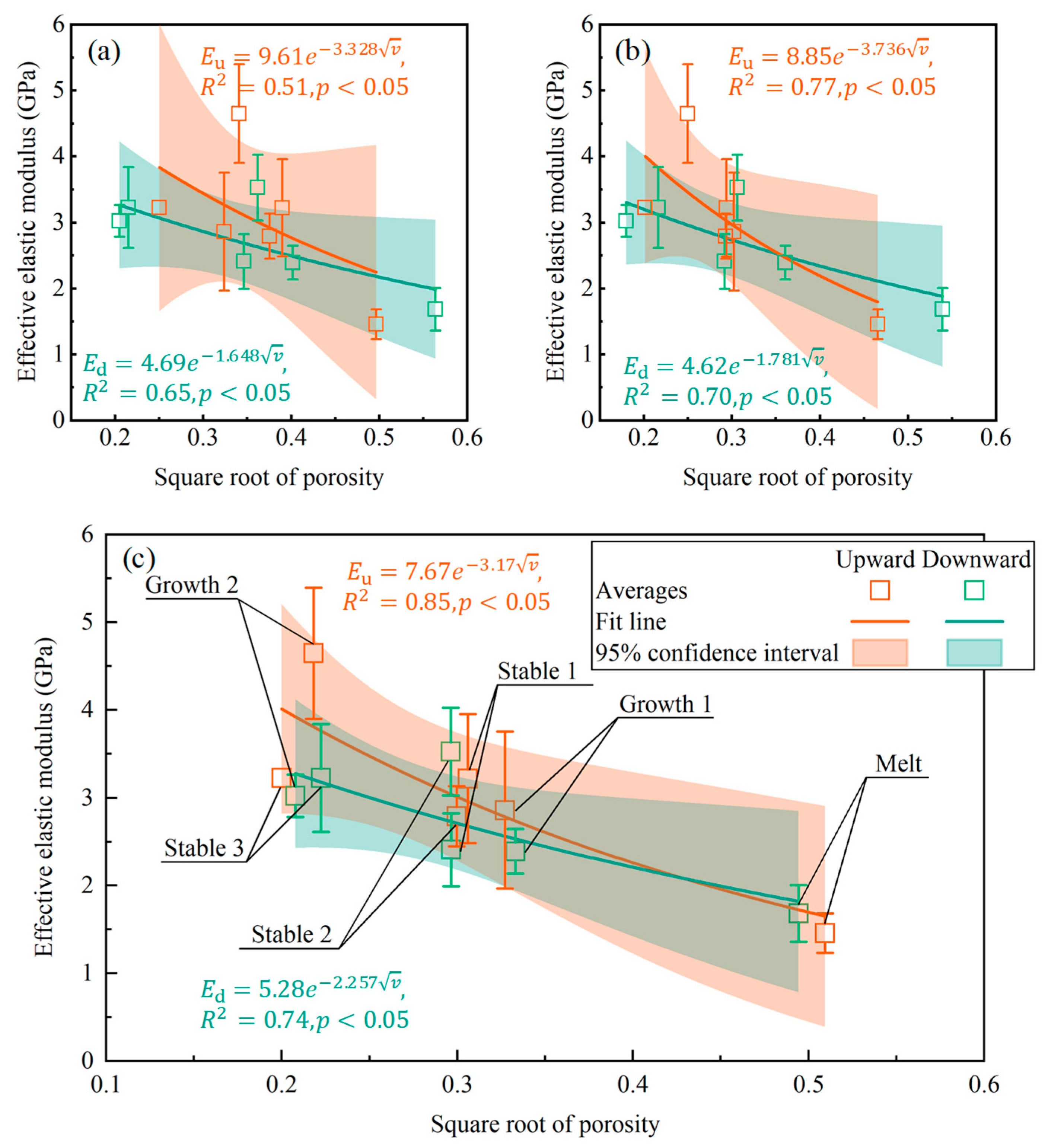
3.2.1. Effects of Physical Parameters
3.2.2. Effects of Loading Direction
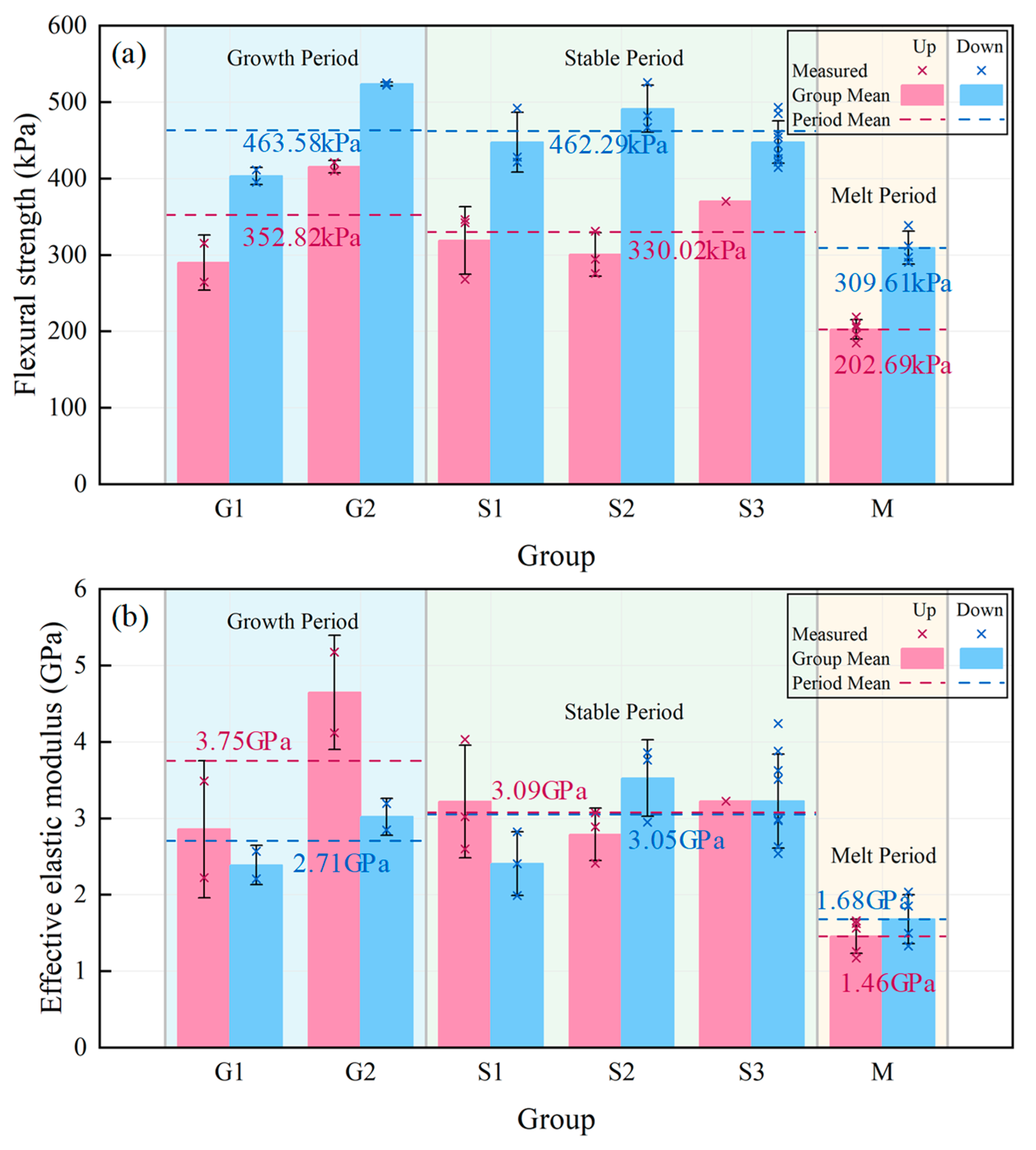
3.2.3. Effects of Ice Period and Beam Volume
3.2.4. Evaluation of Buoyancy Effects on Test Results
4. Discussion
4.1. Differences in Mechanical Properties of Brackish Water Ice from Saline Water Ice and Freshwater Ice
4.2. Fracture of Ice During Melt Period
5. Conclusions
- (1)
- Exponential functions were identified as the most effective form for fitting the relationships between flexural strength, effective elastic modulus, and ice physical properties. Although fracture under different loading modes is governed by the physical properties of different parts of the ice layer, comparison among alternative parameterizations revealed that the bulk mean values of physical properties provided the best predictive performance. Both flexural strength and effective elastic modulus decreased with increasing porosity and gas volume fraction, with porosity yielding the highest goodness-of-fit, highlighting its dominant role in controlling ice mechanical behavior. The empirical formulas for the full-scale flexural mechanical properties of brackish ice, as shown in Equations (3) and (4).
- (2)
- Flexural strength obtained under downward loading was systematically higher than that under upward loading, with differences ranging from 17.3 to 38.8%. This behavior can be attributed to the presence of granular crystals in the upper ice layer and the progressive increase in columnar crystal diameters with depth, which weakened intergranular bonding in the tensile zone and reduced tensile resistance. In contrast, the effective elastic modulus reflects the overall stress–strain response rather than the failure threshold. Although no clear directional dependence of the modulus was observed in this study, the inherent variability of full-scale in situ measurements suggests that more data are needed before a definitive conclusion can be drawn regarding the relationship between loading direction and elastic modulus.
- (3)
- No significant differences were observed in flexural strength or effective elastic modulus between the growth and stable periods, as both exhibited comparable mechanical levels. In contrast, the melt period showed a marked reduction: flexural strength decreased by approximately 33–42%, and effective elastic modulus decreased by 49–61% relative to the growth and stable periods. This deterioration is primarily attributed to the interconnection of brine channels and substantial brine drainage during melting, combined with increased gas volume fraction and porosity, which weakened the load-bearing skeleton. Furthermore, grain-boundary wetting and bubble accumulation reduced the overall stiffness, thereby accelerating the degradation of mechanical properties.
- (4)
- Comparisons with existing datasets indicate that the mechanical properties of brackish ice are lower than those of freshwater ice but higher than those of sea ice. At the same temperature, its flexural strength and effective elastic modulus are about 30–50% lower than freshwater ice, due to brine inclusions and bubbles weakening the load-bearing skeleton. At the same porosity, however, brackish ice outperforms sea ice; for example, at a porosity square root of 0.3, its strength (379 kPa) and modulus (1.56–3.84 GPa) exceed those of sea ice (180–302 kPa, 0.25–2.30 GPa). This difference reflects the denser structure of brackish ice, formed under weaker brine drainage and dynamic forcing.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blagrave, K.; Sharma, S. Projecting climate change impacts on ice phenology across Midwestern and Northeastern United States lakes. Clim. Change 2023, 176, 119. [Google Scholar] [CrossRef]
- Ruan, Y.A.; Zhang, X.; Xin, Q.; Qiu, Y.; Sun, Y. Prediction and analysis of lake ice phenology dynamics under future climate scenarios across the inner Tibetan Plateau. J. Geophys. Res.-Atmos. 2020, 125, e2020JD033082. [Google Scholar] [CrossRef]
- Stroeve, J.; Notz, D. Changing state of Arctic sea ice across all seasons. Environ. Res. Lett. 2018, 13, 103001. [Google Scholar] [CrossRef]
- Huo, P.; Peng, L.; Cheng, B.; Yu, M.; Wang, Q.; Li, X.; Li, Z. Reconstructing ice phenology of a lake with complex surface cover: A case study of Lake Ulansu during 1941–2023. Cryosphere 2025, 19, 849–868. [Google Scholar] [CrossRef]
- Wang, X.; Feng, L.; Qi, W.; Cai, X.; Zheng, Y.; Gibson, L.; Tang, J.; Song, X.; Liu, J.; Zheng, C.; et al. Continuous loss of global lake ice across two centuries revealed by satellite observations and numerical modeling. Geophys. Res. Lett. 2022, 49, e2022GL099022. [Google Scholar] [CrossRef]
- Sharma, S.; Richardson, D.C.; Woolway, R.I.; Imrit, M.A.; Bouffard, D.; Blagrave, K.; Daly, J.; Filazzola, A.; Granin, N.; Korhonen, J.; et al. Loss of ice cover, shifting phenology, and more extreme events in northern hemisphere lakes. J. Geophys. Res-Biogeo. 2021, 126, e2021JG006348. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, X. Theoretical model for predicting the break-up of ice covers due to wave-ice interaction. Appl. Ocean Res. 2021, 112, 102614. [Google Scholar] [CrossRef]
- Masterson, D.M. State of the art of ice bearing capacity and ice construction. Cold Reg. Sci. Technol. 2009, 58, 99–112. [Google Scholar] [CrossRef]
- Aly, M.; Taylor, R.; Dudley, E.B.; Turnbull, I. Scale effect in ice flexural strength. J. Offshore Mech. Arct. 2019, 141, 051501. [Google Scholar] [CrossRef]
- Wei, M.; Dai, F. Laboratory-scale mixed-mode I/II fracture tests on columnar saline ice. Theor. Appl. Fract. Mech. 2021, 114 (Suppl. SC), 102982. [Google Scholar] [CrossRef]
- Wei, M.; Prasanna, M.; Cole, D.M.; Polojärvi, A. Response of dry and floating saline ice to cyclic compression. Geophys. Res. Lett. 2022, 49, e2022GL099457. [Google Scholar] [CrossRef]
- Wei, M.; Polojärvi, A.; Cole, D.M.; Prasanna, M. Strain response and energy dissipation of floating saline ice under cyclic compressive stress. Cryosphere 2020, 14, 2849–2867. [Google Scholar] [CrossRef]
- Marchenko, A.; Karulin, E.; Chistyakov, P.; Karulina, M.; Sakharov, A. Meso-scale stress relaxation test on floating sea ice. In Proceedings of the 27th International Conference on Port and Ocean Engineering under Arctic Conditions, Glasgow, UK, 12–16 June 2023. [Google Scholar]
- Marchenko, A.; Grue, J.; Karulin, E.; Frederking, R.; Lishiman, B.; Chistyakov, P.; Karulina, M.; Sodhi, D.; Renshaw, C.; Sakharov, A.; et al. Elastic moduli of sea ice and lake ice calculated from in-situ and laboratory experiments. In Proceedings of the 25th IAHR International Symposium on Ice, Trondheim, Norway, 23–25 June 2020. [Google Scholar]
- Voermans, J.J.; Rabault, J.; Marchenko, A.; Nose, T.; Waseda, T.; Babanin, A.V. Estimating the elastic modulus of landfast ice from wave observations. J. Glaciol. 2023, 69, 1823–1833. [Google Scholar] [CrossRef]
- Karulina, M.; Marchenko, A.; Karulin, E.; Sodhi, D.; Sakharov, A.; Chistyakov, P. Full-scale flexural strength of sea ice and freshwater ice in Spitsbergen Fjords and North-West Barents Sea. Appl. Ocean Res. 2019, 90, 101853. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, W.; Yu, C.; Gang, X.; Lu, P.; Yue, Q. Investigations on flexural strength of a columnar saline model ice under circular plate central loading. Water 2023, 15, 3371. [Google Scholar] [CrossRef]
- Krupina, N.A.; Kubyshkin, N.V. Flexural strength of drifting level first-year ice in the Barents Sea. In Proceedings of the 17th International Offshore and Polar Engineering Conference, Lisbon, Portugal, 1–6 July 2007. [Google Scholar]
- Timco, G.W.; O’Brien, S. Flexural strength equation for sea ice. Cold Reg. Sci. Technol. 1994, 22, 285–298. [Google Scholar] [CrossRef]
- Lainey, L.; Tinawi, R. The mechanical properties of sea ice — A compilation of available data. Can. J. Civ. Eng. 1984, 11, 884–923. [Google Scholar] [CrossRef]
- Han, H.; Jia, Q.; Huang, W.; Li, Z. Flexural strength and effective modulus of large columnar-grained freshwater ice. Cold Reg. Sci. Technol. 2015, 30, 04015005. [Google Scholar] [CrossRef]
- Murdza, A.; Marchenko, A.; Schulson, E.M.; Renshaw, C.E. Cyclic strengthening of lake ice. J. Glaciol. 2021, 67, 182–185. [Google Scholar] [CrossRef]
- Murdza, A.; Schulson, E.M.; Renshaw, C.E. Behavior of saline ice under cyclic flexural loading. Cryosphere 2021, 15, 2415–2428. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Y.; Lu, P.; Li, Z. The mechanical properties of gas-enriched sea ice. Cold Reg. Sci. Technol. 2025, 239, 104576. [Google Scholar] [CrossRef]
- Frederking, R.M.W.; Timco, G.W. On measuring flexural properties of ice using cantilever beams. Ann. Glaciol. 1983, 4, 58–65. [Google Scholar]
- Frederking, R.M.W.; Svec, O.J. Stress-relieving techniques for cantilever beam tests in an ice cover. Cold Reg. Sci. Technol. 1985, 11, 247–253. [Google Scholar] [CrossRef]
- Hutchings, J.K.; Heil, P.; Lecomte, O.; Stevens, R.; Steer, A.; Lieser, J.L. Comparing methods of measuring sea-ice density in the East Antarctic. Ann. Glaciol. 2015, 56, 385–386. [Google Scholar] [CrossRef]
- Pustogvar, A.; Kulyakhtin, A. Sea ice density measurements: Methods and uncertainties. Cold Reg. Sci. Technol. 2016, 131, 46–52. [Google Scholar] [CrossRef]
- Cox, G.F.N.; Weeks, W.F. Equations for determining the gas and brine volumes in sea ice samples. J. Glaciol. 1983, 29, 306–316. [Google Scholar] [CrossRef] [PubMed]
- Leppäranta, M.; Manninen, T. The Brine and Gas Content of Sea Ice with Attention to Low Salinities and High Temperatures; Finnish Institute of Marine Research: Helsinki, Finland, 1988. [Google Scholar]
- Eicken, H.; Dieckmann, G.S.; Thomas, D.N. From the microscopic, to the macroscopic, to the regional scale: Growth, microstructure and properties of sea ice. In Sea Ice, 2nd ed.; David, N.T., Gerhard, S.D., Eds.; Blackwell Science Ltd: Oxford, UK, 2003; pp. 22–81. [Google Scholar] [CrossRef]
- Wang, J.; Cao, X.; Wang, Q.; Yan, L.; Li, Z. Experimental relationship between flexural strength, elastic modulus of ice sheet and equivalent ice temperature. J. South-North Water Transf. Water Sci. Technol. 2016, 14, 75–380. [Google Scholar] [CrossRef]
- Frankenstein, G.E. Strength data on lake ice. In U.S. Army Snow Ice and Permafrost Research Establishment; Corps of Engineers: Wilmette, IL, USA, 1961; p. 20. [Google Scholar]
- Ervik, Å. Experimental and Numerical Investigations of Cantilever Beam Tests in Floating Ice Covers. Master’s Thesis, Norwegian University of Science and Technology, Lonyearbyen, Norway, 2013. [Google Scholar]
- Bogorodsky, V.V.; Gavrilo, V.P. Ice. Physical properties. In Modern Methods of Glaciology; Gidrometeoizdat: Leningrad, Russia, 1980; p. 384. [Google Scholar]
- Zhang, H.; Yu, M.; Lu, P.; Zhou, J.; Zhou, J.; Xie, F.; Wang, Q.; Li, Z. Experimental investigation of the partitioning of radiation in the melt pond–ice–ocean system. Cold Reg. Sci. Technol. 2024, 219, 104107. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, Y.; Li, Z.; Yu, M.; Xie, F.; Georgiy, K.; Yang, Z. Optical properties of ice in a shallow Chinese lake (Hanzhang) with consequent impacts on primary production. Sci. Total Environ. 2023, 957, 177512. [Google Scholar] [CrossRef]
- Yang, F.; Li, C.; Shi, X.; Zhao, S.; Hao, Y. Impact of seasonal ice structure characteristics on ice cover impurity distributions in Lake Ulansuhai. J. Lake Sci. 2016, 28, 455–462. [Google Scholar] [CrossRef] [PubMed]


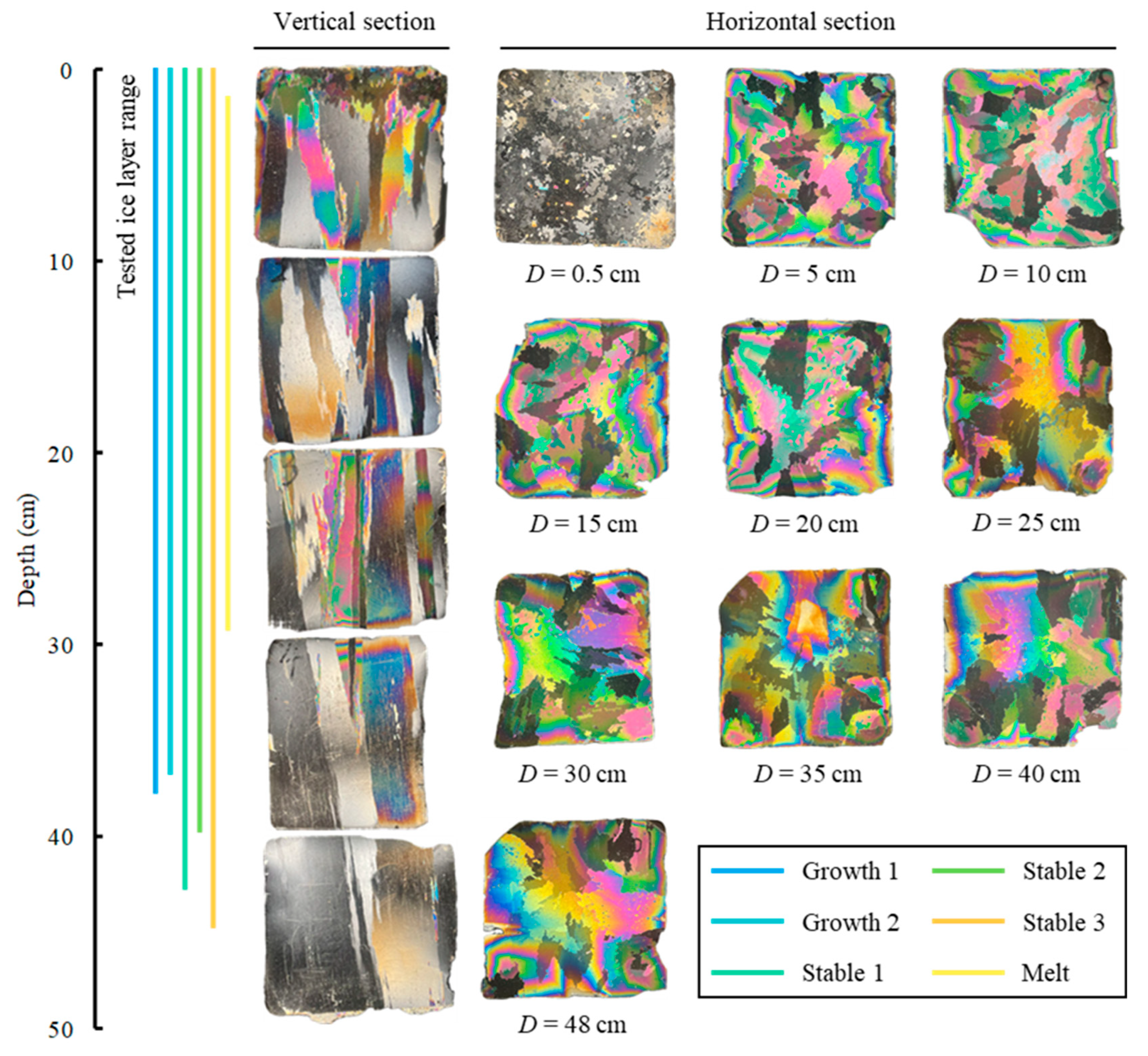
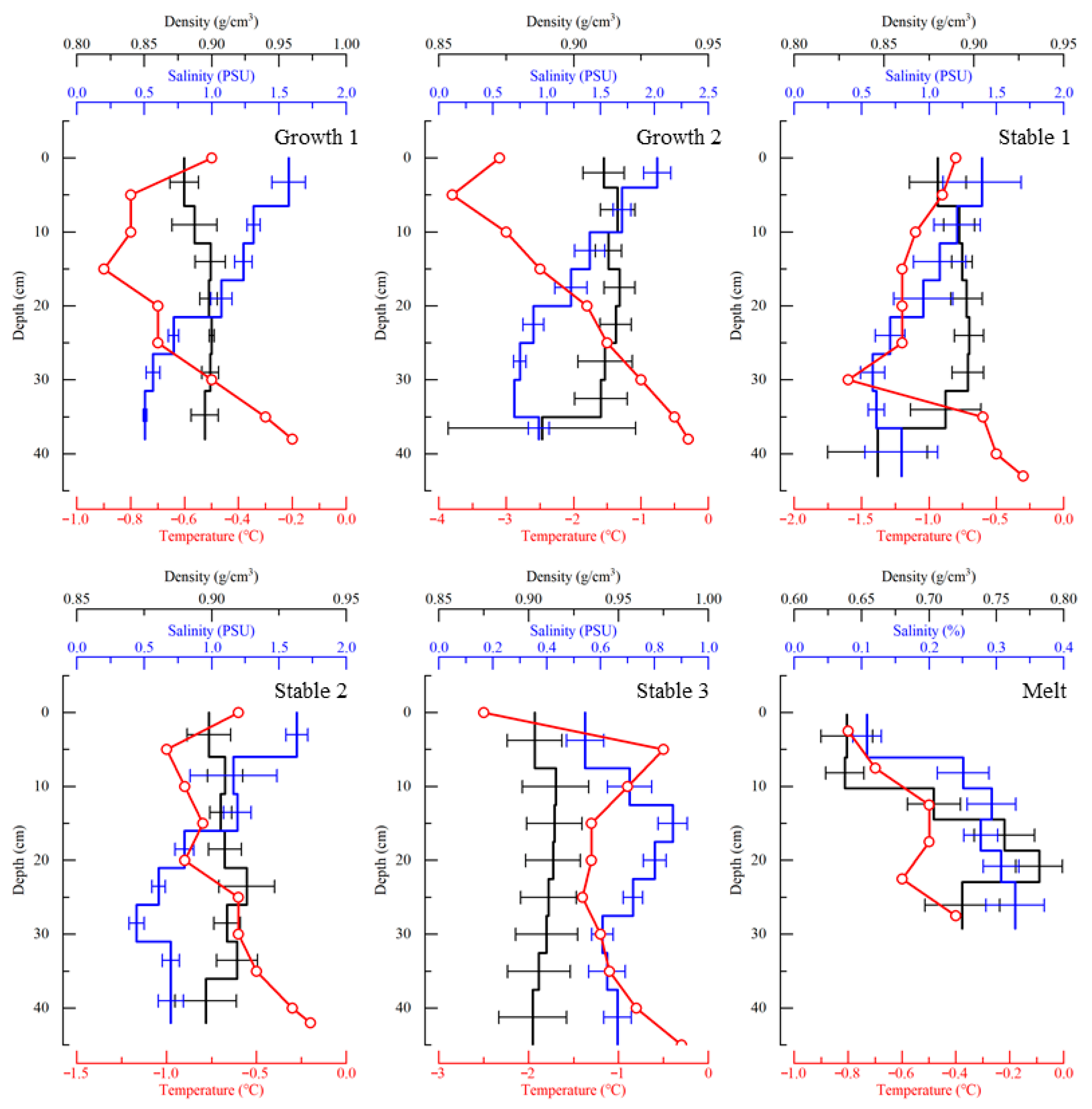
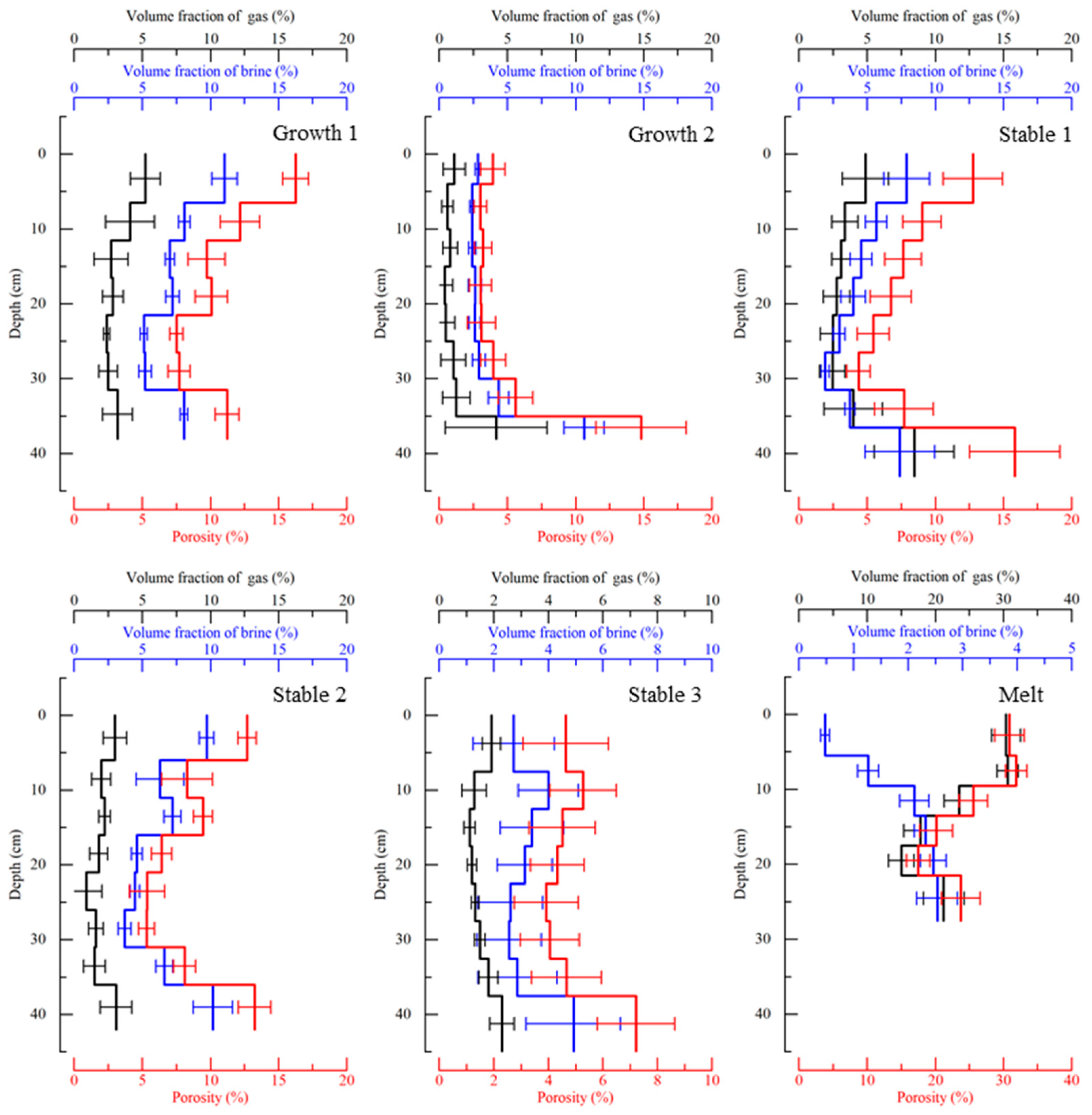





| No. | Date of Test | Ice Period | Ice Thickness (m) | Number of Beams (Upward/Downward) | Ice Surface Condition |
|---|---|---|---|---|---|
| 1 | 17 January 2024 | Growth | 0.38 | 4 (2/2) | Snow-covered and smooth surface |
| 2 | 22 January 2024 | Growth | 0.37 | 4 (2/2) | Snow-covered and smooth surface |
| 3 | 26 January 2024 | Stable | 0.43 | 6 (3/3) | Snow-covered and smooth surface |
| 4 | 30 January 2024 | Stable | 0.40 | 6 (3/3) | Snow-covered and smooth surface |
| 5 | 24 February 2024 | Stable | 0.45 | 10 (1/9) | Rough surface |
| 6 | 12 March 2024 | Melt | 0.28 | 10 (5/5) | Wet surface |
| Group | Beam Volume (m3) | Loading Direction | Number of Valid Datasets (n) | Flexural Strength (kPa) | Effective Modulus (GPa) | Mean Flexural Strength (MPa) | Mean Effective Modulus (GPa) |
|---|---|---|---|---|---|---|---|
| Growth 1 | 0.99 ± 0.005 | Upward | 2 | 290.12 ± 35.91 | 2.86 ± 0.90 | 346.75 ± 68.9 | 2.62 ± 0.60 |
| Downward | 2 | 403.37 ± 11.33 | 2.39 ± 0.26 | ||||
| Growth 2 | 0.99 ± 0.004 | Upward | 2 | 415.52 ± 7.97 | 4.65 ± 0.75 | 469.65 ± 62.69 | 3.84 ± 1.04 |
| Downward | 2 | 523.78 ± 2.34 | 3.02 ± 0.24 | ||||
| Stable 1 | 1.30 ± 0.009 | Upward | 3 | 318.96 ± 44.18 | 3.22 ± 0.74 | 383.24 ± 76.69 | 2.81 ± 0.70 |
| Downward | 3 | 447.53 ± 39.06 | 2.41 ± 0.42 | ||||
| Stable 2 | 1.06 ± 0.011 | Upward | 3 | 300.66 ± 28.34 | 2.79 ± 0.34 | 396.09 ± 107.82 | 3.16 ± 0.56 |
| Downward | 3 | 491.52 ± 30.63 | 3.53 ± 0.50 | ||||
| Stable 3 | 1.37 ± 0.031 | Upward | 1 | 370.46 | 3.22 | 440.07 ± 35.74 | 3.23 ± 0.58 |
| Downward | 9 | 447.81 ± 27.64 | 3.23 ± 0.61 | ||||
| Melt | 0.38 ± 0.022 | Upward | 5 | 202.69 ± 12.88 | 1.46 ± 0.22 | 250.21 ± 58.58 | 1.56 ± 0.28 |
| Downward | 4 | 309.61 ± 21.47 | 1.68 ± 0.32 |
| Ice Type | Author | Location | Test Date | Number of Data Points | Flexural Strength (kPa) | Effective Modulus (GPa) | Fit Line |
|---|---|---|---|---|---|---|---|
| Brackish ice | This study | Lake Hanzhang | 2024 | 39 | 374.21 ± 99.93 | 2.77 ± 0.93 | |
| [35] | Gulf of Finland | 2006 | / | / | / | ||
| Freshwater ice | [16] | Spitsbergen Fjords | 2012–2015 | 15 | 486.60 ± 149.67 | 2.91 ± 1.26 | / |
| [32] | Lake Ulansuhai | 2016 | 9 | 665.75 ± 93.48 | 5.32 ± 1.14 | ||
| [33] | Chassell Bay and Keweenaw Bay | 1957–1958 | 49 | 438.73 ± 170.36 | / | / | |
| Sea ice | [16] | Spitsbergen Fjords and North-West Barents Sea | 2010–2018 | 62 | 258.58 ± 85.38 | 1.24 ± 0.62 | |
| [18] | South-East Barents Sea and North-East Barents Sea | 1996–2006 | 138 | 252.00 ± 84.00 | / | ||
| [19] | Labrador, Greenland, Alaska, Antarctica, Beaufortsea, Baffin, Bothnia, Japan, Spitzbergen | 1955–1992 | 2495 | / | / | ||
| [34] | North-West Barents Sea | 2013 | 12 | 225.25 ± 81.15 | 1.03 ± 0.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, S.; Liu, Y.; Wang, Q.; Lu, P.; Yuan, S. In Situ Tests on the Flexural Strength and Effective Elastic Modulus of Brackish Ice During Different Ice Periods. Water 2025, 17, 3189. https://doi.org/10.3390/w17223189
Ji S, Liu Y, Wang Q, Lu P, Yuan S. In Situ Tests on the Flexural Strength and Effective Elastic Modulus of Brackish Ice During Different Ice Periods. Water. 2025; 17(22):3189. https://doi.org/10.3390/w17223189
Chicago/Turabian StyleJi, Shaopeng, Yubo Liu, Qingkai Wang, Peng Lu, and Shunqi Yuan. 2025. "In Situ Tests on the Flexural Strength and Effective Elastic Modulus of Brackish Ice During Different Ice Periods" Water 17, no. 22: 3189. https://doi.org/10.3390/w17223189
APA StyleJi, S., Liu, Y., Wang, Q., Lu, P., & Yuan, S. (2025). In Situ Tests on the Flexural Strength and Effective Elastic Modulus of Brackish Ice During Different Ice Periods. Water, 17(22), 3189. https://doi.org/10.3390/w17223189






