Assessment and Modeling of the Hydrological Response of Extensive Green Roofs Under High-Intensity Simulated Rainfalls
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Simple Reservoir-Routing Model
2.3. Statistical Analysis
3. Results and Discussion
3.1. Hydrological Performance of Green Roof Columns
3.2. Statistical Evaluation of the Hydrological Performance of Green Roof Columns
3.3. Influence of Substrate–Drainage Combination on the Hydrological Response
3.4. Simple Reservoir-Routing Model Evaluation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Scalenghe, R.; Ajmone Marsan, F. The anthropogenic sealing of soils in urban areas. Landsc. Urban Plan. 2009, 90, 1–10. [Google Scholar] [CrossRef]
- Tobias, S.; Conen, F.; Duss, A.; Wenzel, L.M.; Buser, C.; Alewell, C. Soil sealing and unsealing: State of the art and examples. Land Degrad. Dev. 2018, 29, 2015–2024. [Google Scholar] [CrossRef]
- Bengtsson, L. Peak flows from thin sedum-moss roof. Hydrol. Res. 2005, 36, 269–280. [Google Scholar] [CrossRef]
- Güneralp, B.; Güneralp, I.; Liu, Y. Changing global patterns of urban exposure to flood and drought hazards. Glob. Environ. Change 2015, 31, 217–225. [Google Scholar] [CrossRef]
- Lee, J.Y.; Lee, M.J.; Han, M. A pilot study to evaluate runoff quantity from green roofs. J. Environ. Manag. 2015, 152, 171–176. [Google Scholar] [CrossRef]
- Shafique, M.; Kim, R.; Kyung-Ho, K. Green roof for stormwater management in a highly urbanized area: The case of Seoul, Korea. Sustainability 2018, 10, 584. [Google Scholar] [CrossRef]
- Santamouris, A. Cooling the cities—A review of reflective and green roof mitigation technologies to fight heat island and improve comfort in urban environments. Sol. Energy 2014, 103, 682–703. [Google Scholar] [CrossRef]
- Rowe, B. Green roofs as a means of pollution abatement. Environ. Pollut. 2011, 159, 2100–2110. [Google Scholar] [CrossRef]
- Li, Y.; Babcock Jr, R.W. Green roofs against pollution and climate change. A review. Agron. Sustain. Dev. 2014, 34, 695–705. [Google Scholar] [CrossRef]
- Van Renterghem, T. Green roofs for acoustic insulation and noise reduction. In Nature Based Strategies for Urban and Building Sustainability; Butterworth-Heinemann: Oxford, UK, 2018; pp. 167–179. [Google Scholar]
- Yang, J.; Yu, Q.; Gong, P. Quantifying air pollution removal by green roofs in Chicago. Atmos. Environ. 2008, 42, 7266–7273. [Google Scholar] [CrossRef]
- Wang, L.; Wang, H.; Wang, Y.; Che, Y.; Ge, Z.; Mao, L. The relationship between green roofs and urban biodiversity: A systematic review. Biodivers. Conserv. 2022, 31, 1771–1796. [Google Scholar] [CrossRef]
- Czemiel Berndtsson, J. Green roof performance towards management of runoff water quantity and quality: A review. Ecol. Eng. 2010, 36, 351–360. [Google Scholar] [CrossRef]
- Gregoire, B.G.; Clausen, J.C. Effect of a modular extensive green roof on stormwater runoff and water quality. Ecol. Eng. 2011, 37, 963–969. [Google Scholar] [CrossRef]
- Stovin, V.; Vesuviano, G.; Kasmin, H. The hydrological performance of a green roof test bed under UK climatic conditions. J. Hydrol. 2012, 414, 148–161. [Google Scholar] [CrossRef]
- Voyde, E.; Fassman, E.; Simcock, R. Hydrology of an extensive living roof under sub-tropical climate conditions in Auckland, New Zeland. J. Hydrol. 2010, 394, 384–395. [Google Scholar] [CrossRef]
- De-Ville, S.; Menon, M.; Jia, X.; Reed, G.; Stovin, V. The impact of green roof ageing on substrate characteristics and hydrological performance. J. Hydrol. 2017, 547, 332–344. [Google Scholar] [CrossRef]
- Li, Y.; Babcock Jr, R.W. Green roof hydrologic performance and modeling: A review. Water Sci. Technol. 2014, 69, 4. [Google Scholar] [CrossRef] [PubMed]
- Ampim, P.A.Y.; Sloan, J.J.; Cabrera, R.I.; Harp, D.A.; Jaber, F.H. Green Roof Growing Substrates: Types, Ingredients, Composition and Properties. J. Environ. Hort. 2010, 28, 244–252. [Google Scholar] [CrossRef]
- Charpentier, S. Simulation of Water Regime and Sensible Heat Exchange Phenomena in Green Roof Substrates. Vadose Zone J. 2015, 14, vzj2014-07. [Google Scholar] [CrossRef]
- Dauda, I.; Alibaba, H.Z. Green roof benefits, opportunities and challenges. Int. J. Civ. Struct. Eng. Res. 2020, 7, 106–112. [Google Scholar]
- Zhang, S.; Lin, Z.; Zhang, S.; Ge, D. Stormwater retention and detention performance of green roofs with different substrates: Observational data and hydrological simulations. J. Environ. Manag. 2021, 291, 112682. [Google Scholar] [CrossRef]
- Liu, W.; Engel, B.A.; Feng, Q. Modelling the hydrological responses of green roofs under different substrate designs and rainfall characteristics using a simple water balance model. J. Hydrol. 2021, 602, 126786. [Google Scholar] [CrossRef]
- Yio, M.H.N.; Stovin, V.; Werdin, J.; Vesuviano, G. Experimental analysis of green roof substrate detention characteristics. Water Sci. Technol. 2013, 68, 1477–1486. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Zhang, S.; Zhang, J.; Zhang, S.; Zhang, C.; Yang, H.; Wang, R.; Wei, L. Stormwater retention performance of green roofs with various configurations in different climatic zones. J. Environ. Manag. 2022, 319, 115447. [Google Scholar] [CrossRef] [PubMed]
- Bortolini, L.; Bettella, F.; Zanin, G. Hydrological Behaviour of Extensive Green Roofs with Native Plants in the Humid Subtropical Climate Context. Water 2021, 13, 44. [Google Scholar] [CrossRef]
- Bettella, F.; D’Agostino, V.; Bortolini, L. Drainage flux simulation of green roofs under wet conditions. J. Agric. Eng. XLIX 2018, 838, 242–252. [Google Scholar] [CrossRef]
- Gan, L.; Garg, A.; Wang, H.; Mei, G.; Liu, J. Influence of biochar amendment on stormwater management in green roofs: Experiment with numerical investigation. Acta Geophys. 2021, 69, 2417–2426. [Google Scholar] [CrossRef]
- Huang, S.; Garg, A.; Mei, G.; Huang, D.; Balaji Chandra, R.; Sadasiv, S.G. Experimental study on the hydrological performance of green roofs in the application of novel biochar. Hydrol. Process. 2020, 34, 4512–4525. [Google Scholar] [CrossRef]
- Quinn, R.; Dussaillant, A. The impact of macropores on heavy metal retention in sustainable drainage systems. Hydrol. Res. 2018, 49, 517–527. [Google Scholar] [CrossRef]
- Liu, R.; Fassman-Beck, E. Hydrologic response of engineered media in living roofs and bioretention to large rainfalls: Experiments and modeling. Hydrol. Process. 2017, 31, 556–572. [Google Scholar] [CrossRef]
- Hilten, R.N.; Lawrence, T.M.; Tollner, E.W. Modeling stormwater runoff from green roofs with HYDRUS-1D. J. Hydrol. 2008, 358, 288–293. [Google Scholar] [CrossRef]
- Brunetti, G.; Šimůnek, J.; Piro, P. A Comprehensive Analysis of the Variably Saturated Hydraulic Behavior of a Green Roof in a Mediterranean Climate. Vadose Zone J. 2016, 15, vzj2016.2004.0032. [Google Scholar] [CrossRef]
- Li, Y.; Babcock Jr, R.W. Modeling Hydrologic Performance of a Green Roof System with HYDRUS-2D. J. Environ. Eng. 2015, 141, 04015036. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D.; Ntoulas, N.; Kargas, G.; Nektarios, P.A. Simulation of green roof runoff under different substrate depths and vegetation covers by coupling a simple conceptual and a physically based hydrological model. J. Environ. Manag. 2017, 200, 434e445. [Google Scholar] [CrossRef] [PubMed]
- Kasmin, H.; Stovin, V.R.; Hathway, E.A. Towards a generic rainfall-runoff model for green roofs. Water Sci. Technol. 2010, 62, 898–905. [Google Scholar] [CrossRef]
- Locatelli, L.; Mark, O.; Mikkelsen, P.S.; Arnbjerg-Nielsen, K.; Bergen Jensen, M.; Binning, P.J. Modelling of green roof hydrological performance for urban drainage applications. J. Hydrol. 2014, 519, 3237–3248. [Google Scholar] [CrossRef]
- Stovin, V.; Poë, S.; De-Ville, S.; Berretta, C. The influence of substrate and vegetation configuration on green roof hydrological performance. Ecol. Eng. 2015, 85, 159–172. [Google Scholar] [CrossRef]
- De-Ville, S.; Menon, M.; Stovin, V. Temporal variations in the potential hydrological performance of extensive green roof systems. J. Hydrol. 2018, 558, 564–578. [Google Scholar] [CrossRef]
- Lönnqvist, J.; Broekhuizen, I.; Viklander, M.; Blecken, G. Green roof runoff reduction of 84 rain events: Comparing Sedum, life strategy-based vegetation, unvegetated and conventional roofs. J. Hydrol. 2025, 646, 132325. [Google Scholar] [CrossRef]
- Peng, Z.; Smith, C.; Stovin, V. Internal fluctuations in green roof substrate moisture content during storm events: Monitored data and model simulations. J. Hydrol. 2019, 573, 872–884. [Google Scholar] [CrossRef]
- Skala, V.; Dohnal, M.; Votrubová, J.; Jelínková, V. The use of simple hydrological models to assess outflow of two green roofs systems. Soil Water Res. 2019, 14, 94–103. [Google Scholar] [CrossRef]
- Bondì, C.; Alagna, V.; Iovino, M. Hydrological response of a volcanic medium as a potential substrate for green roofs. In Proceedings of the IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Pisa, Italy, 6–8 November 2023. [Google Scholar]
- Autovino, D.; Alagna, V.; Bondì, C.; Iovino, M. Hydraulic Characterization of Green Roof Substrates by Evaporation Experiments. Appl. Sci. 2024, 14, 1617. [Google Scholar] [CrossRef]
- Wind, G.P. Capillary Conductivity Data Estimated by a Simple Method. In Water in the Unsaturated Zone, Proceedings of the Wageningen Symposium, Wageningen, The Netherlands, 19–23 June 1966; Institute for Land and Water Management Research: Wageningen, The Netherlands, 1969; Volume 1, p. 1. [Google Scholar]
- Dane, J.H.; Hopmans, J.W. Pressure Plate Extractor. In Methods of Soil Analysis, Part 4, Physical Methods; Dane, J.H., Topp, G.C., Eds.; Soil Science Society of America, Inc.: Madison, WI, USA, 2002; pp. 680–683. [Google Scholar]
- van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- De-Ville, S.; Stovin, V. Application of a Conceptual Hydrological Model to Identify the Impacts of Green Roof Substrate Ageing on Detention Performance. In Proceedings of the University of Sheffield Engineering Symposium Conference Proceedings Volume 1, USES 2014, Sheffield, UK, 24 June 2014; The University of Sheffield: Sheffield, UK, 2014. [Google Scholar]
- Lilliefors, H.W. On the Kolmogorov-Smirnov test for normality with mean and variance unknown. J. Am. Stat. Assoc. 1967, 62, 339–402. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Bondì, C.; Concialdi, P.; Iovino, M.; Bagarello, V. Assessing short- and long-term modifications of steady-state water infiltration rate in an extensive Mediterranean green roof. Heliyon 2023, 9, e16829. [Google Scholar] [CrossRef]
- Liu, W.; Feng, Q.; Chen, W.; Wei, W. Assessing the runoff retention of extensive green roofs using runoff coefficients and curve numbers and the impacts of substrate moisture. Hydrol. Res. 2020, 51, 635–647. [Google Scholar] [CrossRef]
- Villarreal, E.L.; Bengtsson, L. Response of a Sedum green-roof to individual rain events. Ecol. Eng. 2005, 25, 1–7. [Google Scholar] [CrossRef]
- Breulmann, M.; Merbach, A.; Bernhard, K.; Moeller, L. Enhancing Urban Resilience: Stormwater Retention and Evapotranspiration Performance of Green Roofs Under Extreme Rainfall Events. Land 2025, 14, 977. [Google Scholar] [CrossRef]
- Cui, E.; Fu, X.; Yang, X.; Zhang, Q.; Duan, D.; Hopton, M. How vertical drainage positions of extensive green roofs affect the runoff control performance. J. Hydrol. 2024, 642, 131855. [Google Scholar] [CrossRef]
- Stovin, V. The potential of green roofs to manage Urban Stormwater. Water Environ. J. 2010, 24, 192–199. [Google Scholar] [CrossRef]
- Volder, A.; Dvorak, B. Event size, substrate water content and vegetation affect storm water retention efficiency of an un-irrigated extensive green roof system in Central Texas. Sustain. Cities Soc. 2014, 10, 59–64. [Google Scholar] [CrossRef]
- Zheng, X.; Zou, Y.; Lounsbury, A.W.; Wang, C.; Wang, R. Green roofs for stormwater runoff retention: A global quantitative synthesis of the performance. Resour. Conserv. Recycl. 2021, 170, 105577. [Google Scholar] [CrossRef]
- Wang, J.P.; Liu, T.H.; Wang, S.H.; Luan, J.Y.; Dadda, A. Investigation of porosity variation on water retention behaviour of unsaturated granular media by using pore scale Micro-CT and lattice Boltzmann method. J. Hydrol. 2023, 626, 130161. [Google Scholar] [CrossRef]
- Gerke, H.H.; van Genuchten, M.T. A dual-porosity model for simulating the preferential movement of water and solutes in structured porous media. Water Resour. Res. 1993, 29, 305–319. [Google Scholar] [CrossRef]
- Russell, A.R. Water retention characteristics of soils with double porosity. Eur. J. Soil Sci. 2010, 61, 412–424. [Google Scholar] [CrossRef]
- Pęczkowski, G.; Szawernoga, K.; Kowalczyk, T.; Orzepowski, W.; Pokładek, R. Runoff and Water Quality in the Aspect of Environmental Impact Assessment of Experimental Area of Green Roofs in Lower Silesia. Sustainability 2020, 12, 4793. [Google Scholar] [CrossRef]
- Wu, L.; Peng, M.; Qiao, S.; Ma, X. Effects of rainfall intensity and slope gradient on runoff and sediment yield characteristics of bare loess soil. Environ. Sci. Pollut. Res. 2018, 25, 3480–3487. [Google Scholar] [CrossRef]
- Ferrans, P.; Rey, C.V.; Pérez, G.; Rodrìguez, J.P.; Dìaz-Granados, M. Effect of Green Roof Configuration and Hydrological Variables on Runoff Water Quantity and Quality. Water 2018, 10, 960. [Google Scholar] [CrossRef]
- Stovin, V.; Vesuviano, G.; De-Ville, S. Defining green roof detention performance. Urban Water J. 2017, 14, 574–588. [Google Scholar] [CrossRef]
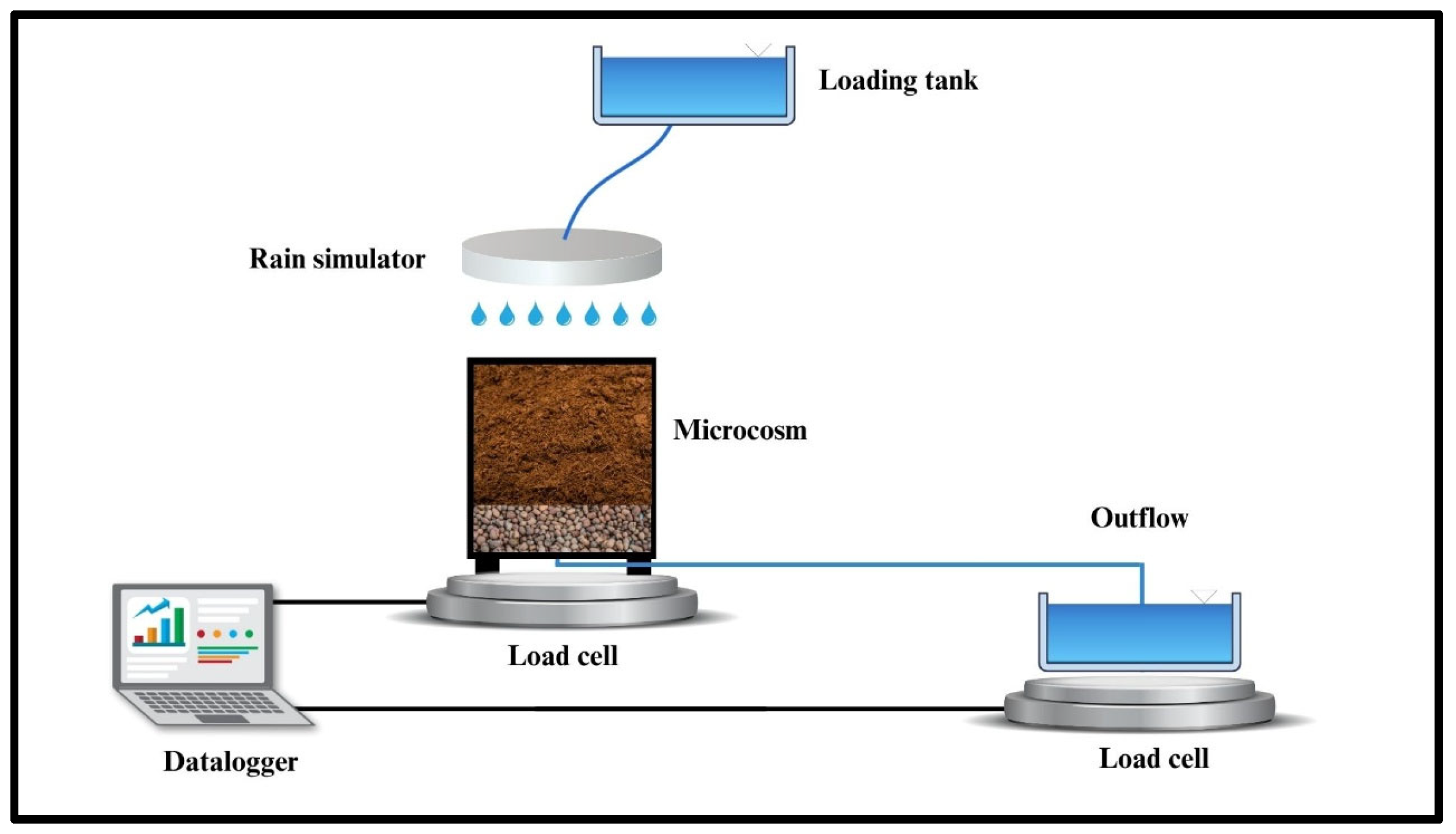

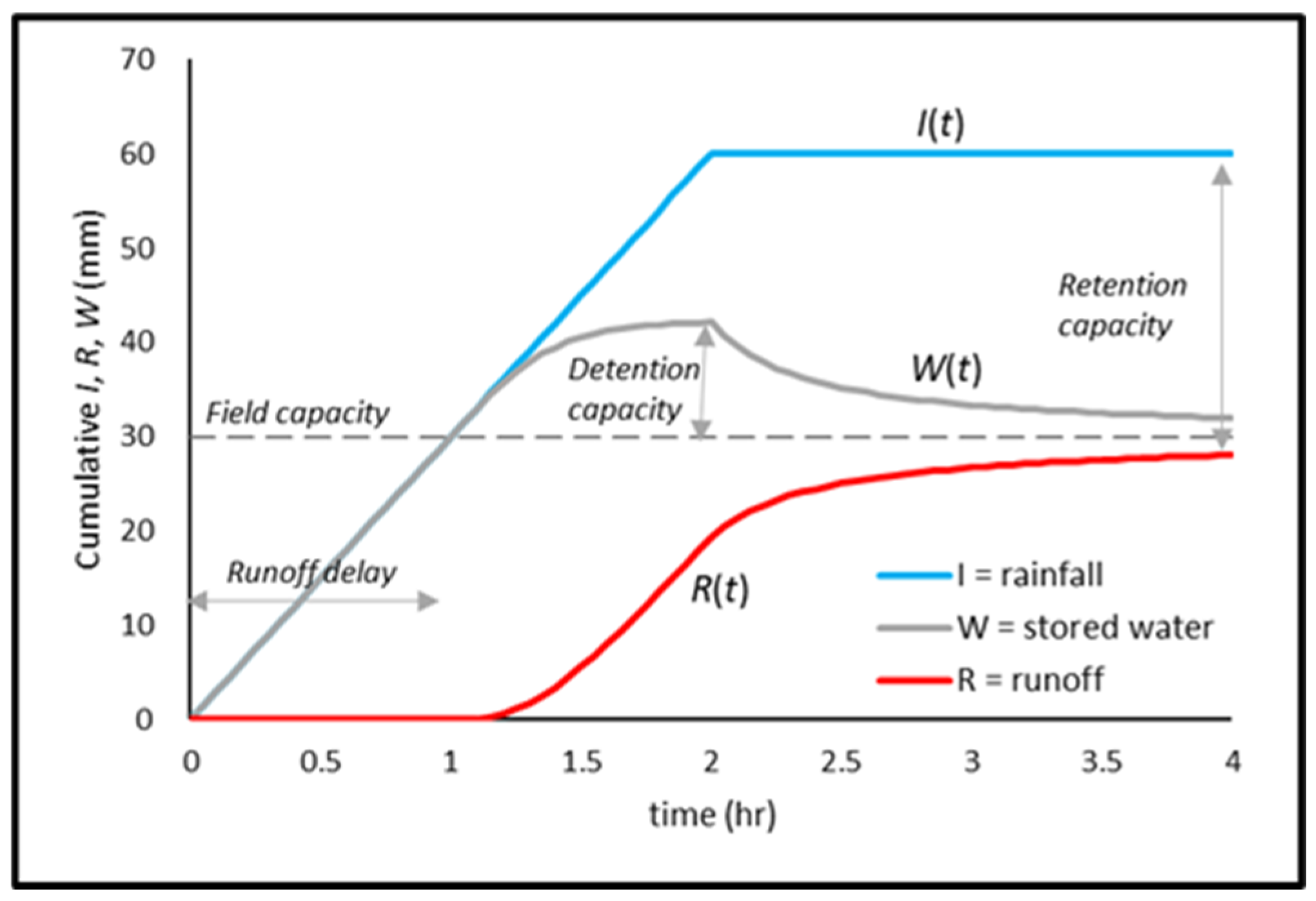


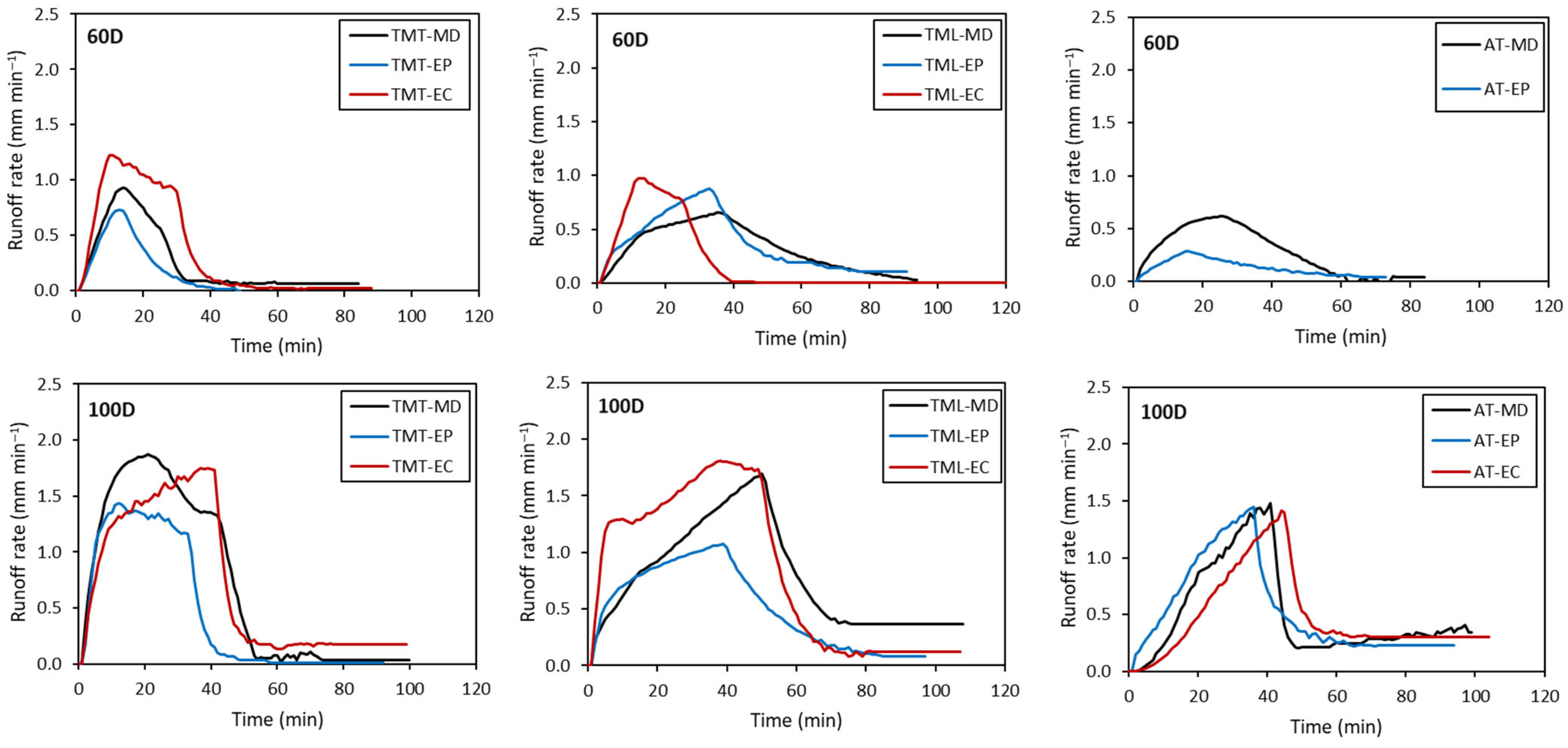

| Layer | Identification | Composition | BD (g cm−3) | θS (cm3 cm−3) | θFC (cm3 cm−3) | θPWP (cm3 cm−3) | Porosity (% V/V) | pH | EC (ds m−1) |
|---|---|---|---|---|---|---|---|---|---|
| Substrate | Terra Mediterranea (TMT) | Green compost, peat, lapillus, pumice and zeolite | 0.939 | 0.475 | 0.289 | 0.073 | 50−60 | 6.0−7.8 | 0.05−0.25 |
| Terra Mediterranea Light (TML) | Lapillus, pumice, Baltic peat and green compost | 0.826 | 0.513 | 0.251 | 0.068 | 60−70 | 7.5−8.0 | 0.30−0.50 | |
| AgriTERRAM® TV (AT) | Peat, lapillus, pumice, Agrilit expanded perlite, bark, coconut fibres, special clays, organic fertilizers | 0.447 | 0.650 | 0.242 | 0.110 | >80 | 6.0−7.0 | 0.40 | |
| Drainage | MediDrain MD 25 (MD) | Preformed polystyrene | ˗ | - | - | - | ˗ | - | - |
| Agrilit 1 expanded perlite (EP) | Expanded perlite with fine grain size | 0.120 | - | - | - | >90 | 6.5−7.5 | 0.02 | |
| Expanded clay (EC) | A balls of 100% expanded clay with controlled pH | 0.360 | - | - | - | >80 | 6.5−7.0 | 0.80 |
| ID | td | WR | WD | RP | DP | RC | MB | td | WR | WD | RP | DP | RC | MB |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (h) | (mm) | (mm) | (%) | (%) | (%) | (%) | (h) | (mm) | (mm) | (%) | (%) | (%) | (%) | |
| 30D | 30W | |||||||||||||
| TMT-MD | ≥1.00 | ≥30.0 | n.d. | 100.0 | n.d. | 0.00 | n.d. | 0.20 | 6.5 | 9.9 | 21.7 | 32.9 | 87.8 | 73.6 |
| TMT-EP | ≥1.00 | ≥30.0 | n.d. | 100.0 | n.d. | 0.00 | n.d. | 0.18 | 8.5 | 9.1 | 28.3 | 30.4 | 90.5 | 79.5 |
| TMT-EC | ≥1.00 | ≥30.0 | n.d. | 100.0 | n.d. | 0.00 | n.d. | 0.13 | 6.9 | 10.9 | 23.1 | 36.2 | 94.7 | 77.6 |
| TML-MD | ≥1.00 | ≥30.0 | n.d. | 100.0 | n.d. | 0.00 | n.d. | 0.15 | 6.5 | 7.7 | 21.7 | 25.8 | 89.9 | 80.4 |
| TML-EP | ≥1.00 | ≥30.0 | n.d. | 100.0 | n.d. | 0.00 | n.d. | 0.02 | 1.0 | 6.7 | 3.5 | 22.4 | 84.7 | 81.1 |
| TML-EC | ≥1.00 | ≥30.0 | n.d. | 100.0 | n.d. | 0.00 | n.d. | 0.05 | 1.9 | 5.3 | 6.3 | 17.6 | 84.6 | 83.5 |
| AT-MD | ≥1.00 | ≥30.0 | n.d. | 100.0 | n.d. | 0.00 | n.d. | 0.15 | 6.5 | 3.5 | 21.8 | 11.7 | 85.5 | 89.0 |
| AT-EP | ≥1.00 | ≥30.0 | n.d. | 100.0 | n.d. | 0.00 | n.d. | 0.03 | 1.5 | 4.7 | 5.0 | 15.7 | 65.4 | 86.1 |
| AT-EC | ≥1.00 | ≥30.0 | n.d. | 100.0 | n.d. | 0.00 | n.d. | 0.27 | 7.5 | 8.6 | 25.0 | 28.7 | 84.0 | 76.7 |
| mean | 0.13 | 5.2 | 7.4 | 17.4 | 24.6 | 85.2 | 80.8 | |||||||
| CV (%) | 63.5 | 55.2 | 33.9 | 55.2 | 33.9 | 9.7 | 5.9 | |||||||
| 60D | 60W | |||||||||||||
| TMT-MD | 0.58 | 35.1 | 7.1 | 58.5 | 11.9 | 35.6 | 88.4 | 0.10 | 6.7 | 3.2 | 11.2 | 5.3 | 86.8 | 94.1 |
| TMT-EP | 0.78 | 52.4 | 8.5 | 87.3 | 14.2 | 19.5 | 88.5 | 0.10 | 7.3 | 4.9 | 12.1 | 8.2 | 87.5 | 92.2 |
| TMT-EC | 0.52 | 37.7 | 6.6 | 62.9 | 11.0 | 45.5 | 91.3 | 0.10 | 7.7 | 2.2 | 12.8 | 3.6 | 87.2 | 96.5 |
| TML-MD | 0.42 | 26.7 | 14.3 | 44.4 | 23.9 | 53.6 | 80.1 | 0.15 | 13.6 | 16.1 | 22.6 | 26.9 | 79.5 | 80.4 |
| TML-EP | 0.47 | 35.8 | 7.3 | 59.6 | 12.2 | 47.3 | 90.3 | 0.22 | 14.8 | 7.3 | 24.7 | 12.1 | 75.2 | 89.2 |
| TML-EC | 0.60 | 36.6 | 8.5 | 61.0 | 14.2 | 37.5 | 87.3 | 0.15 | 14.0 | 6.5 | 23.3 | 10.9 | 79.2 | 91.1 |
| AT-MD | 0.58 | 34.8 | 15.3 | 58.0 | 25.5 | 39.7 | 79.0 | 0.30 | 23.3 | 14.0 | 38.8 | 23.3 | 64.8 | 82.6 |
| AT-EP | 0.77 | 46.8 | 5.4 | 78.0 | 9.0 | 18.4 | 91.4 | 0.35 | 28.4 | 8.5 | 47.4 | 14.2 | 57.3 | 88.6 |
| AT-EC | 0.42 | 32.2 | 1.0 | 53.7 | 1.6 | 52.3 | 98.6 | 0.17 | 12.1 | 4.0 | 20.2 | 6.7 | 80.0 | 93.7 |
| mean | 0.57 | 37.6 | 8.2 | 62.6 | 13.7 | 38.8 | 88.3 | 0.18 | 14.2 | 7.4 | 23.7 | 12.4 | 77.5 | 89.8 |
| CV (%) | 23.7 | 20.4 | 53.1 | 20.4 | 53.1 | 33.1 | 6.7 | 50.0 | 52.0 | 64.7 | 52.0 | 64.7 | 13.4 | 6.0 |
| 100D | 100W | |||||||||||||
| TMT-MD | 0.32 | 36.5 | 14.5 | 36.5 | 14.5 | 65.7 | 88.0 | 0.08 | 10.6 | 1.5 | 10.6 | 1.5 | 87.8 | 98.3 |
| TMT-EP | 0.47 | 51.1 | 5.0 | 51.1 | 5.0 | 45.6 | 94.9 | 0.08 | 9.3 | 9.4 | 9.3 | 9.4 | 90.5 | 91.2 |
| TMT-EC | 0.33 | 40.6 | 5.3 | 40.6 | 5.3 | 62.5 | 95.3 | 0.03 | 6.4 | 5.5 | 6.4 | 5.5 | 94.7 | 95.6 |
| TML-MD | 0.18 | 20.9 | 12.2 | 20.9 | 12.2 | 80.7 | 89.8 | 0.08 | 9.2 | 23.8 | 9.2 | 23.8 | 89.9 | 79.3 |
| TML-EP | 0.37 | 39.4 | 9.6 | 39.4 | 9.6 | 54.8 | 90.0 | 0.12 | 14.0 | 11.1 | 14.0 | 11.1 | 84.7 | 89.2 |
| TML-EC | 0.20 | 23.6 | 9.5 | 23.6 | 9.5 | 78.3 | 92.0 | 0.13 | 16.1 | 15.5 | 16.1 | 15.5 | 84.6 | 87.2 |
| AT-MD | 0.33 | 38.4 | 3.2 | 38.4 | 3.2 | 62.5 | 97.0 | 0.12 | 14.8 | 10.4 | 14.8 | 10.4 | 85.5 | 90.8 |
| AT-EP | 0.42 | 42.5 | 5.6 | 42.5 | 5.6 | 57.0 | 94.6 | 0.30 | 31.6 | 9.9 | 31.6 | 9.9 | 65.4 | 90.2 |
| AT-EC | 0.27 | 29.5 | 4.4 | 29.5 | 4.4 | 69.9 | 95.7 | 0.13 | 16.9 | 11.4 | 16.9 | 11.4 | 84.0 | 90.2 |
| mean | 0.32 | 35.8 | 7.7 | 35.8 | 7.7 | 64.1 | 93.0 | 0.12 | 14.3 | 10.9 | 14.3 | 10.9 | 85.2 | 90.2 |
| CV (%) | 29.1 | 26.8 | 50.7 | 26.8 | 50.7 | 17.4 | 3.4 | 61.9 | 51.6 | 56.8 | 51.6 | 56.8 | 9.7 | 5.9 |
| WR | WD | ||
|---|---|---|---|
| D | W | D + W | |
| 30–60 | - | 0.019 | 0.786 |
| 30–100 | - | 0.019 | 0.745 |
| 60–100 | 0.366 | 0.940 | 0.364 |
| ID | k | n | SSD | k | n | SSD | k | n | SSD |
|---|---|---|---|---|---|---|---|---|---|
| 30D | 60D | 100D | |||||||
| TMT-MD | ˗ | ˗ | ˗ | 0.10 | 1.07 | 4.535 | 0.27 | 0.72 | 8.112 |
| TMT-EP | ˗ | ˗ | ˗ | 0.07 | 1.07 | 1.878 | 0.08 | 1.64 | 0.609 |
| TMT-EC | ˗ | ˗ | ˗ | 0.08 | 1.45 | 2.175 | 0.09 | 1.54 | 9.286 |
| TML-MD | ˗ | ˗ | ˗ | 0.04 | 1.01 | 0.939 | 0.13 | 0.93 | 27.887 |
| TML-EP | ˗ | ˗ | ˗ | 0.12 | 0.95 | 4.189 | 0.12 | 0.93 | 6.006 |
| TML-EC | ˗ | ˗ | ˗ | 0.12 | 0.99 | 3.643 | 0.25 | 0.87 | 9.479 |
| AT-MD | ˗ | ˗ | ˗ | 0.13 | 0.56 | 2.884 | 0.01 | 2.07 | 38.445 |
| AT-EP | ˗ | ˗ | ˗ | 0.07 | 1.07 | 1.878 | 0.08 | 1.64 | 0.609 |
| AT-EC | ˗ | ˗ | ˗ | ˗ | ˗ | ˗ | 0.01 | 1.90 | 40.644 |
| Mean | ˗ | ˗ | ˗ | 0.09 | 1.02 | 2.765 | 0.12 | 1.36 | 15.675 |
| σ | ˗ | ˗ | ˗ | 0.03 | 0.24 | 1.265 | 0.09 | 0.50 | 15.712 |
| 30W | 60W | 100W | |||||||
| TMT-MD | 0.06 | 0.72 | 0.388 | 0.13 | 1.34 | 1.588 | 0.11 | 2.16 | 28.937 |
| TMT-EP | 0.11 | 0.47 | 1.006 | 0.22 | 0.62 | 2.037 | 0.12 | 1.09 | 13.839 |
| TMT-EC | 0.08 | 0.78 | 0.316 | 0.24 | 1.29 | 12.993 | 0.10 | 1.54 | 12.259 |
| TML-MD | 0.04 | 1.03 | 0.218 | 0.04 | 1.04 | 0.960 | 0.05 | 1.00 | 1.942 |
| TML-EP | 0.05 | 1.10 | 0.268 | 0.10 | 1.10 | 1.176 | 0.11 | 0.97 | 7.354 |
| TML-EC | 0.04 | 1.47 | 0.655 | 0.20 | 0.79 | 2.160 | 0.07 | 1.11 | 5.951 |
| AT-MD | 0.08 | 1.10 | 0.816 | 0.09 | 0.67 | 3.406 | 0.15 | 0.99 | 4.019 |
| AT-EP | 0.11 | 0.47 | 1.006 | 0.22 | 0.62 | 2.037 | 0.12 | 1.09 | 13.839 |
| AT-EC | 0.09 | 0.53 | 0.870 | 0.19 | 1.04 | 3.178 | 0.10 | 1.13 | 5.648 |
| Mean | 0.07 | 0.85 | 0.616 | 0.16 | 0.94 | 3.282 | 0.10 | 1.23 | 10.421 |
| σ | 0.03 | 0.34 | 0.322 | 0.07 | 0.28 | 3.731 | 0.03 | 0.39 | 8.175 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bondì, C.; Iovino, M. Assessment and Modeling of the Hydrological Response of Extensive Green Roofs Under High-Intensity Simulated Rainfalls. Water 2025, 17, 3113. https://doi.org/10.3390/w17213113
Bondì C, Iovino M. Assessment and Modeling of the Hydrological Response of Extensive Green Roofs Under High-Intensity Simulated Rainfalls. Water. 2025; 17(21):3113. https://doi.org/10.3390/w17213113
Chicago/Turabian StyleBondì, Cristina, and Massimo Iovino. 2025. "Assessment and Modeling of the Hydrological Response of Extensive Green Roofs Under High-Intensity Simulated Rainfalls" Water 17, no. 21: 3113. https://doi.org/10.3390/w17213113
APA StyleBondì, C., & Iovino, M. (2025). Assessment and Modeling of the Hydrological Response of Extensive Green Roofs Under High-Intensity Simulated Rainfalls. Water, 17(21), 3113. https://doi.org/10.3390/w17213113







